Benchmarking Free Energy Calculations in Liquid Aliphatic Ketone Solvents Using the 3D-RISM-KH Molecular Solvation Theory
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Molecular Simulations of Pure Liquid Ketones
3.2. Solvation Free Energy Calculations
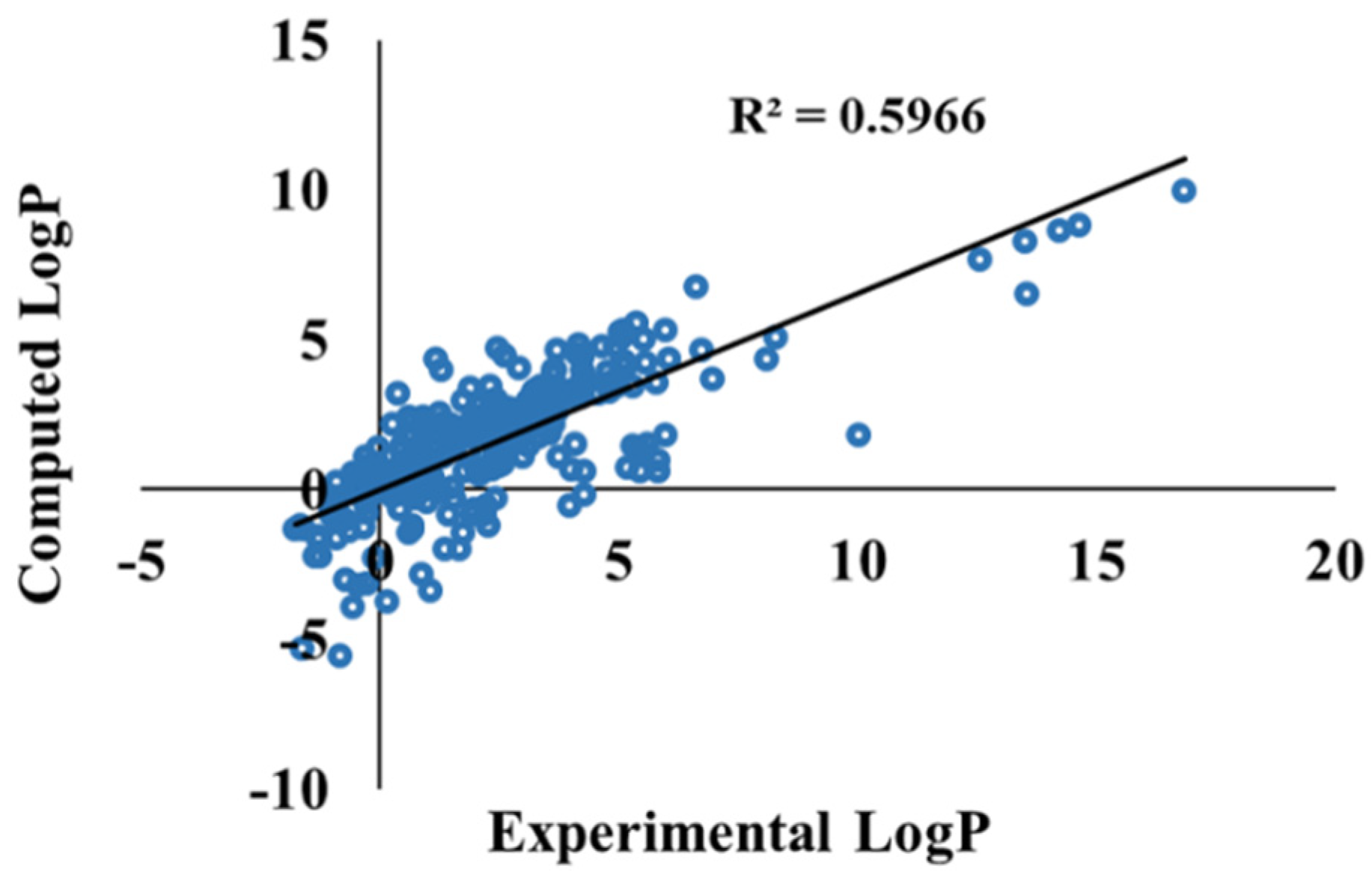
3.3. Ketone–Water Partition Coefficient Calculations Using the 3D-RISM-KH Theory
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D-RISM | 3-Dimensional reference interaction site model |
| AM1 | Austin model 1 |
| CyO | Cyclohexanone |
| GAFF | Generalized amber force field |
| GF | Gaussian fluctuation |
| KH | Kovalenko–Hirata closure |
| MAD | Mean absolute deviation |
| MD | Molecular dynamics |
| MEK | 2-Butanone a.k.a. methyl ethyl ketone |
| MIBK | Methyl isobutyl ketone |
| PMV | Partial molar volume |
| QM | Quantum mechanical |
| RDF | Radial distribution function |
| RMSE | Relative mean square error |
| SFE | Solvation free energy |
References
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourika, T.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef] [Green Version]
- Matos, G.D.R.; Kyu, D.Y.; Loeffler, H.H.; Chodera, J.D.; Shirts, M.R.; Mobley, D.L. Approaches for calculating solvation free energies and enthalpies demonstrated with an update of the FreeSolv database. J. Chem. Eng. Data 2017, 62, 1559–1569. [Google Scholar] [CrossRef] [Green Version]
- Mennucci, B. Polarizable continuum model. WIREs Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; van der Spoel, D. Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999, 99, 2161–2220. [Google Scholar] [CrossRef]
- Pliego, J.R.; Riveros, J.M. The Cluster—Continuum Model for the Calculation of the Solvation Free Energy of Ionic Species. J. Phys. Chem. A 2001, 105, 7241–7247. [Google Scholar] [CrossRef]
- Tomaník, L.; Muchová, E.; Slavíček, P. Solvation energies of ions with ensemble cluster-continuum approach. Phys. Chem. Chem. Phys. 2020, 22, 22357–22368. [Google Scholar] [CrossRef]
- Roy, D.; Dutta, D.; Wishart, D.; Kovalenko, A. Predicting PAMPA permeability using the 3D-RISM-KH theory: Are we there yet? J. Comput.-Aided Mol. Des. 2021, 35, 261–269. [Google Scholar] [CrossRef]
- Roy, D.; Hinge, V.K.; Kovalenko, A. To Pass or Not to Pass: Predicting the Blood—Brain Barrier Permeability with the 3D-RISM-KH Molecular Solvation Theory. ACS Omega 2019, 4, 16774–16780. [Google Scholar] [CrossRef]
- Hinge, V.K.; Blinov, N.; Roy, D.; Wishart, D.; Kovalenko, A. The role of hydration effects in 5-fluorouridine binding to SOD1: Insight from a new 3D-RISM-KH based protocol for including structural water in docking simulations. J. Comput.-Aided Mol. Des. 2019, 33, 913–926. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. MTS-MD of Biomolecules Steered with 3D-RISM-KH Mean Solvation Forces Accelerated with Generalized Solvation Force Extrapolation. J. Chem. Theory Comput. 2015, 11, 1875–1895. [Google Scholar] [CrossRef]
- Imai, T.; Oda, K.; Kovalenko, A.; Hirata, F.; Kidera, A. Ligand Mapping on Protein Surfaces by the 3D-RISM Theory: Toward Computational Fragment-Based Drug Design. J. Am. Chem. Soc. 2009, 131, 12430–12440. [Google Scholar] [CrossRef]
- Sugita, M.; Hamano, M.; Kasahara, K.; Kikuchi, T.; Hirata, F. New Protocol for Predicting the Ligand-Binding Site and Mode Based on the 3D-RISM/KH Theory. J. Chem. Theory Comput. 2020, 16, 2864–2876. [Google Scholar] [CrossRef]
- Sindhikara, D.J.; Hirata, F. Analysis of Biomolecular Solvation Sites by 3D-RISM Theory. J. Phys. Chem. B 2013, 117, 6718–6723. [Google Scholar] [CrossRef]
- Truchon, J.-F.; Pettitt, B.M.; Labute, P. A Cavity Corrected 3D-RISM Functional for Accurate Solvation Free Energies. J. Chem. Theory Comput. 2014, 10, 934–941. [Google Scholar] [CrossRef]
- Misin, M.; Fedorov, M.V.; Palmer, D.S. Communication: Accurate hydration free energies at a wide range of temperatures from 3D-RISM. J. Chem. Phys. 2015, 142, 091105. [Google Scholar] [CrossRef] [Green Version]
- Gavazzoni, C.; Skaf, M.S. Adsorption of CO2 and CH4 in MIL-47 investigated by the 3D-RISM molecular theory of solvation. Phys. Chem. Chem. Phys. 2020, 22, 13240–13247. [Google Scholar] [CrossRef]
- Genheden, S.; Luchko, T.; Gusarov, S.; Kovalenko, A.; Ryde, U. An MM/3D-RISM approach for ligand binding affinities. J. Phys. Chem. B 2010, 114, 8505–8516. [Google Scholar] [CrossRef]
- Kaminski, J.W.; Gusarov, S.; Wesolowski, T.A.; Kovalenko, A. Modeling Solvatochromic Shifts Using the Orbital-Free Embedding Potential at Statistically Mechanically Averaged Solvent Density. J. Phys. Chem. A 2010, 114, 6082–6096. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. I. General formulation. J. Chem. Phys. 1986, 85, 5971–5976. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. II. Rational closures for integral equations. J. Chem. Phys. 1986, 85, 5977–5982. [Google Scholar] [CrossRef]
- Lowden, L.J.; Chandler, D. Solution of a new integral equation for pair correlation functions in molecular liquids. J. Chem. Phys. 1973, 59, 6587–6595. [Google Scholar] [CrossRef]
- Chandler, D. Cluster diagrammatic analysis of the RISM equation. Mol. Phys. 1976, 31, 1213–1223. [Google Scholar] [CrossRef]
- Andersen, H.C.; Chandler, D.; Weeks, J.D. Roles of repulsive and attractive forces in liquids, the equilibrium theory of classical fluids. Adv. Chem. Phys. 1976, 34, 105–155. [Google Scholar]
- Kovalenko, A. Molecular theory of solvation: Methodology summary and illustrations. Cond. Matt. Phys. 2015, 18, 32601. [Google Scholar] [CrossRef] [Green Version]
- Kovalenko, A. Multiscale Modeling of Solvation. In Springer Handbook of Electro-Chemical Energy; Breitkopf, C., Swider-Lyons, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kovalenko, A.; Gusarov, S. Multiscale methods framework: Self-consistent coupling of molecular theory of solvation with quantum chemistry, molecular simulations, and dissipative particle dynamics. Phys. Chem. Chem. Phys. 2017, 20, 2947–2969. [Google Scholar] [CrossRef]
- Ratkova, E.L.; Palmer, D.S.; Fedorov, M.V. Solvation Thermodynamics of Organic Molecules by the Molecular Integral Equation Theory: Approaching Chemical Accuracy. Chem. Rev. 2015, 13, 6312–6356. [Google Scholar] [CrossRef] [Green Version]
- Kovalenko, A.; Hirata, F. A molecular theory of liquid interfaces. Phys. Chem. Chem. Phys. 2005, 7, 1785–1793. [Google Scholar] [CrossRef]
- Palmer, D.S.; Frolov, A.; Ratkova, E.; Fedorov, M.V. Towards a universal method for calculating hydration free energies: A 3D reference interaction site model with partial molar volume correction. J. Phys. Condens. Matt. 2010, 22, 492101. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. (Theochem) 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M.; Tomasi, J. A new definition of cavities for the computation of solvation free energies by the polarizable continuum model. J. Chem. Phys. 1997, 107, 3210–3221. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247260. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameter-ization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638. [Google Scholar] [CrossRef]
- Kobryn, A.E.; Kovalenko, A. Molecular theory of hydrodynamic boundary conditions in nanofluidics. J. Chem. Phys. 2008, 129, 134701. [Google Scholar] [CrossRef] [PubMed]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Head-Gordon, M.; Head-Gordon, T. Analytic MP2 Frequencies without Fifth Order Storage: Theory and Application to Bifurcated Hydrogen Bonds in the Water Hexamer. Chem. Phys. Lett. 1994, 220, 122–128. [Google Scholar] [CrossRef]
- Luchko, T.; Blinov, N.; Limon, G.C.; Joyce, K.P.; Kovalenko, A. SAMPL5: 3D-RISM partition coefficient calculations with partial molar volume corrections and solute conformational sampling. J. Comput.-Aided Mol. Des. 2016, 30, 1115–1127. [Google Scholar] [CrossRef] [PubMed]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminfo. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Marenich, A.V.; Kelly, C.P.; Thompson, J.D.; Hawkins, G.D.; Chambers, C.C.; Giesen, D.J.; Winget, P.; Cramer, C.J.; Truhlar, D.G. Minnesota Solvation Database (MNSOL) Version 2012; University of Minnesota: Minneapolis, MN, USA, 2012. [Google Scholar]
- Michael, H.; Abraham, M.H.; Acree, W.E.; Leoc, A.J.; Hoekmand, D. The partition of compounds from water and from air into wet and dry ketones. New J. Chem. 2009, 33, 568–573. [Google Scholar]
- Mobley, D.L.; Guthire, P. FreeSolv: A database of experimental and calculated hydration free energies, with input files. J. Comput.-Aided Mol. Des. 2014, 28, 711–720. [Google Scholar] [CrossRef] [Green Version]
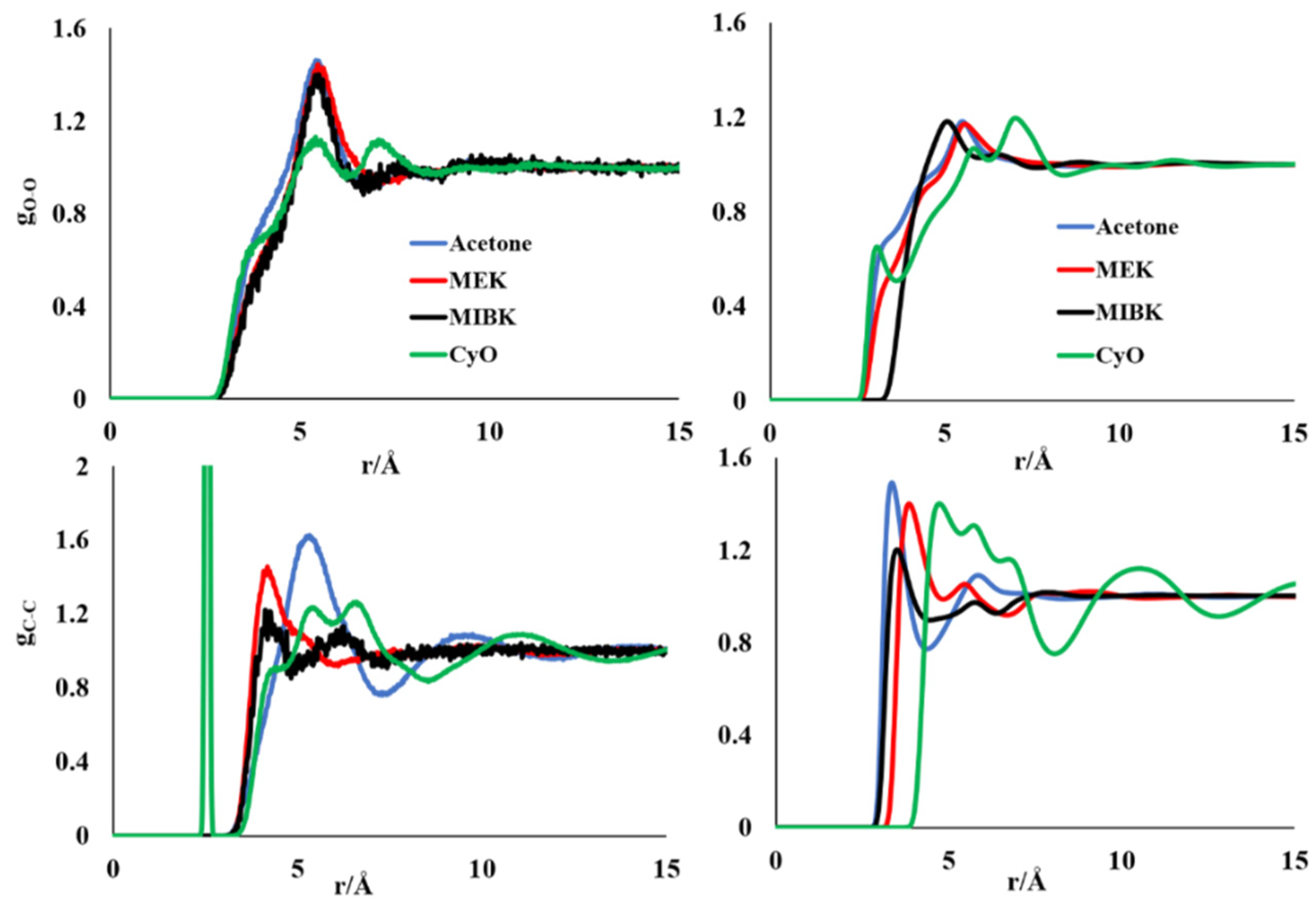
| Atomic Site | σ (Å) | ε (kcal·mol−1) |
|---|---|---|
| C[H3] | 3.775 | 0.207 |
| C[H2] | 3.905 | 0.118 |
| C[H] | 3.850 | 0.080 |
| C[=O] | 3.399 | 0.086 |
| O[=C] | 2.960 | 0.210 |
| OWater | 3.116 | 0.155 |
| HWater | 0.700 | 0.046 |
| C[H2]Cyclohexanone | 4.700 | 0.140 |
| Molecule | Density (Experimental, gm/cm3) | Density (MD, gm/cm3) 1 | Dielectric Constant (Experimental) |
|---|---|---|---|
| Acetone | 0.784 | 0.782 (±0.0009) | 20.493 |
| MEK | 0.805 | 0.784 (±0.0006) | 18.246 |
| MIBK | 0.796 | 0.800 (±0.0003) | 12.887 |
| CyO | 0.942 | 0.929 (±0.0008) | 15.619 |
| Molecule | A (kcal·mol−1·Å−3) | B (kcal·mol−1) |
|---|---|---|
| Acyclic aliphatic ketone | 0.0016 | −4.2669 |
| Cyclohexanone | −0.2286 | −5.0964 |
| Compound | Solvent | ΔG(Exptl.) 1 | ΔG(CPCM) 2 | ΔG(SMD) 3 | ΔG(RISM) 4 |
|---|---|---|---|---|---|
| n-octane | Cyclohexanone | −4.57 | −0.64 | −4.13 | −3.37 |
| Toluene | Cyclohexanone | −5.05 | −2.88 | −6.43 | −4.45 |
| Ethanol | Cyclohexanone | −4.41 | −3.09 | −3.83 | −5.02 |
| 1,4-dioxane | Cyclohexanone | −4.95 | −3.37 | −5.30 | −7.02 |
| 2-butanone | Cyclohexanone | −4.42 | −2.35 | −5.27 | −5.32 |
| Acetic acid | Cyclohexanone | −6.43 | −4.60 | −6.03 | −6.32 |
| Propanoic acid | Cyclohexanone | −7.18 | −4.30 | −6.42 | −6.24 |
| Nitromethane | Cyclohexanone | −5.09 | −5.42 | −5.77 | −6.70 |
| Cyclohexanone | Cyclohexanone | −6.25 | −4.12 | −7.99 | −6.64 |
| Hydrogen peroxide | Cyclohexanone | −9.11 | −4.60 | −7.62 | −6.39 |
| n-octane | Butanone | −4.64 | −0.64 | −5.21 | −2.26 |
| Toluene | Butanone | −5.06 | −2.90 | −7.26 | −3.71 |
| Ethanol | Butanone | −4.46 | −3.13 | −4.34 | −4.46 |
| 1,4-dioxane | Butanone | −5.02 | −3.41 | −5.96 | −6.29 |
| Formaldehyde | Butanone | −1.77 | −3.17 | −3.22 | −4.82 |
| 2-butanone | Butanone | −4.5 | −2.40 | −5.96 | −4.71 |
| Acetic acid | Butanone | −6.88 | −4.65 | −6.51 | −5.99 |
| Propanoic acid | Butanone | −7.05 | −4.35 | −7.00 | −5.88 |
| Butanoic acid | Butanone | −7.34 | −4.40 | −7.63 | −5.83 |
| Pentanoic acid | Butanone | −7.54 | −4.55 | −8.37 | −5.80 |
| Hexanoic acid | Butanone | −8.07 | −4.61 | −9.09 | −5.76 |
| Nitromethane | Butanone | −5.24 | −5.49 | −6.37 | −6.15 |
| γ-butyrolactone | Butanone | −4.47 | −6.50 | −9.69 | −8.12 |
| Naphthalene | Methyl isobutyl ketone | −7.45 | −2.55 | −8.29 | −7.26 |
| Phenol | Methyl isobutyl ketone | −9.38 | −3.98 | −7.86 | −7.13 |
| m-Cresol | Methyl isobutyl ketone | −8.79 | −4.24 | −8.15 | −7.27 |
| Acetic acid | Methyl isobutyl ketone | −6.33 | −4.53 | −6.35 | −6.49 |
| Propanoic acid | Methyl isobutyl ketone | −6.85 | −4.23 | −6.89 | −6.68 |
| Butanoic acid | Methyl isobutyl ketone | −7.44 | −4.28 | −7.55 | −6.98 |
| Trimethylamine | Methyl isobutyl ketone | −2.86 | −1.46 | −3.44 | −5.08 |
| Diethylamine | Methyl isobutyl ketone | −3.63 | −1.99 | −4.86 | −5.01 |
| Pyridine | Methyl isobutyl ketone | −5.33 | −3.11 | −6.36 | −6.37 |
| Aniline | Methyl isobutyl ketone | −7.54 | −4.03 | −8.50 | −7.25 |
| Ammonia | Methyl isobutyl ketone | −2.52 | −3.15 | −3.57 | −3.80 |
| Methylamine | Methyl isobutyl ketone | −4.14 | −2.55 | −3.45 | −4.25 |
| 4-methyl-2-pentanone | Methyl isobutyl ketone | −5.23 | −3.74 | −7.39 | −6.18 |
| MAD 5 | 2.41 | 0.98 | 1.21 | ||
| RMSE 6 | 2.71 | 1.33 | 1.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.; Kovalenko, A. Benchmarking Free Energy Calculations in Liquid Aliphatic Ketone Solvents Using the 3D-RISM-KH Molecular Solvation Theory. J 2021, 4, 604-613. https://doi.org/10.3390/j4040044
Roy D, Kovalenko A. Benchmarking Free Energy Calculations in Liquid Aliphatic Ketone Solvents Using the 3D-RISM-KH Molecular Solvation Theory. J. 2021; 4(4):604-613. https://doi.org/10.3390/j4040044
Chicago/Turabian StyleRoy, Dipankar, and Andriy Kovalenko. 2021. "Benchmarking Free Energy Calculations in Liquid Aliphatic Ketone Solvents Using the 3D-RISM-KH Molecular Solvation Theory" J 4, no. 4: 604-613. https://doi.org/10.3390/j4040044
APA StyleRoy, D., & Kovalenko, A. (2021). Benchmarking Free Energy Calculations in Liquid Aliphatic Ketone Solvents Using the 3D-RISM-KH Molecular Solvation Theory. J, 4(4), 604-613. https://doi.org/10.3390/j4040044






