Nonparametric Conditional Heteroscedastic Hourly Probabilistic Forecasting of Solar Radiation
Abstract
:1. Introduction
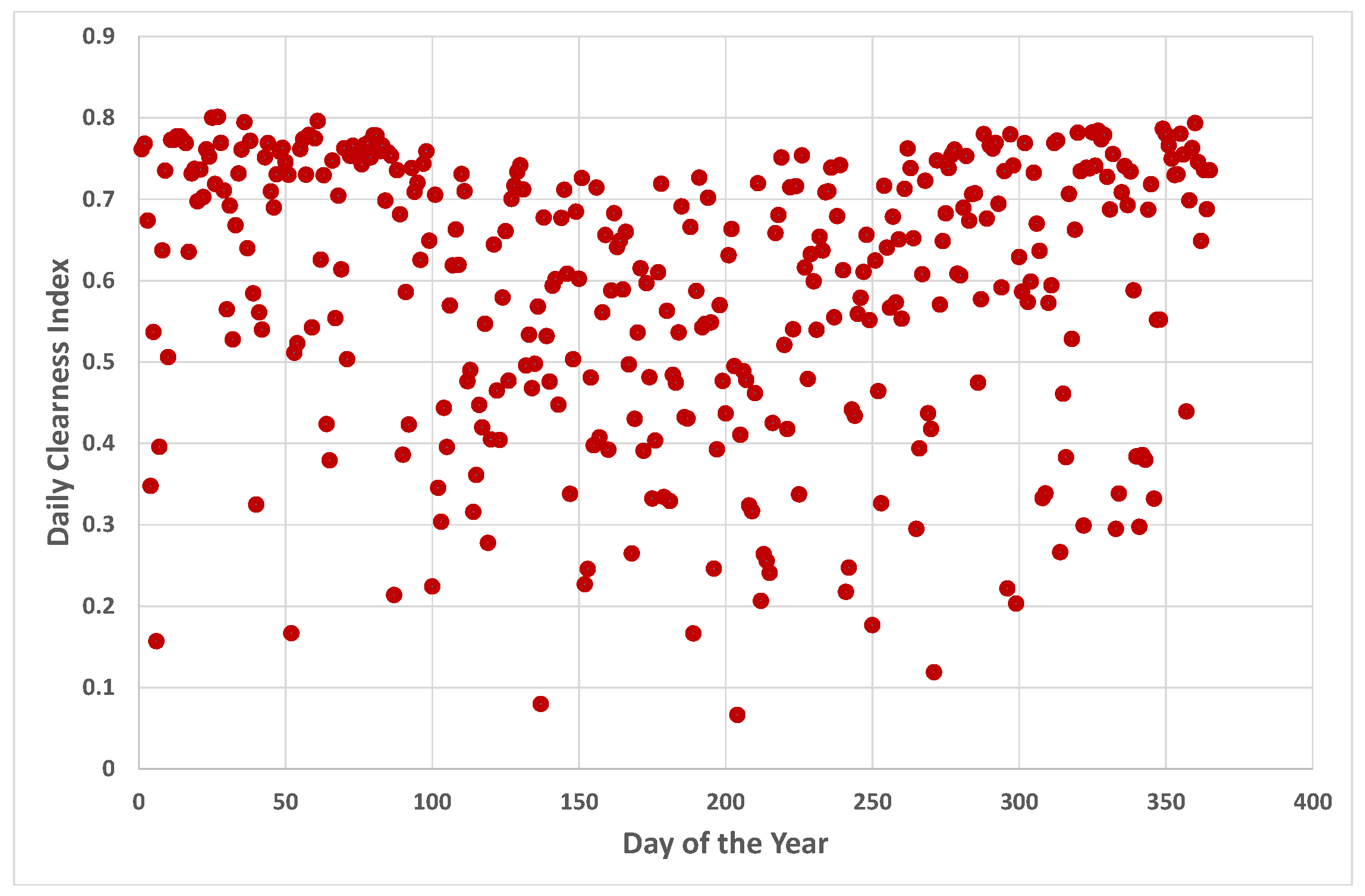
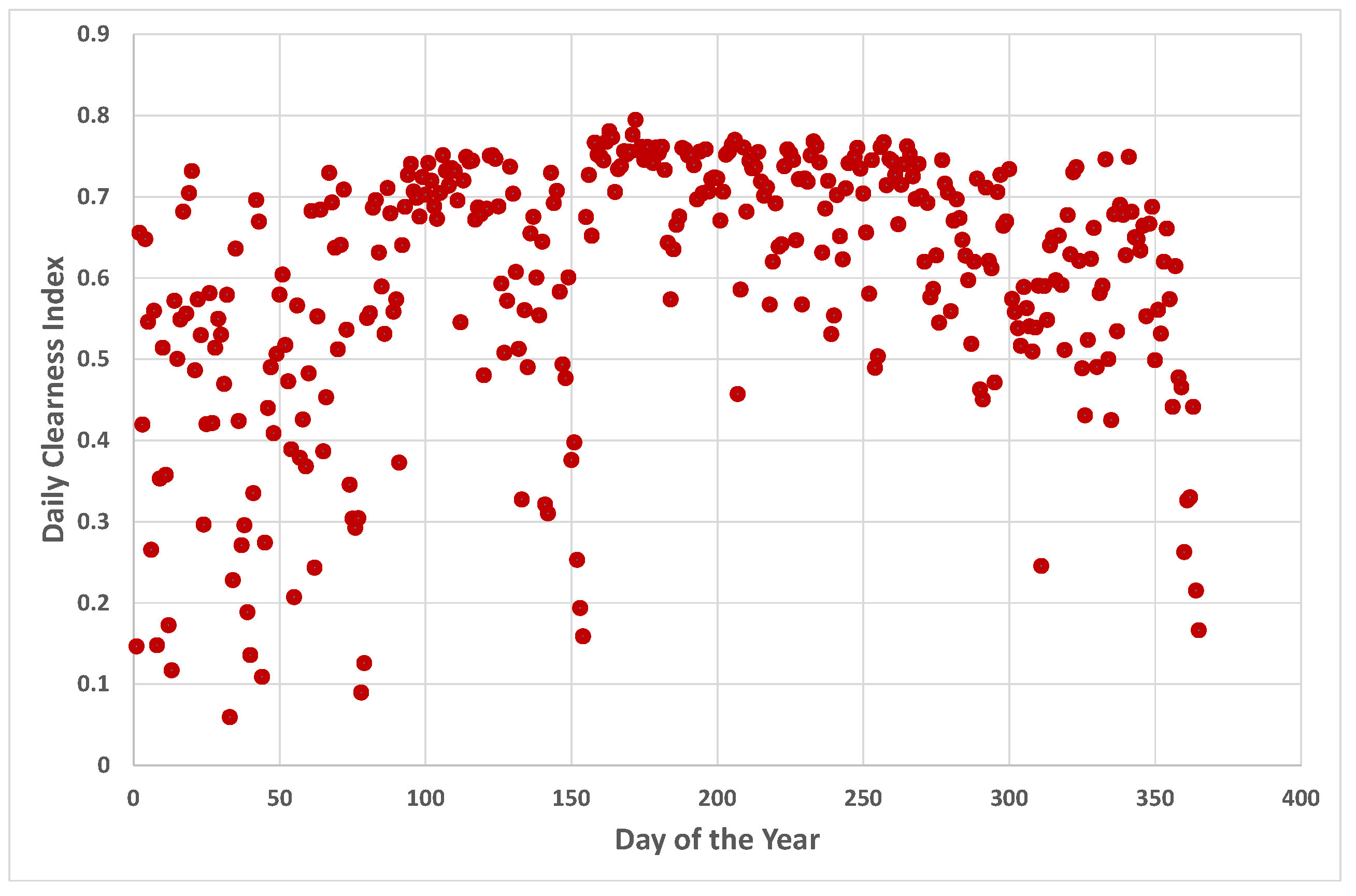
2. Data and Preliminaries
3. Point Forecast
Point Forecast Performance Evaluation
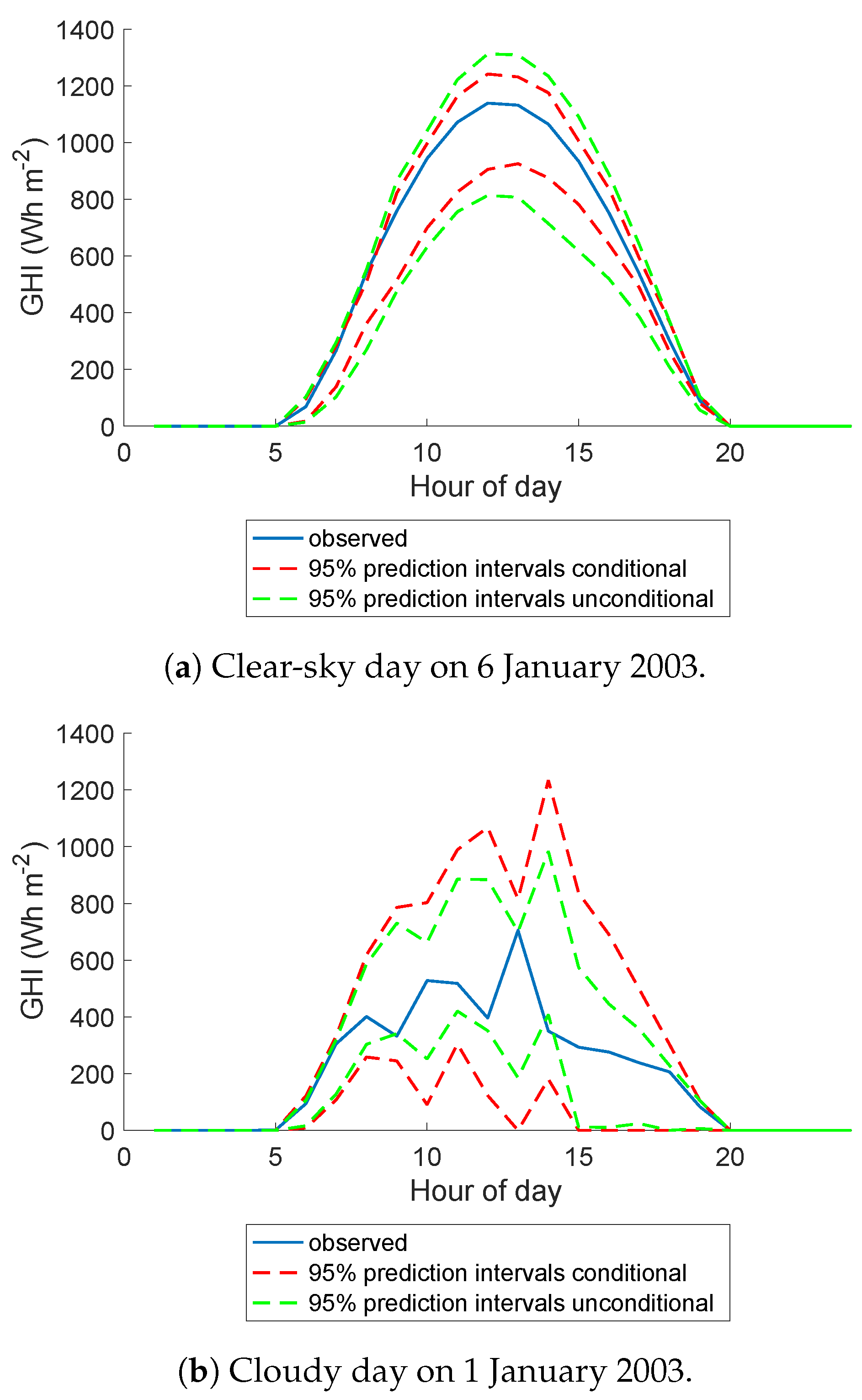
4. Probabilistic Forecasting
| Algorithm 1: Algorithm for generating (100-) prediction intervals using the conditional method. |
 |
5. Probabilistic Forecast Performance Evaluation
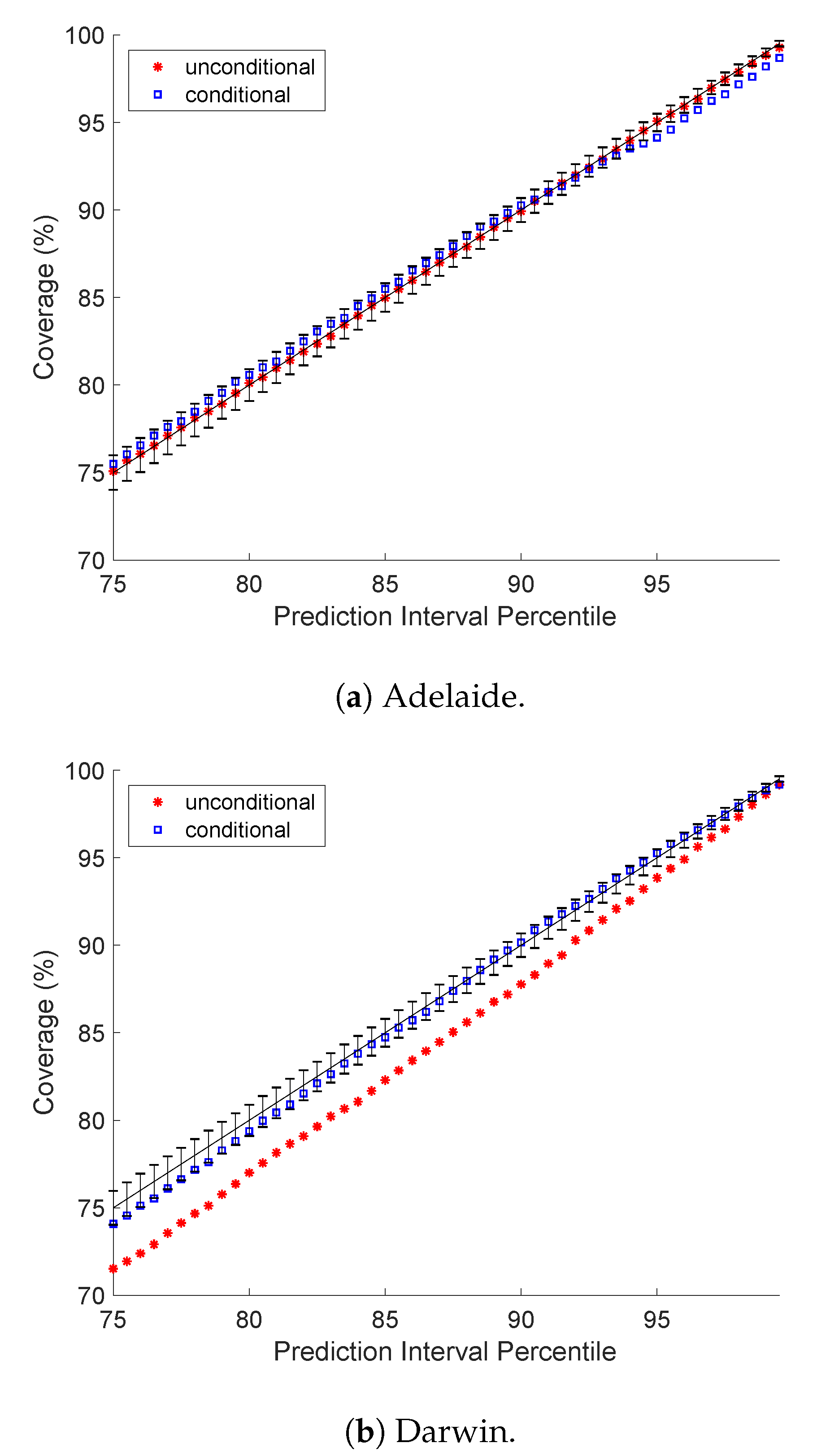
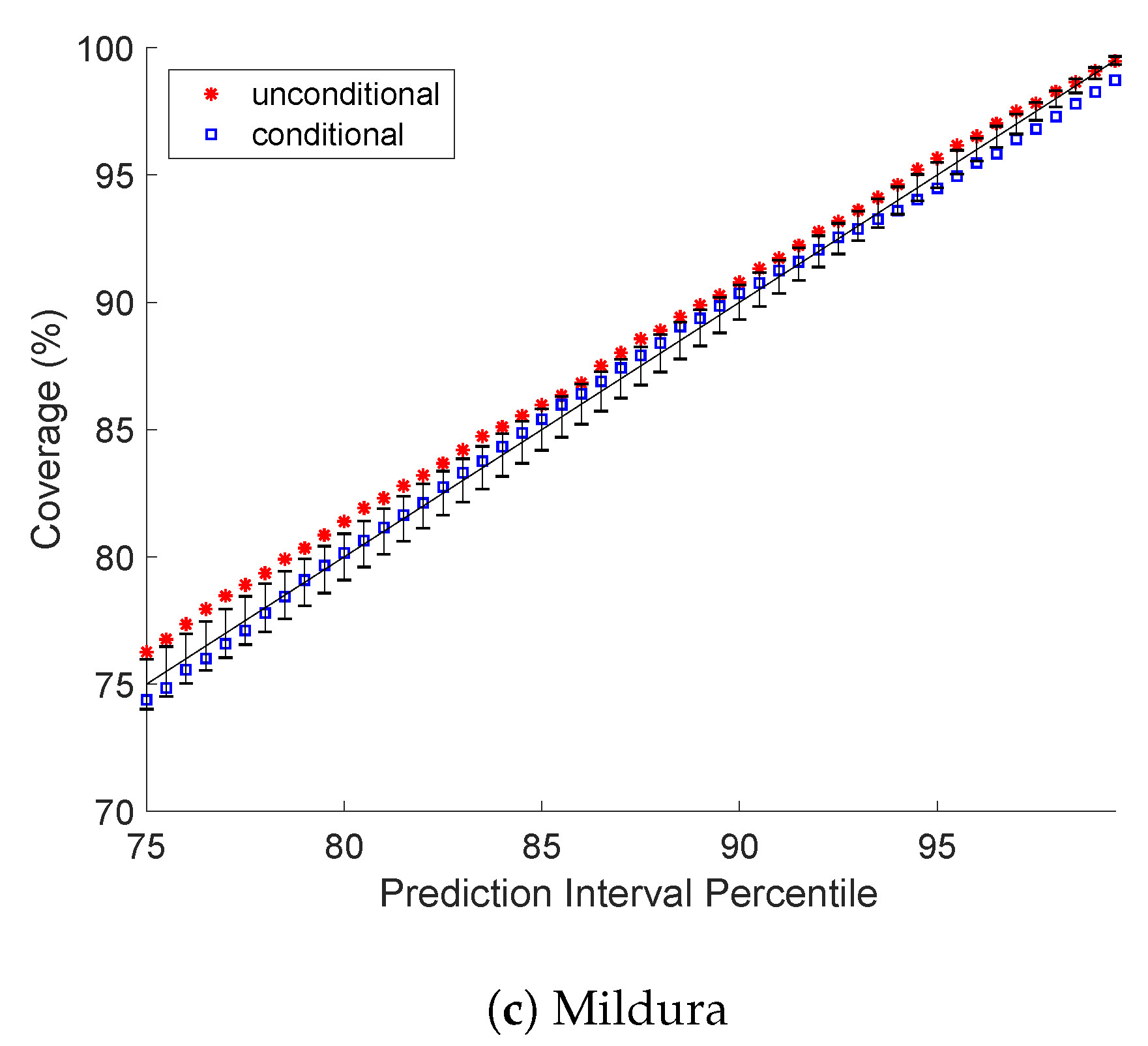
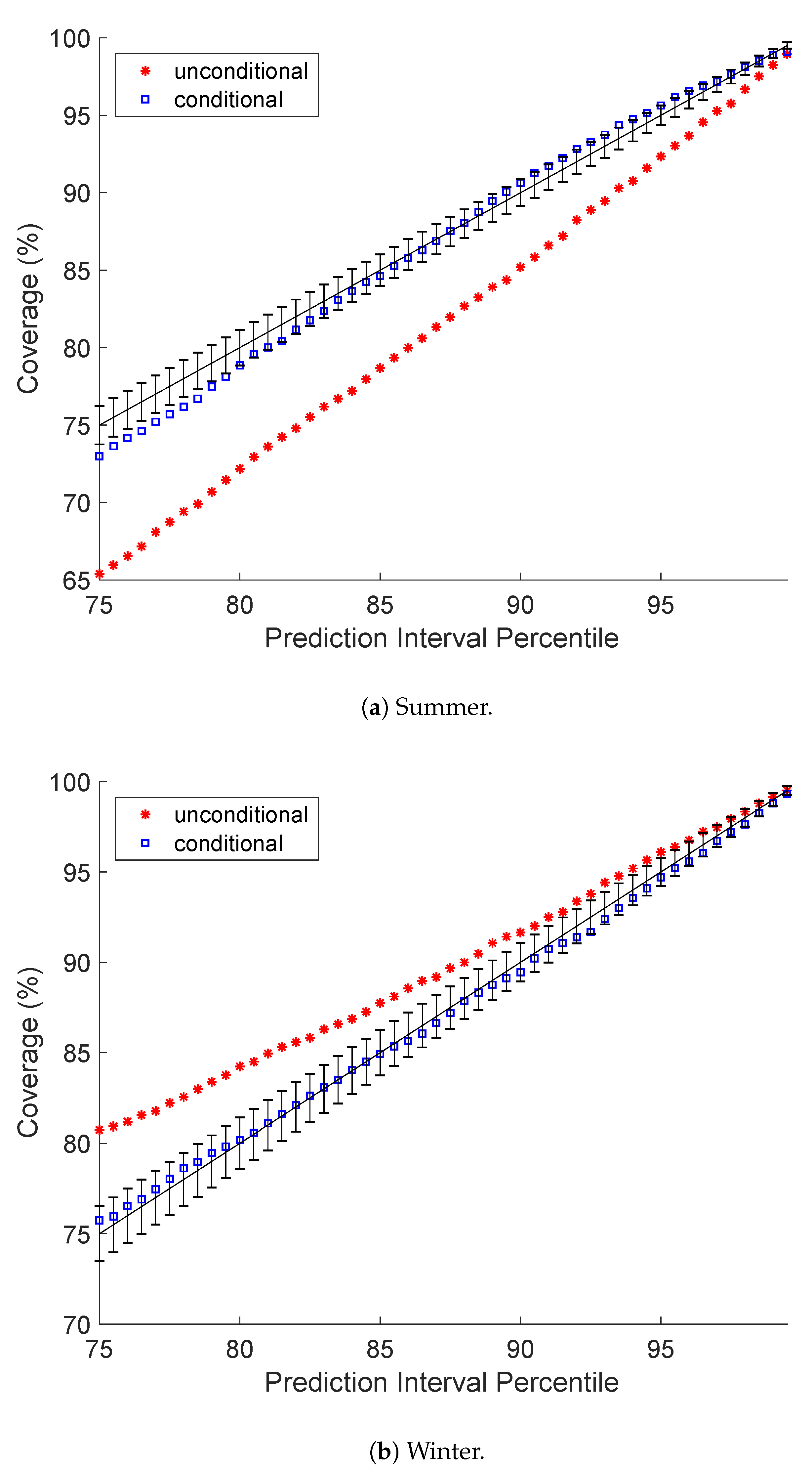
5.1. Prediction Interval Coverage Probability
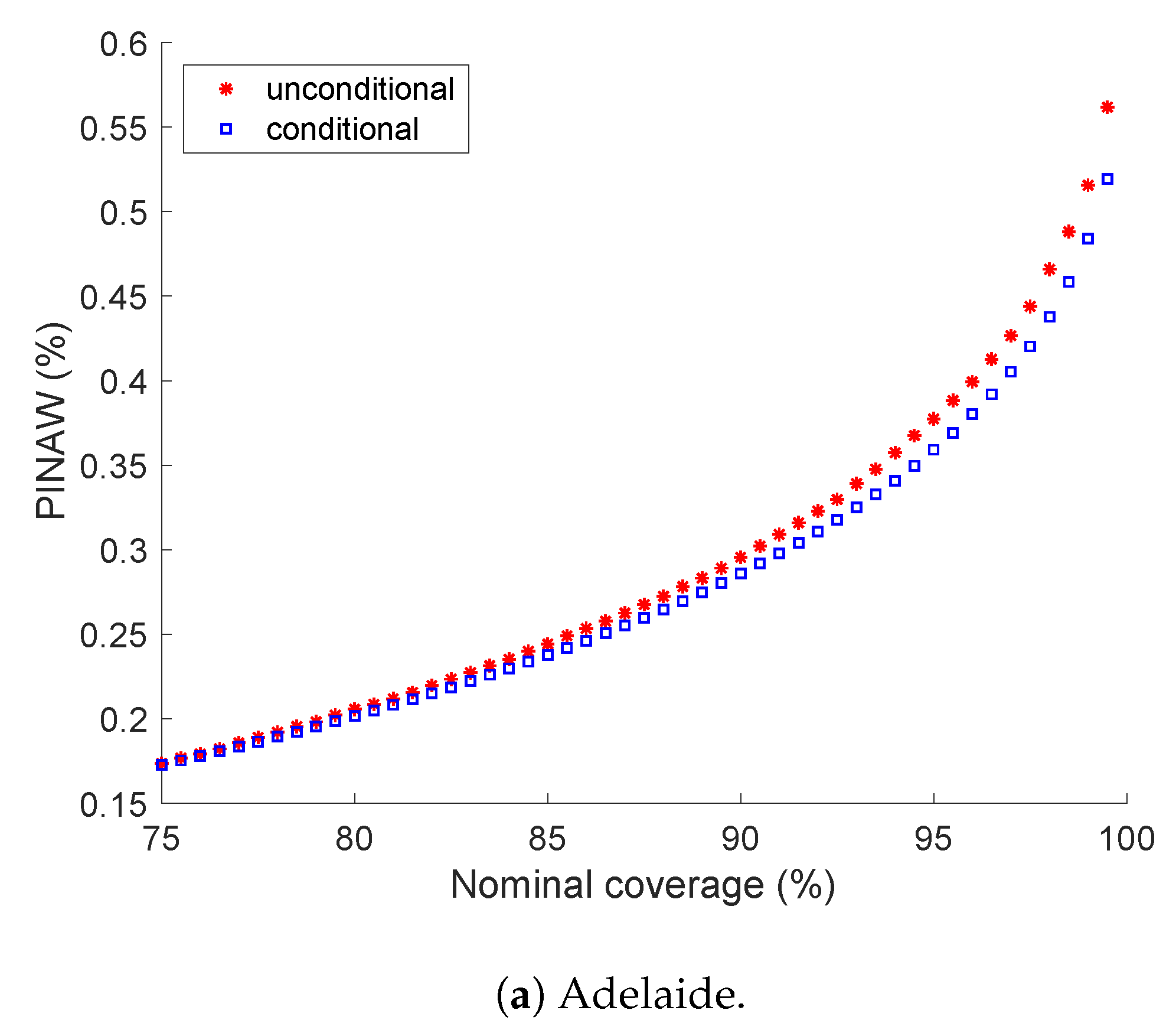
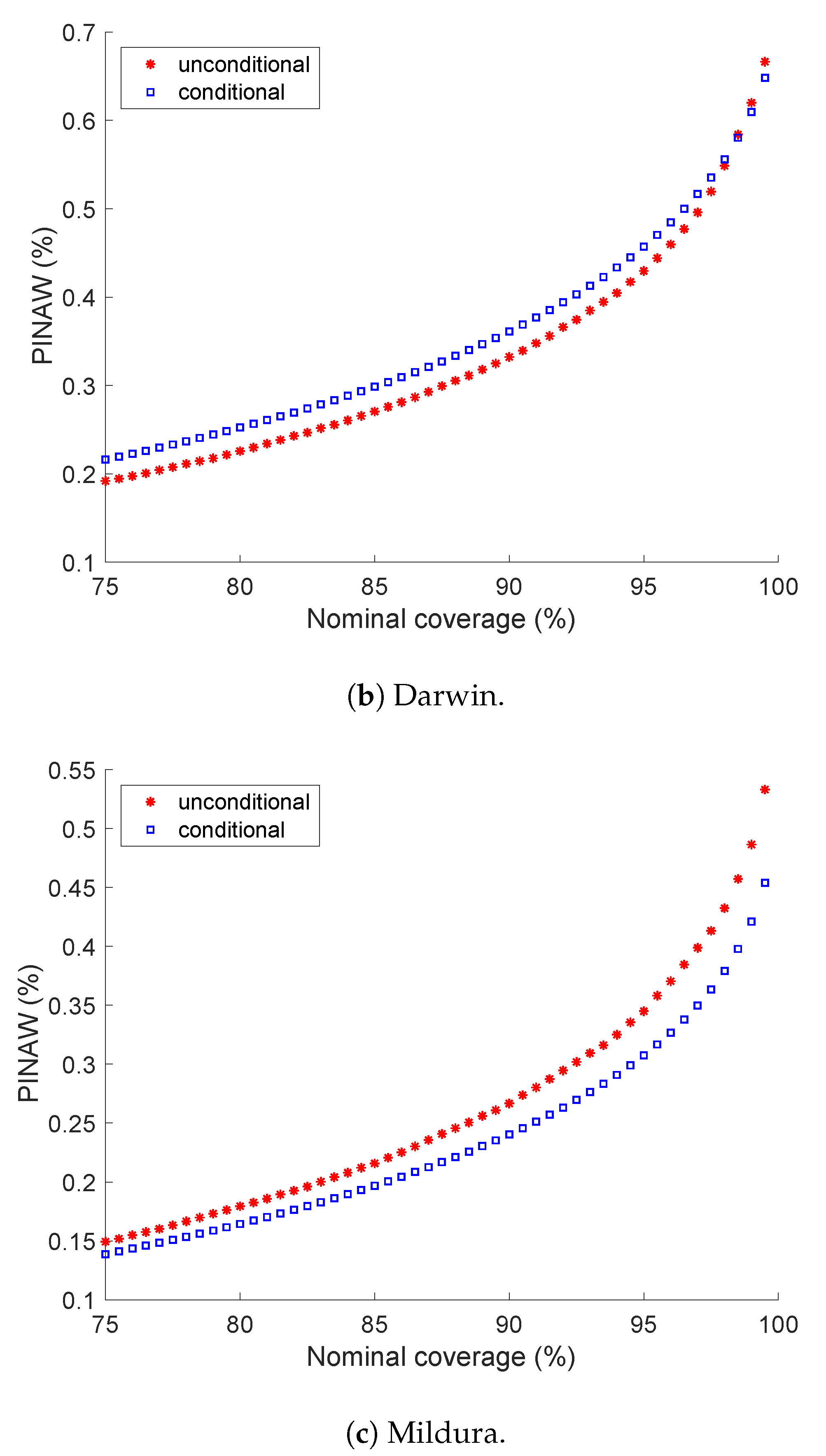
5.2. Prediction Interval Normalized Averaged Width
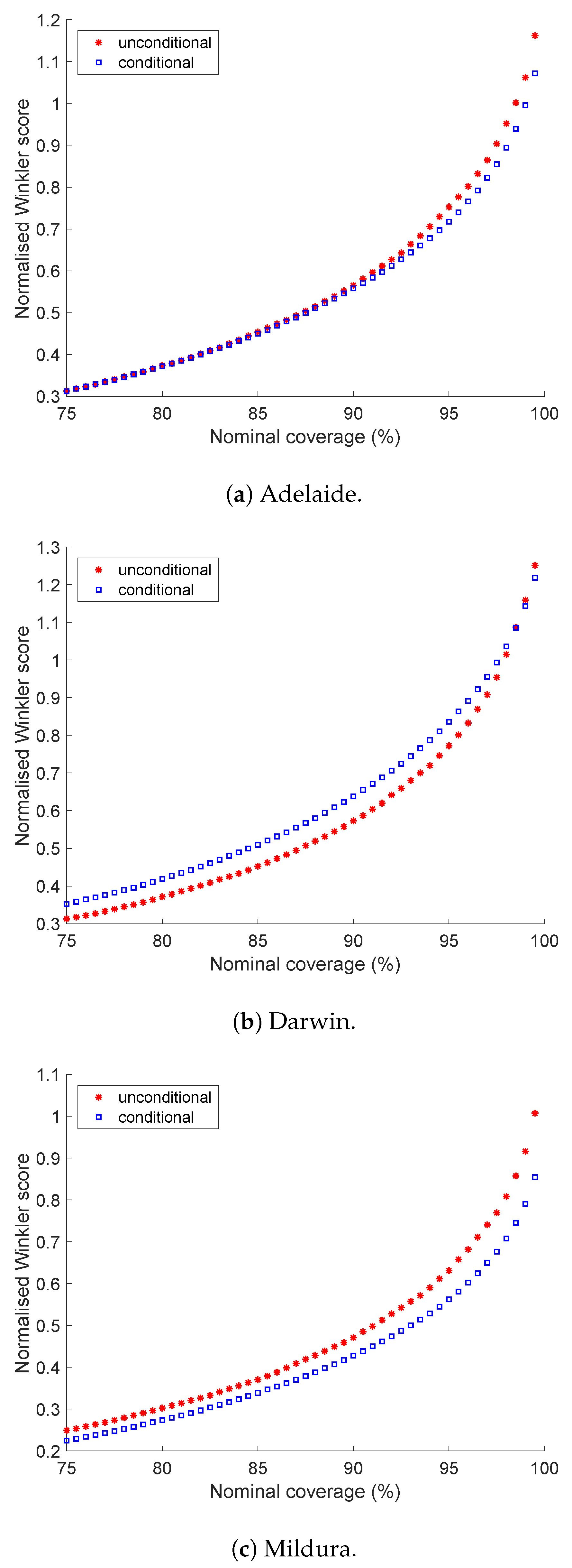
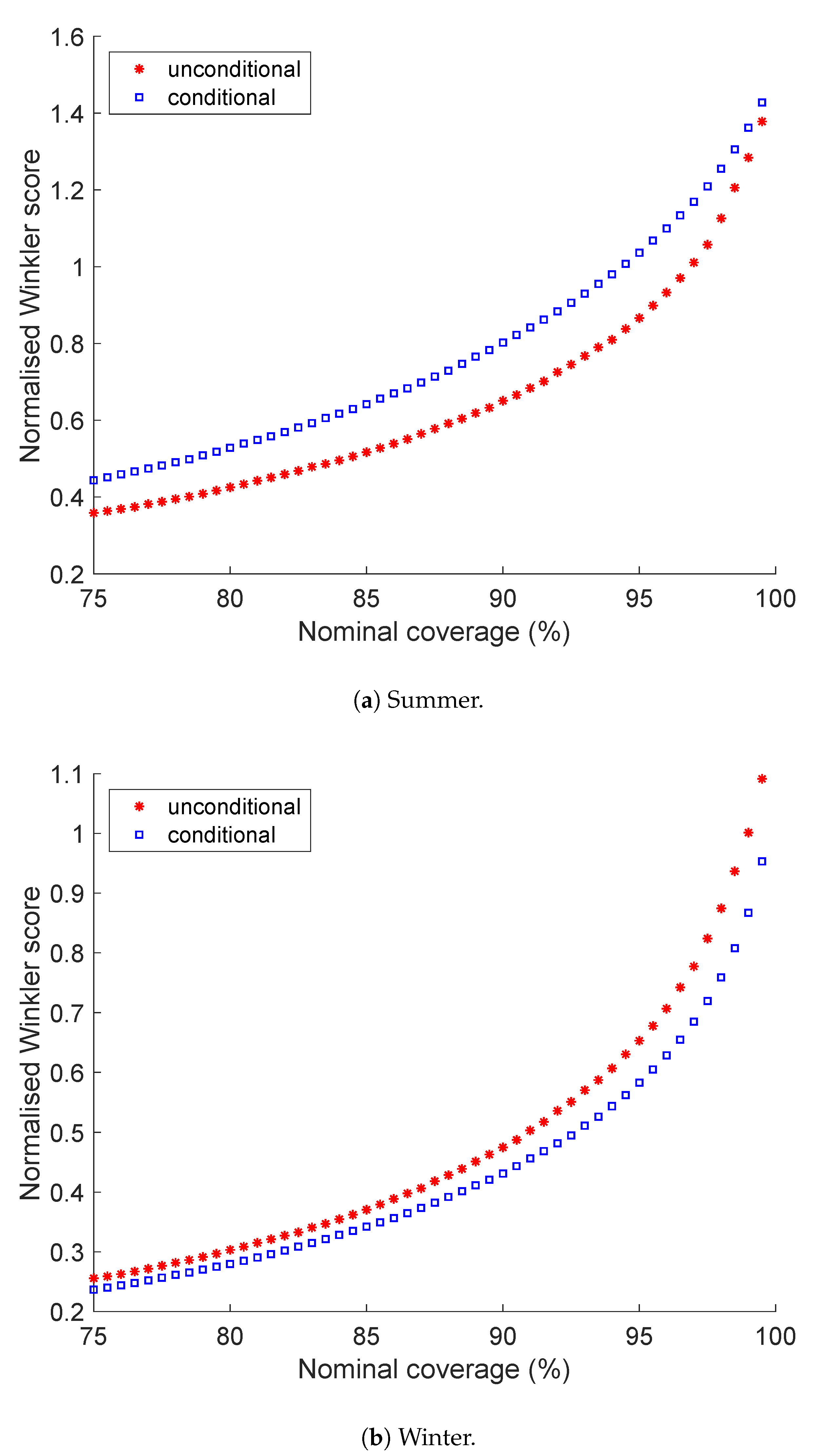
5.3. Winkler Score
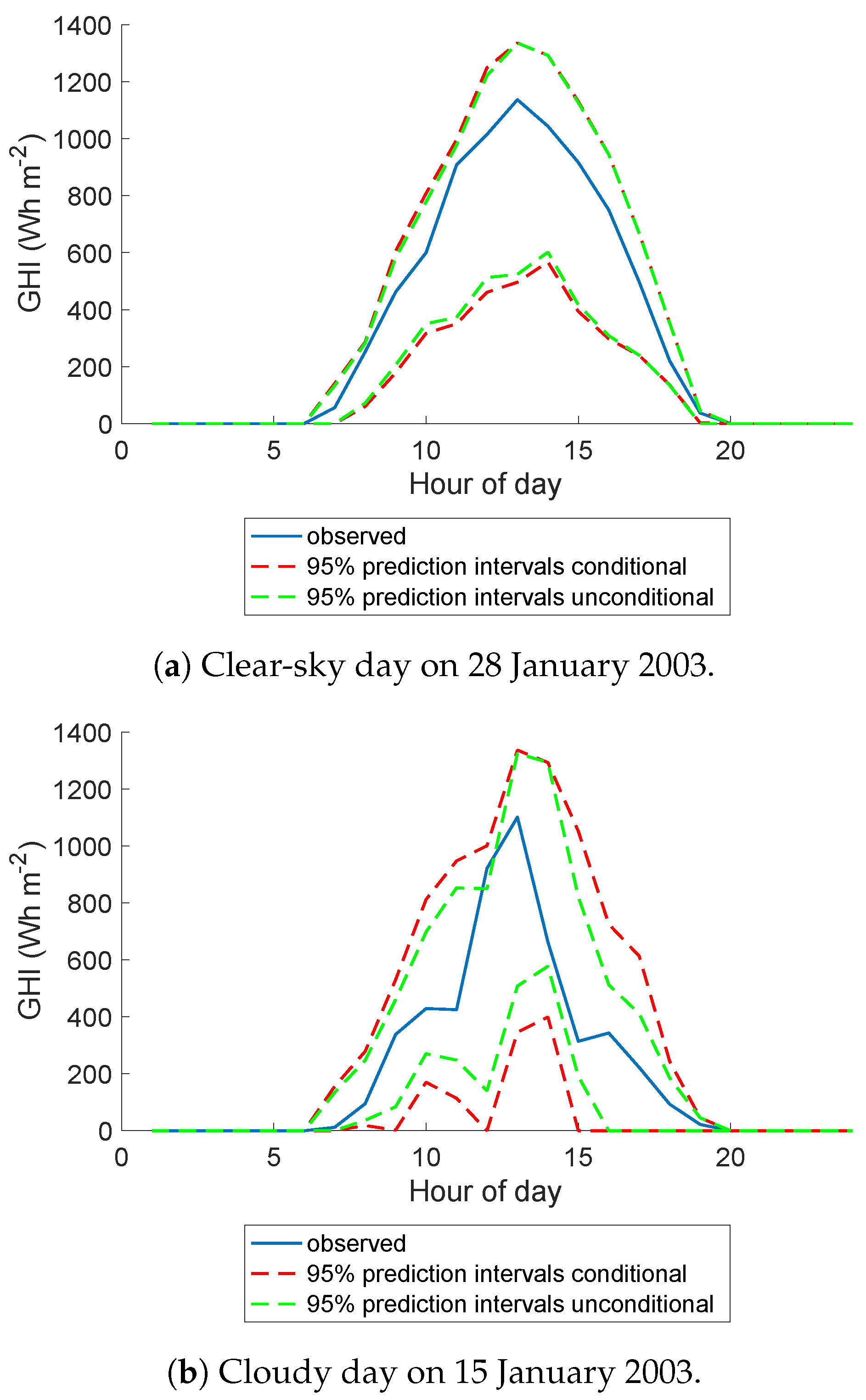
5.4. A Closer Look at Darwin
5.5. Results in the Literature
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Glossary
| hourly solar irradiation | |
| seasonal component of the solar irradiation | |
| autoregressive component of the solar irradiation | |
| noise term for the solar forecast model | |
| two-dimensional array for binning the noise, according to the sun position | |
| i corresponds to the sun elevation and j to the sun hour angle | |
| variance of the noise term at time t | |
| exponential smoothing parameter | |
| forecast of at time | |
| transformation of to the corresponding value in probability in | |
| transformation of to the corresponding value in probability in | |
| empirical cumulative distribution function of the noise term | |
| empirical cumulative distribution function of the solar forecast | |
| lower bound of the prediction interval | |
| upper bound of the prediction interval | |
| probability level for determining the prediction interval. For example, for a 95% prediction interval, | |
| the width of the prediction interval at time t |
References
- Grantham, A.; Gel, Y.R.; Boland, J. ScienceDirect Nonparametric short-term probabilistic forecasting for solar radiation. Sol. Energy 2016, 133, 465–475. [Google Scholar] [CrossRef]
- Lauret, P.; David, M.; Pedro, H.T.C. Probabilistic Solar Forecasting Using Quantile Regression Models. Energies 2017, 10, 1591. [Google Scholar] [CrossRef]
- Scolari, E.; Sossan, F.; Paolone, M. Irradiance prediction intervals for {PV} stochastic generation in microgrid applications. Sol. Energy 2016, 139, 116–129. [Google Scholar] [CrossRef]
- Chu, Y.; Coimbra, C.F.M. Short-term probabilistic forecasts for Direct Normal Irradiance. Renew. Energy 2017, 101, 526–536. [Google Scholar] [CrossRef]
- Pedro, H.T.; Coimbra, C.F.; David, M.; Lauret, P. Assessment of machine learning techniques for deterministic and probabilistic intra-hour solar forecasts. Renew. Energy 2018, 123, 191–203. [Google Scholar] [CrossRef]
- David, M.; Ramahatana, F.; Trombe, P.; Lauret, P. Probabilistic forecasting of the solar irradiance with recursive ARMA and GARCH models. Sol. Energy 2016, 133, 55–72. [Google Scholar] [CrossRef] [Green Version]
- Trapero, J.R. Calculation of solar irradiation prediction intervals combining volatility and kernel density estimates. Energy 2016, 114, 266–274. [Google Scholar] [CrossRef]
- Voyant, C.; Motte, F.; Notton, G.; Fouilloy, A.; Nivet, M.L.; Duchaud, J.L. Prediction intervals for global solar irradiation forecasting using regression trees methods. Renew. Energy 2018, 126, 332–340. [Google Scholar] [CrossRef] [Green Version]
- Grantham, A.; Pudney, P.; Boland, J. Generating synthetic sequences of global horizontal irradiation. Sol. Energy 2018, 162. [Google Scholar] [CrossRef]
- Boland, J.; Soubdhan, T. Spatial-temporal forecasting of solar radiation. Renew. Energy 2015, 75, 607–616. [Google Scholar] [CrossRef]
- Bureau of Meteorology. 2013. Available online: http://www.bom.gov.au/ (accessed on 3 December 2018).
- Boland, J.W. Time Series Modelling of Solar Radiation. In Modeling Solar Radiation at the Earth’s Surface: Recent Advances; Badescu, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Chapter 11; pp. 283–326. [Google Scholar]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting solar radiation on an hourly time scale using a Coupled AutoRegressive and Dynamical System ( CARDS ) model. Sol. Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Coimbra, C.F.M.; Kleissl, J.; Marquez, R. Chapter 8—Overview of Solar-Forecasting Methods and a Metric for Accuracy Evaluation. In Solar Energy Forecasting and Resource Assessment; Kleissl, J., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 171–194. [Google Scholar] [CrossRef]
- Templeton, G.F. A Two-Step Approach for Transforming Continuous Variables to Normal: Implications and Recommendations for IS Research. Commun. Assoc. Inf. Syst. 2011, 28, 41–58. [Google Scholar] [CrossRef]
- Bird, R.; Hulstrom, R.; Solar Energy Research Institute and United States Dept. of Energy. A Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces; Solar Energy Research Institute: Singapore, 1981. [Google Scholar]
- Starke, A.R.; Lemos, L.F.; Boland, J.; Cardemil, J.M.; Colle, S. Resolution of the cloud enhancement problem for one-minute diffuse radiation prediction. Renew. Energy 2018, 125, 472–484. [Google Scholar] [CrossRef]
- Qin, S.; Liu, F.; Wang, J.; Song, Y. Interval forecasts of a novelty hybrid model for wind speeds. Energy Rep. 2015, 1, 8–16. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Prediction intervals for short-term wind farm power generation forecasts. IEEE Trans. Sustain. Energy 2013, 4, 602–610. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Pinson, P.; Tastu, J. Discussion of “prediction intervals for short-term wind farm generation forecasts” and “combined nonparametric prediction intervals for wind power generation”. IEEE Trans. Sustain. Energy 2014, 5, 1019–1020. [Google Scholar] [CrossRef]
- Pinson, P. Very-short-term probabilistic forecasting of wind power with generalized logit-normal distributions. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2012, 61, 555–576. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic Forecasting. Annu. Rev. Stat. Its Appl. 2014, 125–151. [Google Scholar] [CrossRef]
- Bröcker, J.; Smith, L.A. Increasing the Reliability of Reliability Diagrams. Weather Forecast. 2007, 22, 651–661. [Google Scholar] [CrossRef]
- Pinson, P.; McSharry, P.; Madsen, H. Reliability diagrams for non-parametric density forecasts of continuous variables: Accounting for serial correlation. Q. J. R. Meteorol. Soc. 2010, 136, 77–90. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M. Wind-Wave Probabilistic Forecasting Based on Ensemble Predictions. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2012. [Google Scholar]
- Winkler, R.L. A Decision-Theoretic Approach to Interval Estimation. J. Am. Stat. Assoc. 1972, 67, 187–191. [Google Scholar] [CrossRef]
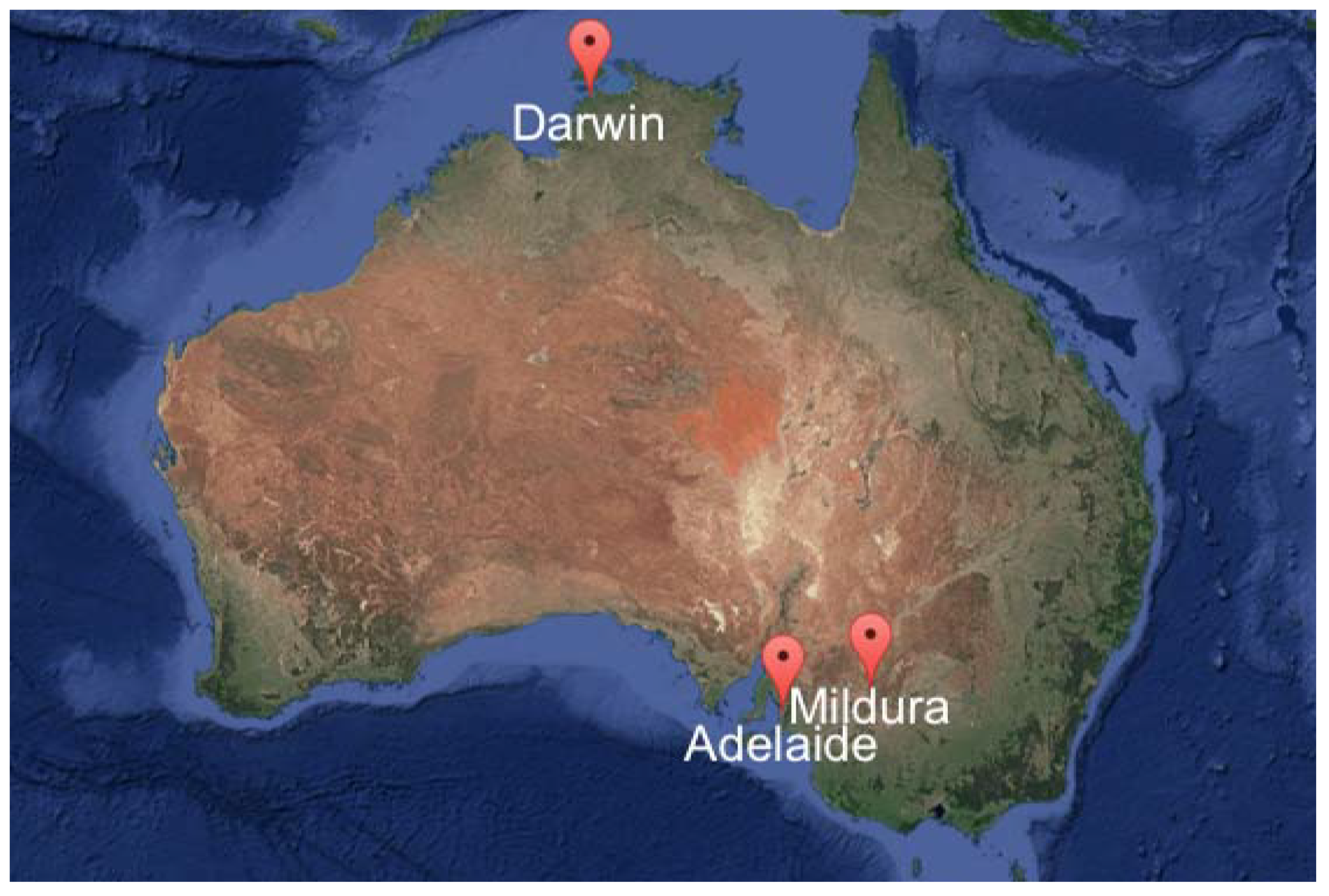
| Location | Data Period | Köppen-Geiger |
|---|---|---|
| Climate Classification | ||
| Adelaide | 2005 to 2014 | Hot Mediterranean |
| Darwin | 1995 to 2004 | Tropical |
| Mildura | 1995 to 2004 | Semi-arid |
| Point Forecast | NRMSE (%) | MBE (%) | MAE (%) |
|---|---|---|---|
| Adelaide | 19.14 | 0.72 | 13.25 |
| Darwin | 22.74 | 0.81 | 15.83 |
| Mildura | 15.29 | 1.32 | 10.83 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boland, J.; Grantham, A. Nonparametric Conditional Heteroscedastic Hourly Probabilistic Forecasting of Solar Radiation. J 2018, 1, 174-191. https://doi.org/10.3390/j1010016
Boland J, Grantham A. Nonparametric Conditional Heteroscedastic Hourly Probabilistic Forecasting of Solar Radiation. J. 2018; 1(1):174-191. https://doi.org/10.3390/j1010016
Chicago/Turabian StyleBoland, John, and Adrian Grantham. 2018. "Nonparametric Conditional Heteroscedastic Hourly Probabilistic Forecasting of Solar Radiation" J 1, no. 1: 174-191. https://doi.org/10.3390/j1010016
APA StyleBoland, J., & Grantham, A. (2018). Nonparametric Conditional Heteroscedastic Hourly Probabilistic Forecasting of Solar Radiation. J, 1(1), 174-191. https://doi.org/10.3390/j1010016






