Defect Properties of Li2NiGe3O8
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
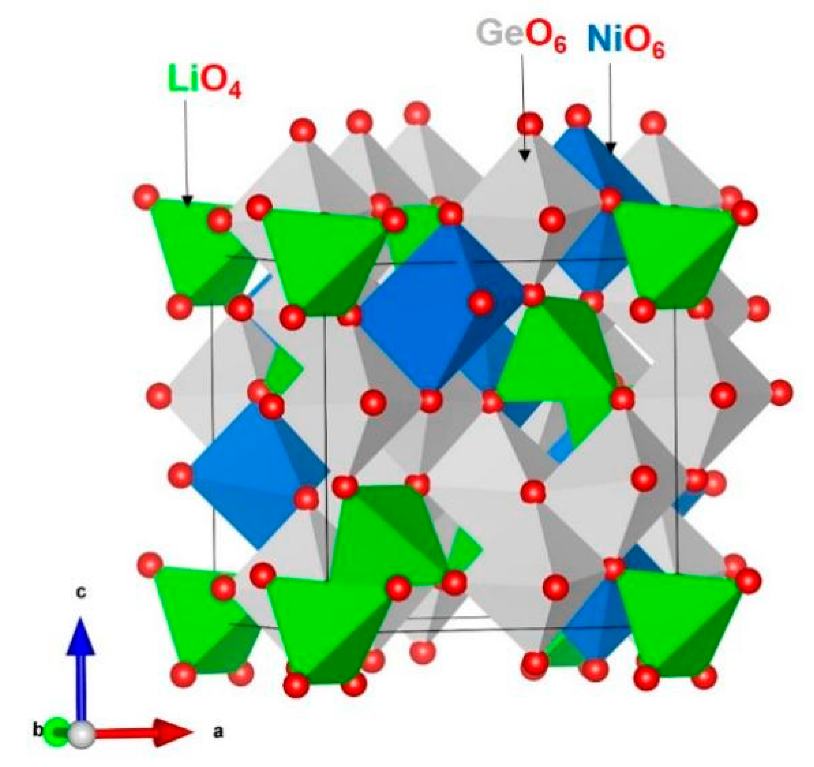
3.1. Modelling of Bulk Li2NiGe3O8
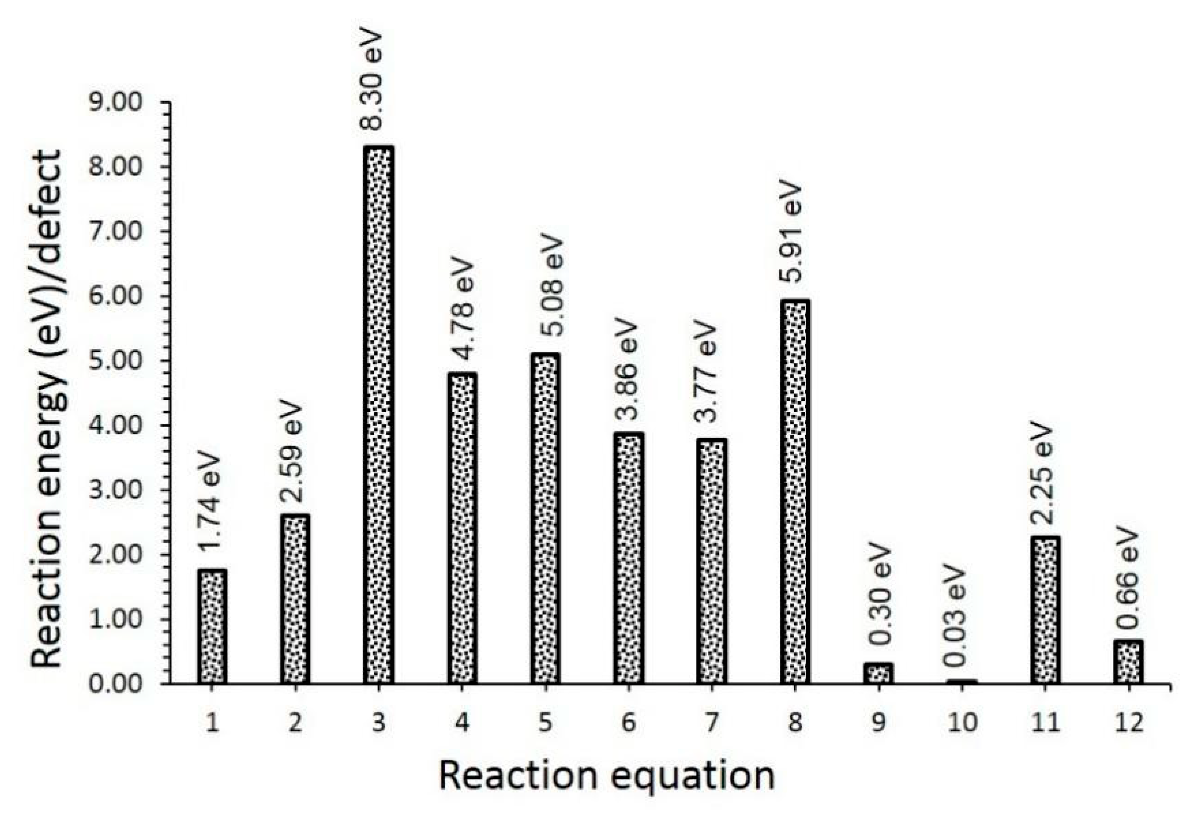
3.2. Intrinsic Defects
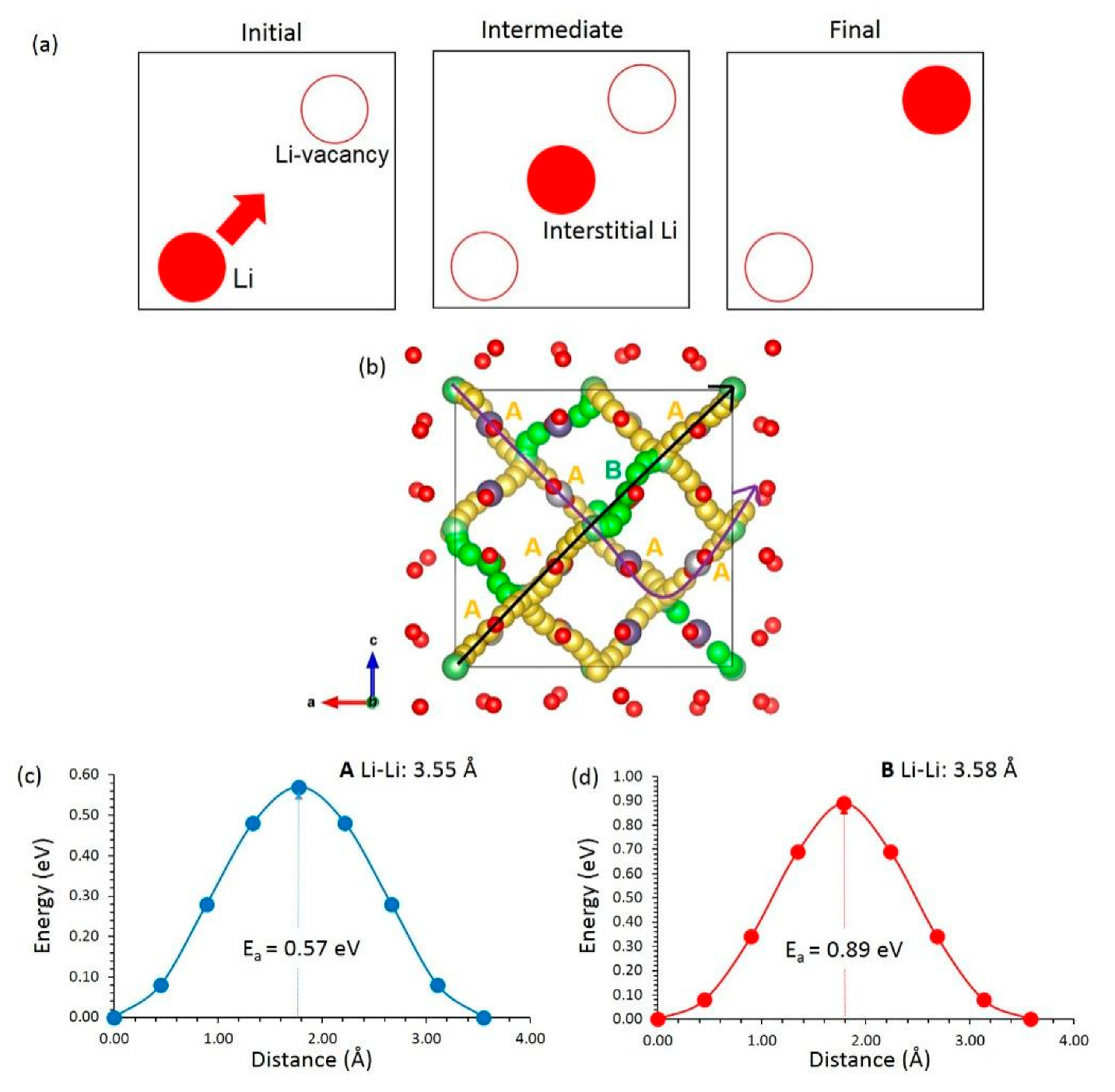
3.3. Li-ion Diffusion
3.4. Solution of Dopants
3.4.1. Alkali Dopants
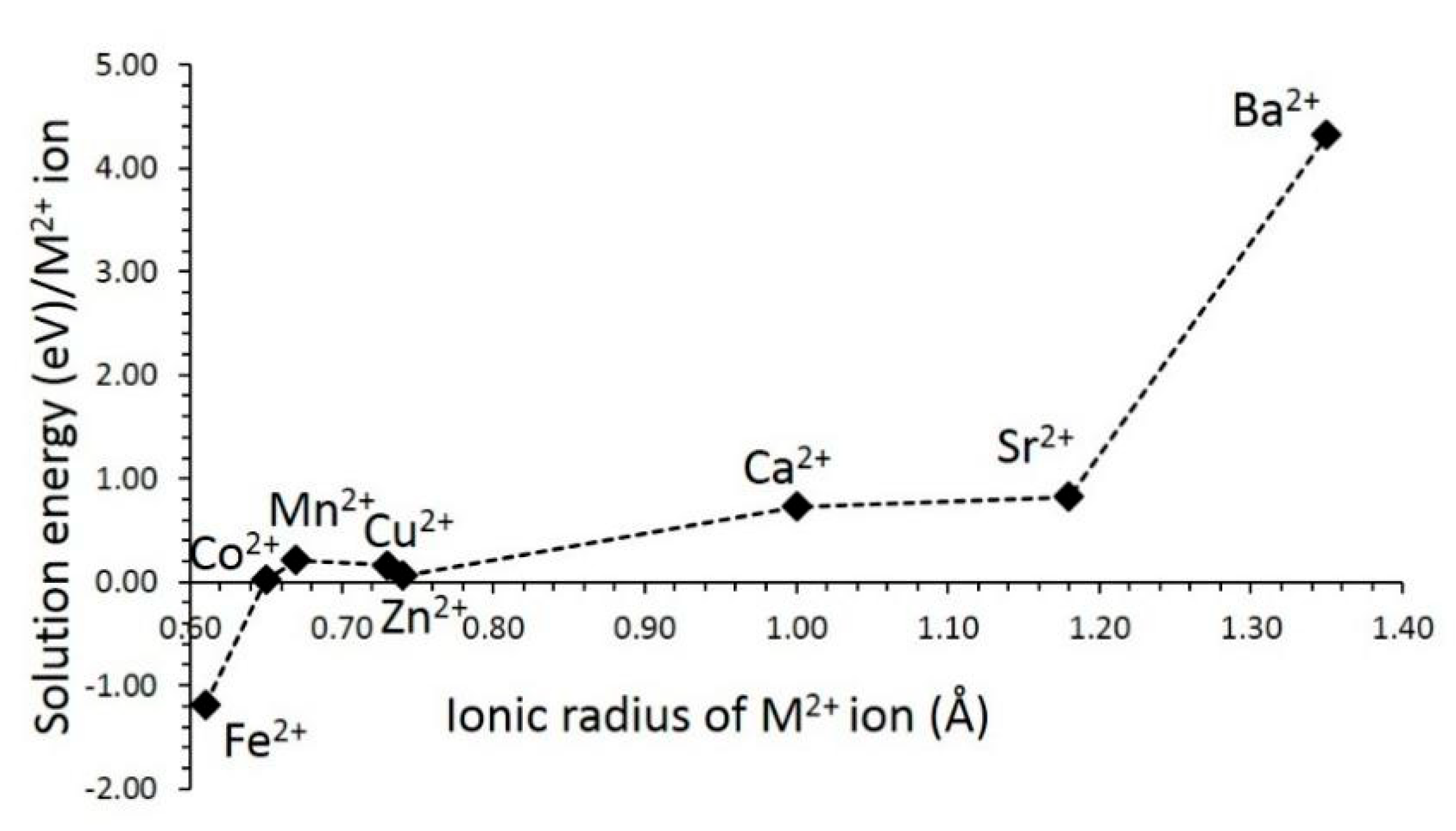
3.4.2. Divalent Dopants
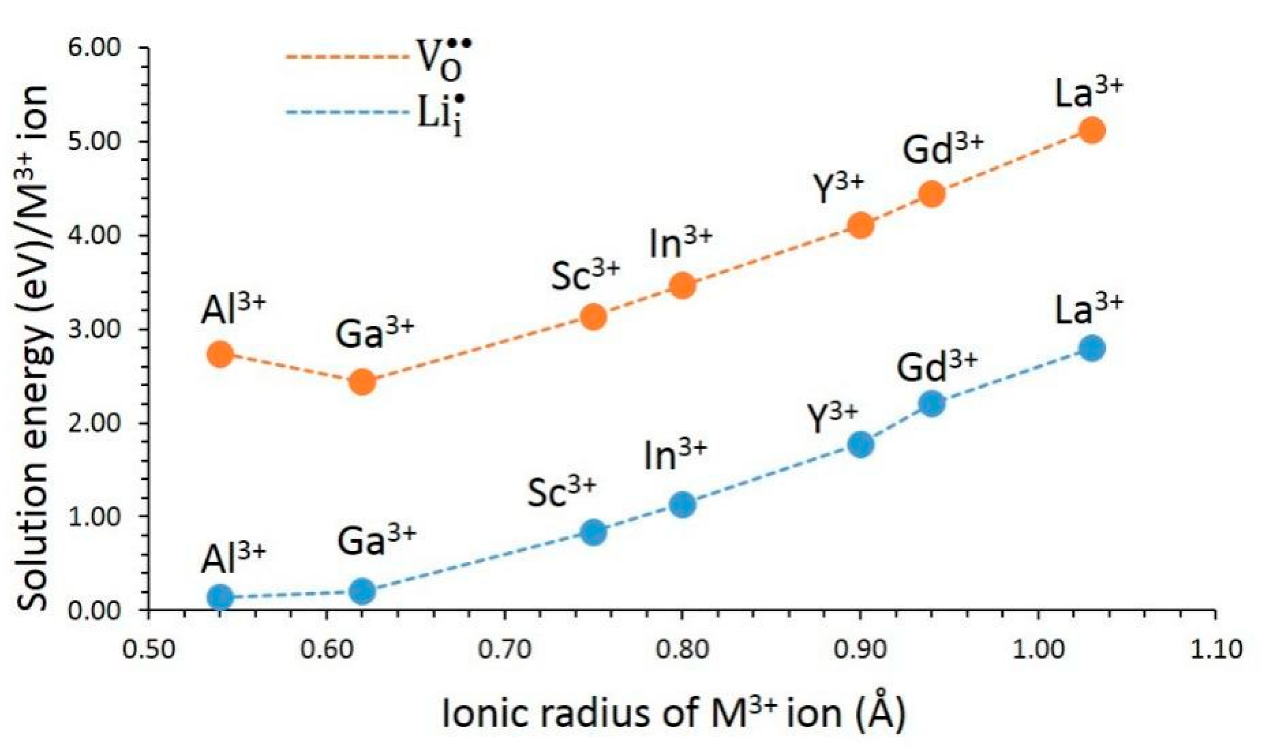
3.4.3. Trivalent Dopants
3.4.4. Tetravalent Dopants
3.5. The Impact of Favorable Dopants on the Diffusion of Li-ions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Armand, M.; Tarascon, J.M. Building better batteries. Nature 2008, 451, 652. [Google Scholar] [CrossRef] [PubMed]
- Whittingham, M.S. Lithium Batteries and Cathode Materials. Chem. Rev. 2004, 104, 4271–4302. [Google Scholar] [CrossRef] [PubMed]
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B. Phospho-olivines as Positive Electrode Materials for Rechargeable Lithium Batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Islam, M.S.; Fisher, C.A.J. Lithium and sodium battery cathode materials: Computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 2014, 43, 185–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masquelier, C.; Croguennec, L. Polyanionic (Phosphates, Silicates, Sulphates) Frameworks as Electrode Materials for Rechargeable Li (or Na) Batteries. Chem. Rev. 2013, 113, 6552–6591. [Google Scholar] [CrossRef]
- Soltani, M.; Beheshti, S.H. A comprehensive review of Lithium-ion capacitor: Development, modelling, thermal management and applications. J. Energy Storage 2021, 34, 102019. [Google Scholar] [CrossRef]
- Delmas, C. Sodium and Sodium-Ion Batteries: 50 Years of Research. Adv. Energy Mater. 2018, 8, 1703137. [Google Scholar] [CrossRef]
- Jeżowski, P.; Crosnier, O.; Brousse, T. Sodium borohydride (NaBH4) as a high-capacity material for next-generation sodium-ion capacitors. Open Chem. 2021, 19, 432–441. [Google Scholar] [CrossRef]
- Hosaka, T.; Kubota, K.; Hameed, A.S.; Komaba, S. Research Development on K-Ion Batteries. Chem. Rev. 2020, 120, 6358–6466. [Google Scholar] [CrossRef]
- Nik, R.M.; Ronald, I.S.; Anthony, R.W. Lithium-Ion conduction pathways in complex lithium spinels Li2MGe3O8 (M = Ni or Zn). Chem. Mater. 2011, 23, 3556–3563. [Google Scholar]
- Daniel, Z.C.M.; Abby, R.H.; Whiney, L.S.; Peter, J.B.; Rebecca, B.; Karen, E.J.; Nik, R.M. Evaluating lithium diffusion mechanisms in the complex spinel Li|NiGe3O8. Phys. Chem. Chem. Phys. 2019, 21, 23111–23118. [Google Scholar]
- Bachman, J.C.; Muy, S.; Grimaud, A.; Chang, H.; Pour, N.; Lux, S.F.; Paschos, O.; Maglia, F.; Lupart, S.; Lamp, P.; et al. Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction. Chem. Rev. 2016, 116, 140–162. [Google Scholar] [CrossRef]
- Orera, A.; Campo, J. Influence of Li+ and H+ Distribution on the Crystal Structure of Li7−xHxLa3Zr2O12 (0 ≤ x ≤ 5) Garnets. Inorg. Chem. 2016, 55, 1324–1332. [Google Scholar] [CrossRef] [Green Version]
- Hofstetter, K.; Samson, A.J.; Narayanan, S.; Thangadurai, V. Present understanding of the stability of Li-stuffed garnets with moisture, carbon dioxide, and metallic lithium. J. Power Sources 2018, 390, 297–312. [Google Scholar] [CrossRef]
- Bragg, W.H. The structure of the spinel group of crystals. Philos. Mag. 1915, 30, 305–315. [Google Scholar] [CrossRef] [Green Version]
- Nishikawa, S. Structure of Some Crystals of Spinel Group. Proc. Math. Phys. Soc. Tokyo 1915, 8, 199–209. [Google Scholar]
- Nakayama, M.; Jalem, R.; Kasuga, T. Electronic structure of spinel-type LiNi1/2Ge3/2O4 and LiNi1/2Mn3/2O4 as positive electrodes for rechargeable Li-ion batteries studied by first-principles density functional theory. Solid State Ionics 2014, 262, 74–76. [Google Scholar] [CrossRef] [Green Version]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Kuganathan, N.; Iyngaran, P.; Chroneos, A. Lithium diffusion in Li5FeO4. Sci. Rep. 2018, 8, 5832. [Google Scholar] [CrossRef] [Green Version]
- Tealdi, C.; Saiful Islam, M.; Malavasi, L.; Flor, G. Defect and dopant properties of MgTa2O6. J. Solid State Chem. 2004, 177, 4359–4367. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [Green Version]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects, diffusion, dopants and encapsulation of Na in NaZr2(PO4)3. Materialia 2021, 16, 101039. [Google Scholar] [CrossRef]
- Kim, Y. Theoretical investigation of the cation antisite defect in layer-structured cathode materials for Li-ion batteries. Phys. Chem. Chem. Phys. 2019, 21, 24139–24146. [Google Scholar] [CrossRef]
- Lin, Q.; Guan, W.; Zhou, J.; Meng, J.; Huang, W.; Chen, T.; Gao, Q.; Wei, X.; Zeng, Y.; Li, J.; et al. Ni–Li anti-site defect induced intragranular cracking in Ni-rich layer-structured cathode. Nano Energy 2020, 76, 105021. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: New York, NY, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Morando, C.; Cofrancesco, P.; Tealdi, C. Zn ion diffusion in spinel-type cathode materials for rechargeable batteries: The role of point defects. Mater. Today Commun. 2020, 25, 101478. [Google Scholar] [CrossRef]
- Li, J.-J.; Dai, Y.; Zheng, J.-C. Strain engineering of ion migration in LiCoO2. Front. Phys. 2021, 17, 13503. [Google Scholar] [CrossRef]
- Azough, F.; Freer, R.; Wright, K.; Jackson, R. A computer simulation study of point defects in diopside and the self-diffusion of Mg and Ca by a vacancy mechanism. Mineral. Mag. 1998, 62, 599–606. [Google Scholar] [CrossRef]
- Kilo, M.; Jackson, R.A.; Borchardt, G. Computer modelling of ion migration in zirconia. Philos. Mag. 2003, 83, 3309–3325. [Google Scholar] [CrossRef]


| Interaction | A/eV | ρ/Å | C/eV•Å6 | Y/e | K/eV•Å−2 |
|---|---|---|---|---|---|
| Li+ – O2− | 632.1018 | 0.2906 | 0 | 1 | 99,999.0 |
| Ni2+ – O2− | 1760.0 | 0.2800 | 0 | 2 | 93.7 |
| Ge4+ − O2− | 1497.3996 | 0.325646 | 16.808599 | 4 | 99,999.0 |
| O2− – O2− | 22,764.30 | 0.1490 | 44.53 | −2.96 | 65.0 |
| Parameter | Calculated | Experiment [11] | |∆|(%) |
|---|---|---|---|
| a = b = c (Å) | 8.218 | 8.180 | 0.46 |
| α = β = γ (°) | 90 | 90 | 0 |
| V (Å3) | 555.11 | 547.39 | 1.41 |
| Dopants | Activation Energy (eV) | |
|---|---|---|
| A | B | |
| Na | 0.58 | 0.93 |
| Fe | 0.55 | 0.87 |
| Al | 0.54 | 0.86 |
| Ga | 0.56 | 0.84 |
| Si | 0.59 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N.; Sukumar, R.; Iyngaran, P. Defect Properties of Li2NiGe3O8. Clean Technol. 2022, 4, 619-628. https://doi.org/10.3390/cleantechnol4030038
Kuganathan N, Sukumar R, Iyngaran P. Defect Properties of Li2NiGe3O8. Clean Technologies. 2022; 4(3):619-628. https://doi.org/10.3390/cleantechnol4030038
Chicago/Turabian StyleKuganathan, Navaratnarajah, Raveena Sukumar, and Poobalasuntharam Iyngaran. 2022. "Defect Properties of Li2NiGe3O8" Clean Technologies 4, no. 3: 619-628. https://doi.org/10.3390/cleantechnol4030038
APA StyleKuganathan, N., Sukumar, R., & Iyngaran, P. (2022). Defect Properties of Li2NiGe3O8. Clean Technologies, 4(3), 619-628. https://doi.org/10.3390/cleantechnol4030038







