Hardware Implementation of Composite Control Strategy for Wind-PV-Battery Hybrid Off-Grid Power Generation System
Abstract
:1. Introduction
- Minimizing the number of power converters to reduce the hardware complexity and increase the system efficiency,
- Development of an indirect control for the buck-boost converter to realize many tasks such as achieving high performance from PV without using any MPPT algorithm, facilitating the bidirectional power flow between the ESS and PCC, and ensuring stable operation during the disturbance,
- Effective and efficient, mechanical-speed sensorless operation of variable-speed WT-based permanent magnet brushless DC generator (PMBLDCG) using hybridization of the root-finding algorithm (secant method) with P&O technique,
- Reinforcement of the SRF based control with virtual impedance active damping to improve the power quality at the PCC while eliminating the 5th and 7th order harmonics, along with the prevention of the 6th order-harmonic generation in the rotor of the synchronous generator (SG), as well as to solve the issue of filter resonance.
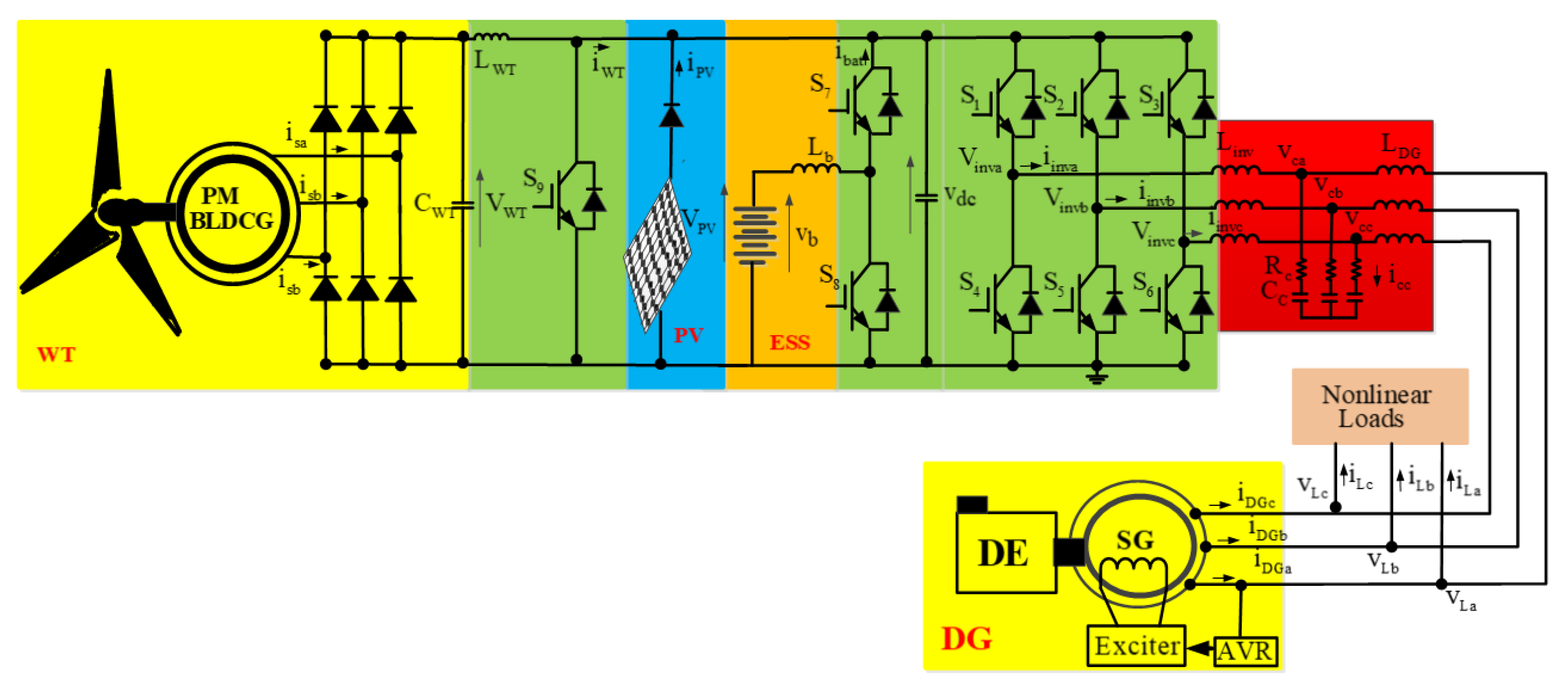
2. System Configuration and Operation
3. Developed Composite Control Strategy
3.1. Control of DC-DC Boost Converter on WT Side
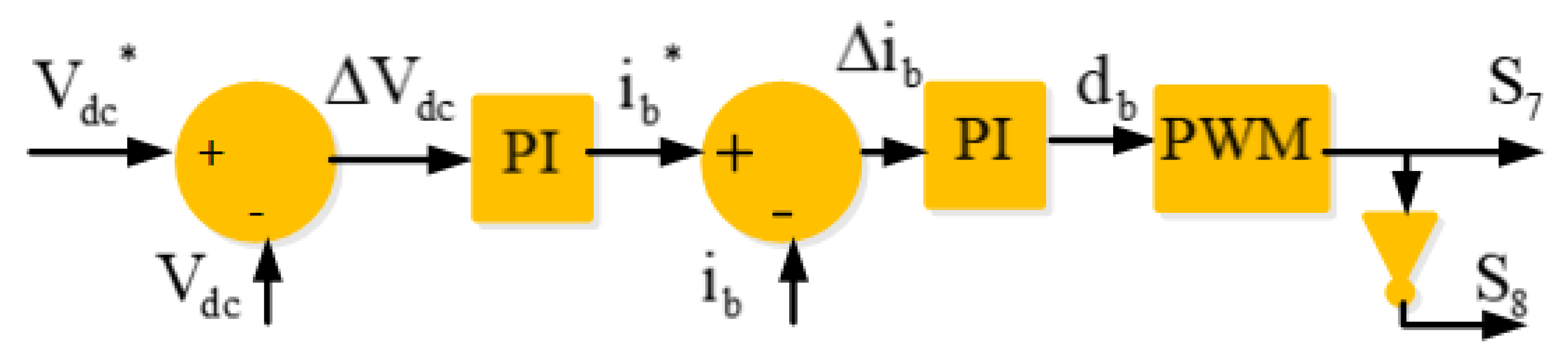
3.2. Control of DC-DC Buck-Boost Converter for ESS Side
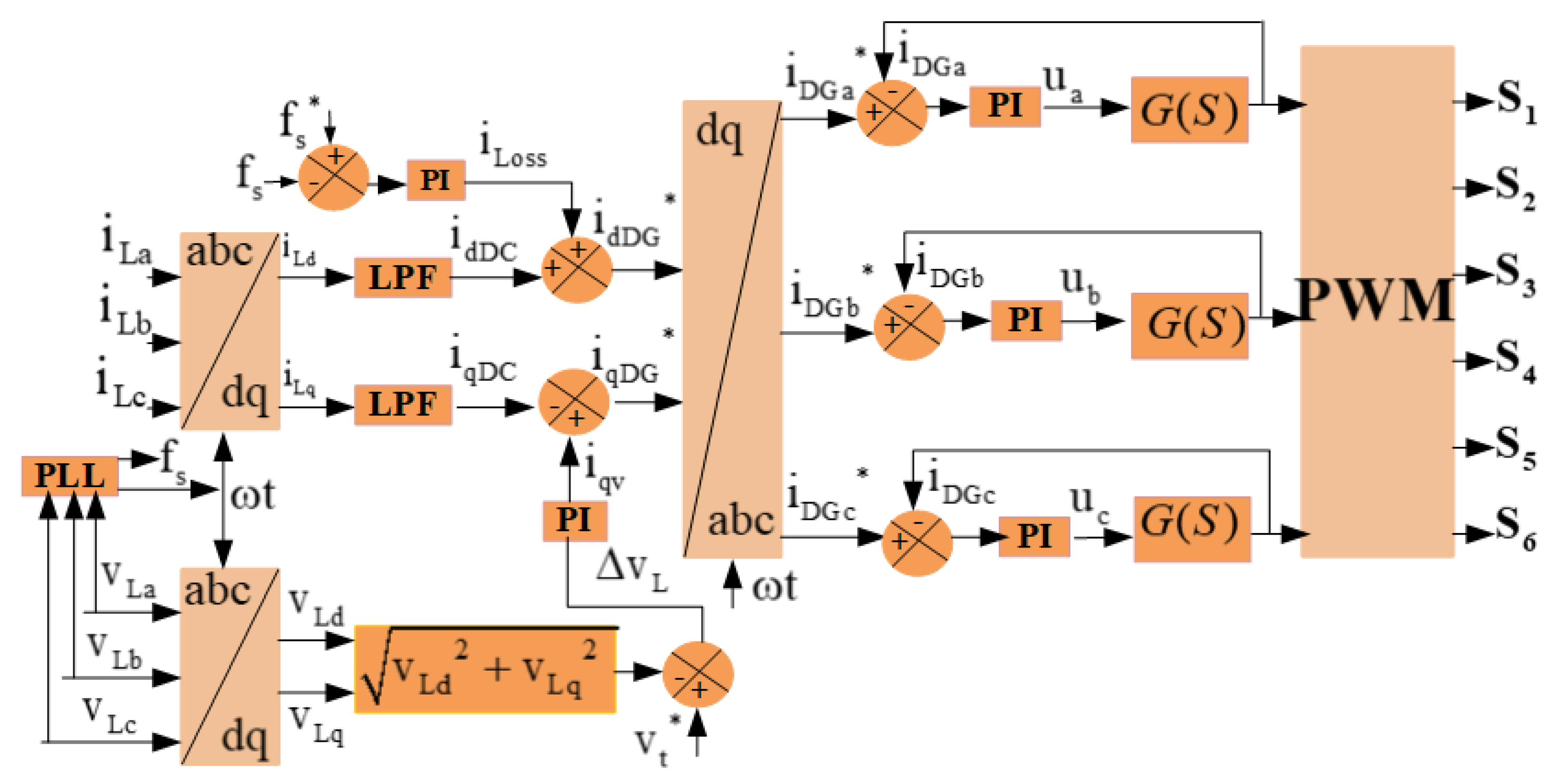
3.3. SRF Control with Virtual Impedance-Based Active Damping
4. Results and Discussion
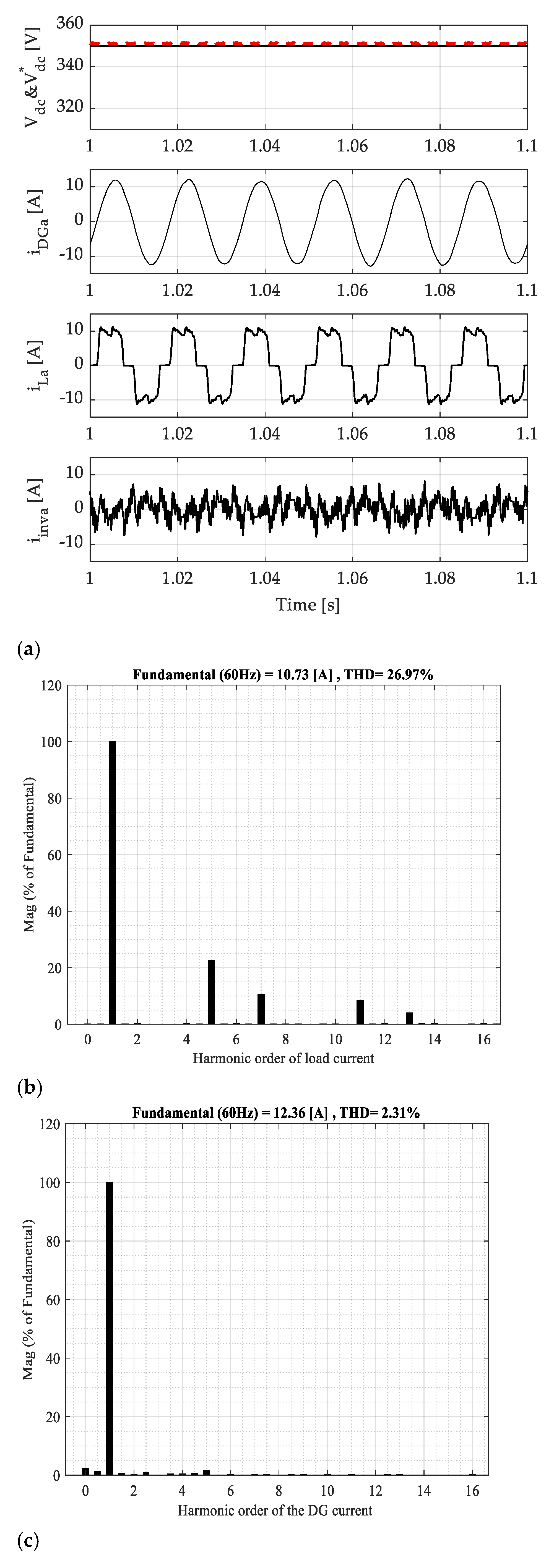
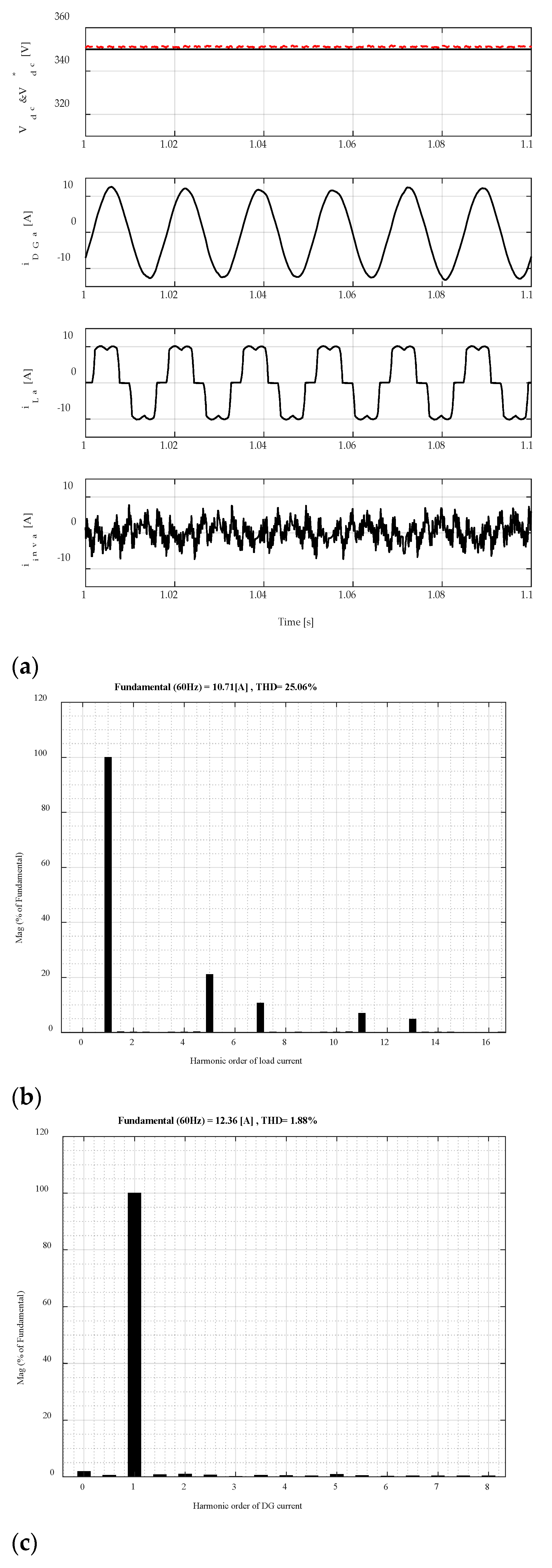
4.1. Performance at the AC Side under Presence of Linear Load
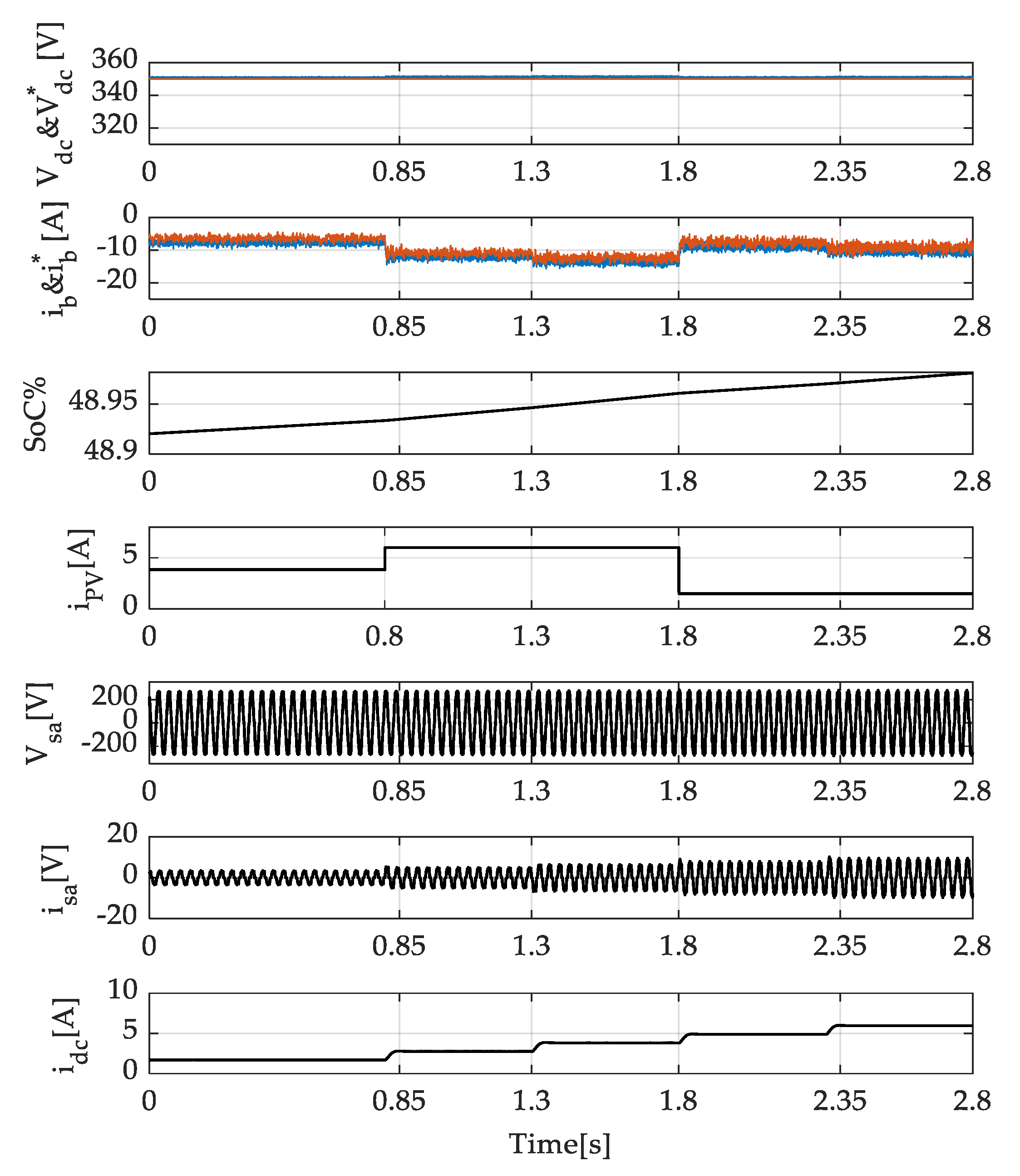
4.2. Performance at the DC Side at Solar Irradiation and Wind Speed Change
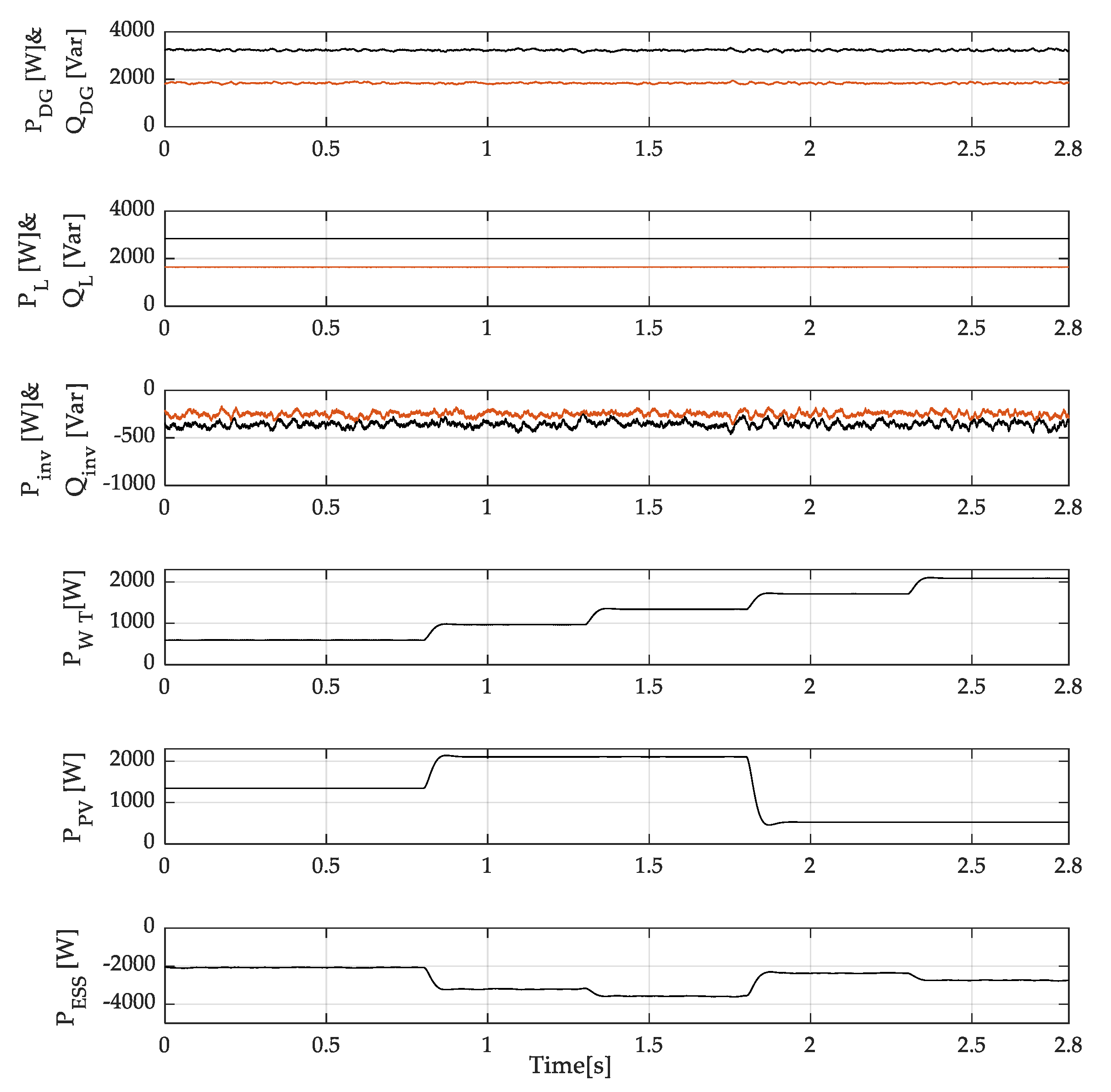
4.3. Generated and Consumed Active and Reactive Powers
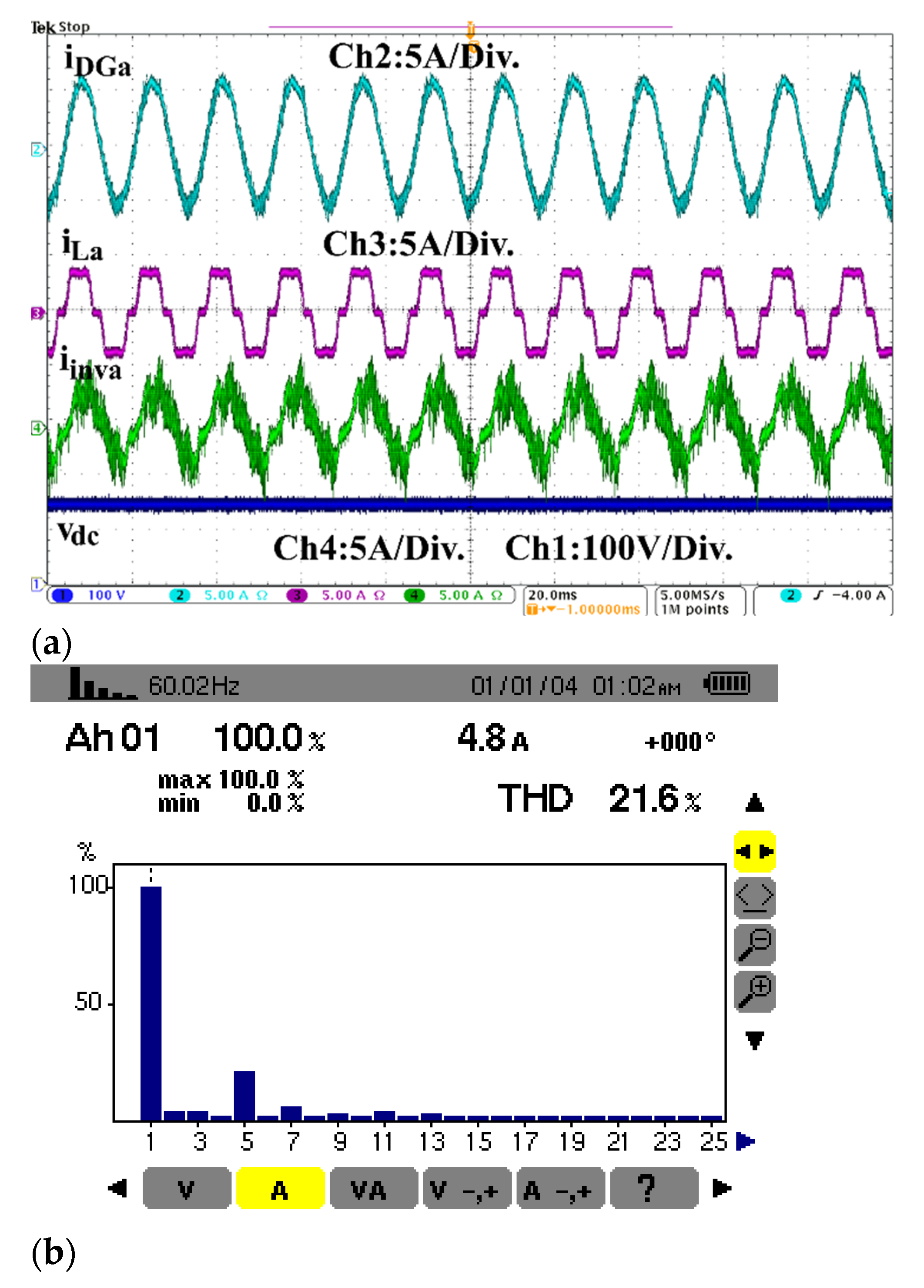
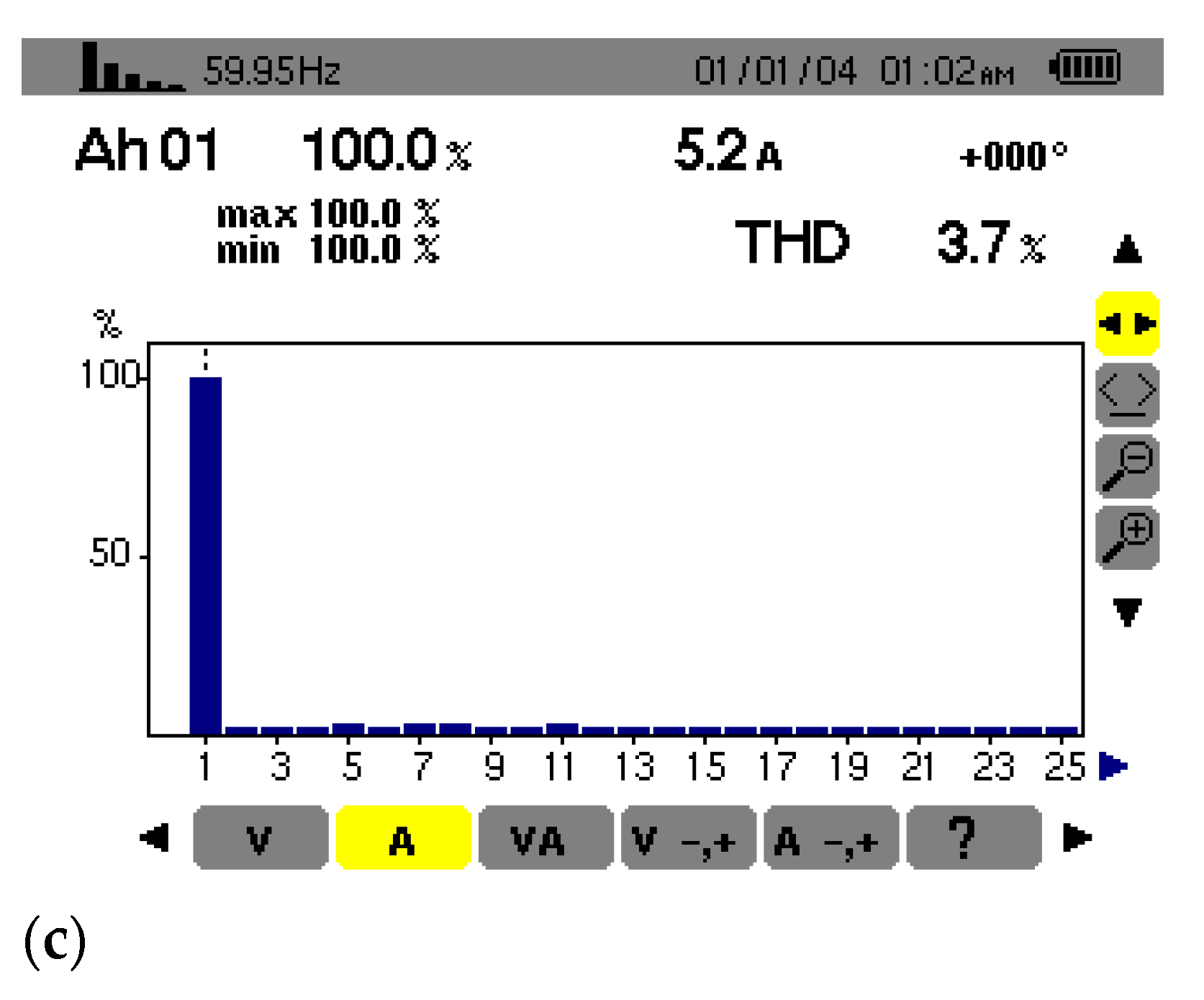
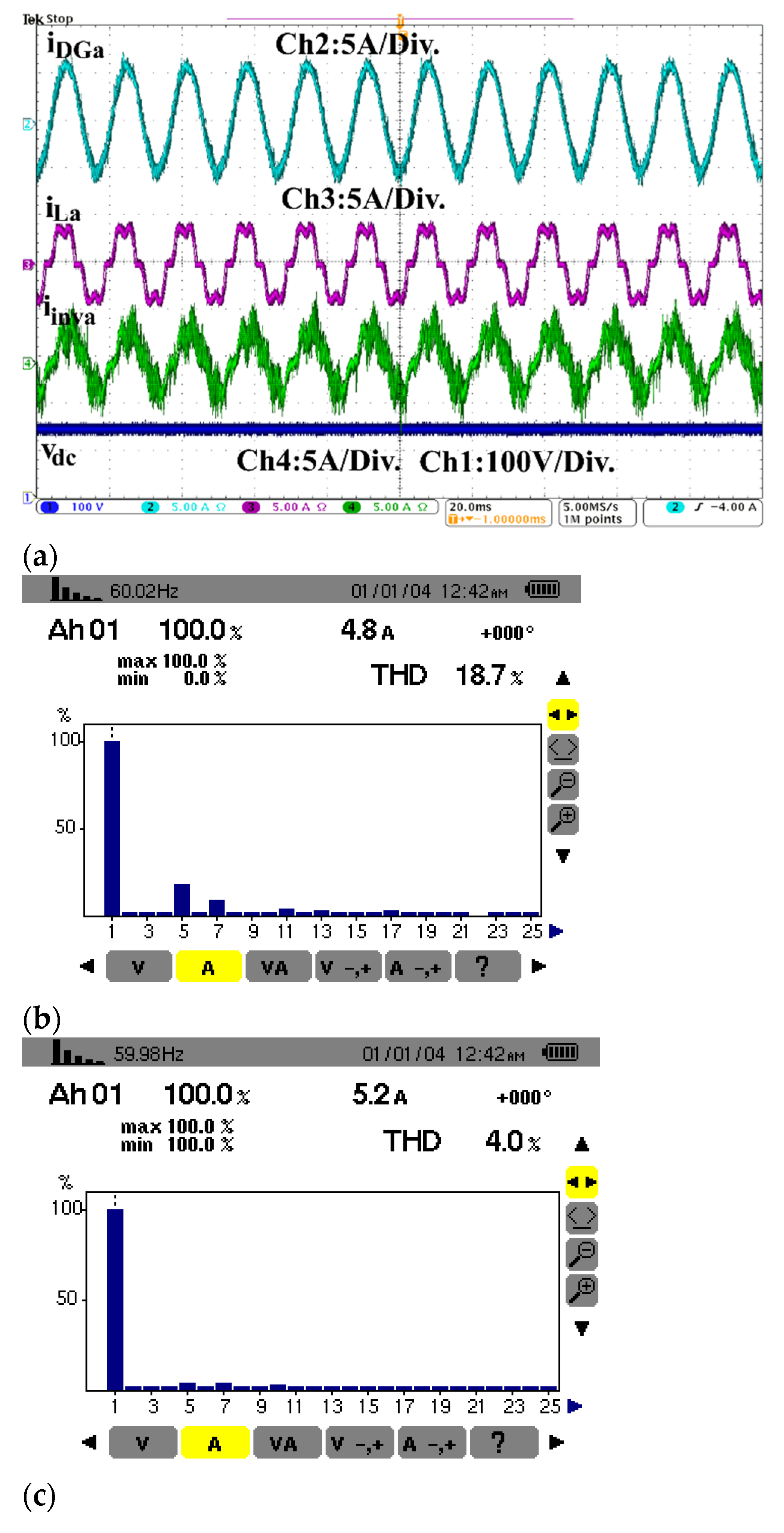
4.4. Performance at PCC under the Presence of Nonlinear Loads
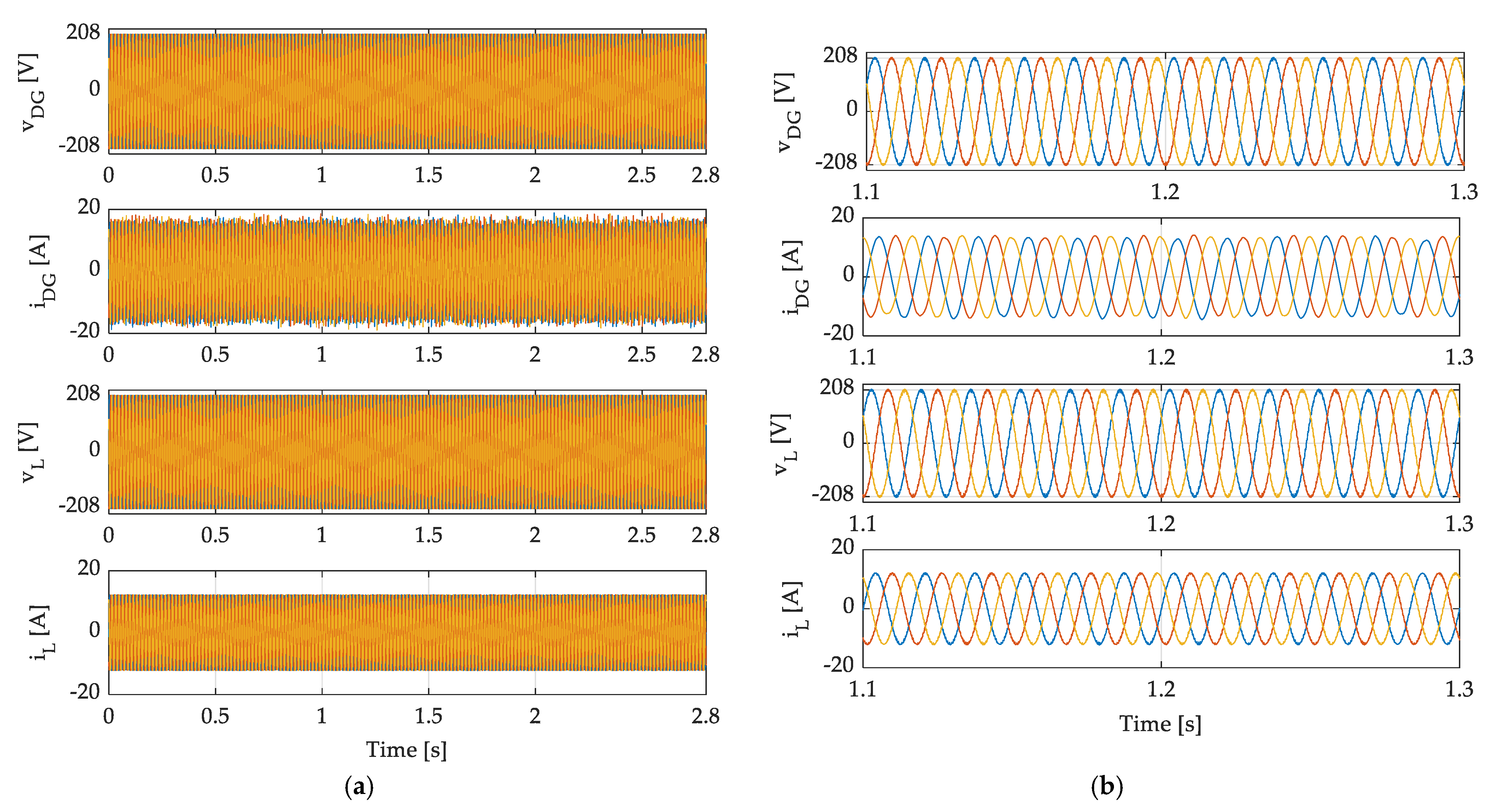
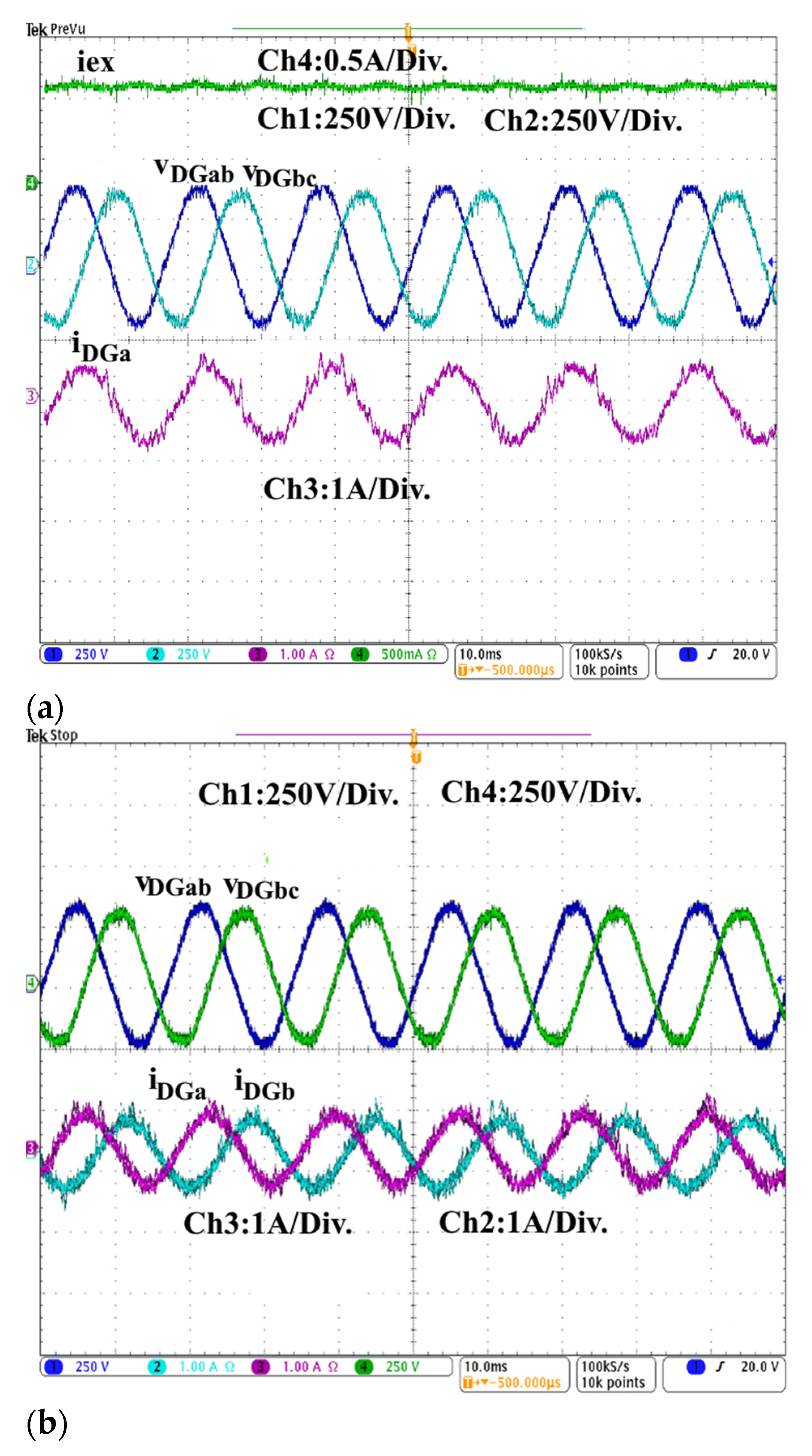
4.5. Experimental Results of the DG under the Presence of Linear Load
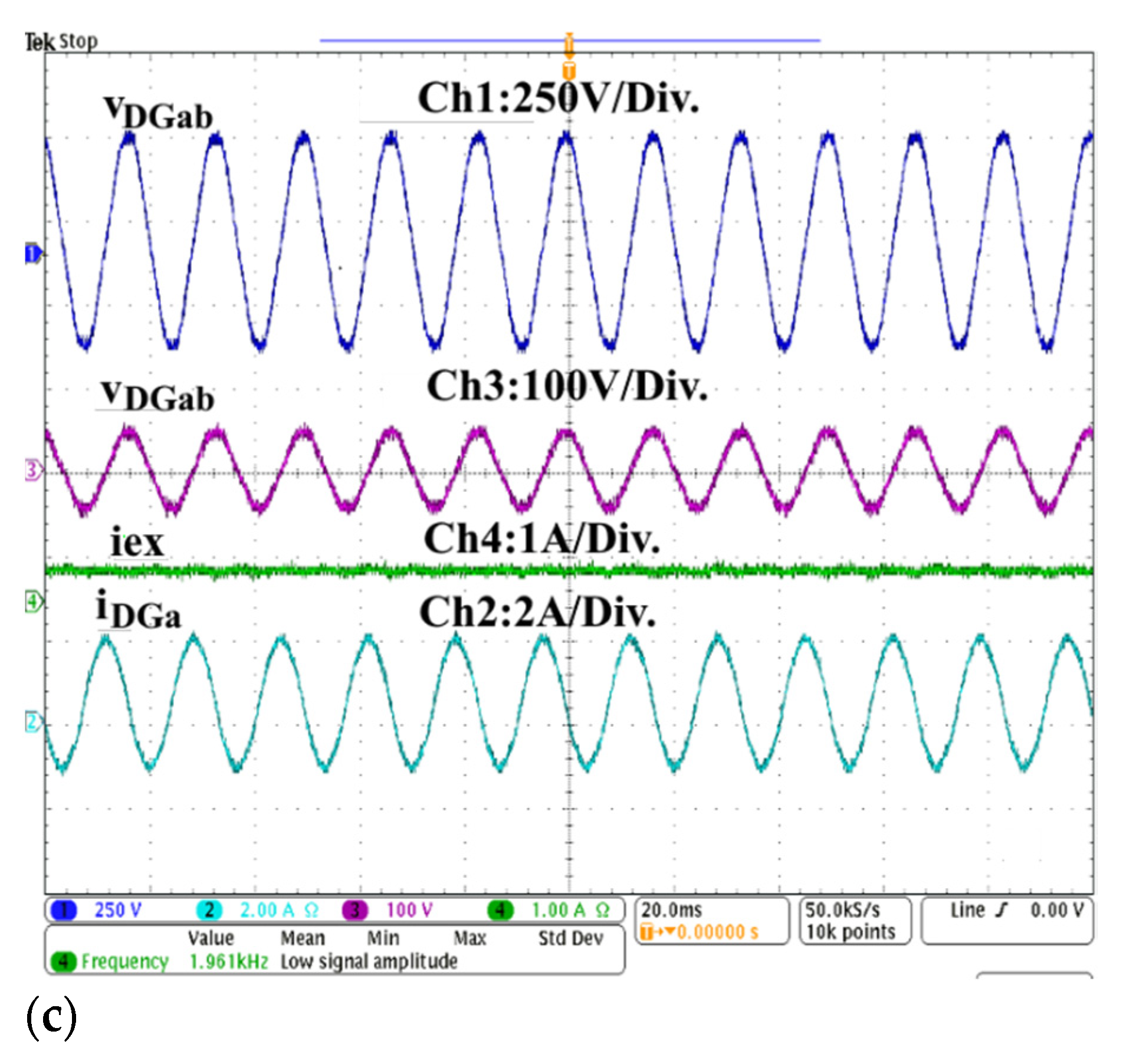
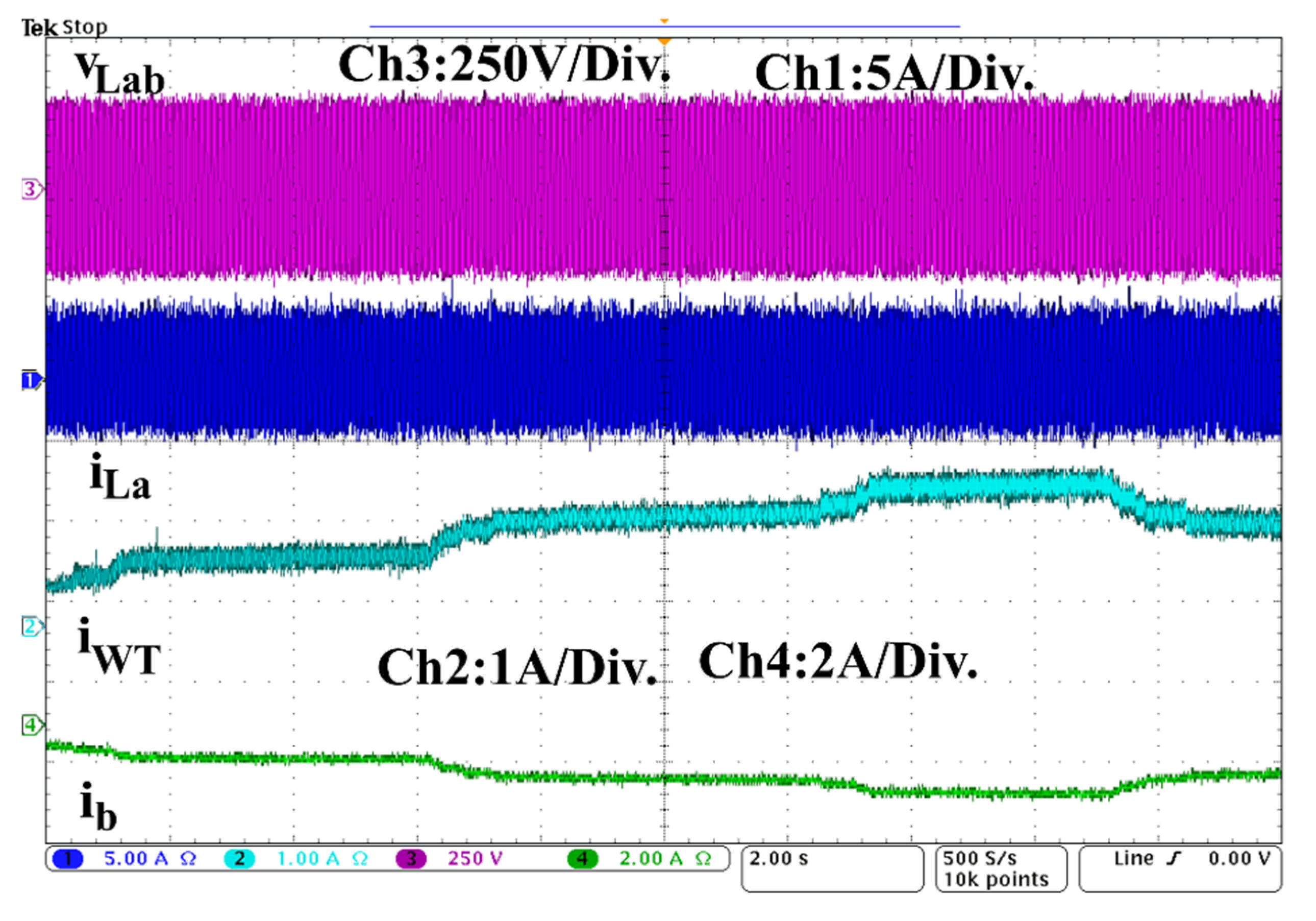
4.6. Performance under Load Variation and Presence of Linear Load
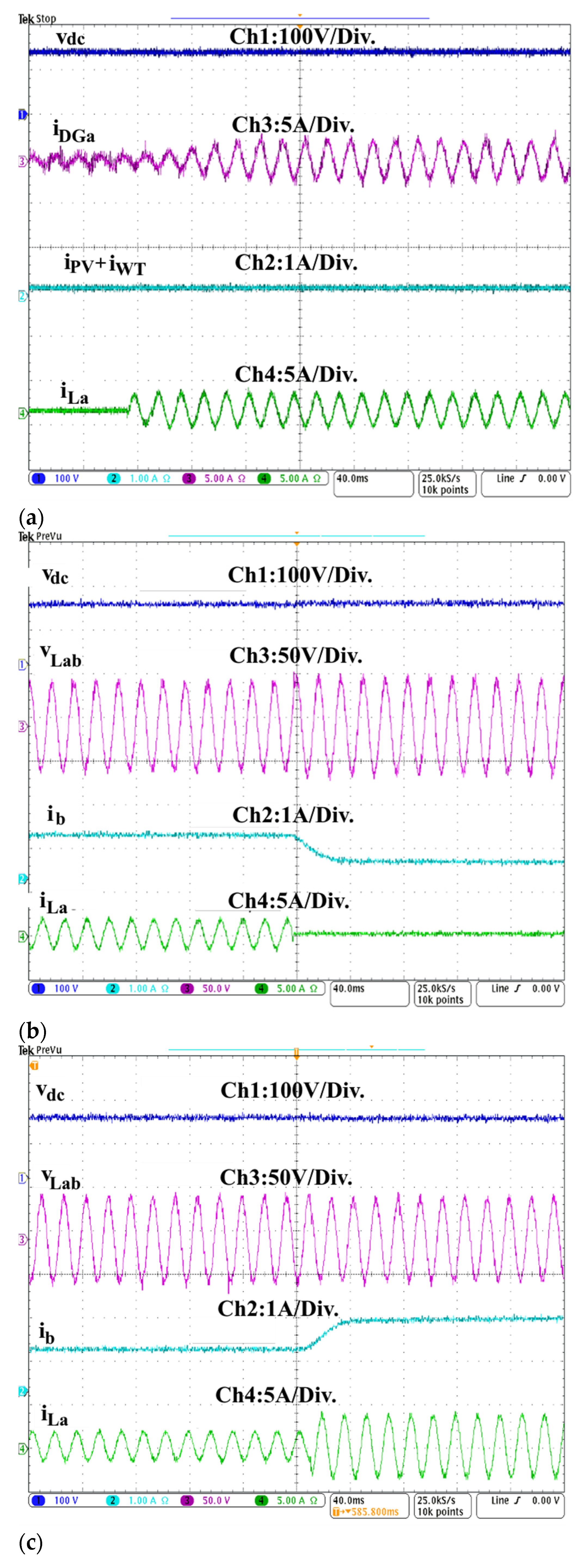
4.7. Performance in Presence of RC and RL Types Nonlinear Loads
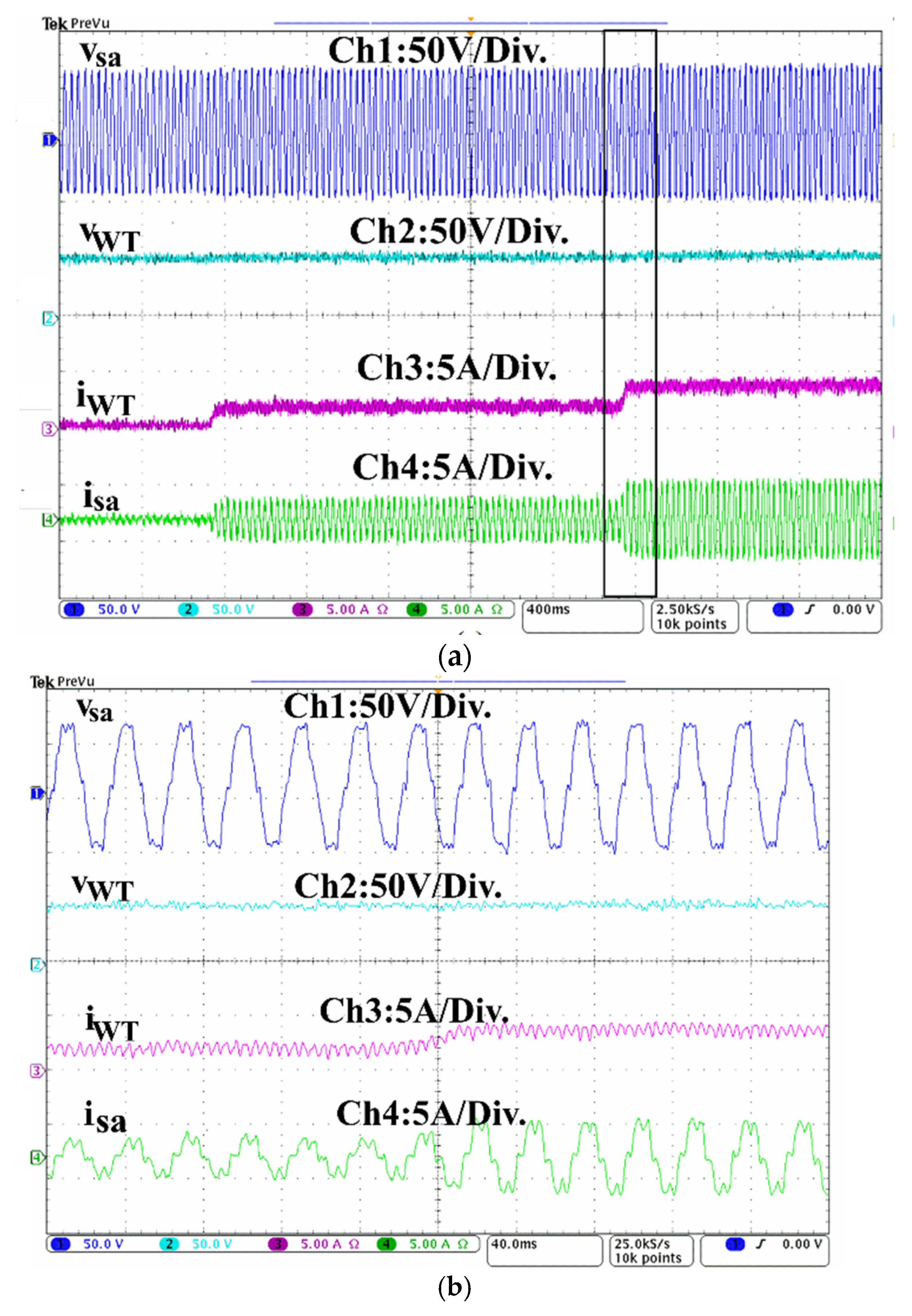
4.8. Performance of the WT at Wind Speed Change
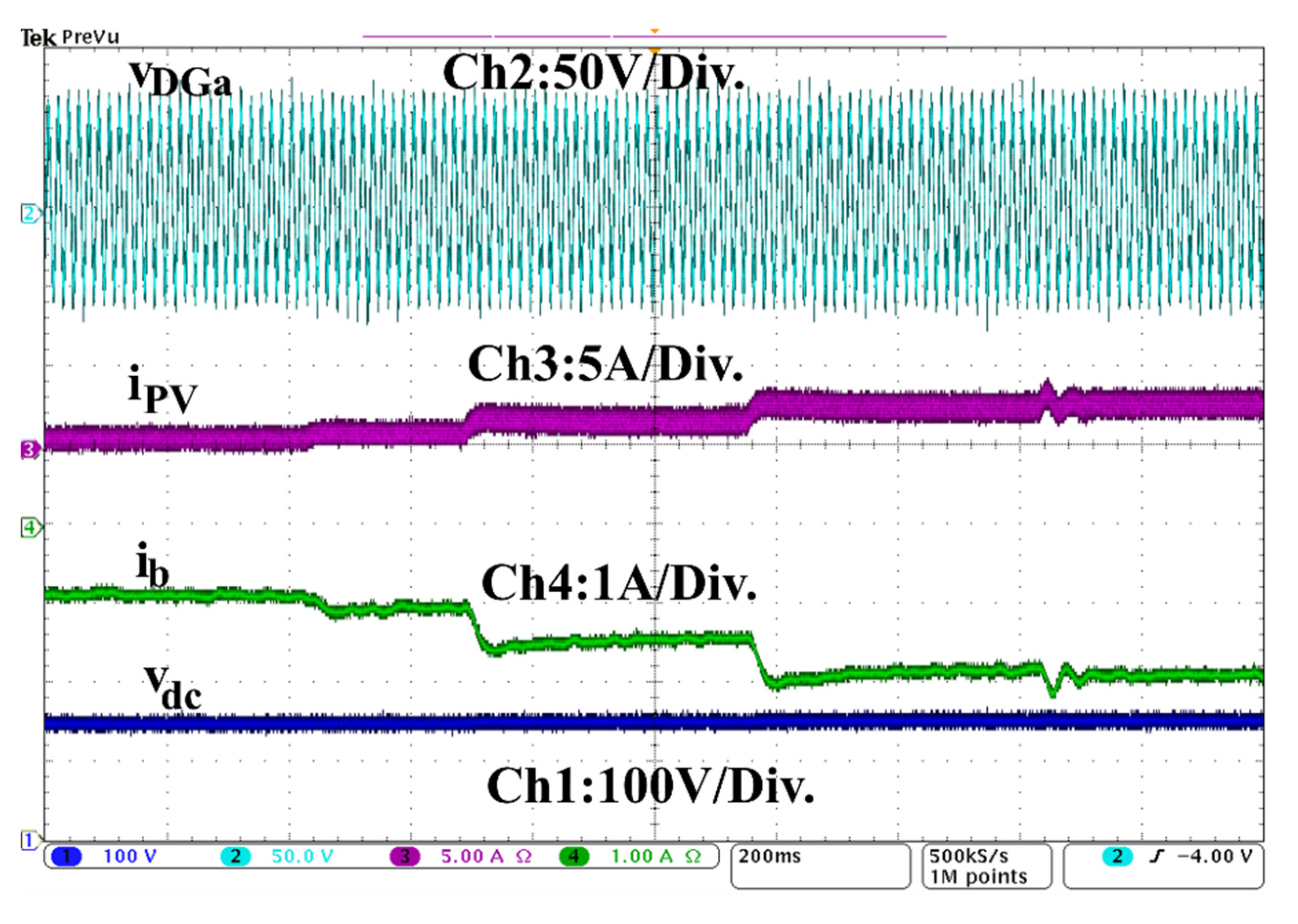
4.9. Performance of the PV Panel at Solar Irradiation Change
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Define Abbreviation
| Symbol | Description |
| WT | Wind turbine |
| PV | Photovoltaic array |
| ESS | Energy storage system |
| DG | Diesel generator |
| PMBLDCG | Permanent magnet brushless DC generator |
| isa, isb, and isc | Stator currents of the PMBLDCG |
| CWT | The capacitor at the output of the diode bridge |
| VWT | DC voltage of the WT |
| LWT | The inductor of the DC-DC boost converter for WT side |
| iWT | DC current of the WT |
| VPV | Output PV voltage |
| iPV | Output PV current |
| vb | Battery voltage |
| Lb | Inductor that connects the battery to the DC-DC buck-boost converter |
| Vdc | Common DC-link voltage |
| Vinva, Vinvb, and Vinvc | Output voltages of the interfacing inverter |
| iinva, iinvb, and iinvc | Output currents of the interfacing inverter |
| Vca, Vcb, and Vcc | Voltages of the output filter |
| Rc and CC | Resistance and capacitor of the output filter |
| icc | The current of the output filter |
| Linv and LDG | Inductors of the output filter |
| VLa, VLb, and VLc | Load voltages |
| iLa, iLb, and iLc | Load currents |
| iDGa, iDGb, and iDGc | Diesel generator currents |
| AVR | Automatic voltage regulator |
| DE | Diesel engine |
| P&O | Perturbation and observation technique |
| VWTmax | The maximum voltage obtained using the P&O technique |
| ΔVWT | Step of variation |
| VWT* | Reference DC voltage of the WT |
| ΔV | WT DC voltage error value |
| PI | Proportional integral regulator |
| iWT* | Reference DC current of the WT |
| ΔiWT | WT DC current error value |
| dWT | Control signal |
| S1 to S9 | Power electronic switches (insulated-gate bipolar transistor (IGBT)) of the power converters |
| PWM | Pulse-width modulation |
| Vdc* | Reference of the common DC-link voltage |
| ΔVdc | Error value of the common DC-link voltage |
| ib* | Reference battery current |
| Δ ib | Error value of battery current |
| db | Control signal |
| fs | System frequency |
| fs* | Reference of the system frequency |
| lLoss | losses of active power |
| d-q | Direct and quadrature axis |
| LPF | Low pass filter |
| PLL | Phased locked loop |
| ωt | Angular frequency |
| iDGa*, iDGb* and iDGc* | Reference of DG currents |
| G(s) | Transfer function of LCL filter |
References
- Hidalgo-Leon, R.; Amoroso, F.; Litardo, J.; Urquizo, J.; Torres, M.; Singh, P.; Soriano, G. Impact of the Reduction of Diesel Fuel Subsidy in the Design of an Off-Grid Hybrid Power System: A Case Study of the Bellavista Community in Ecuador. Energies 2021, 14, 1730. [Google Scholar] [CrossRef]
- Mokhtara, C.; Negrou, B.; Settou, N.; Settou, B.; Samy, M.M. Design optimization of off-grid Hybrid Renewable Energy Systems considering the effects of building energy performance and climate change: Case study of Algeria. Energy 2021, 219, 119605. [Google Scholar] [CrossRef]
- Dubuisson, F.; Rezkallah, M.; Ibrahim, H.; Chandra, A. Real-Time Implementation of the Predictive-Based Control with Bacterial Foraging Optimization Technique for Power Management in Standalone Microgrid Application. Energies 2021, 14, 1723. [Google Scholar] [CrossRef]
- Rezkallah, M.; Singh, S.; Chandra, A.; Singh, B.; Ibrahim, H. Off-Grid System Configurations for Coordinated Control of Renewable Energy Sources. Energies 2020, 13, 4950. [Google Scholar] [CrossRef]
- Rezkallah, M.; Chandra, A.; Singh, B.; Singh, S. Microgrid: Configurations, Control and Applications. IEEE Trans. Smart Grid 2017, 10, 1290–1302. [Google Scholar] [CrossRef]
- Sawle, Y.; Gupta, S.; Bohre, A.K. Review of hybrid renewable energy systems with comparative analysis of off-grid hybrid system. Renew. Sustain. Energy Rev. 2018, 81, 2217–2235. [Google Scholar] [CrossRef]
- Upadhyay, S.; Sharma, M. A review on configurations, control and sizing methodologies of hybrid energy systems. Renew. Sustain. Energy Rev. 2014, 38, 47–63. [Google Scholar] [CrossRef]
- Nehrir, M.H.; Wang, C.; Strunz, K.; Aki, H.; Ramakumar, R.; Bing, J.; Miao, Z.; Salameh, Z. A Review of Hybrid Renewable/Alternative Energy Systems for Electric Power Generation: Configurations, Control, and Applications. IEEE Trans. Sustain. Energy 2011, 2, 392–403. [Google Scholar] [CrossRef]
- Beleiu, H.G.; Maier, V.; Pavel, S.G.; Birou, I.; Pică, C.S.; Dărab, P.C. Harmonics Consequences on Drive Systems with Induction Motor. Appl. Sci. 2020, 10, 1528. [Google Scholar] [CrossRef] [Green Version]
- Rezkallah, M.; Chandra, A.; Ibrahim, H.; Singh, B. Implementation of Two-Level Control Coordinate for Seamless Transfer in Standalone Microgrid. In Proceedings of the 2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 29 September–3 October 2019; Volume 75, pp. 1–6. [Google Scholar] [CrossRef]
- Park, B.; Jaehyeong, L.; Hangkyu, Y.; Gilsoo, J. Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System. Energies 2021, 14, 2278. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd, A.M.R.; Muhammad, A.A.M.Z.; Mohamad, A.M.Z. Shunt active power filter: A review on phase synchronization control techniques. Electronics 2019, 8, 7. [Google Scholar] [CrossRef] [Green Version]
- Bielecka, A.; Wojciechowski, D. Stability Analysis of Shunt Active Power Filter with Predictive Closed-Loop Control of Supply Current. Energies 2021, 14, 2208. [Google Scholar] [CrossRef]
- Bhim, S.; Chandra, A.; Kamal, A.L.-H. Power Quality: Problems and Mitigation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Mehmood, S.; Qureshi, A.; Kristensen, A.S. Risk Mitigation of Poor Power Quality Issues of Standalone Wind Turbines: An Efficacy Study of Synchronous Reference Frame (SRF) Control. Energies 2020, 13, 4485. [Google Scholar] [CrossRef]
- Singh, B.; Sharma, S. SRF theory for voltage and frequency control of IAG based wind power generation. In Proceedings of the International Conference on Power Systems, Kharagpur, India, 27–29 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Naderipour, A.; Asuhaimi Mohd Zin, A.; Bin Habibuddin, M.H.; Miveh, M.R.; Guerrero, J.M. An improved synchronous reference frame current control strategy for a photovoltaic grid-connected inverter under unbalanced and nonlinear load conditions. PLoS ONE 2017, 12, e0164856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benhalima, S.; Miloud, R.; Chandra, A. Real-Time Implementation of Robust Control Strategies Based on Sliding Mode Control for Standalone Microgrids Supplying Non-Linear Loads. Energies 2018, 11, 2590. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Santos, O.; Urrego-Aponte, J.O.; Lezama, S.T.; Almansa-López, J.D. Control of the Bidirectional Buck-Boost Converter Operating in Boundary Conduction Mode to Provide Hold-Up Time Extension. Energies 2018, 11, 2560. [Google Scholar] [CrossRef] [Green Version]
- Ramos-Paja, C.A.; Bastidas-Rodríguez, J.D.; González, D.; Acevedo, S.; Peláez-Restrepo, J. Design and Control of a Buck–Boost Charger-Discharger for DC-Bus Regulation in Microgrids. Energies 2017, 10, 1847. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.Y.; Kim, H.J.; Kim, J.H.; Han, B.M. SoC-based output voltage control for BESS with a lithium-ion battery in a stand-alone DC microgrid. Energies 2016, 11, 924. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Kim, M.K.; Wen, H. Simulation and Analysis of Perturbation and Observation-Based Self-Adaptable Step Size Maximum Power Point Tracking Strategy with Low Power Loss for Photovoltaics. Energies 2018, 12, 92. [Google Scholar] [CrossRef] [Green Version]
- Rezkallah, M.; Hamadi, A.; Chandra, A.; Singh, B. Design and Implementation of Active Power Control With Improved P&O Method for Wind-PV-Battery-Based Standalone Generation System. IEEE Trans. Ind. Electron. 2017, 65, 5590–5600. [Google Scholar] [CrossRef]
- Jung, Y.; So, J.; Yu, G.; Choi, J. Improved perturbation and observation method (IP&O) of MPPT control for photovoltaic power systems. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 1788–1791. [Google Scholar]
- Gunasekaran, M.; Krishnasamy, V.; Selvam, S.; Almakhles, D.J.; Anglani, N. An Adaptive resistance perturbation based MPPT algorithm for Photovoltaic applications. IEEE Access 2020, 8, 1. [Google Scholar] [CrossRef]
- Pathak, G.; Singh, B.; Panigrahi, B.K. Isolated microgrid employing PMBLDCG for wind power generation and synchronous reluctance generator for DG system. In Proceedings of the 2014 IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–6. [Google Scholar]
- Sharma, R.; Singh, B. MDSOGI-FLL Control for SyRG-PMBLDCG-BES-PV Based Microgrid. In Proceedings of the IEEE Industrial and Commercial Power Systems Europe, Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Pathak, G.; Singh, B.; Panigrahi, B.K. Control of Wind-Diesel Microgrid Using Affine Projection-Like Algorithm. IEEE Trans. Ind. Inform. 2016, 12, 524–531. [Google Scholar] [CrossRef]
- Chen, Y.-M.Y.; Liu, C.S.; Hung, C.; Cheng, C.-S. Multi-input inverter for grid-connected hybrid PV/wind power system. IEEE Trans. Power Electron. 2007, 2, 1070–1077. [Google Scholar] [CrossRef]
- Chun, S.; Kwasinski, A. Analysis of classical root-finding methods applied to digital maximum power point tracking for sustainable photovoltaic energy generation. IEEE Trans. Power Electron. 2011, 26, 3730–3743. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Farakhor, A.; Haghighian, S.K. Novel algorithm of maximum power point tracking (MPPT) for variable speed PMSG wind generation systems through model predictive control. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2013; pp. 243–247. [Google Scholar]
- Rezkallah, M.; Chandra, A.; Saad, M.; Tremblay, M.; Singh, B.; Singh, S.; Ibrahim, H. Composite Control Strategy for a PV-Wind-Diesel based Off-Grid Power Generation System Supplying Unbalanced Non-Linear Loads. In Proceedings of the 2018 IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018; pp. 1–6. [Google Scholar]
- Rezkallah, M.; Chandra, A.; Saad, M.; Tremblay, M.; Singh, B.; Singh, S.; Ibrahim, H. Design and Implementation of Decentralized Control for Distributed generation based Off-grid System. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Bao, C.; Ruan, X.; Wang, X.; Li, W.; Pan, D.; Weng, K. Step-by-Step Controller Design for LCL-Type Grid-Connected Inverter with Capacitor–Current-Feedback Active-Damping. IEEE Trans. Power Electron. 2014, 29, 1239–1253. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, Y.; Duan, S.; Yin, J.; Liu, B.; Liu, F. Parameter Design of a Two-Current-Loop Controller Used in a Grid-Connected Inverter System with LCL Filter. IEEE Trans. Ind. Electron. 2009, 56, 4483–4491. [Google Scholar] [CrossRef]


| Mode | Conditions | ES | State of ESS |
|---|---|---|---|
| Mode1 | PPV + PWT + PDG < PL SoC% > 50% | WT, PV&DG | discharging |
| Mode2 | PPV + PWT + PDG > PL SoC% < 50% | WT, PV&DG | charging |
| Mode 3 | PPV + PWT + PDG > PL SoC% < 100% | WT, PV&DG | charging |
| Mode4 | SoC% = 100% Ppv + PWT + PDG > PL Ppv + PWT + PDG = PL | WT, PV&DG | Stop charging |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezkallah, M.; Ibrahim, H.; Dubuisson, F.; Chandra, A.; Singh, S.; Singh, B.; Issa, M. Hardware Implementation of Composite Control Strategy for Wind-PV-Battery Hybrid Off-Grid Power Generation System. Clean Technol. 2021, 3, 821-843. https://doi.org/10.3390/cleantechnol3040048
Rezkallah M, Ibrahim H, Dubuisson F, Chandra A, Singh S, Singh B, Issa M. Hardware Implementation of Composite Control Strategy for Wind-PV-Battery Hybrid Off-Grid Power Generation System. Clean Technologies. 2021; 3(4):821-843. https://doi.org/10.3390/cleantechnol3040048
Chicago/Turabian StyleRezkallah, Miloud, Hussein Ibrahim, Félix Dubuisson, Ambrish Chandra, Sanjeev Singh, Bhim Singh, and Mohamad Issa. 2021. "Hardware Implementation of Composite Control Strategy for Wind-PV-Battery Hybrid Off-Grid Power Generation System" Clean Technologies 3, no. 4: 821-843. https://doi.org/10.3390/cleantechnol3040048
APA StyleRezkallah, M., Ibrahim, H., Dubuisson, F., Chandra, A., Singh, S., Singh, B., & Issa, M. (2021). Hardware Implementation of Composite Control Strategy for Wind-PV-Battery Hybrid Off-Grid Power Generation System. Clean Technologies, 3(4), 821-843. https://doi.org/10.3390/cleantechnol3040048








