1. Introduction
Pet-coke is a carbon-rich and black-colored solid. It is mostly applied as a boiling and combusting fuel in power generation, and cement plants. Pet-coke is considered as a promising replacement for coal in power plants because of its higher heating value, carbon content, and low ash [
1]. The pet-coke produced by delayed cokers is an attractive source of energy due to its very high heating value (over 8500 kcal/kg) that stems from its high carbon (75–80% by weight) and low ash content (under 1%) [
2]. The refiner now decides to add petro-power and shifts production away from high sulfur fuel oil (HSFO) for producing pet-coke fuel [
2]. According to [
3], the coke yield produced by delayed coker is about 33%. Coke burns in several installations inside the refinery. For example, FCC (fluid catalytic cracking) regenerators have been employed for burning the coke-coated catalysts in order to restore catalytic activity and to supply the required heat flux for the cracking reactions in risers [
4].
Computational fluid dynamics (CFD) is considered a powerful tool for predicting the hydrodynamic properties and other characteristics of fluidized beds and other dense multiphase flows [
5].
CFD modeling is an important computational tool for steam reforming design. It includes physical and chemical models with detailed representation of the reformer geometry. It has powerful computational capabilities and visualization to deal with different geometry characteristics, transport equations, and boundary conditions.
Wilde and Froment [
6] have performed CFD computations on the zone-flow reactor. It is a tubular reactor, which contains two types of internals: a core type adjacent to the wall, and a casing type, both of which are coated with a thin layer of catalyst. This reactor is designed for higher energy efficiency and lower steam-to-carbon ratios in methane steam reforming. The CFD is based on the Reynolds-averaged Navier–Stokes (RANS) turbulence model. Convective and radiative heat transfer, detailed reaction kinetics including coking, intraparticle diffusion limitations, and the compressibility of the gas phase were considered in the CFD simulations. The 3D CFD simulations show a better performance of on zone-flow reactor compared to conventional fixed bed reactors in terms of conversion and coke formation. Lao et al. [
7] developed a CFD model of an industrial scale steam methane reforming tube. The numerical simulation was carried out by applying ANSYS software with realistic geometry characteristics to simulate the transport and chemical reactions phenomena occurring in catalyst packing. In the framework of their research, they evaluated different feedback control schemes to drive the area-weighted average hydrogen mole fraction measured at the reforming tube outlet to a desired set-point value area-weighted average hydrogen mole fraction under the influence of a tube-side feed supply disturbance. The CFD simulation results obtained for the closed-loop significantly improve the process dynamics compared to open-loop control.
In my opinion, this is the first work consisting of simulation of pet-coke combustion by using fire dynamics simulator (FDS) software coupled with thermal structural analysis of the burner ceiling lining (in order to verify that the burner lining can withstand the extreme service conditions of the burner) and a multiphysics computation of the methane steam reforming (MSR).
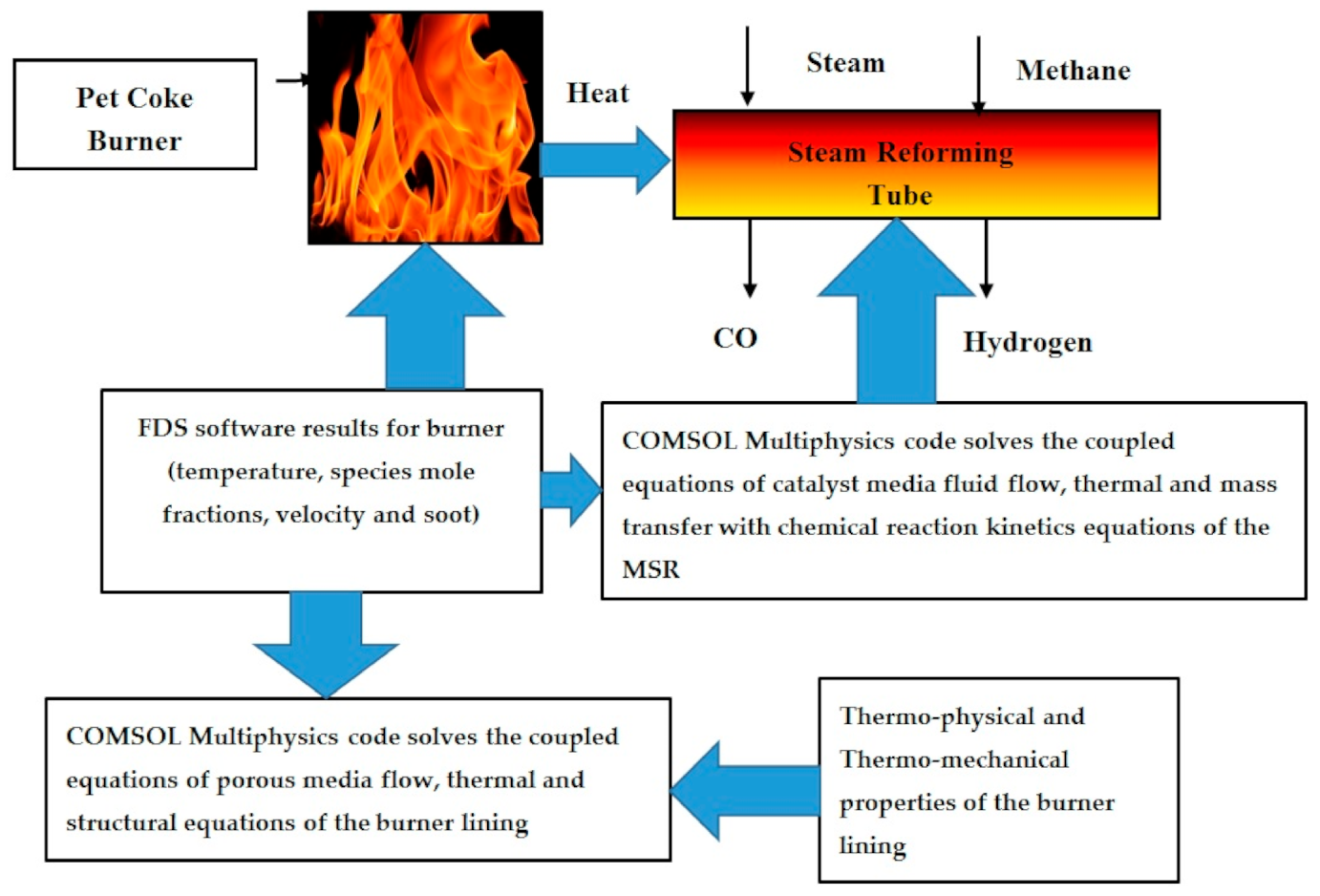
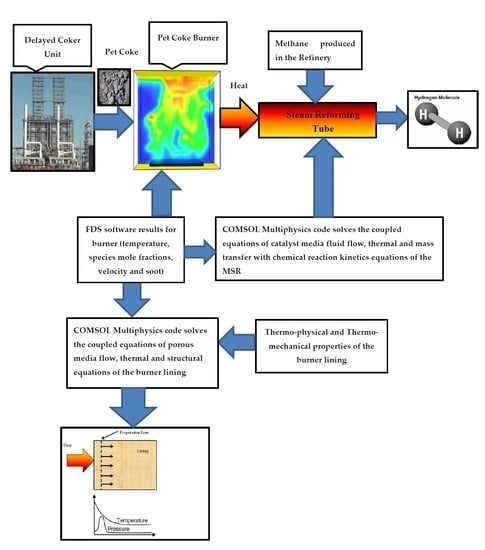
All the papers described above have hardly addressed the issue of structural integrity of the lining. The pet-coke linings rupture may release pollutants such carbon dioxide and soot particles to the atmosphere. By applying the heat loads obtained from FDS software, COMSOL multiphysics software has solved simultaneously the heat conduction equation, Darcy porous media steam flow equation, and structural mechanics equations for the concrete. The computational modeling of the methane steam reforming system is described schematically in
Figure 1.
The computational process algorithm of the pet-coke burner described in the bottom of
Figure 1 contains three components: simulation of coke flame carried out by using FDS simulation, multiphysics transient model which performs heat transfer, porous media flow (Darcy), and structural analyses of burner linings carried out by using COMSOL multiphysics software.
1.1. Mechanism of Methane Steam Reforming (MSR) Process
The major reactions that occur during the MSR process on Ni–Alumina catalyst are [
8]:
1.2. Refractory Lining System Failure
Refractories are used to withstand extreme temperature conditions. They are applied as heat-resistant linings to protect the walls from chemical decomposition, oxidation, and chemical and mechanical erosion [
9]. The main types are made from ceramic materials or brick. Intense heating of the burner lining will cause accumulation of steam inside the refractory lining that may not flow outside through the refractory lining. The accumulated steam trapped inside the lining causes explosive spallation. It should be noted that most ceramic materials are weak under tension and if the ultimate tensile strength (UTS) is locally exceeded, a crack will develop, often leading to the hot outer layer becoming detached from the remaining brick. This process is known as “spallation” [
10]. The process of buildup steam pressure inside the heated lining is illustrated in
Figure 2. As the concrete temperature increases, the moisture trapped inside the lining pores heats and evaporates, leading to further pressure loads on the lining. Under the pressure gradient, water vapor is transported both outwards and inwards in the concrete element. If the stress induced by the pressure gradient is higher than the strength of the concrete, the spallation occurs [
11].
2. Materials and Methods
2.1. Fire Dynamic Simulation (FDS) Modeling of the Pet-Coke Burner
The National Institutes of Standards and Technology (NIST) have developed this software [
12,
13]. It solves simultaneously the momentum transport equation, the equation of state, the energy equation, and the diffusion transport transient equations within each numerical grid cell. It is capable of computing the heat fluxes. This software is composed of three main components:
Hydrodynamic Model—the numerical solution of the momentum equation is carried out by applying large eddy simulation (LES) technique in most of the fire-driven turbulent flows (i.e., natural convection) simulation applications. It is suitable for low Mach numbers.
Combustion Model— FDS software employs two types of combustion models. The first model (default) uses the mixture fraction, a quantity representing the fuel and the products of combustion. The second model applies Arrhenius reaction parameters for individual gas species [
14].
Radiation Transport—FDS uses finite volume method (FVM) technique in order to solve the radiation transport equation (RTE) for a non-scattering gray gaseous mixture [
12].
The “smoke-view” postprocessor software was used in order to simulate the pet-coke burner combustion performance (temperatures and products mass fractions). The governing equations of FDS software are described in [
15].
2.2. FDS Modeling of the Combustor
The geometrical model of the pet-coke burner is shown in
Figure 3.
The height of the pet-coke burner is 4.0 m. The width and the length of the burner are 3 m and 2 m, respectively. The mesh size of the burner is 24,000 cells. At the side of the burner, coke particles are injected and ignited. Seven thermocouples, seven carbon dioxide, seven carbon monoxide, seven oxygen, and seven soot particles concentration sensors are placed inside the burner model.
Table 1 shows the thermocouples locations inside the burner (the coordinate system center is located at the center of the burner bottom plate; see
Figure 3).
According to [
16], the heat of combustion of coke is 38,379 (kJ/kg).
Initial condition—The initial temperature, species concentration in the air, and the pressure are:
Boundary Condition—the burner is opened to the atmosphere (the MSR tubes are exposed to the flame).
A comparison was carried out between the experimental and numerical results reported in [
17]. It was assumed that the mass flow rate of the pet-coke supply is about 3 tons/hour. The temperature of the air entering the burner was 20 °C (293.15 K) [
17].
2.3. Thermal and Structural Properties of the Burner Concrete Lining
It was assumed that the burner linings are made from two different types of concrete: fiber-reinforced carbonate aggregate concrete and fiber-reinforced siliceous aggregate concrete [
18]. The thermal and mechanical properties of steel fiber-reinforced concrete at elevated temperatures were applied. The thermal properties as a function of temperature were evaluated in the temperature range between 0 °C and 1000 °C [
18].
Figure 4 presents the thermal conductivities of the two kinds of concrete.
Figure 4 indicates that the thermal conductivities of the two concrete types decay with the temperature up to approximately 400 °C. The thermal conductivity of fiber-reinforced siliceous concrete is greater than the carbonate concrete because of the higher crystallinity of the siliceous aggregates as compared to that of the carbonate aggregate.
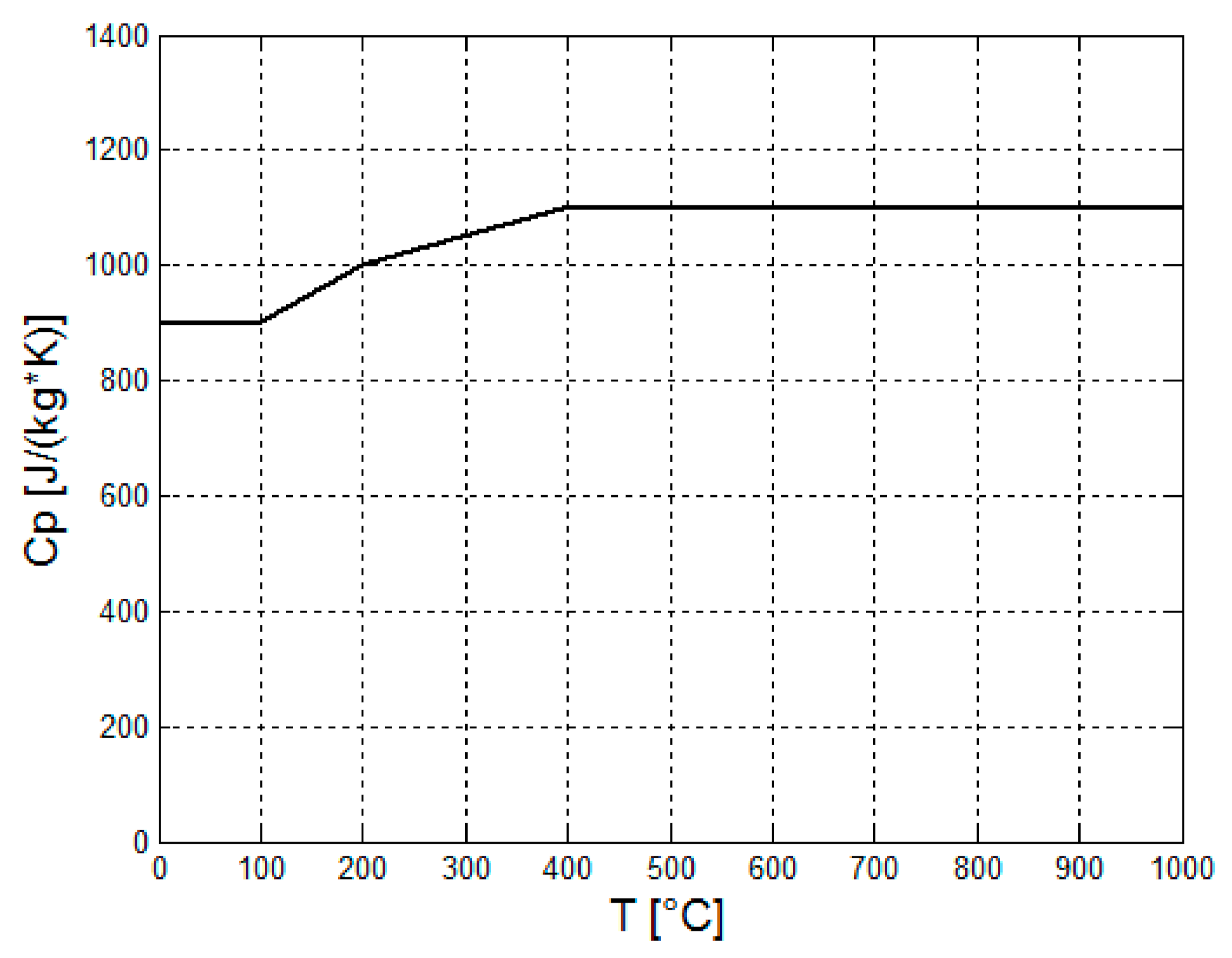
Figure 5 shows the typical graph of the heat capacity of concrete [
19].
Figure 5 shows that the heat capacity of concrete increases with the temperature up to 400 °C. In the temperature range of 400–1000 °C, the heat capacity remains almost constant. The presence of the steel fibers inside the concrete slightly affects the specific heat of the concrete.
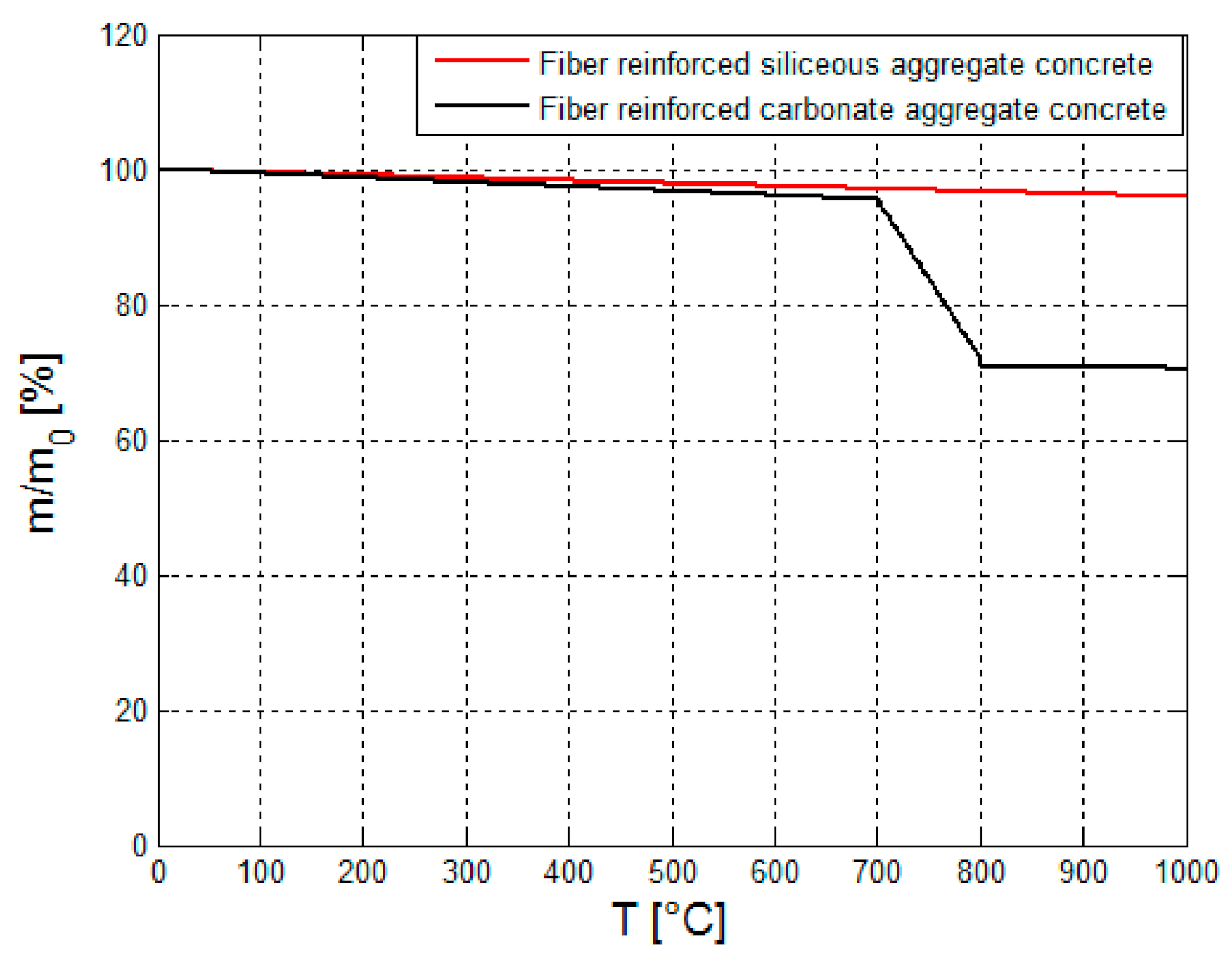
Figure 6 shows the mass loss of the two different types of concrete: fiber-reinforced carbonate aggregate concrete and fiber-reinforced siliceous aggregate concrete [
18].
As can be seen from
Figure 6, the mass loss of the two concrete types is negligible until about 600 °C. Above 600 °C, the mass of plain and fiber-reinforced carbonate aggregate concrete decays considerably. This is caused by thermal decomposition of the dolomite component in the concrete. Above 800 °C, the mass loss again gradually decays with temperature.
Figure 7 shows the coefficient of thermal expansion of the two different types of concrete: fiber-reinforced carbonate aggregate concrete and fiber-reinforced siliceous aggregate concrete [
18].
The thermal expansion of fiber-reinforced siliceous aggregate concrete increases with temperature up to about 600 °C and then remains constant. The CTE is increased considerably near 550 °C. This can be attributed to transformation of quartz in the siliceous aggregate. Above this temperature, the CTE of the fiber-reinforced carbonate concrete increases considerably more than the CTE of the siliceous concrete. This steep increase of CTE with temperature can be caused by the presence of the steel fibers which expand at a growing rate [
18]. The stress–strain curves are shown in
Figure 8.
As can be seen from
Figure 8, the compressive strength tends to decrease at elevated temperatures. The thermophysical and thermomechanical properties shown in
Figure 4,
Figure 5,
Figure 6 and
Figure 7 indicate that the steel fibers have a minor influence on the thermal properties of the concretes. The influence on the mechanical properties is relatively greater and is expected to contribute to the flame resistance of the fiber-reinforced concrete. The porosity,
φ, and permeability,
κ, of both kinds of concrete used in the calculation of COMSOL are shown in
Table 2 [
20].
2.4. Multiphysics Analysis of the Concrete Lining
2.4.1. Porous Media Flow—Concrete Lining
The accumulated steam flows through the lining. It is described by using Darcy’s Law [
21,
22]:
The steam density is represented by
in dimensions of (kg/m
3). The steam viscosity is represented by
in dimensions of (Pa·s).
is the permeability of the porous concrete medium (m
2).
is the pressure of the steam trapped inside the concrete lining (Pa). All the concrete lining boundaries are impervious, corresponding to the condition:
2.4.2. Energy Transport—Concrete Lining
The conduction heat transfer equation inside the concrete lining is [
21,
22]:
In the above equations, the subscript “conc” denotes the concrete lining. Furthermore,
is the temperature in K, and
is the thermal conductivity of the concrete lining in w/(m·K). It is assumed that the left side of the concrete lining is exposed to radiative and convective heat flux.
where
denotes the convective coefficient, and
denotes the flame temperature produced by the coke combustion,
is the emissivity, and
is the Stefan–Boltzmann constant.
2.5. Multiphysics Analysis of the MSR
The methane steam reformer (MSR) is analyzed numerically in the section.
Figure 9 presents the geometrical model of the MSR.
The MSR contains catalyst material and steel casing. The reformer radius is 0.2 m, and its height is 0.5 m. The steel tube thickness is 0.01 m. The steam chemical reforming reactions occur in an MSR catalytic reactor. Heat is transferred to the MSR by using pet-coke burner in order to provide the necessary endothermal steam reforming reaction. A mixture of methane and steam enters into the MSR catalytic reactor. COMSOL multiphysics solves simultaneously the Darcy fluid flow, heat transfer with endothermic chemical reactions, and mass transfer equations with terms of chemical reaction kinetics (Arrhenius equation).
2.5.1. Model Kinetics of the MSR
The steam and methane react to form CO and H
2 in the MSR:
The kinetic rate of the MSR reaction is calculated by applying Equation (6) [
23]:
The frequency factor is (represented by
A) is 1.2 × 10
17 (1/s). The activation energy (represented by
E) is 223,070 (kJ/mole) [
24].
2.5.2. Porous Media Fluid Flow inside the MSR
The flow of the gaseous mixture of the methane and steam is described by Darcy’s Law:
where
denotes the gaseous mixture density (kg/m
3), and
is the viscosity of the gaseous mixture in (Pa·s). The term
is the permeability of the MSR bed (m
2).
represents the pressure inside the reformer bed (Pa). The other boundaries are impervious:
2.5.3. Heat Transfer of Equation inside the MSR
The heat transfer equation is applied to describe the temperature field inside the catalyst bed:
The equivalent heat capacity of the MSR is calculated by:
The subscripts “
s” and “
f” represent solid and fluid phases, respectively. The term
ε represents the volume fraction of the fluid phase.
is the temperature (K) and
is the thermal conductivity of the MSR catalyst bed in w/(m·K).
Q is the thermal source (w/m
3), and
u is the fluid velocity field (m/s) of the mixture inside the MSR. It is assumed that the MSR is homogeneous and isotropic. The steady-state heat transfer conduction equation becomes:
The MSR reaction volumetric heat source is calculated by the following equation:
Here,
r represents the MSR reaction rate. The enthalpy of reforming reaction is:
[
25]. Since there are no chemical reactions taking place in the steel tube, the heat conduction equation reduces to:
where
is the steel thermal conductivity. The temperature of the entering gaseous mixture is 1000 K at the inlet. The convective heat transport is dominant at the outlet:
The thermophysical properties of the reformer are presented in
Table 3 [
7].
2.5.4. Mass Transport of the MSR Bed
The Maxwell–Stefan diffusion and convection equation (mass balance) at steady state condition is:
Here, denotes the density (kg/m3), is the mass fraction of species i, is the mole fraction of component j, is the ij component diffusion coefficient (m2/s), is the generalized thermal diffusion coefficient (kg/(m·s)), and is the reforming reaction rate in (kg/(m3·s)).
2.5.5. Computation of the Species Diffusion Coefficients
The diffusion coefficients of the components,
, are obtained by Chapman–Enskog theory [
26]:
is the Lennard–Jones collision diameter.
is the collision integral between molecule
i and molecule
j. The collision diameter is calculated by
and
is calculated by [
27]:
denotes the dimensionless temperature. The term
denotes the maximum attractive energy between the molecule
i and
j. The numerical values of
and
for each component are described in detail in [
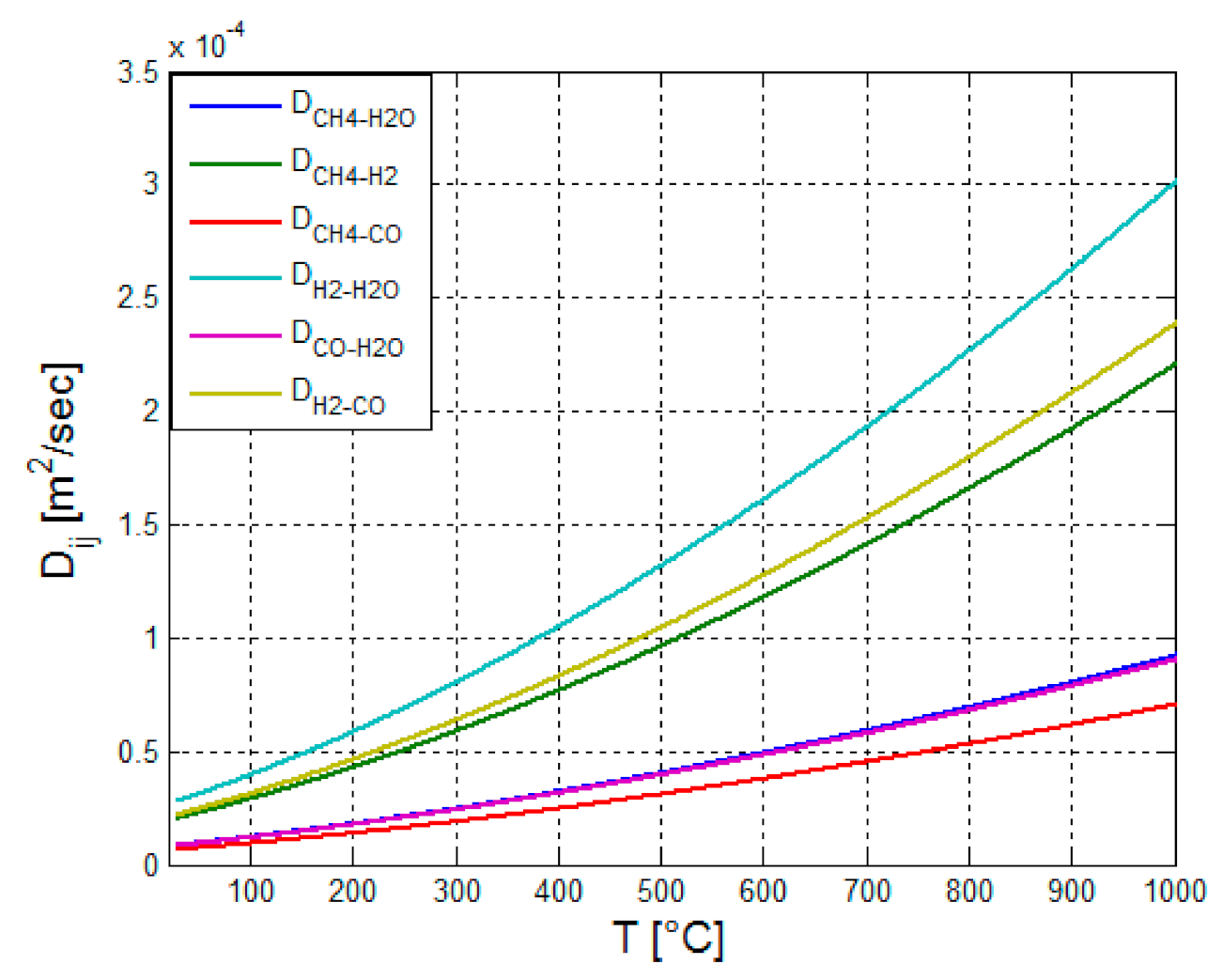
28]. The binary diffusion coefficients are shown in
Figure 10.
According to
Figure 10, the species diffusion coefficient increases with the temperature.
2.6. Computation Process of the Pet-coke Burner
The computational process is described in
Figure 11. The calculation process is composed of three parts: computation of the temperatures and species mass fractions by using FDS software, loading the thermo-physical and thermo-structural properties of the concrete, and finally solving the heat transfer, and structural equations for the burner ceiling by using COMSOL software [
21].
3. Results
The results section is divided into three parts. The thermal results of FDS code are described in
Section 3.1. The multiphysics results (temperature and mass fractions of the species) for MSR are described in
Section 3.3.
3.1. Fire Dynamics Simulator Software Results for Burner
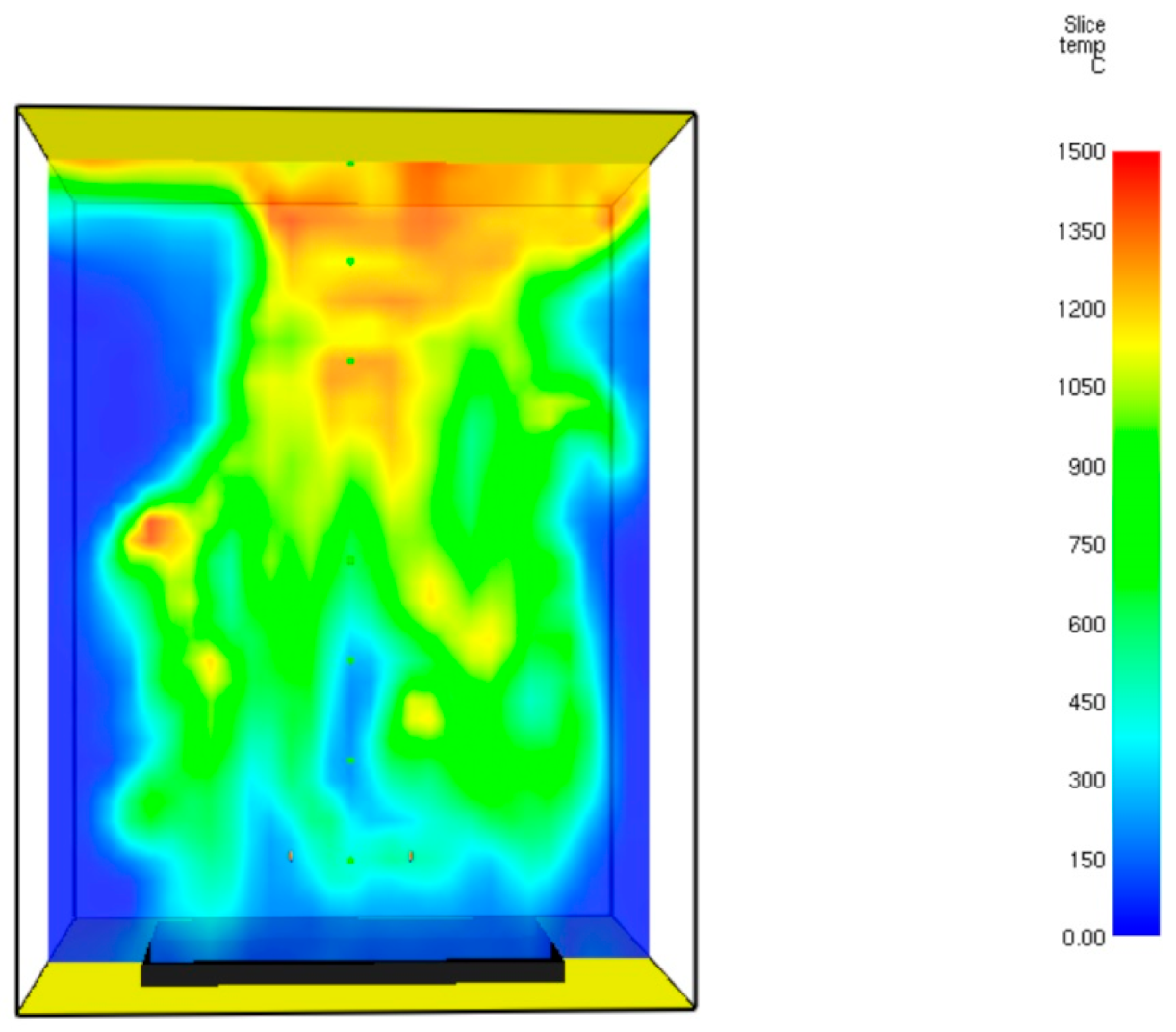
This section provides the results of FDS simulation regarding the coke burner, including the gas velocity, the mixture temperature, heat release rate, and carbon dioxide mole fractions. The temperature field at
t = 60.7 s is presented in
Figure 12.
It can be seen from this figure that the maximal temperature at time = 60.7 s reaches 1440 °C. A similar value was reported in [
18]. The temperature of the gaseous mixture tends to increase at the top of the burner. The calculated temperature at the bottom region of the burner is close to 700 °C. A similar temperature was reported in Ahmed and Ateya [
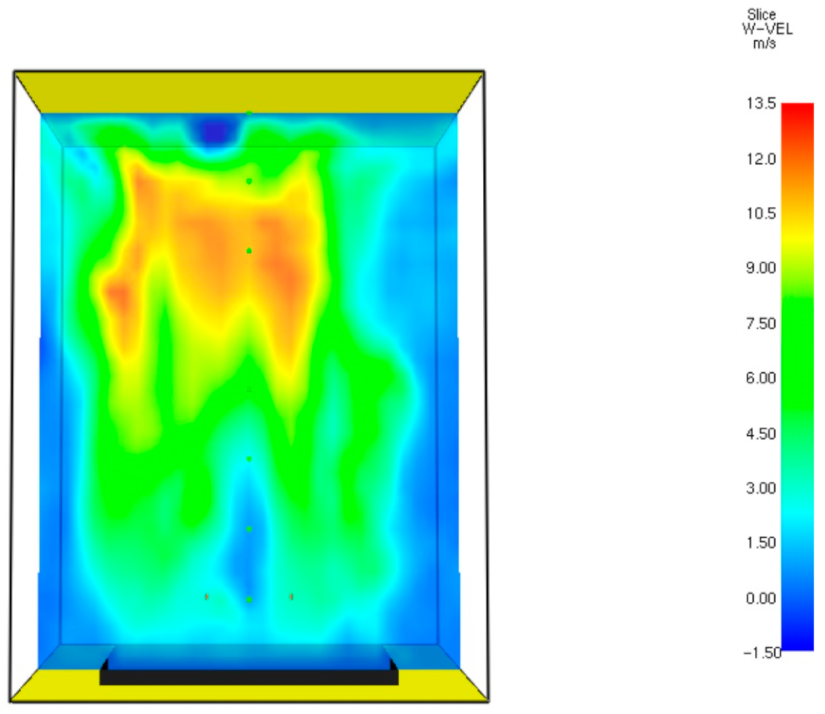
29]. The velocity field of the gaseous mixture at time of t = 60.7 s is presented in
Figure 13.
Figure 13 shows that flue gases flow upwards. This movement is caused by buoyancy. As can be seen from
Figure 10 and
Figure 11, the temperature and velocity of the gaseous mixture tend to be higher in close proximity to the ceiling. The combination of these physical phenomena increases the convective and radiative heat fluxes to the ceiling lining. Thermal stresses are usually generated by temperature distributions caused by the combustion or by generation of heat by internal thermal sources such as joule dissipation [
30]. The temperature gradient leads to thermal expansion. The sharp temperature gradient inside the concrete ceiling lining enhances the thermal stresses.
Figure 14 shows the heat release rate (HRR). Seven soot concentration sensors and thermocouples were positioned at different heights (shown in
Table 1) inside the burner model.
Figure 15 shows the temperature readings of the three thermocouples (TC1, TC4, and TC7).
According to
Figure 15, the temperature readings which are shown by TC1 are much lower than the temperature readings of TC4 and TC7. This is because the hot gaseous mixture tends to concentrate near the burner ceiling because of the buoyancy forces. The maximal temperature obtained from TC7 reading is about 1440 °C. The calculated temperature is similar to the temperature reported in [
18], which is also close to 1400 °C.
Figure 16 shows the carbon dioxide mole fraction readings of the three sensors (CO2-1, CO2-4, and CO2-7).
Figure 16 indicates that the mole fraction readings shown by CO2-1 are much lower than the mole fraction readings obtained by CO2-4 and CO2-7 sensors. This is because the oxidation reactions taking place between the coke particles and the oxygen increases with higher temperatures. The oxidation reactions are governed by the Arrhenius rate equations. The maximal carbon dioxide mole fraction obtained from CO2-7 reading is 15.0%. The calculated carbon dioxide mole fraction is similar to the carbon dioxide mole fractions reported in [
31,
32] which are 14.5% and 13.6%, respectively.
Grid Sensitivity Study Results
In order to verify the CFD numerical results, a grid sensitivity study was carried out on the FDS model developed in this work. An additional FDS model was developed, containing 36,000 cells. The average temperature was calculated by performing numerical integration over the time. The difference between the average temperatures obtained by applying different meshes are shown in
Table 4.
The difference between the average temperatures obtained by applying different meshes is less than 8%.
3.2. Thermomechanical Analysis Results for Burner Ceiling Lining
A thermomechanical analysis was carried out in order to evaluate the von Mises stresses inside the concrete. It is assumed that the convective coefficient of gaseous mixture is 25.0 W/(m
2·K) [
33].
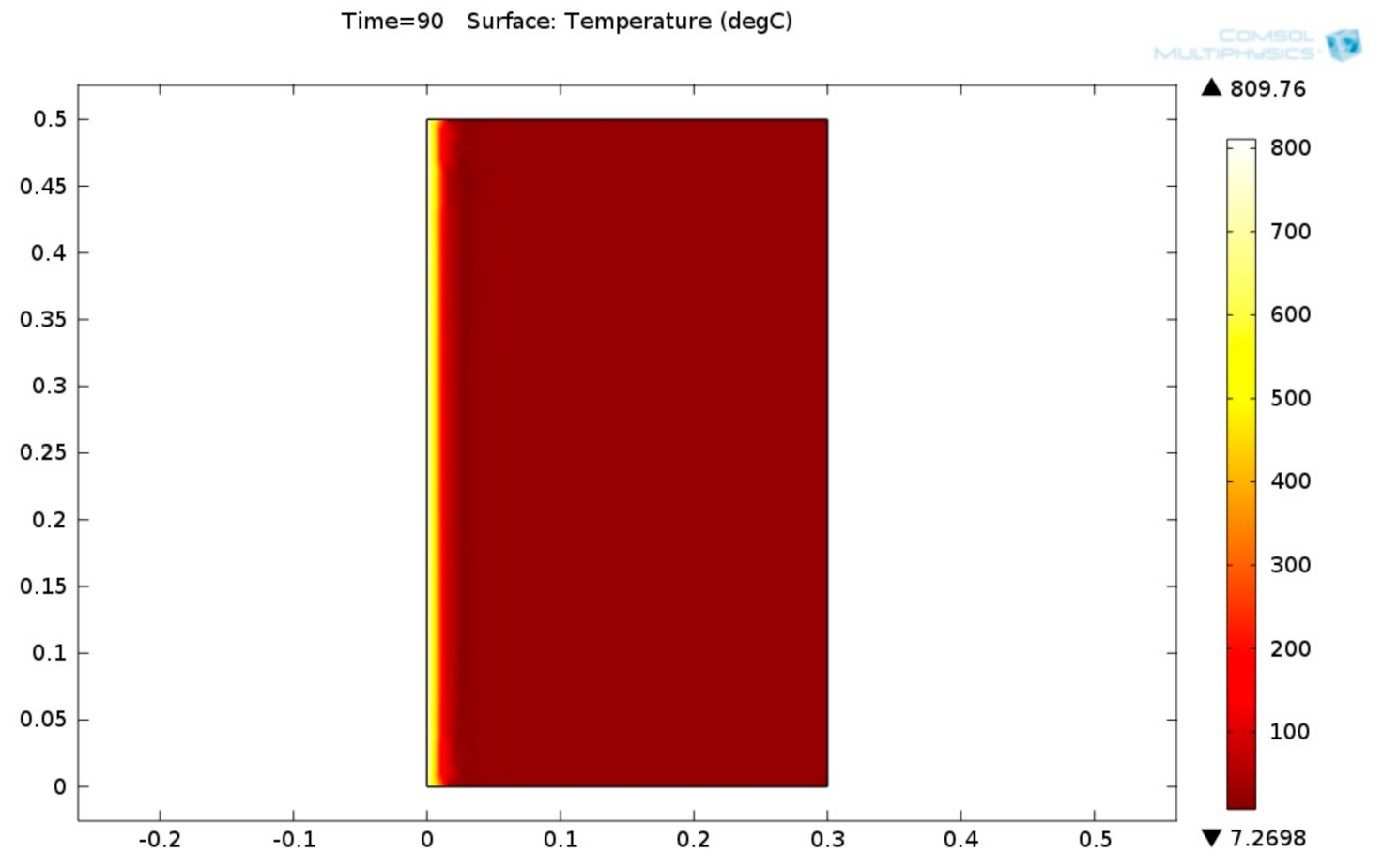
Figure 17 shows the 2D temperature field inside the fiber-reinforced carbonate aggregate concrete lining.
From
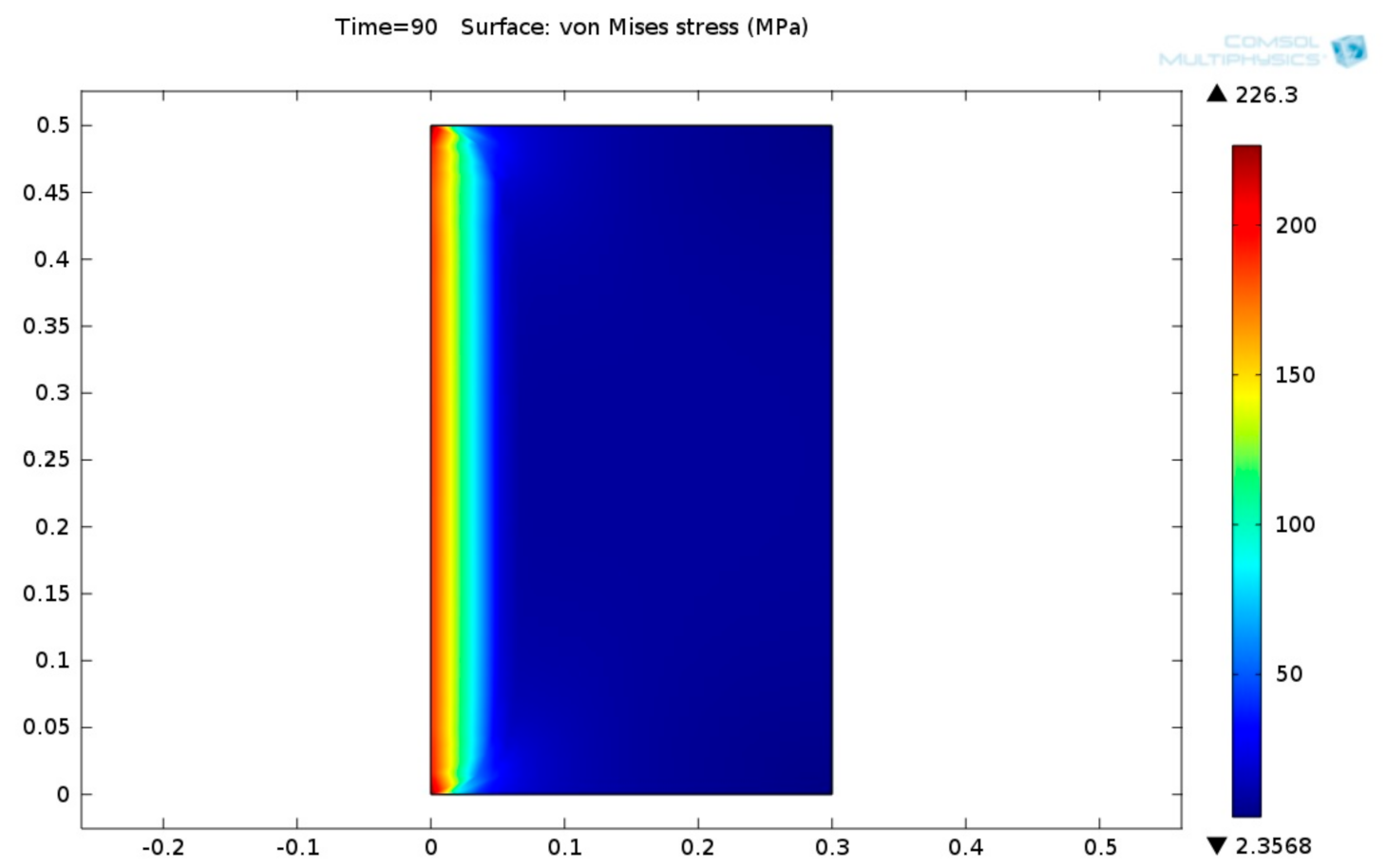
Figure 17, it can be seen that the temperature gradient inside the fiber-reinforced carbonate aggregate concrete is high. This is because the thermal conductivity of this kind of concrete is low. The 2D von Mises stress distribution of burner fiber-reinforced carbonate aggregate concrete lining is shown in
Figure 18.
Figure 18 indicates that the maximal stress reaches 226.3 MPa. These stresses are concentrated at the very narrow zone at the left side of the concrete ceiling lining. The von Mises stress decreases with the concrete thickness. Similar calculations were carried out on fiber-reinforced siliceous aggregate concrete linings. It was found that the maximal temperature obtained in the case of applying siliceous aggregate concrete is lower than carbonate aggregate concrete. This is because the thermal conductivity of siliceous aggregate concrete is greater than the thermal conductivity of carbonate aggregate concrete (see
Figure 4). The maximal stress reaches 217.06 MPa. These stresses are concentrated at the very narrow zone at the left side of the concrete ceiling lining. The von Mises stress decreases along the concrete depth.
3.3. Multiphysics Results for MSR
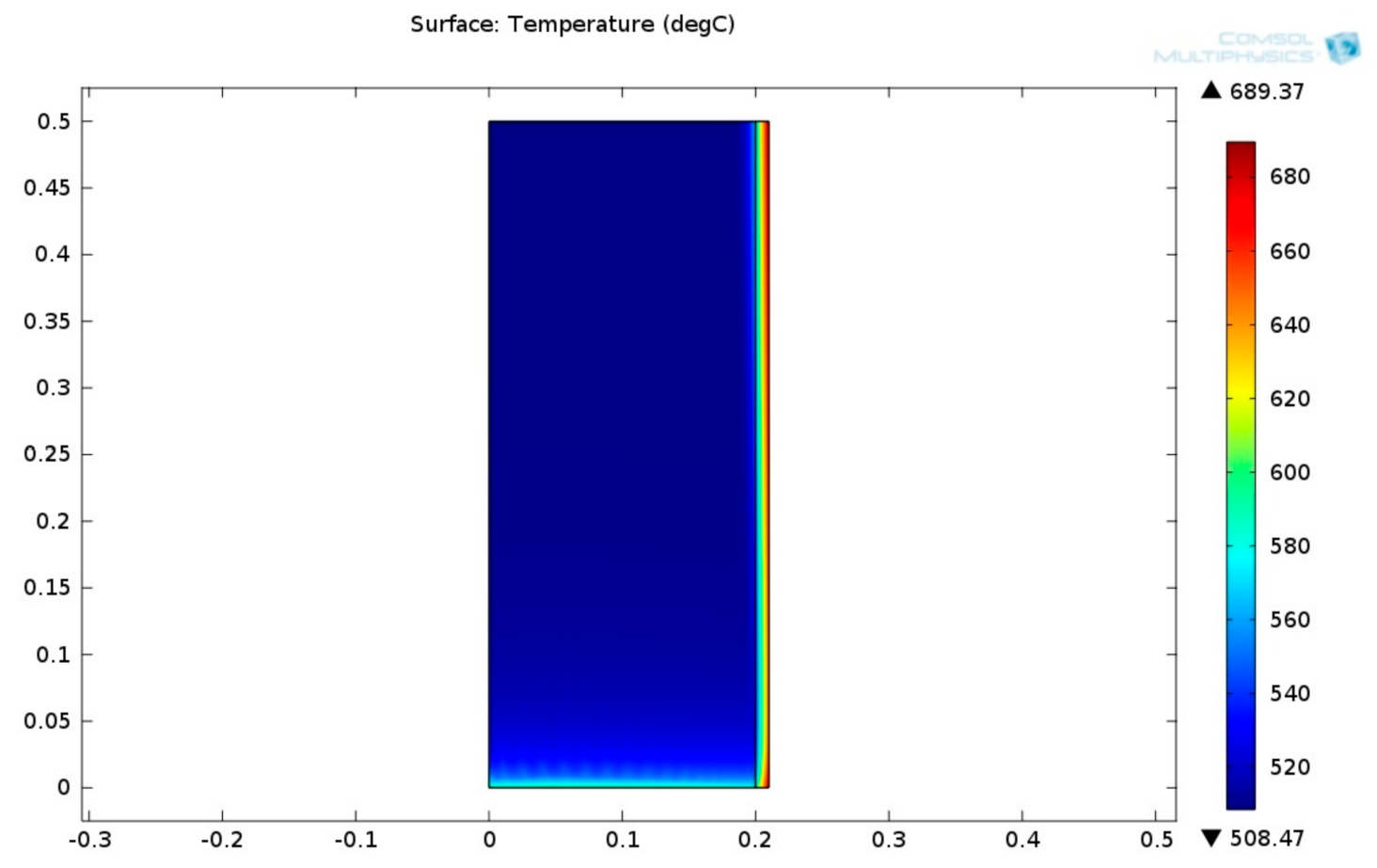
Figure 19 shows the 2D plot of temperature field inside the MSR.
Figure 19 shows that the temperature decays along the MSR height. The temperature of the steel tube is greater than the temperature of the MSR. This phenomenon may be attributed to by three major factors: Firstly, the thermal conductivity of the catalyst is smaller than the steel tube; secondly, the endothermic reactions taking place at the MSR are endothermic and consume the heat; and thirdly, the MSR bed is thicker than the steel casing.
Figure 20 shows the values mass fractions of the components (methane, CO, and H
2O) along the reformer height. The temperature inside the MSR is about 510 °C.
The mass fractions of the reactants (methane and steam) decrease with reformer height. The methane conversion is about 27%. The amounts of methane and the steam are proportional to each other (see Equation (5)). Similar results have been obtained in references [
34,
35]. The results obtained here indicate that heat released by the pet-coke burner provides the necessary heat for performing the endothermic MSR chemical reactions.
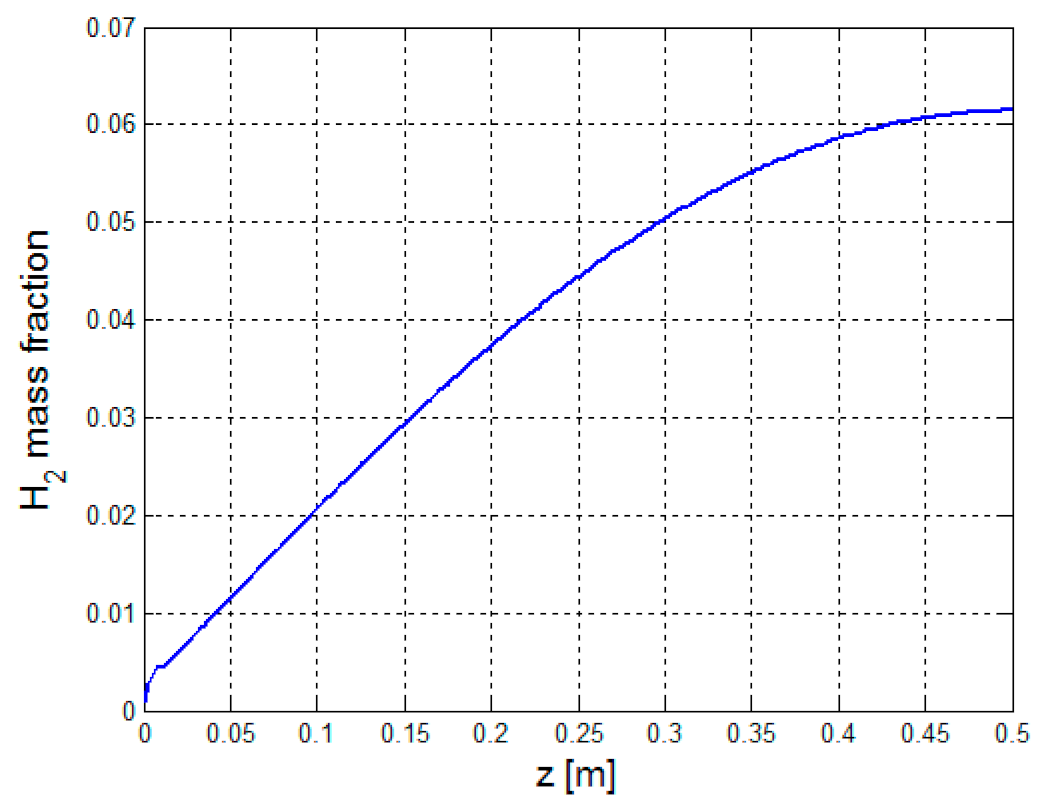
Figure 21 presents the mass fraction of hydrogen along the reformer height.
The hydrogen mass fraction increases considerably with the reformer height, as shown in
Figure 21. It is increased by 98.4%.
3.4. Verification and Validation of the Multiphysics Results for the MSR
The profile of the hydrogen mass fraction shown in this figure is similar to the profile to the hydrogen partial pressure graph (the partial pressure of the hydrogen is a linear function of the mass fraction) shown in [
35]. According to the graphs shown in
Figure 20 and
Figure 21, the methane, steam, hydrogen, and carbon monoxide mass fraction at the upper edge of the MSR are: 0.440, 0.218, 0.062, and 0.28, respectively. The sum of these mass fractions is 1, as expected according to the mass conservation law.
4. Discussion
Multiphysics design of a pet-coke burner and methane steam reforming (MSR) system was carried out in this work. The heat needed for operating the MSR was supplied by using a petroleum coke burner. Pet-coke (petroleum coke) is a black-colored and carbon-rich solid. Pet-coke is produced by delayed cokers. It is an attractive source of energy due to its very high heating value (over 8500 kcal/kg) that stems from its high carbon (75–80% by weight) and low ash content (under 1%). According to the literature, the coke yield produced by delayed coker is about 33%. Coke burns in several installations inside the refinery.
A computational fluid dynamics (CFD) simulation algorithm of pet-coke burner was developed in this work. The proposed computational algorithm includes simulation of a pet-coke burner by using FDS software, and structural analysis of the burner ceiling lining by coupling the solutions of heat conduction equation, Darcy porous media flow equation, and structural mechanics equation. In order to validate the gaseous temperature and carbon dioxide mole fraction obtained by FDS calculation, a comparison was carried out with the literature results. The maximal temperature obtained in the numerical combustion analysis is about 1440 °C. The calculated temperature is similar to the temperature reported in the literature. The maximal carbon dioxide mole fraction obtained in this work is 15.0%. The calculated carbon dioxide mole fraction is similar to the carbon dioxide mole fraction reported in the literature, which is 14.5%.
It is assumed that the ceiling linings are made from concrete with the strength and deformation properties of steel fiber-reinforced siliceous and carbonate aggregate concretes. A thermostructural analyses study was performed in order to analyze the influence of the radiative and convective heat flux on the burner concrete lining structural integrity. The COMSOL software was loaded with the gaseous temperature obtained by FDS software. The proposed work may be applied in the design of wall lining FCC, furnaces, and pet-coke combustion installation in order to mitigate the explosive spallation failure of the linings. The von Mises stress field of the concrete linings was calculated. It was found that the temperature gradient inside the fiber-reinforced carbonate aggregate concrete is high. This is because the thermal conductivity of this kind of concrete is low. The maximal stress reaches 226.3 MPa at the very narrow zone at the left side of the fiber-reinforced carbonate aggregate concrete lining. It was found that the maximal temperature obtained in the case of applying siliceous aggregate concrete is lower than carbonate aggregate concrete. This is because the thermal conductivity of siliceous aggregate concrete is greater than the thermal conductivity of carbonate aggregate concrete. The maximal stress reaches 217.06 MPa at the very narrow zone at the left side of the fiber-reinforced siliceous aggregate concrete lining. The von Mises stress decreases along the concrete thickness. The von Mises strength decreases with enhancement of the heat transfer. The pet-coke burner supplies the necessary heat flux for maintaining the methane steam reforming reaction.
The temperature decays along the MSR height. The temperature of the MSR steel casing is greater than the temperature of the MSR reactor. It was found that the methane and steam mass fractions decrease along the reformer height. The methane conversion is about 27%. The steam and the methane decay along the catalyst bed reactor at the same slope. This is because these two amounts of reactants are proportional to each other. Similar values are reported in the literature for MSR temperature of 510 °C. The hydrogen mass fraction was increased by 98.4%.
5. Conclusions
In my opinion, this is the first work consisting of simulation of pet-coke combustion by using FDS software coupled with thermal structural analysis of the burner ceiling lining (in order to verify that the burner lining can withstand the extreme service conditions of the burner) and a multiphysics computation of the methane steam reforming (MSR).
All the papers described above have hardly addressed the issue of structural integrity of the lining. The pet-coke linings rupture may release pollutants such as carbon dioxide and soot particles to the atmosphere.
This paper presents a CFD modeling of pet-coke combustion and structural analysis of the burner lining. The proposed computational algorithm includes simulation of a pet-coke burner, structural analysis of the burner ceiling lining by coupling the solutions of heat conduction equation, Darcy porous media flow equation, and structural mechanics equation for two kinds of concrete lining—fiber-reinforced carbonate aggregate concrete and fiber-reinforced siliceous aggregate concrete. The relevant thermal and mechanical properties of steel fiber-reinforced concrete at elevated temperatures were applied. It is recommended to apply fiber-reinforced siliceous aggregate concrete. Its mass decays slowly and its maximal stress is much slower. The maximal temperature obtained in the numerical combustion analysis is about 1440 °C. The calculated temperature is similar to the temperature reported in the literature. The maximal carbon dioxide mole fraction obtained in this work is 15.0%. The calculated carbon dioxide mole fraction is similar to the carbon dioxide mole fractions reported in the literature which are 14.5% and 13.6%, respectively. This work may be further extended in order to include power production by applying the Organic Rankine Cycle. The heat liberated from the pet-coke combustion may be exploited in the steam generator order to produce steam. The hydrogen production system is composed of a pet-coke burner and a catalyst bed reactor. The hot gases generated were utilized for convective and radiative heating of the catalyst bed for maintaining the steam reforming reaction of methane into hydrogen and carbon monoxide.