Neutron Star–Dark Matter Admixed Objects in the Mass Gap Region
Abstract
1. Introduction
2. The Two-Fluid Model
NS and DM Equation of State
3. Stability
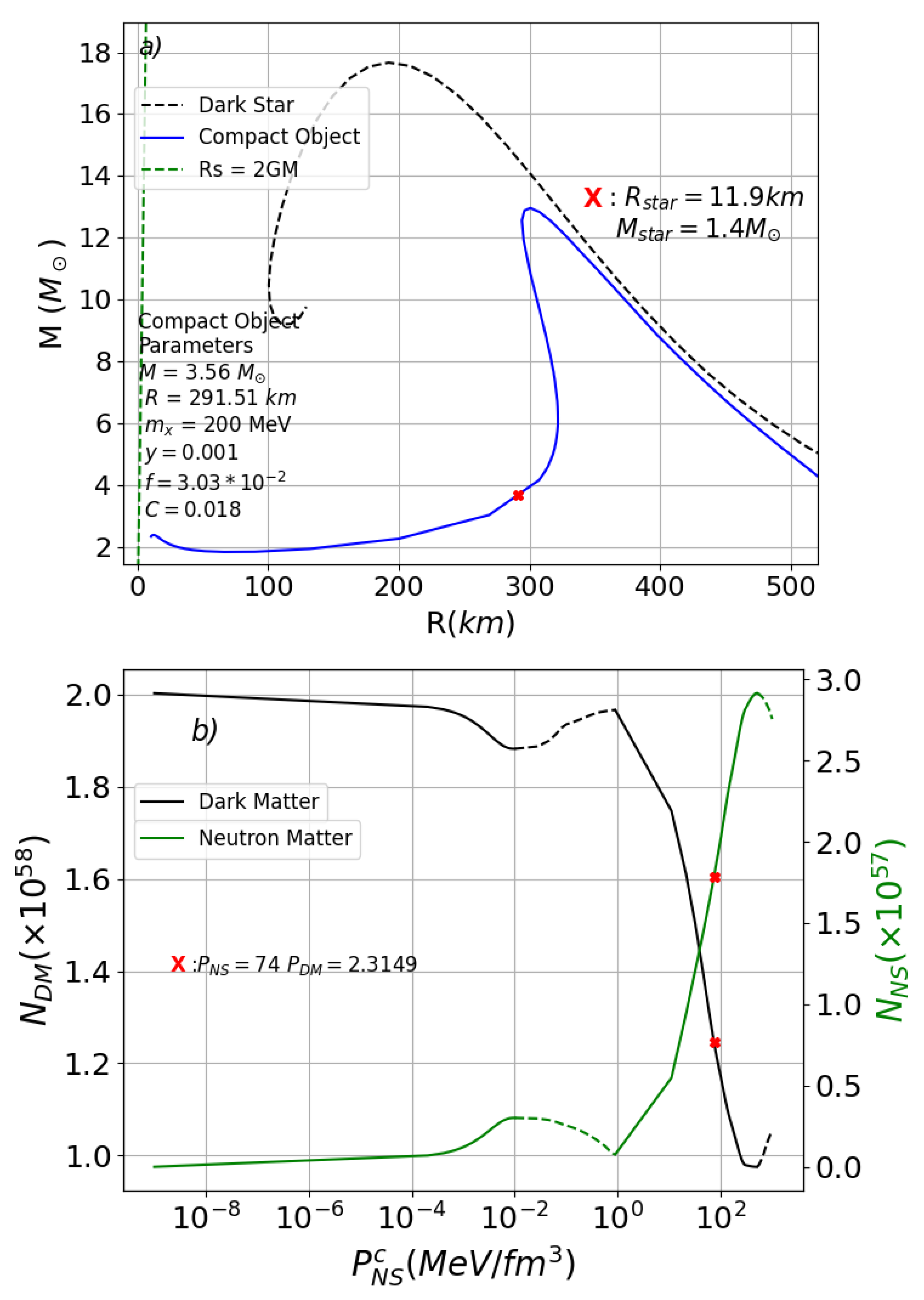
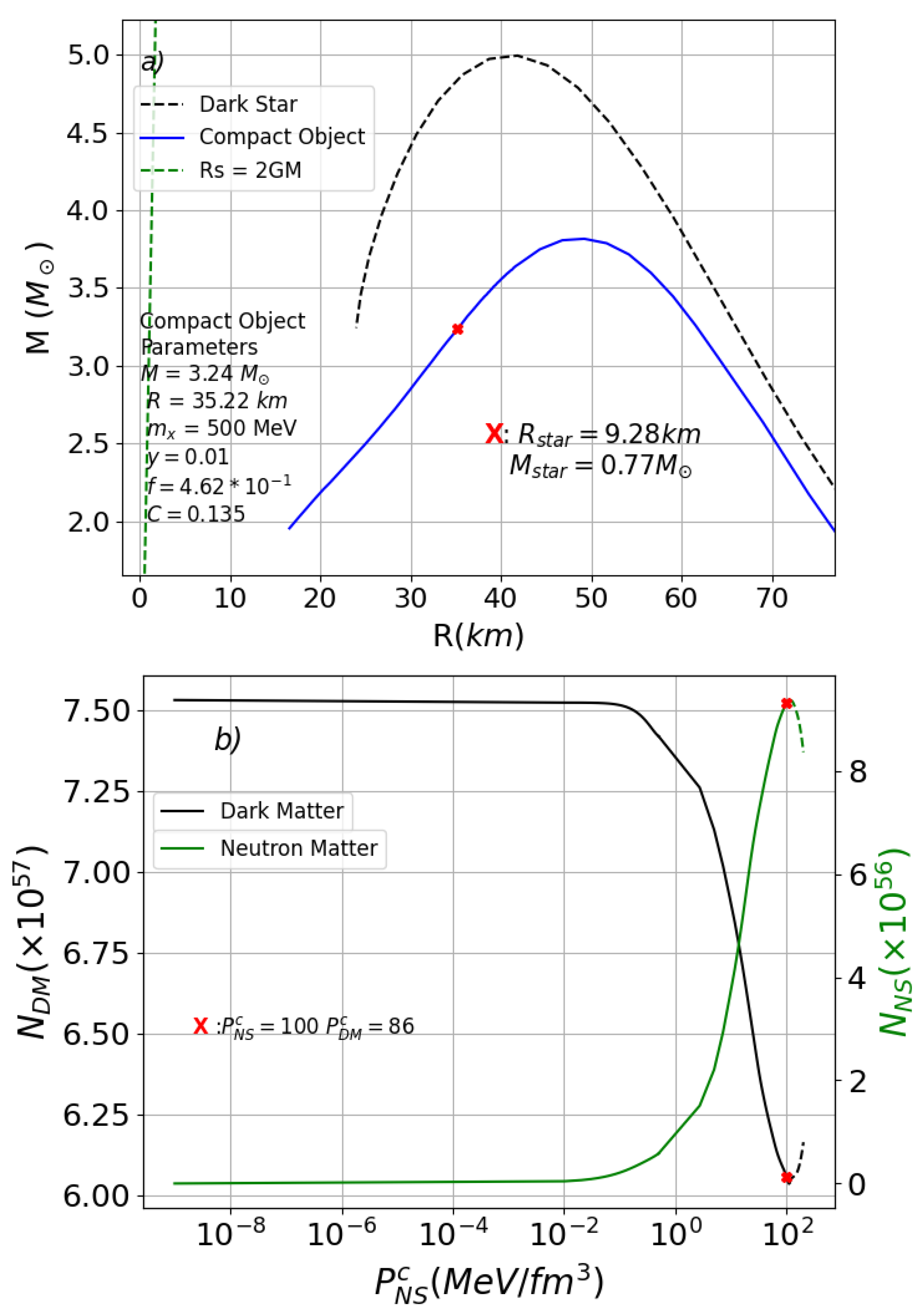
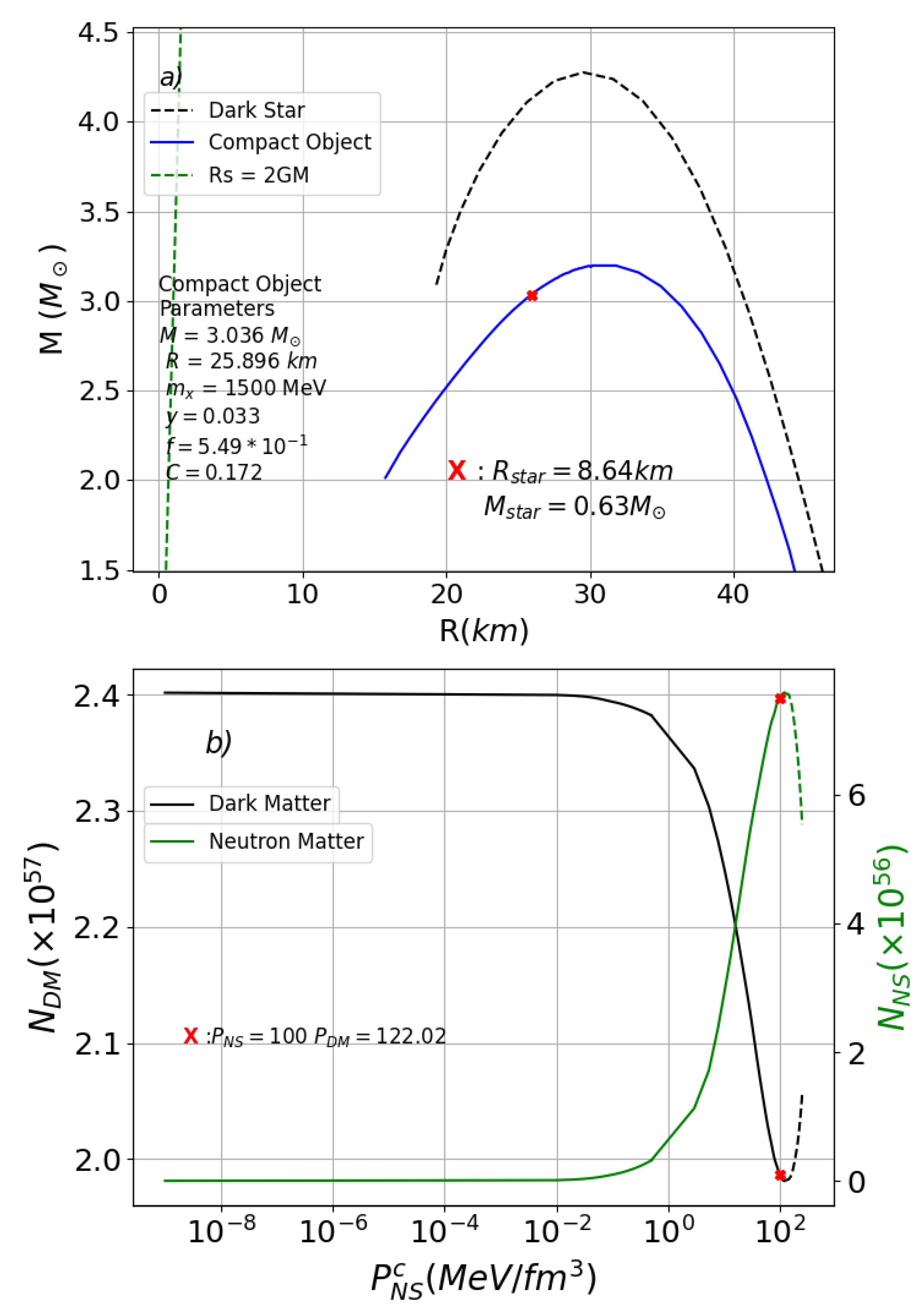
4. Results and Discussion
5. Concluding Remarks
Funding
Data Availability Statement
Conflicts of Interest
References
- Shapiro, T. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley-VCH: New York, NY, USA, 1983. [Google Scholar]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Goldman, I.; Nussinov, S. Weakly interacting massive particles and neutron stars. Phys. Rev. D 1989, 40, 3221. [Google Scholar] [CrossRef] [PubMed]
- Kouvaris, C. WIMP annihilation and cooling of neutron stars. Phys. Rev. D 2008, 77, 023006. [Google Scholar] [CrossRef]
- Bertone, G.; Fairbairn, M. Compact stars as dark matter probes. Phys. Rev. D 2008, 77, 043515. [Google Scholar] [CrossRef]
- de Lavallaz, A.; Fairbairn, M. Neutron stars as dark matter probes. Phys. Rev. D 2010, 81, 123521. [Google Scholar] [CrossRef]
- Kouvaris, C.; Tinyakov, P. Can neutron stars constrain dark matter? Phys. Rev. D 2010, 82, 063531. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Okawa, H. Accretion of Dark Matter by Stars. Phys. Rev. Lett. 2015, 115, 111301. [Google Scholar] [CrossRef]
- Cermeño, M.; Pérez-García, M.Á.; Silk, J. Fermionic light dark matter particles and the new physics of neutron stars. Pub. Astron. Soc. Aust. 2017, 34, e043. [Google Scholar] [CrossRef][Green Version]
- Bramante, J.; Fukushima, K.; Kumar, J. Constraints on bosonic dark matter from observation of old neutron stars. Phys. Rev. D 2013, 87, 055012. [Google Scholar] [CrossRef]
- Bell, N.F.; Melatos, A.; Petraki, K. Realistic neutron star constraints on bosonic asymmetric dark matter. Phys. Rev. D 2013, 87, 123507. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Equilibrium structure and radial oscillations of dark matter admixed neutron stars. Phys. Rev. D 2012, 85, 103528. [Google Scholar] [CrossRef]
- Kouvaris, C. Limits on self-interacting dark matter from neutron stars. Phys. Rev. Lett. 2012, 108, 191301. [Google Scholar] [CrossRef] [PubMed]
- Bertoni, B.; Nelson, A.E.; Reddy, S. Dark matter thermalization in neutron stars. Phys. Rev. D 2013, 88, 123505. [Google Scholar] [CrossRef]
- Ciancarella, R.; Pannarale, F.; Addazi, A.; Marciano, A. Constraining mirror dark matter inside neutron stars. Phys. Dark Universe 2021, 32, 100796. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Dark matter effect on realistic equation of state in neutron stars. Phys. Rev. D 2017, 96, 083004. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with condensed dark matter. Phys. Rev. D 2017, 96, 083013. [Google Scholar] [CrossRef]
- Routaray, P.; Das, H.D.; Sen, S.; Kumarr, B.; Panotopoulos, G.; Zhao, T. Radial oscillations of dark matter admixed neutron stars. Phys. Rev. D 2023, 107, 103039. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Kumar, B.; Biswal, S.K.; Nakatsukasa, T.; Li, A.; Patra, S.K. Effects of dark matter on the nuclear and neutron star matter. Mon. Not. R. Astron. Soc. 2020, 495, 4893. [Google Scholar] [CrossRef]
- Kumar, S.S.; Kentah, A.; Sivaram, C. Effects of dark matter on the upper bound mass of neutron stars. Phys. Dark Universe 2020, 28, 100507. [Google Scholar] [CrossRef]
- Dasgupta, B.; Laha, R.; Ray, A. Low Mass Black Holes from Dark Core Collapse. Phys. Rev. Lett. 2021, 136, 141105. [Google Scholar] [CrossRef]
- Kouvaris, C.; Tinyakov, P. Constraining asymmetric dark matter through observations of compact stars. Phys. Rev. D 2011, 83, 083512. [Google Scholar] [CrossRef]
- Liu, H.M.; Wei, J.B.; Li, Z.H.; Burgio, G.F.; Shulze, H.-J. Dark matter effects on the properties of neutron stars: Optical radii. Phys. Dark Universe 2023, 42, 101338. [Google Scholar] [CrossRef]
- McDermott, S.M.; Yu, H.B.; Zurek, K. Constraints on scalar asymmetric dark matter from black hole formation in neutron stars. Phys. Rev. D 2012, 85, 023519. [Google Scholar] [CrossRef]
- Hippert, M.; Dillingham, E.; Tan, H.; Curtin, D.; Hostler, J.N.; Yunes, N. Dark matter or regular matter in neutron stars? How to tell the difference from the coalescence of compact objects. Phys. Rev. D 2023, 107, 115028. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S.; Rosenbaum, D.; Teplitz, V. Possible implications of asymmetric fermionic dark matter for neutron stars. Phys. Lett. B 2013, 725, 200. [Google Scholar] [CrossRef]
- Dietl, C.; Labun, L.; Rafelski, J. Properties of gravitationally bound dark compact ultra dense objects. Phys. Lett. B 2012, 709, 123. [Google Scholar] [CrossRef]
- Li, X.; Wang, F.; Cheng, K.S. Gravitational effects of condensate dark matter on compact stellar objects. J. Cosmol. Astropart. Phys. 2012, 10, 31. [Google Scholar] [CrossRef]
- Xiang, Q.F.; Jiang, W.Z.; Zhang, D.R.; Yang, R.Y. Effects of fermionic dark matter on properties of neutron stars. Phys. Rev. C 2014, 89, 025803. [Google Scholar] [CrossRef]
- Guver, T.; Erkoca, A.E.; Reno, M.H.; Sarcevic, I. On the capture of dark matter by neutron stars. J. Cosmol. Astropart. Phys. 2014, 5, 13. [Google Scholar] [CrossRef]
- Routaray, P.; Mohantly, S.R.; Das, H.C.; Ghosh, S.; Kalita, P.J.; Parmar, V.; Kumar, B. Investigating dark matter-admixed neutron stars with NITR equation of state in light of PSR J0952-0607. J. Cosmol. Astropart. Phys. 2023, 10, 73. [Google Scholar] [CrossRef]
- Li, A.; Huang, F.; Xu, R.X. Too massive neutron stars: The role of dark matter? Astrop. Phys. 2012, 37, 70. [Google Scholar] [CrossRef]
- Rutherford, N.; Raaijmakers, G.; Weinstein, C.P.; Watts, A. Constraining bosonic asymmetric dark matter with neutron star mass-radius measurements. Phys. Rev. D 2023, 107, 103051. [Google Scholar] [CrossRef]
- Raj, N.; Tanedo, P.; Yu, H.B. Neutron stars at the dark matter direct detection frontier. Phys. Rev. D 2018, 97, 043006. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Sagun, V.; Lopes, I. Neutron stars: New constraints on asymmetric dark matter. Phys. Rev. D 2020, 102, 063028. [Google Scholar] [CrossRef]
- Lopes, L.L.; Das, H.C. Strange stars within bosonic and fermionic admixed dark matter. J. Cosmol. Astropart. Phys. 2023, 5, 34. [Google Scholar] [CrossRef]
- Karkevandi, D.R.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Rezaei, Z. Study of dark matter admixed neutron stars using the equation of state from rotational curves of galaxies. Astrophys. J. 2017, 835, 33. [Google Scholar] [CrossRef]
- Sarkar, N.; Sarkar, S.; Singh, K.N.; Rahaman, F. Relativistic compact stars with dark matter density profile. Eur. Phys. J. C 2020, 80, 255. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Patra, S.K. Dark matter admixed neutron star as a possible compact component in the GW190814 merger event. Phys. Rev. D 2021, 104, 063028. [Google Scholar] [CrossRef]
- Das, A.; Malik, T.; Nayak, A.C. Dark matter admixed neutron star properties in light of gravitational wave observations: A two fluid approach. Phys. Rev. D 2022, 105, 123034. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Robles, S.; Virgato, M. Improved treatment of dark matter capture in neutron stars. J. Cosmol. Astropart. Phys. 2020, 9, 28. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Barranco, J.; Bernal, A.; Rezzolla, L. Constraining scalar fields with stellar kinematics and collisional dark matter. J. Cosmol. Astropart. Phys. 2010, 11, 2. [Google Scholar] [CrossRef]
- Shakeri, S.; Karkevandi, D.R. Bosonic dark matter in light of the NICER precise mass-radius measurements. arXiv 2022, arXiv:2210.17308. [Google Scholar] [CrossRef]
- Mariani, M.; Albertus, C.; Alessandroni, M.d.; Orsaria, M.G.; Garcıa, M.A.P.; Sandoval, I.F.R. Constraining self-interacting fermionic dark matter in admixed neutron stars using multimessenger astronomy. Mon. Not. R. Astron. Soc. 2024, 527, 6795. [Google Scholar] [CrossRef]
- Gresham, M.I.; Zurek, K.M. Asymmetric dark stars and neutron star stability. Phys. Rev. D 2019, 99, 083008. [Google Scholar] [CrossRef]
- Ellis, J.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Dark matter effects on neutron star properties. Phys. Rev. D 2018, 97, 123007. [Google Scholar] [CrossRef]
- Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astropart. Phys. 2009, 32, 278. [Google Scholar] [CrossRef]
- Kodama, T.; Yamada, M. Theory of superdense stars. Prog. Theor. Phys. 1972, 47, 444. [Google Scholar] [CrossRef]
- Henriques, A.B.; Liddle, A.R.; Moorhouse, R.G. Combined Boson-fermion stars. Phys. Lett. B 1989, 233, 99. [Google Scholar] [CrossRef]
- Vikiaris, M.; Petousis, V.; Veselský, M.; Moustakidis, C.C. Supramassive dark objects with neutron star origin. Phys. Rev. D 2024, 109, 123006. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952–0607: The fastest and heaviest known galactic neutron star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Abbott, R. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration. Observation of Gravitational Waves from the Coalescence of a 2.5-4.5 M⊙ Compact Object and a Neutron Star. arXiv 2024, arXiv:2404.04248. [Google Scholar]
- Barr, E.D.; Dutta, A.; Freire, P.C.; Cadelano, M.; Gautam, T.; Kramer, M.; Pallanca, C.; Ransom, S.M.; Ridolfi, A.; Stappers, B.W.; et al. A pulsar in a binary with a compact object in the mass gap between neutron stars and black holes. Science 2024, 383, 275–279. [Google Scholar] [CrossRef] [PubMed]
- Schochet, M.; Tayar, J.; Andrews, J.J. A Lack of Mass-Gap Compact Object Binaries in APOGEE. arXiv 2024, arXiv:2406.13024. [Google Scholar] [CrossRef]
- Nelson, A.; Reddy, S.; Zhou, D. Dark halos around neutron stars, and gravitational waves. J. Cosmol. Astropart. Phys. 2019, 7, 12. [Google Scholar] [CrossRef]
- Naidu, N.F.; Carloni, S.; Dunsby, P. Two-fluid stellar objects in general relativity: The covariant formulation. Phys. Rev. D 2021, 104, 044014. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year data set: High-precision timing of 45 millisecond pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340, 448. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Narain, G.; Schaffner-Bielich, J.; Mishustin, I.N. Compact stars made of fermionic dark matter. Phys. Rev. D 2006, 74, 063003. [Google Scholar] [CrossRef]
- Agnihotri, P.; Schaffner-Bielich, J.; Mishustin, I.N. Boson stars with repulsive self-interactions. Phys. Rev. D 2009, 79, 084033. [Google Scholar] [CrossRef]
- Dengler, Y.; Bielich, J.S.; Tolos, L. Second Love number of dark compact planets and neutron stars with dark matter. Phys. Rev. D 2022, 105, 043013. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Thorne, K.S.; Meltzer, D.W. A catalogue of methods for studying the normal modes of radial pulsation of General-Relativistic stellar models. Astrophys. J. 1966, 145, 505. [Google Scholar] [CrossRef]
- Kain, B. Radial oscillations and stability of multiple-fluid compact stars. Phys. Rev. D 2020, 102, 023001. [Google Scholar] [CrossRef]
- Henriques, A.; Liddle, A.R.; Moorhouse, R. Stability of boson-fermion stars. Phys. Lett. B 1990, 251, 511. [Google Scholar] [CrossRef]
- Henriques, A.; Liddle, A.R.; Moorhouse, R. Combined boson-fermion stars: Configurations and stability. Nucl. Phys. B 1990, 337, 737. [Google Scholar] [CrossRef]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Alvarado, S.V.; Palenzuela, C.; Alic, D.; Lopez, L.A.U. Dynamical evolution of fermion-boson stars. Phys. Rev. D 2013, 87, 084040. [Google Scholar] [CrossRef]
- Alvarado, S.V.; Becerril, R.; Lopez, L.A.U. Fermion-boson stars with a quartic self-interaction in the boson sector. Phys. Rev. D 2020, 102, 064038. [Google Scholar] [CrossRef]
- Giovanni, F.D.; Guerra, D.; Albanesi, S.; Tenes, M.M.; Tseneklidou, D. Fermion-axion stars: Static solutions and dynamical stability. Phys. Rev. D 2022, 106, 084013. [Google Scholar] [CrossRef]
- Fishbach, M. Mystery in the “mass gap”. Science 2024, 383, 259. [Google Scholar] [CrossRef]
- Bauswein, A.; Guo, G.; Lien, J.H.; Lin, Y.H.; Wu, M.R. Compact dark objects in neutron star mergers. Phys. Rev. D 2023, 107, 083002. [Google Scholar] [CrossRef]
- Rhoades, C.E., Jr.; Ruffini, R. Maximum Mass of a Neutron Star. Phys. Rev. Lett. 1974, 32, 324. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vikiaris, M. Neutron Star–Dark Matter Admixed Objects in the Mass Gap Region. Particles 2024, 7, 692-702. https://doi.org/10.3390/particles7030040
Vikiaris M. Neutron Star–Dark Matter Admixed Objects in the Mass Gap Region. Particles. 2024; 7(3):692-702. https://doi.org/10.3390/particles7030040
Chicago/Turabian StyleVikiaris, Michael. 2024. "Neutron Star–Dark Matter Admixed Objects in the Mass Gap Region" Particles 7, no. 3: 692-702. https://doi.org/10.3390/particles7030040
APA StyleVikiaris, M. (2024). Neutron Star–Dark Matter Admixed Objects in the Mass Gap Region. Particles, 7(3), 692-702. https://doi.org/10.3390/particles7030040






