An Empirical Consistent Redshift Bias: A Possible Direct Observation of Zwicky’s TL Theory

Abstract

Recent advancements have shown tensions between observations and our current understanding of the Universe. Such observations may include the $H_0$ tension and massive galaxies at high redshift that are older than traditional galaxy formation models have predict. Since these observations are based on redshift as the primary distance indicator, a bias in the redshift may explain these tensions. While redshift follows an established model, when applied to astronomy it is based on the assumption that the rotational velocity of the Milky Way galaxy relative to the observed galaxies has a negligible effect on redshift. But given the mysterious nature of the physics of galaxy rotation, that assumption needed to be tested. The test was done by comparing the redshift of galaxies rotating in the same direction relative to the Milky Way to the redshift of galaxies rotating in the opposite direction relative to the Milky Way. The results show that the mean redshift of galaxies that rotate in the same direction relative to the Milky Way is higher than the mean redshift of galaxies that rotate in the opposite direction. Additionally, the redshift difference becomes larger as the redshift gets higher. The consistency of the analysis was verified by comparing data collected by three different telescopes, annotated using four different methods, released by three different research teams, and covering both the northern and southern ends of the galactic pole. All the datasets are in excellent agreement with each other, showing consistency in the observed redshift bias. Given the “reproducibility crisis” in science, all the datasets used in this study are publicly available, and the results can be easily reproduced. This observation could be the first direct empirical reproducible observation for the Zwicky’s “tired-light” model.

1. Introduction

The unprecedented imaging power of JWST has revealed new information about the Universe that is not aligned with some of the current fundamental cosmological assumptions. For instance, the presence of galaxies at redshift higher than 13 [1] or even as high as 15 [2] was not expected according to previous assumptions [3]. Mature massive galaxies observed at redshift of ∼11 [4] also challenge the cosmological model and the history of the Universe. The existence of massive galaxies at high redshift was reported also before JWST was launched [5], and JWST provided more and deeper instances of such galaxies, showing that mature galaxies were prevalent in the early Universe. Another example of a puzzling unexplained observation is the $H_0$ tension, reflected by two different messengers that provide two different expansion rates and ages of the Universe [6,7,8,9,10,11,12,13]. Since both measure the same Universe, it can be assumed that at least one of these measurements is biased.

These puzzling observations introduce a challenge to cosmology: if the distance indicators are accurate, the standard cosmological model is incomplete. If the current standard cosmological theories are complete, then the distance indicators may not be fully accurate. That is, either the standard cosmological theories need to be revised, or the redshift as a distance indicator needs to be revised, but the two may not be able to co-exist without modifications. While some solutions include alternative cosmological models, it has also been suggested that the tensions can be solved by changing the redshift model [14,15,16,17,18].

The redshift of an astronomical object is expected to correspond to the linear velocity of the object relative to Earth. But in addition to the linear velocity, the measurement of the redshift of a galaxy can also be affected by the rotational velocity of the galaxy, as well as the rotational velocity of the Milky Way. The rotational velocity of a luminous object can affect the Doppler shift effect [19,20,21], but since the rotational velocity of a galaxy is far smaller than its linear velocity, it is assumed that the effect of the rotational velocity is negligible. When the redshift of the galaxy is higher, the effect of the rotational velocity is expected to be even smaller. In any case, the rotational velocity of galaxies is ignored in common redshift models. However, it should be noted that the physics of a galaxy’s rotation, and, namely, its rotational velocity, are still among the most mysterious and most provocative phenomena in nature.

While the puzzling nature of the physics of galaxy rotation was noted in the first half of the 20th century [22], it was not until five decades later that it became part of mainstream science [23,24]. Common explanations include dark matter [23] or modified Newtonian dynamics [25], but numerous other explanations have also been proposed [26,27,28,29,30,31,32,33,34,35]. However, despite over a century of scientific research, there is no complete explanation for the nature of galaxy rotation [26,36,37,38,39,40,41,42,43,44,45,46,47,48,49].

The purpose of this experiment was to examine the impact of the galaxy rotational velocity on the redshift. This could be done by observing galaxies located around the galactic pole, and comparing the redshift of galaxies rotating in the same direction relative to the Milky Way to the redshift of galaxies rotating in the opposite direction relative to the Milky Way. An observed difference in the redshift could indicate that the redshift is affected by the rotational velocity, and, therefore, that the way it is implemented in astronomy is incomplete.

2. A Possible Link between Galaxy Rotational Velocity and Redshift

A preliminary possible link between redshift and the rotational velocity of galaxies has been proposed through empirical observations showing that galaxies that rotate in the same direction relative to the Milky Way have different redshift compared to galaxies that rotate in the opposite direction relative to the Milky Way [50]. The analysis was based on several different datasets of galaxies acquired by two different telescopes, and annotated by their direction of rotation, using several different annotation methods. Since galaxies with leading arms are extremely rare [51], the direction of rotation was determined by the arms of the galaxies. The analysis was based on galaxies at the ${10}^{\circ }\times {10}^{\circ }$ field centered at the galactic pole and on the ${20}^{\circ }\times {20}^{\circ }$ field, to increase the number of galaxies and, consequently, the statistical significance. The analysis was done for both the northern and southern ends of the galactic pole [50].

The catalogs used in the experiment included galaxies annotated by the Ganalyzer algorithm [52,53], by the SpArcFiRe method [54,55], and by the manual annotation of Galaxy Zoo, such that the “superclean” criterion of 95% agreement between the annotations [56] was used. All of these methods determine the spin direction of the galaxies based on analysis of the shape of the galaxy arms. The datasets are all available publicly. The SDSS and DESI galaxies annotated by the Ganalyzer algorithm are available at https://people.cs.ksu.edu/~lshamir/data/zdifference/ (accessed on 15 July 2024). The set of galaxies annotated by the SpArcFiRe method can be found at https://people.cs.ksu.edu/~lshamir/data/sparcfire/ (accessed on 15 July 2024). The annotations of Galaxy Zoo can be accessed through SDSS CAS server at http://casjobs.sdss.org/CasJobs/default.aspx (accessed on 15 July 2024).

Table 1. The mean redshift of galaxies that rotate in the same direction relative to the Milky Way galaxy (MW) and the mean redshift of galaxies that rotate in the opposite direction relative to the Milky Way (OMW). The p values are the one-tailed p values determined by the Student t-test. All datasets are publicly available. The experiments are described in detail in [50].

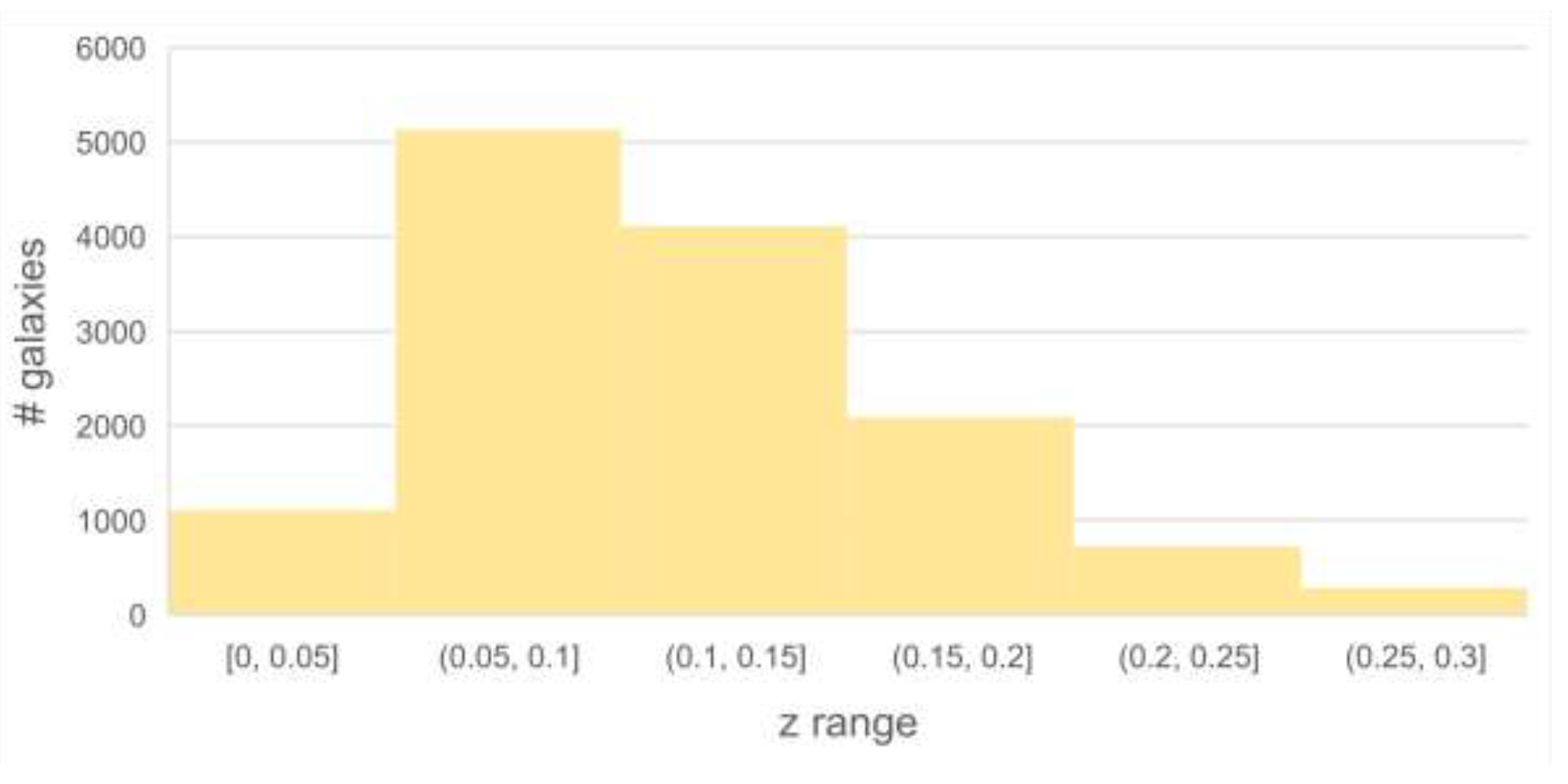
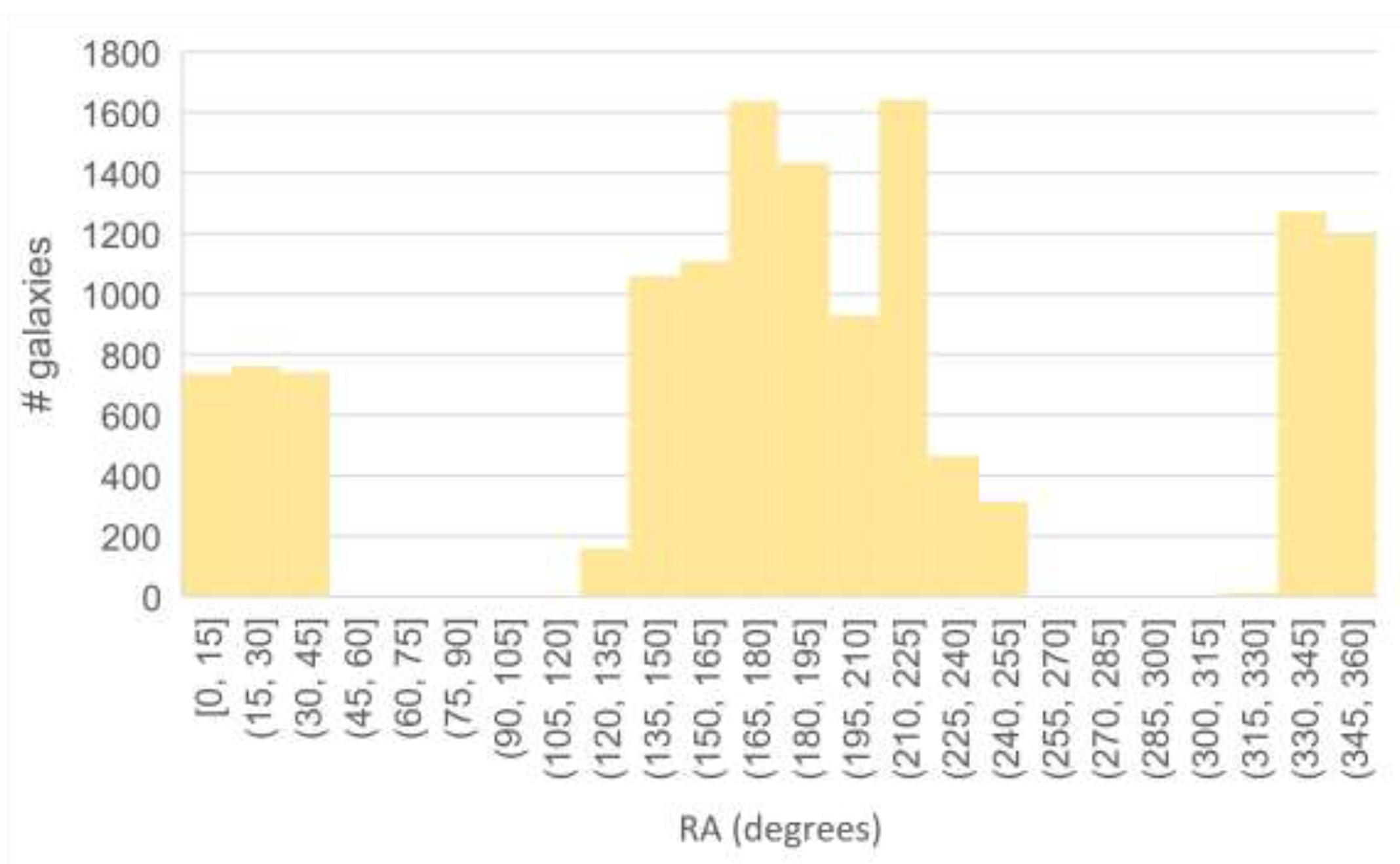
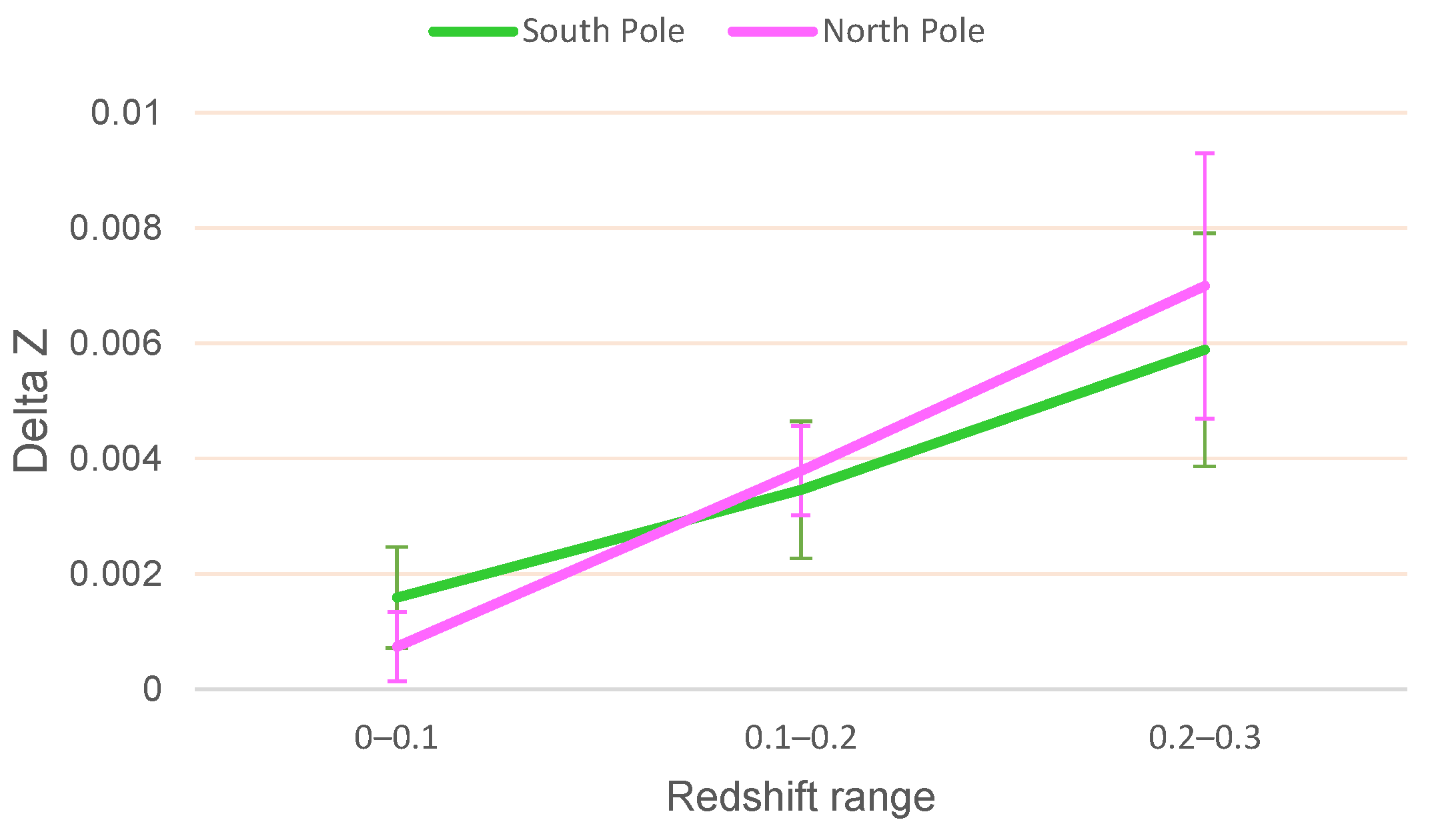
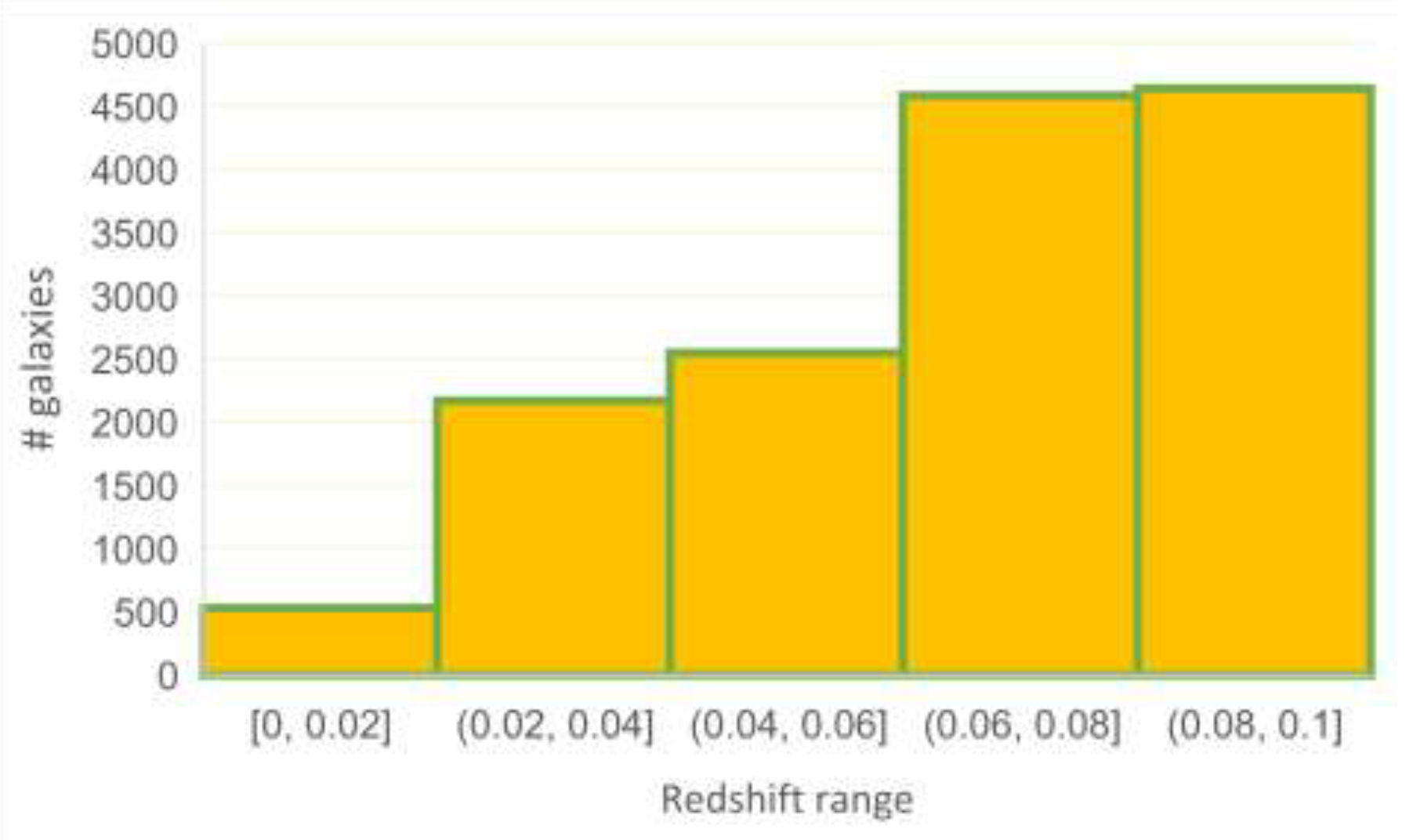
Survey	Pole	Field Size (∘)	Annotation	# MW	# OMW	${\mathit{Z}}_{\mathit{mw}}$	${\mathit{Z}}_{\mathit{omw}}$	$\Delta$z	t-Test p
SDSS	North	10 × 10	Ganalyzer	204	202	0.0996 ± 0.0036	0.08774 ± 0.0036	0.01185 ± 0.005	0.01
SDSS	North	20 × 20	Ganalyzer	817	825	0.09545 ± 0.0017	0.08895 ± 0.0016	0.0065 ± 0.0023	0.0029
SDSS	North	20 × 20	Galaxy Zoo	154	135	0.07384 ± 0.004	0.06829 ± 0.0035	0.0056 ± 0.0053	0.15
SDSS	North	10 × 10	SpArcFiRe	710	732	0.07197 ± 0.0015	0.06234 ± 0.0014	0.00963 ± 0.002	<0.0001
SDSS	North	10 × 10	SpArcFiRe	728	709	0.06375 ± 0.0014	0.07191 ± 0.0014	−0.00816 ± 0.002	<0.0001
			Mirrored
SDSS	North	20 × 20	SpArcFiRe	2903	2976	0.07285 ± 0.0007	0.07116 ± 0.0007	0.00169 ± 0.001	0.04
SDSS	North	20 × 20	SpArcFiRe	3003	2914	0.07113 ± 0.0007	0.07271 ± 0.0007	−0.00158 ± 0.001	0.05
			Mirrored
DESI	South	10 × 10	Ganalyzer	414	376	0.1352 ± 0.0027	0.1270 ± 0.0025	0.0082 ± 0.0036	0.018
DESI	South	20 × 20	Ganalyzer	1702	1681	0.1317 ± 0.0013	0.1273 ± 0.0014	0.0044 ± 0.0018	0.008

shows the mean redshift of galaxies that rotate in the same direction and in the opposite direction relative to the Milky Way.

As the table shows, all the catalogs show lower redshift for galaxies that rotate in the opposite direction relative to the Milky Way. With the exception of the small Galaxy Zoo catalog, in all cases the difference is statistically significant. The observed $\Delta$z difference was higher when using the smaller ${10}^{\circ }\times {10}^{\circ }$ field centered at the galactic pole compared to the larger ${20}^{\circ }\times {20}^{\circ }$ field. This can be explained by the difference in the relative rotational velocity, which is expected to increase when the galaxies are located closer to the galactic pole. The SpArcFiRe algorithm was used with both the original images and with the mirrored images. This was done due to the reported bias of the SpArcFiRe method [57]. SpArcFiRe provided a higher number of galaxies, but at the expense of the accuracy of the annotation, leading to a smaller absolute $\Delta$z though a stronger statistical signal, due to the higher number of galaxies [50]. The Ganalyzer algorithm has a simple “mechanical” symmetric nature [52,58,59], and, therefore, mirroring the galaxies did not change the results [50]. When using SpArcFiRe the results changed when the galaxy images were mirrored, but the change was not substantial, except for the expected inverse $\Delta$z observed when the galaxy images were mirrored.

The p-values shown in Table 1 are based on the Student t-test, which assumes normal distribution of the redshift. Because the redshift distribution does not necessarily follow normal distribution, the Student t-test may not provide the real probability of having such a distribution by chance. To verify the statistical significance, a simulation analysis was used, such that the galaxies were separated randomly into two groups, and the difference between the mean redshift of each of the two groups of galaxies was computed. This was repeated 100,000 times with the dataset of 1642 galaxies of the second row in Table 1. In 307 of the runs the difference between the first group of galaxies and the second group was larger than 0.0016, providing a probability of 0.0031 of occurrence by chance [50].

The DESI Legacy Survey data were collected around the southern galactic pole, and, therefore, galaxies in the southern galactic pole rotating in the same direction relative to the Milky Way would seem to rotate in the opposite direction compared to galaxies in the northern galactic pole rotating in the same direction relative to the Milky Way. This provides an additional verification that the difference is not a feature of some unknown behavior of the galaxy annotation methods, as such an effect would be consistent across the sky, rather than flipping and providing inverse results at the two ends of the galactic pole [50]. An additional control experiment was performed by using SDSS galaxies from the same source that rotate in opposite directions in fields that are perpendicular to the galactic pole. For instance, in the 20 × 20 degree fields centered at $(\alpha ={102}^{\circ },\delta =0^{\circ })$ the $\Delta$z was 0.00022 ± 0.004, which is statistically insignificant.

Table 2. Flux differences in different filters between galaxies that rotate in the same and in the opposite direction relative to the Milky Way. The data are the galaxies and the field shown in the first row of Table 1. The p values were determined by a simple two-tailed Student t-test.

Band	MW	OMW	$\mathbf{\Delta }$	t-Test p
spectroFlux_g	25.969 ± 0.8669	28.554 ± 1.0918	−2.585	0.063
spectroFlux_r	53.2433 ± 1.765	58.6214 ± 2.3422	−5.378	0.066
spectroFlux_i	77.4189 ± 2.513	85.0868 ± 3.407	−7.667	0.067

shows the differences between the flux in different wavelengths. The flux differences between galaxies that rotate in opposite directions show a difference of ∼10% in the different filters, and the absolute difference is larger when the wavelength is shorter [50].

3. Analysis of HSC DR3 Galaxies

The analysis shown in Section 2 and in [50] shows a consistent but relatively small redshift bias. But these analyses are based on galaxies imaged mostly by SDSS, with one experiment with galaxies obtained through the DESI Legacy Survey. Therefore, most galaxies used for the experiments included in Table 1 are of relatively low redshift. This makes it difficult to profile the change in $\Delta$z when the redshift changes. That is, if $\Delta$z increases at a higher redshift, it can provide an indication that the redshift bias is higher for high-redshift galaxies.

To profile the dependence between $\Delta$z and the redshift, an experiment was performed with the third data release (DR3) of the hyper suprime-cam (HSC). Using the 8.2 m Subaru telescope, HSC provides a high level of detail of galaxies with higher redshift compared to galaxies imaged by the SDSS or DESI Legacy Surveys. This allowed us to annotate galaxies with higher redshift by their direction of rotation, and to test whether the redshift bias increases with the redshift.

The galaxies used in the experiment included all the HSC DR3 galaxies that have redshift in SDSS DR17. This included 101,415 galaxies with redshift of $z<0.3$. The purpose of the redshift limit was to avoid galaxies that could not be annotated accurately by their visible spin patterns. The galaxies were annotated by the Ganalyzer algorithm [52,53], as described in [50]. This led to a clean dataset of 13,477 galaxies.

A smaller dataset of annotated galaxies compared to the initial dataset was expected because not all galaxies are necessarily spiral and not all spiral galaxies have a direction of rotation that can be identified. Manual inspection of 100 galaxies, randomly selected, showed that all the galaxies were annotated accurately. The dataset can be accessed at https://people.cs.ksu.edu/~lshamir/data/zdifference_hsc/ (accessed on 15 July 2024). The redshift distribution of the galaxies is displayed in Figure 1. Although most galaxies have a relatively low redshift, the catalog still contains more than 1000 galaxies with $z>0.2$.

While providing better image quality and depth compared to the catalogs summarized in Section 2, the downside of the HSC catalog used here is that it covers neither the south nor the north end of the galactic pole. Therefore, the galaxies used for the analysis were galaxies that are closer to the south end of the galactic pole, as well as galaxies that are close to the north end of the galactic pole. The declination of the galaxies ranged between $-6.{58}^{\circ }$ to $53.{18}^{\circ }$. The distribution of the right ascension is shown in Figure 2. The catalog contains 4724 galaxies that are within 60^∘ from the southern galactic pole and 8753 galaxies that are within 60^∘ from the northern galactic pole.

Table 3. Redshift of the galaxies around the southern galactic pole that rotate in the same direction as the Milky Way galaxy and in the opposite direction relative to the Milky Way. The p values are the Student t-test probabilities of such differences being stronger by chance.

z Range	# MW	# OMW	${\mathit{Z}}_{\mathit{mw}}$	${\mathit{Z}}_{\mathit{omw}}$	$\mathbf{\Delta }$z	t-Test p
0–0.1	871	917	0.072788 ± 0.0006	0.071198 ± 0.0006	0.001589 ± 0.0009	0.03
0.1–0.2	1100	1144	0.149292 ± 0.0008	0.145834 ± 0.0008	0.003458 ± 0.001	0.001
0.2–0.3	342	350	0.242174 ± 0.0015	0.236287 ± 0.001	0.005886 ± 0.002	0.0006
All	2313	2411	0.13421 ± 0.001	0.13058 ± 0.001	0.00363 ± 0.0014	0.005

and

Table 4. Mean redshift of galaxies around the northern galactic pole rotating in the same direction relative to the Milky Way and the mean redshift of galaxies rotating in the opposite direction relative to the Milky Way.

z Range	# MW	# OMW	${\mathit{Z}}_{\mathit{mw}}$	${\mathit{Z}}_{\mathit{omw}}$	$\mathbf{\Delta }$z	t-Test p
0–0.1	2202	2255	0.070232 ± 0.0004	0.069493 ± 0.0004	0.000739 ± 0.0006	0.095
0.1–0.2	1949	2021	0.138494 ± 0.0006	0.134705 ± 0.0005	0.003789 ± 0.0008	0.00005
0.2–0.3	166	160	0.228586 ± 0.0018	0.221593 ± 0.0014	0.006993 ± 0.0023	0.0012
All	4317	4436	0.10714 ± 0.0006	0.104689 ± 0.0006	0.002451 ± 0.0008	0.0019

show the mean redshift of galaxies rotating in the same direction relative to the Milky Way galaxy and the mean redshift of galaxies rotating in the opposite direction relative to the Milky Way galaxy in the southern and northern galactic poles, respectively. The tables show the difference between the mean z among all the galaxies, but also the differences when the galaxy population is separated into 0.1 redshift ranges. As the table shows, in both ends of the galactic pole there is a statistically significant difference between the redshift of the galaxies rotating in the same direction as the galactic pole and the galaxies rotating in the opposite direction relative to the galactic pole.

The directions of rotation of the galaxies observed on the opposite sides of the galactic pole were inverse, such that a galaxy located around the north end of the galactic pole and rotating in the same direction relative to the Milky Way would seem to rotate in the opposite direction if it was located at the south end of the galactic pole. This was naturally taken into account in the analysis, but the consistency between both ends of the galactic pole showed that the differences were not driven by an unknown bias in the annotation, as such a bias would have been consistent at both ends of the galactic pole, and would not flip based on the locations of the galaxies in the sky.

As discussed in Section 2, the p-values were based on the Student t-test, and, therefore, on the assumption that the redshift was distributed normally. Since that assumption might not necessarily have been correct, a simulation was performed, such that the galaxies were separated into two groups randomly, and the mean redshift of one group was compared to the mean redshift of the galaxies of the other group [50]. After 100,000 tests, the galaxies close to the southern galactic pole were separated into two random groups with a mean redshift difference larger than 0.00363 in 518 runs. The same experiment when using the galaxies closer to the northern galactic pole showed a mean redshift difference larger than 0.002451 in 230 of the runs. These simulation experiments show that the probability of such a separation by mere chance is far below 1%.

The simple separation of the analysis into several redshift ranges shows that $\Delta$z increases as the redshift gets higher. That observation is consistent at both ends of the galactic pole. Figure 3 shows the $\Delta$z in the different redshift ranges.

The statistical significance of the increase in $\Delta$z can also be determined by using a simple Pearson correlation after assigning the galaxies that rotate in the same direction relative to the the Milky Way with the value 1 and the galaxies that rotate in the opposite direction relative to the Milky Way as −1. When using galaxies closer to the northern galactic pole the Pearson correlation is 0.0296, and the probability of such a correlation by chance is p = 0.02. When using galaxies closer to the southern galactic pole, the Pearson correlation is 0.02669, and the p is 0.0064.

4. Verification Using a Third-Party Dataset

To further test the consistency of the bias, the observation described in Section 2 and Section 3 was compared to a third-party catalog [60]. That catalog was prepared by five undergraduate students who manually annotated SDSS galaxies, and the galaxy images were also mirrored, to offset for possible human bias [60]. While the purpose of that dataset was not to compare redshift or test the impact of the rotational velocity of the Milky Way, 14,462 of the galaxies in that dataset had redshift, and, therefore, could be used for the analysis. The dataset can be accessed at https://ars.els-cdn.com/content/image/1-s2.0-S0370269311003947-mmc1.txt (accessed on 15 July 2024). The redshift of all the galaxies that had spectra was smaller than 0.1, and the redshift distribution is displayed in Figure 4. The distribution of the RA is displayed in Figure 5. As the figure shows, the majority of the galaxies are in relatively close proximity to the northern galactic pole.

A very simple analysis of the data shows that the mean redshift of the galaxies that rotate clockwise in that catalog is 0.06586 ± 0.00029, while the mean redshift of galaxies rotating counterclockwise is 0.065 ± 0.00029. The probability of such difference being by chance is 0.018. While the statistically significant redshift difference may seem unexpected, most of the galaxies are located near the northern galactic pole, and, therefore, the lower redshift for the galaxies that rotate counterclockwise is in agreement with the results shown in Table 4 using the HSC data taken from the northern galactic pole, as well as the other datasets show in Table 1.

Table 5. Redshift of the galaxies annotated by [60] around the southern and northern galactic poles that rotate in the same direction as the Milky Way galaxy and in the opposite direction relative to the Milky Way. The older third-party dataset was used to confirm the results observed with the other datasets.

Hemisphere	# MW	# OMW	${\mathit{Z}}_{\mathit{mw}}$	${\mathit{Z}}_{\mathit{omw}}$	$\mathbf{\Delta }$z	t-Test p Values
North	6450	6573	0.06598 ± 0.0003	0.06498 ± 0.0003	0.001 ± 0.0004	0.01
South	722	717	0.06516 ± 0.0008	0.06469 ± 0.0009	0.00047 ± 0.0012	0.34

shows the mean z of the galaxies rotating in the same direction as the Milky Way galaxy in the catalog [60], and the mean z of the galaxies that rotate in the opposite direction relative to the Milky Way in the southern and northern galactic poles.

As the table shows, the $\Delta$z around the northern galactic pole agrees well with the $\Delta$z observed by HSC around the northern galactic pole at the same redshift range of 0–0.1, as shown in Table 4. The opposite end of the galactic pole also shows that galaxies that rotate in the opposite direction relative to the Milky Way have lower redshift compared to galaxies that rotate in the same direction, but in the case of the [60] catalog the difference is not statistically significant, possibly due to the low number of galaxies in that part of the sky.

Since the redshift of the galaxies in that catalog is limited to $z<0.1$, a direct comparison to the redshift ranges used in Table 4 is not possible. However, when using the galaxies around the northern galactic pole, the Pearson correlation coefficient between the direction of rotation and the redshift is 0.02033, and the probability of this coefficient being by chance is ∼0.01. This provides an indication that the bias increases with the redshift, as was also observed with the data from HSC DR3. The third-party dataset, therefore, shows the same observation as the dataset of HSC DR3 galaxies and, in fact, the data from all other premier sky surveys.

5. Possible Link to Zwicky’s “Tired-Light” Model

The early Universe as imaged by JWST is different from the early Universe predicted by the standard model. Among other explanations, that tension was proposed to have a link to Fritz Zwicky’s “tired-light” (TL) theory [16,18,61,62,63,64,65,66,67,68,69,70].

According to TL, photons lose their energy along their traveling path through the Universe. This can lead to differences in the redshift as observed from Earth, and, therefore, galaxies that are more distant from Earth can have redshift that differs from galaxies that are closer to Earth. If this theory is correct, it would explain the early mature galaxies observed by JWST, as their true age would not the same age that their redshift indicates. In its extreme form, TL can argue that the Big Bang is merely an artifact created by TL, and that the Universe is in fact in steady state. One of the downsides of the model is that there is no empirical observation showing that photons indeed lose their energy as they travel through the Cosmos.

An empirical experiment that shows a redshift bias that grows as the redshift becomes higher is difficult to perform at cosmological-scale distance, since the only information that can be obtained is the redshift as observed from Earth. While the distances of the galaxies can be estimated through other candles, such as Ia supernovae, it is difficult to prove whether the redshift of a galaxy is higher because the galaxy indeed moves faster away from Earth in accordance to the Big Bang theory, because of TL, or because of a combination of the two. Ia supernovae are also limited in the distance range compared to the redshift, and, therefore, a redshift bias in the very high redshift will be difficult to profile using Ia supernovae.

But when using the rotational velocity of the Earth within the Milky Way galaxy, a small redshift bias is expected, due to the rotational velocity of the Earth. That bias is expected to affect galaxies rotating in the same direction relative to the Milky Way differently than it affects galaxies rotating in the opposite direction relative to the Milky Way. That bias is expected to be small, but according to several datasets, as shown here, it is statistically significant. More importantly, the bias grows with the redshift, suggesting that it is not the velocity alone that leads to the bias. The rotational velocity of the Earth within the Milky Way galaxy is obviously a constant that does not change, and the radial velocity of galaxies rotating in the same direction relative to the Milky Way galaxy is expected to be, on average, the same as the radial velocity of galaxies that rotate in the opposite direction relative to the Milky Way. The idea that the redshift can change with the distance, and not necessarily the velocity, might be an indication supporting Fritz Zwicky’s century-old theory.

That observation can also be related to the far higher number of galaxies that rotate in the opposite direction relative to the Milky Way as imaged by JWST [71]. The JWST deep field images show that 140% more galaxies rotate in the opposite direction relative to the Milky Way [71]. A possible explanation is that galaxies that rotate in the opposite direction relative to the Milky Way are brighter, due to the Doppler shift effect. Due to TL, the brightness difference becomes more significant when the galaxies are more distant from Earth, and, therefore, many more galaxies are observed rotating in the opposite direction relative to the Milky Way. Earlier observations made before JWST saw that first light also showed such asymmetry that grew with the redshift [72,73], although at the lower redshift range the asymmetry was far milder than the asymmetry observed in the early Universe image by JWST.

6. Conclusions

Unexpected observations, such as the $H_0$ tension and galaxies that according to the current theories are expected to be older than traditional galaxy formation models predict, are challenging the standard cosmological model. If the cosmological model is complete and fully accurate, the distance measurements and, primarily, the redshift are biased. If the redshift is fully accurate then the standard cosmological model and basic theories regarding galaxy formation and the history of the Universe are incomplete. In any case, the redshift as used currently and the existing basic cosmological theories cannot co-exist without modifications.

This paper presents empirical observations that show that the redshift model may be biased and that the bias might be driven by the rotational velocity of the Milky Way galaxy relative to the rotational velocity of the observed galaxies. The observed bias is consistent across different telescopes and different annotation methods, and it shows very similar bias at both ends of the galactic pole. It is also consistent in catalogs that were collected for other purposes by different research teams.

The empirical observations described in this paper are provided with the data to ensure that the results can be reproduced. It has been shown that the vast majority of the scientific results cannot be reproduced [74], introducing the challenge known as the “reproducibility crisis” in science [75,76,77,78]. The ability to access the data and reproduce the results allows us to advance science in a transparent manner and to avoid errors that might not be noticeable to a reader unless they have access to the data.

In current astrophysics and cosmology practices, the redshift is used in most cases by ignoring the rotational velocity of the Milky Way, as the rotational velocity is far lower than the linear velocity and can, therefore, be considered negligible. But it should be noted that the physics of galaxy rotation and, in particular, the rotational velocity of galaxies are still not fully understood [22,26,33,36,37,38,39,40,41,42,43,44,45,46,47,49,79,80,81,82,83,84,85]. Theories such as dark matter [23] or MOND [25] have been proposed to explain the anomaly of the rotational velocity of galaxies, but several decades of research still have not led to a proven explanation for the provocative nature of the rotational velocity of galaxies.

It is difficult to identify an immediate explanation for the link between the rotational velocity and the redshift as observed from Earth. A possible explanation is the tired-light theory. But, as mentioned above, the physics of galaxy rotation in general are difficult to explain without making unproven assumptions. Since the redshift is the most common distance indicator in cosmological scales, a bias in the redshift can impact a large number of other studies that make use of the redshift.

Because the bias tends to become larger when the redshift gets higher, it is possible that such bias can explain anomalies, such as galaxies that according to the existing theories are expected to be older than traditional galaxy formation models predict. The experiments described here were based on relatively low redshift ranges and, therefore, it is still unclear whether higher redshift will have significant redshift bias. Studying the bias in higher redshift would require using a large number of galaxies with redshift imaged by space-based instruments, such as JWST, at around the galactic pole.

Because $H_0$ is determined by using the redshift, a redshift bias can also explain the observed $H_0$ tension. For instance, when using the SH0ES catalog [86] of Ia supernovae, by just selecting the galaxies that rotate in the same direction as the Milky Way, $H_0$ drops from ∼73.7 to ∼69.05 km/s Mpc⁻¹ [87], which is within the statistical error from $H_0$ as observed by the CMB. When using only the SH0ES galaxies rotating in the opposite direction relative to the Milky Way, $H_0$ increases to ∼74.2 km/s Mpc⁻¹ [87]. Although SH0ES contains a relatively small number of Ia supernovae with their host galaxies, this suggests that redshift as a distance indicator may depend on the rotational velocity relative to the rotational velocity of the Milky Way. This observation is also aligned with the contention that the $H_0$ tension may require new physics that apply to the entire Universe, rather than certain changes in the physics of the early Universe [88]. Because $H_0$ is determined by using the redshift, redshift bias can also be related to the observed $H_0$ anisotropy [89,90,91,92,93], which is another puzzling observation that does not have an immediate explanation.

It is also possible that the redshift difference is not a bias, and that galaxies that rotate in the opposite direction relative to the Milky Way are indeed closer to Earth compared to galaxies that rotate in the same direction relative to the Milky Way. In that case, the alignment with both ends of the galactic pole is merely a coincidence. Such large-scale alignment is far larger than any known cluster, super-cluster, or filament in the cosmic web. That may be in agreement with numerous other observations that suggest that the cosmological principle is violated [93].

Although alignment in galaxy spin directions is expected [94,95], it is not expected to form a cosmological-scale axis. If such an axis indeed exists and it is not driven by the impact of the rotational velocity on the redshift measurements then it can be linked with theories such as dipole cosmology [96,97,98,99,100] or the rotating Universe [101,102,103,104,105]. Theories that assume a Universe rotating around a cosmological-scale axis include black hole cosmology [106,107,108,109,110,111,112,113,114,115] and ellipsoidal Universe [116,117,118,119,120].

Tensions between the expected age of some galaxies and the age of the Universe, as well as other cosmological-scale anisotropies and observations, such as the $H_o$ tension, challenge our understanding of the Universe. It is clear that the current theories cannot co-exist with the redshift model as it is used currently, and, therefore, if the current theories are complete then this means that the redshift as a distance indicator is incomplete. This paper shows consistent evidence that the redshift depends on the rotational velocity of the Milky Way relative to the observed objects. The bias is small, but if it increases in the redshift ranges of the JWST deep fields then this would potentially explain the existence of mature galaxies in the early Universe.