Abstract
The shape vibrations of a superheavy nucleus with a complete (bubble) or a partially (semi-bubble) depleted density in its central region and sharp-edge inner and outer surfaces are investigated in the frame of the Liquid-Drop Model. The quadrupole oscillations of the two existing surfaces are coupled in both velocity and coordinate and, upon decoupling, a low-energy and a high-energy component are predicted. The electric transition probabilities are estimated for the decay of the low-lying mode first state to the ground state for the entire range of the radius and density of the depleted core.
1. Introduction
Estimates of the binding energies of hyperheavy nuclei using the Bethe–Weiszäcker semiempirical formula [1] predict the existence of spherical shell (bubble) configurations. Previously, it was noted by Wilson that the formation of a shell instead of a sphere may be caused by the saturation of nuclear forces [2]. Arguing that each nucleon cannot be strongly attracted by more than four nearby particles, he conjectured that the electrostatic forces should pull out a sphere into a shell.
Relativistic mean-field (RMF) calculations for nuclei with charges around point to a pronounced central density depletion [3,4,5]. This result stimulated the appetite of Walter Greiner to conjecture that superheavy elements assume a fullerene-like structure formed of -clusters [6]. The RMF framework applied by Greiner and collaborators in 2002 to the nucleus 292120 suggests the existence of a pronounced depletion of matter in the interior of this superheavy nucleus [7]. In [8], a calculation for the superheavy 240120 was reported and it was concluded that the depletion of density is also visible. It was also pointed out in [7] that, due to the density depletion in the central region of the nucleus 292120, the electric multipole transition densities have oscillations for small radii, more pronounced than for the lighter double-magic nucleus 208Pb.
A first evaluation of the macroscopic energy and Strutinsky shell corrections of a bubble nucleus was performed in [9]. A more thorough discussion of shell effects for bubbles in superheavy and hyperheavy nuclei was carried out in [10,11,12,13,14,15,16].
On the other hand, the possible existence of depleted densities in the inner regions of exotic nuclei was frequently called forth in the literature [17,18,19], along with the quest of the stability of nuclear Coulomb bubbles [20] and the occurrence of -matter in the peripheral regions of nuclei [8,21]. Very recently, RMF calculations [22,23,24] have shown the appearance of low nucleonic density in the central regions of lighter nuclei; 22O and 34,36Si were emphasized as good candidates of being spherical bubble nuclei, whereas 24Ne, 32Si and 34Ar were classified as deformed bubble nuclei.
The formation of unstable bubbles and rings (toroidal-like) in the central collision between equal-mass heavy ions at beam energies per nucleon around 50-60 MeV was predicted by BUU transport calculations [25].
Bubble structures of quantum objects also arise in other fields of modern physics. An example from solid-state physics is provided by the vibrations of a hollow spherical molecule composed of a large number of atoms, such as the C60 fullerenes [26]. The problem of collective excitations in triaxial superheavy nuclei was addressed in [27].
In Section 2, the structure of the collective Hamiltonian for the case of arbitrary multipolarity is investigated. The expression of the deformation energy is given within the Liquid-Drop Model (LDM) and the finite-range LDM (FRLDM). We present expressions for the geometrical surface energy and Krappe–Nix energy of a nucleus with uniform densities of the core and the shell.
Section 3 focuses on the expression of quadrupole vibrational energies, depending on the size and density of the core, and the transition rates of the corresponding excited quantum levels to the ground state.
2. Liquid-Drop Hamiltonian
In this paper, we consider a nuclear liquid drop that, in the ground state, consists of a core of radius and a shell of thickness . Both core and shell are separated by an inner surface that is assumed to be impenetrable, i.e., no exchange of nucleon mass and charge between these two regions is allowed.
Below, the outer and the inner nuclear surfaces are described in a laboratory-fixed system with orientation by a volume conserving expansion into spherical harmonics :
Above, are the dynamic multipole deformations of the inner (1) and the outer (2) surfaces. The two surfaces are assumed to be sharp, i.e., they have no thickness, and, if the nuclear matter inside the core can be completely depleted (left panel of Figure 1), one then speaks of a bubble. If the density of the core, containing nucleons,
is smaller than the density of the outer shell, containing nucleons,
as pictured on the right panel of Figure 1, then one deals with a configuration dubbed in this work as a semi-bubble.
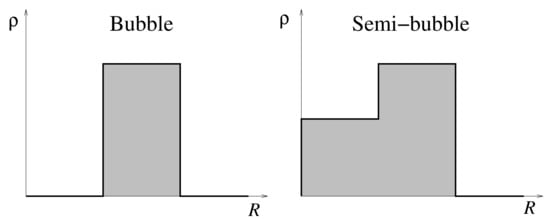
Figure 1.
Artist’s view of the square densities of bubble (left) and semi-bubble (right) nuclei.
At this point, one should remind the reader that the above choice of the nuclear matter density is an ideal one. In Figure 2, the density calculated in [7] within the relativistic mean-field framework, using the NL-Z parametrization for the meson coupling constants, is approximated by a two squares distribution.
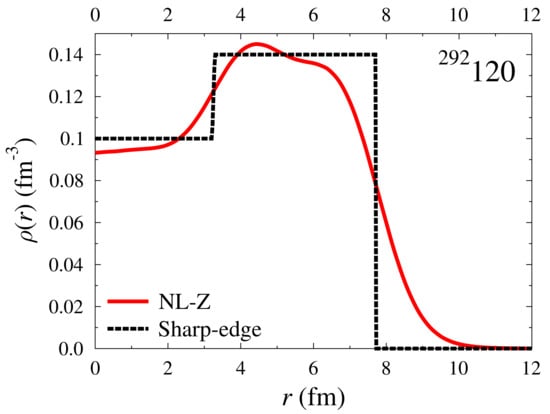
Figure 2.
The nuclear density with depletion in the central region as predicted by the RMF calculations with NL-Z forces [7] (full line) and the simplification to a semi-bubble rectangular-like density (dashed lines).
For sharp surfaces, the total density reads
In what follows, the collective energy of the nuclear drop is computed in the frame of the macroscopic model and consists of a kinetic contribution and a potential part, which accounts for the nuclear energy, calculated with and without finite-range effects, and also the Coulomb energy.
2.1. Kinetic Energy
Similar to the case of a constant density massive nucleus [28], we adopt the assumption that the velocity field is irrotational and incompressible in both inner and outer regions,
Since these conditions are satisfied separately by the nuclear fluids inside the core and the outer shell, we introduce the velocity potential, , as a linear superposition of the contributions from the core and the shell, respectively. Thus, the function satisfies the Laplace equation in each domain:
The solution, regular at the origin, is available in spherical coordinates [29]:
Similar to the case of a massive nucleus, a boundary condition on the nuclear surface of radius is imposed [28]:
A supplementary condition, at the interface between the outer layer of density and the core of density , is derived from the natural requirement in hydrodynamics that, at the frontier between two non-mixing fluids, the normal components of the velocity of both fluids must be equal to the velocity of the separating surface in the direction of momentary normals [30,31]:
where
Using the formula of the nuclear shape (1) and the solutions (8) and (9) in conjunction with the boundary conditions (10) and (11), three equations for the three coefficients , and are obtained:
where the constant , dubbed as breathing deformation in [9], is constant in time due to the incompressibility assumption.
Then, the total kinetic energy splits into a contribution coming from the core (domain enclosed by the surface ) and the outer layer (domain enclosed by the surface ),
The kinetic energy of the fluid inside the core has the same form as that of a massive nucleus of radius [28],
For the outer layer, the calculation is more lengthy. It reads:
2.2. Liquid-Drop Model Macroscopic Deformation Energy
The LDM deformation energy results from the Weiszäcker expansion of the binding energy of a leptodermous nuclear system [32,33]. The first term in the series is the volume energy proportional to the number of particles. For small-amplitude shape fluctuations, this term is considered to have a negligible contribution. This is not the case for giant resonances of a compressional nature. The next term in the expansion is the surface energy that is discussed below.
2.2.1. Surface Energy
The surface energy of the nucleus is proportional to its surface in the LDM,
where is the surface tension (given in units of MeV/fm2). Expressions for the surface energy of a spherical and of a deformed nucleus can be found in the literature (see for example [33]).
For the semi-bubble nucleus, the surface energy is the sum of the outer surface energy, as written in Equations (5.12) and (5.13) of Ref. [9], and the surface energy of the core of radius (taken with minus to compensate the contribution coming from the inner surface of the shell for the case of a nucleus with homogeneous density):
where
and
The number of nucleons in the core and in the shell can be expressed in terms of the nucleus mass number A using the particle number conservation, i.e.,
where is the depletion factor.
The three-dimensional plot of the spherical part of , relative to the ground state value, as a function of p and q is shown in Figure 3 for the superheavy nucleus 292120. This energy increases dramatically with p when the density of the core vanishes (bubble) or is smaller than 1 (semi-bubble). For a nucleus with a homogeneous density distribution (), the surface energy is naturally not dependent on p.
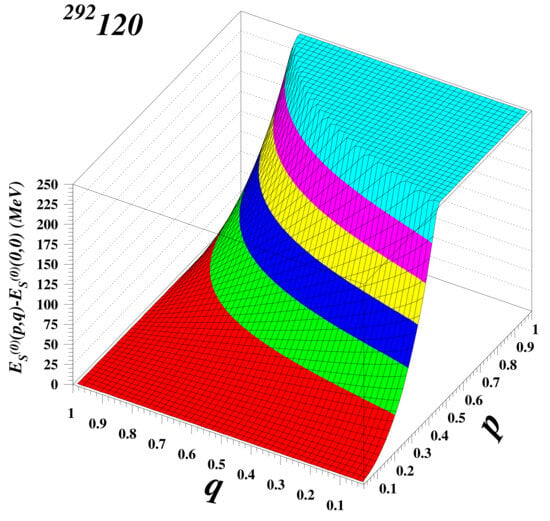
Figure 3.
Three-dimensional plot of the spherical part of the surface energy with respect to the ground state in and coordinates for the nucleus 292120.
2.2.2. Finite-Range Nuclear Energy
A more refined approach to compute the deformation energy consists in folding a phenomenological short-range interaction (e.g., Yukawa, Gauss) into the density distribution:
The surface energy in this case results from subtracting the bulk binding energy from the above expression.
If a Yukawa interaction is employed and the discussion is restricted to uniform density distributions, the single-folded energy (20) is known as the Krappe–Nix (KN) energy [34,35,36]:
For the FRLDM, the physical constants entering the above formula are the surface energy constant , the surface-asymmetry constant , the proton-neutron asymmetry , the nuclear radius constant and the range of the Yukawa potential [37,38].
The integral in the above formula can be expressed as a convolution of the density (4) with the product of the Yukawa kernel and the density [36]. Thus, for a semi-bubble nucleus, the KN energy splits into the following direct and mixed terms:
where and are the KN energies of equivalent massive (with homogeneous density) nuclei of radii . According to [35,36] they read
where and are the modified Bessel functions of rank [39]. It is important to note that the first term in the first square bracket of (22) is the volume energy term and, if subtracted, we are left with the surface energy and the higher-order terms from the leptodermous expansion, customarily known as generalized surface energy [34].
In what follows, instead of the above form, a more concentrated one, deduced in this work, is employed:
Below, we show how to derive the mixed term:
This part of the energy can be split into a spherical and a deformed part if we expand the nuclear form up to quadratic terms in the deformation:
where
and
The three-dimensional plot of the spherical part of , relative to the ground state value, as a function of p and q is shown in Figure 4 for the superheavy nucleus 292120. The qualitative behavior is similar to the surface energy represented in Figure 3.
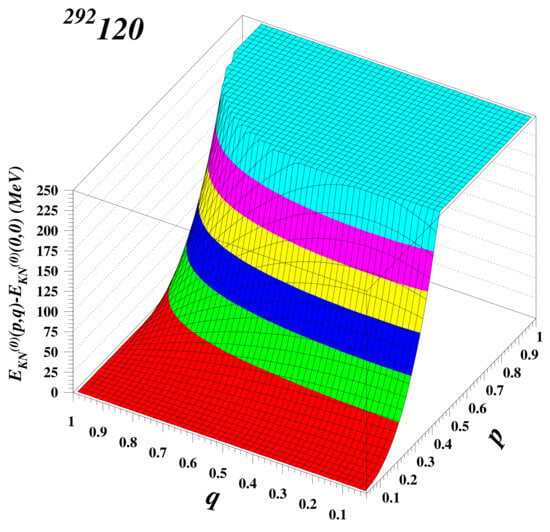
Figure 4.
Three-dimensional plot of the spherical part of the Krappe–Nix energy with respect to the ground state in and coordinates for the nucleus 292120.
2.2.3. Coulomb Energy
For a charge distribution , the Coulomb potential energy is
where the charge density of the semi-bubble reads similar to the mass density (4):
The charge densities of the core, containing protons, are
and of the outer shell, containing protons,
After some lengthy calculations, we arrive at the following expressions for the spherical part,
and the deformation-dependent part,
In the limiting case of a bubble (),
This expression coincides with the form of the Coulomb potential given in Equations (5.24–27) of Wong’s paper [9]. The three-dimensional plot of the spherical part of , relative to the ground state value, as a function of p and q is shown in Figure 5 for the superheavy nucleus 292120. The dip for and indicates the instability of an initially purely charged liquid drop, driven to Coulomb explosion due to the absence of attractive forces.
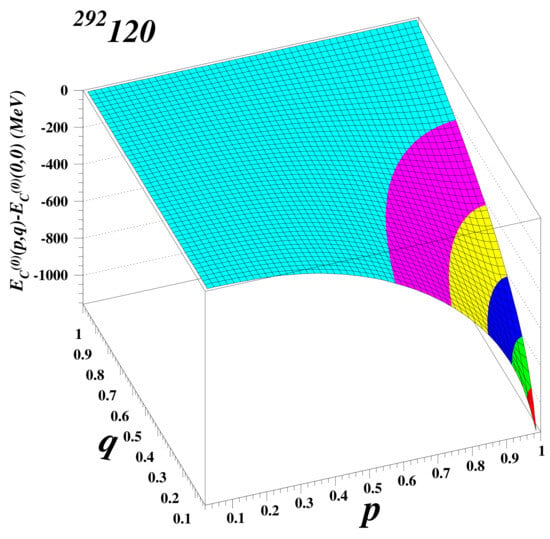
Figure 5.
Three-dimensional plot of the spherical part of the Coulomb energy with respect to the ground state in and coordinates for the nucleus 292120.
3. Coupled Quadrupole Vibrations
In this work, we discuss the mode corresponding to small-amplitude quadrupole oscillations of a bubble/semi-bubble inside an inviscid and irrotational drop around concentric spherical interfaces. More precisely, we are interested in the case when the two surfaces (menisci) are oscillating in phase. This is the bubble mode, which is pictured in Figure 6. If the oscillation of the interfaces occurs in anti-phase, one speaks of a sloshing mode. For an inviscid liquid shell surrounding an incompressible gas bubble, the first mode corresponds to a high-frequency mode [40].
Figure 6.
Schematic illustration of the quadrupole distortions of a bubble nucleus.
According to the findings of the previous section, the classical collective Hamiltonian, including all shape multipolarities, reads
which represents two coupled five-dimensional harmonic oscillators (see Ref. [41] for more details on the harmonic quadrupole oscillator), with couplings of the type coordinate–coordinate () and velocity–velocity () and no coordinate–velocity couplings (). The inertia parameters are given by
where is the LDM inertia moment of a compact nucleus of radius and uniform density .
The Hamiltonian of two coupled harmonic quadrupole oscillators ( in Equation (35)), from which two generalized momenta conjugate to the coordinates can be defined, reads
and is quantized following the standard procedure [28]. For that, we introduce the boson creation and annihilation operators corresponding to the two pairs of conjugate coordinates, i.e., for and for , through the canonical transformations, namely,
where
The quantized Hamiltonian is
We therefore deal with two SU(5) oscillators with , , and couplings, where
Introducing the 20-dimensional column vector
the quadrupole Hamiltonian then acquires the following matrix form:
where the 20 × 20 matrix M reads
The submatrices composing M have the structure
where is the five-dimensional unit matrix, whereas
In order to solve the eigenvalue problem, we have to diagonalize the matrix (see [42] for details), where
and is the ten-dimensional unit matrix. The eigenvalues are
We therefore end up with two decoupled five-dimensional oscillators, one of high-frequency and the other one of low-frequency :
The evolution of the high-frequency mode with p and q is displayed in Figure 7. In the range , increases with the core’s depletion and with a larger . For , attains a maximum for a given q and afterwards starts to decrease with growing depletion. A similar trend can be inferred from Figure 8 for . It should be also pointed out that, for a nucleus with homogeneous matter distribution () and vanishing core radius (), is finite (≈0.4 MeV), whereas the low-frequency mode fades away.
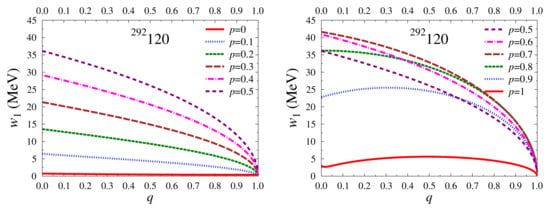
Figure 7.
The high-frequency mode dependence on q for p = 0, 0.1, 0.2, 0.3, 0.4 and 0.5 (left panel) and p = 0.5, 0.6, 0.7, 0.8, 0.9 and 1 (right panel) for the spherical superheavy nucleus 292120.
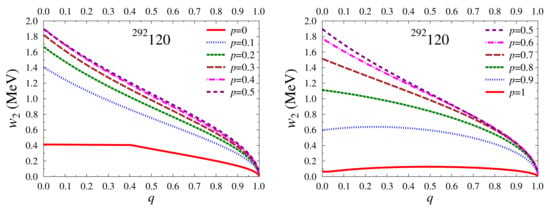
Figure 8.
The low-frequency mode dependence on q for p = 0, 0.1, 0.2, 0.3, 0.4 and 0.5 (left panel) and p = 0.5, 0.6, 0.7, 0.8, 0.9 and 1 (right panel) for the spherical superheavy nucleus 292120.
The strength of these vibrational states can be assessed by estimating the transition probability for the electromagnetic decay from a one-phonon state 2+ to the zero-phonon 0+ state. For that purpose, the quadrupole moment operator is introduced [43]:
Inserting in the formula above, the specific shape parametrization (1) and the nucleon density for a bubble-like nucleus (4), a straightforward calculation, yields
For simplicity, we assumed in the above formula that the ratio of nuclear radii (densities) coincides with the ratio of charge radii . This assumption was already used in deriving the various pieces of the Coulomb potential energy in Section 2.2.3. It is also important to note that the charge numbers of the core, , and of the shell, , are related to p and q according to the formulas
As an example, we take the decay to the ground-state of the quadrupole state corresponding to the low-lying mode, i.e., . The corresponding transition probability reads
The representation of the ratio of to its value in the uniform case, i.e., , is displayed in Figure 9. It indicates a sharp decrease of the transition probability with the growing density depletion of the core. Moreover, for an increase in the size of the core, the decay probability of the low-lying quadrupole state is reduced significantly.
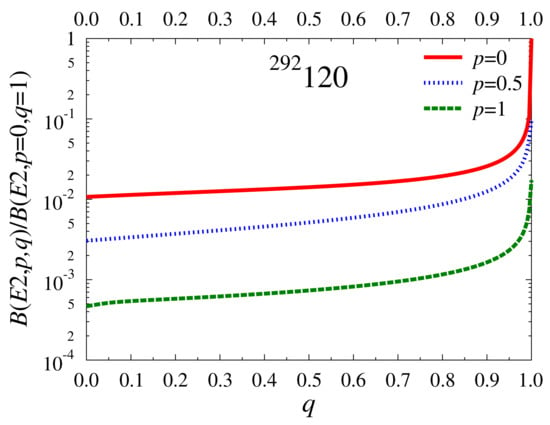
Figure 9.
dependence on q for p=0, 0.1, and 1 for the spherical superheavy nucleus 292120.
4. Summary and Outlook
Compared to the old study of Wong [9], which deals with bubble-shaped nuclei, the present work extends the investigation such that semi-bubble shapes are also dealt with. The analysis introduces an additional parameter in the macroscopic deformation energy, i.e., the ratio q of the core to the shell density.
The main conclusion of the present study concerns the possibility of generating, within the LDM, a new branch of surface oscillations for a nucleus with a significant density depletion in the central region. The standard branch is characterized by high frequencies increasing further with the enhanced depletion of nuclear matter inside the core. The situation changes in the limit of vanishing thickness of the shell (bubble nucleus) when the energies of both modes are drastically diminished compared to the more realistic semi-bubble case when (see Figure 2). On the other hand, transition rates are large only in the vicinity of nuclei with a uniform density.
Studies on viscous and inviscid fluids point out that small perturbations decentering the bubble inside the drop do not induce motion of the liquid and, therefore, the bubble’s center is not restored toward the center of mass of the bubble–shell aggregate [40]. Analogously, for the particular type of nuclei discussed in this work, one could inquire on the possible existence of a dipole oscillation of the core with respect to the outer shell, a type of collective motion which bears some similarities to the pygmy resonance [44].
Regarding the possibility of observing the decay of collective levels discussed in this paper, one could imagine, first, their excitation through the bombardment with intense beams of nuclei, simultaneously with or following the synthesis of the superheavy nucleus with the same projectiles. The formation of bubble nuclei in heavy-ion reactions was discussed in [45,46,47]. In the context discussed in this work, one could envisage a scenario in which, during the formation of the compound semi-bubble superheavy nucleus, phonon levels of the type discussed in this work are also populated and subsequently decay electromagnetically.
One should add that the present analysis can be extended to include protons and neutrons separately. The spectrum of collective states is then expanded with anti-phase vibrations of proton surfaces compared to neutron ones, as discussed in [48] for nuclei with uniform density.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
I am grateful to Joachim Maruhn for his suggestions, going back to 2003, from which the present analysis emerged. This work was supported by the Ministry of Research and Innovation of Romania, through the Project PN 23 21 01 01/2023.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Siemens, P.J.; Bethe, H.A. Shape of heavy nuclei. Phys. Rev. Lett. 1967, 18, 704–706. [Google Scholar] [CrossRef]
- Wilson, H.A. A spherical shell nuclear model. Phys. Rev. 1946, 69, 538. [Google Scholar] [CrossRef]
- Davies, K.T.R.; Wong, C.Y.; Krieger, S.J. Hartree-Fock calculations of bubble nuclei. Phys. Rev. B 1972, 41, 455–457. [Google Scholar] [CrossRef]
- Rutz, K. Struktur von Atomkernen im Relativistic-Mean-Field-Modell; Ibidem-Verlag: Stuttgart, Germany, 1999. [Google Scholar]
- Bender, M.; Rutz, K.; Reinhard, P.-G.; Maruhn, J.A.; Greiner, W. Shell structure of superheavy nuclei in self-consistent mean-field models. Phys. Rev. C 1999, 60, 034304. [Google Scholar] [CrossRef]
- Greiner, W. Nuclear Cluster Structure: Superheavies, cluster-radioactivity and exotic fission processes. Heavy Ion Phys. 2001, 13, 61–78. [Google Scholar] [CrossRef]
- Mişicu, Ş.; Bürvenich, T.; Cornelius, T.; Greiner, W. Properties of some collective excitations in spherical nuclei from the superheavy island. J. Phys. G 2002, 28, 1441–1452. [Google Scholar] [CrossRef]
- Mişicu, Ş.; Mishustin, N.I. The Fullerene-like Structure of Superheavy Element Z = 120 (Greinerium)—A Tribute to Walter Greiner; Walter Greiner Memorial Volume; Hess, P.O., Stöcker, H., Eds.; World Scientific: Singapore, 2018. [Google Scholar]
- Wong, C.Y. Toroidal and spherical bubble nuclei. Ann. Phys. 1973, 77, 279–353. [Google Scholar] [CrossRef]
- Dietrich, K.; Pomorsky, K. Stability of bubble nuclei through shell effects. Phys. Rev. Lett. 1998, 80, 37–40. [Google Scholar] [CrossRef]
- Dechargé, J.; Berger, J.-F.; Dietrich, K.; Weiss, M.S. Superheavy and hyperheavy nuclei in the form of bubbles or semi-bubbles. Phys. Rev. B 1999, 451, 275–282. [Google Scholar] [CrossRef]
- Berger, J.-F.; Bitaud, L.; Dechargé, J.; Girod, M.; Dietrich, K. Superheavy, hyperheavy and bubble nuclei. Nucl. Phys. A 2001, 685, 1–16. [Google Scholar] [CrossRef]
- Dechargé, J.; Berger, J.-F.; Girod, M.; Dietrich, K. Bubbles and semi-bubbles as a new kind of superheavy nuclei. Nucl. Phys. A 2003, 716, 55–86. [Google Scholar] [CrossRef]
- Yu, Y.; Bulgac, A.; Magierski, P. Shell correction energy for bubble nuclei. Phys. Rev. Lett. 2000, 84, 412–415. [Google Scholar] [CrossRef] [PubMed]
- Bulgac, A.; Magierski, P. Bubble nuclei, neutron stars and quantum biliards. In Proceedings of the Bologna 2000: Structure of the Nucleus at the Dawn of the Century, Bologna, Italy, 29 May–3 June 2000; Bonsignori, G.C., Bruno, M., Ventura, A., Vretenar, D., Eds.; World Scientific: Singapore, 2001. [Google Scholar]
- Perera, U.C.; Afanasjev, A.V. Bubble nuclei: Single-particle versus Coulomb interaction effects. Phys. Rev. C 2022, 106, 024321. [Google Scholar] [CrossRef]
- Campi, X.; Sprung, D.W.L. Possible bubble nuclei -36Ar and 200Hg. Phys. Lett. B 1973, 46, 291–295. [Google Scholar] [CrossRef]
- Khan, E.; Grasso, M.; Margueron, J.; Van Giai, N. Detecting bubbles in exotic nuclei. Nucl. Phys. A 2008, 800, 37–46. [Google Scholar] [CrossRef]
- Grasso, M.; Gaudefroy, L.; Khan, E.; Nikšić, T.; Piekarewicz, J.; Sorlin, O.; Van Giai, N.; Vretenar, D. Nuclear “bubble” structure in 34Si. Phys. Rev. C 2009, 79, 034318. [Google Scholar] [CrossRef]
- Moretto, L.G.; Tso, K.; Wozniak, G.J. Stable Coulomb bubbles. Phys. Rev. Lett. 1997, 78, 824–827. [Google Scholar] [CrossRef]
- Tohsaki, A.; Itagaki, N. Coulomb energy of α-aggregates on a soap bubble shape. Phys. Rev. C 2018, 98, 014302. [Google Scholar] [CrossRef]
- Shukla, A.; Åberg, S.; Patra, S.K. Nuclear structure and reaction properties of even–even oxygen isotopes towards drip line. J. Phys. G 2011, 38, 095103. [Google Scholar] [CrossRef]
- Shukla, A.; Åberg, S. Deformed bubble nuclei in the light-mass region. Phys. Rev. C 2014, 89, 014329. [Google Scholar] [CrossRef]
- Shukla, A.; Åberg, S.; Bajpeyi, A. Systematic study of bubble nuclei in relativistic mean field model. Phys. Atom. Nuclei 2016, 79, 11–20. [Google Scholar] [CrossRef]
- Bauer, W.; Bertsch, G.F.; Schulz, H. Bubble and Ring Formation in Nuclear Fragmentation. Phys. Rev. Lett. 2016, 69, 1888–1891. [Google Scholar] [CrossRef]
- Menéndez, J.; Page, J.B. Vibrational Spectroscopy of C60. In Light Scattering in Solids VIII; Cardona, M., Güntherodt, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Hess, P.O.; Mişicu, Ş. Potential energy surfaces and spectra of superheavy elements. Phys. Rev. C 2003, 68, 064303. [Google Scholar] [CrossRef]
- Eisenberg, J.; Greiner, W. Nuclear Models I; Elsevier: Amsterdam, The Netherlands, 1987; p. 747. [Google Scholar]
- Frank, P.; von Mises, R. Die Differential- und Integralgleichungen der Mechanik und Physik: 1 Mathematischer Teil; Dover Publications: New York, NY, USA; Friedr. Vieweg & Sohn: Braunschweig, Germany, 1961; p. 386. [Google Scholar]
- Frank, P.; von Mises, R. Die Differential- und Integralgleichungen der Mechanik und Physik: 2 Physikalischer Teil; Dover Publications: New York, NY, USA; Friedr. Vieweg & Sohn: Braunschweig, Germany, 1961; p. 383. [Google Scholar]
- Greiner, W.; Stock, H. Hydrodynamik; Verlag Harri Deutsch: Frankfurt, Germany, 1991; p. 44. [Google Scholar]
- Myers, W.D. Droplet Model of Atomic Nuclei; IFI/Plenum: New York, NY, USA, 1977; p. 3. [Google Scholar]
- Greiner, W.; Maruhn, J.A. Kernmodelle; Verlag Harri Deutsch,: Frankfurt, Germany, 1996; p. 134. [Google Scholar]
- Krappe, H.J.; Nix, J.R. Modified definition of the surface energy in the liquid drop formula. In Proceedings of the Third International Atomic Energy Agency Symposium on the Physics and Chemistry of Fission, Rochester, NY, USA, 13–17 August 1973; Volume I, pp. 159–175. [Google Scholar]
- Krappe, H.J.; Nix, J.R.; Sierk, A.J. Unified nuclear potential for heavy-ion elastic scattering, fusion, fission, and ground-state masses and deformation. Phys. Rev. C 1979, 20, 992–1013. [Google Scholar] [CrossRef]
- Krappe, H.J. Folding methods in Heavy-Ion Physics. Nucl. Sci. Res. Conf. Ser. 1984, 5, 197–236. [Google Scholar]
- Möller, P.; Nix, J.R.; Myers, W.D.; Świa̧tecki, W.J. Nuclear ground-state masses and deformations. At. Data Nucl. Data Tables 1995, 59, 185–381. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109, 1–204. [Google Scholar] [CrossRef]
- Abramowitz, A.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964. [Google Scholar]
- Tsamopoulos, J.A.; Brown, R.A. Dynamic centering of liquid shells. Phys. Fluids 1987, 30, 27–35. [Google Scholar] [CrossRef]
- Weber, H.J.; Huber, M.G.; Greiner, W. Zur klassifikation der Zustände des 5-dimensionalen harmonischen Oszillators. Z. Phys. 1966, 190, 25–29. [Google Scholar] [CrossRef]
- Blaizot, J.-P.; Ripka, G. Quantum Theory of Finite Systems; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Raman, S.; Nestor, C.W., Jr.; Tikkanen, P. Transition probability from the ground to the first-excited 2+ state of even-even nuclides. At. Data Nucl. Data Tables 2001, 78, 1–128. [Google Scholar] [CrossRef]
- Bastrukov, S.I.; Molodtsova, I.V.; Podgainy, D.V.; Mişicu, Ş.; Chang, H.-K. Elasticity of nuclear medium as a principal macrodynamical promoter of electric pygmy dipole resonance. Phys. Rev. B 2008, 664, 258–264. [Google Scholar] [CrossRef]
- Wong, C.-Y. Hot Toroidal and Bubble Nuclei. Phys. Rev. Lett. 1985, 55, 1973–1975. [Google Scholar] [CrossRef]
- Xu, H.M.; Gagliardi, C.A.; Tribble, R.E.; Wong, C.Y. Multifragmentation of toroidal and bubble nuclei within the BUU approach. Nucl. Phys. A 1994, 569, 575–602. [Google Scholar] [CrossRef]
- Yong, G.-C. Hollow nuclear matter. Phys. Rev. C 2016, 93, 014602. [Google Scholar] [CrossRef]
- Faessler, A. E2-Oberflächenresonanzen in sphärischen Kernen. Nucl. Phys. 1966, 85, 653–669. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).