Abstract
In this article, we highlight that the interaction potential confining Dirac particles in a box must be invariant under the charge conjugation to avoid the Klein paradox, in which an infinite number of negative-energy particles are excited. Furthermore, we derive the quantization rules for a relativistic particle in a cylindrical box, which emulates the volume occupied by a beam of particles with a non-trivial aspect ratio. We apply our results to the evaluation of the quantum limit for emittance in particle accelerators. The developed theory allows the description of quantum beams carrying Orbital Angular Momentum (OAM). We demonstrate how the degeneracy pressure is such to increase the phase–space area of Dirac particles carrying OAM. The results dramatically differ from the classical evaluation of phase–space areas, that would foresee no increase in emittance for beams in a coherent state of OAM. We discuss the quantization of the phase–space cell’s area for single Dirac particles carrying OAM, and, finally, provide an interpretation of the beam entropy as the measure of how much the phase–space area occupied by the beam deviates from its quantum limit.
1. Introduction
We face the problem of a Dirac particle in a box with the aim of applying our findings to the evaluation of the quantum limit for the beam emittance in particle accelerators. Firstly, the physics of the Klein paradox are reviewed, which affect the problem of a particle in a box in relativistic quantum mechanics. It is demonstrated that the correct box potential must be invariant under charge conjugation, which is an equivalent approach to the locally variable particle mass [1,2]. Furthermore, we solve the problem of a Dirac particle within a box in cylindrical symmetry, differently from the cartesian symmetry used in [3,4]. Cylindrical symmetry best fits the description of a particle beam with a transverse dimension (i.e., the size of the beam in the plane orthogonal to the propagation) that is different from the longitudinal dimension (the length of the beam along the axis of propagation). After finding the quantization rules, we derive an analytical expression of the quantum limit for the transverse beam emittance in particle accelerators. Transverse beam emittance is a figure of merit for a particle beam: the lower the emittance, the better the performance for collision or radiation purposes [5]. Our results show that the transverse phase–space can be strongly compressed by the longitudinal (axial) momentum spread. Finally, the cylindrical symmetry naturally allows the consideration of quantum particle beams carrying Orbital Angular Momentum (OAM). Thus, an expression of the emittance for such beams is derived and compared to the one obtained for particle beams without OAM. Analogous discussions are presented for the case of single-particle emittance. A final comment on the relation between emittance and entropy is given.
2. On the Box Potential for Particles and Anti-Particles
The problem of a particle in a box is solved in non-relativistic quantum mechanics by imposing a vanishing wave function at the boundaries of the box, where the box’s potential is sent to infinity. As discussed in [3,4], when approached as in the non-relativistic case, the problem of a Dirac particle in a box leads to the so-called Klein paradox [6,7,8], in which the reflected flux in the walls of the potential is larger than the incident flux. The problem has been avoided in [3,4], introducing a locally variable mass and suitable boundary conditions preserving the continuity of the probability current rather than the wave function. Moreover, the variable mass is such to go to infinity outside the box boundaries, while remaining finite at its proper value inside the box. In the following, we show that the mathematical trick of a locally variable mass is equivalent to the definition of an interaction potential that is invariant under these conditions. For the relativistic particle in a box, we propose a Dirac equation of the following kind:
where H is the Dirac hamiltonian operator, is the bispinor, E is the energy eigenvalue of the equation, m is the mass of the Dirac particle, c is the speed of light in vacuum, is the momentum of the particle, and the and matrices in Dirac representation are defined as:
where is the unit matrix and is the vector of Pauli matrices. It is important to note that the box potential enters Equation (1) as , and not just as V. Considering internally to the box and externally, the same behavior of a variable mass is obtained. Indeed, in our notation, we define the charge conjugation operator as , where is the complex conjugation operator and the matrix is:
Applying C to Equation (1) yields:
where , representing the anti-particle, i.e., the negative energy state. If the box potential entered the Dirac equation in such a way that:
once the charge conjugation operator was applied to Equation (5), one would obtain:
Therefore, sending would bring to the Klein paradox, in which an increasing number of negative-energy particles are excited. Written as in Equation (5), the potential would correspond to an electrostatic potential, changing sign under charge conjugation. However, the box electrostatic potential cannot be of trivial scalar nature. Indeed, such a potential is an artificial representation of a more complicated force able to confine Dirac particles, and it must be invariant under C-symmetry.
3. Relativistic Particle in a Cylindrical Box
The solution of the free Dirac equation is fundamental in constructing the theory of a relativistic particle in a box, since, in addition to the boundary conditions, it corresponds to the wave function inside the box. The Dirac equation for a free particle is:
We remark that the and Dirac matrices in Equation (2) are matrices acting on the bispinor . In this paper, we consider a cylindrical box with transverse radius R and axial length L, as shown in Figure 1. The box potential is assumed to be such that Dirac particles can only be found within the cylinder volume. The cylindrical volume represents the volume occupied by a particle beam, i.e., an ensemble of confined particles, with a non-trivial aspect ratio (such as a sphere or a cube). The beam radius is then R and the bunch length is L. The beam propagation axis is z.
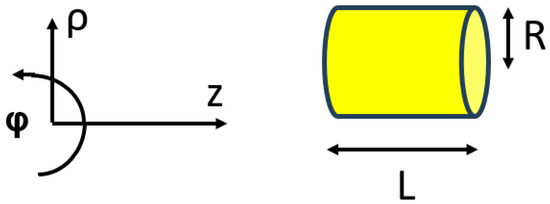
Figure 1.
Left: Cylindrical coordinates system for this paper. Right: Cylindrical box with transverse radius R and axial length L.
The vector of Pauli matrices in cylindrical coordinates is . The latter matrices are represented as:
In cylindrical coordinates and in terms of the upper (u) and lower spinor components (v), the Dirac equation reads:
where the quantum expression of the momentum operator is , with ℏ being the Planck constant. The positive energy solution of Equation (9) is found as:
where A and B are normalization constants, is the particle spinor, and the radial wavenumber is defined as:
Before proceeding to the calculation of the Dirac particle eigenstates in the cylindrical box, let us note that l corresponds to the azimuthal quantum number associated with the operator , i.e., the third component of the OAM. For sake of simplicity, from now on, we consider , returning to the topic at the end of the work. Therefore, the particle wave function will be described by:
As demonstrated in [3,4], the proper boundary condition yielding the quantization rules for the relativistic particle in a box is applied to the probability current instead of the wave function as in non-relativistic quantum mechanics. The vanishing of the outward component of the probability current at the boundaries is obtained by requiring that the condition locally holds there, where the minus sign is used for the outgoing current towards the positive direction of a given axis and vice versa. Given a radial boundary at , i.e., for a particle that cannot be found for , and using the solution of the free Dirac equation, the quantization rule for the radial momentum of the particle is found via:
from which, it is possible to obtain:
where is the Lorentz factor of the particle and pm is the reduced Compton wavelength. It is important to note that, when the Compton wavelength is to be considered negligible on the scale of (in other words, when the radial particle momentum is non-relativistic), the quantization condition at Equation (16) reduces to the non-relativistic one, i.e., . Thus, Equation (16) behaves well in the non-relativistic limit, yielding the same result expected from the Schroedinger equation. In an analogous way, for a limited domain of existence for the particle along z, ranging in , it is possible to obtain the quantization rule for the axial momentum :
Equation (17) is the same as that found in [3] for a Dirac particle within a 1D box. As for the radial case, in the non-relativistic limit , the same quantization expected from the Schroedinger equation is retrieved. The positive energy eigenvalue of the Dirac particle is finally found as:
To conclude, it must be noted that Equations (16) and (17) and coupled via and must hold at the same time.
4. Limit of a Relativistic Particle Beam
For a paraxial relativistic particle beam , and, moreover, . In these conditions, ; therefore, Equation (17) becomes:
The quantization rule for ultra-relativisitc particles is easily found as:
with the axial quantum number ranging within naturals, i.e., . Furthermore, for ultra-relativistic particle beams with bunch length , the average Lorentz factor corresponds to a very large axial quantum number. The particle states fall very close each other along the momentum axis . It is possible, then, to approximate Equation (16) as:
where in the last passage we have considered . In order to count how many states are occupied along the axial momentum space, It is sufficient to recall that the quantum of axial momentum, from Equation (20), is . Therefore, for a full-width-at-half-maximum (FWHM) momentum spread , it is possible to define the number of occupied states along as:
Given a beam made by N particles, each state occupation can be twofold due to spin degeneracy. For counting the number of occupied states in the transverse momentum space, it is necessary to consider the distribution of the zeros . We adopt the McMahon expansion [9]:
where .
Defining the Fermi-line in the radial momentum space as the curve along which the maximum radial momenta are distributed (see Figure 2), the number of states occupied in the transverse momentum space is found counting the zeros up to . Thus, by means of Equation (23), it is possible to obtain:
where is called Fermi level. For , i.e., for a single particle in the system, , while for . Recognizing that , It is finally possible to set the following identity for the case :
Equation (25) establishes the relation between the Fermi level and the beam momentum spread, which acts compressing the Fermi area. This behavior must be expected from the fact that particles with slightly different axial momenta can occupy the same state in the transverse phase–space.
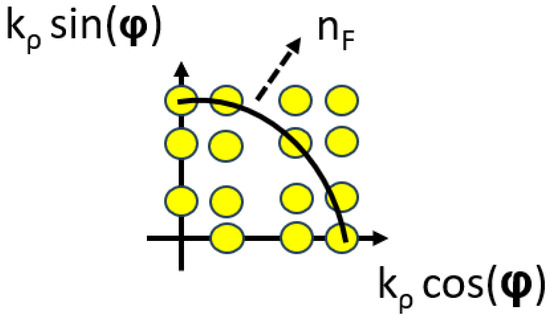
Figure 2.
Occupation of states in the sub-space. The drawn line defines the Fermi level, as the line of maximal transverse momenta.
5. Rms Observables
Root mean square (rms) observables are calculated by standard definitions. For the rms value of the operators on a generic Dirac particle state, we use:
The observable is found via Equation (26) replacing . The final result is found in terms of the generalized hypergeometric function and Bessel functions and , but it can be approximated by introducing the Euler–Mascheroni constant :
It is possible to notice that the approximation at Equation (27) allows the estimation of with an expression which does not depend upon the radial quantum number, i.e., that is the same for all the eigenstates (see Figure 3).
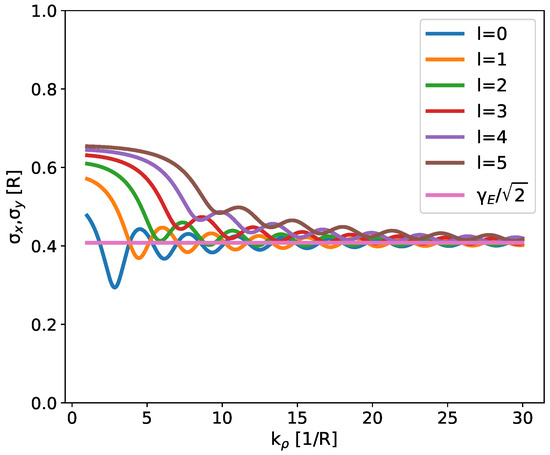
Figure 3.
Value of for different OAM states.
The rms value of the angular operator is found as:
with an identical expression for , obtained replacing . Figure 4 shows that Equation (28) can be approximately valid for higher OAM states.
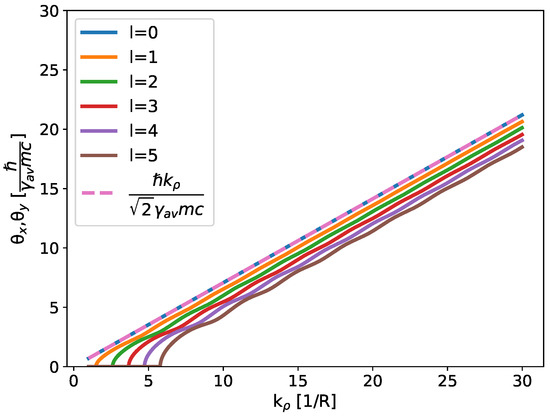
Figure 4.
Value of for different OAM states.
Finally, the correlation observable is found:
Solving the integral in Equation (29) yields:
The observable is found via Equation (29), replacing , leading to the same result of Equation (30). Figure 5 shows that, for large enough occupation numbers (), the correlation term is limited to small values (), even for relatively large OAM states. We note that, due to the axisymmetry of the considered beam, , and , where the subscript “r” stays for “radial”.
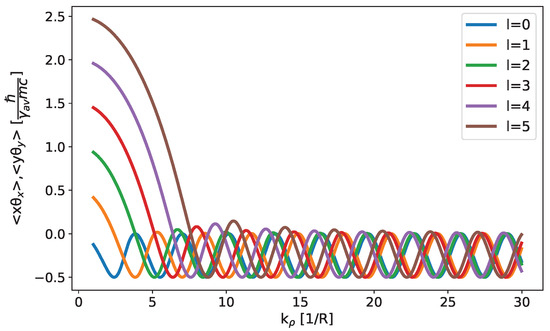
Figure 5.
Value of transverse phase–space correlation for different OAM states.
6. Transverse Beam Emittance: The Quantum Limit
The definition of rms normalized transverse (radial) emittance for the single particle state is:
The rms emittance measures the area occupied by the single state in the horizontal(vertical) phase–space, being just a normalization constant conventionally adopted in particle accelerator physics [5]. The total radial beam emittance is to be calculated summing up all single contributions from the occupied states:
For a momentum spread such that Equation (32) can be further simplified to:
where—performing the sum in Equation (33)—we have used Equation (23). We observe that momentum spread can considerably decrease the beam transverse emittance, for the particles occupy different states of axial momentum so that they can be compacted in a smaller transverse phase–space. This behavior cannot been taken into account when considering a spherically symmetric Fermi-sea, as in [10], but analogous results can be found in [11] for the case of quantum oscillators. For a relativistic bunch of electrons corresponding to , with length m (300 fs) and momentum spread (half a MeV), the quantum limited emittance value is of the order of 1 pm and the Fermi level is .
7. Role of the Transverse Temperature and Classical Limit
It is customary to associate a temperature to the maximal kinetic energy value of a Fermi gas. In particular, for the transverse kinetic energy, the maximum value for is , where is the Boltzmann constant and we have assumed that is non-relativistic. It is important to note that the Fermi temperature that we have introduced here refers only to the radial momentum space. Recalling Equation (33), it is possible to establish the following relation between quantum emittance and Fermi temperature:
where, in this section, the quantum emittance is understood as the radial emittance that has been previously introduced. For a classical beam of particles, we can define the emittance at the source as , where for a thermionic gun is the temperature of the cathode; meanwhile, for a photoelectric gun, , where is the photon energy used to extract charge from the cathode and W the work function of the latter. The scaling of the emittance as a function of temperature is very different for the quantum case compared to the classical one, due to the different equation of state of the two gases. The classical limit for the behavior of a particle beam is not simply obtained by directly comparing with . Indeed, using Equation (27), the ratio between quantum and classical emittance is found:
For a relativistic bunch of electrons corresponding to , with length m and momentum spread , the ratio between the quantum and classical emittances is:
When the temperature is of the order of a fraction of eV, corresponding to a momentum spread of the same order of magnitude at the cathode, the quantum to classical emittance ratio at Equation (36) is of the order of , showing that the above-considered beams behave classically. Moreover, we can define a critical temperature, for which the ratio at Equation (36) is equal to one, implying a quantum behavior of such beams. Given the above choice of parameters, the critical temperature value is K, corresponding to a momentum spread at the source which is below 1 neV. In order to keep quantum effects alive in a particle accelerator, such a spread should be preserved along the acceleration chain, which is demanding.
8. Particle Beams Carrying Orbital Angular Momentum
For Dirac particles carrying OAM, the bispinor solution of the wave equation is determined by Equations (10) and (11). Let us assume that all particle in the ensembles are in the same state of angular momentum, defined by the quantum number l. In these conditions, it is possible to state that the beam carries OAM . In the limit of a relativistic particle beam in the paraxial approximation, the quantization rule for , as for the case , is found as:
which is solved by , where . For counting the number of occupied states in the transverse momentum space, we consider the distribution of the zeros. We adopt an approximation similar to Equation (23) [9]:
The number of occupied states in the transverse momentum space is, therefore:
The Fermi level is determined by inversion of Equation (39). From Figure 3, Figure 4 and Figure 5, it is possible to note that, for relatively large occupation numbers, and mc, for any value of OAM. In the same approximation, the correlation terms are negligible, as was the case for . Therefore, the final transverse emittance is easily found as:
Equation (40) is completely equivalent to Equation (33) for and for all the cases of relatively small OAM . Otherwise, the OAM increases the emittance of the particle beam. For the same parameters used in the example at the end of Section 6, an OAM corresponding to would lead to a non-negligible increase in transverse emittance of ∼30%.
In the classical limit, the radial emittance of a beam with OAM is expected to be [12]:
where has been discussed in Section 7, and the OAM contribution to classical emittance is:
It is interesting to recall that the OAM denotes an coupling that extends the projected transverse phase–space, leading to the increase in emittance compared to the zero OAM case, in both the quantum and classical cases. Equation (42) measures the spread of the OAM within the particle beam, since each particle can carry a different value of OAM. A degenerate beam, with all particles carrying the same OAM, i.e., , as considered at the beginning of this section, would carry zero OAM according to classical theory. Conversely, as we have shown, an appropriate quantum treatment considering the Pauli exclusion principle leads to the correct results given by Equation (40), where a non-negligible correction appears of the order of , leading to emittance increase.
9. Single-Particle Emittance
A single particle with occupies the ground state . The rms value for the position operators becomes:
The rms divergence of the ground state is then:
It is important to notice that , obeying the Heisenberg principle of uncertainty. Furthermore, from Equation (30), it is easily verified that:
Thus, the single-particle transverse emittance is found:
In Table 1, we report the values of single-particle emittance for different states of OAM.

Table 1.
Single-particle transverse emittance for different states of OAM.
It is worth noting that, for large values of l, the difference between single-particle emittance values for different states of OAM tends to be comparable to the ground-state emittance given by Equation (46).
10. Entropy
In the classic paper [13], the entropy formula for the kind of beam considered in this work is reported:
which determines the contribution to the entropy due to the classical emittance . The A parameter, for Lawson, is the elementary area of the transverse phase–space cell. By identifying the elementary area as , the entropy can be interpreted as the measure of how much the emittance of the beam deviates from its quantum limit. Furthermore, using the Sommerfeld expansion [14], one could write , where . When , i.e., for very low temperatures, the entropy goes to zero, recovering the third principle of thermodynamics.
11. Summary and Conclusions
In conclusion, we have presented a work on the the quantum mechanics problem of the relativistic particle in a box. We have highlighted that the box interaction potential figuring in the Dirac equation must be invariant under charge conjugation, in order to avoid the Klein paradox. Furthermore, we have found quantization rules for the particle momentum in a cylindrical 3D box, resembling the shape of a particle beam with a non-trivial aspect ratio. Starting from that, we have estimated the quantum limit for the beam emittance in particle accelerators. Our findings demonstrate that the transverse beam emittance can be compressed by the axial momentum spread. In fact, particles can occupy the same state of transverse momentum as far as they occupy different state of longitudinal momentum. Differently from the plane–wave theory in cartesian coordinates, our theoretical description naturally allows us to study quantum particle beams carrying orbital angular momentum. Finally, we have presented a discussion on the single-particle emittance for different states of OAM. For a relativistic bunch of electrons corresponding to , with length and radius m and momentum spread (half a MeV), we have found that the quantum limited emittance value is of the order of 1 pm. For the above beam parameters and for ordinary beams generated by thermionic or photoelectric electron guns, we have calculated that quantum effects are negligible; this is because, for them to be observable, the momentum spread at the source should reach values well below 1 neV and be preserved along the accelerator.
Author Contributions
Conceptualization, M.F., A.C. (Alessandro Cianchi) and A.C. (Alessandro Curcio); Methodology, A.C. (Alessandro Curcio); Software, A.C. (Alessandro Curcio); Validation, A.C. (Alessandro Curcio); Formal Analysis, A.C. (Alessandro Curcio); Investigation, A.C. (Alessandro Curcio), A.C. (Alessandro Cianchi) and M.F.; Resources, M.F., A.C. (Alessandro Cianchi) and A.C. (Alessandro Curcio); Data Curation, A.C. (Alessandro Curcio), A.C. (Alessandro Cianchi) and M.F.; Writing—Original Draft Preparation, A.C. (Alessandro Curcio); Writing—Review & Editing, M.F., A.C. (Alessandro Cianchi) and A.C. (Alessandro Curcio); Visualization, M.F., A.C. (Alessandro Cianchi) and A.C. (Alessandro Curcio); Supervision, M.F.; Project Administration, M.F.; Funding Acquisition, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results received funding from the European Union co-funding “Next Generation EU”.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Conflicts of Interest
The authors declare no competing interests.
References
- Thomas, A.W. Chiral symmetry and the bag model: A new starting point for nuclear physics. In Advances in Nuclear Physics: Volume 13; Springer: Berlin/Heidelberg, Germany, 1984; pp. 1–137. [Google Scholar]
- Bhaduri, R. Models of the Nucleon: From Quarks to Soliton. In Vol. 22 of Lecture Notes and Supplements in Physics Addison-Wesley; Addison-Wesley: Redwood City, CA, USA, 1988. [Google Scholar]
- Alberto, P.; Fiolhais, C.; Gil, V. Relativistic particle in a box. Eur. J. Phys. 1996, 17, 19. [Google Scholar] [CrossRef]
- Alberto, P.; Das, S.; Vagenas, E.C. Relativistic particle in a three-dimensional box. Phys. Lett. A 2011, 375, 1436–1440. [Google Scholar] [CrossRef]
- Wiedemann, H. Particle Accelerator Physics; Springer Nature: Berlin, Germany, 2015. [Google Scholar]
- Adler, C.G. The relativistic one-dimensional square potential. Am. J. Phys. 1971, 39, 305–309. [Google Scholar] [CrossRef]
- Coutinho, F.A.B.; Nogami, Y.; Toyama, F. General aspects of the bound-state solutions of the one-dimensional Dirac equation. Am. J. Phys. 1988, 56, 904–907. [Google Scholar] [CrossRef]
- Greiner, W. Relativistic Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 2. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1968; Volume 55.
- Mikhailichenko, A. To the quantum limitations in beam physics. In Proceedings of the 1999 Particle Accelerator Conference (Cat. No. 99CH36366), New York, NY, USA, 29 March–2 April 1999; IEEE: Toulouse, France, 1999; Volume 4, pp. 2814–2816. [Google Scholar]
- Kabel, A.C. Quantum ground state and minimum emittance of a fermionic particle beam in a circular accelerator. In Quantum Aspects Of Beam Physics; World Scientific: London, UK, 2002; pp. 67–75. [Google Scholar]
- Burov, A.; Nagaitsev, S.; Shemyakin, A.; Derbenev, Y. Optical principles of beam transport for relativistic electron cooling. Phys. Rev. Spec. Top.-Accel. Beams 2000, 3, 094002. [Google Scholar] [CrossRef]
- Lawson, J.; Gluckstern, R.; Lapostolle, P.M. Emittance, entropy and information. Part. Accel. 1973, 5, 61–65. [Google Scholar]
- Sommerfeld, A. Zur elektronentheorie der metalle. Naturwissenschaften 1927, 15, 825–832. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).