An Improved Core-Corona Model for Λ and Λ Polarization in Relativistic Heavy-Ion Collisions
Abstract
1. Introduction
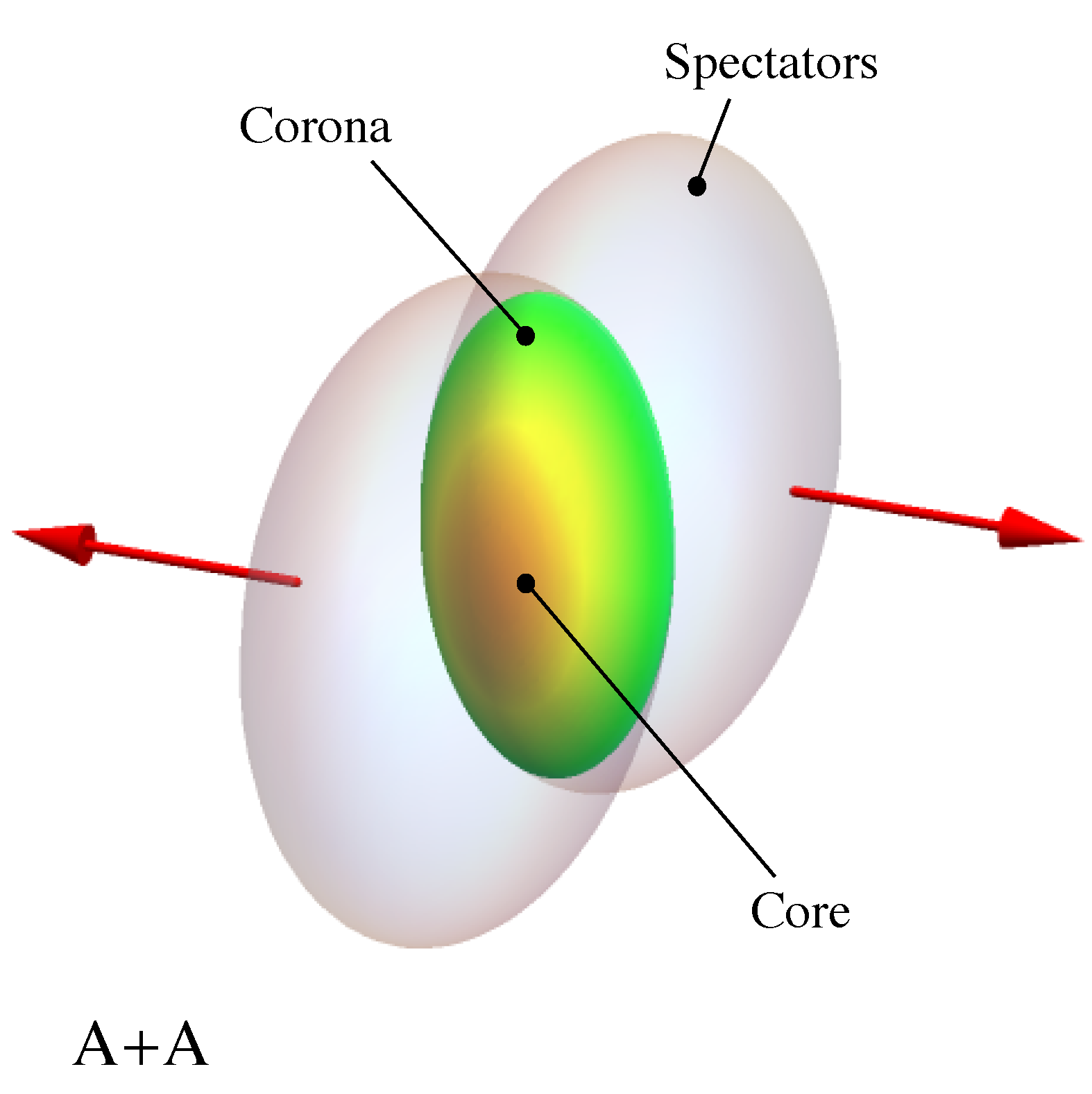
2. A Core-Corona Model for Polarization
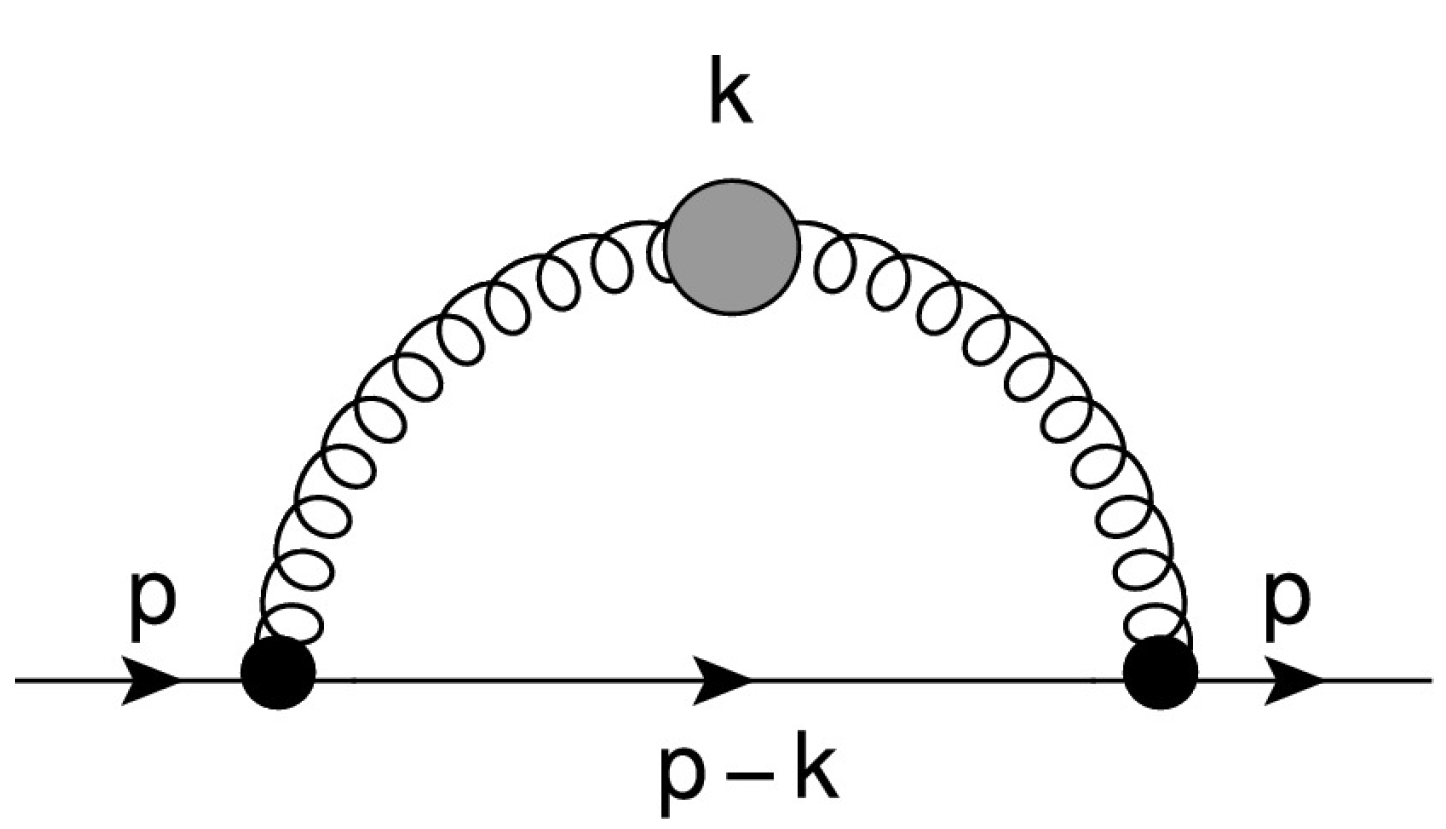
3. () Intrinsic Polarization z ()
4. Polarization in the Corona ()
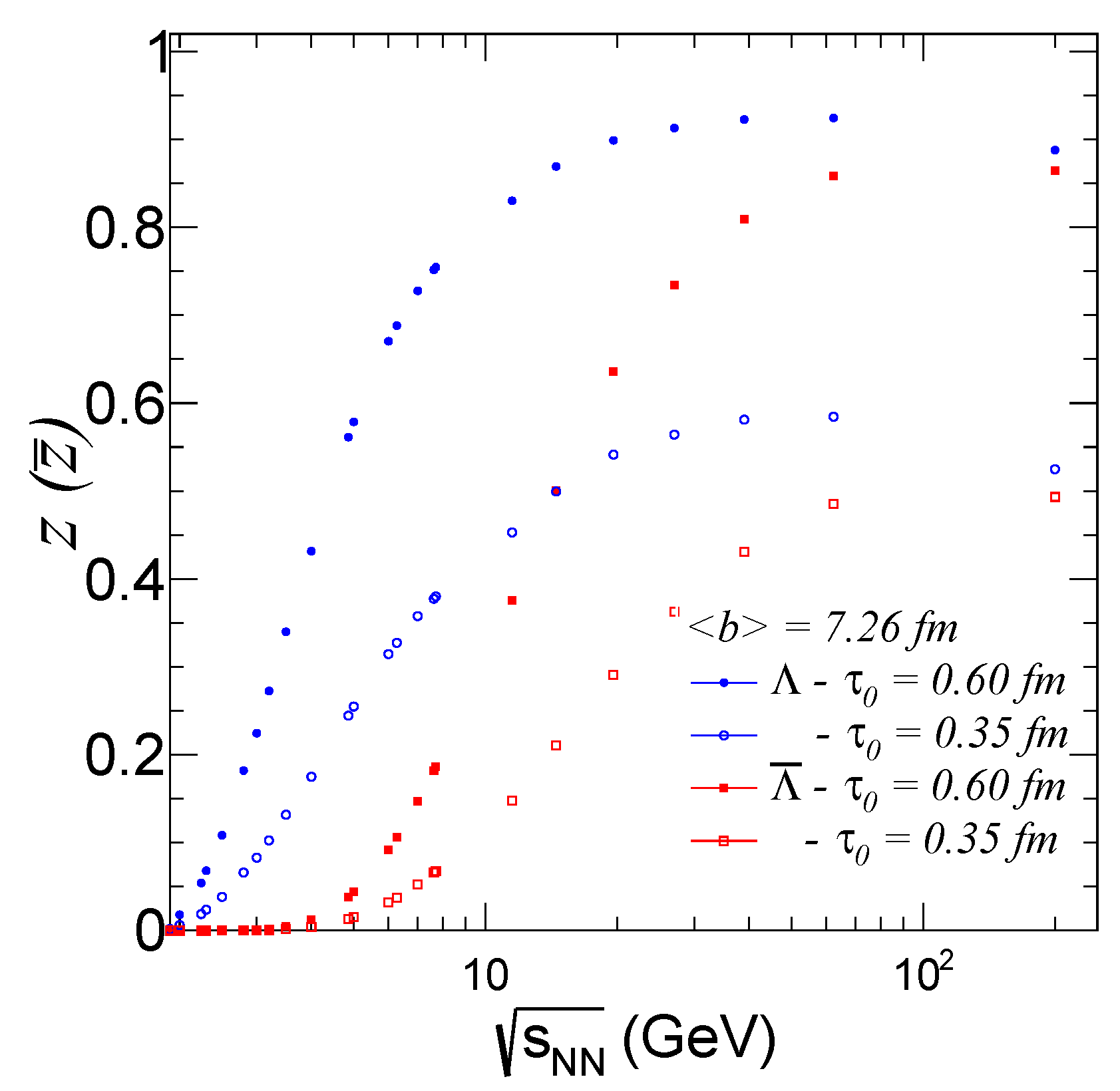
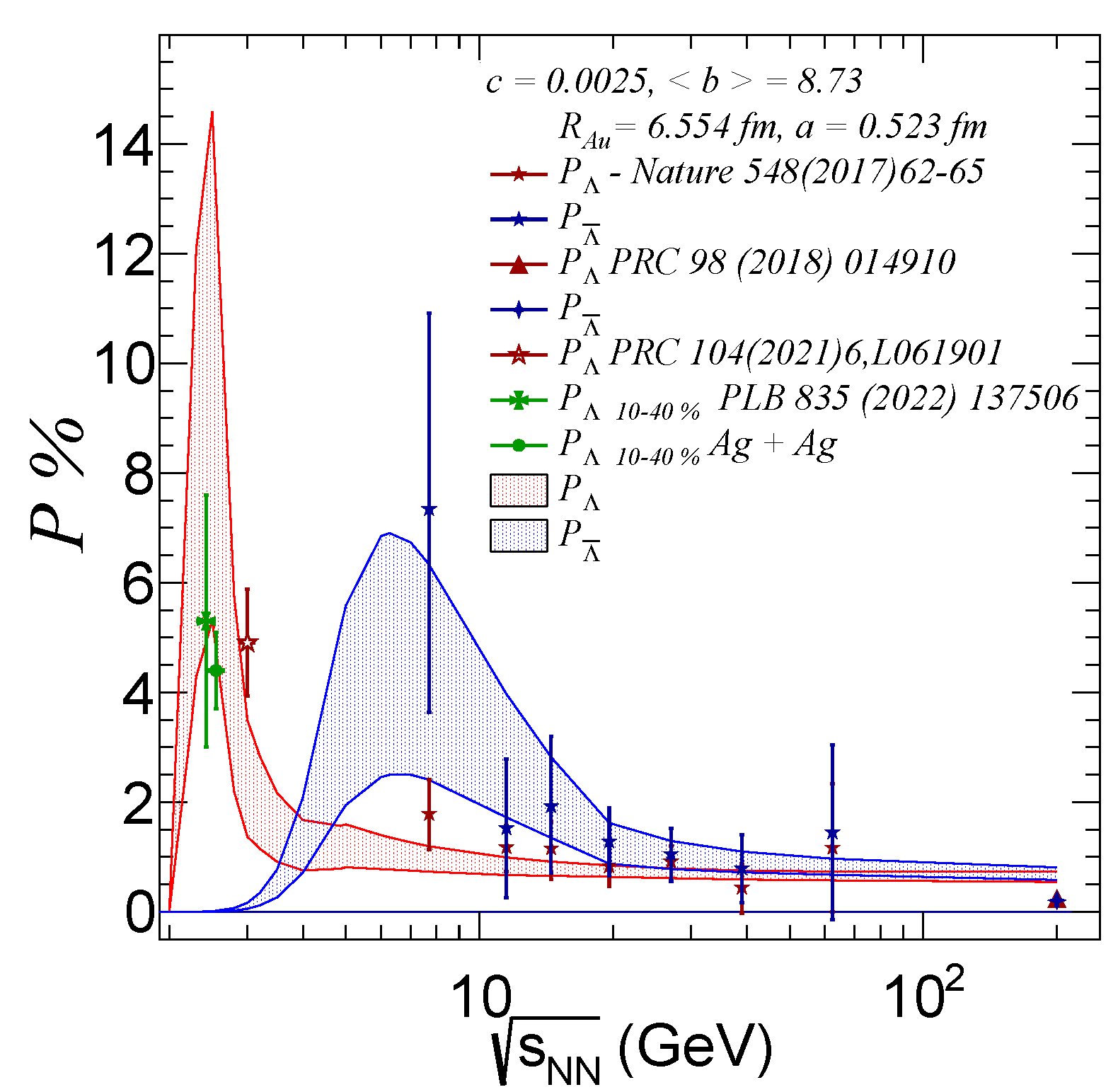
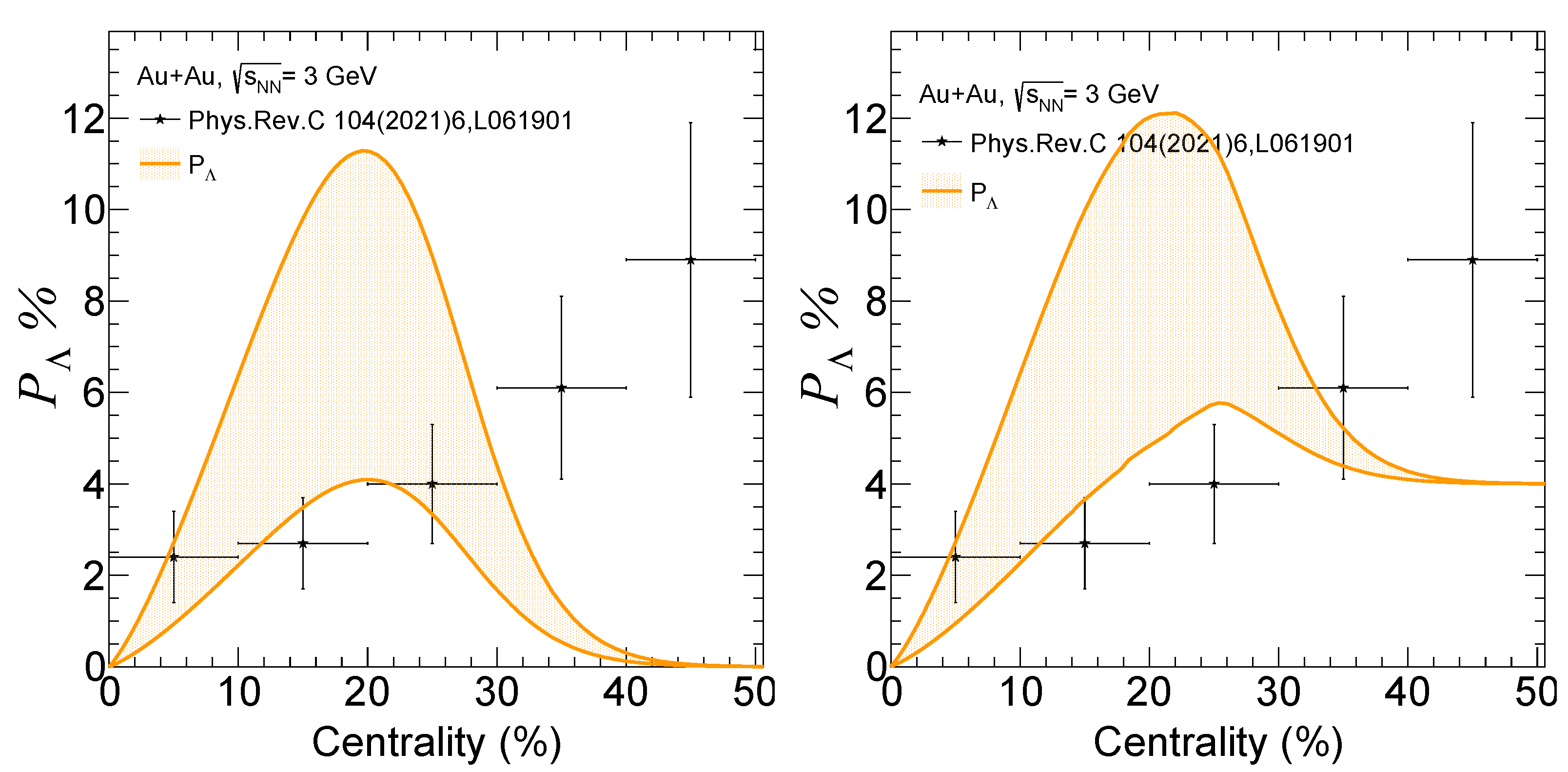
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
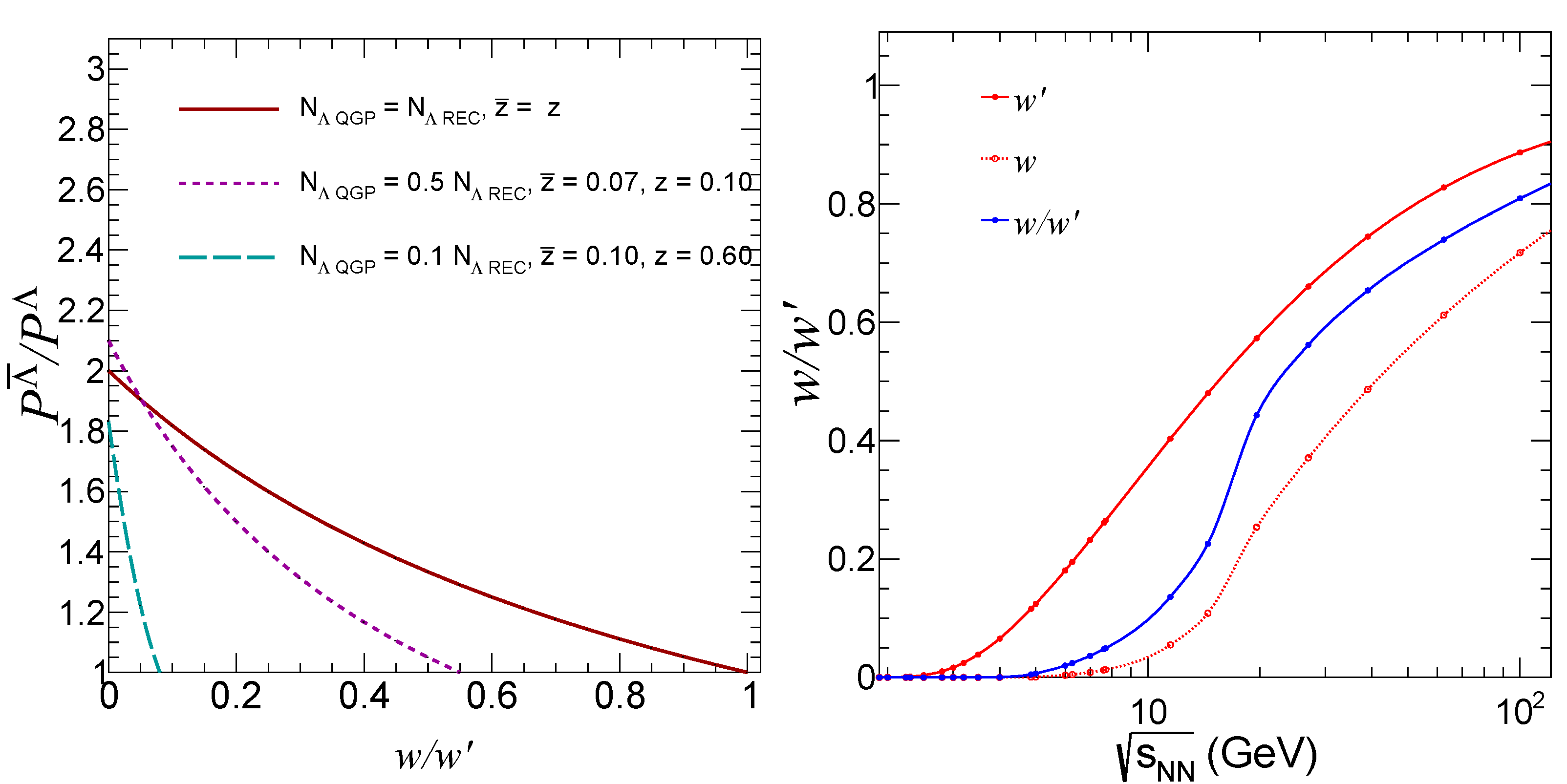
Appendix A. The Ratio w
Appendix B. The Ratio w′
Appendix C. Λ and Λ Production in the Core and Corona
References
- Jacob, M. Lambda (anti-lambda) longitudinal polarization: A signature for the formation of a quark—Gluon plasma in heavy ion collisions. Zeitschrift Phys. Part. Fields 1988, 38, 273–276. [Google Scholar] [CrossRef]
- Barros, C.d.C., Jr.; Hama, Y. Λ and Λ polarization in Au-Au collisions at RHIC. Phys. Lett. B 2011, 699, 74–77. [Google Scholar] [CrossRef]
- Ladygin, V.P.; Jerusalimov, A.P.; Ladygina, N.B. Polarization of Lambda0 hyperons in nucleus-nucleus collisions at high energies. Phys. Part. Nucl. Lett. 2010, 7, 349–354. [Google Scholar] [CrossRef]
- Becattini, F.; Csernai, L.; Wang, D.J. Λpolarization in peripheral heavy ion collisions. Phys. Rev. C 2013, 88, 034905, Erratum in Phys. Rev. C 2016, 93, 069901. [Google Scholar] [CrossRef]
- Xie, Y.; Glastad, R.C.; Csernai, L.P. Λpolarization in an exact rotating and expanding fluid dynamical model for peripheral heavy ion reactions. Phys. Rev. C 2015, 92, 064901. [Google Scholar] [CrossRef]
- Karpenko, I.; Becattini, F. Study of Λpolarization in relativistic nuclear collisions at =7.7 –200 GeV. Eur. Phys. J. C 2017, 77, 213. [Google Scholar] [CrossRef]
- Xie, Y.L.; Bleicher, M.; Stöcker, H.; Wang, D.J.; Csernai, L.P. Λpolarization in peripheral collisions at moderate relativistic energies. Phys. Rev. C 2016, 94, 054907. [Google Scholar] [CrossRef]
- Jiang, Y.; Lin, Z.W.; Liao, J. Rotating quark-gluon plasma in relativistic heavy ion collisions. Phys. Rev. C 2016, 94, 044910, Erratum in Phys. Rev. C 2017, 95, 049904. [Google Scholar] [CrossRef]
- Shi, S.; Li, K.; Liao, J. Searching for the Subatomic Swirls in the CuCu and CuAu Collisions. Phys. Lett. B 2019, 788, 409–413. [Google Scholar] [CrossRef]
- Li, H.; Pang, L.G.; Wang, Q.; Xia, X.L. Global Λpolarization in heavy-ion collisions from a transport model. Phys. Rev. C 2017, 96, 054908. [Google Scholar] [CrossRef]
- Karpenko, I.; Becattini, F. Vorticity in the QGP liquid and Λpolarization at the RHIC Beam Energy Scan. Nucl. Phys. A 2017, 967, 764–767. [Google Scholar] [CrossRef]
- Xia, X.L.; Li, H.; Tang, Z.B.; Wang, Q. Probing vorticity structure in heavy-ion collisions by local Λpolarization. Phys. Rev. C 2018, 98, 024905. [Google Scholar] [CrossRef]
- Suvarieva, D.; Gudima, K.; Zinchenko, A. A Monte Carlo Study of Lambda Hyperon Polarization at BM@N. Phys. Part. Nucl. Lett. 2018, 15, 182–188. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitan, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; Aparin, A.; et al. Global Λhyperon polarization in nuclear collisions: Evidence for the most vortical fluid. Nature 2017, 548, 62–65. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitan, N.; Alekseev, I.; Anderson, D.M.; et al. Global polarization of Λhyperons in Au+Au collisions at = 200 GeV. Phys. Rev. C 2018, 98, 014910. [Google Scholar] [CrossRef]
- Yassine, R.A.; Adamczewski-Musch, J.; Asal, C.; Becker, M.; Belounnas, A.; Blanco, A.; Blume, C.; Chlad, L.; Chudoba, P.; Ciepał, I.; et al. Global Λ-hyperon polarization in Au+Au collisions at =3 GeV. Phys. Rev. C 2021, 104, L061901. [Google Scholar] [CrossRef]
- Yassine, R.A.; Adamczewski-Musch, J.; Asal, C.; Becker, M.; Belounnas, A.; Blanco, A.; Blume, C.; Chlad, L.; Chudoba, P.; Ciepal, I.; et al. Measurement of global polarization of Λhyperons in few-GeV heavy-ion collisions. Phys. Lett. B 2022, 835, 137506. [Google Scholar] [CrossRef]
- Ayala, A.; Torres, M.A.A.; Cuautle, E.; Dominguez, I.; Sanchez, M.A.F.; Maldonado, I.; Moreno-Barbosa, E.; Nieto-Marín, P.A.; Rodriguez-Cahuantzi, M.; Salinas, J.; et al. Core meets corona: A two-component source to explain Λand Λ¯ global polarization in semi-central heavy-ion collisions. Phys. Lett. B 2020, 810, 135818. [Google Scholar] [CrossRef]
- Ayala, A.; Domínguez, I.; Maldonado, I.; Tejeda-Yeomans, M.E. Rise and fall of Λand Λ¯ global polarization in semi-central heavy-ion collisions at HADES, NICA and RHIC energies from the core-corona model. Phys. Rev. C 2022, 105, 034907. [Google Scholar] [CrossRef]
- Ayala, A.; Domínguez, I.; Maldonado, I.; Tejeda-Yeomans, M.E. Λand Λ¯ global polarization from the core-corona model. Rev. Mex. Fis. Suppl. 2022, 3, 040914. [Google Scholar] [CrossRef]
- Ayala, A.; Domínguez, I.; Maldonado, I.; Tejeda-Yeomans, M.E. Core-corona approach to describe hyperon global polarization in semi-central relativistic heavy-ion collisions. arXiv 2023, arXiv:10.48550/ARXIV.2301.07356. [Google Scholar]
- Ayala, A.; De La Cruz, D.; Hernández-Ortíz, S.; Hernández, L.A.; Salinas, J. Relaxation time for quark spin and thermal vorticity alignment in heavy-ion collisions. Phys. Lett. B 2020, 801, 135169. [Google Scholar] [CrossRef]
- Ayala, A.; de la Cruz, D.; Hernández, L.A.; Salinas, J. Relaxation time for the alignment between the spin of a finite-mass quark or antiquark and the thermal vorticity in relativistic heavy-ion collisions. Phys. Rev. D 2020, 102, 056019. [Google Scholar] [CrossRef]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerl, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Bleicher, M.; Zabrodin, E.; Spieles, C.; Bass, S.A.; Ernst, C.; Soff, S.; Bravina, L.; Belkacem, M.; Weber, H.; Stöcker, H.; et al. Relativistic hadron hadron collisions in the ultrarelativistic quantum molecular dynamics model. J. Phys. G 1999, 25, 1859–1896. [Google Scholar] [CrossRef]
- Rogachevsky, O.V.; Bychkov, A.V.; Krylov, A.V.; Krylov, V.A.; Moshkin, A.A.; Voronyuk, V.V. Software Development and Computing for the MPD Experiment. Phys. Part. Nucl. 2021, 52, 817–820. [Google Scholar] [CrossRef]
- MpdRoot Framework. Available online: https://mpdroot.jinr.ru (accessed on 30 January 2023).
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Randrup, J.; Cleymans, J. Maximum freeze-out baryon density in nuclear collisions. Phys. Rev. C 2006, 74, 047901. [Google Scholar] [CrossRef]
- Hagiwara, K.; Hikasa, K.; Nakamura, K.; Tanabashi, M.; Aguilar-Benitez, M.; Amsler, C.; Barnett, R.; Burchat, P.R.; Carone, C.D.; Caso, C.; et al. Review of particle physics. J. Phys. G 2010, 37, 075021. [Google Scholar] [CrossRef]
- Buss, O.; Gaitanos, T.; Gallmeister, K.; van Hees, H.; Kaskulov, M.; Lalakulich, O.; Larionov, A.B.; Leitner, T.; Weil, J.; Mosel, U. Transport-theoretical Description of Nuclear Reactions. Phys. Rept. 2012, 512, 1–124. [Google Scholar] [CrossRef]
- Bystricky, J.; La France, P.; Lehar, F.; Perrot, F.; Siemiarczuk, T.; Winternitz, P. Energy dependence of nucleon-nucleon inelastic total cross-sections. J. Phys. Fr. 1987, 48, 1901–1924. [Google Scholar] [CrossRef]
- Letessier, J.; Tounsi, A.; Rafelski, J. Impact of QCD and QGP properties on strangeness production. Phys. Lett. B 1996, 389, 586–594. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayala, A.; Dominguez, I.; Maldonado, I.; Tejeda-Yeomans, M.E. An Improved Core-Corona Model for Λ and Λ Polarization in Relativistic Heavy-Ion Collisions. Particles 2023, 6, 405-415. https://doi.org/10.3390/particles6010022
Ayala A, Dominguez I, Maldonado I, Tejeda-Yeomans ME. An Improved Core-Corona Model for Λ and Λ Polarization in Relativistic Heavy-Ion Collisions. Particles. 2023; 6(1):405-415. https://doi.org/10.3390/particles6010022
Chicago/Turabian StyleAyala, Alejandro, Isabel Dominguez, Ivonne Maldonado, and Maria Elena Tejeda-Yeomans. 2023. "An Improved Core-Corona Model for Λ and Λ Polarization in Relativistic Heavy-Ion Collisions" Particles 6, no. 1: 405-415. https://doi.org/10.3390/particles6010022
APA StyleAyala, A., Dominguez, I., Maldonado, I., & Tejeda-Yeomans, M. E. (2023). An Improved Core-Corona Model for Λ and Λ Polarization in Relativistic Heavy-Ion Collisions. Particles, 6(1), 405-415. https://doi.org/10.3390/particles6010022





