Abstract
Light-nuclei production in relativistic heavy-ion collisions is simulated within an updated Three-fluid Hydrodynamics-based Event Simulator Extended by UrQMD (Ultra-relativistic Quantum Molecular Dynamics) final State interactions (THESEUS). The simulations are performed in the collision energy range of 6.4–19.6 GeV. The light-nuclei are produced within the thermodynamical approach on an equal basis with hadrons. Since the light nuclei do not participate in the UrQMD evolution, the only additional parameter related to the light nuclei, i.e., the energy density of late freeze-out, is used for the imitation of the afterburner stage of the collision. The updated THESEUS provides a reasonable reproduction of data on bulk observables of the light nuclei, especially their functional dependence on the collision energy and light-nucleus mass. Various ratios, , , , and , are also considered. Imperfect reproduction of the light-nuclei data leaves room for medium effects in produced light nuclei.
1. Introduction
Light-nuclei production in heavy-ion collisions arouses interest in connection with conjectured critical point in the QCD phase diagram. There are some indications of existence of such a critical point from the STAR experiment [1]. An enhanced production of light nuclei close to the critical point with respect to a noncritical scenario is expected [2,3,4], and also may be connected with the formation of baryon clusters, due to spinodal decomposition associated with the mechanically unstable region in the first-order phase transition [5,6,7,8,9].
Currently, there are various 3D dynamical models which include the coalescence mechanism of light-nuclei production [10,11,12,13,14,15,16,17,18,19], see also a recent review [20]. In the simplest case, the models based on coalescence fit the necessary parameters from comparison with experimental data of the light-nuclei production [10,11] and, hence, their predictive power is limited. The refined coalescence calculations are very successful in reproducing data in a wide range of collision energies [17]. Advanced coalescence approaches involve the Wigner functions of light-nuclei [12,13,15,16,18,19] to calculate the coalescence parameters.
The recently developed transport models, such as SMASH (Simulating Many Accelerated Strongly-interacting Hadrons) [21,22,23], PHQMD (Parton-Hadron-Quantum-Molecular-Dynamics) [24,25,26] and a stochastic kinetic approach [27], treat light nuclei microscopically, on an equal basis with other hadrons. These transport models also require extensive additional input for treatment of the light-nuclei production, albeit in a wide range of collision energies.
Another situation is in the thermodynamical approach. This does not need any additional parameters for treatment of the light-nuclei production, because it describes the light nuclei in terms of temperatures and chemical potentials, i.e., on an equal basis with hadrons. Therefore, this approach has a significant advantage, as its predictive power is the same for light nuclei and hadrons. This approach was realized within the statistical model in [28,29]. Deuteron midrapidity yields at the energies (from 7.7 to GeV 200 GeV) of the STAR Beam Energy Scan (BES) at the Relativistic Heavy-Ion Collider (RHIC) [30,31] are described fairly well by this model [32,33], while the yield of tritium is overestimated by roughly a factor of two [33,34]. The statistical model gives a similarly good description of not only the light nuclei but even hypernuclei and antinuclei at energies of the CERN Large Hadron Collider (LHC) [35].
In view of the success of the thermal model, we implemented the thermodynamic approach of light-nuclei production into the updated THESEUS event generator [36]. In this paper, we describe the data on light-nuclei within the thermodynamic approach, keeping in mind that the bulk observables [37,38,39,40] for protons are reasonably well reproduced by the model of the three-fluid dynamics (3FD). It is important to note that the model involves no extra parameters related to the light nuclei, except for the late freeze-out energy density, see Section 3. The results of the THESEUS simulations are compared with available data from NA49 [41] and STAR [31,34] collaborations.
2. The Updated Version of the Generator THESEUS
The THESEUS event generator was first presented and applied to simulations of heavy-ion collisions in Refs. [42,43]. The generator THESEUS is based on the 3FD model [11,38] complemented by the UrQMD [44,45] for the afterburner stage. The output of the 3FD model, i.e., the freeze-out hypersurface, is recorded in terms of local flow velocities and thermodynamic quantities. The THESEUS generator transforms the 3FD output into a set of observed particles, i.e., performs the procedure of particlization.
The 3FD model is designed to simulate heavy-ion collisions at energies of the BES-RHIC, SPS, FAIR and NICA. The nonequilibrium stage is modeled by two counterstreaming baryon-rich fluids. Newly produced particles, which dominantly populate the midrapidity region, are assigned to a so-called fireball fluid. At present, three different equations of state (EoSs) are used in the 3FD simulations: a purely hadronic EoS [46] (hadr. EoS) and two EoSs with deconfinement transition [47], i.e., an EoS with a first-order phase transition (1PT EoS) and one with a smooth crossover transition (crossover EoS). At energies 5 GeV, the deconfinement scenarios reveal definite preference [48]. The 3FD and the original version of the THESEUS [42,43] calculate spectra of the so-called primordial nucleons, i.e., both observable nucleons and those bound in the light nuclei. This is done for the subsequent application of the coalescence model [11,49] for the light-nuclei production.
In the new version of THESEUS the light nuclei were included on an equal basis with hadrons [36]. In THESEUS, only thermodynamical values, such as temperature and chemical potential, are used to calculate the density of each particle, both hadrons and light-nuclei. Each element of the fluid surface (or droplet) is characterized by its own thermodynamical values. The Monte-Carlo method is applied to randomly generate particles according to their densities in each droplet. As result, we have an ensemble of particles, characterized by their mass, energy, coordinates, momenta, etc. Hence, the procedure of recalculation of the yields of protons and neutrons was added, which takes into account light-nuclei production. The list of the light nuclei includes the stable nuclei and low-lying resonances of the He system, the decays of which contribute to the yields of stable species [2], see Table 1. The corresponding anti-nuclei were also included.

Table 1.
Stable light nuclei and low-lying resonances of the He system (from BNL properties of nuclides [50]). J denotes the total angular momentum. The last column represents branching ratios of the decay channels, in percent. The correspond to the emission of protons, neutrons, or deuterons, respectively.
These nuclei are sampled similarly to other hadrons, i.e. according to their phase–space distribution functions. Nevertheless, while the hadrons pass through the UrQMD afterburner stage after particlization, the light nuclei do not, just because the UrQMD is not able to treat them. This is a definite shortcoming, because the light nuclei are destroyed and reproduced during this afterburner stage [22,23,25]. We imitate the afterburner for the light nuclei by late freeze-out. For selection of the parameter of the late freeze-out, we considered protons, because they are closely related to light nuclei.
In Figure 1, transverse-momentum spectra of protons in central Au + Au collisions at collision energies of 20A and 158A GeV are shown. These spectra were calculated by means of the THESEUS simulations without the subsequent UrQMD afterburner, similarly to the light-nuclei simulations based on 3FD calculations with different freeze-out energy densities 0.2 and 0.4 GeV/fm. The conventional for the 3FD results with 0.4 GeV/fm and the subsequent UrQMD afterburner are also presented. The results are presented in linear scale in order to better resolve the low region, which is mostly affected by the afterburner effect [51]. As seen in Figure 1, the late freeze-out with the energy density = 0.2 GeV/fm approximately reproduced the afterburner effect in midrapidity proton spectra at both collision energies. The same also took place in the 1PT-EoS scenario.
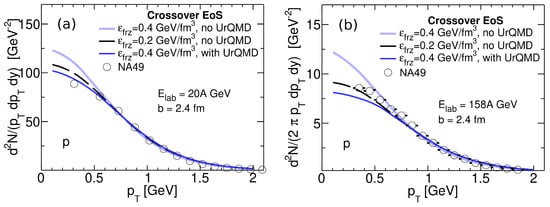
Figure 1.
Transverse-momentum spectra of protons in central Au+Au collisions calculated with the crossover EoS at collision energy of (a) 20A GeV (left panel) and of (b) 158A GeV (right panel). The results of the THESEUS simulations (without the subsequent UrQMD afterburner), based on the 3FD calculations with different freeze-out energy densities 0.2 and 0.4 GeV/fm, are shown. The conventional for the 3FD results with 0.4 GeV/fm and the subsequent UrQMD afterburner are also presented. Experimental data are from the NA49 collaboration [52].
The effect of the late freeze-out on rapidity distribution of net-protons is demonstrated in Figure 2. The late freeze-out with 0.2 GeV/fm reproduced the results for conventional freeze-out with the subsequent UrQMD afterburner in the midrapidity region reasonably well. The reproduction for 20A GeV (not shown) was even better, as could be expected from Figure 1. However, the freeze-out energy density 0.2 GeV/fm was not that good in imitating the afterburner effect at forward/backward rapidities, see Figure 2. Below, we use this late freeze-out with 0.2 GeV/fm for calculations of light nuclei for all considered collision energies and centralities.
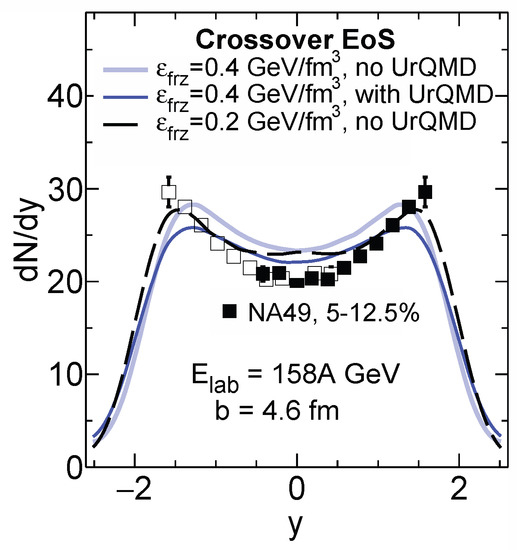
Figure 2.
Rapidity distributions of net-protons in central ( 2.4 fm) Pb + Pb collisions at = 158A GeV calculated with the crossover EoS. The results of the THESEUS simulations (without the subsequent UrQMD afterburner) based on the 3FD calculations with different freeze-out energy densities = 0.2 and 0.4 GeV/fm are shown. The conventional for the 3FD results with = 0.4 GeV/fm, and the subsequent UrQMD afterburner, are also presented. The experimental data filled boxes are from the NA49 collaboration [53]. The open boxes correspond to the NA49 data reflected with respect to .
3. Results
In this section, we demonstrate some results obtained by using the THESEUS generator. We analyze some spectra of light nuclei with the existing experimental data, and present the spectra of protons for comparison.
3.1. Rapidity Distributions
We started our analysis with the rapidity distributions of light nuclei, see Figure 3. We compared our results with NA49 data [41], as well as with the 3FD coalescence results [49]. Let us remind the reader that the light nuclei were simulated without the afterburner stage, and to imitate the afterburner stage, the late freeze-out paremeter 0.2 GeV/fm was used. As seen in the midrapidity region, the THESEUS results overestimated the data on light-nuclei yields, even with the late freeze-out which somewhat improved agreement with the data, but not completely. It is surprising that reproduction of the He data turned out to be better than that of the data on deuterons, in spite of the fact that He has a heavier nucleus.
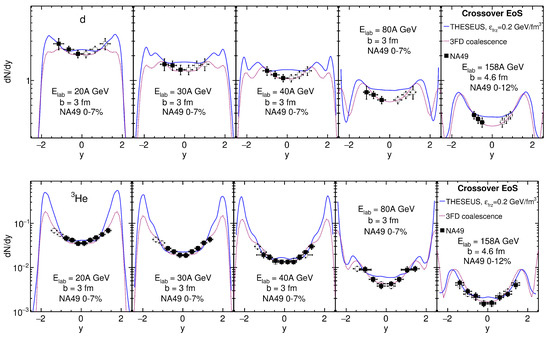
Figure 3.
Rapidity distributions of deuterons (upper raw of panels) and of He nuclei (lower raw of panels) in central Pb+Pb collisions at collision energies of 20A -158A GeV calculated with the crossover EoS. The results of THESEUS simulations with the late freeze-out, 0.2 GeV/fm, are displayed. The 3FD coalescence results [49] are also presented. Experimental data filled boxes are from the NA49 collaboration [41]. The open boxes correspond to the NA49 data reflected with respect to .
The 3FD coalescence [49], also presented in Figure 3 by short-dashed lines, reproduced the data much better because the coalescence coefficients were tuned for each collision energy and each light nucleus. Nevertheless, the THESEUS simulations resulted in good agreement with the dependence of light-nuclei production on collision energy and light nucleus mass. Note that this agreement did not need any additional tuning parameters.
For comparison, the rapidity distributions of net-protons are presented in Figure 4. The net-protons were reproduced much better. The UrQMD afterburner slightly reduced net-proton yield in the midrapidity region and drove it to even better agreement with the data.
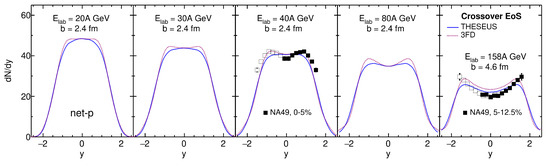
Figure 4.
The same as in Figure 3 but for net-protons in central Pb+Pb collisions. The results of simulations without the UrQMD afterburner and the 3FD results [49] are also displayed. Experimental data filled boxes are from the NA49 collaboration [53]. The open boxes correspond to the NA49 data reflected with respect to .
However, agreement of the form of the net-proton distribution at 40A GeV with the data became worse after application of the UrQMD. This had a consequence for the light-nuclei distributions: a slight peak at the midrapidity appeared. Note that the 3FD coalescence was based on nucleon spectra before UrQMD, where global midrapidity peaks for protons are less pronounced. Therefore, the coalescence results did not reveal these slight peaks at the midrapidity.
3.2. Transverse-Momentum Spectra
The results of the THESEUS simulations of transverse-mass spectra of deuterons and tritons at midrapidity in central Pb + Pb collisions at collision energies of 20A -158A GeV, with conventional freeze-out, 0.4 GeV/fm, and late freeze-out, 0.2 GeV/fm, were compared with the data measured by the NA49 collaboration [41], and presented in Figure 5. The 3FD coalescence results [49] are also shown. The agreement of these spectra with the NA49 data was not perfect. Imitation of the afterburner (THESEUS with 0.2 GeV/fm) somewhat improved the normalization at low , but worsened agreement with the slopes. The overall normalization of the 3FD-coalescence spectra was better but this was achieved by tuning the coalescence parameters.
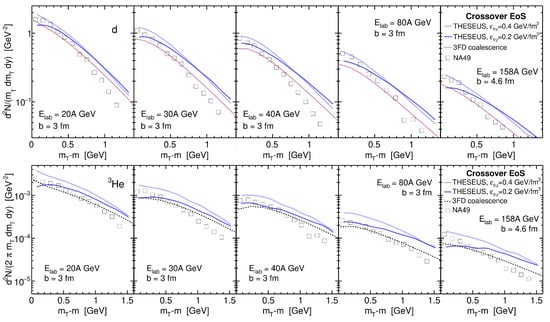
Figure 5.
Transverse-mass spectra of deuterons (upper raw of panels) and tritons (lower raw of panels) in central Pb + Pb collisions at collision energies of 20A -158A GeV calculated with the crossover EoS. The results of THESEUS simulations with conventional freeze-out, 0.4 GeV/fm, and late freeze-out, 0.2 GeV/fm, are displayed. The 3FD coalescence results [49] are also shown. NA49 data are from Ref. [41].
The proton transverse-mass spectra at midrapidity in central Pb + Pb collisions at the same collision energies are presented in Figure 6, and the results of 3FD simulations are also displayed. As seen, the afterburner (THESEUS curves in Figure 6) improved agreement with the NA49 data [52] at low as compared with the 3FD, but the slopes disagreed with the data; though, this disagreement was much smaller than that for light nuclei in Figure 5.
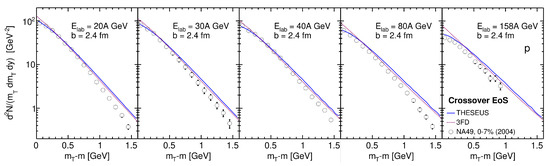
Figure 6.
The same as in Figure 5, but for protons calculated with the crossover EoS. The results of conventional THESEUS simulations (i.e., with the UrQMD afterburner) and the 3FD results [49] are displayed. NA49 data are from Ref. [52].
The calculated He spectra were closer to the data than the deuteron data, which was again surprising. The spectra slopes were better reproduced at lower energies. Together with better agreement with rapidity distributions of light nuclei at lower energies, this maight suggest that the THESEUS was more suitable for simulating light nuclei at NICA and FAIR energies.
Since light nuclei consist of protons and neutrons, their spectra are closely related to proton spectra. The shortcomings of the nucleon spectra are summed up and, thus, amplified in the light-nuclei spectra. As a result, we observed a larger disagreement with data in light-nuclei results than in proton ones.
The UrQMD afterburner, as it is implemented in THESEUS [36,42], does not improve the high- description. The reason is that the grand canonical distributions are sampled in the particlization procedure, rather than the canonical or micro-canonical ones. Thus, the high- overestimation persists. Of course, it is difficult to indicate how much of this overestimation is the grand canonical treatment rather than due to shortcomings of the model.
3.3. Yield Ratios of Light-Nuclei
Energy dependence of , , and midrapidity ratios for central collisions are presented in Figure 7 (left panel). Protons in these ratios do not contain feed-down from weak decays, in accordance with the experimental procedure [30,31]. As can be seen, the model reproduces the energy dependence of experimental data [31] but s the values of these ratios.
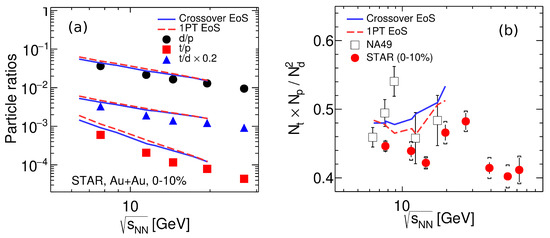
Figure 7.
Energy dependence of (a) , ,and midrapidity ratios for central (0–10%) Au + Au collisions, compared with STAR data [31] for central (0–10%) Au + Au collisions, and (b) of the midrapidity light-nuclei-yield ratio in central Au + Au and Pb + Pb collision, compared with STAR data [31] (filled circles), with the weak-decays feed-down determined by experimental means, for central (0–10%) Au + Au collisions. The experimental results extracted from the NA49 data on Pb + Pb collisions (0–7% at 20A -80A GeV and 0–12% at 158 A GeV) [41] are also displayed (open boxes). Simulations were performed at 4 fm for Au + Au, at 3 fm ( 17.4 GeV) and 4.6 fm ( 17.4 GeV) for Pb + Pb in rapidity bin . is related to protons without feed-down from weak decays. The results with the crossover and 1PT EoSs are presented.
This is not surprising, because calculated light-nuclei yields systematically overestimate the data in the midrapidity.
This reproduction was similar to that within the statistical model in [31].
The yield ratio of light nuclei, is presented in Figure 7 (right panel). Historically, it has been suggested as a probe to neutron density fluctuations associated with the first-order phase transition [54,55]. Later, it was also associated with the possible critical point of the hot and baryon-rich QCD matter [2,3,4]. Near the critical point, this ratio increases monotonically with the nucleon density correlation length [4], and, besides, production of He may increase because of enhanced preclustering and subsequent decay of He-like clusters [2,3]. In its turn, this may result in a maximum in the ratio near the critical point. Recent data on this ratio [31] showed non-monotonic behavior with a peak located around 20–30 GeV (see Figure 7), right panel), which might indicate passing through either the first-order phase transition or critical point at this collision energy.
Energy dependence of the midrapidity ratio in central Au + Au and Pb + Pb collisions is presented in Figure 7) (right panel). The proton yields do not include contribution from the weak-decay feed-down. This weak-decay feed-down was determined by the UrQMD simulation at the afterburner stage, i.e., in the same way as the proton feed-down correction was done in the preliminary STAR data [34]. In the final STAR data [31] (filled circles in Figure 7) (right panel), the feed-down correction was done by experimental means. The STAR Collaboration concluded that the UrQMD simulation underestimates the proton feed-down contributions from weak decays. If so, our simulations suffered from the same shortcoming of the UrQMD. Therefore, the overestimation of the data by THESEUS could be related to the same shortcomings of the UrQMD. An increase of the calculated ratio when the energy approached 20 GeV could also be an artifact of the aforementioned shortcoming.
4. Summary
We performed simulations of the light-nuclei production in relativistic heavy-ion collisions within the updated THESEUS [36] event generator for Pb + Pb and Au + Au collisions in the collision energy range of 6.4–19.6 GeV, and compared the results with available data from the NA49 and STAR collaborations. The light-nuclei production in the updated THESEUS were produced within the thermodynamical approach on an equal basis with hadrons. The only additional parameter related to the light nuclei was the energy density of the late freeze-out, 0.2 GeV/fm, which was the same for all collision energies, centralities and combinations of colliding nuclei. The late freeze-out imitated the afterburner stage of the collision because the light nuclei were not subjected to the UrQMD afterburner. The parameter was not free and was chosen from the condition of the best reproduction of the proton spectrum after the UrQMD afterburner by the spectrum at the late freeze-out without the afterburner.
The reproduction of the data on bulk observables (rapidity distributions, and -spectra) of the light nuclei by the updated generator was not perfect, but reasonable, especially with regard to the functional dependence on the collision energy and light-nucleus mass. It is important to note that this reproduction was achieved with a single universal additional parameter related to late freeze-out.
Different ratios, , , , and were also estimated. We conclude that the feed-down contributions of weak decays should be carefully subtracted from the proton yield in order for the calculated ratio to serve as a probe of production characteristics of light nuclei and of the structure of the QCD phase diagram. The UrQMD was not quite accurate for the subtraction of weak decays from the proton yield.
We can conclude that the THESEUS generator can reasonably well reproduce light-nuclei data; however, with systematical overestimation of data. Although, the underlying 3FD model provided results more consistent with the experimental data, that agreement was achieved by tuning a greater number of coalescence parameters. Therefore, the coalescence predictive power was limited as compared to THESEUS. The shortcomings of the generator could be related to the absence of a light-nuclei afterburner in UrQMD and imperfect proton description. As is argued above, the shortcomings of the proton description are amplified in the case of light nuclei. Imperfect reproduction of the light-nuclei data also leaves room for the medium effects advanced in Refs. [56,57], see also [58].
A more complete account of this study is presented in Ref. [59].
Author Contributions
All the authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on: https://arxiv.org/abs/2210.07334 (accessed on: 31 January 2023).
Acknowledgments
We are grateful to David Blaschke for convincing us to apply the thermodynamic approach to modeling the light-nuclei production in heavy-ion collisions. We are especially grateful to Iurii Karpenko because without his help and expertise this work would hardly have been possible. Useful discussions with V. Kireyeu are gratefully acknowledged. This work was carried out using computing resources of the supercomputer “Govorun” at JINR.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adam, J.; Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Li, X. Net-proton number fluctuations and the Quantum Chromodynamics critical point. arXiv 2020, arXiv:2001.02852. [Google Scholar]
- Shuryak, E.; Torres-Rincon, J.M. Baryon preclustering at the freeze-out of heavy-ion collisions and light-nuclei production. Phys. Rev. C 2020, 101, 034914. [Google Scholar] [CrossRef]
- Shuryak, E.; Torres-Rincon, J.M. Light-nuclei production and search for the QCD critical point. Eur. Phys. J. A 2020, 56, 241. [Google Scholar] [CrossRef]
- Sun, K.J.; Li, F.; Ko, C.M. Effects of QCD critical point on light nuclei production. Phys. Lett. B 2021, 816, 136258. [Google Scholar] [CrossRef]
- Steinheimer, J.; Randrup, J. Spinodal amplification of density fluctuations in fluid-dynamical simulations of relativistic nuclear collisions. Phys. Rev. Lett. 2012, 109, 212301. [Google Scholar] [CrossRef] [PubMed]
- Steinheimer, J.; Pang, L.; Zhou, K.; Koch, V.; Randrup, J.; Stoecker, H. A machine learning study to identify spinodal clumping in high energy nuclear collisions. J. High Energy Phys. 2019, 12, 122. [Google Scholar] [CrossRef]
- Skokov, V.V.; Voskresensky, D.N. Hydrodynamical description of a hadron-quark first-order phase transition. JETP Lett. 2009, 90, 223–227. [Google Scholar] [CrossRef]
- Skokov, V.V.; Voskresensky, D.N. Hydrodynamical description of first-order phase transitions: Analytical treatment and numerical modeling. Nucl. Phys. A 2009, 828, 401–438. [Google Scholar] [CrossRef]
- Randrup, J. Phase transition dynamics for baryon-dense matter. Phys. Rev. C 2009, 79, 054911. [Google Scholar] [CrossRef]
- Russkikh, V.N.; Ivanov, Y.B.; Pokrovsky, Y.E.; Henning, P.A. Analysis of intermediate-energy heavy ion collisions within relativistic mean field two fluid model. Nucl. Phys. A 1994, 572, 749–790. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Russkikh, V.N.; Toneev, V.D. Relativistic heavy-ion collisions within 3-fluid hydrodynamics: Hadronic scenario. Phys. Rev. C 2006, 73, 044904. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; He, S.; Sun, K.J.; Yu, N.; Luo, X. Light nuclei production in Au + Au collisions at = 5–200 GeV from JAM model. Phys. Lett. B 2020, 805, 135452. [Google Scholar] [CrossRef]
- Zhu, L.; Ko, C.M.; Yin, X. Light (anti-)nuclei production and flow in relativistic heavy-ion collisions. Phys. Rev. C 2015, 92, 064911. [Google Scholar] [CrossRef]
- Steinheimer, J.; Gudima, K.; Botvina, A.; Mishustin, I.; Bleicher, M.; Stocker, H. Hypernuclei, dibaryon and antinuclei production in high energy heavy ion collisions: Thermal production versus Coalescence. Phys. Lett. B 2012, 714, 85–91. [Google Scholar] [CrossRef]
- Dong, Z.J.; Chen, G.; Wang, Q.Y.; She, Z.L.; Yan, Y.L.; Liu, F.X.; Zhou, D.M.; Sa, B.H. Energy dependence of light (anti)nuclei and (anti)hypertriton production in the Au-Au collision from = 11.5 to 5020 GeV. Eur. Phys. J. A 2018, 54, 144. [Google Scholar] [CrossRef]
- Sombun, S.; Tomuang, K.; Limphirat, A.; Hillmann, P.; Herold, C.; Steinheimer, J.; Yan, Y.; Bleicher, M. Deuteron production from phase-space coalescence in the UrQMD approach. Phys. Rev. C 2019, 99, 014901. [Google Scholar] [CrossRef]
- Hillmann, P.; Käfer, K.; Steinheimer, J.; Vovchenko, V.; Bleicher, M. Coalescence, the thermal model and multi-fragmentation: The energy and volume dependence of light nuclei production in heavy ion collisions. arXiv 2022, arXiv:2109.05972. [Google Scholar] [CrossRef]
- Zhao, W.; Shen, C.; Ko, C.M.; Liu, Q.; Song, H. Beam-energy dependence of the production of light nuclei in Au + Au collisions. Phys. Rev. C 2020, 102, 044912. [Google Scholar] [CrossRef]
- Zhao, W.; Sun, K.J.; Ko, C.M.; Luo, X. Multiplicity Scaling of Light Nuclei Production in Relativistic Heavy-Ion Collisions. arXiv 2021, arXiv:2105.14204. [Google Scholar] [CrossRef]
- Oliinychenko, D. Overview of light nuclei production in relativistic heavy-ion collisions. arXiv 2020, arXiv:2003.05476. [Google Scholar] [CrossRef]
- Weil, J.; Steinberg, V.; Staudenmaier, J.; Pang, L.G.; Oliinychenko, D.; Mohs, J.; Kretz, M.; Kehrenberg, T.; Goldschmidt, A.; Bäuchle, B.; et al. Particle production and equilibrium properties within a new hadron transport approach for heavy-ion collisions. Phys. Rev. C 2016, 94, 054905. [Google Scholar] [CrossRef]
- Oliinychenko, D.; Pang, L.G.; Elfner, H.; Koch, V. Microscopic study of deuteron production in PbPb collisions at = 2.76TeV via hydrodynamics and a hadronic afterburner. Phys. Rev. C 2019, 99, 044907. [Google Scholar] [CrossRef]
- Staudenmaier, J.; Oliinychenko, D.; Torres-Rincon, J.M.; Elfner, H. Deuteron production in relativistic heavy ion collisions via stochastic multiparticle reactions. Phys. Rev. C 2021, 104, 034908. [Google Scholar] [CrossRef]
- Aichelin, J.; Bratkovskaya, E.; Le Fèvre, A.; Kireyeu, V.; Kolesnikov, V.; Leifels, Y.; Voronyuk, V.; Coci, G. Parton-hadron-quantum-molecular dynamics: A novel microscopic n-body transport approach for heavy-ion collisions, dynamical cluster formation, and hypernuclei production. Phys. Rev. C 2020, 101, 044905. [Google Scholar] [CrossRef]
- Gläßel, S.; Kireyeu, V.; Voronyuk, V.; Aichelin, J.; Blume, C.; Bratkovskaya, E.; Coci, G.; Kolesnikov, V.; Winn, M. Cluster and hyper-cluster production in relativistic heavy-ion collisions within the Parton-Hadron-Quantum-Molecular-Dynamics approach. arXiv 2021, arXiv:2106.14839. [Google Scholar]
- Bratkovskaya, E.; Glässel, S.; Kireyeu, V.; Aichelin, J.; Bleicher, M.; Blume, C.; Coci, G.; Kolesnikov, V.; Steinheimer, J.; Voronyuk, V. Midrapidity cluster formation in heavy-ion collisions. arXiv 2022, arXiv:2208.11802. [Google Scholar] [CrossRef]
- Sun, K.J.; Wang, R.; Ko, C.M.; Ma, Y.G.; Shen, C. Relativistic kinetic approach to light nuclei production in high-energy nuclear collisions. arXiv 2021, arXiv:2106.12742. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Hadron production in central nucleus-nucleus collisions at chemical freeze-out. Nucl. Phys. A 2006, 772, 167–199. [Google Scholar] [CrossRef]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Adam, J.; Suaide, A.A.P. Beam energy dependence of (anti-)deuteron production in Au + Au collisions at the BNL Relativistic Heavy Ion Collider. Phys. Rev. C 2019, 99, 064905. [Google Scholar] [CrossRef]
- STAR Collaboration. Beam Energy Dependence of Triton Production and Yield Ratio (Nt × Np/Nd2) in Au+Au Collisions at RHIC. arXiv 2022, arXiv:2209.08058. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Stocker, H. Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phys. Lett. B 2011, 697, 203–207. [Google Scholar] [CrossRef]
- Vovchenko, V.; Dönigus, B.; Kardan, B.; Lorenz, M.; Stoecker, H. Feeddown contributions from unstable nuclei in relativistic heavy-ion collisions. Phys. Lett. B 2020, 809, 135746. [Google Scholar] [CrossRef]
- Zhang, D. Light Nuclei (d,t) Production in Au + Au Collisions at = 7.7-200GeV. Nucl. Phys. A 2021, 1005, 121825. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Kozhevnikova, M.; Ivanov, Y.B.; Karpenko, I.; Blaschke, D.; Rogachevsky, O. Update of the Three-fluid Hydrodynamics-based Event Simulator: Light-nuclei production in heavy-ion collisions. Phys. Rev. C 2021, 103, 044905. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Baryon Stopping as a Probe of Deconfinement Onset in Relativistic Heavy-Ion Collisions. Phys. Lett. B 2013, 721, 123–130. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: I. Baryon Stopping. Phys. Rev. C 2013, 87, 064904. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: III. Transverse Momentum Spectra. Phys. Rev. C 2014, 89, 024903. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Soldatov, A.A. Bulk Properties of the Matter Produced at Energies of the Beam Energy Scan Program. Phys. Rev. C 2018, 97, 024908. [Google Scholar] [CrossRef]
- Anticic, T.; Baatar, B.; Bartke, J.; Beck, H.; Betev, L.; Bialkowska, H.; Blume, C.; Boimska, B.; Book, J.; Botje, M.; et al. NA49 Collaboration. Production of deuterium, tritium, and He3 in central Pb + Pb collisions at 20A, 30A, 40A, 80A, and 158A GeV at the CERN Super Proton Synchrotron. Phys. Rev. C 2016, 94, 044906. [Google Scholar] [CrossRef]
- Batyuk, P.; Blaschke, D.; Bleicher, M.; Ivanov, Y.B.; Karpenko, I.; Merts, S.; Rogachevsky, O.; Nahrgang, M.; Petersen, H. Event simulation based on three-fluid hydrodynamics for collisions at energies available at the Dubna Nuclotron-based Ion Collider Facility and at the Facility for Antiproton and Ion Research in Darmstadt. Phys. Rev. C 2016, 94, 044917. [Google Scholar] [CrossRef]
- Batyuk, P.; Blaschke, D.; Bleicher, M.; Ivanov, Y.B.; Karpenko, I.; Malinina, L.; Merts, S.; Nahrgang, M.; Petersen, H.; Rogachevsky, O. Three-fluid Hydrodynamics-based Event Simulator Extended by UrQMD final State interactions (THESEUS) for FAIR-NICA-SPSBES/RHIC energies. EPJ Web Conf. 2018, 182, 02056. [Google Scholar] [CrossRef]
- Bass, S.A.; Mattiello, R.; Stöcker, H.; Greiner, W.; Hartnack, C. Is collective pion flow anticorrelated to nucleon flow? Phys. Lett. B 1993, 302, 381. [Google Scholar] [CrossRef]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Amelin, N.; Soff, S.; Spieles, C.; Weber, H.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255. [Google Scholar] [CrossRef]
- Mishustin, I.N.; Russkikh, V.N.; Satarov, L.M. Fluid dynamical model of relativistic heavy ion collision. Sov. J. Nucl. Phys. 1991, 54, 260–314. (In Russian) [Google Scholar]
- Khvorostukin, A.S.; Skokov, V.V.; Toneev, V.D.; Redlich, K. Lattice QCD constraints on the nuclear equation of state. Eur. Phys. J. C 2006, 48, 531. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: II. Particle Production. Phys. Rev. C 2013, 87, 064905. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Soldatov, A.A. Light fragment production at CERN Super Proton Synchrotron. Eur. Phys. J. A 2017, 53, 218. [Google Scholar] [CrossRef]
- ADOPTED LEVELS for 4He. Available online: https://www.nndc.bnl.gov/nudat2/getdataset.jsp?nucleus=4HE&unc=nds (accessed on 31 January 2023).
- Song, H.; Bass, S.A.; Heinz, U. Viscous QCD matter in a hybrid hydrodynamic + Boltzmann approach. Phys. Rev. C 2011, 83, 024912. [Google Scholar] [CrossRef]
- Gazdzicki, M.; NA49 Collaboration. Report from NA49. J. Phys. G 2004, 30, S701–S708. [Google Scholar] [CrossRef]
- Anticic, T.; Baatar, B.; Barna, D.; Bartke, J.; Beck, H.; Betev, L.; NA49 Collaboration. Centrality dependence of proton and antiproton spectra in Pb + Pb collisions at 40A GeV and 158A GeV measured at the CERN SPS. Phys. Rev. C 2011, 83, 014901. [Google Scholar] [CrossRef]
- Sun, K.J.; Chen, L.W.; Ko, C.M.; Xu, Z. Probing QCD critical fluctuations from light nuclei production in relativistic heavy-ion collisions. Phys. Lett. B 2017, 774, 103–107. [Google Scholar] [CrossRef]
- Sun, K.J.; Chen, L.W.; Ko, C.M.; Pu, J.; Xu, Z. Light nuclei production as a probe of the QCD phase diagram. Phys. Lett. B 2018, 781, 499–504. [Google Scholar] [CrossRef]
- Bastian, N.U.; Batyuk, P.; Blaschke, D.; Danielewicz, P.; Ivanov, Y.B.; Karpenko, I.; Röpke, G.; Rogachevsky, O.; Wolter, H.H. Light cluster production at NICA. Eur. Phys. J. A 2016, 52, 244. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Ivanov, Y.B.; Karpenko, I.; Rogachevsky, O.V.; Wolter, H.H. Medium effects on freeze-out of light clusters at NICA energies. Phys. Part. Nucl. Lett. 2018, 15, 225–229. [Google Scholar] [CrossRef]
- Dönigus, B.; Röpke, G.; Blaschke, D. Deuteron yields from heavy-ion collisions at energies available at the CERN Large Hadron Collider: Continuum correlations and in-medium effects. Phys. Rev. C 2022, 106, 044908. [Google Scholar] [CrossRef]
- Kozhevnikova, M.; Ivanov, Y.B. Light-nuclei production in heavy-ion collisions within thermodynamical approach. Phys. Rev. C 2023, 107, 024903. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).