Nucleon Resonance Electroexcitation Amplitudes and Emergent Hadron Mass
Abstract
1. Introduction
2. Basics for Insight into EHM Using CSMs
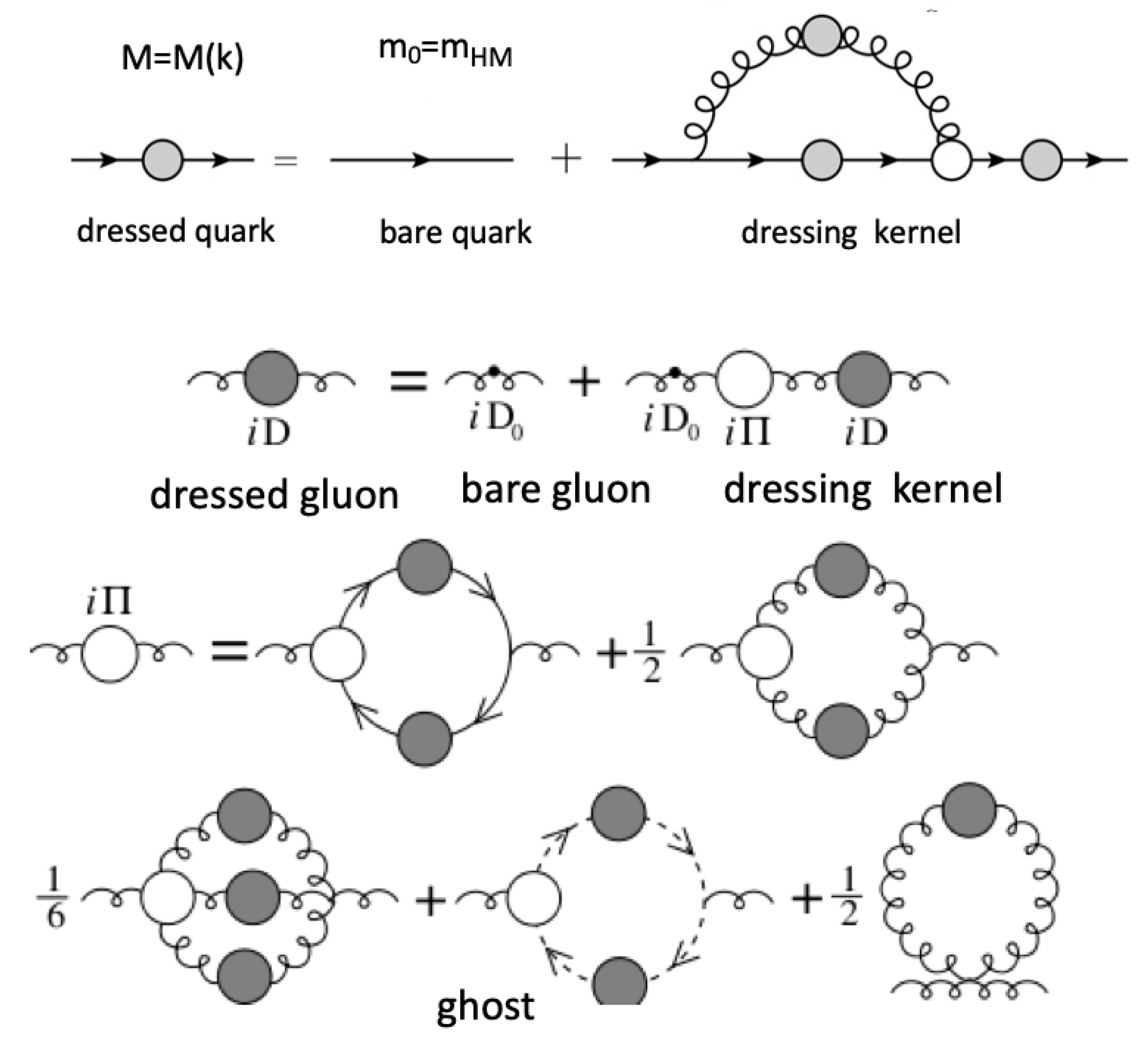
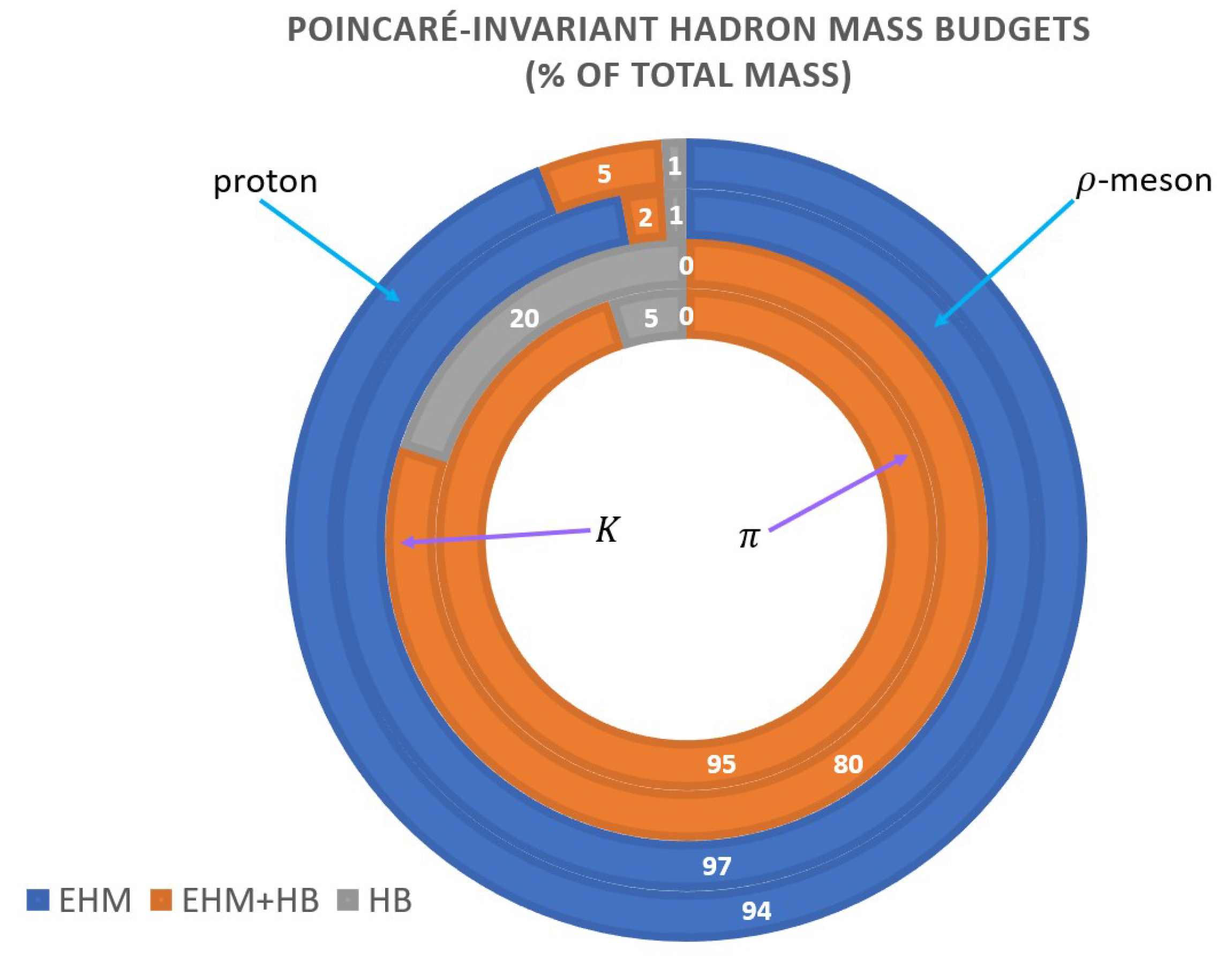
2.1. CSMs and the EHM Paradigm
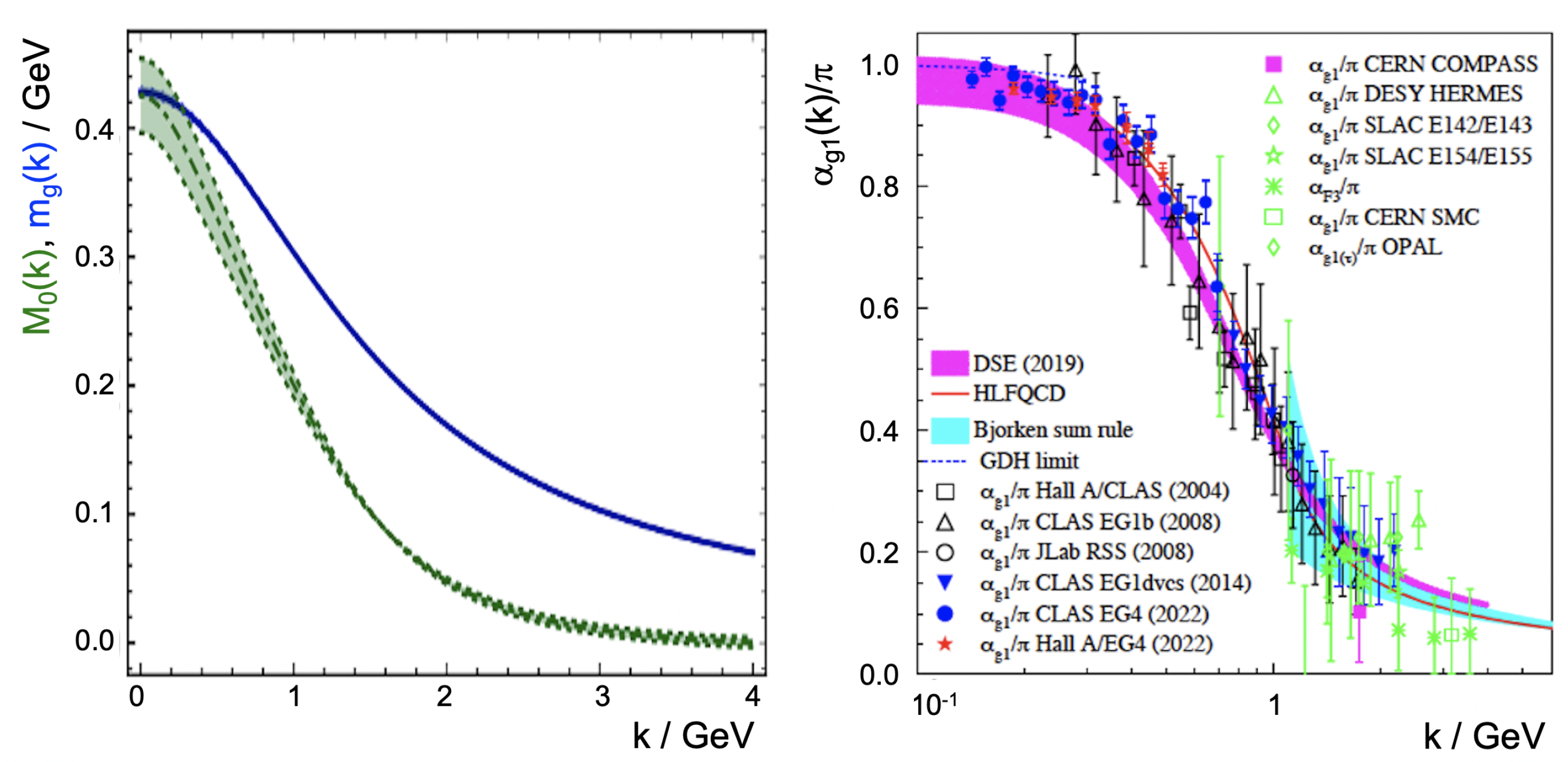
2.2. Some Highlights from the EHM Experiment-Theory Connection
3. Nucleon Resonance Electrocouplings and Their Impact on the Insight into EHM
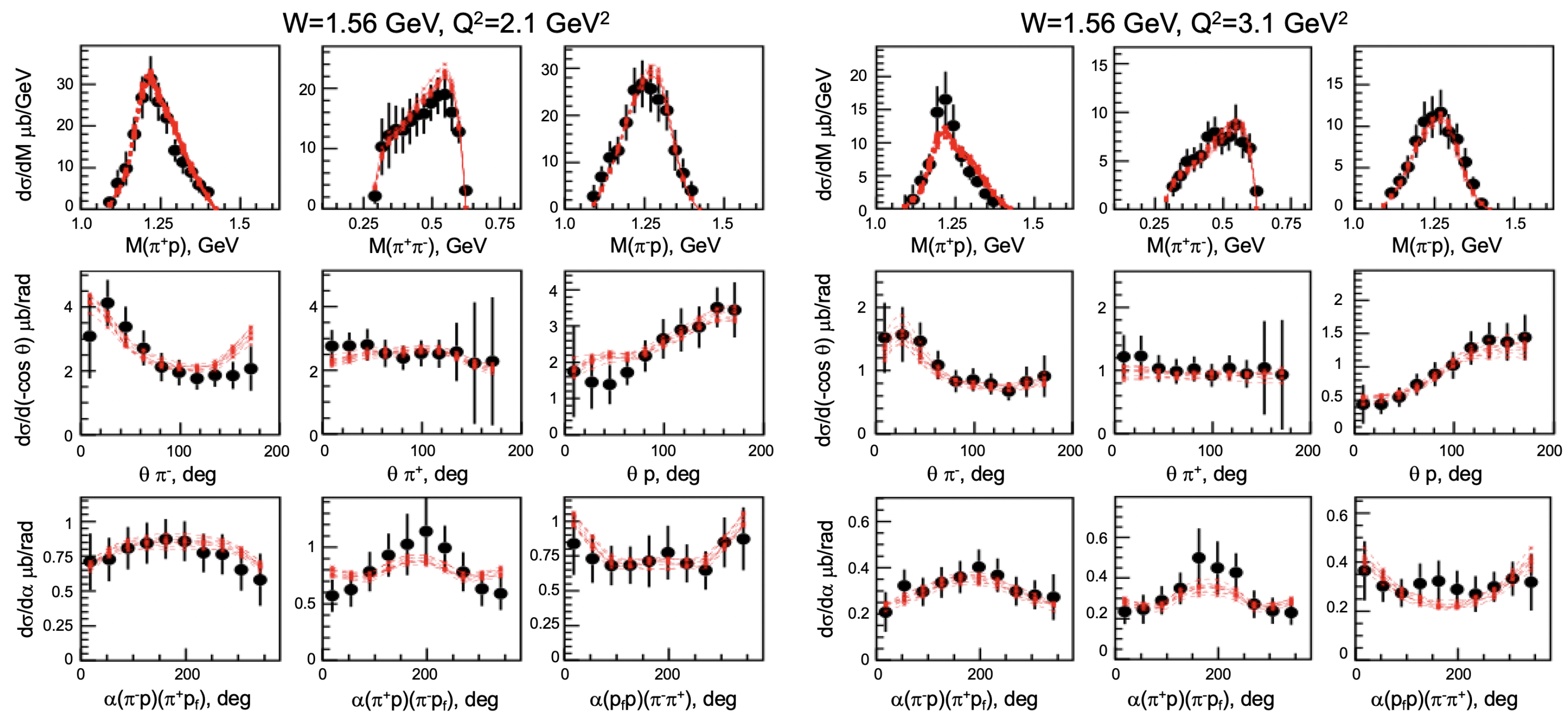
3.1. Extraction of Electrocouplings from Exclusive Meson Electroproduction Data
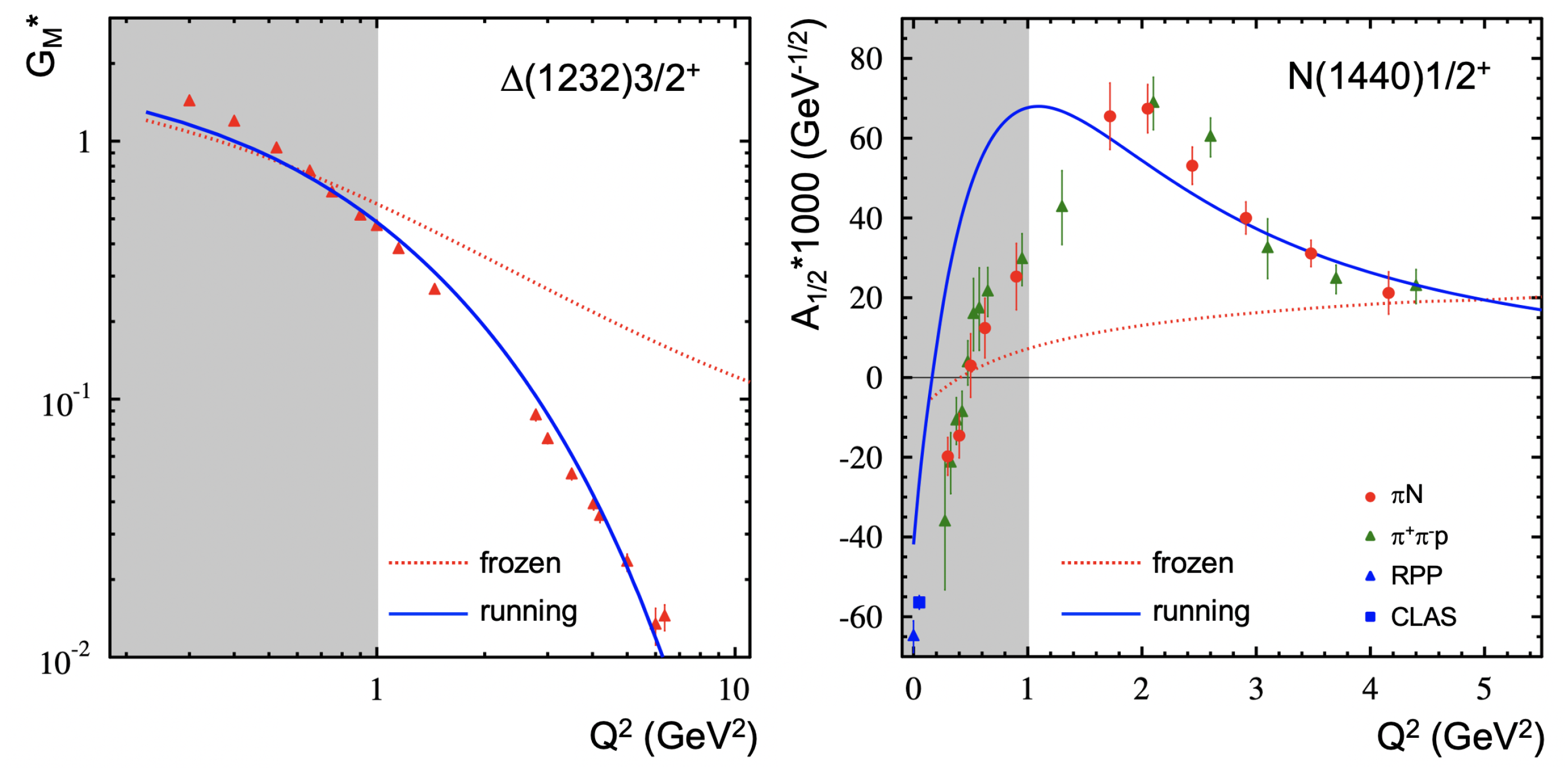
3.2. Insights into the Dressed-Quark Mass Function from the Electrocouplings
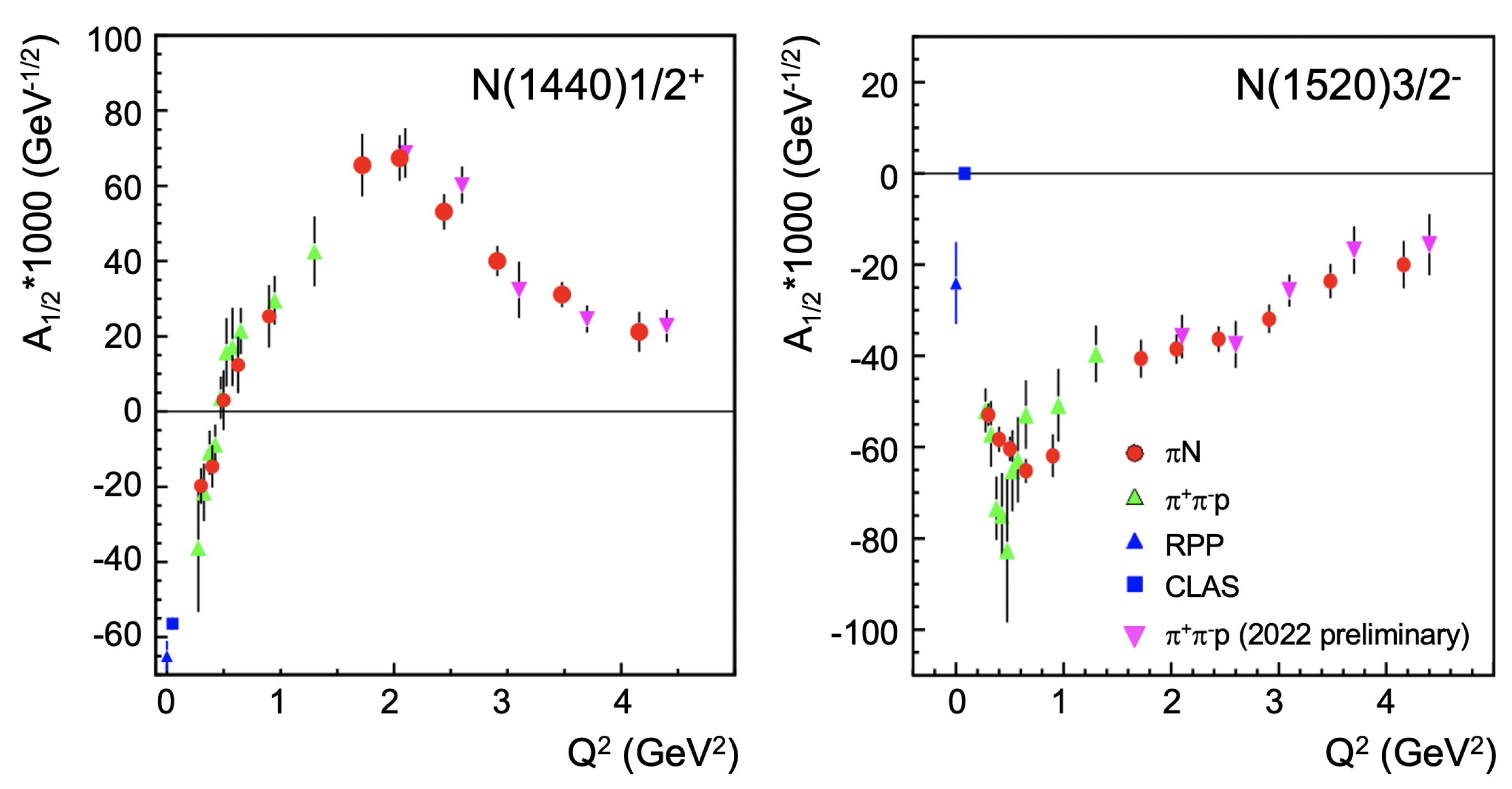
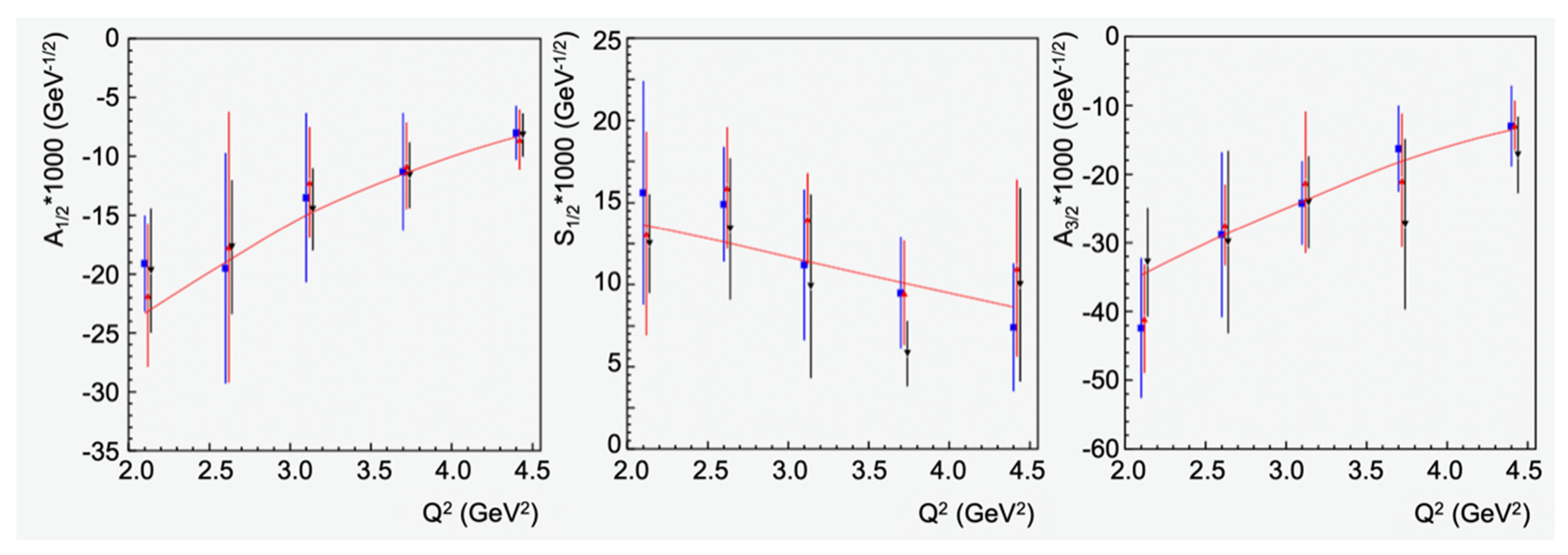
3.3. Novel Tests of CSM Predictions
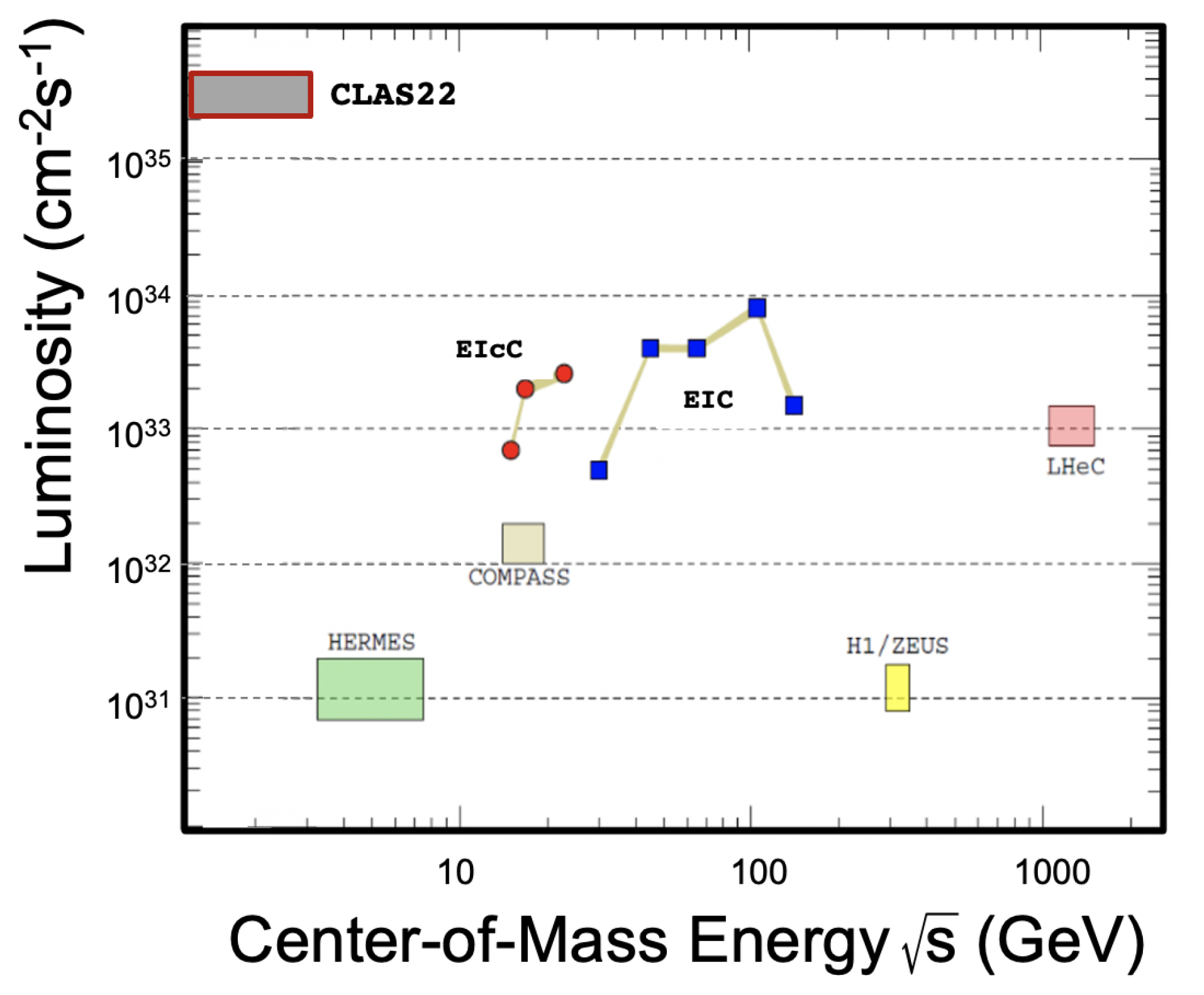
4. Studies of Structure in Experiments with CLAS12 and Beyond
5. Conclusions and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CM | center-of-mass |
| CSM | continuum Schwinger function method |
| DCSB | dynamical chiral symmetry breaking |
| data point | |
| EHM | emergence of hadron mass |
| EIC | Electron-Ion Collider (at Brookhaven National Laboratory) |
| EicC | Electron-ion collider China |
| HB | Higgs boson |
| JLab | Thomas Jefferson National Accelerator Facility (Jefferson Laboratory) |
| JM | JLab-Moscow State University |
| lQCD | lattice-regularized quantum chromodynamics |
| NG (mode/boson) | Nambu-Goldstone (mode/boson) |
| PDFs | Particle Distribution Functions |
| PDG | Particle Data Group (and associated publications) |
| pQCD | perturbative QCD |
| QCD | quantum chromodynamics |
| RMS | root mean square |
| RPP | Review of Particle Properties (and associated publications) |
| sQCD | strong QCD |
| SM | Standard Model of particle physics |
References
- Brodsky, S.J.; Burkert, V.D.; Carman, D.S.; Chen, J.P.; Cui, Z.F.; Döring, M.; Dosch, H.G.; Draayer, J.; Elouadrhiri, L.; Glazier, D.I.; et al. Strong QCD from Hadron Structure Experiments. Int. J. Mod. Phys. E 2020, 29, 2030006. [Google Scholar] [CrossRef]
- Binosi, D.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D.; Rodriguez-Quintero, J. Process-Independent Strong Running Coupling. Phys. Rev. D 2017, 96, 054026. [Google Scholar] [CrossRef]
- Cui, Z.F.; Zhang, J.L.; Binosi, D.; de Soto, F.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D.; Rodríguez-Quintero, J.; Segovia, J.; Zafeiropoulos, S. Effective Charge from Lattice QCD. Chin. Phys. C 2020, 44, 083102. [Google Scholar] [CrossRef]
- Deur, A.; Burkert, V.; Chen, J.P.; Korsch, W. Experimental Determination of the QCD Effective Charge αg1(Q). Particles 2022, 5, 171–179. [Google Scholar] [CrossRef]
- Eichmann, G.; Sanchis-Alepuz, H.; Williams, R.; Alkofer, R.; Fischer, C.S. Baryons as Relativistic Three-Quark Bound States. Prog. Part. Nucl. Phys. 2016, 91, 1–100. [Google Scholar] [CrossRef]
- Fischer, C.S. QCD at Finite Temperature and Chemical Potential from Dyson–Schwinger Equations. Prog. Part. Nucl. Phys. 2019, 105, 1–60. [Google Scholar] [CrossRef]
- Qin, S.X.; Roberts, C.D. Impressions of the Continuum Bound State Problem in QCD. Chin. Phys. Lett. 2020, 37, 121201. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Reflections upon the Emergence of Hadronic Mass. Eur. Phys. J. ST 2020, 229, 3319–3340. [Google Scholar] [CrossRef]
- Roberts, C.D. Empirical Consequences of Emergent Mass. Symmetry 2020, 12, 1468. [Google Scholar] [CrossRef]
- Roberts, C.D. On Mass and Matter. AAPPS Bull. 2021, 31, 6. [Google Scholar] [CrossRef]
- Roberts, C.D.; Richards, D.G.; Horn, T.; Chang, L. Insights into the Emergence of Mass from Studies of Pion and Kaon Structure. Prog. Part. Nucl. Phys. 2021, 120, 103883. [Google Scholar] [CrossRef]
- Binosi, D. Emergent Hadron Mass in Strong Dynamics. Few Body Syst. 2022, 63, 42. [Google Scholar] [CrossRef]
- Papavassiliou, J. Emergence of Mass in the Gauge Sector of QCD. Chin. Phys. C 2022, 46, 112001. [Google Scholar] [CrossRef]
- Ding, M.; Roberts, C.D.; Schmidt, S.M. Emergence of Hadron Mass and Structure. Particles 2023, 6, 57–120. [Google Scholar] [CrossRef]
- Ferreira, M.N.; Papavassiliou, J. Gauge Sector Dynamics in QCD. Particles 2023, 6, 312–363. [Google Scholar] [CrossRef]
- Blum, T.; Boyle, P.A.; Christ, N.H.; Frison, J.; Garron, N.; Hudspith, R.J.; Izubuchi, T.; Janowski, T.; Jung, C.; Jüttner, A.; et al. Domain Wall QCD with Physical Quark Masses. Phys. Rev. D 2016, 93, 074505. [Google Scholar] [CrossRef]
- Boyle, P.A.; Christ, N.H.; Garron, N.; Jung, C.; Jüttner, A.; Kelly, C.; Mawhinney, R.D.; McGlynn, G.; Murphy, D.J.; Ohta, S.; et al. Low Energy Constants of SU(2) Partially Quenched Chiral Perturbation Theory from Nf = 2 + 1 Domain Wall QCD. Phys. Rev. D 2016, 93, 054502. [Google Scholar] [CrossRef]
- Boyle, P.A.; Del Debbio, L.; Jüttner, A.; Khamseh, A.; Sanfilippo, F.; Tsang, J.T. The Decay Constants fD and fDs in the Continuum Limit of Nf = 2 + 1 Domain Wall Lattice QCD. JHEP 2017, 12, 008. [Google Scholar] [CrossRef]
- Gao, F.; Qin, S.X.; Roberts, C.D.; Rodríguez-Quintero, J. Locating the Gribov Horizon. Phys. Rev. D 2018, 97, 034010. [Google Scholar] [CrossRef]
- Oliveira, O.; Silva, P.J.; Skullerud, J.I.; Sternbeck, A. Quark Propagator with Two Flavors of O(a)-Improved Wilson Fermions. Phys. Rev. D 2019, 99, 094506. [Google Scholar] [CrossRef]
- Boucaud, P.; De Soto, F.; Raya, K.; Rodríguez-Quintero, J.; Zafeiropoulos, S. Discretization Effects on Renormalized Gauge-Field Green’s Functions, Scale Setting, and the Gluon Mass. Phys. Rev. D 2018, 98, 114515. [Google Scholar] [CrossRef]
- Zafeiropoulos, S.; Boucaud, P.; De Soto, F.; Rodríguez-Quintero, J.; Segovia, J. Strong Running Coupling from the Gauge Sector of Domain Wall Lattice QCD with Physical Quark Masses. Phys. Rev. Lett. 2019, 122, 162002. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, A.C.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J. Infrared Facets of the Three-Gluon Vertex. Phys. Lett. B 2021, 818, 136352. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ambrósio, C.O.; De Soto, F.; Ferreira, M.N.; Oliveira, B.M.; Papavassiliou, J.; Rodríguez-Quintero, J. Ghost Dynamics in the Soft Gluon Limit. Phys. Rev. D 2021, 104, 054028. [Google Scholar] [CrossRef]
- Pinto-Gómez, F.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J. Lattice Three-Gluon Vertex in Extended Kinematics: Planar Degeneracy. arXiv 2022, arXiv:2208.01020. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Bashir, A.; Braun, V.M.; Brodsky, S.J.; Burkert, V.D.; Chang, L.; Chen, C.; El-Bennich, B.; Cloët, I.C.; Cole, P.L.; et al. Studies of Nucleon Resonance Structure in Exclusive Meson Electroproduction. Int. J. Mod. Phys. E 2013, 22, 1330015. [Google Scholar] [CrossRef]
- Horn, T.; Roberts, C.D. The Pion: An Enigma within the Standard Model. J. Phys. G. 2016, 43, 073001. [Google Scholar] [CrossRef]
- Burkert, V.D.; Roberts, C.D. Colloquium: Roper Resonance: Toward a Solution to the Fifty-Year Puzzle. Rev. Mod. Phys. 2019, 91, 011003. [Google Scholar] [CrossRef]
- Burkert, V.D. Nucleon Resonances and Transition Form Factors. arXiv 2022, arXiv:2212.08980. Available online: https://arxiv.org/abs/2212.08980 (accessed on 1 March 2023).
- Beričič, J.; Correa, L.; Benali, M.; Achenbach, P.; Gayoso, C.A.; Bernauer, J.C.; Blomberg, A.; Böhm, R.; Bosnar, D.; Debenjak, L.; et al. New Insight in the Q2-Dependence of Proton Generalized Polarizabilities. Phys. Rev. Lett. 2019, 123, 192302. [Google Scholar] [CrossRef]
- Blomberg, A.; Atac, H.; Sparveris, N.; Paolone, M.; Achenbach, P.; Benali, M.; Beričič, J.; Böhm, R.; Correa, L.; Distler, M.O.; et al. Virtual Compton Scattering Measurements in the Nucleon Resonance Region. Eur. Phys. J. A 2019, 55, 182. [Google Scholar] [CrossRef]
- Mihovilovič, M.; Weber, A.B.; Achenbach, P.; Beranek, T.; Beričič, J.; Bernauer, J.C.; Böhm, R.; Bosnar, D.; Cardinali, M.; Correa, L.; et al. First Measurement of Proton’s Charge Form Factor at Very Low Q2 with Initial State Radiation. Phys. Lett. B 2017, 771, 194–198. [Google Scholar] [CrossRef]
- Friščić, I.; Achenbach, P.; Gayoso, C.A.; Baumann, D.; Böhm, R.; Bosnar, D.; Debenjak, L.; Denig, A.; Ding, M.; Distler, M.O.; et al. Measurement of the p(e,e′π+)n Reaction Close to Threshold and at Low Q2. Phys. Lett. B 2017, 766, 301–305. [Google Scholar] [CrossRef]
- Bernauer, J.C.; Distler, M.O.; Friedrich, J.; Walcher, T.; Achenbach, P.; Gayoso, C.A.; Böhm, R.; Bosnar, D.; Debenjak, L.; Doria, L.; et al. Electric and Magnetic Form Factors of the Proton. Phys. Rev. C 2014, 90, 015206. [Google Scholar] [CrossRef]
- Sparveris, N.; Stave, S.; Achenbach, P.; Gayoso, C.A.; Baumann, D.; Bernauer, J.; Bernstein, A.M.; Bohm, R.; Bosnar, D.; Botto, T.; et al. Measurements of the γ*p→Δ Reaction at Low Q2. Eur. Phys. J. A 2013, 49, 136. [Google Scholar] [CrossRef]
- Bevan, A.J.; Golob, B.; Mannel, T.; Prell, S.; Yabsley, B.D.; Aihara, H.; Anulli, F.; Arnaud, N.; Aushev, T.; Beneke, M.; et al. The Physics of the B Factories. Eur. Phys. J. C 2014, 74, 3026. [Google Scholar] [CrossRef]
- Kou, E.; Urquijo, P.; Altmannshofer, W.; Beaujean, F.; Bell, G.; Beneke, M.; Bigi, I.I.; Bishara, F.; Blanke, M.; Bobeth, C.; et al. The Belle II Physics Book. PTEP 2019, 2019, 123C01, Erratum in PTEP 2020, 2020, 029201. [Google Scholar] [CrossRef]
- Burkert, V.D. Jefferson Lab at 12 GeV: The Science Program. Ann. Rev. Nucl. Part. Sci. 2018, 68, 405–428. [Google Scholar] [CrossRef]
- Barabanov, M.Y.; Bedolla, M.A.; Brooks, W.K.; Cates, G.D.; Chen, C.; Chen, Y.; Cisbani, E.; Ding, M.; Eichmann, G.; Ent, R.; et al. Diquark Correlations in Hadron Physics: Origin, Impact and Evidence. Prog. Part. Nucl. Phys. 2021, 116, 103835. [Google Scholar] [CrossRef]
- Accardi, A.; Afanasev, A.; Albayrak, I.; Ali, S.F.; Amaryan, M.; Annand, J.R.M.; Arrington, J.; Asaturyan, A.; Atac, H.; Avakian, H.; et al. An Experimental Program with High Duty-Cycle Polarized and Unpolarized Positron Beams at Jefferson Lab. Eur. Phys. J. A 2021, 57, 261. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ahmed, Z.; Aidala, C.; Ali, S.; Andrieux, V.; Arrington, J.; Bashir, A.; Berdnikov, V.; Binosi, D.; Chang, L.; et al. Pion and Kaon Structure at the Electron-Ion Collider. Eur. Phys. J. A 2019, 55, 190. [Google Scholar] [CrossRef]
- Khalek, R.A.; Accardi, A.; Adam, J.; Adamiak, D.; Akers, W.; Albaladejo, M.; Al-bataineh, A.; Alexeev, M.G.; Ameli, F.; Antonioli, P.; et al. Science Requirements and Detector Concepts for the Electron-Ion Collider: EIC Yellow Report. Nucl. Phys. A 2022, 1026, 122447. [Google Scholar] [CrossRef]
- Arrington, J.; Gayoso, C.A.; Barry, P.C.; Berdnikov, V.; Binosi, D.; Chang, L.; Diefenthaler, M.; Ding, M.; Ent, R.; Frederico, T. Revealing the Structure of Light Pseudoscalar Mesons at the Electron–Ion Collider. J. Phys. G 2021, 48, 075106. [Google Scholar] [CrossRef]
- Chen, X.; Guo, F.K.; Roberts, C.D.; Wang, R. Selected Science Opportunities for the EicC. Few Body Syst. 2020, 61, 43. [Google Scholar] [CrossRef]
- Anderle, D.P.; Bertone, V.; Cao, X.; Chang, L.; Chang, N.; Chen, G.; Chen, X.; Chen, Z.; Cui, Z.; Dai, L.; et al. Electron-Ion Collider in China. Front. Phys. (Beijing) 2021, 16, 64701. [Google Scholar] [CrossRef]
- Quintans, C. The New AMBER Experiment at the CERN SPS. Few Body Syst. 2022, 63, 72. [Google Scholar] [CrossRef]
- Mokeev, V.I.; Carman, D.S. Photo- and Electrocouplings of Nucleon Resonances. Few Body Syst. 2022, 63, 59. [Google Scholar] [CrossRef]
- Carman, D.S.; Joo, K.; Mokeev, V.I. Strong QCD Insights from Excited Nucleon Structure Studies with CLAS and CLAS12. Few Body Syst. 2020, 61, 29. [Google Scholar] [CrossRef]
- Aznauryan, I.; Burkert, V. Electroexcitation of Nucleon Resonances. Prog. Part. Nucl. Phys. 2012, 67, 1–54. [Google Scholar] [CrossRef]
- Villano, A.N.; Stoler, P.; Bosted, P.E.; Connell, S.H.; Dalton, M.M.; Jones, M.K.; Kubarovsky, V.; Adams, G.S.; Ahmidouch, A.; Arrington, J.; et al. Neutral Pion Electroproduction in the Resonance Region at High Q2. Phys. Rev. D 2009, 80, 035203. [Google Scholar]
- Dalton, M.M.; Adams, G.S.; Ahmidouch, A.; Angelescu, T.; Arrington, J.; Asaturyan, R.; Baker, O.K.; Benmouna, N.; Bertoncini, C.; Boeglin, W.U.; et al. Electroproduction of η Mesons in the S11(1535) Resonance Region at High Momentum Transfer. Phys. Rev. C 2009, 80, 015205. [Google Scholar] [CrossRef]
- Anikin, I.V.; Braun, V.M.; Offen, N. Electroproduction of the N*(1535) Nucleon Resonance in QCD. Phys. Rev. D 2015, 92, 014018. [Google Scholar] [CrossRef]
- Giannini, M.M.; Santopinto, E. The Hypercentral Constituent Quark Model and its Application to Baryon Properties. Chin. J. Phys. 2015, 53, 020301. [Google Scholar]
- Braun, V.M. Hadron Wave Functions from Lattice QCD. Few Body Syst. 2016, 57, 1019. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Burkert, V.D. Electroexcitation of Nucleon Resonances in a Light-Front Relativistic Quark Model. Few Body Syst. 2018, 59, 98. [Google Scholar] [CrossRef]
- Qin, S.X.; Roberts, C.D.; Schmidt, S.M. Poincaré-Covariant Analysis of Heavy-Quark Baryons. Phys. Rev. D 2018, 97, 114017. [Google Scholar] [CrossRef]
- Ramalho, G. Quark Model Calculations of Transition Form Factors at High Photon Virtualities. EPJ Web Conf. 2020, 241, 02007. [Google Scholar] [CrossRef]
- Lyubovitskij, V.E.; Schmidt, I. Nucleon Resonances with Higher Spins in Soft-Wall AdS/QCD. Phys. Rev. D 2020, 102, 094008. [Google Scholar] [CrossRef]
- Raya, K.; Gutiérrez-Guerrero, L.X.; Bashir, A.; Chang, L.; Cui, Z.F.; Lu, Y.; Roberts, C.D.; Segovia, J. Dynamical Diquarks in the γ(*)p→N(1535) Transition. Eur. Phys. J. A 2021, 57, 266. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Roberts, C.D. Wave Functions of (I,JP) = (, ) Baryons. arXiv 2022, arXiv:2208.12353. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Lu, Y.; Roberts, C.D.; Segovia, J. Composition of Low-Lying J = 3/2± Δ-Baryons. Phys. Rev. D 2022, 105, 114047. [Google Scholar] [CrossRef]
- Blin, A.N.H.; Melnitchouk, W.; Mokeev, V.I.; Burkert, V.D.; Chesnokov, V.V.; Pilloni, A.; Szczepaniak, A.P. Resonant Contributions to Inclusive Nucleon Structure Functions from Exclusive Meson Electroproduction data. Phys. Rev. C 2021, 104, 025201. [Google Scholar] [CrossRef]
- Hiller Blin, A.N.; Mokeev, V.; Albaladejo, M.; Fernández-Ramírez, C.; Mathieu, V.; Pilloni, A.; Szczepaniak, A.; Burkert, V.D.; Chesnokov, V.V.; Golubenko, A.A.; et al. Nucleon Resonance Contributions to Unpolarised Inclusive Electron Scattering. Phys. Rev. C 2019, 100, 035201. [Google Scholar] [CrossRef]
- Klimenko, V. Inclusive Electron Scattering in the Resonance Region from a Hydrogen Target with CLAS12. 2023, in progress.
- Wilson, D.J.; Cloet, I.C.; Chang, L.; Roberts, C.D. Nucleon and Roper Electromagnetic Elastic and Transition Form Factors. Phys. Rev. C 2012, 85, 025205. [Google Scholar] [CrossRef]
- Segovia, J.; Chen, C.; Cloet, I.C.; Roberts, C.D.; Schmidt, S.M.; Wan, S.L. Elastic and Transition Form Factors of the Δ(1232). Few Body Syst. 2014, 55, 1–33. [Google Scholar] [CrossRef]
- Mokeev, V.I.; Burkert, V.D.; Carman, D.S.; Elouadrhiri, L.; Fedotov, G.V.; Golovatch, E.N.; Gothe, R.W.; Hicks, K.; Ishkhanov, B.S.; Isupov, E.L.; et al. New Results from the Studies of the N(1440)1/2+, N(1520)3/2−, and Δ(1620)1/2− Resonances in Exclusive ep→e′p′π+π− Electroproduction with the CLAS Detector. Phys. Rev. C 2016, 93, 025206. [Google Scholar] [CrossRef]
- Segovia, J.; Cloet, I.C.; Roberts, C.D.; Schmidt, S.M. Nucleon and Δ Elastic and Transition Form Factors. Few Body Syst. 2014, 55, 1185–1222. [Google Scholar] [CrossRef]
- Segovia, J.; El-Bennich, B.; Rojas, E.; Cloet, I.C.; Roberts, C.D.; Xu, S.S.; Zong, H.S. Completing the Picture of the Roper Resonance. Phys. Rev. Lett. 2015, 115, 171801. [Google Scholar] [CrossRef]
- Segovia, J.; Roberts, C.D. Dissecting Nucleon Transition Electromagnetic Form Factors. Phys. Rev. C 2016, 94, 042201(R). [Google Scholar] [CrossRef]
- Chen, C.; Lu, Y.; Binosi, D.; Roberts, C.D.; Rodríguez-Quintero, J.; Segovia, J. Nucleon-to-Roper Electromagnetic Transition Form Factors at Large Q2. Phys. Rev. D 2019, 99, 034013. [Google Scholar] [CrossRef]
- Burkert, V.D.; Mokeev, V.I.; Ishkhanov, B.S. The Nucleon Resonance Structure from the π+π−p Electroproduction Reaction off Protons. Moscow Univ. Phys. Bull. 2019, 74, 243, Vestn. Mosk. Univ. Ser. III Fiz. Astron.2019, 74, 28–38. [Google Scholar] [CrossRef]
- Roberts, C.D. Resonance Electroproduction and the Origin of Mass. EPJ Web Conf. 2020, 241, 02008. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, C.; Cui, Z.F.; Roberts, C.D.; Schmidt, S.M.; Segovia, J.; Zong, H.S. Transition Form Factors: γ* + p→Δ(1232), Δ(1600). Phys. Rev. D 2019, 100, 034001. [Google Scholar] [CrossRef]
- Mokeev, V.I. Two Pion Photo- and Electroproduction with CLAS. EPJ Web Conf. 2020, 241, 03003. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C. Review of Particle Physics. PTEP 2022, 2022, 083C01. [Google Scholar]
- Binosi, D.; Chang, L.; Papavassiliou, J.; Qin, S.X.; Roberts, C.D. Natural Constraints on the Gluon-Quark Vertex. Phys. Rev. D 2017, 95, 031501(R). [Google Scholar] [CrossRef]
- Chang, L.; Cloet, I.C.; Roberts, C.D.; Schmidt, S.M.; Tandy, P.C. Pion Electromagnetic Form Factor at Spacelike Momenta. Phys. Rev. Lett. 2013, 111, 141802. [Google Scholar] [CrossRef]
- Cui, Z.F.; Chen, C.; Binosi, D.; de Soto, F.; Roberts, C.D.; Rodríguez-Quintero, J.; Schmidt, S.M.; Segovia, J. Nucleon Elastic Form Factors at Accessible Large Spacelike Momenta. Phys. Rev. D 2020, 102, 014043. [Google Scholar] [CrossRef]
- Ripani, M.; Mokeev, V.; Anghinolfi, M.; Battaglieri, M.; Fedotov, G.; Golovach, E.; Ishkhanov, B.; Osipenko, M.; Ricco, G.; Sapunenko, V.; et al. A Phenomenological Description of π−Δ++ Photoproduction and Electroproduction in Nucleon Resonance Region. Nucl. Phys. A 2000, 672, 220–248. [Google Scholar] [CrossRef]
- Burkert, V.D.; Mokeev, V.I.; Shvedunov, N.V.; Boluchevskii, A.A.; Battaglieri, M.; Golovach, E.N.; Elouardrhiri, L.; Joo, K.; Isupov, E.L.; Ishkhanov, B.S.; et al. Isobar Channels in the Production of π+π− Pairs on a Proton by Virtual Photons. Phys. Atom. Nucl. 2007, 70, 427. [Google Scholar] [CrossRef]
- Mokeev, V.I.; Burkert, V.D.; Lee, T.S.H.; Elouadrhiri, L.; Fedotov, G.V.; Ishkhanov, B.S. Model Analysis of the pπ+π− Electroproduction Reaction on the Proton. Phys. Rev. C 2009, 80, 045212. [Google Scholar] [CrossRef]
- Mokeev, V.I.; Biselli, A. Experimental Study of the P11(1440) and D13(1520) Resonances from CLAS Data on ep→e′π+π−p′. Phys. Rev. C 2012, 86, 035203. [Google Scholar] [CrossRef]
- Roberts, C.D.; Williams, A.G. Dyson-Schwinger Equations and their Application to Hadronic Physics. Prog. Part. Nucl. Phys. 1994, 33, 477–575. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D. π- and K Meson Bethe-Salpeter Amplitudes. Phys. Rev. C 1997, 56, 3369. [Google Scholar] [CrossRef]
- Cornwall, J.M. Dynamical Mass Generation in Continuum QCD. Phys. Rev. D 1982, 26, 1453. [Google Scholar] [CrossRef]
- Schwinger, J.S. Gauge Invariance and Mass. Phys. Rev. 1962, 125, 397. [Google Scholar] [CrossRef]
- Schwinger, J.S. Gauge Invariance and Mass. 2. Phys. Rev. 1962, 128, 2425. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Gluon and Ghost Propagators in the Landau Gauge: Deriving Lattice Results from Schwinger-Dyson Qquations. Phys. Rev. D 2008, 78, 025010. [Google Scholar] [CrossRef]
- Boucaud, P.; Leroy, J.P.; Le-Yaouanc, A.; Micheli, J.; Pene, O.; Rodríguez-Quintero, J. The Infrared Behaviour of the Pure Yang-Mills Green Functions. Few Body Syst. 2012, 53, 387–436. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. The Gluon Mass Generation Mechanism: A Concise Primer. Front. Phys. China 2016, 11, 111203. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Papavassiliou, J. Exploring Smoking-Gun Signals of the Schwinger Mechanism in QCD. Phys. Rev. D 2022, 105, 014030. [Google Scholar] [CrossRef]
- Aguilar, A.C.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Pinto-Gómez, F.; Roberts, C.D.; Rodríguez-Quintero, J. Schwinger Mechanism for Gluons from Lattice QCD. arXiv 2022, arXiv:2211.12594. Available online: https://arxiv.org/abs/2211.12594 (accessed on 1 March 2023).
- Grunberg, G. Renormalization Scheme Independent QCD and QED: The Method of Effective Charges. Phys. Rev. D 1984, 29, 2315. [Google Scholar] [CrossRef]
- Grunberg, G. On Some Ambiguities in the Method of Effective Charges. Phys. Rev. D 1989, 40, 680. [Google Scholar] [CrossRef]
- Bjorken, J.D. Applications of the Chiral U(6) × (6) Algebra of Current Densities. Phys. Rev. 1966, 148, 1467. [Google Scholar] [CrossRef]
- Bjorken, J.D. Inelastic Scattering of Polarized Leptons from Polarized Nucleons. Phys. Rev. D 1970, 1, 1376. [Google Scholar] [CrossRef]
- Gell-Mann, M. A Schematic Model of Baryons and Mesons. Phys. Lett. 1964, 8, 214. [Google Scholar] [CrossRef]
- Eichmann, G.; Ramalho, G. Nucleon Resonances in Compton Scattering. Phys. Rev. D 2018, 98, 093007. [Google Scholar] [CrossRef]
- Ding, M.; Raya, K.; Binosi, D.; Chang, L.; Roberts, C.D.; Schmidt, S.M. Symmetry, Symmetry Breaking, and Pion Parton Distributions. Phys. Rev. D 2020, 101, 054014. [Google Scholar] [CrossRef]
- Chen, C.; Roberts, C.D. Nucleon Axial Form Factor at Large Momentum Transfers. Eur. Phys. J. A 2022, 58, 206. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D.; Tandy, P.C. Pion Mass and Decay Constant. Phys. Lett. B 1998, 420, 267–273. [Google Scholar] [CrossRef]
- Höll, A.; Krassnigg, A.; Roberts, C.D. Pseudoscalar Meson Radial Excitations. Phys. Rev. C 2004, 70, 042203(R). [Google Scholar] [CrossRef]
- Brodsky, S.J.; Roberts, C.D.; Shrock, R.; Tandy, P.C. Confinement Contains Condensates. Phys. Rev. C 2012, 85, 065202. [Google Scholar] [CrossRef]
- Qin, S.X.; Roberts, C.D.; Schmidt, S.M. Ward–Green–Takahashi Identities and the Axial-Vector Vertex. Phys. Lett. B 2014, 733, 202–208. [Google Scholar] [CrossRef]
- Nambu, Y. Quasiparticles and Gauge Invariance in the Theory of Superconductivity. Phys. Rev. 1960, 117, 648. [Google Scholar] [CrossRef]
- Goldstone, J. Field Theories with Superconductor Solutions. Nuovo Cim. 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Roberts, C.D. Perspective on the Origin of Hadron Masses. Few Body Syst. 2017, 58, 5. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Holl, A.; Jaikumar, P.; Roberts, C.D.; Wright, S.V. Sigma Terms of Light-Quark Hadrons. Few Body Syst. 2006, 38, 31–51. [Google Scholar] [CrossRef]
- Ruiz de Elvira, J.; Hoferichter, M.; Kubis, B.; Meißner, U.G. Extracting the σ-Term from Low-Energy Pion-Nucleon Scattering. J. Phys. G 2018, 45, 024001. [Google Scholar] [CrossRef]
- Aoki, S.; Aoki, Y.; Bečirević, D.; Blum, T.; Colangelo, G.; Collins, S.; Della Morte, M.; Dimopoulos, P.; Dürr, S.; Fukaya, H.; et al. FLAG Review 2019. Eur. Phys. J. C 2020, 80, 113. [Google Scholar] [CrossRef]
- Obukhovsky, I.T.; Faessler, A.; Fedorov, D.K.; Gutsche, T.; Lyubovitskij, V.E. Transition Form Factors and Helicity Amplitudes for Electroexcitation of Negative- and Positive Parity Nucleon Resonances in a Light-Front Quark Model. Phys. Rev. D 2019, 100, 094013. [Google Scholar] [CrossRef]
- Carman, D.S. Nucleon Resonance Structure Studies Via Exclusive KY Electroproduction. Few Body Syst. 2016, 57, 941–948. [Google Scholar] [CrossRef]
- Carman, D.S. CLAS N* Excitation Results from Pion and Kaon Electroproduction. Few Body Syst. 2018, 59, 82. [Google Scholar] [CrossRef]
- CLAS Physics Database. Available online: https://clasweb.jlab.org/physicsdb/ (accessed on 1 March 2023).
- Chesnokov, V.V.; Golubenko, A.A.; Ishkhanov, B.S.; Mokeev, V.I. CLAS Database for Studies of the Structure of Hadrons in Electromagnetic Processes. Phys. Part. Nucl. 2022, 53, 184–190. [Google Scholar] [CrossRef]
- Aznauryan, I.G. Multipole Amplitudes of Pion Photoproduction on Nucleons up to 2-GeV Within Dispersion Relations and Unitary Isobar Model. Phys. Rev. C 2003, 67, 015209. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Burkert, V.D.; Fedotov, G.V.; Ishkhanov, B.S.; Mokeev, V.I. Electroexcitation of Nucleon Resonances at Q2 = 0.65 (GeV/c)2 from a Combined Analysis of Single- and Double-Pion Electroproduction Data. Phys. Rev. C 2005, 72, 045201. [Google Scholar] [CrossRef]
- Arndt, R.; Briscoe, W.; Strakovsky, I.; Workman, R. Partial-Wave Analysis And Spectroscopy: From πN Scattering To Pion-Electroproduction. eConf 2007, C070910, 166. [Google Scholar]
- Drechsel, D.; Kamalov, S.S.; Tiator, L. Unitary Isobar Model - MAID2007. Eur. Phys. J. A 2007, 34, 69–97. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Burkert, V.D.; Biselli, A.S.; Egiyan, H.; Joo, K.; Kim, W.; Park, K.; Smith, L.C.; Ungaro, M.; Adhikari, K.P.; et al. Electroexcitation of Nucleon Resonances from CLAS Data on Single Pion Electroproduction. Phys. Rev. C 2009, 80, 055203. [Google Scholar] [CrossRef]
- Tiator, L.; Drechsel, D.; Kamalov, S.S.; Vanderhaeghen, M. Electromagnetic Excitation of Nucleon Resonances. Eur. Phys. J. ST 2011, 198, 141–170. [Google Scholar] [CrossRef]
- Park, K.; Aznauryan, I.G.; Burkert, V.D.; Adhikari, K.P.; Amaryan, M.J.; Pereira, S.A.; Avakian, H.; Battaglieri, M.; Badui, R.; Bedlinskiy, I.; et al. Measurements of ep→e′π+n at W = 1.6 − 2.0 GeV and Extraction of Nucleon Resonance Electrocouplings at CLAS. Phys. Rev. C 2015, 91, 045203. [Google Scholar] [CrossRef]
- Tiator, L.; Döring, M.; Workman, R.L.; Hadžimehmedović, M.; Osmanović, H.; Omerović, R.; Stahov, J.; Švarc, A. Baryon Transition Form Factors at the Pole. Phys. Rev. C 2016, 94, 065204. [Google Scholar] [CrossRef]
- Tiator, L.; Workman, R.L.; Wunderlich, Y.; Haberzettl, H. Amplitude Reconstruction from Complete Electroproduction Experiments and Truncated Partial-Wave Expansions. Phys. Rev. C 2017, 96, 025210. [Google Scholar] [CrossRef]
- Tiator, L. The MAID Legacy and Future. Few Body Syst. 2018, 59, 21. [Google Scholar] [CrossRef]
- Knochlein, G.; Drechsel, D.; Tiator, L. Photoproduction and Electroproduction of η Mesons. Z. Phys. A 1995, 352, 327–343. [Google Scholar] [CrossRef]
- Chiang, W.T.; Yang, S.N.; Tiator, L.; Drechsel, D. An Isobar Model for η Photoproduction and Electroproduction on the Nucleon. Nucl. Phys. A 2002, 700, 429–453. [Google Scholar] [CrossRef]
- Chiang, W.T.; Yang, S.N.; Drechsel, D.; Tiator, L. An Isobar Model Study of η Photoproduction and Electroproduction. PiN Newslett. 2002, 16, 299. [Google Scholar]
- Aznauryan, I. Resonance Contributions to η Photoproduction on Protons Found Using Dispersion Relations and an Isobar Model. Phys. Rev. C 2003, 68, 065204. [Google Scholar] [CrossRef]
- Kamano, H. Electromagnetic N* Transition Form Factors in the ANL-Osaka Dynamical Coupled-Channels Approach. Few Body Syst. 2018, 59, 24. [Google Scholar] [CrossRef]
- Mai, M.; Döring, M.; Granados, C.; Haberzettl, H.; Hergenrather, J.; Meißner, U.G.; Rönchen, D.; Strakovsky, I.; Workman, R. Coupled-Channels Analysis of Pion and η Electroproduction within the Jülich-Bonn-Washington Model. Phys. Rev. C 2022, 106, 015201. [Google Scholar] [CrossRef]
- Mai, M.; Döring, M.; Granados, C.; Haberzettl, H.; Meißner, U.G.; Rönchen, D.; Strakovsky, I.; Workman, R. Jülich-Bonn-Washington Model for Pion Electroproduction Multipoles. Phys. Rev. C 2021, 103, 065204. [Google Scholar] [CrossRef]
- Hwang, S.; Ahn, J.K.; Bassalleck, B.; Fujioka, H.; Guo, L.; Han, Y.; Hasegawa, S.; Hicks, K.; Honda, R.; Hosomi, K.; et al. Measurement of 3-Body Hadronic Reactions with HypTPC at J-PARC. JPS Conf. Proc. 2015, 8, 022008. [Google Scholar]
- Hicks, K.H.; Sako, H.; Imai, K.; Hasegawa, S.; Sato, S.; Shirotori, K.; Chandavar, S.; Goetz, J.; Tang, W.; Ahn, J.K.; et al. 3-Body Hadronic Reactions for New Aspects of Baryon Spectroscopy. Available online: https://j-parc.jp/researcher/Hadron/en/pac_1207/pdf/P45_2012-3.pdf (accessed on 1 March 2023).
- Mokeev, V.I. New Opportunities for Insight into the Emergence of Hadron Mass from Studies of Nucleon Resonance Electroexcitation. In Proceedings of the Fall 2022 Meeting of the APS Division of Nuclear Physics, New Orleans, LA, USA, 27–30 October 2022. [Google Scholar]
- Mokeev, V.I. Nucleon Resonance Electrocouplings and the Emergence of Hadron Mass. In Proceedings of the Baryons 2022—International Conference on the Structure of Baryons, Andalusia, Spain, 7–11 November 2022. [Google Scholar]
- Dugger, M.; Ritchie, B.G.; Ball, J.P.; Collins, P.; Pasyuk, E.; Arndt, R.A.; Briscoe, W.J.; Strakovsky, I.I.; Workman, R.L.; Amaryan, M.J.; et al. π+ Photoproduction on the Proton for Photon Energies from 0.725 to 2.875 GeV. Phys. Rev. C 2009, 79, 065206. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Burkert, V.D. Extracting Meson-Baryon Contributions to the Electroexcitation of the N(1675) Nucleon Resonance. Phys. Rev. C 2015, 92, 015203. [Google Scholar] [CrossRef]
- Roberts, H.L.L.; Chang, L.; Cloet, I.C.; Roberts, C.D. Masses of Ground and Excited-state Hadrons. Few Body Syst. 2011, 51, 1. [Google Scholar] [CrossRef]
- Chen, C.; Fischer, C.S.; Roberts, C.D.; Segovia, J. Nucleon Axial-Vector and Pseudoscalar Form Factors and PCAC Relations. Phys. Rev. D 2022, 105, 094022. [Google Scholar] [CrossRef]
- Chang, L.; Cloet, I.C.; Cobos-Martinez, J.J.; Roberts, C.D.; Schmidt, S.M.; Tandy, P.C. Imaging Dynamical Chiral Symmetry Breaking: Pion Wave Function on the Light Front. Phys. Rev. Lett. 2013, 110, 132001. [Google Scholar] [CrossRef]
- Raya, K.; Chang, L.; Bashir, A.; Cobos-Martinez, J.J.; Gutiérrez-Guerrero, L.X.; Roberts, C.D.; Tandy, P.C. Structure of the Neutral Pion and its Electromagnetic Transition Form Factor. Phys. Rev. D 2016, 93, 074017. [Google Scholar] [CrossRef]
- Mokeev, V.I. Insight into EHM from Results on Electroexcitation of Δ(1600)3/2+ Resonance. In Proceedings of the Workshop on perceiving the Emergence of Hadron Mass through AMBER @ CERN—VII, Geneve, Switzerland, 10–13 May 2022. [Google Scholar]
- Isupov, E.L.; Burkert, V.D.; Carman, D.S.; Gothe, R.W.; Hicks, K.; Ishkhanov, B.S.; Mokeev, V.I. Measurements of ep→e′π+π−p′ Cross Sections with CLAS at 1.40 GeV < W < 2.0 GeV and 2.0 GeV2 < Q2 < 5.0 GeV2. Phys. Rev. C 2017, 96, 025209. [Google Scholar]
- Trivedi, A. Measurement of New Observables from the π+π− p Electroproduction Off the Proton. Few Body Syst. 2019, 60, 5. [Google Scholar] [CrossRef]
- Mokeev, V.I.; Burkert, V.D.; Carman, D.S.; Elouadrhiri, L.; Golovatch, E.; Gothe, R.W.; Hicks, K.; Ishkhanov, B.S.; Isupov, E.L.; Joo, K.; et al. Evidence for the N′(1720)3/2+ Nucleon Resonance from Combined Studies of CLAS π+π−p Photo- and Electroproduction Data. Phys. Lett. B 2020, 805, 135457. [Google Scholar] [CrossRef]
- Mokeev, V.I.; Carman, D.S. New Baryon States in Exclusive Meson Photo-/Electroproduction with CLAS. Rev. Mex. Fis. Suppl. 2022, 3, 0308024. [Google Scholar] [CrossRef]
- Burkert, V.D.; Elouadrhiri, L.; Adhikari, K.P.; Adhikari, S.; Amaryan, M.J.; Anderson, D.; Angelini, G.; Antonioli, M.; Atac, H.; Aune, S.; et al. The CLAS12 Spectrometer at Jefferson Laboratory. Nucl. Instrum. Meth. A 2020, 959, 163419. [Google Scholar] [CrossRef]
- Gothe, R.W.; Mokeev, V.; Burkert, V.D.; Cole, P.L.; Joo, K.; Stoler, P. Nucleon Resonance Studies with CLAS12. JLab Experiment E12-09-003. Available online: https://www.jlab.org/exp_prog/proposals/09/PR12-09-003.pdf (accessed on 1 March 2023).
- Carman, D.S.; Mokeev, V.I.; Burkert, V.D. Exclusive N*→KY Studies with CLAS12. JLab Experiment E12-06-108A. Available online: https://www.jlab.org/exp_prog/proposals/14/E12-06-108A.pdf (accessed on 1 March 2023).
- D’Angelo, A.; Burkert, V.D.; Carman, D.S.; Golovatch, E.; Gothe, R.; Mokeev, V. A Search for Hybrid Baryons in Hall B with CLAS12. JLab Experiment E12-16-010. Available online: https://www.jlab.org/exp_prog/proposals/16/PR12-16-010.pdf (accessed on 1 March 2023).
- Carman, D.S.; d’Angelo, A.; Lanza, L.; Mokeev, V.I.; Adhikari, K.P.; Amaryan, M.J.; Armstrong, W.R.; Atac, H.; Avakian, H.; Gayoso, C.A.; et al. Beam-Recoil Transferred Polarization in K+Y Electroproduction in the Nucleon Resonance Region with CLAS12. Phys. Rev. C 2022, 105, 065201. [Google Scholar] [CrossRef]
- Burkert, V.D. N* Experiments and Their Impact on Strong QCD Physics. Few Body Syst. 2018, 59, 57. [Google Scholar] [CrossRef]
- Aznauryan, I.; Burkert, V.; Lee, T.S.; Mokeev, V. Results from the N* Program at JLab. J. Phys. Conf. Ser. 2011, 299, 012008. [Google Scholar] [CrossRef]



| Proton | Neutron | |
|---|---|---|
| Measured masses (MeV) | 938.2720813 ± 0.0000058 | 939.5654133± 0.0000058 |
| Sum of the current quark masses (MeV) | 8.09 | 11.50 |
| Contribution of the current quark masses to the measured nucleon mass (%) | <1.1 | <1.4 |
| Meson Electroproduction Channels | Excited Proton States | Ranges for Extracted Electrocouplings, GeV |
|---|---|---|
| , | 0.16–6 | |
| , | 0.30–4.16 | |
| 0.30–4.16 | ||
| , | 1.6-4.5 | |
| 0.2–2.9 | ||
| , | 0.25–1.50 | |
| , | 2.0–5.0 | |
| , , | ||
| 0.50–1.50 | ||
| , | 0.50-1.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carman, D.S.; Gothe, R.W.; Mokeev, V.I.; Roberts, C.D. Nucleon Resonance Electroexcitation Amplitudes and Emergent Hadron Mass. Particles 2023, 6, 416-439. https://doi.org/10.3390/particles6010023
Carman DS, Gothe RW, Mokeev VI, Roberts CD. Nucleon Resonance Electroexcitation Amplitudes and Emergent Hadron Mass. Particles. 2023; 6(1):416-439. https://doi.org/10.3390/particles6010023
Chicago/Turabian StyleCarman, Daniel S., Ralf W. Gothe, Victor I. Mokeev, and Craig D. Roberts. 2023. "Nucleon Resonance Electroexcitation Amplitudes and Emergent Hadron Mass" Particles 6, no. 1: 416-439. https://doi.org/10.3390/particles6010023
APA StyleCarman, D. S., Gothe, R. W., Mokeev, V. I., & Roberts, C. D. (2023). Nucleon Resonance Electroexcitation Amplitudes and Emergent Hadron Mass. Particles, 6(1), 416-439. https://doi.org/10.3390/particles6010023








