Generalised Parton Distributions in Continuum Schwinger Methods: Progresses, Opportunities and Challenges
Abstract
1. Introduction
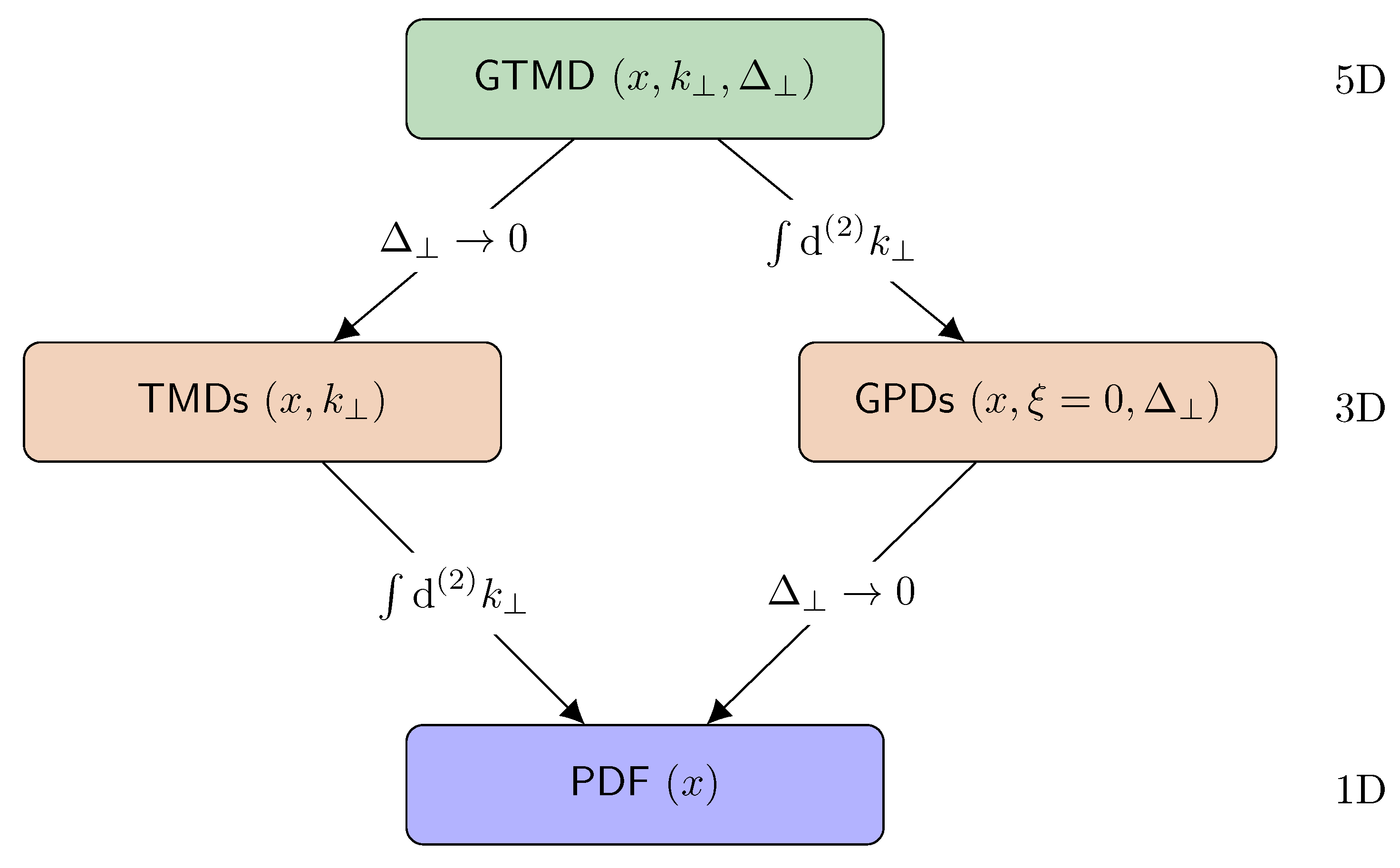
2. Generalised Parton Distributions
2.1. Formal Definitions and First Properties
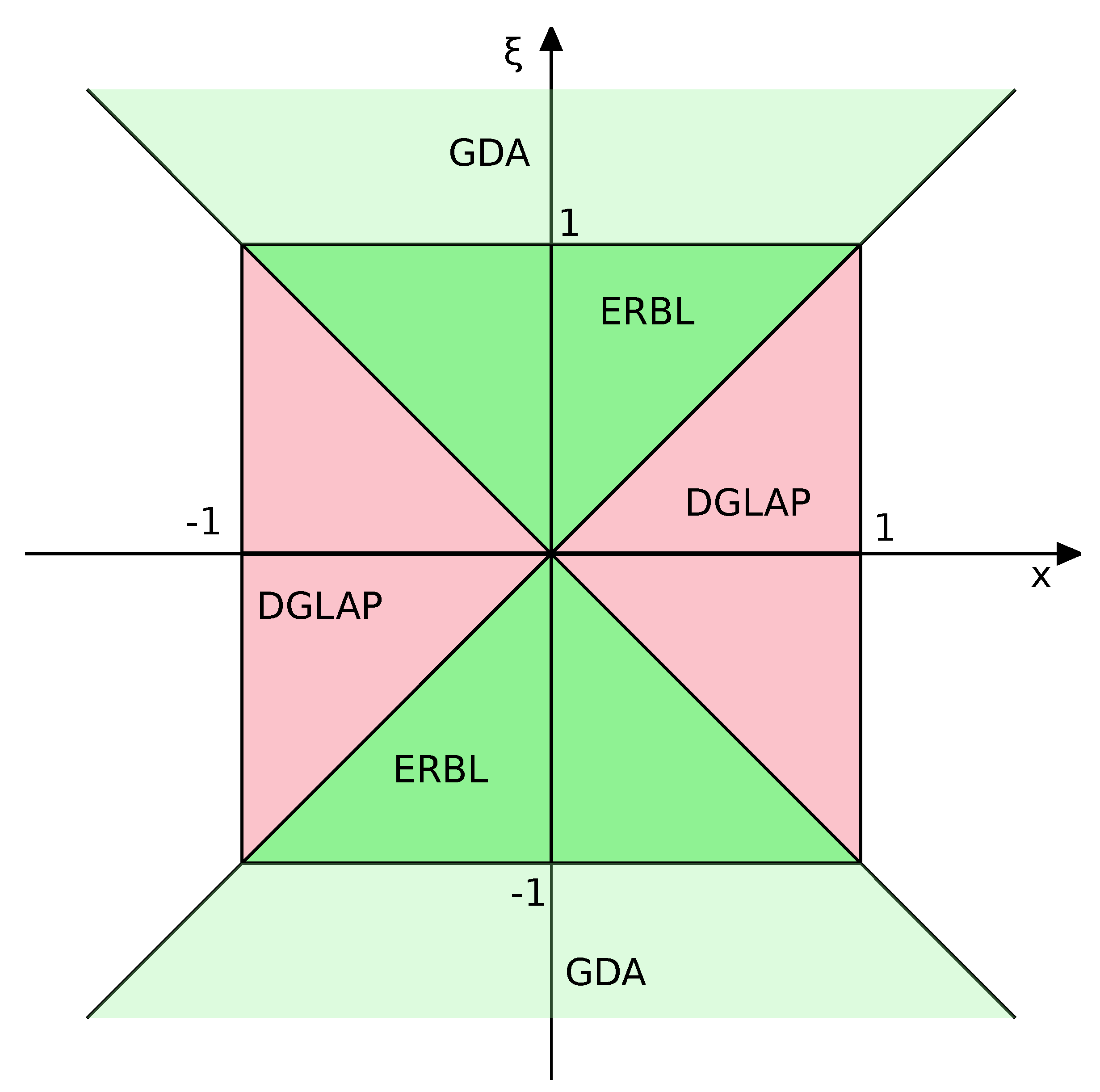
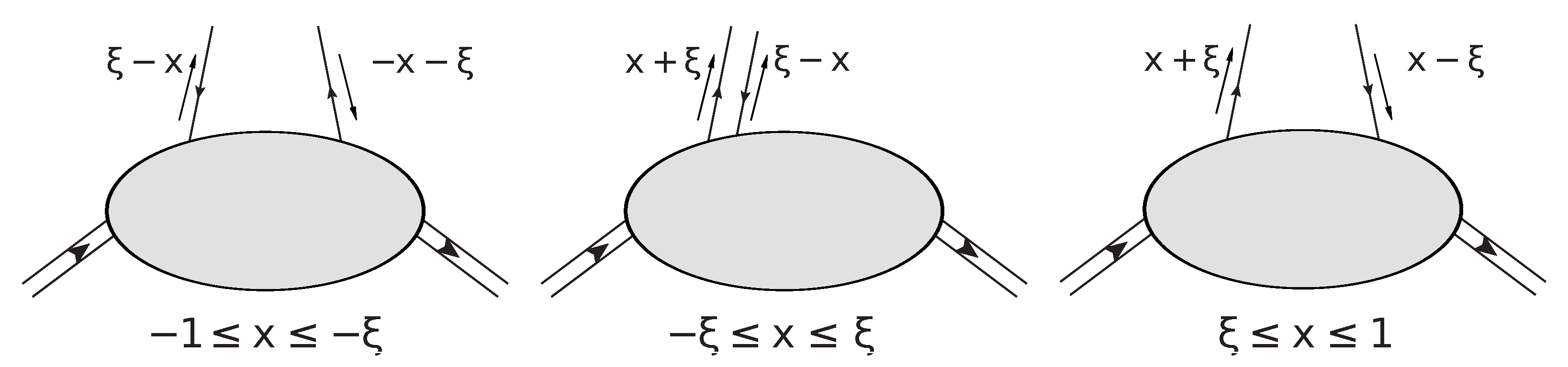
2.2. Reduction to Unidimensional Distributions
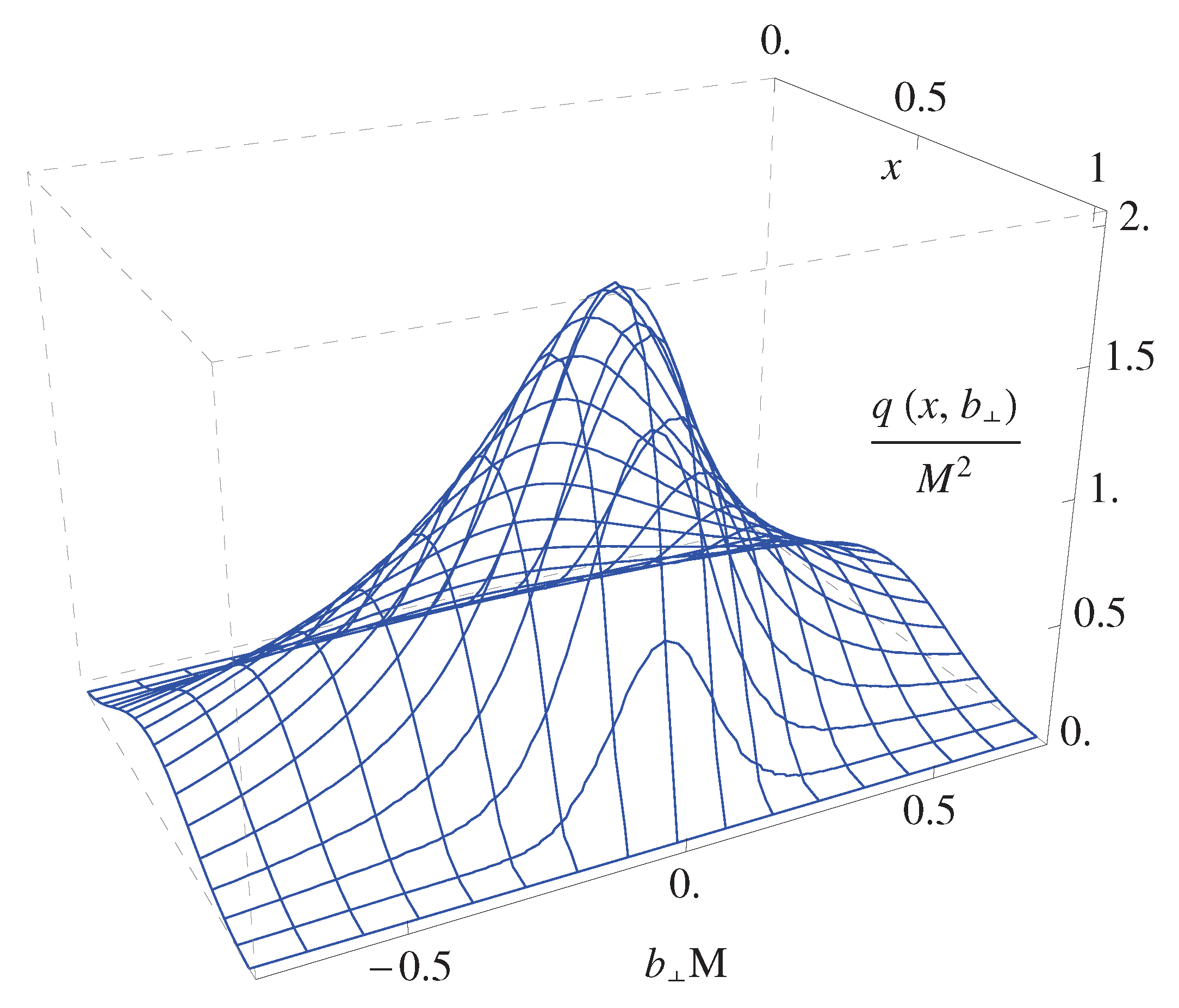
2.3. Interpretation in Coordinate Space
- Collinear factorisation allows one to interpret exclusive processes in terms of GPDs for values of t much smaller than the typical hard scale of the system;
- Yet, performing the Fourier transform requires to integrate over t up to infinity, introducing model-dependent extrapolations;
- Furthermore, no experimental data is available for vanishing values of , meaning that additional extrapolations generating more model biases are required.
2.4. Connection with the Energy-Momentum Tensor
2.5. Double Distribution Representation
2.5.1. Local Operators Analysis
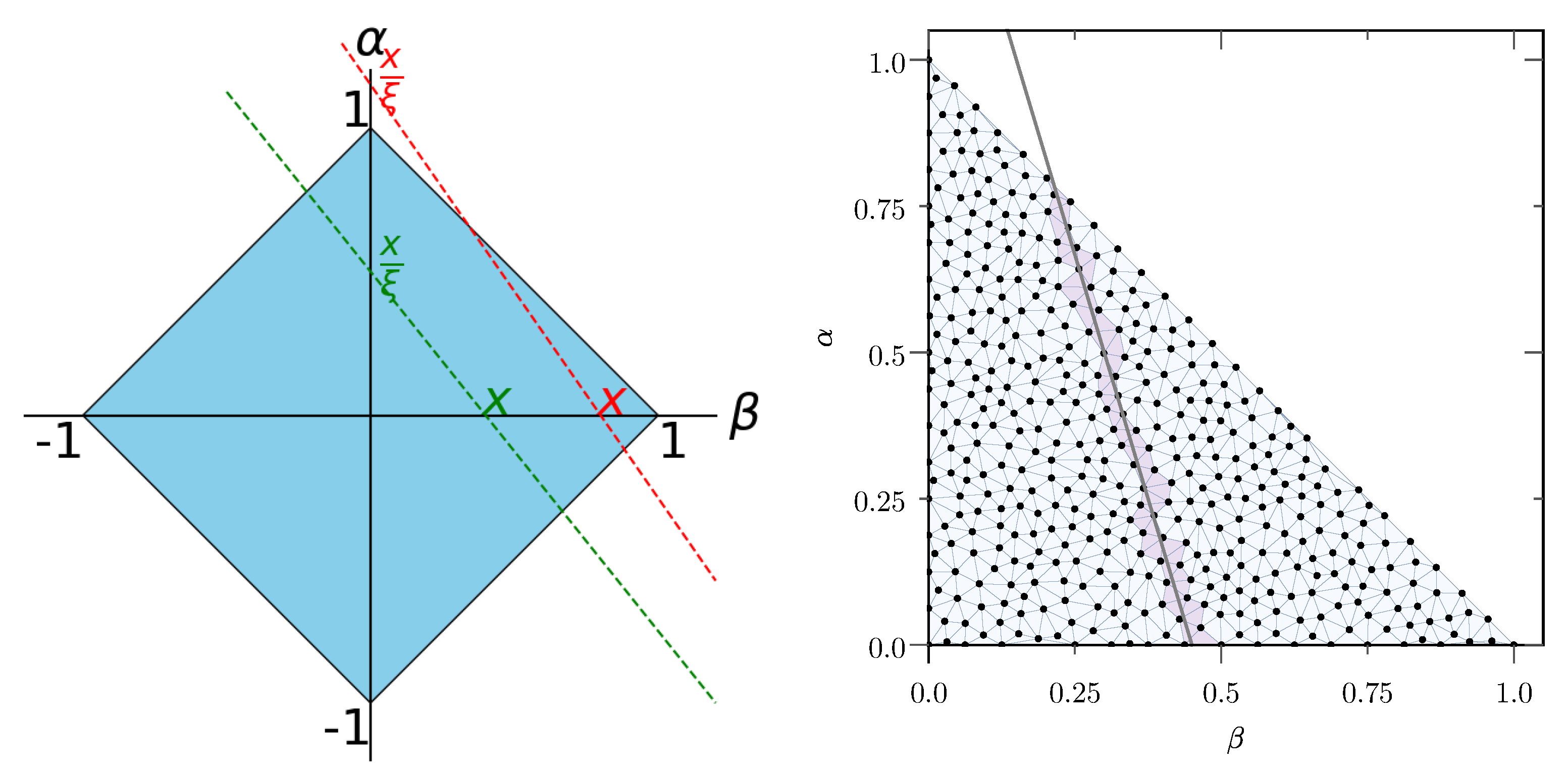
2.5.2. The Radon Transform and the Specific Role of the D-Term
2.6. Positivity and Lightfront Wave Function Picture
2.6.1. The Lightfront Wave Function Picture
2.6.2. The Positivity Property
2.7. Scale Dependence and Evolution
2.7.1. Discussion in Momentum Space
2.7.2. Properties of the Momentum-Dependent Anomalous Dimensions
2.7.3. Evolution in Conformal Space
3. Continuum Results for Mesons
3.1. Impulse Approximation and Its Limitations
- The computation (or modelling) of non-perturbative QCD correlation functions such as the Bethe–Salpeter wave function, the quark propagator and the local operator;
- The validity of the impulse approximation.

3.2. From Bethe–Salpeter Wave Funtions to Lightfront Wave Functions
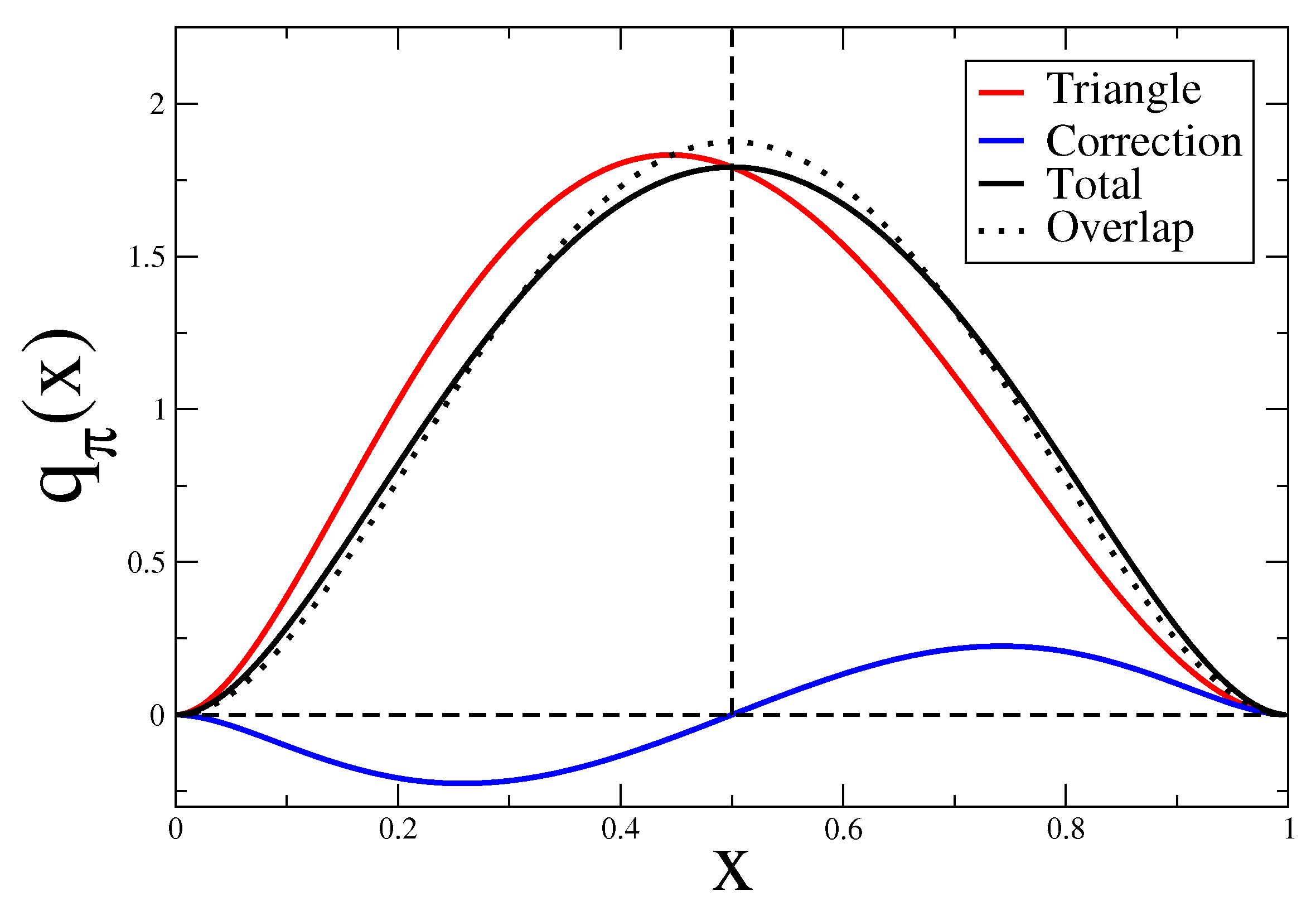
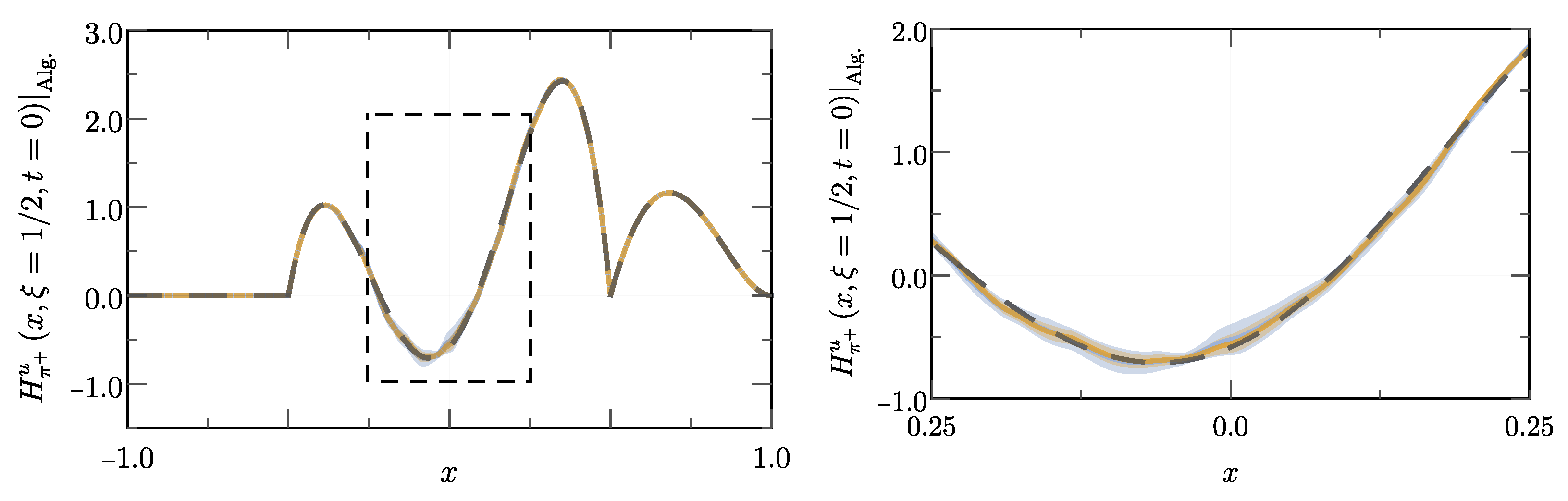
3.3. The Covariant Extension
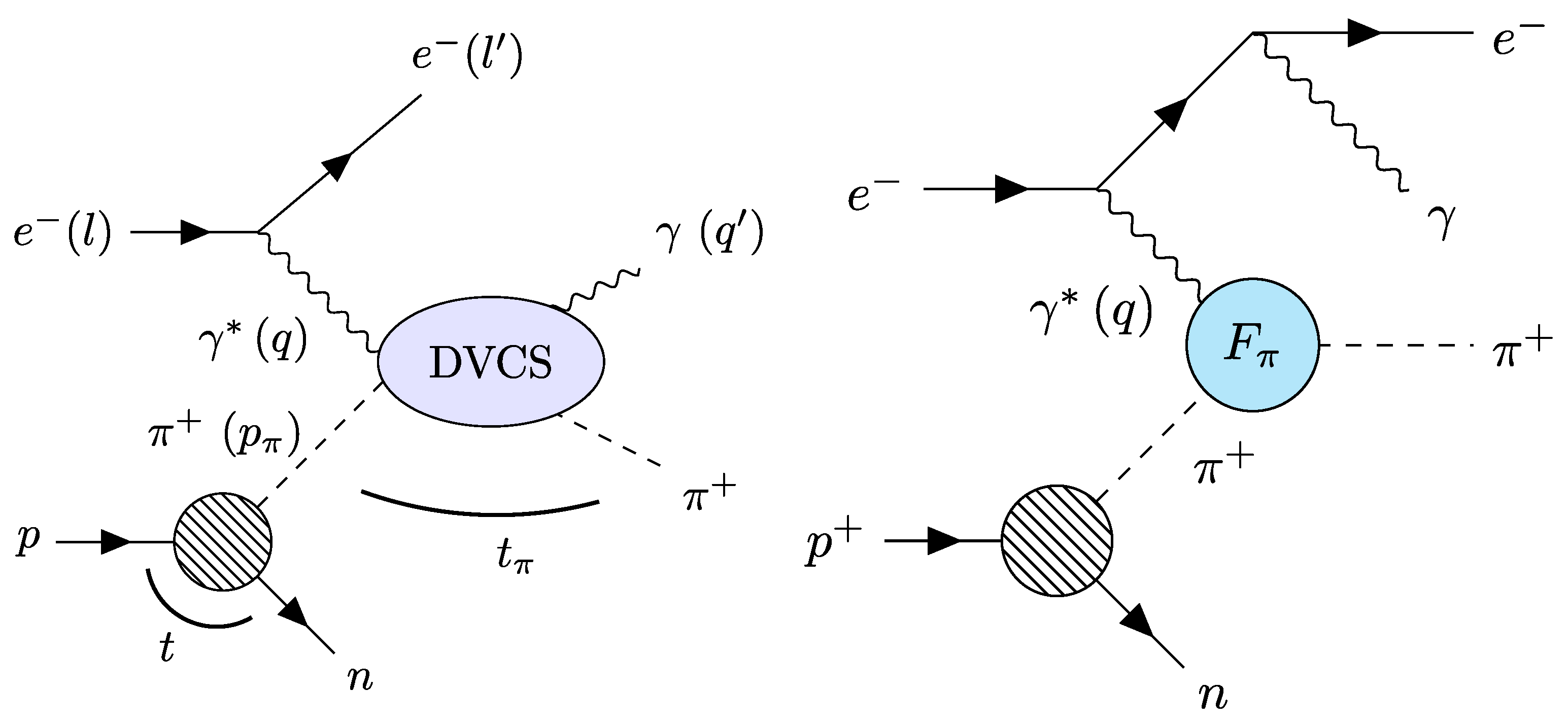
3.4. The Sullivan Process
3.4.1. Introduction to the Sullivan Process
3.4.2. From the Sullivan Process to GPDs
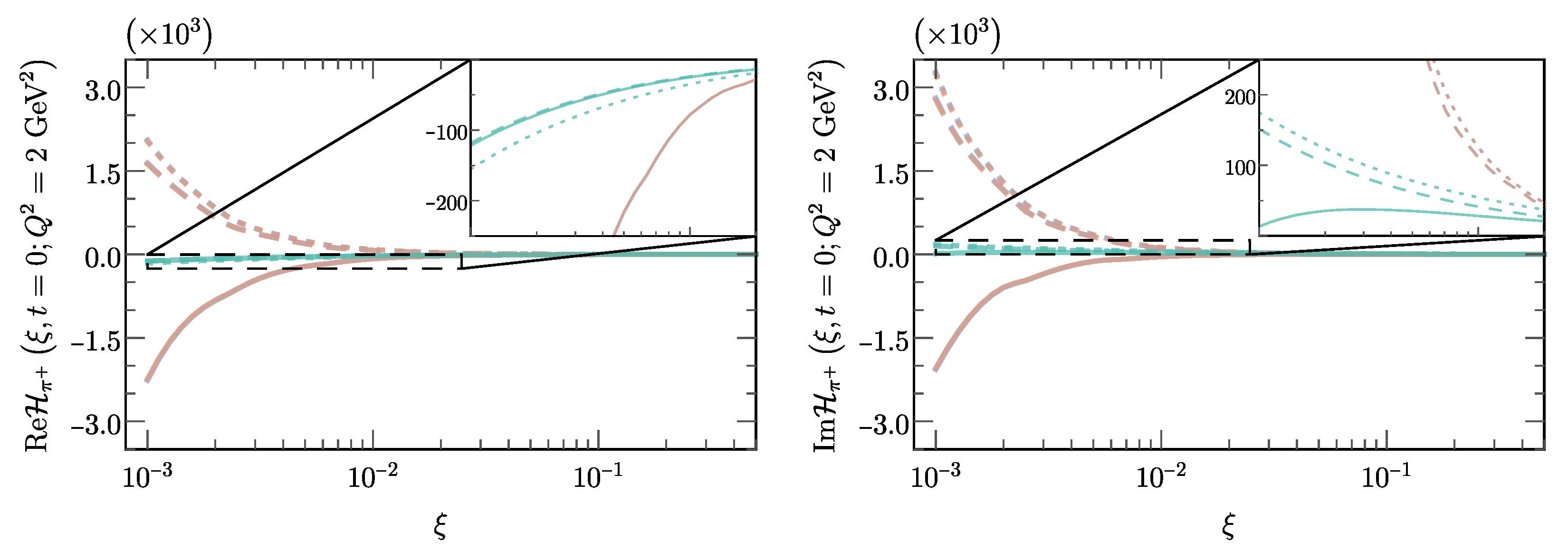
3.4.3. A Smoking Gun for Gluons at the EIC and EicC
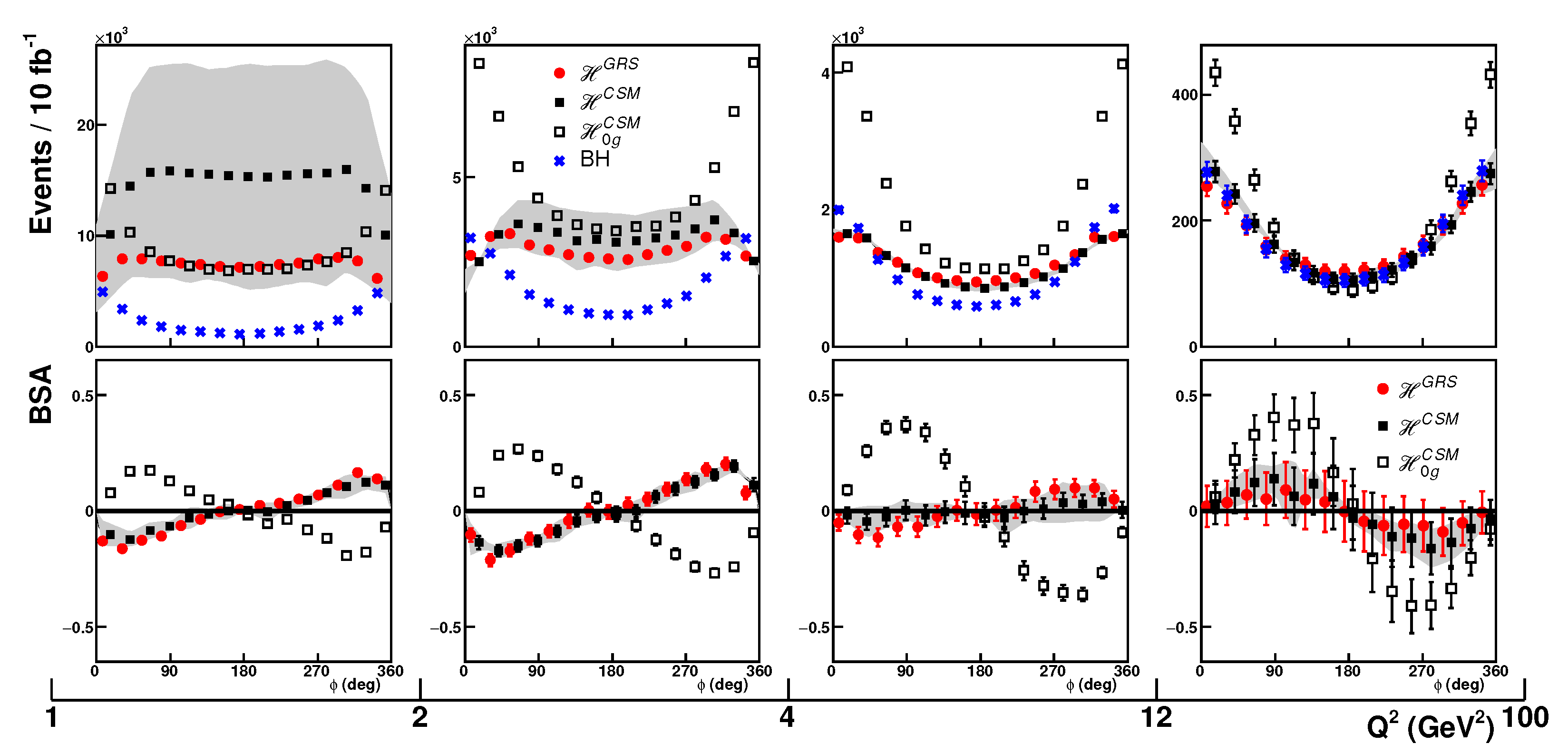
3.5. Challenges
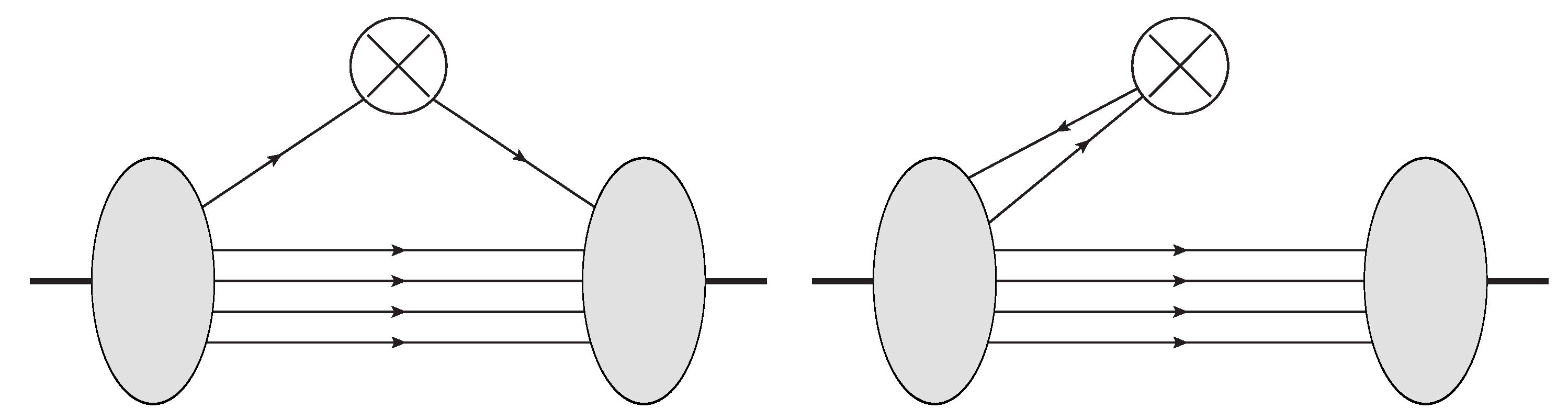
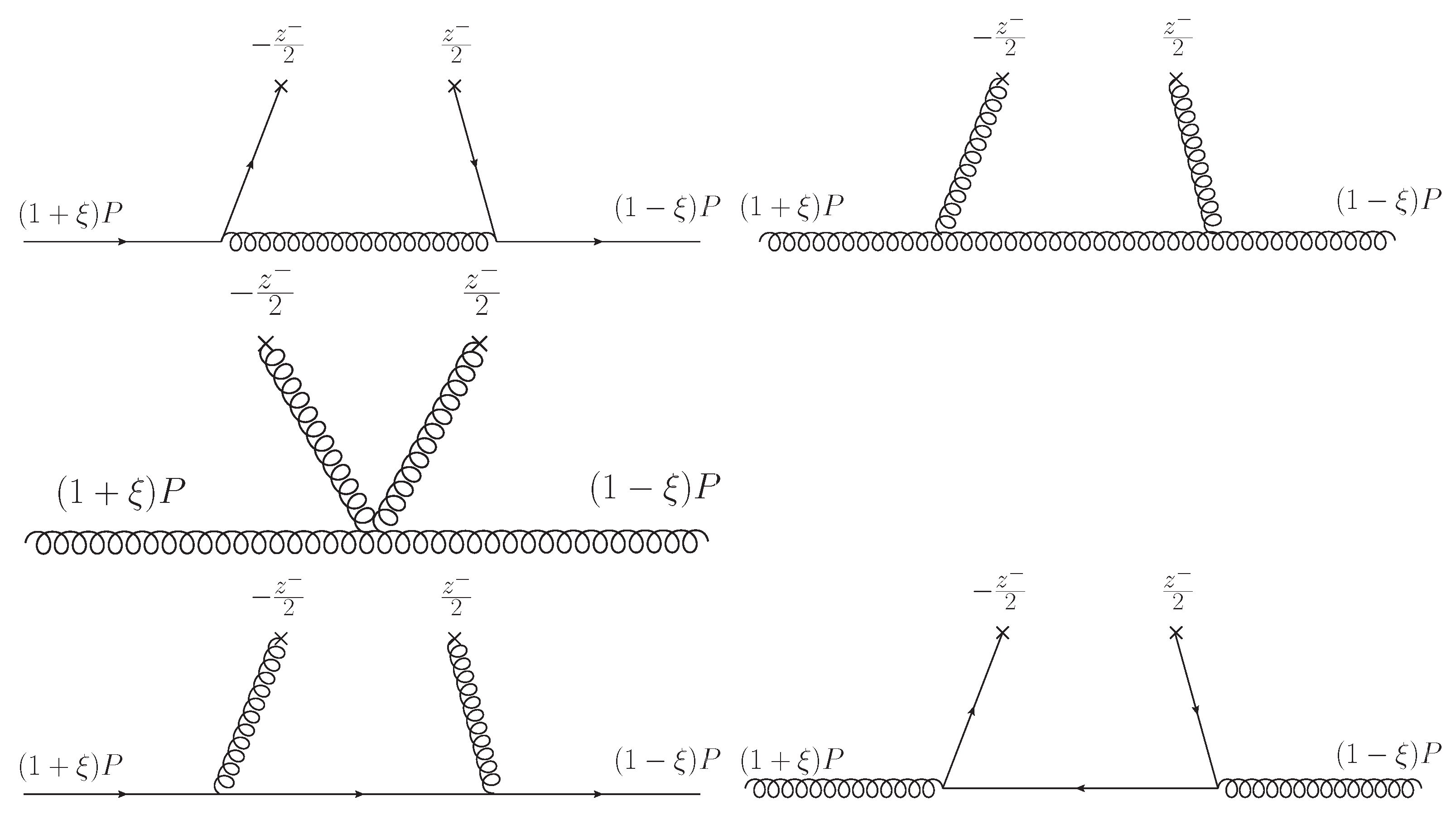
3.5.1. The Wilson Line
3.5.2. Non-Perturbative Renormalisation
3.5.3. The D-Term
4. From Mesons to Baryons
4.1. Nucleon LFWFs
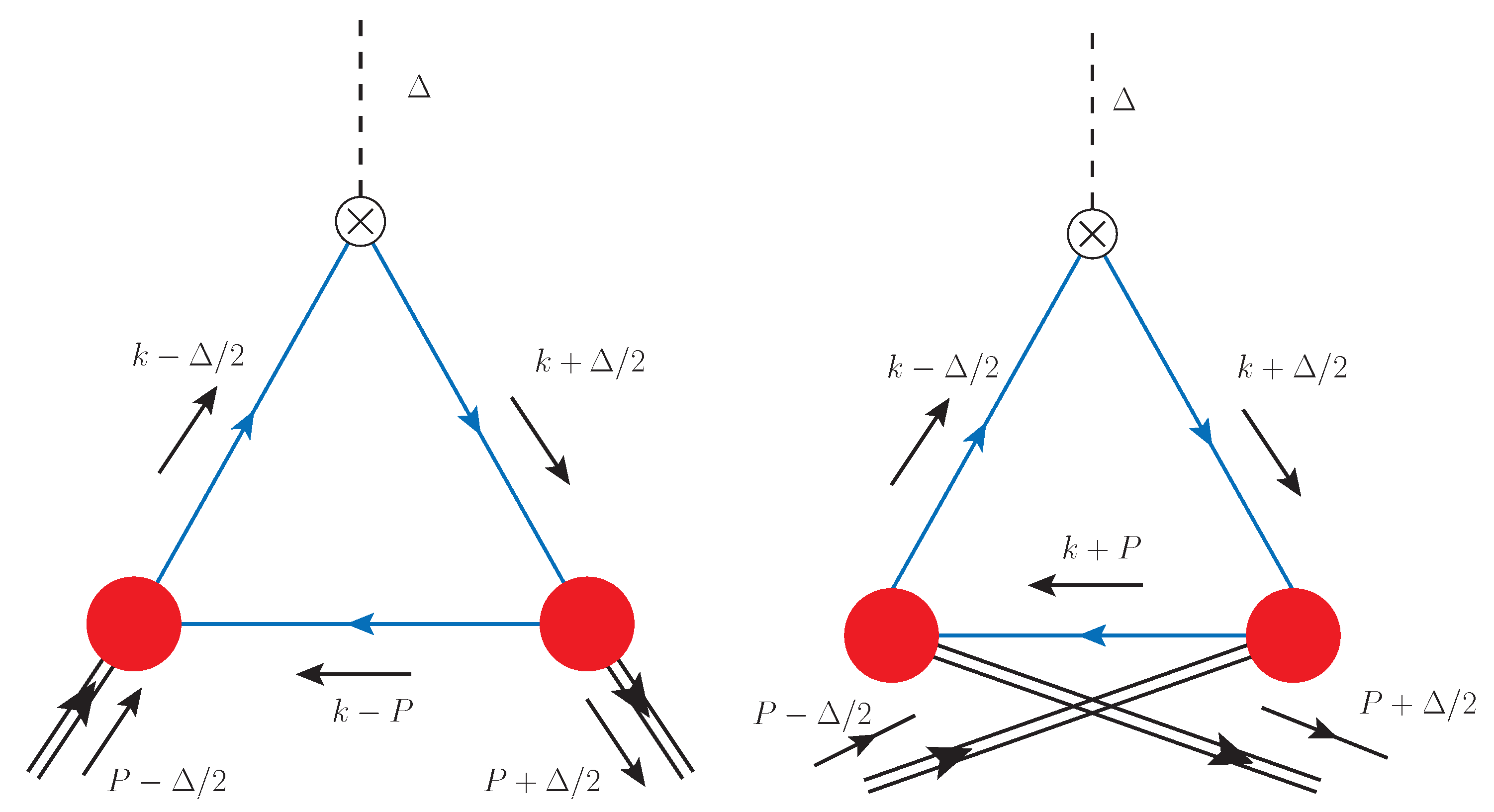
4.2. Nucleon GPDs
4.3. Transition GPDs
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DDs | Double Distributions |
| DGLAP | Dokshitzer–Gribov–Lipatov–Altarelli–Parisi |
| DVCS | Deep Virtual Compton Scattering |
| EFFs | Electromagnetic Form Factors |
| EIC | Electron Ion Collider |
| EicC | Electron Ion collider in China |
| EMT | Energy Momentum Tensor |
| ERBL | Efremov–Radyushkin–Brodsky–Lepage |
| GPDs | Generalised Parton Distribution |
| GTMDs | Generalised Transverse Momentum dependent Distributions |
| JLab | Jefferson Laboratory |
| LFWFs | Lightfront Wave Functions |
| NJL | Nambu–Jona-Lasinio |
| PDFs | Parton Distribution Functions |
| QCD | Quantum Chromodynamics |
| RGE | Renormalisation Group Equation |
| TMDs | Transverse Momentum dependent Distributions |
References
- Bjorken, J. Asymptotic Sum Rules at Infinite Momentum. Phys. Rev. 1969, 179, 1547–1553. [Google Scholar] [CrossRef]
- Altarelli, G.; Parisi, G. Asymptotic Freedom in Parton Language. Nucl. Phys. 1977, B126, 298. [Google Scholar] [CrossRef]
- Gribov, V.; Lipatov, L. Deep inelastic e p scattering in perturbation theory. Sov. J. Nucl. Phys. 1972, 15, 438–450. [Google Scholar]
- Dokshitzer, Y.L. Calculation of the Structure Functions for Deep Inelastic Scattering and e+ e- Annihilation by Perturbation Theory in Quantum Chromodynamics. Sov. Phys. JETP 1977, 46, 641–653. [Google Scholar]
- Ji, X.D. Gauge-Invariant Decomposition of Nucleon Spin. Phys. Rev. Lett. 1997, 78, 610–613. [Google Scholar] [CrossRef]
- Mueller, D.; Robaschik, D.; Geyer, B.; Dittes, F.; Hořeǰsi, J. Wave functions, evolution equations and evolution kernels from light ray operators of QCD. Fortsch. Phys. 1994, 42, 101–141. [Google Scholar] [CrossRef]
- Radyushkin, A. Nonforward parton distributions. Phys. Rev. 1997, D56, 5524–5557. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E.; Sterman, G.F. Transverse Momentum Distribution in Drell-Yan Pair and W and Z Boson Production. Nucl. Phys. B 1985, 250, 199–224. [Google Scholar] [CrossRef]
- Collins, J. Foundations of Perturbative QCD; Cambridge University Press: Cambridge, UK, 2013; Volume 32. [Google Scholar]
- Burkardt, M. Impact parameter dependent parton distributions and off forward parton distributions for zeta —> 0>. Phys. Rev. 2000, D62, 071503, Erratum in Phys. Rev. 2002, D66, 119903. [Google Scholar] [CrossRef]
- Diehl, M. Generalized parton distributions in impact parameter space. Eur. Phys. J. 2002, C25, 223–232. [Google Scholar] [CrossRef]
- Ji, X.d. Viewing the proton through `color’ filters. Phys. Rev. Lett. 2003, 91, 062001. [Google Scholar] [CrossRef] [PubMed]
- Belitsky, A.V.; Ji, X.d.; Yuan, F. Quark imaging in the proton via quantum phase space distributions. Phys. Rev. 2004, D69, 074014. [Google Scholar] [CrossRef]
- Meissner, S.; Metz, A.; Schlegel, M. Generalized parton correlation functions for a spin-1/2 hadron. J. High Energy Phys. 2009, 0908, 056. [Google Scholar] [CrossRef]
- Meissner, S.; Metz, A.; Schlegel, M.; Goeke, K. Generalized parton correlation functions for a spin-0 hadron. J. High Energy Phys. 2008, 0808, 038. [Google Scholar] [CrossRef]
- Lorce, C.; Pasquini, B. Quark Wigner Distributions and Orbital Angular Momentum. Phys. Rev. 2011, D84, 014015. [Google Scholar] [CrossRef]
- Echevarria, M.G.; Idilbi, A.; Kanazawa, K.; Lorcé, C.; Metz, A.; Pasquini, B.; Schlegel, M. Proper definition and evolution of generalized transverse momentum dependent distributions. Phys. Lett. B 2016, 759, 336–341. [Google Scholar] [CrossRef]
- Hatta, Y.; Xiao, B.W.; Yuan, F. Probing the Small- x Gluon Tomography in Correlated Hard Diffractive Dijet Production in Deep Inelastic Scattering. Phys. Rev. Lett. 2016, 116, 202301. [Google Scholar] [CrossRef] [PubMed]
- Georges, F.; Rashad, M.N.H.; Stefanko, A.; Dlamini, M.; Karki, B.; Ali, S.F.; Lin, P.; Ko, H.; Israel, N.; Adikaram, D.; et al. Deeply Virtual Compton Scattering Cross Section at High Bjorken xB. Phys. Rev. Lett. 2022, 128, 252002. [Google Scholar] [CrossRef]
- Christiaens, G.; Defurne, M.; Sokhan, D.; Achenbach, P.; Akbar, Z.; Amaryan, M.J.; Atac, H.; Avakian, H.; Gayoso, C.A.; Baashen, L.; et al. First CLAS12 measurement of DVCS beam-spin asymmetries in the extended valence region. arXiv 2022, arXiv:2211.11274. [Google Scholar]
- Catani, S.; de Florian, D.; Grazzini, M. Universality of nonleading logarithmic contributions in transverse momentum distributions. Nucl. Phys. B 2001, 596, 299–312. [Google Scholar] [CrossRef]
- Echevarria, M.G.; Scimemi, I.; Vladimirov, A. Unpolarized Transverse Momentum Dependent Parton Distribution and Fragmentation Functions at next-to-next-to-leading order. J. High Energy Phys. 2016, 2016, 4. [Google Scholar] [CrossRef]
- Bertone, V. Matching generalised transverse-momentum-dependent distributions onto generalised parton distributions at one loop. Eur. Phys. J. C 2022, 82, 941. [Google Scholar] [CrossRef]
- Braun, V.; Müller, D. Exclusive processes in position space and the pion distribution amplitude. Eur. Phys. J. C 2008, 55, 349–361. [Google Scholar] [CrossRef]
- Ji, X. Parton Physics on a Euclidean Lattice. Phys. Rev. Lett. 2013, 110, 262002. [Google Scholar] [CrossRef]
- Radyushkin, A.V. Quasi-parton distribution functions, momentum distributions, and pseudo-parton distribution functions. Phys. Rev. D 2017, 96, 034025. [Google Scholar] [CrossRef]
- Alexandrou, C.; Cichy, K.; Constantinou, M.; Jansen, K.; Scapellato, A.; Steffens, F. Light-Cone Parton Distribution Functions from Lattice QCD. Phys. Rev. Lett. 2018, 121, 112001. [Google Scholar] [CrossRef]
- Egerer, C.; Edwards, R.G.; Kallidonis, C.; Orginos, K.; Radyushkin, A.V.; Richards, D.G.; Romero, E.; Zafeiropoulos, S. Towards high-precision parton distributions from lattice QCD via distillation. J. High Energy Phys. 2021, 11, 148. [Google Scholar] [CrossRef]
- Constantinou, M.; Courtoy, A.; Ebert, M.A.; Engelhardt, M.; Giani, T.; Hobbs, T.; Hou, T.-J.; Kusina, A.; Kutak, K.; Liang, J.; et al. Parton distributions and lattice-QCD calculations: Toward 3D structure. Prog. Part. Nucl. Phys. 2021, 121, 103908. [Google Scholar] [CrossRef]
- Nakanishi, N. A General survey of the theory of the Bethe-Salpeter equation. Prog. Theor. Phys. Suppl. 1969, 43, 1–81. [Google Scholar] [CrossRef]
- Nakanishi, N. Graph Theory and Feynman Integrals; Gordon and Breach: New York, NY, USA, 1971. [Google Scholar]
- Binosi, D.; Tripolt, R.A. Spectral functions of confined particles. Phys. Lett. B 2020, 801, 135171. [Google Scholar] [CrossRef]
- Eichmann, G.; Ferreira, E.; Stadler, A. Going to the light front with contour deformations. Phys. Rev. D 2022, 105, 034009. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Cardona, J.C.; Ferreira, M.N.; Papavassiliou, J. Non-Abelian Ball-Chiu vertex for arbitrary Euclidean momenta. Phys. Rev. 2017, D96, 014029. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Figueiredo, C.T.; Papavassiliou, J. Nonperturbative Ball-Chiu construction of the three-gluon vertex. Phys. Rev. D 2019, 99, 094010. [Google Scholar] [CrossRef]
- Aguilar, A.C.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J.; Zafeiropoulos, S. Gluon propagator and three-gluon vertex with dynamical quarks. Eur. Phys. J. C 2020, 80, 154. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Papavassiliou, J. Exploring smoking-gun signals of the Schwinger mechanism in QCD. Phys. Rev. D 2022, 105, 014030. [Google Scholar] [CrossRef]
- Diehl, M. Generalized parton distributions. Phys. Rep. 2003, 388, 41–277. [Google Scholar] [CrossRef]
- Belitsky, A.; Radyushkin, A. Unraveling hadron structure with generalized parton distributions. Phys. Rep. 2005, 418, 1–387. [Google Scholar] [CrossRef]
- Kumericki, K.; Liuti, S.; Moutarde, H. GPD phenomenology and DVCS fitting. Eur. Phys. J. 2016, A52, 157. [Google Scholar] [CrossRef]
- Mezrag, C. An Introductory Lecture on Generalised Parton Distributions. Few Body Syst. 2022, 63, 62. [Google Scholar] [CrossRef]
- Mezrag, C.; Moutarde, H.; Rodriguez-Quintero, J. From Bethe–Salpeter Wave functions to Generalised Parton Distributions. Few Body Syst. 2016, 57, 729–772. [Google Scholar] [CrossRef]
- Ji, X.D. Deeply virtual Compton scattering. Phys. Rev. 1997, D55, 7114–7125. [Google Scholar] [CrossRef]
- Radyushkin, A. Asymmetric gluon distributions and hard diffractive electroproduction. Phys. Lett. 1996, B385, 333–342. [Google Scholar] [CrossRef]
- Diehl, M.; Gousset, T.; Pire, B.; Teryaev, O. Probing partonic structure in gamma* gamma —> pi pi near threshold. Phys. Rev. Lett. 1998, 81, 1782–1785. [Google Scholar] [CrossRef]
- Polyakov, M.V. Hard exclusive electroproduction of two pions and their resonances. Nucl. Phys. 1999, B555, 231. [Google Scholar] [CrossRef]
- Kivel, N.; Mankiewicz, L.; Polyakov, M.V. NLO corrections and contribution of a tensor gluon operator to the process gamma* gamma —> pi pi. Phys. Lett. B 1999, 467, 263–270. [Google Scholar] [CrossRef]
- Diehl, M.; Gousset, T.; Pire, B. Exclusive production of pion pairs in gamma* gamma collisions at large Q**2. Phys. Rev. 2000, D62, 073014. [Google Scholar] [CrossRef]
- Diehl, M.; Gousset, T. Time ordering in off diagonal parton distributions. Phys. Lett. 1998, B428, 359–370. [Google Scholar] [CrossRef]
- Efremov, A.; Radyushkin, A. Asymptotical Behavior of Pion Electromagnetic Form-Factor in QCD. Theor. Math. Phys. 1980, 42, 97–110. [Google Scholar] [CrossRef]
- Efremov, A.; Radyushkin, A. Factorization and Asymptotical Behavior of Pion Form-Factor in QCD. Phys. Lett. 1980, B94, 245–250. [Google Scholar] [CrossRef]
- Lepage, G.P.; Brodsky, S.J. Exclusive Processes in Quantum Chromodynamics: Evolution Equations for Hadronic Wave Functions and the Form-Factors of Mesons. Phys. Lett. 1979, B87, 359–365. [Google Scholar] [CrossRef]
- Lepage, G.P.; Brodsky, S.J. Exclusive Processes in Perturbative Quantum Chromodynamics. Phys. Rev. 1980, D22, 2157. [Google Scholar] [CrossRef]
- Vanderhaeghen, M.; Guichon, P.A.; Guidal, M. Deeply virtual electroproduction of photons and mesons on the nucleon: Leading order amplitudes and power corrections. Phys. Rev. 1999, D60, 094017. [Google Scholar] [CrossRef]
- Musatov, I.; Radyushkin, A. Evolution and models for skewed parton distributions. Phys. Rev. 2000, D61, 074027. [Google Scholar] [CrossRef]
- Goloskokov, S.; Kroll, P. Vector meson electroproduction at small Bjorken-x and generalized parton distributions. Eur. Phys. J. 2005, C42, 281–301. [Google Scholar] [CrossRef]
- Mezrag, C.; Moutarde, H.; Sabatié, F. Test of two new parameterizations of the Generalized Parton Distribution. H. Phys. Rev. 2013, D88, 014001. [Google Scholar] [CrossRef]
- Chavez, J.M.M.; Bertone, V.; De Soto Borrero, F.; Defurne, M.; Mezrag, C.; Moutarde, H.; Rodríguez-Quintero, J.; Segovia, J. Pion generalized parton distributions: A path toward phenomenology. Phys. Rev. D 2022, 105, 094012. [Google Scholar] [CrossRef]
- Raya, K.; Cui, Z.F.; Chang, L.; Morgado, J.M.; Roberts, C.D.; Rodriguez-Quintero, J. Revealing pion and kaon structure via generalised parton distributions. Chin. Phys. C 2022, 46, 013105. [Google Scholar] [CrossRef]
- Mezrag, C.; Chang, L.; Moutarde, H.; Roberts, C.D.; Rodríguez-Quintero, J.; Sabatié, F.; Schmidt, S.M. Sketching the pion’s valence-quark generalised parton distribution. Phys. Lett. 2014, B741, 190–196. [Google Scholar] [CrossRef]
- Moutarde, H.; Sznajder, P.; Wagner, J. Border and skewness functions from a leading order fit to DVCS data. Eur. Phys. J. 2018, C78, 890. [Google Scholar] [CrossRef]
- Khalek, R.A.; Accardi, A.; Adam, J.; Adamiak, D.; Akers, W.; Albaladejo, M.; Al-bataineh, A.; Alexeev, M.G.; Ameli, F.; Antonioli, P.; et al. Science Requirements and Detector Concepts for the Electron-Ion Collider: EIC Yellow Report. arXiv 2021, arXiv:2103.05419. [Google Scholar]
- Anderle, D.P.; Bertone, V.; Cao, X.; Chang, L.; Chang, N.; Chen, G.; Chen, X.; Chen, Z.; Cui, Z.; Dai, L.; et al. Electron-ion collider in China. Front. Phys. 2021, 16, 64701. [Google Scholar] [CrossRef]
- Polyakov, M.V.; Schweitzer, P. Forces inside hadrons: Pressure, surface tension, mechanical radius, and all that. Int. J. Mod. Phys. A 2018, 33, 1830025. [Google Scholar] [CrossRef]
- Bakker, B.L.G.; Leader, E.; Trueman, T.L. A Critique of the angular momentum sum rules and a new angular momentum sum rule. Phys. Rev. D 2004, 70, 114001. [Google Scholar] [CrossRef]
- Leader, E.; Lorcé, C. The angular momentum controversy: What’s it all about and does it matter? Phys. Rep. 2014, 541, 163–248. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Ma, B.Q.; Schmidt, I. Light cone representation of the spin and orbital angular momentum of relativistic composite systems. Nucl. Phys. B 2001, 593, 311–335. [Google Scholar] [CrossRef]
- Lowdon, P.; Chiu, K.Y.J.; Brodsky, S.J. Rigorous constraints on the matrix elements of the energy-momentum tensor. Phys. Lett. B 2017, 774, 1–6. [Google Scholar] [CrossRef]
- Lorcé, C.; Lowdon, P. Universality of the Poincaré gravitational form factor constraints. Eur. Phys. J. C 2020, 80, 207. [Google Scholar] [CrossRef]
- Lorcé, C.; Mantovani, L.; Pasquini, B. Spatial distribution of angular momentum inside the nucleon. Phys. Lett. B 2018, 776, 38–47. [Google Scholar] [CrossRef]
- Dutrieux, H.; Lorcé, C.; Moutarde, H.; Sznajder, P.; Trawiński, A.; Wagner, J. Phenomenological assessment of proton mechanical properties from deeply virtual Compton scattering. Eur. Phys. J. C 2021, 81, 300. [Google Scholar] [CrossRef]
- Polyakov, M.V. Generalized parton distributions and strong forces inside nucleons and nuclei. Phys. Lett. 2003, B555, 57–62. [Google Scholar] [CrossRef]
- Lorcé, C.; Moutarde, H.; Trawiński, A.P. Revisiting the mechanical properties of the nucleon. Eur. Phys. J. C 2019, 79, 89. [Google Scholar] [CrossRef]
- Ji, X.D. Off forward parton distributions. J. Phys. 1998, G24, 1181–1205. [Google Scholar] [CrossRef]
- Radyushkin, A. Symmetries and structure of skewed and double distributions. Phys. Lett. 1999, B449, 81–88. [Google Scholar] [CrossRef]
- Hausdorff, F. Summationsmethoden und Momentfolgen. I. Math. Z. 1921, 9, 74–109. [Google Scholar] [CrossRef]
- Hausdorff, F. Summationsmethoden und Momentfolgen. II. Math. Z. 1921, 9, 280–299. [Google Scholar] [CrossRef]
- Hertle, A. Continuity of the Radon transform and its inverse on euclidean space. Math. Z. 1983, 184, 165–192. [Google Scholar] [CrossRef]
- Radon, J. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten. Akad. Wiss. 1917, 69, 262. [Google Scholar]
- Radon, J. On the determination of functions from their integral values along certain manifolds. IEEE Trans. Med. Imaging 1986, 5, 170–176. [Google Scholar] [CrossRef]
- Polyakov, M.V.; Weiss, C. Skewed and double distributions in pion and nucleon. Phys. Rev. 1999, D60, 114017. [Google Scholar] [CrossRef]
- Teryaev, O. Crossing and radon tomography for generalized parton distributions. Phys. Lett. 2001, B510, 125–132. [Google Scholar] [CrossRef]
- Chouika, N.; Mezrag, C.; Moutarde, H.; Rodríguez-Quintero, J. Covariant Extension of the GPD overlap representation at low Fock states. Eur. Phys. J. 2017, C77, 906. [Google Scholar] [CrossRef]
- Diehl, M.; Feldmann, T.; Jakob, R.; Kroll, P. The Overlap representation of skewed quark and gluon distributions. Nucl. Phys. 2001, B596, 33–65. [Google Scholar] [CrossRef]
- Chouika, N.; Mezrag, C.; Moutarde, H.; Rodríguez-Quintero, J. A Nakanishi-based model illustrating the covariant extension of the pion GPD overlap representation and its ambiguities. Phys. Lett. 2018, B780, 287–293. [Google Scholar] [CrossRef]
- Rinaldi, M. GPDs at non-zero skewness in ADS/QCD model. Phys. Lett. B 2017, 771, 563–567. [Google Scholar] [CrossRef]
- Shi, C.; Bednar, K.; Cloët, I.C.; Freese, A. Spatial and Momentum Imaging of the Pion and Kaon. Phys. Rev. D 2020, 101, 074014. [Google Scholar] [CrossRef]
- Radyushkin, A. Double distributions and evolution equations. Phys. Rev. 1999, D59, 014030. [Google Scholar] [CrossRef]
- Pire, B.; Soffer, J.; Teryaev, O. Positivity constraints for off-forward parton distributions. Eur. Phys. J. 1999, C8, 103–106. [Google Scholar] [CrossRef]
- Pobylitsa, P. Disentangling positivity constraints for generalized parton distributions. Phys. Rev. 2002, D65, 114015. [Google Scholar] [CrossRef]
- Pobylitsa, P. Inequalities for generalized parton distributions H and E. Phys. Rev. 2002, D65, 077504. [Google Scholar] [CrossRef]
- Bertone, V.; Dutrieux, H.; Mezrag, C.; Morgado, J.M.; Moutarde, H. Revisiting evolution equations for generalised parton distributions. Eur. Phys. J. C 2022, 82, 888. [Google Scholar] [CrossRef]
- Vinnikov, A. Code for prompt numerical computation of the leading order GPD evolution. arXiv 2006, arXiv:hep-ph/hep-ph/0604248. [Google Scholar]
- Bertone, V.; Carrazza, S.; Rojo, J. APFEL: A PDF Evolution Library with QED corrections. Comput. Phys. Commun. 2014, 185, 1647–1668. [Google Scholar] [CrossRef]
- Bertone, V.; Carrazza, S.; Hartland, N.P. APFELgrid: A high performance tool for parton density determinations. Comput. Phys. Commun. 2017, 212, 205–209. [Google Scholar] [CrossRef]
- Bertone, V. APFEL++: A new PDF evolution library in C++. PoS 2018, DIS2017, 201. [Google Scholar] [CrossRef]
- Berthou, B.; Binosi, D.; Chouika, N.; Colaneri, L.; Guidal, M.; Mezrag, C.; Moutarde, H.; Rodríguez-Quintero, J.; Sabatié, F.; Sznajder, P.; et al. PARTONS: PARtonic Tomography Of Nucleon Software. A computing framework for the phenomenology of Generalized Parton Distributions. Eur. Phys. J. 2018, C78, 478. [Google Scholar] [CrossRef]
- Ohrndorf, T. Constraints From Conformal Covariance on the Mixing of Operators of Lowest Twist. Nucl. Phys. B 1982, 198, 26–44. [Google Scholar] [CrossRef]
- Mueller, D.; Schafer, A. Complex conformal spin partial wave expansion of generalized parton distributions and distribution amplitudes. Nucl. Phys. 2006, B739, 1–59. [Google Scholar] [CrossRef]
- Kumericki, K.; Mueller, D.; Passek-Kumericki, K. Towards a fitting procedure for deeply virtual Compton scattering at next-to-leading order and beyond. Nucl. Phys. B 2008, 794, 244–323. [Google Scholar] [CrossRef]
- Müller, D.; Lautenschlager, T.; Passek-Kumericki, K.; Schaefer, A. Towards a fitting procedure to deeply virtual meson production—The next-to-leading order case. Nucl. Phys. 2014, B884, 438–546. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Mueller, D. Next-to-leading order evolution of twist-2 conformal operators: The Abelian case. Nucl. Phys. 1998, B527, 207–234. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Mueller, D. Exclusive evolution kernels in two loop order: Parity even sector. Phys. Lett. 1999, B464, 249–256. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Mueller, D.; Freund, A. Reconstruction of nonforward evolution kernels. Phys. Lett. 1999, B461, 270–279. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Freund, A.; Mueller, D. Evolution kernels of skewed parton distributions: Method and two loop results. Nucl. Phys. 2000, B574, 347–406. [Google Scholar] [CrossRef]
- Braun, V.M.; Manashov, A.N.; Moch, S.; Strohmaier, M. Two-loop evolution equations for flavor-singlet light-ray operators. J. High Energy Phys. 2019, 02, 191. [Google Scholar] [CrossRef]
- Braun, V.M.; Manashov, A.N.; Moch, S.; Strohmaier, M. Three-loop evolution equation for flavor-nonsinglet operators in off-forward kinematics. J. High Energy Phys. 2017, 06, 037. [Google Scholar] [CrossRef]
- Mueller, D. The Evolution of the pion distribution amplitude in next-to-leading-order. Phys. Rev. 1995, D51, 3855–3864. [Google Scholar] [CrossRef]
- Braun, V.M.; Manashov, A.N.; Moch, S.; Schoenleber, J. Two-loop coefficient function for DVCS: Vector contributions. J. High Energy Phys. 2020, 09, 117. [Google Scholar] [CrossRef]
- Pobylitsa, P.V. Integral representations for nonperturbative GPDs in terms of perturbative diagrams. Phys. Rev. D 2003, 67, 094012. [Google Scholar] [CrossRef]
- Theussl, L.; Noguera, S.; Vento, V. Generalized parton distributions of the pion in a Bethe-Salpeter approach. Eur. Phys. J. 2004, A20, 483–498. [Google Scholar] [CrossRef]
- Tiburzi, B.; Miller, G. Generalized parton distributions and double distributions for q anti-q pions. Phys. Rev. 2003, D67, 113004. [Google Scholar] [CrossRef]
- Mezrag, C.; Moutarde, H.; Rodríguez-Quintero, J.; Sabatié, F. Towards a Pion Generalized Parton Distribution Model from Dyson-Schwinger Equations. arXiv 2014, arXiv:1406.7425. [Google Scholar]
- Chang, L.; Mezrag, C.; Moutarde, H.; Roberts, C.D.; Rodriguez-Quintero, J.; Tandy, P.C. Basic features of the pion valence-quark distribution function. Phys. Lett. 2014, B737, 23–29. [Google Scholar] [CrossRef]
- Binosi, D.; Chang, L.; Papavassiliou, J.; Qin, S.X.; Roberts, C.D. Symmetry preserving truncations of the gap and Bethe-Salpeter equations. Phys. Rev. D 2016, 93, 096010. [Google Scholar] [CrossRef]
- Qin, S.X.; Roberts, C.D. Resolving the Bethe–Salpeter Kernel. Chin. Phys. Lett. 2021, 38, 071201. [Google Scholar] [CrossRef]
- Nguyen, T.; Bashir, A.; Roberts, C.D.; Tandy, P.C. Pion and kaon valence-quark parton distribution functions. Phys. Rev. 2011, C83, 062201. [Google Scholar] [CrossRef]
- Ding, M.; Raya, K.; Binosi, D.; Chang, L.; Roberts, C.D.; Schmidt, S.M. Symmetry, symmetry breaking, and pion parton distributions. Phys. Rev. D 2020, 101, 054014. [Google Scholar] [CrossRef]
- Broniowski, W.; Ruiz Arriola, E.; Golec-Biernat, K. Generalized parton distributions of the pion in chiral quark models and their QCD evolution. Phys. Rev. 2008, D77, 034023. [Google Scholar] [CrossRef]
- Freese, A.; Cloët, I.C. Impact of dynamical chiral symmetry breaking and dynamical diquark correlations on proton generalized parton distributions. Phys. Rev. C 2020, 101, 035203. [Google Scholar] [CrossRef]
- Freese, A.; Cloët, I.C. Quark spin and orbital angular momentum from proton generalized parton distributions. Phys. Rev. C 2021, 103, 045204. [Google Scholar] [CrossRef]
- Zhang, J.L.; Cui, Z.F.; Ping, J.; Roberts, C.D. Contact interaction analysis of pion GTMDs. Eur. Phys. J. C 2021, 81, 6. [Google Scholar] [CrossRef]
- Xing, Z.; Ding, M.; Raya, K.; Chang, L. A fresh look at the generalized parton distributions of light pseudoscalar mesons. arXiv 2023, arXiv:2301.02958. [Google Scholar]
- Lan, J.; Mondal, C.; Jia, S.; Zhao, X.; Vary, J.P. Pion and kaon parton distribution functions from basis light front quantization and QCD evolution. Phys. Rev. D 2020, 101, 034024. [Google Scholar] [CrossRef]
- de Teramond, G.F.; Liu, T.; Sufian, R.S.; Dosch, H.G.; Brodsky, S.J.; Deur, A. Universality of Generalized Parton Distributions in Light-Front Holographic QCD. Phys. Rev. Lett. 2018, 120, 182001. [Google Scholar] [CrossRef]
- Burkardt, M.; Ji, X.d.; Yuan, F. Scale dependence of hadronic wave functions and parton densities. Phys. Lett. 2002, B545, 345–351. [Google Scholar] [CrossRef]
- Chang, L.; Cloet, I.; Cobos-Martinez, J.; Roberts, C.; Schmidt, S.; Tandy, P.C. Imaging dynamical chiral symmetry breaking: Pion wave function on the light front. Phys. Rev. Lett. 2013, 110, 132001. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.S.; Chang, L.; Roberts, C.D.; Zong, H.S. Pion and kaon valence-quark parton quasidistributions. Phys. Rev. D 2018, 97, 094014. [Google Scholar] [CrossRef]
- Albino, L.; Higuera-Angulo, I.M.; Raya, K.; Bashir, A. Pseudoscalar mesons: Light front wave functions, GPDs, and PDFs. Phys. Rev. D 2022, 106, 034003. [Google Scholar] [CrossRef]
- Mezrag, C.; Salmé, G. Fermion and Photon gap-equations in Minkowski space within the Nakanishi Integral Representation method. Eur. Phys. J. C 2021, 81, 34. [Google Scholar] [CrossRef]
- Hwang, D.; Mueller, D. Implication of the overlap representation for modelling generalized parton distributions. Phys. Lett. 2008, B660, 350–359. [Google Scholar] [CrossRef]
- Müller, D. Double distributions and generalized parton distributions from the parton number conserved light front wave function overlap representation. arXiv 2017, arXiv:1711.09932. [Google Scholar]
- Boman, J.; Quinto, E.T. Support theorems for real-analytic Radon transforms. Duke Math. J. 1987, 55, 943–948. [Google Scholar] [CrossRef]
- Chavez, J.M.M.; Dall’Olio, P.; De Soto Borrero, F.; Mezrag, C.; Moutarde, H.; Rodriguez Quintero, J.; Sznajder, P.; Segovia, J. Reconstruction of Double distributions from limited GPD knowledge. 2023; in preparation. [Google Scholar]
- Müller, D.; Semenov-Tian-Shansky, K.M. J=0 fixed pole and D-term form factor in deeply virtual Compton scattering. Phys. Rev. 2015, D92, 074025. [Google Scholar] [CrossRef]
- Hadamard, J. Sur les problèmes aux dérivées partielles et leur signification physique. Princet. Univ. Bull. 1902, 13, 49–52. [Google Scholar]
- Maz’ya, V.; Shaposhnikova, T. Jacques Hadamard, a Universal Mathematician. History of Mathematics 14; American Mathematical Society: Providence, RI, USA, 1998. [Google Scholar]
- Natterer, F. The Mathematics of Computerized Tomography; Classics in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Fong, D.; Saunders, M. LSMR: An iterative algorithm for sparse least-squares problems. arXiv 2010, arXiv:1006.0758. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Sullivan, J.D. One pion exchange and deep inelastic electron—Nucleon scattering. Phys. Rev. D 1972, 5, 1732–1737. [Google Scholar] [CrossRef]
- Bebek, C.J.; Brown, C.N.; Holmes, S.D.; Kline, R.V.; Pipkin, F.M.; Raither, S.; Sisterson, L.K.; Browman, A.; Hanson, K.M.; Larson, D.; et al. Electroproduction of single pions at low epsilon and a measurement of the pion form-factor up to q2=10GeV2. Phys. Rev. D 1978, 17, 1693. [Google Scholar] [CrossRef]
- Volmer, J.; Abbott, D.; Anklin, H.; Armstrong, C.; Arrington, J.; Assamagan, K.; Avery, S.; Baker, O.K.; Blok, H.P.; Bochna, C.; et al. Measurement of the Charged Pion Electromagnetic Form-Factor. Phys. Rev. Lett. 2001, 86, 1713–1716. [Google Scholar] [CrossRef] [PubMed]
- Huber, G.; Blok, H.P.; Horn, T.; Beise, E.J.; Gaskell, D.; Mack, D.J.; Tadevosyan, V.; Volmer, J.; Abbott, D.; Aniol, K.; et al. Charged pion form-factor between Q**2 = 0.60-GeV**2 and 2.45-GeV**2. II. Determination of, and results for, the pion form-factor. Phys. Rev. 2008, C78, 045203. [Google Scholar] [CrossRef]
- Barry, P.C.; Sato, N.; Melnitchouk, W.; Ji, C.R. First Monte Carlo Global QCD Analysis of Pion Parton Distributions. Phys. Rev. Lett. 2018, 121, 152001. [Google Scholar] [CrossRef]
- Barry, P.C.; Ji, C.R.; Sato, N.; Melnitchouk, W. Global QCD Analysis of Pion Parton Distributions with Threshold Resummation. Phys. Rev. Lett. 2021, 127, 232001. [Google Scholar] [CrossRef]
- Amrath, D.; Diehl, M.; Lansberg, J.P. Deeply virtual Compton scattering on a virtual pion target. Eur. Phys. J. 2008, C58, 179–192. [Google Scholar] [CrossRef]
- Chávez, J.M.M.; Bertone, V.; De Soto Borrero, F.; Defurne, M.; Mezrag, C.; Moutarde, H.; Rodríguez-Quintero, J.; Segovia, J. Accessing the Pion 3D Structure at US and China Electron-Ion Colliders. Phys. Rev. Lett. 2022, 128, 202501. [Google Scholar] [CrossRef] [PubMed]
- Belitsky, A.V.; Mueller, D. Refined analysis of photon leptoproduction off spinless target. Phys. Rev. 2009, D79, 014017. [Google Scholar] [CrossRef]
- Freund, A. On the extraction of skewed parton distributions from experiment. Phys. Lett. B 2000, 472, 412–419. [Google Scholar] [CrossRef]
- Bertone, V.; Dutrieux, H.; Mezrag, C.; Moutarde, H.; Sznajder, P. The deconvolution problem of deeply virtual Compton scattering. Phys. Rev. D 2021, 103, 114019. [Google Scholar] [CrossRef]
- Guidal, M.; Vanderhaeghen, M. Double deeply virtual Compton scattering off the nucleon. Phys. Rev. Lett. 2003, 90, 012001. [Google Scholar] [CrossRef] [PubMed]
- Braun, V.M.; Ji, Y.; Schoenleber, J. Deeply Virtual Compton Scattering at Next-to-Next-to-Leading Order. Phys. Rev. Lett. 2022, 129, 172001. [Google Scholar] [CrossRef] [PubMed]
- Novikov, I.; Abdolmaleki, H.; Britzger, D.; Cooper-Sarkar, A.; Giuli, F.; Glazov, A.; Kusina, A.; Luszczak, A.; Olness, F.; Starovoitov, P.; et al. Parton Distribution Functions of the Charged Pion Within The xFitter Framework. Phys. Rev. D 2020, 102, 014040. [Google Scholar] [CrossRef]
- Gluck, M.; Reya, E.; Schienbein, I. Pionic parton distributions revisited. Eur. Phys. J. C 1999, 10, 313–317. [Google Scholar] [CrossRef]
- Cornwall, J.M. Dynamical Mass Generation in Continuum QCD. Phys. Rev. D 1982, 26, 1453. [Google Scholar] [CrossRef]
- Costa, C.S.R.; Freese, A.; Cloët, I.C.; El-Bennich, B.; Krein, G.a.; Tandy, P.C. Intrinsic glue and Wilson lines within dressed quarks. Phys. Rev. C 2021, 104, 045201. [Google Scholar] [CrossRef]
- Ji, C.R.; Sill, A.F.; Lombard, R.M. Leading Order Perturbative QCD Calculation of Nucleon Dirac Form-factors. Phys. Rev. 1987, D36, 165. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Quintero, J.; Binosi, D.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D. Process-independent effective coupling. From QCD Green’s functions to phenomenology. Few Body Syst. 2018, 59, 121. [Google Scholar] [CrossRef]
- Hoodbhoy, P.; Ji, X.d.; Yuan, F. Probing quark distribution amplitudes through generalized parton distributions at large momentum transfer. Phys. Rev. Lett. 2004, 92, 012003. [Google Scholar] [CrossRef]
- Riberdy, M.; Mezrag, C.; Segovia, J. Computing 3D nucleonic orbitals:an exploratory path with continuum QCD methods. 2023; Under preparation. [Google Scholar]
- Segovia, J.; Cloet, I.C.; Roberts, C.D.; Schmidt, S.M. Nucleon and Δ elastic and transition form factors. Few Body Syst. 2014, 55, 1185–1222. [Google Scholar] [CrossRef]
- Gutiérrez-Guerrero, L.X.; Paredes-Torres, G.; Bashir, A. Mesons and baryons: Parity partners. Phys. Rev. D 2021, 104, 094013. [Google Scholar] [CrossRef]
- Yin, P.L.; Cui, Z.F.; Roberts, C.D.; Segovia, J. Masses of positive- and negative-parity hadron ground-states, including those with heavy quarks. Eur. Phys. J. C 2021, 81, 327. [Google Scholar] [CrossRef]
- Eichmann, G.; Alkofer, R.; Krassnigg, A.; Nicmorus, D. Nucleon mass from a covariant three-quark Faddeev equation. Phys. Rev. Lett. 2010, 104, 201601. [Google Scholar] [CrossRef]
- Eichmann, G.; Sanchis-Alepuz, H.; Williams, R.; Alkofer, R.; Fischer, C.S. Baryons as relativistic three-quark bound states. Prog. Part. Nucl. Phys. 2016, 91, 1–100. [Google Scholar] [CrossRef]
- Wang, Q.W.; Qin, S.X.; Roberts, C.D.; Schmidt, S.M. Proton tensor charges from a Poincaré-covariant Faddeev equation. Phys. Rev. 2018, D98, 054019. [Google Scholar] [CrossRef]
- Ji, X.d.; Ma, J.P.; Yuan, F. Three quark light cone amplitudes of the proton and quark orbital motion dependent observables. Nucl. Phys. 2003, B652, 383–404. [Google Scholar] [CrossRef]
- Mezrag, C.; Segovia, J.; Chang, L.; Roberts, C.D. Parton distribution amplitudes: Revealing correlations within the proton and Roper. Phys. Lett. 2018, B783, 263–267. [Google Scholar] [CrossRef]
- Mezrag, C.; Segovia, J.; Ding, M.; Chang, L.; Roberts, C.D. Nucleon Parton Distribution Amplitude: A scalar diquark picture. In Proceedings of the 22nd International Conference on Few-Body Problems in Physics (FB22), Caen, France, 9–13 July 2018. [Google Scholar]
- Barabanov, M.Y.; Bedolla, M.A.; Brooks, W.K.; Cates, G.D.; Chen, C.; Chen, Y.; Cisbani, E.; Ding, M.; Eichmann, G.; Ent, R.; et al. Diquark correlations in hadron physics: Origin, impact and evidence. Prog. Part. Nucl. Phys. 2021, 116, 103835. [Google Scholar] [CrossRef]
- Radyushkin, A. Modeling Nucleon Generalized Parton Distributions. Phys. Rev. 2013, D87, 096017. [Google Scholar] [CrossRef]
- Anikin, I.V.; Teryaev, O.V. Dispersion relations and subtractions in hard exclusive processes. Phys. Rev. D 2007, 76, 056007. [Google Scholar] [CrossRef]
- Diehl, M.; Ivanov, D.Y. Dispersion representations for hard exclusive processes: Beyond the Born approximation. Eur. Phys. J. C 2007, 52, 919–932. [Google Scholar] [CrossRef]
- Kumerički, K. Measurability of pressure inside the proton. Nature 2019, 570, E1–E2. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Mossé, L.; Vanderhaeghen, M. Pion production in deeply virtual Compton scattering. Phys. Rev. D 2003, 68, 034018. [Google Scholar] [CrossRef]
- Guidal, M.; Bouchigny, S.; Didelez, J.P.; Hadjidakis, C.; Hourany, E.; Vanderhaeghen, M. Generalized parton distributions and nucleon resonances. Nucl. Phys. A 2003, 721, 327–332. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mezrag, C. Generalised Parton Distributions in Continuum Schwinger Methods: Progresses, Opportunities and Challenges. Particles 2023, 6, 262-296. https://doi.org/10.3390/particles6010015
Mezrag C. Generalised Parton Distributions in Continuum Schwinger Methods: Progresses, Opportunities and Challenges. Particles. 2023; 6(1):262-296. https://doi.org/10.3390/particles6010015
Chicago/Turabian StyleMezrag, Cédric. 2023. "Generalised Parton Distributions in Continuum Schwinger Methods: Progresses, Opportunities and Challenges" Particles 6, no. 1: 262-296. https://doi.org/10.3390/particles6010015
APA StyleMezrag, C. (2023). Generalised Parton Distributions in Continuum Schwinger Methods: Progresses, Opportunities and Challenges. Particles, 6(1), 262-296. https://doi.org/10.3390/particles6010015








