Abstract
The dynamics of the QCD gauge sector give rise to non-perturbative phenomena that are crucial for the internal consistency of the theory; most notably, they account for the generation of a gluon mass through the action of the Schwinger mechanism, the taming of the Landau pole, the ensuing stabilization of the gauge coupling, and the infrared suppression of the three-gluon vertex. In the present work, we review some key advances in the ongoing investigation of this sector within the framework of the continuum Schwinger function methods, supplemented by results obtained from lattice simulations.
| Contents | ||
| 1 | Introduction | 2 |
| 2 | Basic Concepts and General Theoretical Framework | 5 |
| 3 | Schwinger Mechanism in Yang–Mills Theories | 10 |
| 4 | Dynamical formation of Massless Poles | 13 |
| 5 | Generation of the Gluon Mass | 16 |
| 5.1 Gluon Mass from the qμqν Component | 17 | |
| 5.2 Gluon Mass from the gμν Component: Seagull Identity and Ward Identity Displacement | 18 | |
| 6 | Renormalization Group Invariant Interaction Strength | 20 |
| 7 | Three-Gluon Vertex and Its Planar Degeneracy | 23 |
| 8 | Ghost Dynamics from Schwinger–Dyson Equations | 25 |
| 9 | Divergent Ghost Loops and Their Impact on the QCD Green’s Functions | 30 |
| 10 | Ward Identity Displacement of the Three-Gluon Vertex | 34 |
| 11 | The Ghost-Gluon Kernel Contribution to the Ward Identity | 35 |
| 12 | Displacement Function from Lattice Inputs | 39 |
| 13 | Conclusions | 40 |
| A. | Appendix A | 41 |
| B. | Appendix B | 43 |
| References | 43 | |
1. Introduction
The systematic exploration of Green’s functions (n-point correlation functions) of quantum chromodynamics (QCD) [1] by means of continuous Schwinger function methods [2,3,4,5,6,7,8,9], such as Schwinger–Dyson equations (SDEs) [10,11,12,13,14,15,16,17,18,19,20,21] and the functional renormalization group [22,23,24,25,26,27,28,29,30,31], together with a plethora of gauge-fixed lattice simulations [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88], has afforded ample access to the dynamical mechanisms responsible for the non-perturbative properties of this remarkable theory. Particularly prominent in this quest is the notion of the emergent hadron mass (EHM) [3,8,9,89,90,91,92,93], together with its three supporting pillars: first, the generation of a gluon mass [18,32,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126] through the action of the Schwinger mechanism [127,128]; second, the construction of the process-independent effective charge [3,16,20,79,96,129,130,131], which arises as the QCD analog of the Gell-Mann–Low charge is known from quantum electrodynamics (QED) [132,133], and is associated with a renormalization-group invariant (RGI) scale of about half of the proton mass [20,79]; and third, the dynamical breaking of chiral symmetry and the generation of constituent quark masses [10,17,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158].
The dynamics of the gauge sector of QCD, which encompasses both gluonic and ghost interactions, is instrumental in the physical picture of the EHM outlined above. In fact, the basic concepts and pivotal mechanisms sustaining the first two pillars of the EHM have their original inception and most genuine realization in the realm of pure Yang–Mills theories [18,93,94,96,109,112,117,159,160,161]. Therefore, in the present review, we focus precisely on the rich dynamical content of the gauge sector, especially in relation to the generation of a gluon mass scale out of the intricate gluon self-interactions.
The formulation of the non-perturbative QCD physics in terms of Green’s functions of the fundamental degrees of freedom, such as gluon and ghost propagators and vertices, provides an intuitive framework for unraveling a wide array of subtle mechanisms; in fact, certain distinctive features of these functions have been inextricably connected with key phenomena such as gluon mass generation, violation of reflection positivity, and confinement, to name a few. Thus, the saturation of the gluon propagator in the deep infrared [37,45,46,47,48,49,52,55,56,57,58,59,63,65,66,67,77,81] has been interpreted as an unequivocal signal of a gluon mass [32,96,97,98,99,100,103,105,107,108,109,112,160,161,162,163,164,165,166]; and the existence of an inflection point in the same function has been argued to lead to a non-positive gluon spectral density [8], and the ensuing loss of reflection positivity [8,11,13,16,167,168,169,170,171] for the dressed gluons. Similarly, the masslessness of the ghost induces [172] a maximum in the gluon propagator, and a zero crossing in the form factors of the three-gluon vertex [28,50,68,69,71,72,81,84,172,173,174,175,176,177,178,179,180], followed by an infrared divergence for vanishing momenta. The dynamic origin of these special traits will be the focal point of the analysis presented in the main body of this article.
The integral equations that govern the full momentum evolution of Green’s functions, known as SDEs, constitute the indispensable formal and practical instrument for unraveling the special characteristics mentioned above. In their primordial form, the SDEs are rigorously derived from the generating functional of the theory [133,181], and encode all dynamical information on the correlation functions, within the entire range of physical momenta. In practice, due to the enormous complexity of these equations, truncation approximations need to be implemented; but, unlike perturbation theory, no expansion parameter is available in the strongly coupled regime of the theory for carrying out such a task. Despite this intrinsic shortcoming, in recent years, the SDE predictions have become particularly robust, in part due to various theoretical advances, and in part thanks to the intense synergy with gauge-fixed lattice simulations, as will be evidenced in subsequent sections.
Typically, Green’s QCD function is defined within the quantization scheme obtained by implementing the linear covariant () gauges [182]. The corresponding SDEs are derived and solved within this same quantization scheme, particularly in the Landau gauge (), where lattice simulations are almost exclusively performed; for studies away from the Landau gauge, see e.g., [55,58,66,74,75,110,114,120,183,184,185,186,187,188,189,190,191]. A great deal may be learned, however, by considering Green’s functions and corresponding SDEs formulated within the “PT-BFM” scheme [109,192], namely the framework that arises from the fusion of the pinch technique (PT) [14,96,100,193,194,195] with the background field method (BFM) [196,197,198,199,200,201,202,203,204,205,206]. The main advantage of the PT-BFM originates from the fact that certain appropriately chosen Green’s functions satisfy Abelian Slavnov–Taylor identities (STIs), whose tree-level form does not get modified by quantum corrections. This situation is to be contrasted to the standard STIs [207,208] obtained in the conventional framework of the linear covariant gauges, which are deformed by non-trivial contributions stemming from the gauge sector of the theory. In the present work, we will carry out computations and develop arguments within both frameworks ( and PT-BFM), and will elaborate on their connection by means of the so-called background-quantum identities (BQIs) [14,209,210,211].
The article is organized as follows:
- In Section 2, we introduce some basic notations and review certain prominent features of Green’s functions within the linear gauges and the PT-BFM formalism [109,192]. We stress, in particular, the properties of the auxiliary function [16,131,212,213], which relates the gluon propagators with quantum and background gluons, and is intimately connected with the definition of the process-independent and RGI interaction strength [16], to be discussed in detail in Section 6. In addition, we elucidate (with a concrete example) the important property of “block-wise” transversality, displayed by the background gluon self-energy [18,109,112].
- In Section 3, we review the general principles associated with the Schwinger mechanism [127,128] that endows gauge bosons with an effective mass, focusing on the details associated with its realization in the context of Yang–Mills theories. We place particular emphasis on the pivotal requirement that must be satisfied by the fundamental vertices of the theory, namely the appearance of massless poles in their form factors [18,93,109,111,112,113,117,159,214].
- In Section 4, we examine the dynamical formation of colored composite excitations (bound states) of vanishing masses, which provide the required structures in the vertices in order for the Schwinger mechanism to be activated [18,117,159,214]. The formation of these states out of a pair of gluons or a ghost–anti-ghost pair is controlled by a set of coupled Bethe–Salpeter equations (BSEs) [18,117,124,214,215], which are found to have nontrivial solutions for the corresponding Bethe–Salpeter (BS) amplitudes, to be denoted by and , respectively.
- In Section 5, we explain in detail how the presence of the massless poles in the dressed vertices that enter the SDE of the gluon propagator give rise to a gluon mass. The demonstration is carried out separately for the and components of the gluon self-energy. The former case requires the evasion of the so-called “seagull identity” [113,166]; this becomes possible by virtue of the crucial Ward identity (WI) displacement, to be further considered in Section 10.
- In Section 6, we go over the basic notions underpinning the PT [14,96,100,193,194], and show how their application leads naturally to the definition of a dimensionful process-independent RGI interaction strength [3,16,20,79,96,129,130,131], denoted by . The genuine process independence of this quantity is concretely exemplified by demonstrating its appearance in two processes involving fundamentally different external fields. Next, is computed by combining lattice data for the gluon propagator and SDE results for the function . Finally, the dimensionless quantity is derived that constitutes the physical definition of the one-gluon exchange interaction appearing in standard bound-state computations [15,16,17,216,217,218,219,220,221,222].
- In Section 7, we focus on the structure of the “transversely projected” three-gluon vertex [126,174,175,223], and discuss briefly the property of planar degeneracy [86], satisfied, at a high level of accuracy [86,87,88,174,175,223], by the vertex form factors. This special property induces a striking simplification to the structure of this vertex, captured by a particularly compact expression [86], which will be extensively used in some of the following sections.
- In Section 8, we take a close look at the ghost sector of the theory, and solve the coupled system of SDEs governing the ghost propagator and ghost–gluon vertex [85,224,225,226,227,228]; as is well-known, the ghost remains massless, but its dressing function saturates at the origin [21,42,47,49,51,56,62,63,73,79,85,112,178,225,227,228,229,230,231,232,233], because the infrared-finite gluon propagator used in the ghost SDE provides an effective infrared cutoff. In the SDE of the ghost–gluon vertex, we employ as central input the compact expression for the three-gluon vertex presented in the previous section. The results are in excellent agreement with the available lattice data for the ghost dressing function [73,85] and the form factor of the ghost–gluon vertex evaluated in the soft-gluon limit [42,43].
- In Section 9, we discuss two important consequences of the masslessness of the ghost propagator, which manifest themselves at the level of both the gluon propagator and the three-gluon vertex. Specifically, the diagrams comprised by a ghost loop induce “unprotected” logarithms, i.e., of the type ; instead, gluonic loops give rise to “protected” logarithms, of the type , where m is the effective gluon mass [172,234]. As , the unprotected contributions diverge, driving the appearance of a maximum in the gluon propagator and a divergence in its first derivative, as well as a zero-crossing and a corresponding divergence in the form factors of the three-gluon vertex. As we comment in this section, of particular phenomenological importance [234,235,236,237,238,239,240] is the relative suppression that the above features induce to the dominant vertex form factors in the intermediate range of momenta.
- In Section 10, we discuss an outstanding feature of the WI satisfied by the pole-free part of the three-gluon vertex, namely the displacement induced by the presence of the aforementioned massless poles [93,124]. In this context, we introduce the key quantity denominated “displacement function”, whose appearance serves as a smoking gun signal of the action of the Schwinger mechanism in QCD; quite interestingly, it coincides [93,124] with the BS amplitude for the formation of a massless scalar out of a pair of gluons, introduced in Section 4. In addition, we derive a crucial relation, which ultimately permits the indirect determination of from lattice QCD [93,124,126]; an important ingredient in this relation is a partial derivative [124,241], denoted by , of the ghost–gluon kernel [228], to be determined in the next section.
- In Section 11, we set up and solve the SDE that governs the evolution of [124,126,241,242]; the main component of this SDE is a special projection of the three-gluon vertex, which is computed by appealing to formulas established in Section 7, and allows for the accurate determination of in the entire range of relevant momenta [126].
- In Section 12, we substitute into the central relation derived in Section 10 the solution for found in the previous section, together with the lattice data [84,85] for the gluon propagator, the ghost dressing function, and the form factor of the three-gluon vertex associated with the soft-gluon limit, in order to obtain the form of the displacement function [124,126]. As we discuss, the results exclude—with near-absolute certainty—the null hypothesis (absence of Schwinger mechanism, ), and corroborate the action of the Schwinger mechanism in QCD [126]. In addition, we show that the form of found is statistically completely compatible with that obtained from the BSE-based analysis presented in Section 4.
- In Section 13, we present our conclusions.
- Finally, in Appendix A, we derive the BQIs related to the displacement functions of the conventional and background vertices, while in Appendix B, we provide details about the renormalization scheme employed in our computations.
2. Basic Concepts and General Theoretical Framework
We start by considering the Lagrangian density of an SU(N) Yang–Mills theory, comprised of the classical part, , the contribution from the ghosts, , and the covariant gauge-fixing term, , namely
where
In the above formula, denotes the gauge field, while and represent the ghost and anti-ghost fields, respectively, with .
In addition,
is the antisymmetric field tensor, where stands for the totally antisymmetric structure constants of the SU(N) gauge group, and g is the gauge coupling, while
denotes the covariant derivative in the adjoint representation. Finally, represents the gauge-fixing parameter; corresponds to the Landau gauge, while specifies the Feynman–´t Hooft gauge.
The transition from the pure Yang–Mills theory of Equation (1) to QCD is implemented by supplementing the corresponding kinetic and interaction terms for the quark fields. However, since throughout this work we do not consider effects due to dynamical quarks, the aforementioned terms will be omitted entirely.
The most fundamental correlation function is the gluon propagator, whose non-perturbative features are inextricably connected with key dynamical properties of the theory. In the Landau gauge that we will employ throughout, the gluon propagator, , is completely transverse, i.e.,
In the continuum, the dynamical properties of the gluon propagator are encoded in the corresponding SDE, given by
where is the gluon self-energy, shown diagrammatically in the first row of Figure 1. The fully-dressed vertices entering the diagrams are determined by their own SDEs, obtaining finally a tower of coupled integral equations, which, for practical purposes, must be truncated or treated approximately.
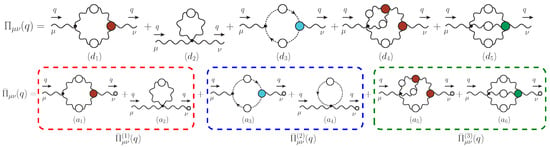
Figure 1.
Upper panel: the diagrammatic representation of the conventional gluon self-energy, . Bottom panel: the diagrammatic representation of the , self-energy ; the grey circles at the end of the gluon lines indicate a background gluon. The corresponding Feynman rules are given in Appendix B of [14].
Given that, by virtue of the fundamental STI satisfied by the two-point function, the self-energy is transverse,
we have that
and from Equation (6) follows that
Of particular importance is the exact way that Equation (7) is enforced at the level of the SDE given in Figure 1 which governs the gluon evolution. In particular, if we were to contract the corresponding diagrams by , the entire set of diagrams must be considered in order for Equation (7) to emerge from the SDE. This pattern manifests itself already at the one-loop level, where it is known that the ghost loop must be included in order to guarantee the transversality of the self-energy. The main practical drawback stemming from this observation is that truncations, in the form of the omission of certain subsets of graphs, are likely to distort this fundamental property.
Quite interestingly, within the PT-BFM framework the transversality property of Equation (7) is enforced in a very special way, which permits physically meaningful truncations. In what follows we will predominantly employ the language of the BFM; for the basic principles of the PT and its connection with the BFM, the reader is referred to the extended literature on the subject [14,96,100,193,194,211,243], as well as to Section 6 of the present work.
The BFM is a powerful quantization procedure, where the gauge-fixing is implemented without compromising explicit gauge invariance. Within this framework, gauge field A appearing in the classical action is decomposed as , where B and Q are the background and quantum (fluctuating) fields, respectively. Note that the variable of integration in the generating functional is the quantum field, which couples to the external sources, as . The background field does not appear in loops. Instead, it couples externally to the Feynman diagrams, connecting them with the asymptotic states to form elements of the S-matrix. Then, if the gauge-fixing term
is used, the resulting gauge-fixed action retains its invariance under gauge transformations of the background field. As a result of this invariance, when Green’s functions are contracted by the momentum carried by a background gluon, they satisfy Abelian (ghost-free) STIs, akin to the Takahashi identities known from QED. In particular, the STIs of the BFM retain their tree-level forms in all orders, in contradistinction to the STIs of the gauges, whose forms are modified by contributions stemming from the ghost sector.
Within the BFM, one may consider three kinds of propagators, by choosing the types of incoming and outgoing gluons [244]. In particular, we have:
- (i)
- The propagator that connects two quantum gluons. Notice that this propagator coincides with the conventional gluon propagator of the covariant gauges, defined in Equation (5), under the assumption that the corresponding gauge-fixing parameters, and , are identified, i.e., .
- (ii)
- The propagator that connects a with a , to be denoted by .
- (iii)
- The propagator that connects a with a , to be denoted by . Note that its full definition requires an additional gauge-fixing term, with the associated “classical” gauge-fixing parameter, [14,202,206].
Given that the relations captured by Equations (5) and (6) apply also in the cases of and , one may define the corresponding self-energies and , as well as the functions and .
Quite interestingly, the three propagators defined in (i)-(iii) are related by a set of exact identities, known as BQIs [14,209,210,211]. In particular, we have that (see also Table 1)
where the function is the component of a particular two-point ghost function, , given by [209,211,213,245]
where is the Casimir eigenvalue of the adjoint representation [N for SU], is the ghost propagator, and denotes the ghost–gluon kernel defined in Figure 2.

Table 1.
The different types of gluon propagators of the background field method (BFM), together with their diagrammatic representations, symbols, corresponding self-energies, and the background quantum identities (BQIs) that relate them to the conventional propagator.
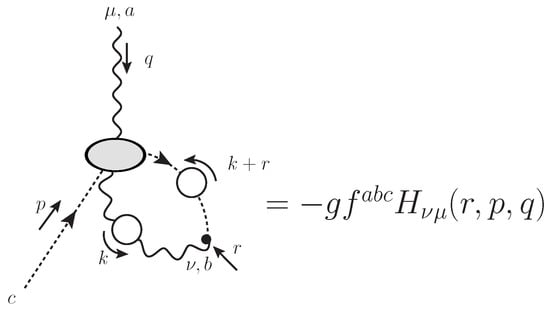
Figure 2.
Diagrammatic definition of the ghost–gluon scattering kernel, . At the tree level, .
In the Landau gauge, a special identity relates the form factors of to the ghost dressing function, , defined as , namely [16,131,213]
which is valid before renormalization. In fact, in this particular gauge, coincides with the so-called Kugo–Ojima function [212,245,246,247].
To determine the renormalized form of Equation (13), we introduce the renormalization constants of the conventional Green’s functions
where we denote by and the conventional ghost–gluon [] and three-gluon [] vertices, respectively. Note that, by virtue of Taylor’s theorem [207], is finite in the Landau gauge; its precise value depends on the renormalization scheme adopted, see Section 8. Moreover, denoting by the (wave-function) renormalization constant of , the Abelian STIs of the BFM impose the validity of the pivotal relation [14,202,206]
which is the non-Abelian analog of the textbook relation [133], relating the renormalization constants of the electric charge and the photon propagator in QED.
Then, since the BQIs of Equation (11) are direct consequences of the Becchi–Rouet–Stora–Tyutin (BRST) symmetry [248,249,250] of the theory [209,211,213,245], the form is preserved by renormalization. Hence, by combining Equations (11), (14) and (15), we obtain
which yields (note that in the original and widely used [3,8,16,20,79,131] version of Equation (17) the renormalization is performed in the so-called Taylor scheme, where .)
As has been shown in [131], the dynamical equation governing yields , provided that the gluon propagator entering it is finite at the origin. Thus, one obtains from Equation (17) the useful identity [212]
According to numerous lattice simulations and studies in the continuum (see e.g., [21,42,47,49,51,56,62,63,73,79,85,112,178,225,227,228,229,230,231,232,233]), the ghost dressing function reaches a finite (nonvanishing) value at the origin, which, due to Equation (18), furnishes also the value of .
The final upshot of the above considerations is that one may use the BQIs in Equation (11) to express the SDE given in Equation (6) in terms of the or , at the modest cost of introducing in the dynamics the quantities or . Focusing on the former possibility, Equation (11) becomes
where the diagrammatic representation of the self-energy is shown in the lower panel of Figure 1.
The principal advantage of this formulation is that the self-energy contains fully-dressed vertices with a background gluon of momentum q exiting from them, which satisfy Abelian STIs. In particular, denoting by , , and the BQQ, Bcc, and BQQQ vertices, respectively, we have that [14,100,109]
In contrast, the conventional three-gluon and ghost–gluon vertices, and , respectively, satisfy the STIs [1,251,252,253,254,255]
where is an interaction kernel containing only ghost fields; its tree-level value is . The STI for the conventional four-gluon vertex is given in Equation (C.24) of [14].
The special STIs listed in Equations (20)–(22) are responsible for the remarkable property of “block-wise” transversality [109,192,244], displayed by . To appreciate this point, notice that the diagrams comprising in Figure 1 were separated into three different subsets (blocks), consisting of (i) one-loop dressed diagrams containing only gluons, (ii) one-loop dressed diagrams containing a ghost loop, and (iii) two-loop dressed diagrams containing only gluons. The corresponding contributions of each block to are denoted by , with .
The block-wise transversality is a stronger version of the standard transversality relation ; it states that each block of diagrams mentioned above is individually transverse, namely
In order to appreciate in detail the reason why the STIs in Equations (20)–(22) are instrumental for the block-wise transversality, we will consider the case of ; the relevant diagrams are enclosed in the blue box of Figure 1.
The diagrams and are given by
where a color factor is suppressed in both expressions. In addition, for the formal manipulations of integrals, we employ dimensional regularization [256]; to that end, we introduce the short-hand notation
where is the dimension of the space-time, and denotes the ’t Hooft mass.
The contraction of graph by triggers the STI satisfied by [given by Equation (21)], and we obtain
which is precisely the negative of the contraction . Hence,
3. Schwinger Mechanism in Yang–Mills Theories
The BRST symmetry of the Yang–Mills Lagrangian given in Equation (1) prohibits the inclusion of a mass term of the form . Moreover, a symmetry-preserving regularization scheme, such as dimensional regularization, prevents the generation of a mass term at any finite order in perturbation theory. Nonetheless, as affirmed four decades ago [94,95,96,97,98,99], the non-perturbative Yang–Mills dynamics endow the gluons with an effective mass, which sets the scale for all dimensionful quantities, and tames the instabilities originating from the infrared divergences of the perturbative expansion ( e.g., Landau pole). In addition, the presence of this mass causes the effective decoupling (screening) of the gluonic modes beyond a “maximum gluon wavelength” [257], and leads to the dynamical suppression of the Gribov copies, see e.g., [16,258,259] and references therein.
The generation of a gluon mass proceeds through the non-perturbative realization of the Schwinger mechanism [127,128]. Even though the technical details associated with the implementation of this mechanism in a four-dimensional non-Abelian setting are particularly elaborate, the general underlying idea is relatively easy to convey.
To that end, consider the dimensionless vacuum polarization , defined through , such that
The Schwinger mechanism is based on the fundamental observation that, if develops a pole at (to be referred to as “massless pole”) then the vector meson (gluon) picks up a mass, regardless of any “prohibition” imposed by the gauge symmetry at the level of the original Lagrangian. Thus, in Euclidean space, the above sequence of ideas leads to
and the gauge boson propagator saturates to a non-zero value at the origin. This effect of infrared saturation of the propagator signifies the generation of a mass, which is identified with the positive residue of the pole.
At this descriptive level, Schwinger’s argument is completely general, making no particular reference to the specific dynamics that would lead to the appearance of the required massless pole inside . In fact, depending on the particular theory, the field-theoretic circumstances that trigger the crucial sequence captured by Equation (32) may be very distinct, see e.g., [260,261]. In the case of Yang–Mills theories, the origin of the massless poles is purely non-perturbative [159]: the strong dynamics produce scalar composite excitations, which carry color and have vanishing masses. These poles are carried by the fully-dressed vertices of the theory; and since these vertices enter the gluon SDE shown in Figure 1 (upper (lower) panel for the QQ (QB) propagator), the massless poles find their way into the gluon self-energy (or, equivalently, the gluon vacuum polarization). The detailed implementation of this idea has been presented in a series of works [18,93,96,112,116,117,118,159,160,161,166,189,262], and will be summarized in the rest of this section.
Let us focus for now on the conventional three-gluon and ghost–gluon vertices, and , respectively, introduced above Equation (23). When the formation of massless poles is triggered, these vertices assume the general form (see Figure 3)
where and are their pole-free components, while and contain longitudinally coupled poles, whose special tensorial structure is given by
such that
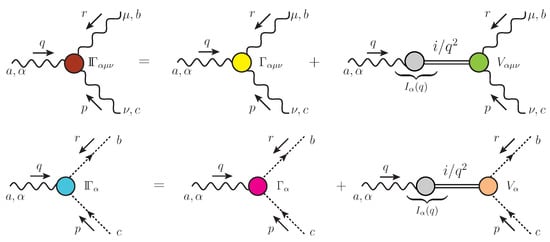
Figure 3.
The diagrammatic representation of the three-gluon and ghost–gluon vertices introduced in Equation (33): (first row) and (second row). The first term on the r.h.s. indicates the pole-free part, or , while the second denotes the pole term or .
We emphasize that the reason why and are longitudinally coupled may be directly inferred from their special decomposition, shown in Figure 3. In particular, let us denote by the transition amplitude that connects a gluon with a massless composite scalar, depicted as a gray circle in Figure 3. Since depends solely on the momentum q, and carries a single Lorentz index, , its general form is given by , where is a scalar form factor [117,214]. This observation accounts directly for the form of given in Equation (34); to deduce the form of , one must, in addition, appeal to Bose symmetry, which imposes the structures and in the remaining two channels.
Returning to the SDE of Figure 1, the component will enter in it through graphs () and , while the component through graph (). Since has poles for each one of its three momenta, let us point out that only the pole associated with the q-channel, i.e., the channel that carries the momentum entering the gluon propagator is relevant for the Schwinger mechanism that will generate mass for . In fact, in the Landau gauge that we employ, the gluon propagators inside the diagrams () and are transverse, leading to a considerable reduction in the number of the form factors of that participate actively, since
Consequently, for the ensuing analysis, one requires only the tensorial decomposition of the component in Equation (34), which is given by
where . Then, the substitution of Equation (37) into Equation (36), and use of the relation , reveals that only two form factors survive inside () and , namely
Since the main function of the Schwinger mechanism is to make the gluon propagator saturate at the origin, it is important to explore the properties of the structures appearing in Equation (38) near . To that end, we expand the r.h.s. of Equation (38), keeping terms at most linear in q. After noticing that the term proportional to in Equation (38) is of order , we end up with a single relevant form factor associated with , namely , which survives the limit of graphs () and . As for , its unique component, , enters directly in ().
The continuation of this analysis entails the Taylor expansion of and around . In carrying out this expansion, one employs the following two key relations,
The first one follows directly from the Bose symmetry of the three-gluon vertex, which implies that ; as we will see in Section 10, it may also be derived in a completely independent way from the fundamental STIs satisfied by the three-gluon vertex. The justification of the second relation in Equation (39) is less straightforward; its derivation, presented in Appendix A, relies on the BQI [14,211] linking the conventional ghost–gluon vertex, , with its background counterpart, .
Thus, after taking Equation (39) into account, the Taylor expansion of and around yields
with
The functions and are of central importance for the rest of this review. In particular, there are three key points related to them that will be elucidated in detail in what follows:
- 1.
- and are the BS amplitudes describing the formation of gluon–gluon and ghost–anti-ghost colored composite bound states, respectively, see Section 4.
- 2.
- The gluon mass is determined by certain integrals that involve and , given explicitly in Section 5.
- 3.
- and lead to smoking-gun displacements of the WIs. In fact, the displacement induced by , has been confirmed by lattice QCD, by combining judiciously the results of several lattice simulations, see Section 5.2.
We emphasize that the BFM vertices develop poles in exactly the same way as their conventional counterparts. In particular, the main relations Equations (33), (34), (39) and (41) remain valid, with the only modification that all quantities carry hats or tildes; these BFM vertices will be used extensively in Section 5. Note that the conventional and background vertices, including their pole content, are related through appropriate BQIs, see e.g., Equations (A3) and (A6).
We end this section by commenting briefly on the implementation of the Schwinger mechanism away from the Landau gauge, i.e., when the gluon propagator is given by
for further details, the reader is referred to [189].
(ı) The massless poles remain longitudinally coupled for every value of , i.e., the form of and given in Equation (34) persists, with the only difference that the form factors comprising , , , and depend in general on . Indeed, as explained right below Equation (35), the longitudinal nature of the poles is dictated solely by Lorentz invariance, which forces the transition amplitude to assume the form ; clearly, this fundamental argument holds for every .
(ii) Since the gluon propagators entering the graphs and of Figure 1 are now given by Equation (42), the l.h.s. of Equation (36) becomes , and, as a result, the terms in Equation (34) proportional to and are not fully annihilated. Note, however, that the presence of poles in and poses no problem, given that one integrates over the loop momentum k. Similar observations hold for the BSE discussed in the next section, which acquires a more complicated form, involving not only the and , but also additional form factors [189].
(iii) A general property of the massless excitations that trigger the Schwinger mechanism is that they do not induce divergences to physical amplitudes; their contributions are completely vanishing, or, at most, finite [260,261]. As was shown recently in [93], in Landau gauge QCD this property hinges on the validity of Equations (35) and (39). Away from the Landau gauge, Equation (39) persists, because its validity relies on Bose symmetry [189]. However, in Equation (35) the substitution must be carried out for all projectors; as a result, the r.h.s. no longer vanishes, but includes -dependent longitudinal contributions. Even though this issue has not been addressed in the literature, the longitudinal nature of the additional terms heralds their cancellation through the same general mechanism that renders physical amplitudes -independent.
4. Dynamical formation of Massless Poles
One crucial aspect of the implementation of the Schwinger mechanism in a Yang–Mills context is that the poles that comprise the components and in Equation (34) are not introduced by hand; rather, they are generated dynamically, as massless composite excitations that carry color. In fact, this subtle process is controlled by a system of coupled linear BSEs for the functions and , which play the role of the BS amplitudes for generating composite massless scalars out of two gluons and a ghost–anti-ghost pair, respectively.
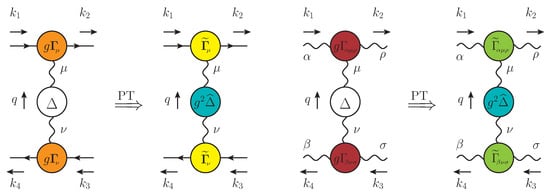
The starting points for the derivations of the aforementioned BSEs are the SDEs for and , shown diagrammatically in Figure 4, and given by [124]
where
and the tree-level expressions for the vertices and are given by
Note that, for compactness, all momentum arguments have been suppressed; they may be easily restored by appealing to Figure 4.
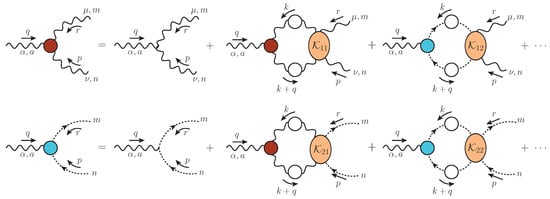
Figure 4.
The coupled system of Schwinger–Dyson equations (SDEs) for the three-gluon and ghost–gluon vertices, and , respectively. The orange ellipses represent four-point scattering kernels, denoted by . We omit diagrams containing five-point scattering kernels.
The following steps are subsequently implemented:
- In order to exploit Equation (38), multiply the first equation by the factor .
- Take the limit of the system as : this activates Equation (40) and introduces the functions and .
- Isolate the tensor structures proportional to , and match the terms on both sides.
- Employ the “one-particle exchange” approximation for the kernels , to be denoted by , shown in Figure 5.
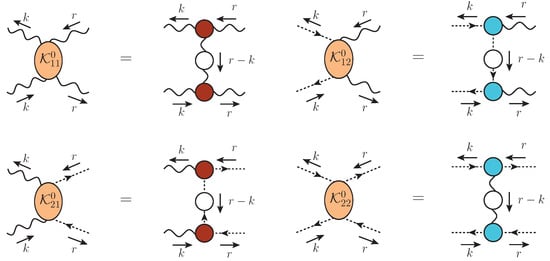 Figure 5. The one-particle exchange approximations, , of the kernels appearing in Figure 4.
Figure 5. The one-particle exchange approximations, , of the kernels appearing in Figure 4.
Thus, we arrive at a system of homogeneous equations involving and ,
where ; the system is diagrammatically depicted in Figure 6.
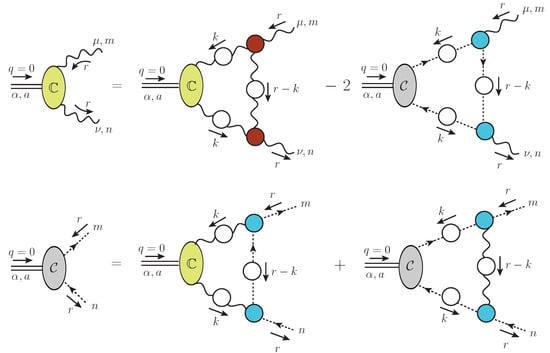
Figure 6.
The diagrammatic representation of the coupled system of Bethe–Salpeter equations (BSEs) that governs the evolution of the functions and .
Before turning to the numerical analysis, the BSE system must be passed to the Euclidean space, following standard conversion rules. In doing so, we note that the integral measure is modified according to ; this extra factor of i combines with the defined in Equation (44) to give real expressions.
As announced, the system of coupled equations given in Equation (46) represents the BSEs that govern the formation of massless colored bound states out of two gluons and a ghost–anti-ghost pair. The functions and are the corresponding BS amplitudes; finding nontrivial solutions for them, i.e., something other than identically, is crucial for the implementation of the Schwinger mechanism.
The equations in Equation (46) are linear and homogeneous in the unknown functions. There are two main consequences arising from this fact. First, the numerical solution of the system will be reduced to an eigenvalue problem. Second, the overall scale of the solutions is undetermined, since the multiplication of a given solution by an arbitrary real constant produces another solution (The ambiguity originates from considering only leading terms in the expansion around , and may be resolved if further orders in q are kept, see e.g., [219,263,264]).
It turns out that the condition for obtaining nontrivial solutions, when expressed in terms of the strong coupling, , states that they exist for when the renormalization point GeV. The solutions obtained when acquires this special value are shown in Figure 7; they have undergone scale fixing (The scale was fixed by requiring the best possible matching with the result obtained for from the WI displacement, see Section 12), and are denoted by and . Observe that is significantly larger in magnitude than , implying that the three-gluon vertex accounts for the bulk of the gluon mass, as originally claimed in [215].
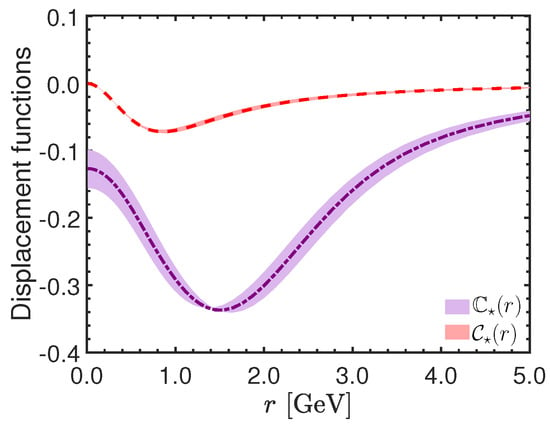
Figure 7.
The solutions for (purple dot-dashed) and (red dashed) obtained from the coupled BSE system of Equation (46).
It is important to compare the value of , imposed by the BSE eigenvalue, with the expected value for for the renormalization scheme employed: within the asymmetric momentum subtraction (MOM) scheme (see Appendix B), we have that [71]. This numerical discrepancy in the values of is clearly an artifact of the truncation employed, and concretely of the approximation of the kernels by their one-particle exchange diagrams, . A preliminary analysis reveals that mild modifications of the kernels lead to considerable variations in the value of , but leave the form of the solutions for and practically unaltered. This observation suggests that, while a more complete knowledge of the BSE kernels is required in order to bring closer to its MOM value, the solutions obtained with the present approximations should be considered as particularly stable.
5. Generation of the Gluon Mass
We next demonstrate in detail how the presence of the massless poles in the vertices that enter the SDE of the gluon propagator generate a gluon mass.
Since the fundamental STIs of the theory remain intact under the action of the Schwinger mechanism, Equations (7) and (8) remain valid, and the mass term will appear in the transverse combination . However, the determination of the mass proportional to exposes an entirely different array of principles compared to the corresponding computation for the component.
The calculation with respect to the component is rather direct; since the massless poles in the vertices are themselves longitudinally coupled, their contribution to the component of is easily worked out, as will be illustrated in Section 5.1. In contrast, the emergence of a mass proportional to is intimately connected with a powerful relation, known as seagull identity [113,166], which in the absence of the Schwinger mechanism would enforce the masslessness of the propagator, as will be discussed in Section 5.2. In fact, one main conceptual difference between the two approaches is that in the case, the use of the PT-BFM-based version of the SDE given in Equation (19) is crucial for the emergence of the correct result.
In order to simplify the technical aspects of the calculation without compromising its conceptual content, we will determine the contribution to the gluon mass due to the pole in the ghost–gluon vertex, namely in the case of , and in the case of . To that end, we will focus on the subset of self-energy graphs containing only ghost loops, i.e., graph in the case of , and graphs and in the case of , shown in the upper and lower row of Figure 1, respectively.
5.1. Gluon Mass from the Component
Let us calculate the contribution to the gluon mass stemming from the ghost loop, i.e., the diagram of Figure 1, which, for general values of q, reads
To isolate the component of Equation (47) at the origin, we first decompose the full vertex as in Equations (33) and (34), and drop directly the pole-free part since it does not contribute at . Then, denoting by the contribution of to , we obtain
Next, a Taylor expansion around , using Equations (39) and (40), yields
Evidently, the integral above can only be proportional to , such that
where the tensor structure is already isolated.
Then, let us denote by the contribution to the mass originating in the of the ghost loop. Noting that the contribution of to the propagator is i times the negative of its form factor, we obtain that
At this point, we set and renormalize Equation (51). This leads to the appearance of the finite renormalization constant of the ghost–gluon vertex, .
Next, we express the result in terms of the ghost dressing function F, pass to Euclidean space, and employ hyperspherical coordinates, to obtain the final expression
where .
The derivation of the contributions from the diagrams and proceeds in a completely analogous way, but is algebraically more involved, see [166] for details.
It is instructive to consider how the result of Equation (52) emerges in the context of Equation (19). To this end, we consider the ghost block of Figure 1, whose diagrams have the expressions given in Equation (27); clearly, only diagram can contribute to the component of .
Then, we decompose in complete analogy with Equations (33) and (34), i.e.,
and expand the of Equation (27) around , isolating its component. These steps eventually lead to
where is defined in the exact same way as , namely through Equation (41) but with tildes over all relevant quantities. It is now easy to establish that Equation (54) is completely equivalent to Equation (51), simply by multiplying both of its sides by , and then using Equation (A4) on the r.h.s. and Equations (19) and (18) on the l.h.s.
Hence, when the mass is computed through the component of the self-energy, the contributions originating from the ghost diagrams of either the BQ or the QQ propagator furnish the same result. The same is not true for the calculation through the component, since the ghost diagram of the QQ propagator is not by itself transverse, and a meaningful analysis is preferably carried out within the BFM.
5.2. Gluon Mass from the Component: Seagull Identity and Ward Identity Displacement
The fact that the activation of the Schwinger mechanism is crucial for the self-consistent generation of a gluon mass may be best appreciated in conjunction with the so-called seagull identity [113,166]. The content of this identity is that
for functions that satisfy Wilson’s criterion [265]; the cases of physical interest are . The general demonstration of the validity of Equation (55) has been given in [166]; for a detailed discussion of how Equation (55) prevents the photon from acquiring a mass in scalar electrodynamics, see [18].
What is so special about Equation (55) is that, within the PT-BFM formalism, the l.h.s. of Equation (55) coincides with the contributions of loop diagrams to the component of the gluon mass. Therefore, Equation (55) enforces the non-perturbative masslessness of the gluon in the absence of the Schwinger mechanism: even if a massive gluon propagator (made “massive” through a procedure other than the Schwinger mechanism) were to be substituted inside Equation (55), one would obtain zero as a contribution to the gluon mass! For example, the simple choice , reduces the l.h.s of Equation (55) to (dimensionally regularized) textbook integrals, which add up to give precisely zero [18].
In order to appreciate in some detail how the seagull identity prevents the component of the propagator from acquiring a mass in the absence of the Schwinger mechanism, let us consider once again the ghost block of Figure 1; now both graphs, () and (), contribute to the component.
Let us assume that the Schwinger mechanism is turned off; at the level of the Bcc vertex this means that vanishes identically, and . Consequently, saturates the STI of Equation (21),
Since the form factors of the vertex do not contain any poles, the derivation from Equation (56) of the corresponding WI proceeds in the standard textbook way: both sides of Equation (56) undergo a Taylor expansion around , and terms at most linear in q are retained. Thus, one arrives at the simple QED-like WI
We now compute the component of at , or, equivalently, . From Equation (27), we see that is proportional to in its entirety. On the other hand, contains both and components; however, the latter vanishes in the limit if the vertex is pole-free. Then, it is straightforward to show that, as ,
At this point, employing the WI of Equation (57) (with ), we get
Hence, the WI satisfied by the vertex in the absence of the Schwinger mechanism triggers the seagull identity, which, in turn, enforces the masslessness of the propagator.
When the Schwinger mechanism is activated, the STIs that are satisfied by the vertices of the theory retain their original forms but are resolved through the nontrivial participation of the terms containing the massless poles [96,112,159,160,161,166,262,266]. In particular, the full vertex precisely satisfies Equation (21), namely
Notice in particular that the contraction of by cancels the massless pole in , leading to a completely pole-free result. Therefore, the WI obeyed by may be derived as before, through a standard Taylor expansion, leading to
Evidently, the unique zeroth-order contribution appearing in Equation (61), namely , must vanish,
Note that this particular property may be independently derived from the antisymmetry of under , , which is a consequence imposed by the ghost–anti-ghost symmetry of the vertex. The above result, together with Equation (A3), is used to prove Equation (39) in Appendix A.
Thus, Equation (61) becomes
and the matching of the terms linear in q yields the WI
Comparing Equations (57) and (64), it becomes clear that the Schwinger mechanism induces a characteristic displacement to the WIs that are satisfied by the pole-free parts of the vertices [166].
Returning to Equation (58), but now substituting in it the displaced version of Equation (57), namely
When Equation (65) is substituted into Equation (58), the first term of its r.h.s. triggers the seagull identity and vanishes, exactly as before; however, the second term survives, precisely furnishing the result given in Equation (54).
Completely analogous procedures may be applied to the remaining two blocks, and , by exploiting the Abelian STIs of Equations (20) and (22), respectively [161].
6. Renormalization Group Invariant Interaction Strength
The PT-BFM formalism provides the natural framework for the construction of the RGI version of the naive one-gluon exchange interaction.
To fix the ideas, recall that in QED, the one-photon exchange interaction, defined as , where is the hyper-fine structure constant and the photon propagator, is an RGI combination, by virtue of the relation ; see comments following Equation (15). Moreover, this particular combination is universal (process-independent) because it may be identified within any two-to-two scattering process, regardless of the nature of the initial and final states (electrons, muons, taus, etc). Instead, in QCD, the corresponding combination is (trivially) universal but not RGI. When the vertices that connect the gluon to the external particles are “dressed” (), the combination becomes RGI; however, it is no longer process-independent, because the vertices contain information on the characteristics of the external particles, e.g., the is not the same if the external particles are quarks or gluons. This apparent conundrum may be resolved by resorting to the PT, which reconciles harmoniously the notions of RGI and process independence.
Within the PT framework, the starting point of the construction involves “on-shell” processes [14,96,100,193,194], such as those depicted in Figure 8. The fundamental observation is that the dressed vertices appearing there contain propagator-like contributions, which may be unambiguously identified by means of a well-defined diagrammatic procedure. After discarding terms that vanish on the shell, the contributions extracted from a vertex have a two-fold effect: (i) the genuine vertex contributions left behind form a new vertex, , which satisfies Abelian STIs, and (ii) when the propagator-like pieces from both vertices are allotted to the conventional propagator, , the resulting effective propagator, , captures all RG logarithms associated with the running of the coupling; for example, at one loop and for large , one has
where is the first coefficient of the Yang–Mills function. We emphasize that the PT construction goes through all orders in perturbation theory, as well as non-perturbatively, and all key properties of the PT Green’s function persist unaltered [194,195].
The correspondence between the PT and the BFM may be summarized by stating that the PT rearrangement outlined above amounts effectively to replacing the Q-type gluon that is being exchanged (carrying momentum q) by a B-type gluon [193,267,268,269]; external (on-shell) fields are always of the Q-type. Thus, the notation used above for the PT effective Green’s functions (“tildes” and “hats”) corresponds precisely to the BFM notation introduced in Section 2. Note that the formal expression of all PT rearrangements implemented diagrammatically are the BQIs that relate conventional Green’s functions to their BFM counterparts [14]. For example, in the case of the quark–gluon vertex, we have that the vertices [with external fields ] and [] are related by the BQI [270]
where the ellipsis denotes terms that vanish on the shell. Similarly, the BQI of Equation (A5), when evaluated on-shell, yields a completely analogous result, to wit,
It is now clear how the PT gives rise to a process-independent propagator-like component: regardless of the process ( i.e., the type of vertex connecting the internal gluon to the external states), each vertex contributes to the conventional a factor of , finally leading to the BQI of Equation (11) [16].
The culmination of the above sequence of ideas is reached by noting that, by virtue of Equation (15), the combination
is RGI: it retains exactly the same form before and after renormalization, and, consequently, does not depend on the renormalization point [96]. The quantity has a mass dimension of , and is known in the literature as the “RGI running interaction strength” [16].
The steps leading to the natural appearance of within any given process may be summarized in the case of quark–antiquark, or gluon–gluon scattering.
Consider the S-matrix elements , for the scattering of a quark and an antiquark, and , for the scattering of two gluons. The quark–antiquark scattering is depicted in the left panel of Figure 8. Using the BQI of Equation (11) we obtain
where we omit color structures.
Similarly, the scattering of two gluons depicted in the right panel of Figure 8, yields
Evidently, the same , defined in Equation (69), appears naturally in both Equations (70) and (71): it is, in that sense, a process-independent RGI interaction capturing faithfully the one-gluon exchange dynamics [3,16,20,79,96,129,130,131].
The actual determination of proceeds by means of the second equality in Equation (69), i.e., by combining the standard gluon propagator, , together with the function . In the top left panel of Figure 9 we show lattice data for the conventional gluon propagator from [85] (points) and a physically motivated fit (blue continuous), given by Equation (C11) of [124]. In the top right panel of the same figure, we show the auxiliary function, which can be computed by contracting Equation (12) with (see e.g., [131]), using the results of [228] for the ghost–gluon kernel, . Then, in the bottom left panel of Figure 9 we show the that results from combining the fit for and the shown in the top panels of the same figure and using [71] and [see Section 8].
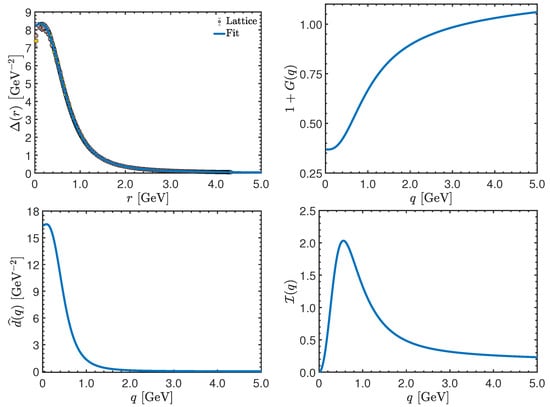
Figure 9.
Top left: Gluon propagator, , from lattice simulations of Reference [85] (points) and a fit given by Equation (C11) of [124] (blue continuous). Top right: The auxiliary function , defined in Equation (12). Bottom left: The renormalization group invariant (RGI) running interaction strength defined in Equation (69), computed using the and shown in the top panels, with [71] and [see Section 8]. Bottom right: The corresponding dimensionless RGI interaction , defined in Equation (72).
From the of Equation (69) one may define the dimensionless RGI interaction [16], ,
As explained in [16], this quantity provides the strength required in order to describe ground-state hadron observables using SDEs in the matter sector of the theory. In that sense, bridges a longstanding gap that has existed between non-perturbative continuum QCD and ab initio predictions of basic hadron properties.
7. Three-Gluon Vertex and Its Planar Degeneracy
The three-gluon vertex, , plays a pivotal role in the dynamics of QCD [234], manifesting its non-Abelian nature through the gluon self-interaction. In fact, the most celebrated perturbative feature of QCD, namely asymptotic freedom, hinges on the properties of this particular interaction vertex. Its importance in the non-perturbative domain has led to an intense effort for unveiling its elaborate features [21,28,33,34,35,36,41,50,68,69,71,78,81,86,87,122,172,173,174,175,176,177,178,179,180,271]. Indeed, as we have seen in Section 3 and Section 4, the pole structure of the three-gluon vertex is crucial for the onset of the Schwinger mechanism and the dynamical generation of a gluon mass. Moreover, its pole-free part provides highly nontrivial contributions to the SDEs of several Green’s functions, most notably the gluon propagator (cf. Figure 1), as well as in the Bethe–Salpeter and Faddeev equations that determine the properties of glue balls [235,236,238,239,240] and hybrid mesons [237], respectively.
For general momenta, is a particularly complicated function, comprised by 14 tensor structures and their associated form factors [251]. Fortunately, in the Landau gauge, considerable simplifications take place, making the treatment of the three-gluon vertex less cumbersome. Indeed, in the latter gauge, quantities of interest require only the knowledge of the transversely projected three-gluon vertex [126,174,175,223], , defined as
Note that does not contain massless poles, by virtue of Equation (35). Furthermore, can be parameterized in terms of only 4 independent tensor structures, i.e.,
Due to the Bose symmetry of , the can be chosen to be individually Bose symmetric, such that its form factors are symmetric under the exchange of any two arguments [86]. In fact, they can only depend on three totally symmetric combinations of momenta.
Quite remarkably, lattice [86,87,88] and continuum [174,175,223] studies alike, have demonstrated that, to a very good level of accuracy, the depend exclusively on a single judiciously chosen variable. Specifically, the computed on the lattice in [86,87,88] can be parameterized in terms of the special Bose symmetry combination
Thus, the are the same for any combination of , , and that fulfils Equation (75) for a given value of . This property has been denominated planar degeneracy, because Equation (75) with fixed s defines a plane, normal to the vector , in the first octant of the coordinate system .
In particular, the form factor of the classical tensor structure is rather accurately approximated by
In the above equation, is the single transverse form factor of the three-gluon vertex in the soft gluon limit [124], and is obtained in lattice simulations as the limit of the following totally transverse projection [84]
A particular realization of the planar degeneracy property is shown in Figure 10, where we show the classical form factor , obtained from the lattice simulation of [86]; we consider three different kinematic configurations, characterized by a single momentum. Specifically, the orange stars correspond to the soft-gluon limit, , which implies ; the green diamonds denote the symmetric limit, where all of the momenta have the same magnitude, ; and the purple circles represent points with and . When plotted against the momentum r, the three configurations of produce three clearly distinct curves; however, when plotted in terms of the Bose symmetry variable s of Equation (75), they become statistically indistinguishable, manifesting the validity of Equation (76).
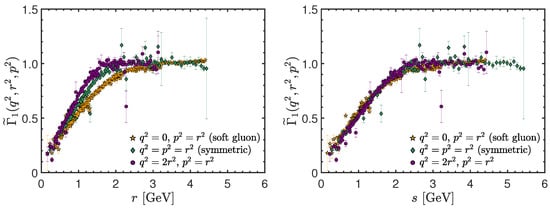
Figure 10.
Lattice data from Reference [86] for the classical form factor, , of the transversely projected three-gluon vertex in three different kinematic configurations: the soft-gluon (, , orange stars), the symmetric limit (, green diamonds), and the case with (purple circles). In the left panel is plotted as a function of r, while in the right it is plotted as a function of the Bose symmetry variable s defined in Equation (75).
In addition to the planar degeneracy property, lattice [84,86,87,88] and continuum [174,175,179,223] results show a clear dominance of the classical form factor over the remaining ones. Based on these considerations, the special approximation
has been put forth, where is the tree-level value of , i.e., Equation (73) with , and the form factor has been defined in Equation (77). We emphasize that the shape of has been very precisely determined through dedicated lattice studies with large-volume simulations [68,71,84,85]. The outcome of this exploration is shown in Figure 11, where we plot the lattice data of [84] for , together with a physically motivated fit given by Equation (C12) of [124] (blue continuous curve). The corresponding fitting formula is rather complicated and will not be reported here; note, however, that the simple expression given in Equation (102) captures rather well the qualitative behavior of .
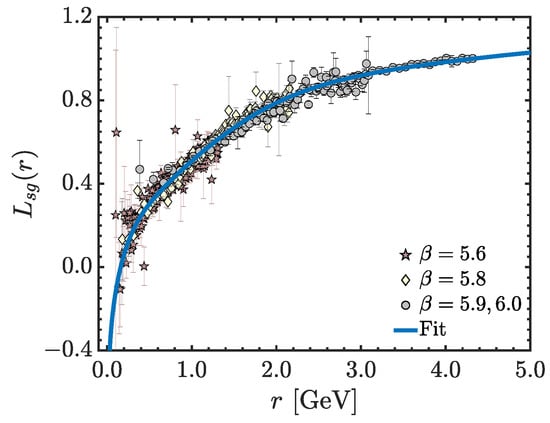
Figure 11.
Lattice data from Reference [84] for , compared to the fit for it given by Equation (C12) of [124] (blue continuous curve).
Equation (78) provides an accurate and exceptionally compact approximation for in general kinematics. This approximation, with the fit for shown in Figure 11, will be used explicitly in Section 8 and Section 11, where the in general kinematics will be needed as input for the determination of other physically important quantities.
8. Ghost Dynamics from Schwinger–Dyson Equations
We next turn our attention to the ghost sector of the theory, whose scrutiny is important for several reasons. First, it has been connected to particular scenarios of color confinement [272,273]. Second, Green’s functions associated with the ghost sector appear as ingredients in the SDEs of several key functions, such as the gluon propagator and the three-gluon vertex [41,50,68,69,71,81,122,172,173,174,175,176,177,178,179,274], affecting their non-perturbative behavior in nontrivial ways, as will be discussed in Section 9. Third, the SDEs governing the ghost sector are simpler than their gluonic counterparts because they are comprised by fewer diagrams; in fact, the SDE of the ghost propagator contains a single diagram, see Figure 12. Fourth, in the Landau gauge, the validity of Taylor’s theorem [207] facilitates considerably the task of renormalization.
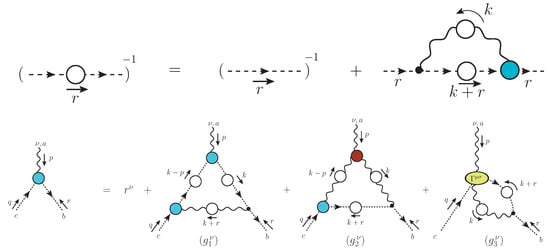
Figure 12.
Top: SDE governing the momentum evolution of the ghost propagator. Bottom: SDE for the ghost–gluon vertex, .
Consequently, the SDEs of the ghost sector are an excellent testing ground for probing the impact of the gluonic Green’s functions that contribute to them [85]; assessing the reliability of truncation schemes [275,276]; and testing the agreement between lattice and continuum approaches.
One of the central results of numerous studies in the continuum [21,62,85,112,178,225,227,228,229,230,231,232,233] as well as a variety of lattice simulations [42,47,49,51,56,63,73,79] may be summarized by stating that the ghost propagator, , remains massless, while the corresponding dressing function, , saturates at the origin. As we will discuss in Section 9, the non-perturbative masslessness of the ghost has important implications for the infrared behavior of the gluon propagator and the three-gluon vertex.
In what follows we provide a concrete example of the state-of-the-art SDE analysis of the ghost sector, by solving the coupled system of equations that governs the ghost-dressing function and the ghost–gluon vertex. In order to obtain a closed system of equations, we use lattice results for the gluon propagator, the three-gluon vertex, and the value of the coupling constant in the particular renormalization scheme employed.
The main points of this analysis may be summarized as follows.
(i) We begin by considering the coupled system of SDEs given in Figure 12, which determines the ghost propagator and ghost–gluon vertex. The treatment will be simplified by neglecting the diagram of Figure 12, thus eliminating the dependence on the ghost–ghost–gluon–gluon vertex, . This is a particularly robust truncation, because the impact of the neglected diagram on the ghost–gluon vertex has been shown to be less than [275].
(ii) Note that due to the fully transverse nature of the gluon propagators in the Landau gauge, in conjunction with the fact that various projections need to be implemented during the treatment of this system, the pole parts V of all fully dressed vertices appearing in Figure 12 will be annihilated; thus, we will have throughout the replacement .
(iii) We proceed by decomposing the pole-free part, , of the ghost–gluon vertex into its most general Lorentz structure, namely
whose scalar form factors reduce to and at the tree level. Evidently, due to the transversality of the gluon propagator, only the classical tensor , accompanied by the form factor , will survive in all SDE diagrams of Figure 12.
(v) Next, we note that the form factor can be extracted from through the projection
Hence, acting with on the diagrams in the second line of Figure 12, we obtain
where
(vi) At this point, we invoke the property of the planar degeneracy of , discussed in Section 7. Employing Equation (78) into the SDE for , the term of Equation (84) becomes
with .
We emphasize that although Equation (78) constitutes in general an approximation, there is one particular kinematic limit in which the expression for given in Equation (85) becomes exact. Specifically, in the soft gluon limit (), it can be shown exactly that [85]
Then, starting from either the general expression for of Equation (84) and using Equation (86), or the approximate version given by Equation (85), it can easily be shown that the limit is the same. As such, the use of Equation (78) yields not only an excellent approximation in general kinematics, but also the exact soft gluon limit for the contribution of the three-gluon vertex to the form factor .
(vii) Now we consider the renormalization of the coupled system of equations. Since the ghost–gluon vertex is finite in the Landau gauge [207], most SDE treatments [85,224,225,226,227,228] of the ghost sector employ the so-called Taylor renormalization scheme (see Appendix B), defined in such a way that the finite renormalization constant of the ghost–gluon vertex has the exact value [54,60,80,85,207].
However, in order to employ Equation (78) most expeditiously, it is more convenient to renormalize in the so-called asymmetric MOM scheme, defined in Appendix B, because this is precisely the scheme employed in the lattice calculations of [68,71,84,85]. Past this point, we denote by the finite value of the ghost–gluon renormalization constant in the asymmetric MOM scheme. Evidently, Equations (15) and (79) imply that .
The renormalization of Equations (80) and (83) proceeds by substitution of the unrenormalized quantities by their renormalized counterparts, following Equation (15), and imposing Equation (A8) for .
Note that, in principle, , may be determined from the relation , imposed by the corresponding STI [277]; however, these renormalization constants are not available to us, given that Green’s functions have been obtained from the lattice. Therefore, is treated as an adjustable parameter, whose value is determined by requiring that the solution of the SDE for reproduces the corresponding lattice data of [73,85] as well as possible.
(viii) Finally, we transform Equations (80) and (83) from Minkowski to the Euclidean space, using standard conversion rules. Note that, once in Euclidean space, we will express the functional dependence of in terms of the squared momenta of the anti-ghost and gluon legs, and , and the angle, , between them, i.e., .
The result of these manipulations is that Equations (80) and (83) become
and
respectively, with
In the above equations, we employ the notation and , and define the following variables
Finally, the kernels and are given by
We are now in a position to solve Equations (87) and (88) numerically. We choose the renormalization point at GeV and employ for and the fits to the lattice data shown in Figure 9 and Figure 11, respectively. Note that for large momenta these fits recover the behaviors dictated by the corresponding anomalous dimensions [124]. For the strong coupling, we use the value , determined from the lattice simulations of [71].
Below, we discuss the main results of this analysis:
The value of was obtained by solving the SDE system for various values of this constant until the of the comparison between the solution for and the lattice data of [73,85] was minimized. This procedure yields .
In the left panel of Figure 13, we show as a blue continuous line the SDE result for , with the above value of . The result is compared to the lattice data of [73,85], which have been cured from discretization artifacts. As it turns out, the SDE and lattice results for F agree within .
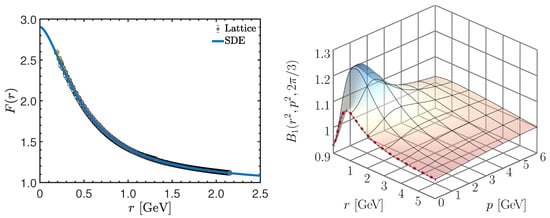
Figure 13.
(Left): ghost dressing function obtained from the coupled system of SDEs of Equations (80) and (83) (blue continuous line) compared to the lattice data of References [73,85]. (Right): The corresponding result for for arbitrary magnitudes of the anti-ghost and gluon momenta, r and p, respectively, and a representative value of for the angle between them. The red dot-dashed curve highlights the soft gluon limit ().
We next consider the form factor . In the right panel of Figure 13 we show as a surface, for arbitrary values of the magnitudes of the momenta r and p, and for the angle formed between them at . In the same panel, we highlight as a red dot-dashed curve the soft gluon limit of the general kinematics (The soft gluon limit is approached by taking in ; in the non-perturbative case, this limit is independent of the value of ).
The only available SU(3) lattice data for were obtained in the soft gluon limit [42,43], and have sizable error bars. Furthermore, they have been computed within the Taylor scheme, while in the present work, we used the asymmetric MOM scheme. Nevertheless, we can meaningfully compare our SDE results with those of the lattice, and perform a statistical analysis to assess their agreement.
Specifically, denoting by the Taylor scheme value of the form factor , it can easily be shown that
which allows us to carry out the desired comparison.
Then, we use Equation (90) to compute from the slice (red dot-dashed curve) in the right panel of Figure 13, and compare the result to the lattice data of [42,43] (points) in Figure 14. Evidently, the SDE determination agrees with the lattice results.
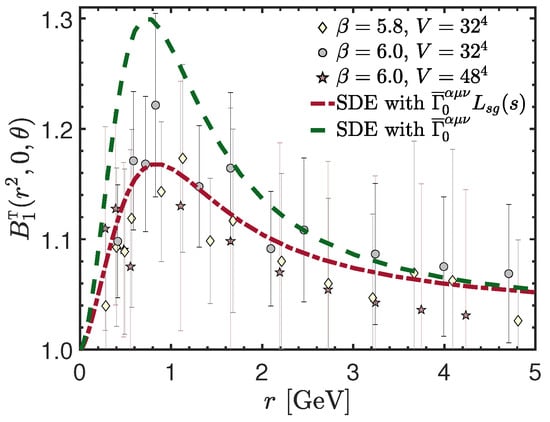
Figure 14.
Soft gluon limit, , of the classical form factor of the ghost–gluon vertex in the Taylor scheme. The points correspond to the lattice data of References [42,43]. The red dot-dashed line shows the SDE solution with the three-gluon vertex dressed according to Equation (78), while the green dashed represents the SDE solution with tree-level three-gluon vertex.
In order to quantify this agreement, we next conduct a analysis. To this end, we consider only the 22 lattice points in the interval GeV, where the signal is most pronounced. Then, we compute the of the data through
where are the lattice points shown in Figure 14, are their respective errors, and are the three hypotheses that we will compare to the lattice data. Specifically, for the we consider the three cases
i.e., is the tree-level value of , is the solution of the SDE using Equation (78) for dressing the three-gluon vertex, corresponding to the red dot-dashed curve of Figure 14, and is the solution of the SDE obtained by setting the three-gluon vertex to the tree level, which amounts to the substitution in Equation (88), and is represented by a green dashed curve in Figure 14.
Then, for each we compute the probability that normally distributed errors would yield a at least as large as , through
In the above equation, denotes the probability distribution function with n degrees of freedom, while is the incomplete function.
The results of the above analyses are collected in Table 2. We note that the case , i.e., the tree-level value of , is discarded at the confidence level. As for case , it is discarded at the level. On the other hand, the SDE result with dressed three-gluon vertex, , is statistically indistinguishable from the lattice data.

Table 2.
Statistical results of the analysis for the three hypotheses given in Equation (92) for the form factor . For each case (first column), we give the corresponding computed from Equation (91) (second column), probability computed from Equation (93) (third row), and the same expressed in terms of confidence levels (fourth row).
Lastly, we point out that for both F and , we find a good qualitative agreement with various related studies [21,29,178,179,224,226,227,228,278,279], including kinematics other than the soft gluon limit considered in Figure 14.
9. Divergent Ghost Loops and Their Impact on the QCD Green’s Functions
The masslessness of the ghost propagator, discussed in Section 8, has important implications for the infrared behavior of Green’s functions. Specifically, while the saturation of the gluon propagator renders gluon loops infrared finite, ghost loops furnish infrared divergent contributions [172], akin to those encountered in perturbation theory. In this section, we highlight (with two characteristic examples) how the effects of ghost loops manifest themselves at the level of the two- and three-point functions. Specifically, the ghost loops induce the appearance of a moderate maximum in the gluon propagator and are responsible for the zero-crossing and the logarithmic divergence at the origin displayed by the dominant form factors of the three-gluon vertex.
The basic observation at the level of the gluon SDE shown in Figure 1 is that, the ghost loop of , due to the masslessness of its ingredients, furnishes “unprotected” logarithms, i.e., terms of the type , which diverge as . Instead, gluonic loops contain infrared finite gluon propagators and, therefore, give rise to contributions that remain finite as , i.e., they may be described in terms of “protected” logarithms of the type .
The circumstances described above may be modeled by
where m is the gluon mass, the mass scale of QCD, and , , and are constants; note that
Differentiating Equation (94) with respect to , we obtain
The second term on the r.h.s. of Equation (95) is infrared divergent, and necessarily dominates the behavior of the derivative of the propagator for sufficiently small q. Moreover, the value of the coefficient can be computed explicitly by expanding the ghost block of Figure 1 around and using Equation (19), which yields
Therefore, has the asymptotic behavior
which diverges to as . Now, since the gluon propagator is a decreasing function in the ultraviolet, we have that is positive for large momenta. Therefore, there must exist a special momentum, denoted by , such that , which corresponds to a maximum of (Note that is an increasing function since it is negative in the infrared and positive in the ultraviolet, i.e., . Therefore, assuming that only crosses zero once, must be a maximum of ).
The maximum of , predicted by means of the simple arguments presented above, is observed in lattice simulations of the gluon propagator [49,56,85]. In particular, it is clearly visible in Figure 15, where the data from the two largest volume lattice setups of [49] are shown. The red dashed lines represent smooth functions, fitted to each of the data sets, in the window GeV. For each of the volumes considered, (left panel) and (right panel), the estimate obtained for is MeV.
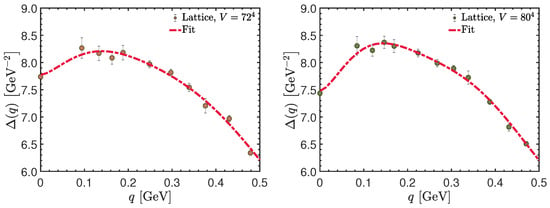
Figure 15.
Lattice data for the gluon propagator in the deep infrared. The data displayed correspond to the two lattice setups with the largest volumes of [49], namely, (left) and (right). The red dashed lines are smooth fits from which the position of the maximum can be estimated.
It is interesting to observe in passing that the existence of a maximum of has an interesting implication on the form of the spectral function of the gluon propagator [280,281,282,283,284,285]. In particular, the standard Källén-Lehmann representation [286,287] states that
where is the gluon spectral function (with a factor absorbed in it). Thus, the differentiation of both sides of Equation (98) with respect to yields
Then, from Equation (99) follows that the existence of a maximum for at leads necessarily to the violation of reflection positivity [11,167,168,171], because the condition
may be fulfilled only if reverses its sign. Note that an analogous argument based on the existence of an inflection point has been presented recently in [8].
Turning to the three-gluon vertex, it is well-known that the corresponding ghost loops induce characteristic features to the form factors associated with its classical (tree-level) tensors. There are two complementary continuum descriptions of the dynamics that determine the behavior of these form factors: the SDE of the three-gluon vertex [174,175,176,226], depicted diagrammatically in Figure 16, and the STI of Equation (23) [172], which, in the limit of vanishing gluon momentum, and when the displacement function and the ghost sector are neglected, yields the approximate WI
which transmits the properties of the propagator derivative to the vertex form factors, as shown schematically in Figure 17.
Figure 16.
The SDE of the three-gluon vertex at the one-loop dressed level. Diagrams and are the gluon and the ghost triangle contributions entering the skeleton expansion of the three-gluon vertex.
Figure 17.
The ghost triangle present in the three-gluon vertex SDE (top) and the ghost loop contributing to the gluon propagator in the corresponding equation (middle). The infrared divergences arising from these diagrams are connected through the Slavnov–Taylor identity (STI) of Equation (23), as shown schematically in the bottom panel.
In the simplified kinematic circumstances where only a single representative momentum is considered, to be denoted by r, the conclusions drawn by either method may be qualitatively described in terms of a simple model, namely
where denotes the particular combination of form factors, such that, at tree level, , and , , and are positive constants. The model in Equation (102) encompasses two important cases studied on the lattice [68,69,71,81], namely the soft gluon limit, , corresponding to the kinematic choice , defined in Equation (77), and totally symmetric limit, , corresponding to .
Upon inspection of Equation (102) we note that, as , the term with the unprotected logarithm will eventually dominate, forcing to reverse its sign (zero crossing), and finally display a logarithmic divergence, . Given that, in practice, is considerably larger than , the unprotected logarithm overtakes the protected one rather deep in the infrared: the location of the zero-crossing is at about 160 MeV [71]. Consequently, in the intermediate region of momenta, which is considered relevant for the onset of non-perturbative dynamics, we have ; this effect is known in the literature as the infrared suppression of the three-gluon vertex.
Most importantly, the special features of infrared suppression, zero-crossing, and logarithmic divergence at the origin have been corroborated through a variety of lattice results [50,68,69,71,72,81,84], as shown, e.g., in Figure 11. The central curve of this figure is presented as the blue line in Figure 18, where the aforementioned characteristics have been explicitly marked for the benefit of the reader. Note the close proximity of the blue curve to the (red dashed line), especially below 1 GeV.
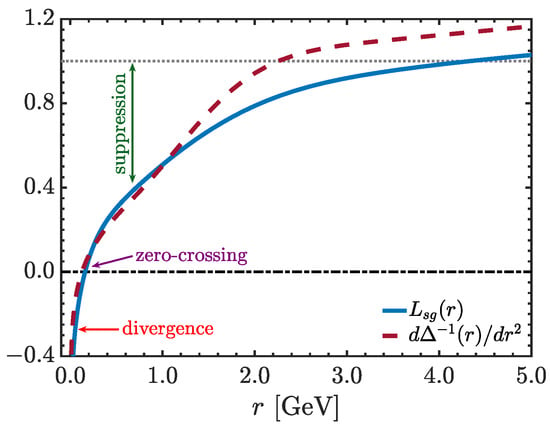
Figure 18.
Comparison of (blue continuous) from Figure 11 and (red dashed) resulting from the fit for of Figure 9. Note that both display the characteristic features of infrared suppression with respect to their tree-level values (which is 1 for both quantities), zero-crossing, and logarithmic divergence at the origin.
We end this section by pointing out that, in the case of Yang–Mills in [28,172,223,288,289,290,291,292,293,294,295,296,297,298,299,300,301,302], the situation is qualitatively similar to the one described above, but the divergences induced due to the masslessness of the ghost are stronger. Specifically, as may be already established at the level of a simple one-loop calculation [302], the first derivative of the gluon propagator diverges at the origin as rather than . Consequently, the corresponding effects are significantly enhanced; in particular, the maximum of the gluon propagator is considerably more pronounced, becoming plainly visible on the lattice [53]. Similarly, an abrupt negative divergence is observed in the corresponding vertex form factors [41,82].
10. Ward Identity Displacement of the Three-Gluon Vertex
In complete analogy to the case of the ghost–gluon vertex discussed in Section 5.2, the WI satisfied by the pole-free part of the three-gluon vertex is also displaced in the presence of longitudinally coupled massless poles. Quite importantly, the associated displacement function, , coincides with the BS amplitude that controls the formation of a (colored) scalar bound state with vanishing mass out of a gluon pair. The displacement of the WI circumvents the seagull cancellation involving the gluon propagator [ i.e., in Equation (55)], furnishing to the component the mass originating from graphs and in Figure 1. In addition, it permits the indirect determination of the displacement function from the lattice; this is particularly important, given that, by virtue of Equation (35), the lattice “observables” do not perceive directly the presence of the massless poles.
The starting point of the analysis is the STI satisfied by the three-gluon vertex, , given by Equation (23). In order to eliminate the poles in r and p, thus isolating the displacement of the WI originating from the pole in the channel q, we contract that equation with . Note that this procedure also eliminates any longitudinal pole terms in the ghost kernels and ; for the diagrammatic definition of the ghost–gluon kernel, see Figure 2.
Then, we decompose into pole-free and longitudinally coupled massless pole parts, as in Equation (33), and use Equation (38), to obtain
where
At this point, we expand Equation (103) around and match coefficients of equal orders. At the zeroth order in this expansion, we immediately obtain that
in exact analogy to Equation (62). Note that we have arrived once again at the result of Equation (39), but through an entirely different path: while Equation (39) is enforced by the Bose symmetry of the three-gluon vertex, Equation (105) is a direct consequence of the STI that this vertex satisfies.
We next gather the terms in the expansion of Equation (103) that are of first order in q. Evidently, the term does not contribute to this order. Then, the expansion leads to the appearance of derivatives of the gluon propagator, in analogy to Equation (64), but also of the ghost–gluon kernel. Specifically, we obtain for the WI of the three-gluon vertex and its displacement the expression
In the above equation, is the form factor of the three-gluon vertex defined in Equation (77) and with lattice results shown in Figure 11, while is a particular derivative of the ghost–gluon kernel, namely [124,241]
For the detailed derivation of Equation (106), we refer to [93,124].
In the following section, we will use Equation (106) to determine the displacement amplitude from lattice inputs. To this end, we must first pass to Euclidean space, where we note that
with the extra sign originating from the fact that is a derivative [see Equation (41)]. Then, suppressing the indices “” and solving for , we obtain the central relation
For the determination of , we use lattice inputs for all the quantities that appear on the r.h.s. of Equation (109), with the exception of the function , which will be computed from the SDE satisfied by the ghost–gluon kernel derived and analyzed in the next section.
11. The Ghost-Gluon Kernel Contribution to the Ward Identity
In this section, we derive the SDE that determines the key function ; the resulting SDE will be solved using lattice inputs for the various quantities entering it. In addition, the infrared behavior of will be analyzed in detail, following an analytic procedure.
Our discussion starts with the SDE of the ghost–gluon kernel, , shown diagrammatically in Figure 19, from which can be obtained using Equation (107).
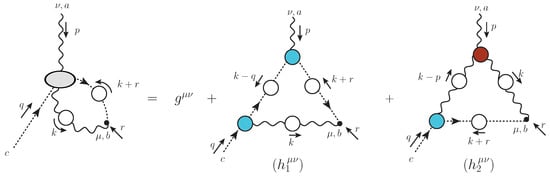
Figure 19.
SDE for the ghost–gluon scattering kernel, . We omit a diagram containing a 1PI four-point function.
Note that the similarity between the diagrams shown in Figure 19 and those in the bottom panel of Figure 12, depicting the SDE of the ghost–gluon vertex, is a simple reflection of the fundamental STI relating the ghost–gluon kernel with the ghost–gluon vertex,
Specifically, Equation (110) is preserved by the SDEs of and ; indeed, contraction of each diagram of Figure 19 by yields the corresponding diagram of Figure 12 (up to a shift of for , introduced to simplify certain expressions). Note that, in Figure 19, the diagram corresponding to the of Figure 12 has been omitted, for the reason explained in item (i) of Section 8.
It is well-known that, in the Landau gauge, the momentum q of the ghost field in factors out of its quantum corrections [1], allowing us to write [124,228,241]
where no particular assumptions are made about the structure of the function . Following Equation (107), we differentiate the r.h.s. of Equation (111) with respect to q and subsequently set , to obtain
Lastly, the finite renormalization of in the asymmetric MOM scheme proceeds through the use of Equation (15), which leads to the appearance of an overall factor of in the equations.
The outcome of the above steps is that can be written as
where the are the contributions originating from the diagrams in Figure 19, respectively, and read
where is given by Equation (81), and we define the specific contribution of the three-gluon vertex to the kernel of as
Note that, from Equation (115) and the Bose symmetry of the under the exchange , it follows that
At this point, by capitalizing on the planar degeneracy of discussed in Section 7, we obtain a compact, and yet accurate, approximation for . Specifically, using Equation (78), we find
where is the tree-level value of , given by
We remark that the approximation given by Equation (117) becomes exact in the limit .
Using the above approximation for , the contribution reads
where we now have .
Lastly, we transform of Equation (114) and of Equation (119) to Euclidean space to obtain the final expression to be used for the numerical determination of ,
where z has been defined below Equation (89) and
We emphasize that for the SDEs of both and , given by Equations (88) and (120), respectively, we used the same approximation for the three-gluon vertex, namely Equation (78). Therefore, our analyses of and are self-consistent, in the sense that the STI in Equation (110) is strictly preserved.
Before embarking on the numerical determination of for the entire range of Euclidean momenta, we discuss the infrared behavior of this function and demonstrate an important self-consistency proof involving .
Specifically, as discussed in Section 9, the and that appear in Equation (109) are infrared divergent, due to the massless ghost loops present in their SDEs. Nevertheless, the BSE solutions for the amplitude are all found to be finite at , (cf. Figure 7) [117,121,124,215]. Therefore, in order for the WI displacement of Equation (109) to be consistent with the finite obtained from BSE solutions, the infrared divergences of the ingredients appearing in Equation (109) must cancel against each other.
Indeed, a careful analysis of diagram of Figure 16 yields
up to infrared finite terms (We note that the results identical to Equations (97) and (122) for the infrared divergences of and , respectively, have been previously derived within the Curci–Ferrari model [180]). Then, assuming that only and diverge, and using the asymptotic form of given in Equation (97) to Equation (109), we find that the divergences do not fully cancel. Therefore, the finiteness of demands that the term appearing in the WI must be infrared divergent.
Now, it is evident from Equation (120) that vanishes as . Nevertheless, the ratio is found to diverge at the origin. Specifically, expanding Equation (120) around , it can be shown that has the asymptotic behavior
Then, combining Equations (97), (122) and (123) we find that the infrared divergences in Equation (109) cancel out exactly, leaving a finite , in full agreement with the BSE results.
We finish the discussion of the infrared finiteness of with a remark. In the absence of the Schwinger mechanism, i.e., for an identically zero , the infrared divergences of , , and must also cancel in Equation (109). For instance, this cancellation can be explicitly verified at the one-loop level (in the perturbative realization of Equation (109) also diverges, participating in the overall cancellation of infrared divergences), where, evidently, . In that case, however, the gluon propagator is also massless, causing the gluonic loops that contribute to the functions that enter Equation (109) to also diverge, such that the cancellation occurs among all radiative diagrams. In contrast, in the presence of a gluon mass, the cancellation of the remaining infrared divergences takes place at the level of the ghost loops only, as illustrated diagrammatically in Figure 20.
Figure 20.
Diagrammatic representation of the cancellation of the infrared divergences originating from massless ghost loops in Equation (109) to yield a finite . The red cross indicates that the overall ghost momentum is factored out before being set to zero.
We now return to the numerical determination of from Equation (120). To this end, we employ the fits to the lattice data of [84] for and , shown in Figure 9 and Figure 11, respectively, and the SDE solution for is shown in the left panel of Figure 13. All of the fits employed are constructed so as to reproduce the correct ultraviolet behavior of Green’s functions. For the value of the coupling in the asymmetric MOM scheme, defined in Appendix B, we employ , with , as determined in the lattice study of [71]. Lastly, for we use the SDE result of Section 8, shown in the right panel of Figure 13, which reproduces accurately the available lattice data for the ghost–gluon vertex.
Using the above ingredients in Equation (120) we obtain the shown as the blue solid curve in Figure 21. The blue band in Figure 21 represents the error estimate on our results; the procedures followed to obtain it are described in detail in [126].
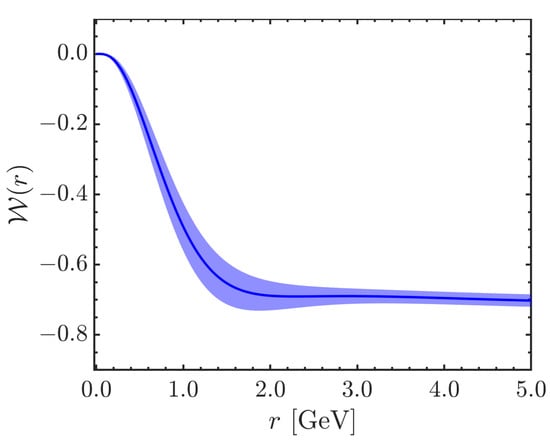
Figure 21.
obtained using the approximation Equation (117) based on the observed planar degeneracy of the three-gluon vertex in its kernel (blue solid curve) together with uncertainty estimate (blue band).
12. Displacement Function from Lattice Inputs
In this section, we determine from the main relation given in Equation (109).
For we use the result shown in Figure 21, together with the curves for from Figure 11, and from Figure 9 and Figure 18, respectively, and the of Figure 13. The obtained is shown as a black solid curve in the left panel of Figure 22. In the same panel, we show as points the estimates of obtained by using into Equation (109) the lattice data points of [84] directly, rather than a fit. Note that these data points, as well as those used for the propagators [85], have been carefully extrapolated to the continuum, through the methods explained in [73,85]. These methods exploit the symmetry of the hypercubic lattice, and are quite effective at minimizing discretization artifacts [54,60,62,63,70,71,73,76,80,85]. As a result of this treatment, the systematic errors are expected to be small. To estimate the uncertainty in the resulting , we combine the error estimate of , represented by the blue band in Figure 21, with the statistical error of the lattice data points for of [84], and neglect the error in the gluon propagator, which is much smaller than the errors in and . Then, a conservative error propagation analysis was carried out in [126], which takes into account an observed correlation between the errors in and ; the results of the analysis are the error bars shown in Figure 22.
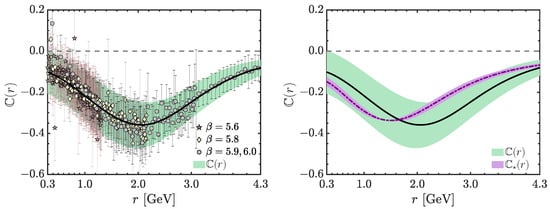
Figure 22.
Left: Result for (black continuous line) obtained from Equation (109) using the shown in Figure 21, the fits to lattice data for and are shown in Figure 9 and Figure 18, respectively, and the SDE solution for shown in Figure 13. The points are obtained using for the data in Reference [84], with error bars denoting the error propagated from and . The green band is obtained by fitting the upper and lower bounds of the points and guiding the eye to the typical error associated with . Right: The of the left panel is compared to the BSE prediction (purple dot-dashed and error band) of Figure 7.
At this point, we quantify the significance of the obtained above, in comparison to the null hypothesis result; evidently, in the absence of the Schwinger mechanism, this latter quantity, to be denoted by in what follows, vanishes identically, namely . To this end, we first compute the of our points as
i.e., the null hypothesis is taken as the estimator for our data. The sum runs over the indices i such that GeV, the interval of momenta for which the systematic error in our calculation of is best known, and denotes the error estimate of . Then we obtain , corresponding to . The probability that our result for is consistent with the null hypothesis s vanishingly small, given by the formula
Naturally, further correlations in the input data, as well as residual systematic errors, may have escaped the analysis leading to the error estimates shown in Figure 7 for . Since changes rapidly with , these unknown errors can substantially alter its value. As such, Equation (125) is to be understood as meaning that in the absence of additional uncertainties, the null hypothesis is excluded. Moreover, it is apparent in Figure 22 that even if the errors had been significantly underestimated, the null hypothesis would still be unlikely. In fact, even if the errors in all data points for were larger, i.e., nearly doubled, we could still discard at the confidence level.
In the right panel of Figure 22, we compare to the BSE prediction, , of Figure 7, shown as a purple dot-dashed curve and corresponding error band. In that panel, we observe an excellent qualitative agreement between the two results. The most noticeable quantitative difference is in the position of the minimum. Specifically, reaches the minimum value of at GeV, while the minimum of is at .
Nevertheless, it is clear in the right panel of Figure 22 that the BSE prediction lies within the error estimate of the lattice-derived . In fact, defining a measure for the discrepancy between and as
we obtain , which is smaller than the number of degrees of freedom. Then, this value of amounts to a probability of
showing that is statistically compatible with the lattice-derived , with probability extremely near the unit.
13. Conclusions
The gauge sector of QCD is host to a wide array of subtle mechanisms that are of vital importance for the self-consistency and infrared stability of the theory. In the present work, we offered a comprehensive review of the intricate dynamics that account for some of the most prominent infrared phenomena, such as the generation of a gluon mass through the action of the Schwinger mechanism, the non-perturbative masslessness of the ghost, and the characteristic features induced by this particular mass pattern to the form factors of the three-gluon vertex.
The SDEs, supplemented by the judicious use of certain key results from lattice QCD, provide a robust continuum framework for carrying out such a demanding investigation. In fact, the results obtained from the SDEs are increasingly reliable, passing successfully all sorts of tests imposed on them. A particularly impressive, and certainly not isolated, case of such a success has been outlined in detail in Section 6.
Symmetry and dynamics are tightly interwoven; therefore, the information encoded in the STIs and WIs of the theory is particularly decisive for unraveling basic dynamical patterns. A striking manifestation of the profound connection between symmetry and dynamics is provided by the dual role played by the function , i.e., the BS amplitudes of the massless states composed by a pair of gluons, and the quantity that embodies the displacement induced to the WIs by the presence of these states.
In our opinion, the determination of described in Section 12 represents a major success of the entire set of concepts and techniques surrounding the generation of a gluon mass through the action of the Schwinger mechanism. Thus, fifty years after the genesis of QCD, we seem to be closing in on the mechanism that the theory uses for curing the infrared instabilities endemic to perturbation theory. We hope to be able to report further progress in this direction in the near future.
Funding
The authors are supported by the Spanish MICINN grant PID2020-113334GB-I00. M.N.F. acknowledges financial support from Generalitat Valenciana through contract CIAPOS/2021/74. J.P. also acknowledges funding from the regional Prometeo/2019/087 from Generalitat Valenciana.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank A.C. Aguilar, D. Binosi, D. Ibá nez, J. Pawlowski, C.D. Roberts, and J. Rodríguez-Quintero for the collaborations.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this work:
| BFM | background field method |
| BQI | background-quantum identity |
| BRST | Becchi–Rouet–Stora–Tyutin |
| BS | Bethe–Salpeter |
| BSE | Bethe–Salpeter equation |
| EHM | emergent hadron mass |
| MOM | momentum subtraction (renormalization scheme) |
| PT | pinch technique |
| QCD | quantum chromodynamics |
| QED | quantum electrodynamics |
| RGI | renormalization group invariant |
| SDE | Schwinger–Dyson equation |
| STI | Slavnov–Taylor identity |
| WI | Ward identity |
Appendix A. BQIs for the BSE Amplitudes
In this appendix, we use two BQIs in order to relate the displacement functions ( and ) with their BFM counterparts, i.e., and , respectively.
The ghost–gluon vertices and are related via a BQI [14], which reads
where and are two auxiliary functions, shown diagrammatically in Figure A1, while and are the form factors of , defined in Equation (12).
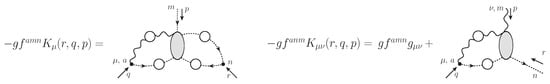
Figure A1.
The auxiliary functions and in the BQI of Equation (A1).
Next, we decompose the and in Equation (A1) into their regular and pole parts, using Equations (33) and (53), respectively. Note that the second and third terms in Equation (A1) do not contain poles in ; this is so because can contain (longitudinally coupled) poles only in the channel, whereas has no external gluon legs (and, hence, no poles).
Then, multiplying Equation (A1) by we obtain
Setting in Equation (A2) and using Equation (18), we find
Hence, using Equation (62), we obtain the result in Equation (39).
Then, expanding Equation (A2) to first order in q, using Equation (41) for and Equation (63) for , entails
which is one of the main results of this appendix.
A relation identical to Equation (A4) can be obtained for and its BFM analog, . The starting point of the derivation is the BQI [14]
where is the function defined in Equation (111).
Then, we note that the only longitudinal poles at present in Equation (A5) are those contained in the and vertices, with the auxiliary functions having poles only in the and channels. As such, isolating the pole and expanding around , one eventually finds
and
where and are defined in analogy to Equations (37) and (41), and we used Equation (39).
Appendix B. The Asymmetric MOM Scheme
In this appendix, we provide a brief overview of the asymmetric MOM scheme [68,71,84,85,241] that we employ throughout this work.
The set of boundary conditions imposed on the renormalized quantities defines the renormalization scheme employed. Within the MOM schemes [277], propagators assume their tree-level values at the subtraction point , namely
Past this point, the various MOM schemes are differentiated according to the way the three-point functions are renormalized.
In Landau gauge, a common choice of renormalization prescription is the so-called “Taylor scheme” [54,60,80,85,207]. This scheme capitalizes on the Taylor theorem [207], i.e., the observation that the unrenormalized ghost–gluon vertex in the Landau gauge reduces to its tree-level form in the soft-ghost configuration,
The Taylor scheme is defined by requiring Equation (A9) to hold after renormalization [54,60,80,85,207]. Using Equation (15), this requirement yields .
Alternatively, in lattice simulations of the three-gluon vertex, it is convenient to impose a renormalization prescription for its classical tensor structure. For example, one may choose the classical form factor to reduce to tree-level in the symmetric point, . This condition defines the “symmetric scheme” [68,71,84].
In the present work, the classical form factor of the three-gluon vertex in the soft-gluon limit, which is denoted by and defined in Equation (77), plays a key role. Indeed, it is the central ingredient in the approximation of the three-gluon vertex given by Equation (78), which is used in the SDE analysis of the ghost–gluon vertex and kernel in Section 8 and Section 11, respectively. Moreover, is one of the inputs necessary for the determination of the displacement amplitude in Section 12, which signals the activation of the Schwinger mechanism. As such, it is convenient to employ throughout the scheme where is most readily renormalized in lattice simulations, which is the so-called “asymmetric scheme” [68,71,84,85,241].
The asymmetric MOM scheme is defined by imposing that reduces to the tree-level at , i.e.,
Note that in this scheme the finite renormalization constant of the ghost–gluon vertex is no longer equal to 1 [85,241]. Instead, the special value of in the asymmetric scheme is denoted by , and is determined to be [126], at GeV, through the SDE analysis discussed in Section 8.
References
- Marciano, W.J.; Pagels, H. Quantum Chromodynamics: A Review. Phys. Rep. 1978, 36, 137. [Google Scholar] [CrossRef]
- Qin, S.X.; Roberts, C.D. Impressions of the Continuum Bound State Problem in QCD. Chin. Phys. Lett. 2020, 37, 121201. [Google Scholar] [CrossRef]
- Roberts, C.D. Empirical Consequences of Emergent Mass. Symmetry 2020, 12, 1468. [Google Scholar] [CrossRef]
- Cui, Z.F.; Ding, M.; Gao, F.; Raya, K.; Binosi, D.; Chang, L.; Roberts, C.D.; Rodríguez-Quintero, J.; Schmidt, S.M. Kaon and pion parton distributions. Eur. Phys. J. C 2020, 80, 1064. [Google Scholar] [CrossRef]
- Chang, L.; Roberts, C.D. Regarding the Distribution of Glue in the Pion. Chin. Phys. Lett. 2021, 38, 081101. [Google Scholar] [CrossRef]
- Cui, Z.F.; Ding, M.; Morgado, J.M.; Raya, K.; Binosi, D.; Chang, L.; De Soto, F.; Roberts, C.D.; Rodríguez-Quintero, J.; Schmidt, S.M. Emergence of pion parton distributions. Phys. Rev. D 2022, 105, L091502. [Google Scholar]
- Lu, Y.; Chang, L.; Raya, K.; Roberts, C.D.; Rodríguez-Quintero, J. Proton and pion distribution functions in counterpoint. Phys. Lett. B 2022, 830, 137130. [Google Scholar] [CrossRef]
- Ding, M.; Roberts, C.D.; Schmidt, S.M. Emergence of Hadron Mass and Structure. Particles 2023, 6, 57–120. [Google Scholar] [CrossRef]
- Roberts, C.D. Origin of the Proton Mass. arXiv 2022, arXiv:2211.09905. [Google Scholar]
- Roberts, C.D.; Williams, A.G. Dyson-Schwinger equations and their application to hadronic physics. Prog. Part. Nucl. Phys. 1994, 33, 477–575. [Google Scholar] [CrossRef]
- Alkofer, R.; von Smekal, L. The Infrared behavior of QCD Green’s functions: Confinement dynamical symmetry breaking, and hadrons as relativistic bound states. Phys. Rep. 2001, 353, 281. [Google Scholar] [CrossRef]
- Fischer, C.S. Infrared properties of QCD from Dyson-Schwinger equations. J. Phys. G 2006, 32, R253–R291. [Google Scholar] [CrossRef]
- Roberts, C.D. Hadron Properties and Dyson-Schwinger Equations. Prog. Part. Nucl. Phys. 2008, 61, 50–65. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. Pinch Technique: Theory and Applications. Phys. Rep. 2009, 479, 1–152. [Google Scholar] [CrossRef]
- Bashir, A.; Chang, L.; Cloet, I.C.; El-Bennich, B.; Liu, Y.X.; Roberts, C.D.; Tandy, P.C. Collective perspective on advances in Dyson-Schwinger Equation QCD. Commun. Theor. Phys. 2012, 58, 79–134. [Google Scholar] [CrossRef]
- Binosi, D.; Chang, L.; Papavassiliou, J.; Roberts, C.D. Bridging a gap between continuum-QCD and ab initio predictions of hadron observables. Phys. Lett. 2015, B742, 183–188. [Google Scholar] [CrossRef]
- Cloet, I.C.; Roberts, C.D. Explanation and Prediction of Observables using Continuum Strong QCD. Prog. Part. Nucl. Phys. 2014, 77, 1–69. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. The Gluon Mass Generation Mechanism: A Concise Primer. Front. Phys. (Beijing) 2016, 11, 111203. [Google Scholar] [CrossRef]
- Binosi, D.; Chang, L.; Papavassiliou, J.; Qin, S.X.; Roberts, C.D. Symmetry preserving truncations of the gap and Bethe–Salpeter equations. Phys. Rev. 2016, D93, 096010. [Google Scholar] [CrossRef]
- Binosi, D.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D.; Rodriguez-Quintero, J. Process-independent strong running coupling. Phys. Rev. 2017, D96, 054026. [Google Scholar] [CrossRef]
- Huber, M.Q. Nonperturbative properties of Yang-Mills theories. Phys. Rep. 2020, 879, 1–92. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Litim, D.F.; Nedelko, S.; von Smekal, L. Infrared behavior and fixed points in Landau gauge QCD. Phys. Rev. Lett. 2004, 93, 152002. [Google Scholar] [CrossRef] [PubMed]
- Pawlowski, J.M. Aspects of the functional renormalisation group. Ann. Phys. 2007, 322, 2831–2915. [Google Scholar] [CrossRef]
- Fischer, C.S.; Maas, A.; Pawlowski, J.M. On the infrared behavior of Landau gauge Yang-Mills theory. Ann. Phys. 2009, 324, 2408–2437. [Google Scholar] [CrossRef]
- Carrington, M.E. Renormalization group flow equations connected to the n-particle-irreducible effective action. Phys. Rev. 2013, D87, 045011. [Google Scholar] [CrossRef]
- Carrington, M.E.; Fu, W.J.; Pickering, D.; Pulver, J.W. Renormalization group methods and the 2PI effective action. Phys. Rev. D 2015, 91, 025003. [Google Scholar] [CrossRef]
- Cyrol, A.K.; Mitter, M.; Pawlowski, J.M.; Strodthoff, N. Nonperturbative quark, gluon, and meson correlators of unquenched QCD. Phys. Rev. 2018, D97, 054006. [Google Scholar] [CrossRef]
- Corell, L.; Cyrol, A.K.; Mitter, M.; Pawlowski, J.M.; Strodthoff, N. Correlation functions of three-dimensional Yang-Mills theory from the FRG. SciPost Phys. 2018, 5, 066. [Google Scholar] [CrossRef]
- Huber, M.Q. Correlation functions of Landau gauge Yang-Mills theory. Phys. Rev. D 2020, 101, 114009. [Google Scholar] [CrossRef]
- Dupuis, N.; Canet, L.; Eichhorn, A.; Metzner, W.; Pawlowski, J.M.; Tissier, M.; Wschebor, N. The nonperturbative functional renormalization group and its applications. Phys. Rep. 2021, 910, 1–114. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Pawlowski, J.M.; Reinosa, U. Functional renormalization group and 2PI effective action formalism. Ann. Phys. 2021, 431, 168549. [Google Scholar] [CrossRef]
- Mandula, J.; Ogilvie, M. The Gluon Is Massive: A Lattice Calculation of the Gluon Propagator in the Landau Gauge. Phys. Lett. B 1987, 185, 127–132. [Google Scholar] [CrossRef]
- Parrinello, C. Exploratory study of the three gluon vertex on the lattice. Phys. Rev. 1994, D50, R4247–R4251. [Google Scholar] [CrossRef] [PubMed]
- Alles, B.; Henty, D.; Panagopoulos, H.; Parrinello, C.; Pittori, C.; Richards, D.G. αs from the nonperturbatively renormalised lattice three gluon vertex. Nucl. Phys. 1997, B502, 325–342. [Google Scholar] [CrossRef]
- Parrinello, C.; Richards, D.; Alles, B.; Panagopoulos, H.; Pittori, C. Status of alpha-s determinations from the nonperturbatively renormalized three gluon vertex. Nucl. Phys. B Proc. Suppl. 1998, 63, 245–247. [Google Scholar] [CrossRef]
- Boucaud, P.; Leroy, J.P.; Micheli, J.; Pene, O.; Roiesnel, C. Lattice calculation of alpha(s) in momentum scheme. J. High Energy Phys. 1998, 10, 017. [Google Scholar] [CrossRef]
- Alexandrou, C.; de Forcrand, P.; Follana, E. The gluon propagator without lattice Gribov copies on a finer lattice. Phys. Rev. 2002, D65, 114508. [Google Scholar] [CrossRef]
- Bowman, P.O.; Heller, U.M.; Williams, A.G. Lattice quark propagator with staggered quarks in Landau and Laplacian gauges. Phys. Rev. D 2002, 66, 014505. [Google Scholar] [CrossRef]
- Skullerud, J.I.; Bowman, P.O.; Kizilersu, A.; Leinweber, D.B.; Williams, A.G. Nonperturbative structure of the quark gluon vertex. J. High Energy Phys. 2003, 4, 047. [Google Scholar] [CrossRef]
- Bowman, P.O.; Heller, U.M.; Leinweber, D.B.; Parappilly, M.B.; Williams, A.G. Unquenched gluon propagator in Landau gauge. Phys. Rev. D 2004, 70, 034509. [Google Scholar] [CrossRef]
- Cucchieri, A.; Maas, A.; Mendes, T. Exploratory study of three-point Green’s functions in Landau-gauge Yang-Mills theory. Phys. Rev. 2006, D74, 014503. [Google Scholar] [CrossRef]
- Ilgenfritz, E.M.; Muller-Preussker, M.; Sternbeck, A.; Schiller, A.; Bogolubsky, I. Landau gauge gluon and ghost propagators from lattice QCD. Braz. J. Phys. 2007, 37, 193–200. [Google Scholar] [CrossRef]
- Sternbeck, A. The Infrared Behavior of Lattice QCD Green’s Functions. Ph.D. Thesis, Humboldt-University Berlin, Berlin, Germany, 2006. [Google Scholar]
- Furui, S.; Nakajima, H. Unquenched Kogut-Susskind quark propagator in lattice Landau gauge QCD. Phys. Rev. D 2006, 73, 074503. [Google Scholar] [CrossRef]
- Bowman, P.O.; Heller, U.M.; Leinweber, D.B.; Parappilly, M.B.; Sternbeck, A.; von Smekal, L.; Williams, A.G.; Zhang, J.b. Scaling behavior and positivity violation of the gluon propagator in full QCD. Phys. Rev. D 2007, 76, 094505. [Google Scholar] [CrossRef]
- Kamleh, W.; Bowman, P.O.; Leinweber, D.B.; Williams, A.G.; Zhang, J. Unquenching effects in the quark and gluon propagator. Phys. Rev. 2007, D76, 094501. [Google Scholar] [CrossRef]
- Cucchieri, A.; Mendes, T. What’s up with IR gluon and ghost propagators in Landau gauge? A puzzling answer from huge lattices. PoS 2007, LATTICE2007, 297. [Google Scholar] [CrossRef]
- Cucchieri, A.; Mendes, T. Constraints on the IR behavior of the gluon propagator in Yang-Mills theories. Phys. Rev. Lett. 2008, 100, 241601. [Google Scholar] [CrossRef]
- Bogolubsky, I.; Ilgenfritz, E.; Muller-Preussker, M.; Sternbeck, A. The Landau gauge gluon and ghost propagators in 4D SU(3) gluodynamics in large lattice volumes. PoS 2007, LATTICE2007, 290. [Google Scholar] [CrossRef]
- Cucchieri, A.; Maas, A.; Mendes, T. Three-point vertices in Landau-gauge Yang-Mills theory. Phys. Rev. 2008, D77, 094510. [Google Scholar] [CrossRef]
- Cucchieri, A.; Mendes, T. Constraints on the IR behavior of the ghost propagator in Yang-Mills theories. Phys. Rev. D 2008, 78, 094503. [Google Scholar] [CrossRef]
- Cucchieri, A.; Mendes, T. Landau-gauge propagators in Yang-Mills theories at beta = 0: Massive solution versus conformal scaling. Phys. Rev. 2010, D81, 016005. [Google Scholar] [CrossRef]
- Cucchieri, A.; Mendes, T. Numerical test of the Gribov-Zwanziger scenario in Landau gauge. PoS 2009, QCD-TNT09, 026. [Google Scholar] [CrossRef]
- Boucaud, P.; De Soto, F.; Leroy, J.P.; Le Yaouanc, A.; Micheli, J.; Pene, O.; Rodriguez-Quintero, J. Ghost-gluon running coupling, power corrections and the determination of Lambda(MS-bar). Phys. Rev. 2009, D79, 014508. [Google Scholar]
- Cucchieri, A.; Mendes, T.; Santos, E.M.S. Covariant gauge on the lattice: A New implementation. Phys. Rev. Lett. 2009, 103, 141602. [Google Scholar] [CrossRef]
- Bogolubsky, I.; Ilgenfritz, E.; Muller-Preussker, M.; Sternbeck, A. Lattice gluodynamics computation of Landau gauge Green’s functions in the deep infrared. Phys. Lett. 2009, B676, 69–73. [Google Scholar] [CrossRef]
- Oliveira, O.; Silva, P. The Lattice infrared Landau gauge gluon propagator: The Infinite volume limit. PoS 2009, LAT2009, 226. [Google Scholar] [CrossRef]
- Cucchieri, A.; Mendes, T.; Nakamura, G.M.; Santos, E.M.S. Gluon Propagators in Linear Covariant Gauge. PoS 2010, FACESQCD, 026. [Google Scholar] [CrossRef]
- Oliveira, O.; Bicudo, P. Running Gluon Mass from Landau Gauge Lattice QCD Propagator. J. Phys. G 2011, G38, 045003. [Google Scholar] [CrossRef]
- Blossier, B.; Boucaud, P.; De soto, F.; Morenas, V.; Gravina, M.; Pene, O.; Rodriguez-Quintero, J. Ghost-gluon coupling, power corrections and from twisted-mass lattice QCD at Nf = 2. Phys. Rev. D 2010, 82, 034510. [Google Scholar] [CrossRef]
- Maas, A. Describing gauge bosons at zero and finite temperature. Phys. Rep. 2013, 524, 203–300. [Google Scholar] [CrossRef]
- Boucaud, P.; Leroy, J.P.; Yaouanc, A.L.; Micheli, J.; Pene, O.; Rodriguez-Quintero, J. The Infrared Behaviour of the Pure Yang-Mills Green Functions. Few Body Syst. 2012, 53, 387–436. [Google Scholar] [CrossRef]
- Ayala, A.; Bashir, A.; Binosi, D.; Cristoforetti, M.; Rodriguez-Quintero, J. Quark flavour effects on gluon and ghost propagators. Phys. Rev. 2012, D86, 074512. [Google Scholar] [CrossRef]
- Oliveira, O.; Silva, P.J. The lattice Landau gauge gluon propagator: Lattice spacing and volume dependence. Phys. Rev. 2012, D86, 114513. [Google Scholar] [CrossRef]
- Sternbeck, A.; Müller-Preussker, M. Lattice evidence for the family of decoupling solutions of Landau gauge Yang-Mills theory. Phys. Lett. B 2013, 726, 396–403. [Google Scholar] [CrossRef]
- Bicudo, P.; Binosi, D.; Cardoso, N.; Oliveira, O.; Silva, P.J. Lattice gluon propagator in renormalizable ξ gauges. Phys. Rev. 2015, D92, 114514. [Google Scholar] [CrossRef]
- Duarte, A.G.; Oliveira, O.; Silva, P.J. Lattice Gluon and Ghost Propagators, and the Strong Coupling in Pure SU(3) Yang-Mills Theory: Finite Lattice Spacing and Volume Effects. Phys. Rev. D 2016, 94, 014502. [Google Scholar] [CrossRef]
- Athenodorou, A.; Binosi, D.; Boucaud, P.; De Soto, F.; Papavassiliou, J.; Rodriguez-Quintero, J.; Zafeiropoulos, S. On the zero crossing of the three-gluon vertex. Phys. Lett. 2016, B761, 444–449. [Google Scholar] [CrossRef]
- Duarte, A.G.; Oliveira, O.; Silva, P.J. Further Evidence For Zero Crossing On The Three Gluon Vertex. Phys. Rev. 2016, D94, 074502. [Google Scholar] [CrossRef]
- Oliveira, O.; Kizilersu, A.; Silva, P.J.; Skullerud, J.I.; Sternbeck, A.; Williams, A.G. Lattice Landau gauge quark propagator and the quark-gluon vertex. Acta Phys. Pol. Suppl. 2016, 9, 363–368. [Google Scholar] [CrossRef]
- Boucaud, P.; De Soto, F.; Rodríguez-Quintero, J.; Zafeiropoulos, S. Refining the detection of the zero crossing for the three-gluon vertex in symmetric and asymmetric momentum subtraction schemes. Phys. Rev. 2017, D95, 114503. [Google Scholar] [CrossRef]
- Sternbeck, A.; Balduf, P.H.; Kizilersu, A.; Oliveira, O.; Silva, P.J.; Skullerud, J.I.; Williams, A.G. Triple-gluon and quark-gluon vertex from lattice QCD in Landau gauge. PoS 2017, LATTICE2016, 349. [Google Scholar] [CrossRef]
- Boucaud, P.; De Soto, F.; Raya, K.; Rodríguez-Quintero, J.; Zafeiropoulos, S. Discretization effects on renormalized gauge-field Green’s functions, scale setting, and the gluon mass. Phys. Rev. 2018, D98, 114515. [Google Scholar] [CrossRef]
- Cucchieri, A.; Dudal, D.; Mendes, T.; Oliveira, O.; Roelfs, M.; Silva, P.J. Lattice Computation of the Ghost Propagator in Linear Covariant Gauges. PoS 2018, LATTICE2018, 252. [Google Scholar] [CrossRef]
- Cucchieri, A.; Dudal, D.; Mendes, T.; Oliveira, O.; Roelfs, M.; Silva, P.J. Faddeev-Popov Matrix in Linear Covariant Gauge: First Results. Phys. Rev. D 2018, 98, 091504. [Google Scholar] [CrossRef]
- Oliveira, O.; Silva, P.J.; Skullerud, J.I.; Sternbeck, A. Quark propagator with two flavors of O(a)-improved Wilson fermions. Phys. Rev. D 2019, 99, 094506. [Google Scholar] [CrossRef]
- Dudal, D.; Oliveira, O.; Silva, P.J. High precision statistical Landau gauge lattice gluon propagator computation vs. the Gribov–Zwanziger approach. Ann. Phys. 2018, 397, 351–364. [Google Scholar] [CrossRef]
- Vujinovic, M.; Mendes, T. Probing the tensor structure of lattice three-gluon vertex in Landau gauge. Phys. Rev. 2019, D99, 034501. [Google Scholar] [CrossRef]
- Cui, Z.F.; Zhang, J.L.; Binosi, D.; de Soto, F.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D.; Rodríguez-Quintero, J.; Segovia, J.; Zafeiropoulos, S. Effective charge from lattice QCD. Chin. Phys. C 2020, 44, 083102. [Google Scholar] [CrossRef]
- Zafeiropoulos, S.; Boucaud, P.; De Soto, F.; Rodríguez-Quintero, J.; Segovia, J. Strong Running Coupling from the Gauge Sector of Domain Wall Lattice QCD with Physical Quark Masses. Phys. Rev. Lett. 2019, 122, 162002. [Google Scholar] [CrossRef]
- Aguilar, A.C.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J.; Zafeiropoulos, S. Gluon propagator and three-gluon vertex with dynamical quarks. Eur. Phys. J. 2020, C80, 154. [Google Scholar] [CrossRef]
- Maas, A.; Vujinović, M. More on the three-gluon vertex in SU(2) Yang-Mills theory in three and four dimensions. SciPost Phys. Core 2022, 5, 019. [Google Scholar] [CrossRef]
- Kızılersü, A.; Oliveira, O.; Silva, P.J.; Skullerud, J.I.; Sternbeck, A. Quark-gluon vertex from Nf = 2 lattice QCD. Phys. Rev. D 2021, 103, 114515. [Google Scholar] [CrossRef]
- Aguilar, A.C.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J. Infrared facets of the three-gluon vertex. Phys. Lett. B 2021, 818, 136352. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ambrósio, C.O.; De Soto, F.; Ferreira, M.N.; Oliveira, B.M.; Papavassiliou, J.; Rodríguez-Quintero, J. Ghost dynamics in the soft gluon limit. Phys. Rev. D 2021, 104, 054028. [Google Scholar] [CrossRef]
- Pinto-Gómez, F.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J. Lattice three-gluon vertex in extended kinematics: Planar degeneracy. Phys. Lett. B 2023, 838, 137737. [Google Scholar] [CrossRef]
- Pinto-Gomez, F.; de Soto, F. Three-gluon vertex in Landau-gauge from quenched-lattice QCD in general kinematics. In Proceedings of the 15th Conference on Quark Confinement and the Hadron Spectrum, Stavanger, Norway, 1–6 August 2022. [Google Scholar]
- Pinto-Gómez, F.; de Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Rodríguez-Quintero, J. General kinematics of the three-gluon vertex from quenched lattice QCD. arXiv 2022, arXiv:2212.11894. [Google Scholar]
- Roberts, C.D.; Schmidt, S.M. Reflections upon the emergence of hadronic mass. Eur. Phys. J. ST 2020, 229, 3319–3340. [Google Scholar] [CrossRef]
- Roberts, C.D. On Mass and Matter. AAPPS Bull. 2021, 31, 6. [Google Scholar] [CrossRef]
- Roberts, C.D.; Richards, D.G.; Horn, T.; Chang, L. Insights into the emergence of mass from studies of pion and kaon structure. Prog. Part. Nucl. Phys. 2021, 120, 103883. [Google Scholar] [CrossRef]
- Binosi, D. Emergent Hadron Mass in Strong Dynamics. Few Body Syst. 2022, 63, 42. [Google Scholar] [CrossRef]
- Papavassiliou, J. Emergence of mass in the gauge sector of QCD*. Chin. Phys. C 2022, 46, 112001. [Google Scholar] [CrossRef]
- Cornwall, J.M. Quark Confinement and Vortices in Massive Gauge Invariant QCD. Nucl. Phys. 1979, B157, 392. [Google Scholar] [CrossRef]
- Parisi, G.; Petronzio, R. On Low-Energy Tests of QCD. Phys. Lett. 1980, B94, 51. [Google Scholar] [CrossRef]
- Cornwall, J.M. Dynamical Mass Generation in Continuum QCD. Phys. Rev. D 1982, 26, 1453. [Google Scholar] [CrossRef]
- Bernard, C.W. Monte Carlo Evaluation of the Effective Gluon Mass. Phys. Lett. B 1982, 108, 431–434. [Google Scholar] [CrossRef]
- Bernard, C.W. Adjoint Wilson Lines and the Effective Gluon Mass. Nucl. Phys. B 1983, 219, 341–357. [Google Scholar] [CrossRef]
- Donoghue, J.F. The Gluon ’Mass’ in the Bag Model. Phys. Rev. D 1984, 29, 2559. [Google Scholar] [CrossRef]
- Cornwall, J.M.; Papavassiliou, J. Gauge Invariant Three Gluon Vertex in QCD. Phys. Rev. D 1989, 40, 3474. [Google Scholar] [CrossRef]
- Lavelle, M. Gauge invariant effective gluon mass from the operator product expansion. Phys. Rev. D 1991, 44, 26–28. [Google Scholar] [CrossRef]
- Halzen, F.; Krein, G.I.; Natale, A.A. Relating the QCD pomeron to an effective gluon mass. Phys. Rev. 1993, D47, 295–298. [Google Scholar] [CrossRef]
- Wilson, K.G.; Walhout, T.S.; Harindranath, A.; Zhang, W.M.; Perry, R.J.; Glazek, S.D. Nonperturbative QCD: A Weak coupling treatment on the light front. Phys. Rev. 1994, D49, 6720–6766. [Google Scholar] [CrossRef]
- Mihara, A.; Natale, A.A. Dynamical gluon mass corrections in heavy quarkonia decays. Phys. Lett. 2000, B482, 378–382. [Google Scholar] [CrossRef]
- Philipsen, O. On the nonperturbative gluon mass and heavy quark physics. Nucl. Phys. 2002, B628, 167–192. [Google Scholar] [CrossRef]
- Kondo, K.I. Vacuum condensate of mass dimension 2 as the origin of mass gap and quark confinement. Phys. Lett. 2001, B514, 335–345. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Natale, A.A.; Rodrigues da Silva, P.S. Relating a gluon mass scale to an infrared fixed point in pure gauge QCD. Phys. Rev. Lett. 2003, 90, 152001. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Natale, A.A. A Dynamical gluon mass solution in a coupled system of the Schwinger-Dyson equations. J. High Energy Phys. 2004, 8, 057. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Papavassiliou, J. Gluon mass generation in the PT-BFM scheme. J. High Energy Phys. 2006, 12, 012. [Google Scholar] [CrossRef]
- Epple, D.; Reinhardt, H.; Schleifenbaum, W.; Szczepaniak, A.P. Subcritical solution of the Yang-Mills Schroedinger equation in the Coulomb gauge. Phys. Rev. 2008, D77, 085007. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Papavassiliou, J. On dynamical gluon mass generation. Eur. Phys. J. 2007, A31, 742–745. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Gluon and ghost propagators in the Landau gauge: Deriving lattice results from Schwinger-Dyson equations. Phys. Rev. 2008, D78, 025010. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Papavassiliou, J. Gluon mass generation without seagull divergences. Phys. Rev. 2010, D81, 034003. [Google Scholar] [CrossRef]
- Campagnari, D.R.; Reinhardt, H. Non-Gaussian wave functionals in Coulomb gauge Yang–Mills theory. Phys. Rev. 2010, D82, 105021. [Google Scholar] [CrossRef]
- Fagundes, D.A.; Luna, E.G.S.; Menon, M.J.; Natale, A.A. Aspects of a Dynamical Gluon Mass Approach to Elastic Hadron Scattering at LHC. Nucl. Phys. A 2012, 886, 48–70. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. The dynamical equation of the effective gluon mass. Phys. Rev. 2011, D84, 085026. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ibanez, D.; Mathieu, V.; Papavassiliou, J. Massless bound-state excitations and the Schwinger mechanism in QCD. Phys. Rev. 2012, D85, 014018. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Gluon mass through ghost synergy. J. High Energy Phys. 2012, 01, 050. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Gluon mass generation in the presence of dynamical quarks. Phys. Rev. 2013, D88, 074010. [Google Scholar] [CrossRef]
- Glazek, S.D.; Gómez-Rocha, M.; More, J.; Serafin, K. Renormalized quark–antiquark Hamiltonian induced by a gluon mass ansatz in heavy-flavor QCD. Phys. Lett. 2017, B773, 172–178. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. Coupled dynamics in gluon mass generation and the impact of the three-gluon vertex. Phys. Rev. 2018, D97, 054029. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Figueiredo, C.T.; Papavassiliou, J. Gluon mass scale through nonlinearities and vertex interplay. Phys. Rev. D 2019, 100, 094039. [Google Scholar] [CrossRef]
- Eichmann, G.; Pawlowski, J.M.; Silva, J.M. Mass generation in Landau-gauge Yang-Mills theory. Phys. Rev. D 2021, 104, 114016. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Papavassiliou, J. Exploring smoking-gun signals of the Schwinger mechanism in QCD. Phys. Rev. D 2022, 105, 014030. [Google Scholar] [CrossRef]
- Horak, J.; Ihssen, F.; Papavassiliou, J.; Pawlowski, J.M.; Weber, A.; Wetterich, C. Gluon condensates and effective gluon mass. SciPost Phys. 2022, 13, 042. [Google Scholar] [CrossRef]
- Aguilar, A.C.; De Soto, F.; Ferreira, M.N.; Papavassiliou, J.; Pinto-Gómez, F.; Roberts, C.D.; Rodríguez-Quintero, J. Schwinger mechanism for gluons from lattice QCD. arXiv 2022, arXiv:2211.12594. [Google Scholar]
- Schwinger, J.S. Gauge Invariance and Mass. Phys. Rev. 1962, 125, 397–398. [Google Scholar] [CrossRef]
- Schwinger, J.S. Gauge Invariance and Mass. 2. Phys. Rev. 1962, 128, 2425–2429. [Google Scholar] [CrossRef]
- Watson, N.J. The gauge-independent QCD effective charge. Nucl. Phys. 1997, B494, 388–432. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. The QCD effective charge to all orders. Nucl. Phys. Proc. Suppl. 2003, 121, 281–284. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J.; Rodriguez-Quintero, J. Non-perturbative comparison of QCD effective charges. Phys. Rev. 2009, D80, 085018. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Low, F.E. Quantum electrodynamics at small distances. Phys. Rev. 1954, 95, 1300–1312. [Google Scholar] [CrossRef]
- Itzykson, C.; Zuber, J.B. Quantum Field Theory; International Series in Pure and Applied Physics; Mcgraw-Hill: New York, NY, USA, 1980; 705p. [Google Scholar]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Lane, K.D. Asymptotic Freedom and Goldstone Realization of Chiral Symmetry. Phys. Rev. 1974, D10, 2605. [Google Scholar] [CrossRef]
- Politzer, H.D. Effective Quark Masses in the Chiral Limit. Nucl. Phys. 1976, B117, 397. [Google Scholar] [CrossRef]
- Miransky, V.A.; Fomin, P.I. Chiral symmetry breakdown and the spectrum of pseudoscalar mesons in quantum chromodynamics. Phys. Lett. 1981, B105, 387–391. [Google Scholar] [CrossRef]
- Atkinson, D.; Johnson, P.W. Chiral Symmetry Breaking in QCD. 2. Running Coupling Constant. Phys. Rev. 1988, D37, 2296–2299. [Google Scholar] [CrossRef]
- Brown, N.; Pennington, M.R. Studies of confinement: How quarks and gluons propagate. Phys. Rev. 1988, D38, 2266. [Google Scholar] [CrossRef]
- Williams, A.G.; Krein, G.; Roberts, C.D. Quark propagator in an Ansatz approach to QCD. Ann. Phys. 1991, 210, 464–485. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Cornwall, J.M. Coupled fermion gap and vertex equations for chiral symmetry breakdown in QCD. Phys. Rev. 1991, D44, 1285–1297. [Google Scholar] [CrossRef]
- Hawes, F.T.; Roberts, C.D.; Williams, A.G. Dynamical chiral symmetry breaking and confinement with an infrared vanishing gluon propagator. Phys. Rev. 1994, D49, 4683–4693. [Google Scholar] [CrossRef]
- Natale, A.A.; Rodrigues da Silva, P.S. Critical coupling for dynamical chiral-symmetry breaking with an infrared finite gluon propagator. Phys. Lett. 1997, B392, 444–451. [Google Scholar] [CrossRef]
- Fischer, C.S.; Alkofer, R. Nonperturbative propagators, running coupling and dynamical quark mass of Landau gauge QCD. Phys. Rev. 2003, D67, 094020. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D. Dyson-Schwinger equations: A Tool for hadron physics. Int. J. Mod. Phys. 2003, E12, 297–365. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Nesterenko, A.; Papavassiliou, J. Infrared enhanced analytic coupling and chiral symmetry breaking in QCD. J. Phys. 2005, G31, 997. [Google Scholar] [CrossRef]
- Bowman, P.O.; Heller, U.M.; Leinweber, D.B.; Parappilly, M.B.; Williams, A.G.; Zhang, J.b. Unquenched quark propagator in Landau gauge. Phys. Rev. 2005, D71, 054507. [Google Scholar] [CrossRef]
- Sauli, V.; Adam, J., Jr.; Bicudo, P. Dynamical chiral symmetry breaking with integral Minkowski representations. Phys. Rev. 2007, D75, 087701. [Google Scholar] [CrossRef]
- Cornwall, J.M. Center vortices, the functional Schrodinger equation, and CSB. In Proceedings of the 419th WE-Heraeus-Seminar: Approaches to Quantum Chromodynamics, Oberwoelz, Austria, 7–13 September 2022. [Google Scholar]
- Alkofer, R.; Fischer, C.S.; Llanes-Estrada, F.J.; Schwenzer, K. The Quark-gluon vertex in Landau gauge QCD: Its role in dynamical chiral symmetry breaking and quark confinement. Ann. Phys. 2009, 324, 106–172. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Papavassiliou, J. Chiral symmetry breaking with lattice propagators. Phys. Rev. 2011, D83, 014013. [Google Scholar] [CrossRef]
- Rojas, E.; de Melo, J.; El-Bennich, B.; Oliveira, O.; Frederico, T. On the Quark-Gluon Vertex and Quark-Ghost Kernel: Combining Lattice Simulations with Dyson-Schwinger equations. J. High Energy Phys. 2013, 10, 193. [Google Scholar] [CrossRef]
- Mitter, M.; Pawlowski, J.M.; Strodthoff, N. Chiral symmetry breaking in continuum QCD. Phys. Rev. 2015, D91, 054035. [Google Scholar] [CrossRef]
- Braun, J.; Fister, L.; Pawlowski, J.M.; Rennecke, F. From Quarks and Gluons to Hadrons: Chiral Symmetry Breaking in Dynamical QCD. Phys. Rev. 2016, D94, 034016. [Google Scholar] [CrossRef]
- Heupel, W.; Goecke, T.; Fischer, C.S. Beyond Rainbow-Ladder in bound state equations. Eur. Phys. J. 2014, A50, 85. [Google Scholar] [CrossRef]
- Binosi, D.; Chang, L.; Papavassiliou, J.; Qin, S.X.; Roberts, C.D. Natural constraints on the gluon-quark vertex. Phys. Rev. 2017, D95, 031501. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Cardona, J.C.; Ferreira, M.N.; Papavassiliou, J. Quark gap equation with non-abelian Ball-Chiu vertex. Phys. Rev. 2018, D98, 014002. [Google Scholar] [CrossRef]
- Gao, F.; Papavassiliou, J.; Pawlowski, J.M. Fully coupled functional equations for the quark sector of QCD. Phys. Rev. D 2021, 103, 094013. [Google Scholar] [CrossRef]
- Eichten, E.; Feinberg, F. Dynamical Symmetry Breaking of Nonabelian Gauge Symmetries. Phys. Rev. D 1974, 10, 3254–3279. [Google Scholar] [CrossRef]
- Smit, J. On the Possibility That Massless Yang-Mills Fields Generate Massive Vector Particles. Phys. Rev. D 1974, 10, 2473. [Google Scholar] [CrossRef]
- Binosi, D.; Iba nez, D.; Papavassiliou, J. The all-order equation of the effective gluon mass. Phys. Rev. 2012, D86, 085033. [Google Scholar] [CrossRef]
- Tissier, M.; Wschebor, N. Infrared propagators of Yang-Mills theory from perturbation theory. Phys. Rev. D 2010, 82, 101701. [Google Scholar] [CrossRef]
- Serreau, J.; Tissier, M. Lifting the Gribov ambiguity in Yang-Mills theories. Phys. Lett. 2012, B712, 97–103. [Google Scholar] [CrossRef]
- Peláez, M.; Tissier, M.; Wschebor, N. Two-point correlation functions of QCD in the Landau gauge. Phys. Rev. D 2014, 90, 065031. [Google Scholar] [CrossRef]
- Siringo, F. Analytical study of Yang–Mills theory in the infrared from first principles. Nucl. Phys. 2016, B907, 572–596. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Figueiredo, C.T.; Papavassiliou, J. Unified description of seagull cancellations and infrared finiteness of gluon propagators. Phys. Rev. 2016, D94, 045002. [Google Scholar] [CrossRef]
- Osterwalder, K.; Schrader, R. Axioms for Euclidean Green’S Functions. Commun. Math. Phys. 1973, 31, 83–112. [Google Scholar] [CrossRef]
- Osterwalder, K.; Schrader, R. Axioms for Euclidean Green’s Functions. 2. Commun. Math. Phys. 1975, 42, 281. [Google Scholar] [CrossRef]
- Glimm, J.; Jaffe, A.M. Quantum Physics. A Functional Integral Point of View; Springer: New York, NY, USA, 1981. [Google Scholar]
- Krein, G.; Roberts, C.D.; Williams, A.G. On the implications of confinement. Int. J. Mod. Phys. 1992, A7, 5607–5624. [Google Scholar] [CrossRef]
- Cornwall, J.M. Positivity violations in QCD. Mod. Phys. Lett. 2013, A28, 1330035. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Iba nez, D.; Papavassiliou, J. Effects of divergent ghost loops on Green’s functions of QCD. Phys. Rev. 2014, D89, 085008. [Google Scholar] [CrossRef]
- Pelaez, M.; Tissier, M.; Wschebor, N. Three-point correlation functions in Yang-Mills theory. Phys. Rev. 2013, D88, 125003. [Google Scholar] [CrossRef]
- Blum, A.; Huber, M.Q.; Mitter, M.; von Smekal, L. Gluonic three-point correlations in pure Landau gauge QCD. Phys. Rev. 2014, D89, 061703. [Google Scholar] [CrossRef]
- Eichmann, G.; Williams, R.; Alkofer, R.; Vujinovic, M. The three-gluon vertex in Landau gauge. Phys. Rev. 2014, D89, 105014. [Google Scholar] [CrossRef]
- Williams, R.; Fischer, C.S.; Heupel, W. Light mesons in QCD and unquenching effects from the 3PI effective action. Phys. Rev. 2016, D93, 034026. [Google Scholar] [CrossRef]
- Blum, A.L.; Alkofer, R.; Huber, M.Q.; Windisch, A. Unquenching the three-gluon vertex: A status report. Acta Phys. Pol. Suppl. 2015, 8, 321. [Google Scholar] [CrossRef]
- Cyrol, A.K.; Fister, L.; Mitter, M.; Pawlowski, J.M.; Strodthoff, N. Landau gauge Yang-Mills correlation functions. Phys. Rev. 2016, D94, 054005. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Figueiredo, C.T.; Papavassiliou, J. Nonperturbative Ball-Chiu construction of the three-gluon vertex. Phys. Rev. 2019, D99, 094010. [Google Scholar] [CrossRef]
- Barrios, N.; Peláez, M.; Reinosa, U. Two-loop three-gluon vertex from the Curci-Ferrari model and its leading infrared behavior to all loop orders. Phys. Rev. D 2022, 106, 114039. [Google Scholar] [CrossRef]
- Rivers, R.J. Path Integral Methods in Quantum Field Theory; Cambridge Monographs on Mathematical Physics. Cambridge University Press: Cambridge, UK, 1988. [Google Scholar] [CrossRef]
- Fujikawa, K.; Lee, B.W.; Sanda, A.I. Generalized Renormalizable Gauge Formulation of Spontaneously Broken Gauge Theories. Phys. Rev. D 1972, 6, 2923–2943. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Papavassiliou, J. Infrared finite ghost propagator in the Feynman gauge. Phys. Rev. 2008, D77, 125022. [Google Scholar] [CrossRef]
- Huber, M.Q.; Schwenzer, K.; Alkofer, R. On the infrared scaling solution of SU(N) Yang-Mills theories in the maximally Abelian gauge. Eur. Phys. J. C 2010, 68, 581–600. [Google Scholar] [CrossRef]
- Siringo, F. Gluon propagator in Feynman gauge by the method of stationary variance. Phys. Rev. D 2014, 90, 094021. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Yang-Mills two-point functions in linear covariant gauges. Phys. Rev. 2015, D91, 085014. [Google Scholar] [CrossRef]
- Huber, M.Q. Gluon and ghost propagators in linear covariant gauges. Phys. Rev. 2015, D91, 085018. [Google Scholar] [CrossRef]
- Capri, M.A.L.; Fiorentini, D.; Guimaraes, M.S.; Mintz, B.W.; Palhares, L.F.; Sorella, S.P.; Dudal, D.; Justo, I.F.; Pereira, A.D.; Sobreiro, R.F. Exact nilpotent nonperturbative BRST symmetry for the Gribov-Zwanziger action in the linear covariant gauge. Phys. Rev. D 2015, 92, 045039. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Schwinger mechanism in linear covariant gauges. Phys. Rev. 2017, D95, 034017. [Google Scholar] [CrossRef]
- De Meerleer, T.; Dudal, D.; Sorella, S.P.; Dall’Olio, P.; Bashir, A. Landau-Khalatnikov-Fradkin Transformations, Nielsen Identities, Their Equivalence and Implications for QCD. Phys. Rev. D 2020, 101, 085005. [Google Scholar] [CrossRef]
- Napetschnig, M.; Alkofer, R.; Huber, M.Q.; Pawlowski, J.M. Yang-Mills propagators in linear covariant gauges from Nielsen identities. Phys. Rev. D 2021, 104, 054003. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. Gauge-invariant truncation scheme for the Schwinger-Dyson equations of QCD. Phys. Rev. 2008, D77, 061702. [Google Scholar] [CrossRef]
- Pilaftsis, A. Generalized pinch technique and the background field method in general gauges. Nucl. Phys. B 1997, 487, 467–491. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. The Pinch technique to all orders. Phys. Rev. D 2002, 66, 111901. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. Pinch technique selfenergies and vertices to all orders in perturbation theory. J. Phys. G 2004, G30, 203. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory of Gravity. 2. The Manifestly Covariant Theory. Phys. Rev. 1967, 162, 1195–1239. [Google Scholar] [CrossRef]
- ’t Hooft, G. Renormalizable Lagrangians for Massive Yang-Mills Fields. Nucl. Phys. B 1971, 35, 167–188. [Google Scholar] [CrossRef]
- Honerkamp, J. The Question of invariant renormalizability of the massless Yang-Mills theory in a manifest covariant approach. Nucl. Phys. B 1972, 48, 269–287. [Google Scholar] [CrossRef]
- Kallosh, R.E. The Renormalization in Nonabelian Gauge Theories. Nucl. Phys. B 1974, 78, 293–312. [Google Scholar] [CrossRef]
- Kluberg-Stern, H.; Zuber, J.B. Renormalization of Nonabelian Gauge Theories in a Background Field Gauge. 1. Green Functions. Phys. Rev. D 1975, 12, 482–488. [Google Scholar] [CrossRef]
- Arefeva, I.Y.; Faddeev, L.D.; Slavnov, A.A. Generating Functional for the s Matrix in Gauge Theories. Teor. Mat. Fiz. 1974, 21, 311–321. [Google Scholar] [CrossRef]
- Abbott, L. The Background Field Method Beyond One Loop. Nucl. Phys. B 1981, 185, 189–203. [Google Scholar] [CrossRef]
- Weinberg, S. Effective Gauge Theories. Phys. Lett. B 1980, 91, 51–55. [Google Scholar] [CrossRef]
- Abbott, L.F. Introduction to the Background Field Method. Acta Phys. Polon. 1982, B13, 33. [Google Scholar]
- Shore, G.M. Symmetry Restoration and the Background Field Method in Gauge Theories. Ann. Phys. 1981, 137, 262. [Google Scholar] [CrossRef]
- Abbott, L.F.; Grisaru, M.T.; Schaefer, R.K. The Background Field Method and the S Matrix. Nucl. Phys. B 1983, 229, 372–380. [Google Scholar] [CrossRef]
- Taylor, J. Ward Identities and Charge Renormalization of the Yang-Mills Field. Nucl. Phys. B 1971, 33, 436–444. [Google Scholar] [CrossRef]
- Slavnov, A. Ward Identities in Gauge Theories. Theor. Math. Phys. 1972, 10, 99–107. [Google Scholar] [CrossRef]
- Grassi, P.A.; Hurth, T.; Steinhauser, M. Practical algebraic renormalization. Ann. Phys. 2001, 288, 197–248. [Google Scholar] [CrossRef]
- Grassi, P.A.; Hurth, T.; Steinhauser, M. The Algebraic method. Nucl. Phys. B 2001, 610, 215–250. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. Pinch technique and the Batalin-Vilkovisky formalism. Phys. Rev. 2002, D66, 025024. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Indirect determination of the Kugo-Ojima function from lattice data. J. High Energy Phys. 2009, 11, 066. [Google Scholar] [CrossRef]
- Binosi, D.; Quadri, A. AntiBRST symmetry and Background Field Method. Phys. Rev. 2013, D88, 085036. [Google Scholar] [CrossRef]
- Iba nez, D.; Papavassiliou, J. Gluon mass generation in the massless bound-state formalism. Phys. Rev. 2013, D87, 034008. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Figueiredo, C.T.; Papavassiliou, J. Evidence of ghost suppression in gluon mass scale dynamics. Eur. Phys. J. 2018, C78, 181. [Google Scholar] [CrossRef]
- Munczek, H. Dynamical chiral symmetry breaking, Goldstone’s theorem and the consistency of the Schwinger-Dyson and Bethe–Salpeter Equations. Phys. Rev. 1995, D52, 4736–4740. [Google Scholar] [CrossRef]
- Bender, A.; Roberts, C.D.; Von Smekal, L. Goldstone theorem and diquark confinement beyond rainbow ladder approximation. Phys. Lett. 1996, B380, 7–12. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D.; Tandy, P.C. Pion mass and decay constant. Phys. Lett. 1998, B420, 267–273. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D. Pi- and K meson Bethe–Salpeter amplitudes. Phys. Rev. C 1997, 56, 3369–3383. [Google Scholar] [CrossRef]
- Chang, L.; Roberts, C.D. Sketching the Bethe–Salpeter kernel. Phys. Rev. Lett. 2009, 103, 081601. [Google Scholar] [CrossRef]
- Chang, L.; Roberts, C.D.; Tandy, P.C. Selected highlights from the study of mesons. Chin. J. Phys. 2011, 49, 955–1004. [Google Scholar]
- Qin, S.X.; Roberts, C.D. Resolving the Bethe–Salpeter Kernel. Chin. Phys. Lett. 2021, 38, 071201. [Google Scholar] [CrossRef]
- Huber, M.Q. Correlation functions of three-dimensional Yang-Mills theory from Dyson-Schwinger equations. Phys. Rev. D 2016, 93, 085033. [Google Scholar] [CrossRef]
- Schleifenbaum, W.; Maas, A.; Wambach, J.; Alkofer, R. Infrared behaviour of the ghost–gluon vertex in Landau gauge Yang-Mills theory. Phys. Rev. D 2005, 72, 014017. [Google Scholar] [CrossRef]
- Boucaud, P.; Leroy, J.; A., L.Y.; Micheli, J.; Pène, O.; Rodríguez-Quintero, J. On the IR behaviour of the Landau-gauge ghost propagator. J. High Energy Phys. 2008, 06, 099. [Google Scholar] [CrossRef]
- Huber, M.Q.; von Smekal, L. On the influence of three-point functions on the propagators of Landau gauge Yang-Mills theory. J. High Energy Phys. 2013, 04, 149. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Iba nez, D.; Papavassiliou, J. Ghost propagator and ghost–gluon vertex from Schwinger-Dyson equations. Phys. Rev. 2013, D87, 114020. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Figueiredo, C.T.; Papavassiliou, J. Nonperturbative structure of the ghost–gluon kernel. Phys. Rev. 2019, D99, 034026. [Google Scholar] [CrossRef]
- Dudal, D.; Gracey, J.A.; Sorella, S.P.; Vandersickel, N.; Verschelde, H. A refinement of the Gribov-Zwanziger approach in the Landau gauge: Infrared propagators in harmony with the lattice results. Phys. Rev. 2008, D78, 065047. [Google Scholar] [CrossRef]
- Boucaud, P.; Leroy, J.P.; Le Yaouanc, A.; Micheli, J.; Pene, O.; Rodríguez-Quintero, J. IR finiteness of the ghost dressing function from numerical resolution of the ghost SD equation. J. High Energy Phys. 2008, 06, 012. [Google Scholar] [CrossRef]
- Kondo, K.I. Infrared behavior of the ghost propagator in the Landau gauge Yang-Mills theory. Prog. Theor. Phys. 2010, 122, 1455–1475. [Google Scholar] [CrossRef]
- Pennington, M.R.; Wilson, D.J. Are the Dressed Gluon and Ghost Propagators in the Landau Gauge presently determined in the confinement regime of QCD? Phys. Rev. D 2011, 84, 094028, Erratum in Phys. Rev. D 2011, 84, 119901. [Google Scholar] [CrossRef]
- Dudal, D.; Oliveira, O.; Rodriguez-Quintero, J. Nontrivial ghost–gluon vertex and the match of RGZ, DSE and lattice Yang-Mills propagators. Phys. Rev. 2012, D86, 105005, Erratum in Phys. Rev. D 2012, 86, 109902. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Aguilar, A.C.; Ferreira, M.N. Theory and phenomenology of the three-gluon vertex. Rev. Mex. Fis. Suppl. 2022, 3, 0308112. [Google Scholar] [CrossRef]
- Meyers, J.; Swanson, E.S. Spin Zero Glueballs in the Bethe–Salpeter Formalism. Phys. Rev. 2013, D87, 036009. [Google Scholar] [CrossRef]
- Sanchis-Alepuz, H.; Fischer, C.S.; Kellermann, C.; von Smekal, L. Glueballs from the Bethe–Salpeter equation. Phys. Rev. 2015, D92, 034001. [Google Scholar] [CrossRef]
- Xu, S.S.; Cui, Z.F.; Chang, L.; Papavassiliou, J.; Roberts, C.D.; Zong, H.S. New perspective on hybrid mesons. Eur. Phys. J. 2019, A55, 113. [Google Scholar] [CrossRef]
- Souza, E.V.; Ferreira, M.N.; Aguilar, A.C.; Papavassiliou, J.; Roberts, C.D.; Xu, S.S. Pseudoscalar glueball mass: A window on three-gluon interactions. Eur. Phys. J. A 2020, 56, 25. [Google Scholar] [CrossRef]
- Huber, M.Q.; Fischer, C.S.; Sanchis-Alepuz, H. Spectrum of scalar and pseudoscalar glueballs from functional methods. Eur. Phys. J. C 2020, 80, 1077. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.Q.; Fischer, C.S.; Sanchis-Alepuz, H. Higher spin glueballs from functional methods. Eur. Phys. J. C 2021, 81, 1083, Erratum in Eur. Phys. J. C 2022, 82, 38. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Papavassiliou, J. Novel sum rules for the three-point sector of QCD. Eur. Phys. J. C 2020, 80, 887. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Papavassiliou, J. Gluon dynamics from an ordinary differential equation. Eur. Phys. J. C 2021, 81, 54. [Google Scholar] [CrossRef]
- Cornwall, J.M.; Papavassiliou, J.; Binosi, D. The Pinch Technique and its Applications to Non-Abelian Gauge Theories; Cambridge University Press: Cambridge, UK, 2010; Volume 31. [Google Scholar]
- Binosi, D.; Papavassiliou, J. New Schwinger-Dyson equations for non-Abelian gauge theories. J. High Energy Phys. 2008, 11, 063. [Google Scholar] [CrossRef]
- Grassi, P.A.; Hurth, T.; Quadri, A. On the Landau background gauge fixing and the IR properties of YM Green functions. Phys. Rev. 2004, D70, 105014. [Google Scholar]
- Kugo, T. The Universal renormalization factors Z(1) / Z(3) and color confinement condition in nonAbelian gauge theory. arXiv 1995, arXiv:9511033. [Google Scholar]
- Kondo, K.I. Kugo-Ojima color confinement criterion and Gribov-Zwanziger horizon condition. Phys. Lett. B 2009, 678, 322–330. [Google Scholar] [CrossRef]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of the Abelian Higgs-Kibble Model. Commun. Math. Phys. 1975, 42, 127–162. [Google Scholar] [CrossRef]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of Gauge Theories. Ann. Phys. 1976, 98, 287–321. [Google Scholar] [CrossRef]
- Tyutin, I.V. Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism. arXiv 1975, arXiv:0812.0580. [Google Scholar]
- Ball, J.S.; Chiu, T.W. Analytic Properties of the Vertex Function in Gauge Theories. 2. Phys. Rev. D 1980, 22, 2550, Erratum in Phys. Rev. D 1981, 23, 3085. [Google Scholar] [CrossRef]
- Davydychev, A.I.; Osland, P.; Tarasov, O. Three gluon vertex in arbitrary gauge and dimension. Phys. Rev. D 1996, 54, 4087–4113, Erratum in Phys. Rev. D 1999, 59, 109901. [Google Scholar] [CrossRef]
- von Smekal, L.; Hauck, A.; Alkofer, R. A Solution to Coupled Dyson–Schwinger Equations for Gluons and Ghosts in Landau Gauge. Ann. Phys. 1998, 267, 1–60, Erratum in Ann. Phys. 1998, 269, 182. [Google Scholar] [CrossRef]
- Binosi, D.; Papavassiliou, J. Gauge invariant Ansatz for a special three-gluon vertex. J. High Energy Phys. 2011, 03, 121. [Google Scholar] [CrossRef]
- Gracey, J.; Kißler, H.; Kreimer, D. Self-consistency of off-shell Slavnov-Taylor identities in QCD. Phys. Rev. D 2019, 100, 085001. [Google Scholar] [CrossRef]
- Collins, J.C. Renormalization. An Introduction To Renormalization, The Renormalization Group, And The Operator Product Expansion; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Brodsky, S.J.; Shrock, R. Maximum Wavelength of Confined Quarks and Gluons and Properties of Quantum Chromodynamics. Phys. Lett. 2008, B666, 95–99. [Google Scholar] [CrossRef]
- Braun, J.; Gies, H.; Pawlowski, J.M. Quark Confinement from Color Confinement. Phys. Lett. 2010, B684, 262–267. [Google Scholar] [CrossRef]
- Gao, F.; Qin, S.X.; Roberts, C.D.; Rodriguez-Quintero, J. Locating the Gribov horizon. Phys. Rev. 2018, D97, 034010. [Google Scholar] [CrossRef]
- Jackiw, R.; Johnson, K. Dynamical Model of Spontaneously Broken Gauge Symmetries. Phys. Rev. D 1973, 8, 2386–2398. [Google Scholar] [CrossRef]
- Jackiw, R. Dynamical Symmetry Breaking. In Proceedings of the 11th International School of Subnuclear Physics: Laws of Hadronic Matter, Erice, Italy, 8–26 July 1973. [Google Scholar]
- Papavassiliou, J. Gauge Invariant Proper Selfenergies and Vertices in Gauge Theories with Broken Symmetry. Phys. Rev. D 1990, 41, 3179. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, N. A General survey of the theory of the Bethe–Salpeter equation. Prog. Theor. Phys. Suppl. 1969, 43, 1–81. [Google Scholar] [CrossRef]
- Blank, M.; Krassnigg, A. Matrix algorithms for solving (in)homogeneous bound state equations. Comput. Phys. Commun. 2011, 182, 1391–1401. [Google Scholar] [CrossRef] [PubMed]
- Wilson, K.G. Quantum field theory models in less than four-dimensions. Phys. Rev. 1973, D7, 2911–2926. [Google Scholar]
- Poggio, E.C.; Tomboulis, E.; Tye, S.H.H. Dynamical Symmetry Breaking in Nonabelian Field Theories. Phys. Rev. 1975, D11, 2839. [Google Scholar] [CrossRef]
- Denner, A.; Weiglein, G.; Dittmaier, S. Gauge invariance of green functions: Background field method versus pinch technique. Phys. Lett. 1994, B333, 420–426. [Google Scholar] [CrossRef]
- Hashimoto, S.; Kodaira, J.; Yasui, Y.; Sasaki, K. The Background field method: Alternative way of deriving the pinch technique’s results. Phys. Rev. D 1994, 50, 7066–7076. [Google Scholar] [CrossRef]
- Papavassiliou, J. On the connection between the pinch technique and the background field method. Phys. Rev. 1995, D51, 856–861. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Iba nez, D.; Papavassiliou, J. New method for determining the quark-gluon vertex. Phys. Rev. 2014, D90, 065027. [Google Scholar] [CrossRef]
- Alkofer, R.; Fischer, C.S.; Llanes-Estrada, F.J. Vertex functions and infrared fixed point in Landau gauge SU(N) Yang-Mills theory. Phys. Lett. B 2005, 611, 279–288, Erratum in Phys. Lett. B 2009, 670, 460–461. [Google Scholar] [CrossRef]
- Kugo, T.; Ojima, I. Local Covariant Operator Formalism of Nonabelian Gauge Theories and Quark Confinement Problem. Prog. Theor. Phys. Suppl. 1979, 66, 1–130. [Google Scholar] [CrossRef]
- Nakanishi, N.; Ojima, I. Covariant Operator Formalism of Gauge Theories and Quantum Gravity; World Scientific Lectures Notes in Physics: Singapore, 1990; Volume 27. [Google Scholar] [CrossRef]
- Alkofer, R.; Huber, M.Q.; Schwenzer, K. Infrared singularities in Landau gauge Yang-Mills theory. Phys. Rev. D 2010, 81, 105010. [Google Scholar] [CrossRef]
- Huber, M.Q. On non-primitively divergent vertices of Yang–Mills theory. Eur. Phys. J. 2017, C77, 733. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Ferreira, M.N.; Oliveira, B.M.; Papavassiliou, J. Schwinger-Dyson truncations in the all-soft limit: A case study. Eur. Phys. J. C 2022, 82, 1068. [Google Scholar] [CrossRef]
- Celmaster, W.; Gonsalves, R.J. The Renormalization Prescription Dependence of the QCD Coupling Constant. Phys. Rev. 1979, D20, 1420. [Google Scholar]
- Mintz, B.W.; Palhares, L.F.; Sorella, S.P.; Pereira, A.D. Ghost-gluon vertex in the presence of the Gribov horizon. Phys. Rev. 2018, D97, 034020. [Google Scholar] [CrossRef]
- Barrios, N.; Peláez, M.; Reinosa, U.; Wschebor, N. The ghost-antighost–gluon vertex from the Curci-Ferrari model: Two-loop corrections. Phys. Rev. D 2020, 102, 114016. [Google Scholar] [CrossRef]
- Cyrol, A.K.; Pawlowski, J.M.; Rothkopf, A.; Wink, N. Reconstructing the gluon. SciPost Phys. 2018, 5, 065. [Google Scholar] [CrossRef]
- Binosi, D.; Tripolt, R.A. Spectral functions of confined particles. Phys. Lett. B 2020, 801, 135171. [Google Scholar] [CrossRef]
- Kern, W.; Huber, M.Q.; Alkofer, R. The spectral dimension as a tool for analyzing non-perturbative propagators. Phys. Rev. 2019, D100, 094037. [Google Scholar] [CrossRef]
- Horak, J.; Papavassiliou, J.; Pawlowski, J.M.; Wink, N. Ghost spectral function from the spectral Dyson-Schwinger equation. Phys. Rev. D 2021, 104, 074017. [Google Scholar] [CrossRef]
- Horak, J.; Pawlowski, J.M.; Rodríguez-Quintero, J.; Turnwald, J.; Urban, J.M.; Wink, N.; Zafeiropoulos, S. Reconstructing QCD spectral functions with Gaussian processes. Phys. Rev. D 2022, 105, 036014. [Google Scholar] [CrossRef]
- Horak, J.; Pawlowski, J.M.; Wink, N. On the complex structure of Yang-Mills theory. arXiv 2022, arXiv:2202.09333. [Google Scholar]
- Kallen, G. On the definition of the Renormalization Constants in Quantum Electrodynamics. Helv. Phys. Acta 1952, 25, 417. [Google Scholar] [CrossRef]
- Lehmann, H. On the Properties of propagation functions and renormalization contants of quantized fields. Nuovo Cim. 1954, 11, 342–357. [Google Scholar] [CrossRef]
- Gross, D.J.; Pisarski, R.D.; Yaffe, L.G. QCD and Instantons at Finite Temperature. Rev. Mod. Phys. 1981, 53, 43. [Google Scholar] [CrossRef]
- Jackiw, R.; Templeton, S. How Superrenormalizable Interactions Cure their Infrared Divergences. Phys. Rev. D 1981, 23, 2291. [Google Scholar] [CrossRef]
- Appelquist, T.; Pisarski, R.D. High-Temperature Yang-Mills Theories and Three-Dimensional Quantum Chromodynamics. Phys. Rev. D 1981, 23, 2305. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R.; Templeton, S. Three-Dimensional Massive Gauge Theories. Phys. Rev. Lett. 1982, 48, 975–978. [Google Scholar] [CrossRef]
- Cornwall, J.M. HOW d = 3 QCD RESEMBLES d = 4 QCD. Physica 1989, A158, 97–110. [Google Scholar] [CrossRef]
- Cornwall, J.M. Exact zero momentum sum rules in d = 3 gauge theory. Nucl. Phys. B 1994, 416, 335–350. [Google Scholar] [CrossRef]
- Alexanian, G.; Nair, V.P. A Selfconsistent inclusion of magnetic screening for the quark - gluon plasma. Phys. Lett. 1995, B352, 435–439. [Google Scholar] [CrossRef]
- Cornwall, J.M.; Yan, B. String tension and Chern-Simons fluctuations in the vortex vacuum of d = 3 gauge theory. Phys. Rev. D 1996, 53, 4638–4649. [Google Scholar] [CrossRef]
- Cornwall, J.M. On the phase transition in D = 3 Yang-Mills Chern-Simons gauge theory. Phys. Rev. D 1996, 54, 1814–1825. [Google Scholar] [CrossRef]
- Buchmuller, W.; Philipsen, O. Magnetic screening in the high temperature phase of the standard model. Phys. Lett. 1997, B397, 112–118. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Seeking an even-parity mass term for 3-D gauge theory. Phys. Lett. 1997, B403, 297–303. [Google Scholar] [CrossRef]
- Cornwall, J.M. On one-loop gap equations for the magnetic mass in d = 3 gauge theory. Phys. Rev. 1998, D57, 3694–3700. [Google Scholar]
- Karabali, D.; Kim, C.j.; Nair, V. On the vacuum wave function and string tension of Yang-Mills theories in (2+1)-dimensions. Phys. Lett. 1998, B434, 103–109. [Google Scholar] [CrossRef]
- Eberlein, F. Two loop gap equations for the magnetic mass. Phys. Lett. 1998, B439, 130–136. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Nonperturbative gluon and ghost propagators for d=3 Yang-Mills. Phys. Rev. 2010, D81, 125025. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).