Masses of Compact (Neutron) Stars with Distinguished Cores
Abstract
1. Introduction
2. One-Component Static Cool Compact Stars: TOV Equations
2.1. Scaling of TOV Equations and Compact/Neutron Star Masses and Radii
| PSR | [km] | |
| 1.4 | [12], [13], [15] | |
| J0030+0451 | [16] | |
| [14], [17] | ||
| J1614–2230 | [78] | |
| J0348+0432 | [79] | |
| J0740+6620 | [15] | |
| [80] | [13], [12] | |
| 0952-0607 | [81] |
2.2. Solving TOV Equations
3. Small-Core Approximation and Beyond
3.1. One-Component Core
3.2. Multi-Component Cores
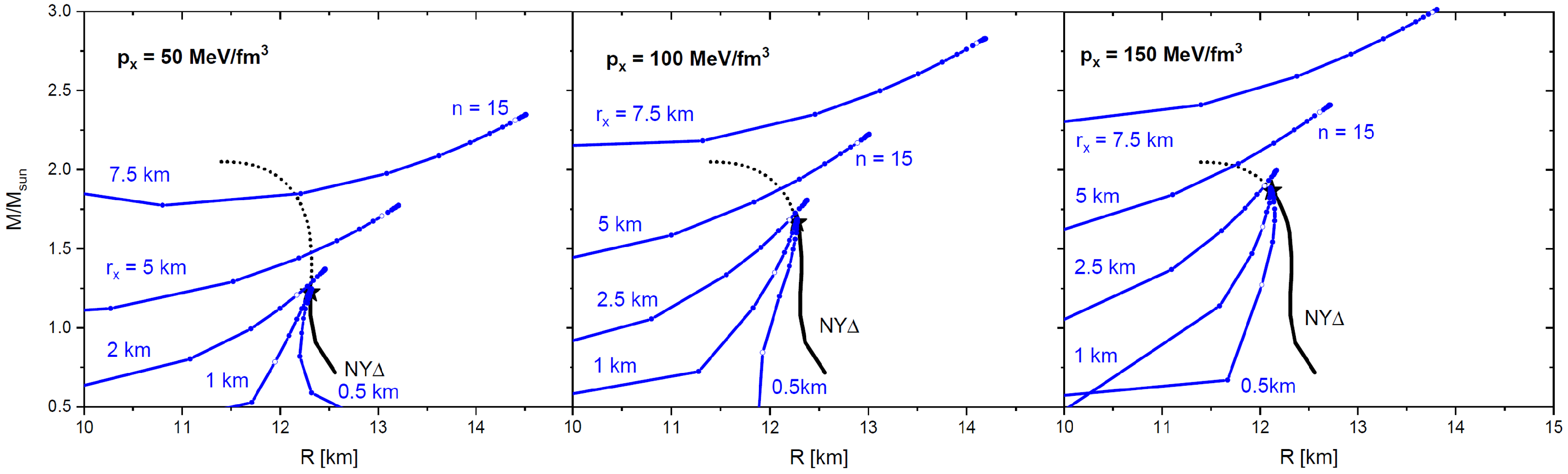
4. Core-Corona Decomposition with NY DD-EM2 EoS
4.1. Trace Anomaly
4.2. Distinguished Cores with NY Envelope
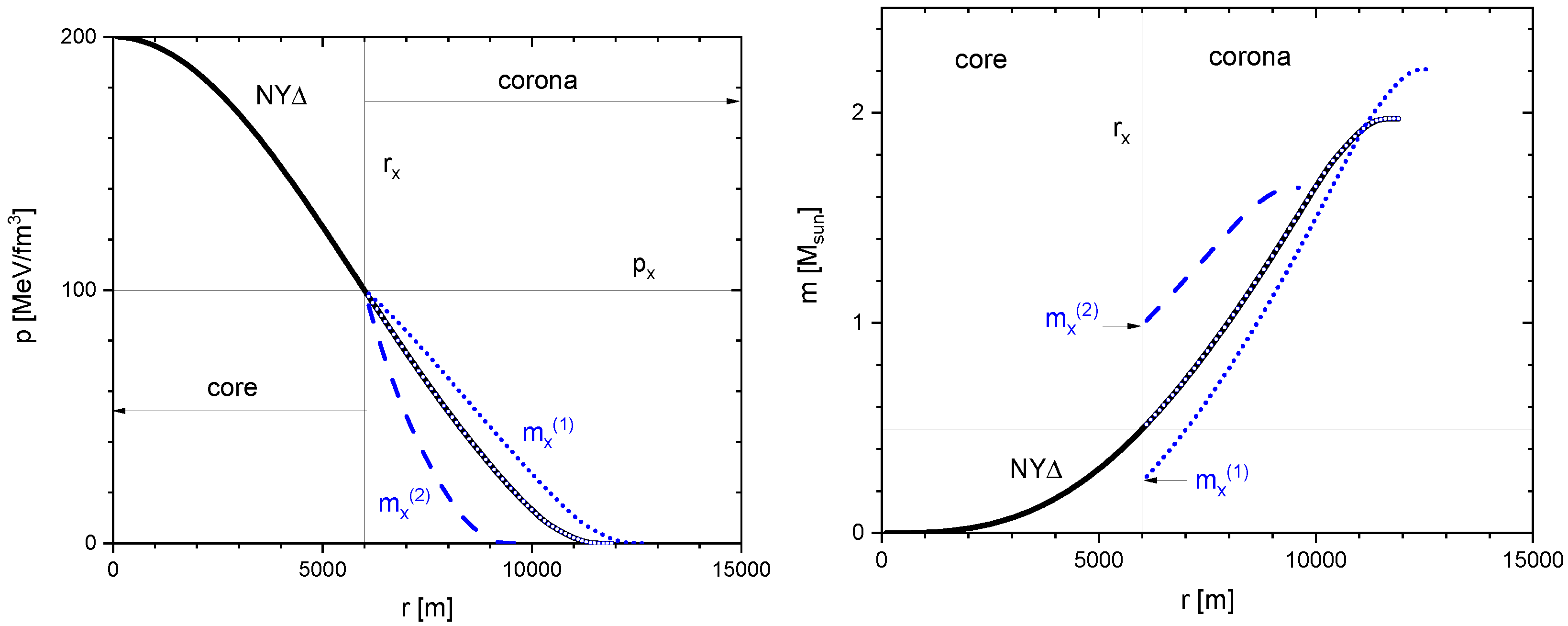
4.3. Example of Radial Pressure and Mass Profiles
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Emergence of Hadron Masses
Appendix A.1. Three Pillars of EHM
Appendix A.1.1. Running Quark Mass
Appendix A.1.2. Running Gluon Mass
Appendix A.1.3. Process-Independent Effective Charge
Appendix A.2. Hadrons in Vacuum
Appendix A.3. Hadrons in Cold Dense Medium
Appendix A.4. Supplementary Remarks

Appendix B. Holographic Approach to the EoS

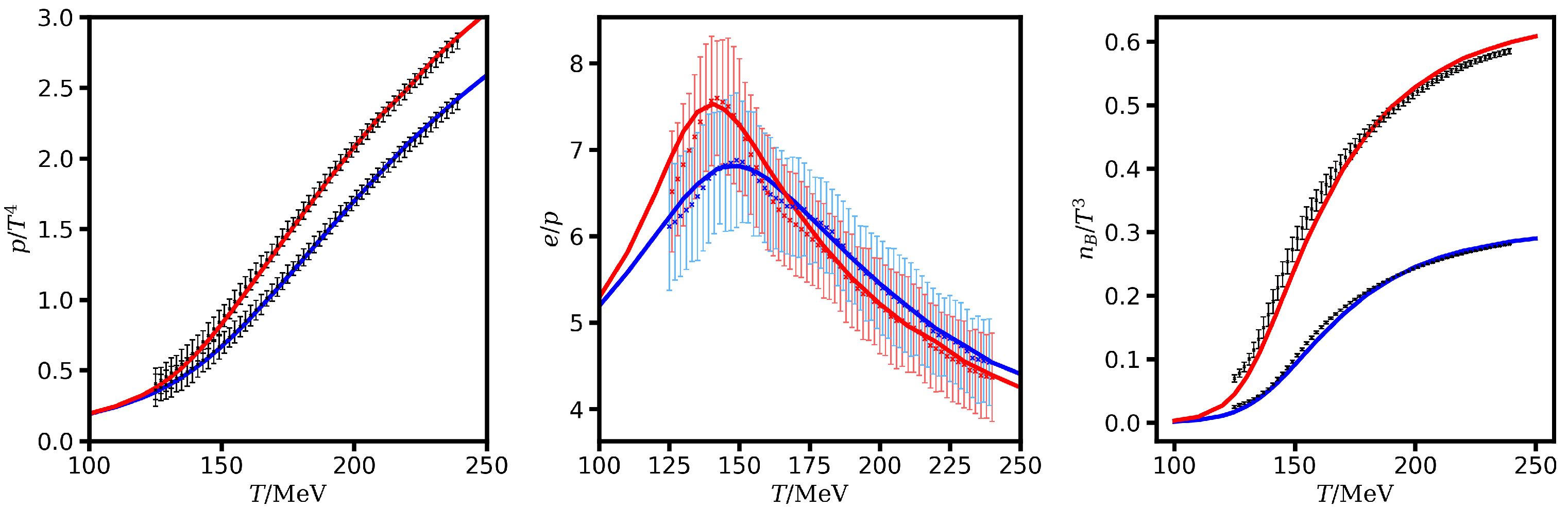
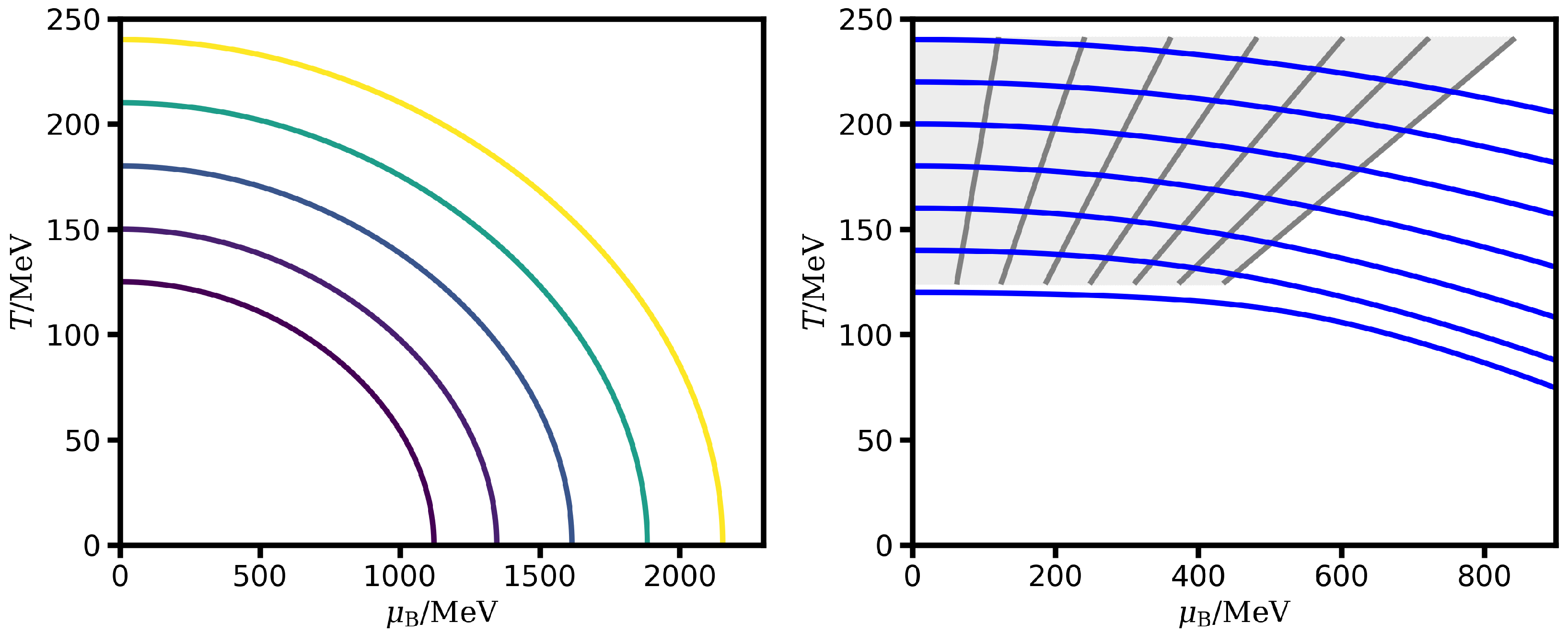
References
- Brandt, B.B.; Endrodi, G.; Fraga, E.S.; Hippert, M.; Schaffner-Bielich, J.; Schmalzbauer, S. New class of compact stars: Pion stars. Phys. Rev. D 2018, 98, 094510. [Google Scholar] [CrossRef]
- Roberts, C.D.; Richards, D.G.; Horn, T.; Chang, L. Insights into the emergence of mass from studies of pion and kaon structure. Prog. Part. Nucl. Phys. 2021, 120, 103883. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Reflections upon the emergence of hadronic mass. Eur. Phys. J. ST 2020, 229, 3319–3340. [Google Scholar] [CrossRef]
- Tolos, L.; Fabbietti, L. Strangeness in Nuclei and Neutron Stars. Prog. Part. Nucl. Phys. 2020, 112, 103770. [Google Scholar] [CrossRef]
- Silva, H.O.; Holgado, A.M.; Cárdenas-Avendaño, A.; Yunes, N. Astrophysical and theoretical physics implications from multimessenger neutron star observations. Phys. Rev. Lett. 2021, 126, 181101. [Google Scholar] [CrossRef]
- Tews, I.; Pang, P.T.H.; Dietrich, T.; Coughlin, M.W.; Antier, S.; Bulla, M.; Heinzel, J.; Issa, L. On the Nature of GW190814 and Its Impact on the Understanding of Supranuclear Matter. Astrophys. J. Lett. 2021, 908, L1. [Google Scholar] [CrossRef]
- Tang, S.P.; Jiang, J.L.; Gao, W.H.; Fan, Y.Z.; Wei, D.M. Constraint on phase transition with the multimessenger data of neutron stars. Phys. Rev. D 2021, 103, 063026. [Google Scholar] [CrossRef]
- Margutti, R.; Chornock, R. First Multimessenger Observations of a Neutron Star Merger. Ann. Rev. Astron. Astrophys. 2021, 59, 155–202. [Google Scholar] [CrossRef]
- Nicholl, M.; Margalit, B.; Schmidt, P.; Smith, G.P.; Ridley, E.J.; Nuttall, J. Tight multimessenger constraints on the neutron star equation of state from GW170817 and a forward model for kilonova light-curve synthesis. Mon. Not. R. Astron. Soc. 2021, 505, 3016–3032. [Google Scholar] [CrossRef]
- Yu, J.; Song, H.; Ai, S.; Gao, H.; Wang, F.; Wang, Y.; Lu, Y.; Fang, W.; Zhao, W. Multimessenger Detection Rates and Distributions of Binary Neutron Star Mergers and Their Cosmological Implications. Astrophys. J. 2021, 916, 54. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Katerini, E.; Kurkela, A.; Nättilä, J.; Paschalidis, V.; Vuorinen, A. Multimessenger Constraints for Ultradense Matter. Phys. Rev. X 2022, 12, 011058. [Google Scholar] [CrossRef]
- Pang, P.T.H.; Tews, I.; Coughlin, M.W.; Bulla, M.; Broeck, C.V.D.; Dietrich, T. Nuclear Physics Multimessenger Astrophysics Constraints on the Neutron Star Equation of State: Adding NICER’s PSR J0740+6620 Measurement. Astrophys. J. 2021, 922, 14. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Hebeler, K.; Hinderer, T.; Nissanke, S.; Schwenk, A.; Riley, T.E.; Watts, A.L.; Lattimer, J.M.; Ho, W.C.G. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass–Radius Estimate of PSR J0740+6620 and Multimessenger Observations. Astrophys. J. Lett. 2021, 918, L29. [Google Scholar] [CrossRef]
- Pereira, J.P.; Bejger, M.; Tonetto, L.; Lugones, G.; Haensel, P.; Zdunik, J.L.; Sieniawska, M. Probing elastic quark phases in hybrid stars with radius measurements. Astrophys. J. 2021, 910, 145. [Google Scholar] [CrossRef]
- Christian, J.E.; Schaffner-Bielich, J. Twin Stars and the Stiffness of the Nuclear Equation of State: Ruling Out Strong Phase Transitions below 1.7n0 with the New NICER Radius Measurements. Astrophys. J. Lett. 2020, 894, L8. [Google Scholar] [CrossRef]
- Chatziioannou, K. Neutron star tidal deformability and equation of state constraints. Gen. Rel. Grav. 2020, 52, 109. [Google Scholar] [CrossRef]
- Motta, T.F.; Thomas, A.W. The role of baryon structure in neutron stars. Mod. Phys. Lett. A 2022, 37, 2230001. [Google Scholar] [CrossRef]
- Jokela, N.; Järvinen, M.; Remes, J. Holographic QCD in the NICER era. Phys. Rev. D 2022, 105, 086005. [Google Scholar] [CrossRef]
- Kovensky, N.; Poole, A.; Schmitt, A. Building a realistic neutron star from holography. Phys. Rev. D 2022, 105, 034022. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Impact of NICER’s Radius Measurement of PSR J0740+6620 on Nuclear Symmetry Energy at Suprasaturation Densities. Astrophys. J. 2021, 921, 111. [Google Scholar] [CrossRef]
- Christian, J.E.; Schaffner-Bielich, J. Supermassive Neutron Stars Rule Out Twin Stars. Phys. Rev. D 2021, 103, 063042. [Google Scholar] [CrossRef]
- Gerlach, U.H. Equation of State at Supranuclear Densities and the Existence of a Third Family of Superdense Stars. Phys. Rev. 1968, 172, 1325. [Google Scholar] [CrossRef]
- Kämpfer, B. On the Possibility of Stable Quark and Pion Condensed Stars. J. Phys. A 1981, 14, L471. [Google Scholar] [CrossRef]
- Kämpfer, B. On stabilizing effects of relativity in cold spheric stars with a phase transition in the interior. Phys. Lett. B 1981, 101, 366–368. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Haensel, P.; Schaeffer, R. Phase transitons in stellar cores, II Equilibrium configurations in general relativity. Astron. Astrophys. 1987, 172, 95–110. [Google Scholar]
- Zdunik, J.L.; Haensel, P.; Schaeffer, R. Phase transitons in stellar cores, I Equilibrium configurations. Astron. Astrophys. 1983, 126, 121–145. [Google Scholar]
- Li, J.J.; Sedrakian, A.; Alford, M. Relativistic hybrid stars with sequential first-order phase transitions and heavy-baryon envelopes. Phys. Rev. D 2020, 101, 063022. [Google Scholar] [CrossRef]
- Alford, M.G.; Sedrakian, A. Compact stars with sequential QCD phase transitions. Phys. Rev. Lett. 2017, 119, 161104. [Google Scholar] [CrossRef] [PubMed]
- Malfatti, G.; Orsaria, M.G.; Ranea-Sandoval, I.F.; Contrera, G.A.; Weber, F. Delta baryons and diquark formation in the cores of neutron stars. Phys. Rev. D 2020, 102, 063008. [Google Scholar] [CrossRef]
- Pereira, J.P.; Bejger, M.; Zdunik, J.L.; Haensel, P. Differentiating sharp phase transitions from mixed states in neutron stars. arXiv 2022, arXiv:2201.01217. [Google Scholar]
- Bejger, M.; Blaschke, D.; Haensel, P.; Zdunik, J.L.; Fortin, M. Consequences of a strong phase transition in the dense matter equation of state for the rotational evolution of neutron stars. Astron. Astrophys. 2017, 600, A39. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Alford, M. Relativistic hybrid stars in light of the NICER PSR J0740+6620 radius measurement. Phys. Rev. D 2021, 104, L121302. [Google Scholar] [CrossRef]
- Cierniak, M.; Blaschke, D. The special point on the hybrid star mass–radius diagram and its multi–messenger implications. Eur. Phys. J. ST 2020, 229, 3663–3673. [Google Scholar] [CrossRef]
- Ranea-Sandoval, I.F.; Han, S.; Orsaria, M.G.; Contrera, G.A.; Weber, F.; Alford, M.G. Constant-sound-speed parametrization for Nambu–Jona-Lasinio models of quark matter in hybrid stars. Phys. Rev. C 2016, 93, 045812. [Google Scholar] [CrossRef]
- Alford, M.G.; Han, S. Characteristics of hybrid compact stars with a sharp hadron-quark interface. Eur. Phys. J. A 2016, 52, 62. [Google Scholar] [CrossRef]
- Tan, H.; Dore, T.; Dexheimer, V.; Noronha-Hostler, J.; Yunes, N. Extreme matter meets extreme gravity: Ultraheavy neutron stars with phase transitions. Phys. Rev. D 2022, 105, 023018. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Kettner, C. Nonidentical neutron star twins. Astron. Astrophys. 2000, 353, L9. [Google Scholar]
- Jakobus, P.; Motornenko, A.; Gomes, R.O.; Steinheimer, J.; Stoecker, H. The possibility of twin star solutions in a model based on lattice QCD thermodynamics. Eur. Phys. J. C 2021, 81, 41. [Google Scholar] [CrossRef]
- Alford, M.; Braby, M.; Paris, M.W.; Reddy, S. Hybrid stars that masquerade as neutron stars. Astrophys. J. 2005, 629, 969. [Google Scholar] [CrossRef]
- Klahn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Most, E.R.; Motornenko, A.; Steinheimer, J.; Dexheimer, V.; Hanauske, M.; Rezzolla, L.; Stoecker, H. Probing neutron-star matter in the lab: Connecting binary mergers to heavy-ion collisions. arXiv 2022, arXiv:2201.13150. [Google Scholar]
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.C.; Biernat, J.; Blanco, A.; Blume, C.; Böhmer, M.; et al. Probing dense baryon-rich matter with virtual photons. Nature Phys. 2019, 15, 1040–1045. [Google Scholar]
- Stephanov, M.A.; Rajagopal, K.; Shuryak, E.V. Event-by-event fluctuations in heavy ion collisions and the QCD critical point. Phys. Rev. D 1999, 60, 114028. [Google Scholar] [CrossRef]
- Karsch, F. Lattice QCD at high temperature and density. Lect. Notes Phys. 2002, 583, 209–249. [Google Scholar]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rept. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Halasz, A.M.; Jackson, A.D.; Shrock, R.E.; Stephanov, M.A.; Verbaarschot, J.J.M. On the phase diagram of QCD. Phys. Rev. D 1998, 58, 096007. [Google Scholar] [CrossRef]
- Blacker, S.; Bastian, N.U.F.; Bauswein, A.; Blaschke, D.B.; Fischer, T.; Oertel, M.; Soultanis, T.; Typel, S. Constraining the onset density of the hadron-quark phase transition with gravitational-wave observations. Phys. Rev. D 2020, 102, 123023. [Google Scholar] [CrossRef]
- Blaschke, D.; Cierniak, M. Studying the onset of deconfinement with multi-messenger astronomy of neutron stars. Astron. Nachr. 2021, 342, 227–233. [Google Scholar] [CrossRef]
- Orsaria, M.G.; Malfatti, G.; Mariani, M.; Ranea-Sandoval, I.F.; García, F.; Spinella, W.M.; Contrera, G.A.; Lugones, G.; Weber, F. Phase transitions in neutron stars and their links to gravitational waves. J. Phys. G 2019, 46, 073002. [Google Scholar] [CrossRef]
- Cierniak, M.; Blaschke, D. Hybrid neutron stars in the mass-radius diagram. Astron. Nachr. 2021, 342, 819. [Google Scholar] [CrossRef]
- Kämpfer, B. Phase transitions in dense nuclear matter and explosive neutron star phenomena. Phys. Lett. B 1985, 153, 121–123. [Google Scholar] [CrossRef]
- Kämpfer, B. Phase transitions in nuclear matter and consequences for neutron stars. J. Phys. G 1983, 9, 1487. [Google Scholar] [CrossRef]
- Schertler, K.; Greiner, C.; Schaffner-Bielich, J.; Thoma, M.H. Quark phases in neutron stars and a ’third family’ of compact stars as a signature for phase transitions. Nucl. Phys. A 2000, 677, 463–490. [Google Scholar] [CrossRef]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Classifications of Twin Star Solutions for a Constant Speed of Sound Parameterized Equation of State. Eur. Phys. J. A 2018, 54, 28. [Google Scholar] [CrossRef]
- Migdal, A.B.; Chernoutsan, A.I.; Mishustin, I.N. Pion condensation and dynamics of neutron stars. Phys. Lett. B 1979, 83, 158–160. [Google Scholar] [CrossRef]
- Kämpfer, B. On the collapse of neutron stars and stellar cores to pion-condensed stars. Astrophys. Space Sci. 1983, 93, 185–197. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rept. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Luzio, L.D.; Gavela, B.; Quilez, P.; Ringwald, A. Dark matter from an even lighter QCD axion: Trapped misalignment. JCAP 2021, 10, 001. [Google Scholar] [CrossRef]
- Hodges, H.M. Mirror baryons as the dark matter. Phys. Rev. D 1993, 47, 456. [Google Scholar] [CrossRef] [PubMed]
- Tulin, S.; Yu, H.B. Dark Matter Self-interactions and Small Scale Structure. Phys. Rept. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Karkevandi, D.R.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Dengler, Y.; Schaffner-Bielich, J.; Tolos, L. Second Love number of dark compact planets and neutron stars with dark matter. Phys. Rev. D 2022, 105, 043013. [Google Scholar] [CrossRef]
- Hippert, M.; Dillingham, E.; Tan, H.; Curtin, D.; Noronha-Hostler, J.; Yunes, N. Dark Matter or Regular Matter in Neutron Stars? How to tell the difference from the coalescence of compact objects. arXiv 2022, arXiv:2211.08590. [Google Scholar]
- Beradze, R.; Gogberashvili, M.; Sakharov, A.S. Binary Neutron Star Mergers with Missing Electromagnetic Counterparts as Manifestations of Mirror World. Phys. Lett. B 2020, 804, 135402. [Google Scholar] [CrossRef]
- Alizzi, A.; Silagadze, Z.K. Dark photon portal into mirror world. Mod. Phys. Lett. A 2021, 36, 2150215. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S. Bounds on neutron-mirror neutron mixing from pulsar timing. Phys. Rev. D 2019, 100, 123021. [Google Scholar] [CrossRef]
- Berezhiani, Z. Antistars or antimatter cores in mirror neutron stars? Universe 2022, 8, 313. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Biondi, R.; Mannarelli, M.; Tonelli, F. Neutron-mirror neutron mixing and neutron stars. Eur. Phys. J. C 2021, 81, 1036. [Google Scholar] [CrossRef]
- Beacham, J.; Burrage, C.; Curtin, D.; Roeck, A.D.; Evans, J.; Feng, J.L.; Gatto, C.; Gninenko, S.; Hartin, A.; Irastorza, I.; et al. Physics Beyond Colliders at CERN: Beyond the Standard Model Working Group Report. J. Phys. G 2020, 47, 010501. [Google Scholar] [CrossRef]
- Zöllner, R.; Kämpfer, B. Exotic Cores with and without Dark-Matter Admixtures in Compact Stars. Astronomy 2022, 1, 36–48. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J. Compact Star Physics; Cambridge University Press: Cambridge UK, 2020. [Google Scholar]
- Schulze, R.; Kämpfer, B. Cold quark stars from hot lattice QCD. arXiv 2009, arXiv:0912.2827. [Google Scholar]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L18. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Ecker, C.; Rezzolla, L. Impact of large-mass constraints on the properties of neutron stars. arXiv 2022, arXiv:2209.08101. [Google Scholar] [CrossRef]
- Shao, Y. On the Neutron Star/Black Hole Mass Gap and Black Hole Searches. Res. Astron. Astrophys. 2022, 22, 122002. [Google Scholar] [CrossRef]
- Farah, A.M.; Fishbach, M.; Essick, R.; Holz, D.E.; Galaudage, S. Bridging the Gap: Categorizing Gravitational-wave Events at the Transition between Neutron Stars and Black Holes. Astrophys. J. 2022, 931, 108. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef] [PubMed]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nature Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Altiparmak, S.; Ecker, C.; Rezzolla, L. On the Sound Speed in Neutron Stars. Astrophys. J. Lett. 2022, 939, L34. [Google Scholar] [CrossRef]
- Ayriyan, A.; Blaschke, D.; Grunfeld, A.G.; Alvarez-Castillo, D.; Grigorian, H.; Abgaryan, V. Bayesian analysis of multimessenger M-R data with interpolated hybrid EoS. Eur. Phys. J. A 2021, 57, 318. [Google Scholar] [CrossRef]
- Oter, E.L.; Windisch, A.; Llanes-Estrada, F.J.; Alford, M. nEoS: Neutron Star Equation of State from hadron physics alone. J. Phys. G 2019, 46, 084001. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Equation of State of Hot, Dense Matter and Neutron Stars. Phys. Rept. 2016, 621, 127–164. [Google Scholar] [CrossRef]
- Greif, S.K.; Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state constraints from nuclear physics, neutron star masses, and future moment of inertia measurements. Astrophys. J. 2020, 901, 155. [Google Scholar] [CrossRef]
- Anzuini, F.; Bell, N.F.; Busoni, G.; Motta, T.F.; Robles, S.; Thomas, A.W.; Virgato, M. Improved treatment of dark matter capture in neutron stars III: Nucleon and exotic targets. JCAP 2021, 11, 056. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Robles, S. Capture of Leptophilic Dark Matter in Neutron Stars. JCAP 2019, 06, 054. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Kumar, B.; Patra, S.K. Dark Matter Effects on the Compact Star Properties. Galaxies 2022, 10, 14. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Patra, S.K. Dark matter admixed neutron star as a possible compact component in the GW190814 merger event. Phys. Rev. D 2021, 104, 063028. [Google Scholar] [CrossRef]
- Blaschke, D.; Ayriyan, A.; Alvarez-Castillo, D.E.; Grigorian, H. Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars. Universe 2020, 6, 81. [Google Scholar] [CrossRef]
- Newton, W.G.; Balliet, L.; Budimir, S.; Crocombe, G.; Douglas, B.; Head, T.B.; Langford, Z.; Rivera, L.; Sanford, J. Ensembles of unified crust and core equations of state in a nuclear-multimessenger astrophysics environment. Eur. Phys. J. A 2022, 58, 69. [Google Scholar] [CrossRef]
- Huth, S.; Pang, P.T.H.; Tews, I.; Dietrich, T.; Fèvre, A.L.; Schwenk, A.; Trautmann, W.; Agarwal, K.; Bulla, M.; Coughlin, M.W.; et al. Constraining Neutron-Star Matter with Microscopic and Macroscopic Collisions. Nature 2022, 606, 276–280. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Riley, T.E.; Watts, A.L.; Greif, S.K.; Morsink, S.M.; Hebeler, K.; Schwenk, A.; Hinderer, T.; Nissanke, S.; Guillot, S.; et al. A NICER view of PSR J0030+0451: Implications for the dense matter equation of state. Astrophys. J. Lett. 2019, 887, L22. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Riley, T.E.; Hinderer, T.; Hebeler, K.; Schwenk, A.; Watts, A.L.; Nissanke, S.; Guillot, S.; Lattimer, J.M.; et al. Constraining the dense matter equation of state with joint analysis of NICER and LIGO/Virgo measurements. Astrophys. J. Lett. 2020, 893, L21. [Google Scholar] [CrossRef]
- Gorda, T.; Komoltsev, O.; Kurkela, A. Ab-initio QCD calculations impact the inference of the neutron-star-matter equation of state. arXiv 2022, arXiv:2204.11877. [Google Scholar]
- Cassing, M.; Brisebois, A.; Azeem, M.; Schaffner-Bielich, J. Exotic Compact Objects with Two Dark Matter Fluids. arXiv 2022, arXiv:2210.13697. [Google Scholar]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; McLerran, L.D.; Praszalowicz, M. Trace anomaly as signature of conformality in neutron stars. Phys. Rev. Lett. 2022, 129, 252702. [Google Scholar] [CrossRef]
- Marczenko, M.; McLerran, L.; Redlich, K.; Sasaki, C. Reaching percolation and conformal limits in neutron stars. arXiv 2022, arXiv:2207.13059. [Google Scholar] [CrossRef]
- Hippert, M.; Fraga, E.S.; Noronha, J. Insights on the peak in the speed of sound of ultradense matter. Phys. Rev. D 2021, 104, 034011. [Google Scholar] [CrossRef]
- Marczenko, M.; Redlich, K.; Sasaki, C. Reconciling Multi-messenger Constraints with Chiral Symmetry Restoration. arXiv 2022, arXiv:2208.03933. [Google Scholar] [CrossRef]
- Suleiman, L.; Fortin, M.; Zdunik, J.L.; Haensel, P. Influence of the crust on the neutron star macrophysical quantities and universal relations. Phys. Rev. C 2021, 104, 015801. [Google Scholar] [CrossRef]
- Gao, H.; Ai, S.K.; Cao, Z.J.; Zhang, B.; Zhu, Z.Y.; Li, A.; Zhang, N.B.; Bauswein, A. Relation between gravitational mass and baryonic mass for non-rotating and rapidly rotating neutron stars. Front. Phys. (Beijing) 2020, 15, 24603. [Google Scholar] [CrossRef]
- Ding, M.; Roberts, C.D.; Schmidt, S.M. Emergence of Hadron Mass and Structure. Particles 2023, 6, 57–120. [Google Scholar] [CrossRef]
- Dorkin, S.M.; Kaptari, L.P.; Hilger, T.; Kampfer, B. Analytical properties of the quark propagator from a truncated Dyson-Schwinger equation in complex Euclidean space. Phys. Rev. C 2014, 89, 034005. [Google Scholar] [CrossRef]
- Dorkin, S.M.; Kaptari, L.P.; Kämpfer, B. Accounting for the analytical properties of the quark propagator from the Dyson-Schwinger equation. Phys. Rev. C 2015, 91, 055201. [Google Scholar] [CrossRef]
- Greifenhagen, R.; Kämpfer, B.; Kaptari, L.P. Regge Trajectories of Radial Meson Excitations: Exploring the Dyson–Schwinger and Bethe–Salpeter Approach. In Discoveries at the Frontiers of Science; FIAS Interdisciplinary Science Series; Springer Nature: Berlin/Heidelberg, Germany, 2020; p. 55. [Google Scholar]
- Dorkin, S.M.; Hilger, T.; Kaptari, L.P.; Kampfer, B. Heavy pseudoscalar mesons in a Schwinger-Dyson–Bethe-Salpeter approach. Few Body Syst. 2011, 49, 247–254. [Google Scholar] [CrossRef]
- Dorkin, S.M.; Hilger, T.; Kampfer, B.; Kaptari, L.P. A Combined Solution of the Schwinger-Dyson and Bethe-Salpeter Equations for Mesons as qq¯ Bound States. arXiv 2010, arXiv:1012.5372. [Google Scholar]
- Kaptari, L.P.; Kämpfer, B. Mass Spectrum of Pseudo-Scalar Glueballs from a Bethe–Salpeter Approach with the Rainbow–Ladder Truncation. Few Body Syst. 2020, 61, 28. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D.; Schmidt, S.M. Chemical potential dependence of pi and rho properties. Phys. Rev. C 1998, 57, R28215. [Google Scholar] [CrossRef]
- Bender, A.; Poulis, G.I.; Roberts, C.D.; Schmidt, S.M.; Thomas, A.W. Deconfinement at finite chemical potential. Phys. Lett. B 1998, 431, 263–269. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Dyson-Schwinger equations: Density, temperature and continuum strong QCD. Prog. Part. Nucl. Phys. 2000, 45, S1. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Roberts, C.D.; Shrock, R.; Tandy, P.C. Confinement contains condensates. Phys. Rev. C 2012, 85, 065202. [Google Scholar] [CrossRef]
- Brambilla, N.; Eidelman, S.; Foka, P.; Gardner, S.; Kronfeld, A.S.; Alford, M.G.; Alkofer, R.; Butenschoen, M.; Cohen, T.D.; Erdmenger, J.; et al. QCD and Strongly Coupled Gauge Theories: Challenges and Perspectives. Eur. Phys. J. C 2014, 74, 2981. [Google Scholar]
- Thomas, R.; Zschocke, S.; Kampfer, B. Evidence for in-medium changes of four-quark condensates. Phys. Rev. Lett. 2005, 95, 232301. [Google Scholar] [CrossRef] [PubMed]
- Buchheim, T.; Hilger, T.; Kampfer, B. Wilson coefficients and four-quark condensates in QCD sum rules for medium modifications of D mesons. Phys. Rev. C 2015, 91, 015205. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Shrock, R. Condensates in Quantum Chromodynamics and the Cosmological Constant. Proc. Nat. Acad. Sci. USA 2011, 108, 45–50. [Google Scholar] [CrossRef]
- Gubler, P.; Satow, D. Recent Progress in QCD Condensate Evaluations and Sum Rules. Prog. Part. Nucl. Phys. 2019, 106. [Google Scholar] [CrossRef]
- Thomas, R.; Hilger, T.; Kampfer, B. Four-quark condensates in nucleon QCD sum rules. Nucl. Phys. A 2007, 795. [Google Scholar] [CrossRef]
- Fischer, C.S.; Kubrak, S.; Williams, R. Mass spectra and Regge trajectories of light mesons in the Bethe-Salpeter approach. Eur. Phys. J. A 2014, 50, 126. [Google Scholar] [CrossRef]
- DeWolfe, O.; Gubser, S.S.; Rosen, C. A holographic critical point. Phys. Rev. D 2011, 83, 086005. [Google Scholar] [CrossRef]
- Grefa, J.; Noronha, J.; Noronha-Hostler, J.; Portillo, I.; Ratti, C.; Rougemont, R. Hot and dense quark-gluon plasma thermodynamics from holographic black holes. Phys. Rev. D 2021, 104, 034002. [Google Scholar] [CrossRef]
- Critelli, R.; Noronha, J.; Noronha-Hostler, J.; Portillo, I.; Ratti, C.; Rougemont, R. Critical point in the phase diagram of primordial quark-gluon matter from black hole physics. Phys. Rev. D 2017, 96, 096026. [Google Scholar] [CrossRef]
- Järvinen, M. Holographic modeling of nuclear matter and neutron stars. Eur. Phys. J. C 2022, 82, 282. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Guenther, J.N.; Kara, R.; Katz, S.D.; Parotto, P.; Pásztor, A.; Ratti, C.; Szabó, K.K. Lattice QCD equation of state at finite chemical potential from an alternative expansion scheme. Phys. Rev. Lett. 2021, 126, 232001. [Google Scholar] [CrossRef] [PubMed]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabo, K.K. Full result for the QCD equation of state with 2+1 flavors. Phys. Lett. B 2014, 730. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Equation of state in ( 2+1 )-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Bellwied, R.; Borsanyi, S.; Fodor, Z.; Katz, S.D.; Pasztor, A.; Ratti, C.; Szabo, K.K. Fluctuations and correlations in high temperature QCD. Phys. Rev. D 2015, 92, 114505. [Google Scholar] [CrossRef]

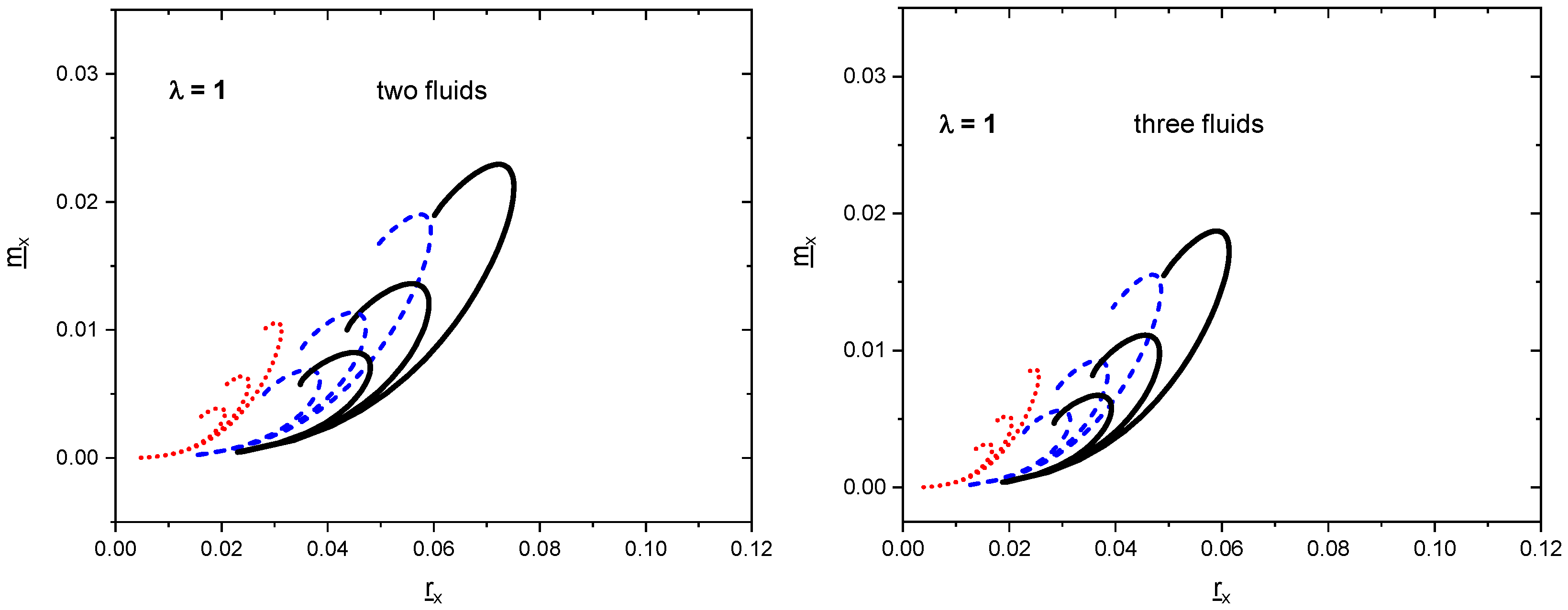
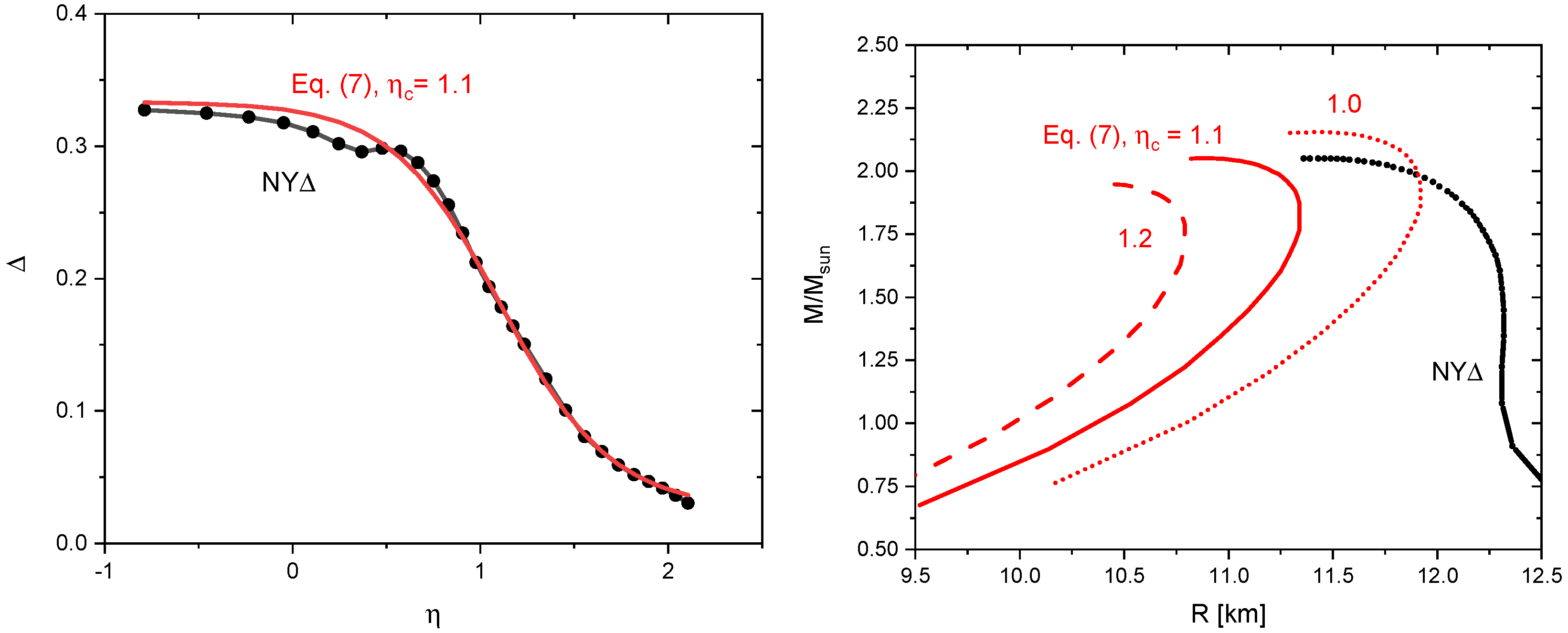
| 0.1 | 0.2 | 0.3 | ||
|---|---|---|---|---|
| 1 | 0.64 | 0.67 | 0.70 | |
| 1/3 | 0.49 | 0.51 | 0.53 | |
| 1/6 | 0.37 | 0.38 | 0.40 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zöllner, R.; Ding, M.; Kämpfer, B. Masses of Compact (Neutron) Stars with Distinguished Cores. Particles 2023, 6, 217-238. https://doi.org/10.3390/particles6010012
Zöllner R, Ding M, Kämpfer B. Masses of Compact (Neutron) Stars with Distinguished Cores. Particles. 2023; 6(1):217-238. https://doi.org/10.3390/particles6010012
Chicago/Turabian StyleZöllner, Rico, Minghui Ding, and Burkhard Kämpfer. 2023. "Masses of Compact (Neutron) Stars with Distinguished Cores" Particles 6, no. 1: 217-238. https://doi.org/10.3390/particles6010012
APA StyleZöllner, R., Ding, M., & Kämpfer, B. (2023). Masses of Compact (Neutron) Stars with Distinguished Cores. Particles, 6(1), 217-238. https://doi.org/10.3390/particles6010012







