Abstract
We review recent studies of vortical motion and the resulting polarization of hyperons in heavy-ion collisions at NICA energies, in particular, within the model of three-fluid dynamics (3FD). This includes predictions of the global polarization and ring structures that appear in Au+Au collisions. The global polarization in Au+Au collisions is calculated, including its rapidity and centrality dependence. The contributions of the thermal vorticity and meson-field term (proposed by Csernai, Kapusta, and Welle) to the global polarization are considered. The results are compared with data from recent STAR and HADES experiments. It is predicted that the polarization maximum is reached at 3 GeV if the measurements are performed with the same acceptance. It is demonstrated that a pair of vortex rings are formed, one at forward rapidities and another at backward rapidities, in ultra-central Au+Au collisions at 4 GeV. The vortex rings carry information about the early stage of the collision, in particular, the stopping of baryons. It is shown that these rings can be detected by measuring the ring observable , even in the midrapidity region at 5–20 GeV. At forward/backward rapidities, the signal is expected to be stronger. The possibility of observing the vortex-ring signal against the background of non-collective transverse polarization is discussed.
PACS:
25.75.-q; 25.75.Nq; 24.10.Nz
1. Introduction
Non-central heavy-ion collisions at high energies are characterized by a huge global angular momentum. It rapidly rises with the collision energy, exceeding the value of at NICA energies. However, only a part of the total angular momentum is accumulated in the participant region, i.e., in the overlap region of the interacting nuclei, which is of prime interest to us. According to the 3FD simulations, 25–30% of the total angular momentum is deposited into the participant matter in the Au+Au collisions at 8 fm, which is a huge amount. As the angular momentum is accumulated in the participant region, the motion of the matter becomes vortical. The vortical motion significantly affects the evolution of the system. However, theoretical and experimental studies of the relevant effects only began relatively recently. In particular, in Ref. [1], it was suggested that parton interaction in non-central heavy-ion collisions leads to a global quark polarization along the direction of the global angular momentum. This global polarization is essentially a local manifestation of the global angular momentum of the colliding system through spin-orbital coupling [2,3].
This phenomenon of the global polarization along the total angular momentum is closely related to the Barnett effect [4] (magnetization by rotation). The Barnett effect consists of the transformation of a fraction of the orbital angular momentum associated with the body rotation into the spin angular momenta of the atoms, which, on average, become directed along the orbital angular momentum. Because of the proportionality between the spin and magnetic moment, this polarization results in the magnetization of the rotating body.
The formation of vortex rings in heavy-ion collisions at high collision energies, 40–200 GeV, was predicted in hydrodynamic [5] and transport [6,7] simulations. Later, the vortex rings were reported at a lower energy of 7.7 GeV in the simulations of Refs. [8,9]. Earlier, ring-like structures, i.e., half rings, were noticed in semi-central Au+Au collisions at an even lower energy of 5 GeV [10,11]. The authors of Refs. [10,11] called this specific toroidal structure a femto-vortex sheet. In a recent paper [12], the formation of the vortex rings was predicted in Au+Au collisions at 7.7–11.5 GeV and even at 4.5 GeV, where the ring structure turns out to be more diffuse.
In Ref. [13], the analysis of the toroidal vortex structures was extended to proton–nucleus collisions. It was predicted that vortex rings are created in such collisions at an energy of 200 GeV. Vortex rings produced by jets propagating through the quark–gluon matter were considered in Ref. [14]. The above predictions [5,6,7,8,9,10,11,12,13,14] were obtained within different models. Thus, it appears that vortex rings are quite common for high-energy nucleus(proton)–nucleus collisions.
In the present paper, we review recent studies of vortical motion and the resulting polarization of hyperons in heavy-ion collisions at NICA energies, in particular, within the 3FD model [15]. This includes predictions of the global polarization [16,17] and ring structures that appear in Au+Au collisions [18].
The 3FD model takes into account the finite stopping power resulting in the counterstreaming of leading baryon-rich matter in the early stage of nuclear collisions [15]. This nonequilibrium stage is modeled using two counterstreaming baryon-rich fluids initially associated with the constituent nucleons of the projectile (p) and target (t) nuclei. Later on, these fluids may consist of any type of hadrons and/or partons (quarks and gluons), rather than only nucleons. Newly produced particles, dominantly populating the midrapidity region, are associated with a fireball (f) fluid. These fluids are governed by conventional hydrodynamic equations coupled with friction terms in the right-hand sides of the Euler equations. The friction results in energy–momentum loss of the baryon-rich fluids. A part of this loss is transformed into thermal excitation of these fluids, whereas another part leads to the formation of the fireball fluid. Thus, the 3FD approximation is a minimal way to implement the early-stage nonequilibrium of the produced strongly interacting matter at high collision energies. The 3FD model describes the major part of the bulk observables: the baryon stopping [19,20], yields of different hadrons, their rapidity and transverse momentum distributions [21,22,23], and also the elliptic [24] and directed [25] flow.
Three different equations of state (EoSs) were used in the simulations of Refs. [19,20,21,22,23,24,25]: a purely hadronic EoS [26] and two versions of the EoS with the deconfinement transition [27], i.e., a first-order phase transition (1PT) and a crossover one. In the present review, only the 1PT and crossover EoSs are discussed, as they are most relevant to the various observables. The physical input of the present 3FD calculations is described in Ref. [19].
2. Global Polarization at NICA Energies
All available data on the polarization of particles produced in heavy-ion collisions refer to hyperons because their weak decays present the most straightforward possibility for measuring polarization. In parity-violating weak decays, the daughter particle distribution in the rest frame of the hyperon directly depends on the hyperon polarization [28,29,30,31]. Measurements of the polarization of particles produced in heavy-ion collisions give us access to a new class of collective phenomena, i.e., the collective rotation of the nuclear medium. The STAR Collaboration at the Relativistic Heavy-Ion Collider (RHIC) observed the nonzero global polarization of and at collision energies 7.7 200 GeV [28,29] and, recently, multi-strange hyperons [30] at 200 GeV. Local polarization along the beam direction was also measured [31]. These measurements demonstrated the increase in global polarization with decreasing .
The spin polarization below 7.7 GeV is less explored. Although a simple extrapolation of this trend suggests that the global polarization continues to increase as decreases, we expect vanishing global polarization at due to the lack of system angular momentum. Therefore, a peak in global polarization should exist in the region 1.9 7.7 GeV. Recent model calculations predict this peak in different places: at 3 GeV [16,17,32,33] and 7.7 GeV [34].
The first data (some of them preliminary) on the global polarization of were presented in Refs. [35,36,37] for energies 3 GeV, 7.2 GeV, and 2.4 GeV, respectively. The first two energy points were obtained within the STAR fixed-target program (FXT-STAR) at RHIC, whereas the third point was obtained by the HADES Collaboration. These data indicate that the peak in global polarization is reached certainly below the energy of 7.7 GeV.
Below, we briefly review the consideration of Ref. [17].
2.1. Thermal-Vorticity Polarization
In the thermodynamic approach [38,39], particle polarization is related to so-called thermal vorticity, defined as
where , is the collective local four-velocity of the matter and T is the local temperature. Here, we deal with and T of the unified fluid because the system is equilibrated at the freeze-out stage, as argued in Ref. [17]. In the leading order in the thermal vorticity, it is directly related to the mean spin vector of spin 1/2 particles with four-momentum p, produced around point x on the freeze-out hypersurface
where is the Fermi-Dirac distribution function and m is the mass of the considered particle. The polarization vector of the S-spin particle is defined as
The polarization of the hyperon is measured in its rest frame; therefore, the polarization is
where is the mean spin vector of the hyperon in its rest frame. The zeroth component identically vanishes in the rest frame and the spatial component becomes [40]
where . Substituting the expression for from Equation (2) and averaging this expression over the direction (i.e., over ) results in the following polarization in the direction orthogonal to the reaction plane () [40]
where is the mass and and are the energy and momentum of the emitted hyperon, respectively. Here, we put because the production takes place only in high-temperature regions, where Boltzmann statistics dominates.
Particles are produced across the entire freeze-out hypersurface. Therefore, to calculate the global polarization vector, the above expression should be averaged over the freeze-out hypersurface and particle momenta
Here, is averaged over the whole system and the momenta of emitted particles. Application of the experimental rapidity acceptance is performed in terms of a so-called hydrodynamical rapidity
based on hydrodynamical 4-velocity . The integration runs only over those cells, where the condition is met. Let us denote this restricted freeze-out hypersurface as . Of course, this is only an imitation of the actual experimental acceptance. Unfortunately, imitation of transverse-momentum acceptance in a similar manner is impossible because the transverse momentum is mainly determined by thermal motion in the cell.
Similar to previous 3FD simulations [8,16], a simplified version of the freeze-out is used. The freeze-out is isochronous that, in particular, implies . The freeze-out instant is associated with the time when the energy density averaged over the central region (i.e., slab 4 fm) reaches the value of the average freeze-out energy density in the same central region obtained in conventional 3FD simulations with a differential, i.e., cell-by-cell, freeze-out [41,42]. It is important to note that the values of this actual freeze-out energy density, , averaged over the frozen-out system, are not parameters of the 3FD model. They are automatically generated in the 3FD simulations as a result of the implemented freeze-out dynamics described in Refs. [41,42]. The only freeze-out parameter is GeV/fm , which is the “trigger” energy density at which the freeze-out procedure starts. This parameter is the same for all EoSs and all collision energies.
We can simplify Equation (7) by explicitly performing an integration over . We reorganize the terms in parentheses in Equation (6) and use the following relations:
where is the density in the frame of calculation and is the 00 component of the partial energy–momentum tensor related to the contribution
with and being the corresponding partial energy density and pressure, respectively. , , and are determined by the ideal–gas relations in terms of the temperature, baryon, and strange chemical potentials. Note that the system is described by the ideal–gas EoS at the freeze-out stage. Thus, by inserting Expression (6) for into Equation (7) and performing the above-described manipulations, we arrive at
This is the final expression with which we perform our simulations.
2.2. Meson-Field Induced Polarization
The meson-field-induced contribution to the global polarization was proposed in Refs. [43,44] primarily to explain the observed - splitting in the global polarization. We do not discuss this splitting in the present paper because it deserves a special separate discussion, but rather study the effect of the meson-field-induced contribution on the polarization.
The relativistic mean-field (RMF) model [45,46] assumes that interaction among baryons are mediated by a scalar field and a vector field . The effective Lagrangian of this model is
Here, j labels the spin-1/2 baryons, and the field strength tensor for the vector field is
In general, the Lagrangian may include a potential of -field self-interaction, but its exact form is irrelevant here. Therefore, we put for definiteness. The V field is usually associated with the vector meson and with the meson. The field results in an attractive interaction and , a repulsive interaction. and are the coupling constants, the possible values of which can be found, e.g., in Ref. [47].
The and fields are treated in the mean-field approximation [45,46,47]:
where is the baryon current of j baryons in which baryons and antibaryons contribute with opposite signs, and
where is the scalar density in which baryons and antibaryons contribute with the same signs. It is expected that these interactions in terms of hadrons are relevant at the freeze-out stage, even if the preceding evolution was dominated by the quark–gluon phase. At this stage, the corresponding energy scale is much less than MeV and MeV. Therefore, the derivatives in Equations (15) and (16) can be neglected, and thus we arrive at the following solution for the fields
The field can be approximately expressed through the baryon current , where is the baryon density and is the mean coupling constant of the vector meson.
Derivation along the lines of Ref. [17] results in the mean spin vector of the hyperons ( or ) with four-momentum p, produced around point x
where and . The vector meson field enters this expression similar to the electromagnetic field interacting with the magnetic moment of the Y-hyperon [39]. This expression is valid [39] in the leading order in the thermal vorticity and field-strength tensor. The Fermi factor was again omitted because of its negligible effect at high temperatures achieved in nuclear collisions.
The further derivation is identical to that performed in the previous subsection with the substitution instead of . Finally, we arrive at the following expression for the meson-field contribution to the global polarization of the Y hyperon ( or ):
which should be added to the thermal-vorticity term (12). Here, and , and is defined in terms of the baryon current, , by Equation (17).
For practical calculations, the coupling constant and the mean coupling constant of the vector meson are needed. A brief survey of the various parametrizations of the RMF model is presented in Ref. [43] (see also [48,49]). We use just one of the possible parametrizations: 8.646, , and 783 MeV [50]. The mean coupling constant is associated with the nucleon one because nucleons dominate in the baryonic content of the system at low energies considered here. The uncertainty in the RMF model parametrization results in the corresponding uncertainty in the calculation.
It is important to note that we do not apply the RMF model to describe the matter dynamics. These dynamics are still described by the 3FD model with the aforementioned EoSs. Only the interaction that splits the polarization of and is taken from the RMF model. This splitting is an additional contribution to the global polarization, which is absent in the 3FD model.
2.3. Results
Only a fraction of all detected s are produced directly in the freeze-out stage. These are primary s. A fraction of s originates from decays of heavier hyperons. The most important feed-down channels are strong decays of and electromagnetic decays . When polarized particles decay, their daughters are themselves polarized because of angular momentum conservation. The amount of polarization that is transferred to the daughter particle depends on the momentum of the daughter in the rest frame of the parent. For the mean, momentum-integrated spin vector in the rest frame, a simple linear rule takes place, which is summarized in Table I of Ref. [39]. This feed-down from higher-lying resonances reduces the global polarization by ≈15–20% at NICA energies. All the results presented below are calculated considering the feed-down from higher-lying resonances.
Figure 1 demonstrates the effects of the thermal-vorticity and meson-field contributions to the midrapidity global polarization in a broader range of collision energies than those of NICA. This is done in order to correlate the predictions for the NICA range with a wider energy range, where there are more experimental data. As can be seen, the additional meson-field term reduces the polarization in the rapidity window at low collision energies and makes it closer to the STAR data at 3 GeV [35]. The overall agreement with the available data is quite good. The results at 4 GeV 7.7 GeV can be considered predictions for the NICA experiments.
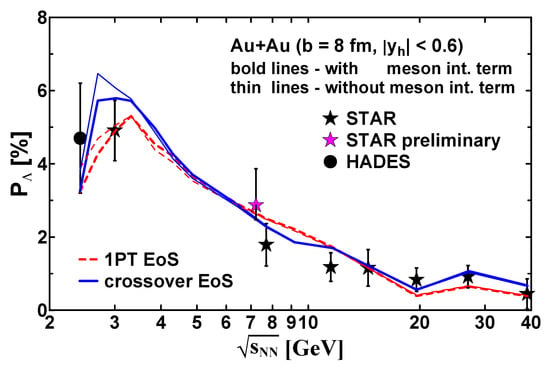
Figure 1.
Global polarization in midrapidity regions , originating from the thermal vorticity with (bold lines) and without (thin lines) the meson-field contribution in Au+Au collisions at 8 fm as a function of the collision energy . The results for different EoSs are presented. Data are from Refs. [28,35,36] (STAR) and [37] (HADES).
The meson-field effect becomes larger in wider rapidity windows, which capture the participant–spectator boundaries more strongly. This is because the baryon-current vorticity achieves the highest absolute values at the participant–spectator border, as argued in Ref. [17]. In particular, this is the reason that the rapidity dependence of the polarization is strongly affected by the meson-field contribution, as discussed below.
The rapidity dependence of the global polarization at 7.7 GeV is shown in Figure 2. The STAR centrality selection is 20–60%, which corresponds to the impact-parameter range 5.6–9.7 fm based on the overlap calculator [51]. Therefore, 8 fm can be chosen to represent this range. Although the STAR data are presented by four subsets corresponding to different selections of transverse momentum, , the 3FD results correspond to averaging over the whole range.
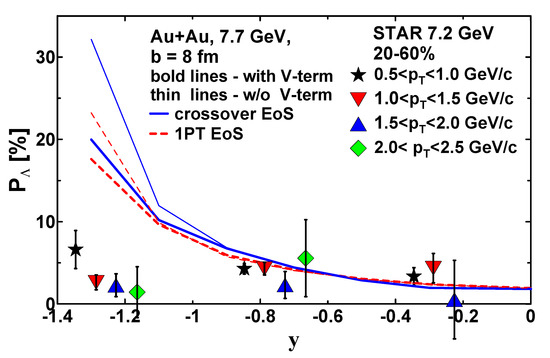
Figure 2.
Rapidity dependence of the global polarization in Au+Au collisions at 7.7 GeV ( 8 fm), originating from only the thermal vorticity (thin lines) and the one with the additional vector–meson contribution (bold lines). The results for different EoSs are presented. Preliminary STAR data for Au+Au collisions at 7.2 GeV and centrality 20–60% are from Ref. [36].
Both the thermal vorticity and the one with the additional vector–meson contribution (bold lines in Figure 2) describe the preliminary STAR data quite well [36] at . However, they overestimate the data at . The vector–meson contribution somewhat improves the agreement but the overestimation at persists. This observation demonstrates that once again, the effects of the thermal vorticity and vector–meson interaction become large in rapidity ranges overlapping with the participant–spectator border. Moreover, the above contributions produce effects of opposite signs. Therefore, the observed global polarization is a result of a delicate cancellation of the above contributions.
The global polarization of hyperons in Au+Au collisions is calculated at the impact parameters 2, 4, 6, 8, and 11 fm. The displayed impact parameters are associated with collision centrality using the Glauber simulations based on the nuclear overlap calculator [51]. In Figure 3, the centrality dependence of the global polarization in the midrapidity region () in Au+Au collisions at 7.7 GeV is displayed. The effect of the additional vector–meson contribution is negligible because the rapidity window does not cover the regions of the participant–spectator borders, as already discussed. The 3FD results describe the preliminary STAR data for 7.2 GeV energy reasonably well.
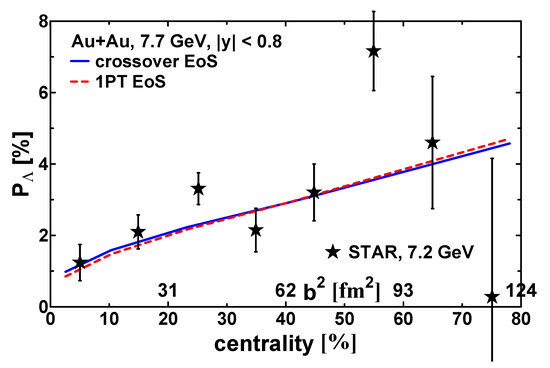
Figure 3.
Centrality dependence of the global polarization in the midrapidity region () in Au+Au collisions at 7.7 GeV. The results for different EoSs are presented. Preliminary STAR data for Au+Au collisions at 7.2 GeV are from Ref. [36]; only statistical errors are displayed.
We can conclude that the 3FD model describes the available data on the global polarization in and around the NICA energy range reasonably well. Keeping this in mind, we can proceed to an even less-explored topic, i.e., the production of vortical rings in heavy-ion collisions.
3. Vortical Rings
Vortex rings are inherent in fluid dynamics. They are developed in a cylindrically symmetric flow of fluid with longitudinal velocity depending on the radius. This flow results in the formation of toroidal vorticity structures, i.e., the vortex rings. An example of these vortex rings is smoke rings.
The formation of vortex rings is a consequence of the partial transparency of colliding nuclei at high energies. The matter in the central region is decelerated more strongly because there is thicker matter in the center than that at the periphery. Therefore, two vortex rings are formed at the periphery of the stronger stopped matter in the central region, one at forward rapidities and another at backward rapidities. The peripheral matter acquires a rotational motion. Matter rotation is opposite in these two rings. A schematic picture of the vortex rings is presented in Figure 4.
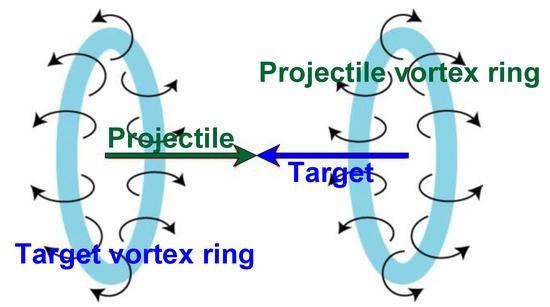
Figure 4.
Schematic picture of the vortex rings at forward/backward rapidities. Curled arrows indicate the direction of the circulation of the matter.
Partial transparency takes place in the early stage of the collision, even before the equilibration of the produced matter. It determines the strength of vorticity in the vortex rings. Therefore, the vortex rings carry information about this early stage of the collision.
3.1. Vortical Rings in Central Collisions
Let us first consider the structure of the thermal-vorticity field in heavy-ion collisions in the plane, where is the longitudinal space–time rapidity and z is the coordinate along the beam direction. The advantage of this is that it is equal to the kinematic longitudinal rapidity defined in terms of the particle momenta in the self-similar one-dimensional expansion of the system.
The plot of in ultra-central ( fm) Au+Au collisions at 4.9–11.5 GeV in the plane is presented in Figure 5. In order to suppress the contributions of almost empty regions, the displayed thermal vorticity is averaged with the weight of proper energy density (also presented in Figure 5) similar to that in Refs. [5,8]. The plane would be a reaction plane in case of non-central collisions. In our case ( fm), all the planes passing through the z-axis are equivalent because of the axial symmetry. These are the plots at the time instants close to the freeze-out. In order to see the correlations of the thermal vorticity with other quantities, plots of the proper energy density, x-component of the baryon current (), and proper baryon density are also displayed. As can be seen, the thermal vorticity reveals a ring structure similar to that schematically displayed in Figure 4. The plane is a cut of these rings by the plane passing through the axis of these rings. This ring structure is seen even at 4.9 GeV.
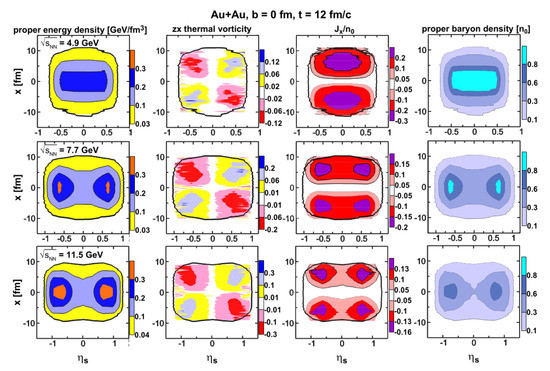
Figure 5.
Columns from left to right: the proper energy density (GeV/fm), the proper-energy-density-weighted relativistic thermal vorticity, x-component of the baryon current () in units of normal nuclear density ( 1/fm), and the proper baryon density () in units of in the plane at time instant 12 fm/c in the ultra-central ( 0 fm) Au+Au collisions at 4.9–11.5 GeV. is the space–time rapidity along the beam (z-axis) direction. Calculations are performed with the crossover EoS. The bold solid contour indicates the border of the nuclear matter with .
As seen in Figure 5, these thermal-vorticity rings correlate with the transverse component of the baryon current (). This means that the vortical rings expand, which is important for their observation. At the same time, the proper energy and density distributions reveal a disk rather than a ring structure, although at the same space–time rapidities. At 4.9 GeV, this is already a central fireball rather than two disks.
At the considered moderately relativistic energies, the expansion dynamics of the system are not of a self-similar one-dimensional character. Therefore, the space–time rapidity is not equal to the kinematic longitudinal rapidity in terms of the particle momenta. Nevertheless, it can be used to approximately estimate the rapidity location of these vortex rings. As seen in Figure 5, at 4.9 GeV, these rings are located slightly below 0.5 and at 0.5 if 7.7 GeV. This location does not restrict their observation because the FXT-STAR experiments allow measurements at very backward rapidities. At 11.5 GeV, where the estimation in terms of is more reliable, these vortex rings are already located at 0.5–1.0, which is slightly beyond the rapidity window of the collider experiment. Nevertheless, the inner parts of these rings are still at 0.5. Therefore, their effect can be observed.
3.2. Ring Observable
The authors of Refs. [13,14] suggested a ring observable
where is the polarization of the hyperon, is its spacial momentum, and is the unit vector along the beam, i.e., along the z-axis. Averaging runs over all momenta with fixed rapidity y. As argued in Refs. [13,14], the ring structure may be quantified using . This ring observable was applied to the analysis of ultra-central Au+Au collisions at 200 GeV [13]. It was found that nonzero values of appear only at rapidities 4, i.e., far beyond the midrapidity window accessible in collider experiments.
However, the same ring observable turns out to be nonzero in proton–proton and proton–nucleus collisions (see, e.g., Refs. [52,53], where a brief survey of earlier experiments is also presented). It is referred to as a transverse polarization in those experiments. At least in proton–proton reactions, the nonzero is related to the correlation of the produced with the beam direction rather than to the collective ring structure. To be precise, only the collective contribution to due to the vortex rings is estimated below, and the discussion of the background of direct production can be found in a later section of this paper.
To quantify the qualitative considerations in the preceding subsection, let us turn to the ring observable in Equation (21). Our goal is to estimate the expected ring observable in the ultra-central ( 0 fm) Au+Au collisions rather than to calculate it.
In terms of hydrodynamic quantities, the contribution of an element of the freeze-out surface to the ring observable reads
where is the unit vector along the beam (z) axis and is the normal vector to the element of the freeze-out surface.
To calculate the ring observable , should be averaged over the whole freeze-out surface and particle momenta
where is the distribution function of s. Here, the approximation has already been made: the constraint of fixed rapidity (y) imposed on the momentum integration is replaced by that of fixed hydrodynamical rapidity (8), similar to that in the preceding subsection [17]. The constraint is imposed on the freeze-out surface integration and is denoted as in Equation (23). At moderately relativistic energies, the hydrodynamical rapidity is a more reliable approximation of the true rapidity than the space–time rapidity .
Let us further proceed with the approximations. Similar to that in the preceding subsection [17], let us use a simplified version of the freeze-out, i.e., an isochronous one, that implies and . Expression (2) for is also simplified. The factor is taken because the production takes place only in high-temperature regions, where Boltzmann statistics dominates. As spatial components of are of prime interest, the approximation is made. The latter approximation, , reduces , which is quite suitable for the upper estimate of the ring observable. The boost of is neglected, which also reduces . After the application of all these approximations, , and hence, , becomes momentum-independent. Therefore, the momentum averaging in Equation (23) can be performed first, leaving beyond the scope of this averaging:
where is the density of s, is the transverse component of the fluid velocity, and T is the temperature. This expression is obtained in the non-relativistic approximation for the transverse collective motion. Indeed, at the freeze-out, 100 MeV and ≲ 0.4 at midrapidity [54]. At the forward/backward rapidities considered here, these values are even smaller. Here, ( + 2T/mΛ)1/2 stand for ⟨|pT|⟩/mΛ. It is important that the system, together with the vortex rings, radially expands at the freeze-out stage. This expansion even determines the sign of RΛ, as seen in Equation (24).
Based on the axial symmetry of the ultra-central ( 0) collisions, the averaging in Equation (24) can be restricted by the quadrant () of the “reaction” plane , [the () quadrant in Figure 5] if . For negative , it is the () quadrant. Thus, this averaging becomes identical to that carried out in the preceding subsection [17] for the calculation of the global polarization but in a restricted region, i.e., the () quadrant. The only difference is that the averaging over cells runs with additional weight , where x takes into account that the integration runs over in cylindrical coordinates at a fixed azimuthal angle.
The estimation of the quantity, averaged over different rapidity ranges, in the ultra-central ( 0) Au+Au collisions as a function of is displayed in Figure 6. For definiteness, all these rapidity ranges are located at positive rapidities because is an odd function of y. In the fixed rapidity region, the magnitude of first increases with the increase in the collision energy; reaches a maximum, the position and height of which depend on the rapidity window; and then decreases. The height of the maximum is larger in wider rapidity windows. All these features are expected from the above qualitative consideration. The presented calculations have a numerical uncertainty of 10–15%. These numerical fluctuations result from averaging over a very restricted spacial region, rather than the whole volume of the system, as performed for the global polarization [17]. These fluctuations are larger for at fixed y because the averaging runs over even more restricted spacial regions in this case.
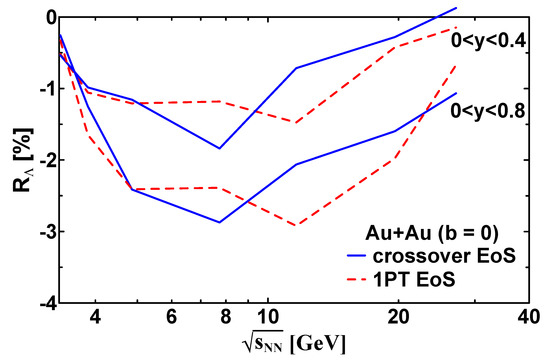
Figure 6.
The quantity averaged over different rapidity ranges in the ultra-central Au+Au collisions as a function of . Calculations are performed with the crossover and 1PT EoSs.
The calculations are performed with the crossover and 1PT EoSs. The predictions of the different EoSs differ but this difference is comparable with the numerical uncertainty at energies below 7 GeV and above 12 GeV. However, at 7 ≲ ≲ 12 GeV, this difference exceeds the numerical uncertainty. This energy range correlates with that of the earlier predicted irregularity in the excitation function of the baryon stopping [19,20], where the results of different EoSs also differ. This is not surprising because the incomplete baryon stopping (or partial transparency) is the driving force for the vortex ring formation. In particular, this is the reason for the correlation between the thermal vorticity and baryon current (see Figure 5).
The rapidity dependence of the quantity in the ultra-central Au+Au collisions at different is shown in Figure 7. Given the large numerical fluctuations, the lines in Figure 7 are smoothed using orthogonal-polynomial fit. Again, as expected, extreme values of are reached at forward/backward rapidities, where the vortex rings are located. The positions of these extreme values move to larger with the increase in the collision energy. However, even at 5 19.6 GeV, sizable values of can be expected at 0.5, attainable in the collider mode. Feed-down from higher-lying resonances ( and ) in has been taken into account similar to the global polarization in Ref. [17]. This feed-down reduces by ≈15%.
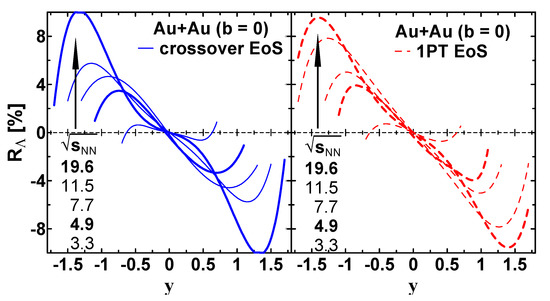
Figure 7.
Rapidity dependence of the quantity in the ultra-central ( 0) Au+Au collisions at 3.3–19.6 GeV (upwards at −1). Distributions at 4.9 and 19.6 GeV are indicated by bold lines. Calculations are performed with the crossover (left panel) and 1PT (right panel) EoSs.
4. Summary and Discussion
The global polarization in Au+Au collisions at NICA energies was calculated. The contributions of the thermal vorticity and meson-field interaction [43] to the global polarization were considered. The results were compared with recent data [36]. It was predicted that the global polarization increases with a decrease in the collision energy. The maximum was reached at 3 GeV if the measurements were performed with the same acceptance. The meson-field contribution was large at the participant–spectator border and hence considerably reduced the polarization at forward/backward rapidities, whereas it was practically insignificant at the midrapidity region. This improved the agreement of the calculated polarization with the available data.
The ring structures that appear in Au+Au collisions at energies 4–20 GeV were studied and the resulting ring observable was estimated. The calculations were performed within the 3FD model [15]. It was demonstrated that a pair of vortex rings are formed, one at forward rapidities and another at backward rapidities, in ultra-central Au+Au collisions at ≳ 4 GeV. The matter rotation is opposite in these two rings. They are formed because in the early stage of the collision, the matter in the vicinity of the beam axis decelerates more strongly than that at the periphery. Thus, the vortex rings carry information about this early stage, in particular, the stopping of baryons.
These rings can be detected by measuring the ring observable , even in the rapidity range (or ). The signal is stronger in wider rapidity ranges. For instance, the magnitude of the ring observable may reach values of 2–3% at 5–20 GeV if the rapidity window is extended to . Measurements in fixed-target experiments, such as FXT-STAR and the forthcoming experiments at FAIR, provide additional advantages. They allow measurements at backward rapidities, where the signal is expected to be more pronounced.
Only ultra-central Au+Au collisions were considered in this paper because the axial symmetry of the system makes the estimation easier in this case. Asymmetric vortex rings are also formed in semi-central collisions at 5 GeV. The corresponding polarization should be asymmetric in the reaction plain.
The quantity also contains the contribution of direct production with the polarization correlated with the beam direction. In heavy-ion collisions, this type of polarization is expected to be diluted due to rescatterings in the medium [55,56]. A vanishing polarization has been proposed as a possible signature for the formation of a Quark Gluon Plasma (QGP) in relativistic heavy-ion collisions [55]. This prediction was one of the motivations for the experimental study of the transverse polarization of hyperons produced in Au+Au collisions (10.7A GeV) [57]. The results revealed no significant differences in polarization from those observed in and collisions. However, the question of the nature of the obtained polarization remains open, i.e., which part results from direct production and which part results from the vortex rings.
Different transverse-momentum dependencies may be used to distinguish these two mechanisms of the transverse polarization. Although the magnitude of transverse polarization due to direct production linearly increases with transverse momentum, low- s should dominate in the due to the vortex rings because these rings are collective phenomena. The dependence of the vortex-ring is expected to decrease, similar to that for the global polarization [35,36,58]. Therefore, limiting the transverse momentum from above would enhance the contribution of the vortex rings.
In any case, the calculations of the due to the vortex rings should be complemented by simulations of the transverse polarization due to the direct production, similar to those performed for the ultra-central Au+Au collisions at 9 GeV in Ref. [59]. That simulation disregarded the polarization dilution due to rescatterings in the medium. Therefore, it gave the upper limit (≈−5%) on the magnitude of the mean transverse polarization. For practical use, such simulations should consider this dilution [56].
The transverse polarization measured in collisions so far is consistent with zero [60]. On the other hand, the collective fluid vorticity in collisions polarizes all emitted particles and, hence, should take place. Therefore, looks to be a good observable for detecting vortex rings.
Author Contributions
All the authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the MEPhI program Priority 2030 and the Ministry of Science and Higher Education of the Russian Federation, Project “New Phenomena in Particle Physics and the Early Universe” No FSWU-2023-0073.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Fruitful discussions with A. Ayala, E. E. Kolomeitsev, O. V. Teryaev, and D. N. Voskresensky are gratefully acknowledged. This work was carried out using computing resources of the federal collective usage center “Complex for simulation and data processing for mega-science facilities” at NRC “Kurchatov Institute” (http://ckp.nrcki.ru/). This work was partially supported by MEPhI within the Federal Program “Priority-2030”.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NICA | Nuclotron-based Ion Collider Facility |
| RHIC | Relativistic Heavy Ion Collider |
| FAIR | Facility for Antiproton and Ion Research |
| FXT-STAR | STAR fixed-target program at RHIC |
| 3FD | three-fluid dynamics |
| EoS | equation of state |
| 1PT EoS | EoS with the first-order phase transition |
References
- Liang, Z.T.; Wang, X.N. Globally polarized quark-gluon plasma in non-central A+A collisions. Phys. Rev. Lett. 2005, 94, 102301, Erratum: [Phys. Rev. Lett. 2006, 96, 039901]. [Google Scholar] [CrossRef] [PubMed]
- Betz, B.; Gyulassy, M.; Torrieri, G. Polarization probes of vorticity in heavy ion collisions. Phys. Rev. C 2007, 76, 044901. [Google Scholar] [CrossRef]
- Gao, J.H.; Chen, S.W.; Deng, W.t.; Liang, Z.T.; Wang, Q.; Wang, X.N. Global quark polarization in non-central A+A collisions. Phys. Rev. C 2008, 77, 044902. [Google Scholar] [CrossRef]
- Barnett, S.J. Magnetization by rotation. Phys. Rev. 1915, 6, 239. [Google Scholar]
- Ivanov, Y.B.; Soldatov, A.A. Vortex rings in fragmentation regions in heavy-ion collisions at = 39 GeV. Phys. Rev. C 2018, 97, 044915. [Google Scholar] [CrossRef]
- Xia, X.L.; Li, H.; Tang, Z.B.; Wang, Q. Probing vorticity structure in heavy-ion collisions by local Λ polarization. Phys. Rev. C 2018, 98, 024905. [Google Scholar] [CrossRef]
- Wei, D.X.; Deng, W.T.; Huang, X.G. Thermal vorticity and spin polarization in heavy-ion collisions. Phys. Rev. C 2019, 99, 014905. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Toneev, V.D.; Soldatov, A.A. Vorticity and Particle Polarization in Relativistic Heavy-Ion Collisions. Phys. Atom. Nucl. 2020, 83, 179–187. [Google Scholar] [CrossRef]
- Zinchenko, A.; Sorin, A.; Teryaev, O.; Baznat, M. Vorticity structure and polarization of Λ hyperons in heavy-ion collisions. J. Phys. Conf. Ser. 2020, 1435, 012030. [Google Scholar] [CrossRef]
- Baznat, M.; Gudima, K.; Sorin, A.; Teryaev, O. Helicity separation in Heavy-Ion Collisions. Phys. Rev. C 2013, 88, 061901. [Google Scholar] [CrossRef]
- Baznat, M.I.; Gudima, K.K.; Sorin, A.S.; Teryaev, O.V. Femto-vortex sheets and hyperon polarization in heavy-ion collisions. Phys. Rev. C 2016, 93, 031902. [Google Scholar] [CrossRef]
- Tsegelnik, N.S.; Kolomeitsev, E.E.; Voronyuk, V. Helicity and vorticity in heavy-ion collisions at NICA energies. arXiv 2022, arXiv:2211.09219. [Google Scholar]
- Lisa, M.A.; Barbon, J.G.P.; Chinellato, D.D.; Serenone, W.M.; Shen, C.; Takahashi, J.; Torrieri, G. Vortex rings from high energy central p+A collisions. Phys. Rev. C 2021, 104, 011901. [Google Scholar] [CrossRef]
- Serenone, W.M.; Barbon, J.G.P.; Chinellato, D.D.; Lisa, M.A.; Shen, C.; Takahashi, J.; Torrieri, G. Λ polarization from thermalized jet energy. Phys. Lett. B 2021, 820, 136500. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Russkikh, V.N.; Toneev, V.D. Relativistic heavy-ion collisions within 3-fluid hydrodynamics: Hadronic scenario. Phys. Rev. C 2006, 73, 044904. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Global Λ polarization in moderately relativistic nuclear collisions. Phys. Rev. C 2021, 103, L031903. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Soldatov, A.A. Global Λ polarization in heavy-ion collisions at energies 2.4–7.7 GeV: Effect of meson-field interaction. Phys. Rev. C 2022, 105, 034915. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Vortex rings in heavy-ion collisions at energies = 3–30 GeV and possibility of their observation. arXiv 2022, arXiv:2211.17190. [Google Scholar]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: I. Baryon Stopping. Phys. Rev. C 2013, 87, 064904. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Baryon Stopping as a Probe of Deconfinement Onset in Relativistic Heavy-Ion Collisions. Phys. Lett. B 2013, 721, 123. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: II. Particle Production. Phys. Rev. C 2013, 87, 064905. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: III. Transverse Momentum Spectra. Phys. Rev. C 2014, 89, 024903. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Soldatov, A.A. Bulk Properties of the Matter Produced at Energies of the Beam Energy Scan Program. Phys. Rev. C 2018, 97, 024908. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Soldatov, A.A. Elliptic Flow in Heavy-Ion Collisions at Energies = 2.7–39 GeV. Phys. Rev. C 2015, 91, 024914. [Google Scholar] [CrossRef]
- Konchakovski, V.P.; Cassing, W.; Ivanov, Y.B.; Toneev, V.D. Examination of the directed flow puzzle in heavy-ion collisions. Phys. Rev. C 2014, 90, 014903. [Google Scholar] [CrossRef]
- Mishustin, I.N.; Russkikh, V.N.; Satarov, L.M. Fluid dynamical model of relativistic heavy ion collision. Sov. J. Nucl. Phys. 1991, 54, 260–314. (In Russian) [Google Scholar]
- Khvorostukin, A.S.; Skokov, V.V.; Toneev, V.D.; Redlich, K. Lattice QCD constraints on the nuclear equation of state. Eur. Phys. J. C 2006, 48, 531–543. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Global Λ hyperon polarization in nuclear collisions: Evidence for the most vortical fluid. Nature 2017, 548, 62. [Google Scholar]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; et al. Global polarization of Λ hyperons in Au+Au collisions at = 200 GeV. Phys. Rev. C 2018, 98, 014910. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; et al. Global Polarization of Ξ and Ω Hyperons in Au+Au Collisions at = 200 GeV. Phys. Rev. Lett. 2021, 126, 162301. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; et al. Polarization of Λ () hyperons along the beam direction in Au+Au collisions at = 200 GeV. Phys. Rev. Lett. 2019, 123, 132301. [Google Scholar] [CrossRef]
- Deng, X.G.; Huang, X.G.; Ma, Y.G.; Zhang, S. Vorticity in low-energy heavy-ion collisions. Phys. Rev. C 2020, 101, 064908. [Google Scholar] [CrossRef]
- Ayala, A.; Domínguez, I.; Maldonado, I.; Tejeda-Yeomans, M.E. Rise and fall of Λ and global polarization in semi-central heavy-ion collisions at HADES, NICA and RHIC energies from the core-corona model. Phys. Rev. C 2022, 105, 034907. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, J.; Wang, E.; Xing, H.; Zhang, H. Hyperon polarization from the vortical fluid in low-energy nuclear collisions. Phys. Rev. C 2021, 104, L041902. [Google Scholar] [CrossRef]
- Abdallah, M.S.; Aboona, B.E.; Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, I.; Aggarwal, M.M.; Ahammed, Z.; et al. Global Λ-hyperon polarization in Au+Au collisions at = 3 GeV. Phys. Rev. C 2021, 104, L061901. [Google Scholar] [CrossRef]
- Okubo, K. Measurement of global polarization of Λ hyperons in Au+Au = 7.2 GeV fixed target collisions at RHIC-STAR experiment. EPJ Web Conf. 2022, 259, 06003. [Google Scholar] [CrossRef]
- Abou Yassine, R.; Adamczewski-Musch, J.; Asal, C.; Becker, M.; Belounnas, A.; Blanco, A.; Blume, C.; Chlad, L.; Chudoba, P.; Ciepa, I.; et al. Measurement of global polarization of Λ hyperons in few-GeV heavy-ion collisions. Phys. Lett. B 2022, 835, 137506. [Google Scholar] [CrossRef]
- Becattini, F.; Chandra, V.; Del Zanna, L.; Grossi, E. Relativistic distribution function for particles with spin at local thermodynamical equilibrium. Ann. Phys. 2013, 338, 32. [Google Scholar] [CrossRef]
- Becattini, F.; Karpenko, I.; Lisa, M.; Upsal, I.; Voloshin, S. Global hyperon polarization at local thermodynamic equilibrium with vorticity, magnetic field and feed-down. Phys. Rev. C 2017, 95, 054902. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Toneev, V.D.; Voronyuk, V. Vorticity and hyperon polarization at energies available at JINR Nuclotron-based Ion Collider fAcility. Phys. Rev. C 2018, 97, 064902. [Google Scholar] [CrossRef]
- Russkikh, V.N.; Ivanov, Y.B. Dynamical freeze-out in 3-fluid hydrodynamics. Phys. Rev. C 2007, 76, 054907. [Google Scholar] [CrossRef]
- Ivanov, Y.B.; Russkikh, V.N. On freeze-out problem in relativistic hydrodynamics. Phys. Atom. Nucl. 2009, 72, 1238. [Google Scholar] [CrossRef]
- Csernai, L.; Kapusta, J.; Welle, T. Λ and spin interaction with meson fields generated by the baryon current in high energy nuclear collisions. Phys. Rev. C 2019, 99, 021901. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, G.; Csernai, L.P. A study of Λ and polarization splitting by meson field in PICR hydrodynamic model. Eur. Phys. J. C 2021, 81, 12. [Google Scholar] [CrossRef]
- Walecka, J.D. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491. [Google Scholar] [CrossRef]
- Serot, B.D. Quantum hadrodynamics. Rep. Prog. Phys. 1992, 55, 1855. [Google Scholar] [CrossRef]
- Kapusta, J.I.; Gale, C. Finite Temperature Field Theory; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802, [Erratum: Phys. Rev. C 2014, 90, 019904]. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic Mean-Field Models with Scaled Hadron Masses and Couplings: Hyperons and Maximum Neutron Star Mass. Nucl. Phys. A 2016, 950, 64–109. [Google Scholar] [CrossRef]
- Cohen, J.; Weber, H.J. Relativistic sigma—Omega mean field theory for hyperons from a quark model. Phys. Rev. C 1991, 44, 1181–1187. [Google Scholar] [CrossRef]
- Web Interface for a Nuclear Overlap Calculation Code. Available online: http://web-docs.gsi.de/~misko/overlap/interface.html (accessed on 23 January 2023).
- Hauenstein, F.; Borodina, E.; Clement, H.; Doroshkevich, E.; Dzhygadlo, R.; Ehrhardt, K.; Eyrich, W.; Gast, W.; Gillitzer, A.; Grzonka, D.; et al. Measurement of polarization observables of the associated strangeness production in proton proton interactions. Eur. Phys. J. A 2016, 52, 337. [Google Scholar] [CrossRef]
- Agakishiev, G.; Arnold, O.; Balanda, A.; Belver, D.; Belyaev, A.V.; Berger-Chen, J.C.; Blanco, A.; Bohmer, M.; Boyard, J.L.; Cabanelas, P.; et al. Lambda hyperon production and polarization in collisions of p(3.5 GeV)+Nb. Eur. Phys. J. A 2014, 50, 81. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Bulk Properties of the Medium Produced in Relativistic Heavy-Ion Collisions from the Beam Energy Scan Program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Panagiotou, A.D. Λ0 Nonpolarization: Possible Signature of Quark Matter. Phys. Rev. C 1986, 33, 1999–2002. [Google Scholar] [CrossRef]
- Ayala, A.; Cuautle, E.; Herrera, G.; Montano, L.M. Λ0 polarization as a probe for production of deconfined matter in ultrarelativistic heavy ion collisions. Phys. Rev. C 2002, 65, 024902. [Google Scholar] [CrossRef]
- Bellwied, R. Transverse polarization of Lambda hyperons in relativistic Au—Au collisions at the AGS. Acta Phys. Hung. A 2002, 15, 437–444. [Google Scholar] [CrossRef]
- Adams, J.R. Differential measurements of Λ polarization in Au+Au collisions and a search for the magnetic field by STAR. Nucl. Phys. A 2021, 1005, 121864. [Google Scholar] [CrossRef]
- Nazarova, E.; Akhat, R.; Baznat, M.; Teryaev, O.; Zinchenko, A. Monte Carlo Study of Λ Polarization at MPD. Phys. Part. Nucl. Lett. 2021, 18, 429–438. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; et al. Measurement of the transverse polarization of Λ and hyperons produced in proton-proton collisions at = 7 TeV using the ATLAS detector. Phys. Rev. D 2015, 91, 032004. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).