Bayesian Exploration of Phenomenological EoS of Neutron/Hybrid Stars with Recent Observations
Abstract
1. Introduction
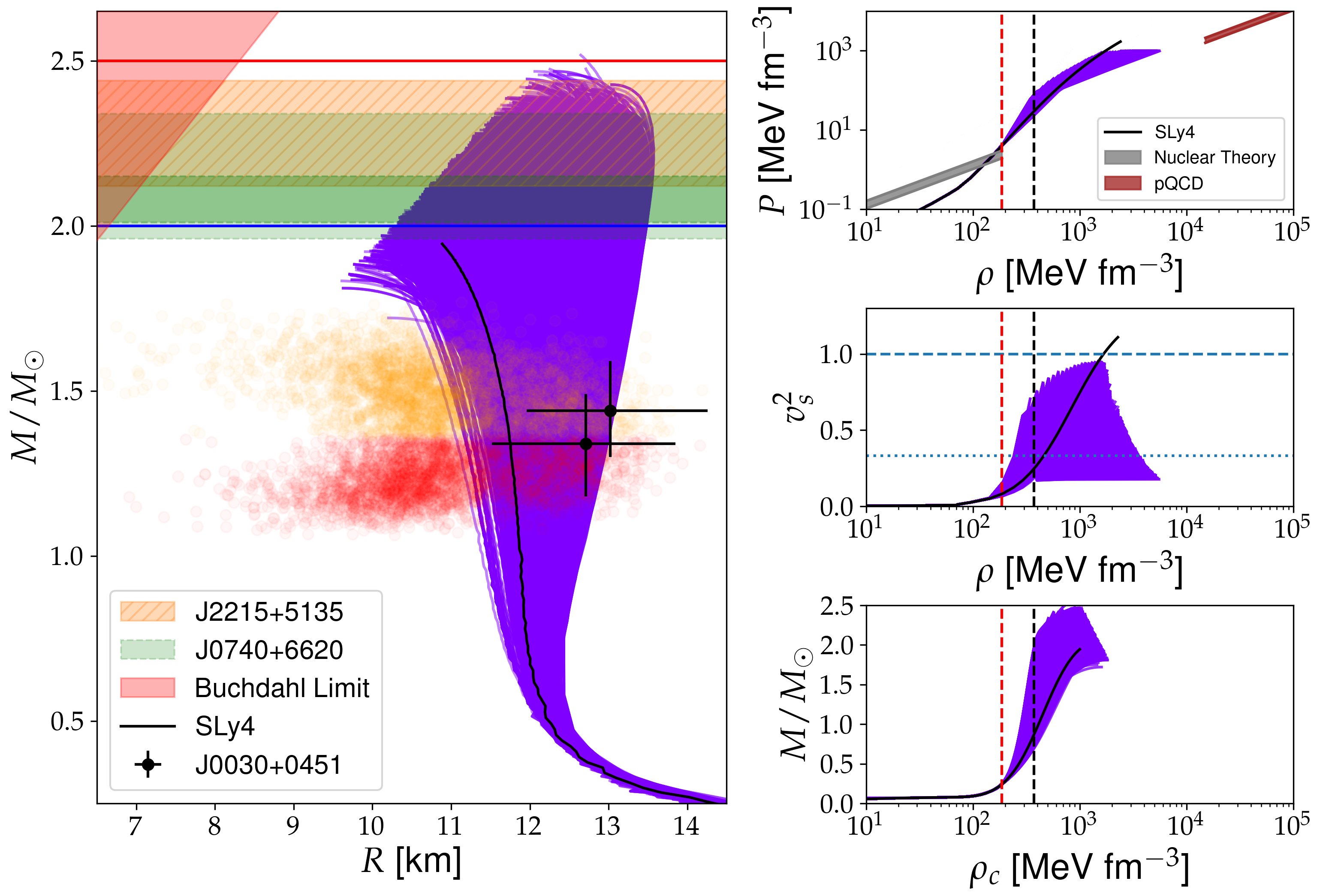
2. The Structure of Neutron Stars
3. The Equation of State
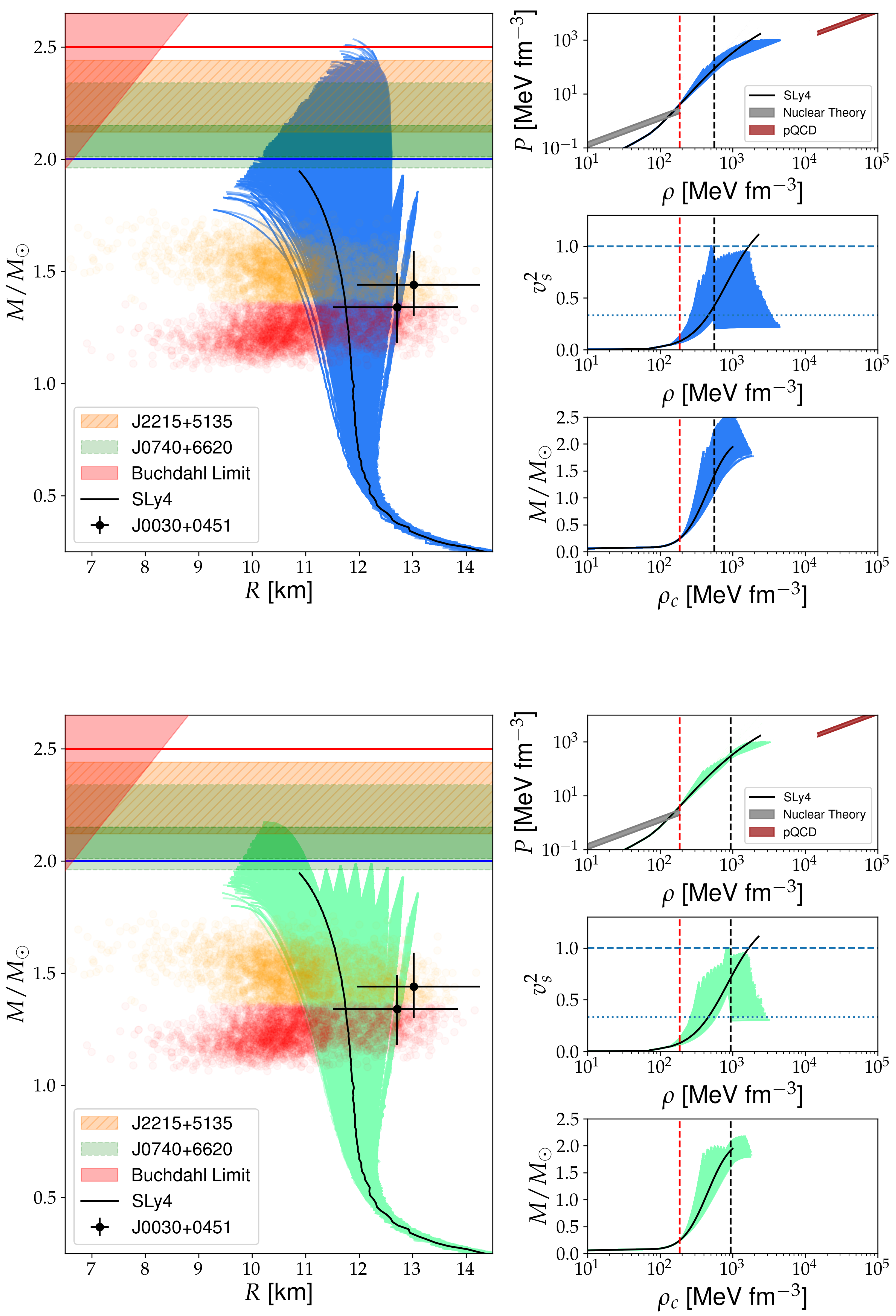
Piecewise Polytropic Representation
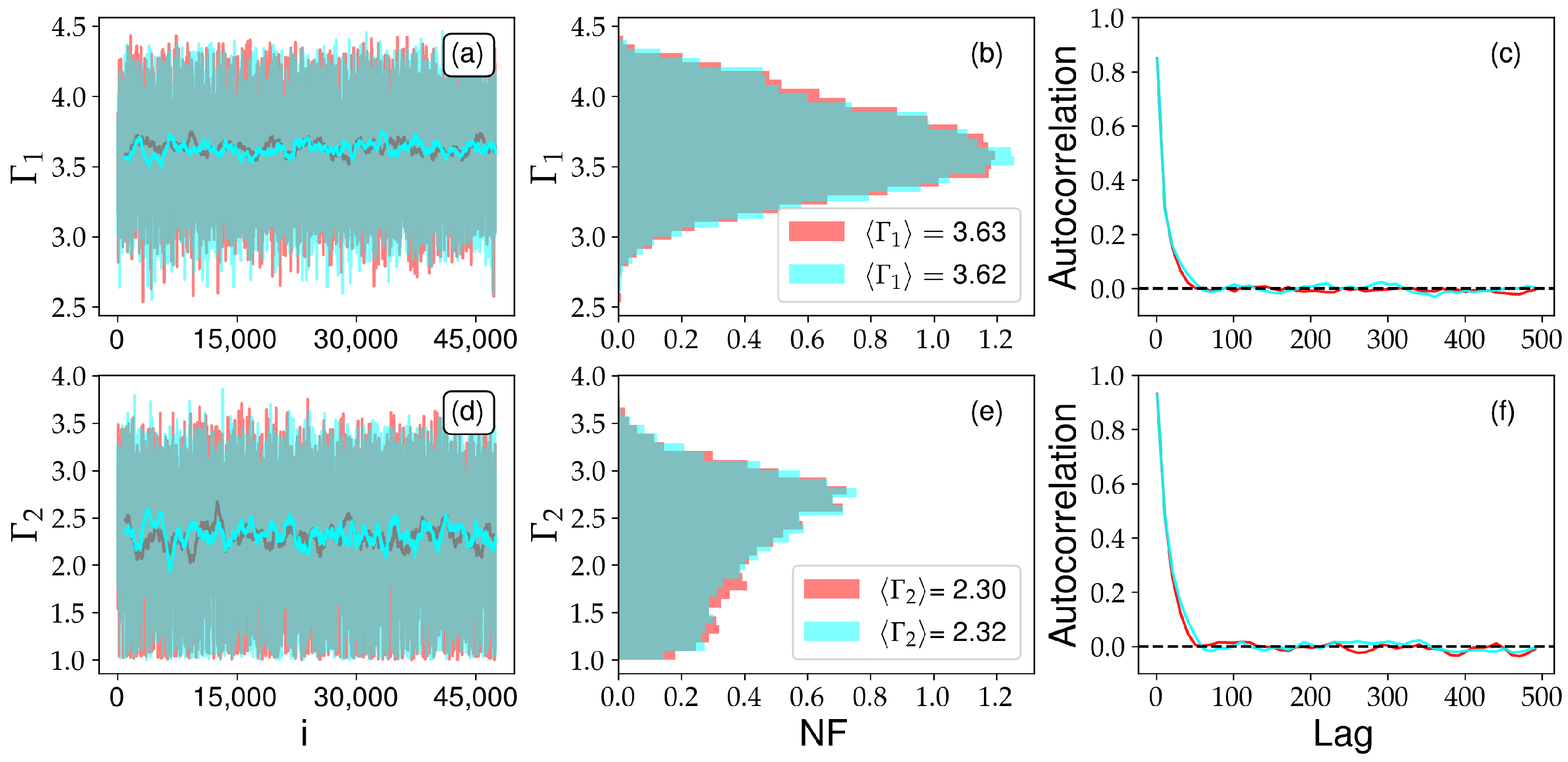
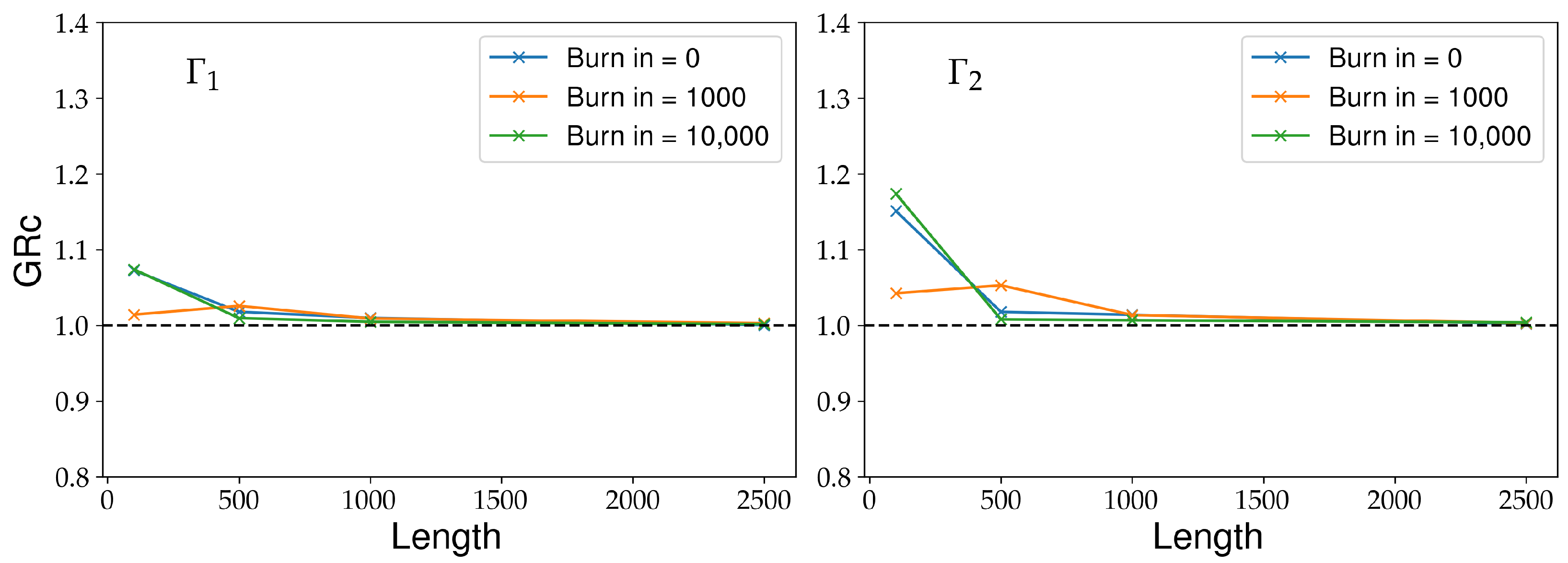
4. Markov Chain Monte Carlo and Bayesian Inference
5. Bayesian Power Regression Model with Heteroscedastic Errors
6. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a Rapidly Pulsating Radio Source. Nature 1968, 217, 709. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-Star Radius Constraints from GW170817 and Future Detections. Astrophys. J. 2017, 850, L34. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and the Virgo Collaboration. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Gamba, R.; Read, J.S.; Wade, L.E. The Impact of the Crust Equation of State on the Analysis of GW170817. Class. Quantum Gravity 2019, 37, 025008. [Google Scholar] [CrossRef]
- Motta, T.F.; Kalaitzis, A.M.; Antić, S.; Guichon, P.A.M.; Stone, J.R.; Thomas, A.W. Isovector Effects in Neutron Stars, Radii, and the GW170817 Constraint. Astrophys. J. 2019, 878, 159. [Google Scholar] [CrossRef]
- Lourenço, O.; Dutra, M.; Lenzi, C.H.; Biswal, S.K.; Bhuyan, M.; Menezes, D.P. Consistent Skyrme Parametrizations Constrained by GW170817. Eur. Phys. J. A 2020, 56, 32. [Google Scholar] [CrossRef]
- Essick, R.; Landry, P.; Holz, D.E. Nonparametric Inference of Neutron Star Composition, Equation of State, and Maximum Mass with GW170817. Phys. Rev. D 2020, 101, 063007. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Critical Examination of Constraints on the Equation of State of Dense Matter Obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining Neutron-Star Tidal Love Numbers with Gravitational-Wave Detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic Tidal Properties of Neutron Stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Zhou, E. Tidal Deformability of Compact Stars. In Studying Compact Star Equation of States with General Relativistic Initial Data Approach; Zhou, E., Ed.; Springer Theses; Springer: Singapore, 2020; pp. 17–36. [Google Scholar] [CrossRef]
- Lim, Y.; Holt, J.W. Neutron Star Tidal Deformabilities Constrained by Nuclear Theory and Experiment. Phys. Rev. Lett. 2018, 121, 062701. [Google Scholar] [CrossRef]
- Traversi, S.; Char, P.; Pagliara, G. Bayesian Inference of Dense Matter Equation of State within Relativistic Mean Field Models Using Astrophysical Measurements. Astrophys. J. 2020, 897, 165. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Adkins, P.W.; Albert, C.L.; Anders, J.F.; Aylward, A.T.; Baker, C.; Balsamo, E.R.; Bamford, W.A.; Benegalrao, S.S.; et al. The Neutron Star Interior Composition Explorer (NICER): Design and Development. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; SPIE: Washington, DC, USA, 2016; Volume 9905, p. 99051H. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. 2019, 887, L21. [Google Scholar] [CrossRef]
- Landry, P.; Essick, R.; Chatziioannou, K. Nonparametric Constraints on Neutron Star Matter with Existing and Upcoming Gravitational Wave and Pulsar Observations. Phys. Rev. D 2020, 101, 123007. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; Murase, K. Mapping Neutron Star Data to the Equation of State Using the Deep Neural Network. Phys. Rev. D 2020, 101, 054016. [Google Scholar] [CrossRef]
- Morawski, F.; Bejger, M. Neural Network Reconstruction of the Dense Matter Equation of State Derived from the Parameters of Neutron Stars. Astron. Astrophys. 2020, 642, A78. [Google Scholar] [CrossRef]
- Soma, S.; Wang, L.; Shi, S.; Stöcker, H.; Zhou, K. Neural Network Reconstruction of the Dense Matter Equation of State from Neutron Star Observables. J. Cosmol. Astropart. Phys. 2022, 2022, 71. [Google Scholar] [CrossRef]
- Krastev, P.G. Translating Neutron Star Observations to Nuclear Symmetry Energy via Deep Neural Networks. Galaxies 2022, 10, 16. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Kurkela, A.; Fraga, E.S.; Schaffner-Bielich, J.; Vuorinen, A. Constraining neutron star matter with Quantum Chromodynamics. Astrophys. J. 2014, 789, 127. [Google Scholar] [CrossRef]
- Gorda, T.; Kurkela, A.; Romatschke, P.; Säppi, S.; Vuorinen, A. Next-to-Next-to-Next-to-Leading Order Pressure of Cold Quark Matter: Leading Logarithm. Phys. Rev. Lett. 2018, 121, 202701. [Google Scholar] [CrossRef]
- Zhou, E.P.; Zhou, X.; Li, A. Constraints on interquark interaction parameters with GW170817 in a binary strange star scenario. Phys. Rev. D 2018, 97, 083015. [Google Scholar] [CrossRef]
- Li, A.; Zhu, Z.Y.; Zhou, E.P.; Dong, J.M.; Hu, J.N.; Xia, C.J. Neutron star equation of state: Quark mean-field (QMF) modeling and applications. J. High Energy Astrophys. 2020, 28, 19–46. [Google Scholar] [CrossRef]
- Sedaghat, J.; Zebarjad, S.M.; Bordbar, G.H.; Panah, B.E.; Moradi, R. Is the compact binary coalescence, GW190425, a strange quark star? arXiv 2021, arXiv:2104.00544. [Google Scholar] [CrossRef]
- Traversi, S.; Char, P.; Pagliara, G.; Drago, A. Speed of sound in dense matter and two families of compact stars. Astron. Astrophys. 2022, 660, A62. [Google Scholar] [CrossRef]
- Miao, Z.; Jiang, J.L.; Li, A.; Chen, L.W. Bayesian Inference of Strange Star Equation of State Using the GW170817 and GW190425 Data. Astrophys. J. Lett. 2021, 917, L22. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a Phenomenologically Parametrized Neutron-Star Equation of State. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Astrophysics and Space Science Library, Neutron Stars; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Bethe, H.A. Theory of Nuclear Matter. Annu. Rev. Nucl. Sci. 1971, 21, 93–244. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Theoretical and Mathematical Physics, The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Blaizot, J.P.; Ripka, G. Quantum Theory of Finite Systems; The MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Machleidt, R. The Meson Theory of Nuclear Forces and Nuclear Structure. In Advances in Nuclear Physics; Negele, J.W., Vogt, E., Eds.; Springer: Boston, MA, USA, 1989; pp. 189–376. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R. Spin-Isospin Structure and Pion Condensation in Nucleon Matter. Phys. Rev. C 1997, 56, 2261–2279. [Google Scholar] [CrossRef]
- Nikolaus, B.A.; Hoch, T.; Madland, D.G. Nuclear Ground State Properties in a Relativistic Point Coupling Model. Phys. Rev. C 1992, 46, 1757–1781. [Google Scholar] [CrossRef] [PubMed]
- Friar, J.L.; Madland, D.G.; Lynn, B.W. QCD Scales in Finite Nuclei. Phys. Rev. C 1996, 53, 3085–3087. [Google Scholar] [CrossRef] [PubMed]
- Skyrme, T.H.R. The Effective Nuclear Potential. Nucl. Phys. 1958, 9, 615–634. [Google Scholar] [CrossRef]
- Bell, J.S.; Skyrme, T.H.R. CVIII. The Nuclear Spin-Orbit Coupling. Philos. Mag. J. Theor. Exp. Appl. Phys. 1956, 1, 1055–1068. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. CVII. The Nuclear Surface. Philos. Mag. 2006, 1, 1043–1054. [Google Scholar] [CrossRef]
- Dechargé, J.; Gogny, D. Hartree-Fock-Bogolyubov Calculations with the $D1$ Effective Interaction on Spherical Nuclei. Phys. Rev. C 1980, 21, 1568–1593. [Google Scholar] [CrossRef]
- Berger, J.F.; Girod, M.; Gogny, D. Time-Dependent Quantum Collective Dynamics Applied to Nuclear Fission. Comput. Phys. Commun. 1991, 63, 365–374. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Sá Martins, J.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme Interaction and Nuclear Matter Constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic Mean-Field Hadronic Models under Nuclear Matter Constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Lourenço, O.; Dutra, M.; Lenzi, C.H.; Flores, C.V.; Menezes, D.P. Consistent Relativistic Mean-Field Models Constrained by GW170817. Phys. Rev. C 2019, 99, 045202. [Google Scholar] [CrossRef]
- Mueller, E.; Eriguchi, Y. Equilibrium Models of Differentially Rotating, Completely Catalyzed, Zero-Temperature Configurations with Central Densities Intermediate to White Dwarf and Neutron Star Densities. Astron. Astrophys. 1985, 152, 325–335. [Google Scholar]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar] [CrossRef] [PubMed]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Equation Of State From Observed Masses And Radii Of Neutron Stars. Astrophys. J. 2010, 722, 33. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Güver, T.; Baym, G.; Heinke, C.; Guillot, S. The Dense Matter Equation Of State From Neutron Star Radius And Mass Measurements. Astrophys. J. 2016, 820, 28. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. From Neutron Star Observables to the Equation of State. I. An Optimal Parametrization. Astrophys. J. 2016, 831, 44. [Google Scholar] [CrossRef]
- O’Boyle, M.F.; Markakis, C.; Stergioulas, N.; Read, J.S. Parametrized Equation of State for Neutron Star Matter with Continuous Sound Speed. Phys. Rev. D 2020, 102, 083027. [Google Scholar] [CrossRef]
- Lindblom, L.; Indik, N.M. Spectral Approach to the Relativistic Inverse Stellar Structure Problem. Phys. Rev. D 2012, 86, 084003. [Google Scholar] [CrossRef]
- Lindblom, L.; Indik, N.M. Spectral Approach to the Relativistic Inverse Stellar Structure Problem II. Phys. Rev. D 2014, 89, 064003. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D. Reconstructing the Neutron-Star Equation of State from Astrophysical Measurements. Phys. Rev. D 2009, 80, 103003. [Google Scholar] [CrossRef]
- Lackey, B.D.; Wade, L. Reconstructing the Neutron-Star Equation of State with Gravitational-Wave Detectors from a Realistic Population of Inspiralling Binary Neutron Stars. Phys. Rev. D 2015, 91, 043002. [Google Scholar] [CrossRef]
- Carney, M.F.; Wade, L.E.; Irwin, B.S. Comparing Two Models for Measuring the Neutron Star Equation of State from Gravitational-Wave Signals. Phys. Rev. D 2018, 98, 063004. [Google Scholar] [CrossRef]
- Ma, P.X.; Jiang, J.L.; Wang, H.; Jin, Z.P.; Fan, Y.Z.; Wei, D.M. GW170817 and the Prospect of Forming Supramassive Remnants in Neutron Star Mergers. Astrophys. J. 2018, 858, 74. [Google Scholar] [CrossRef]
- East, W.E.; Paschalidis, V.; Pretorius, F.; Tsokaros, A. Binary Neutron Star Mergers: Effects of Spin and Post-Merger Dynamics. Phys. Rev. D 2019, 100, 124042. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Further Stable Neutron Star Models from f (R) Gravity. J. Cosmol. Astropart. Phys. 2013, 2013, 040. [Google Scholar] [CrossRef]
- Teppa Pannia, F.A.; García, F.; Perez Bergliaffa, S.E.; Orellana, M.; Romero, G.E. Structure of Compact Stars in R-squared Palatini Gravity. Gen. Relativ. Gravit. 2017, 49, 25. [Google Scholar] [CrossRef]
- Lobato, R.; Lourenço, O.; Moraes, P.H.R.S.; Lenzi, C.H.; de Avellar, M.; de Paula, W.; Dutra, M.; Malheiro, M. Neutron Stars in f(R,T) Gravity Using Realistic Equations of State in the Light of Massive Pulsars and GW170817. J. Cosmol. Astropart. Phys. 2020, 2020, 039. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y. Analytical Representations of Unified Equations of State of Neutron-Star Matter. Astron. Astrophys. 2004, 428, 191–197. [Google Scholar] [CrossRef]
- Fraga, E.S.; Kurkela, A.; Vuorinen, A. Interacting Quark Matter Equation Of State For Compact Stars. Astrophys. J. 2014, 781, L25. [Google Scholar] [CrossRef]
- Altiparmak, S.; Ecker, C.; Rezzolla, L. On the Sound Speed in Neutron Stars. arXiv 2022, arXiv:2203.14974. [Google Scholar] [CrossRef]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gill, J. Bayesian Methods: A Social and Behavioral Sciences Approach, 3rd ed.; Chapman & Hall/CRC Statistics in the Social and Behavioral Sciences; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Betancourt, M. A Conceptual Introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Gelman, A.; Rubin, D.B. (Eds.) A Single Series from the Gibbs Sampler Provides a False Sense of Security; Statistics Department, University of California at Berkeley: Berkeley, CA, USA, 1991. [Google Scholar]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and the Virgo Collaboration; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. 2020, 896, L44. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro Delay Measurements of an Extremely Massive Millisecond Pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Linares, M.; Shahbaz, T.; Casares, J. Peering into the Dark Side: Magnesium Lines Establish a Massive Neutron Star in PSR J2215+5135. Astrophys. J. 2018, 859, 54. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A Two-Solar-Mass Neutron Star Measured Using Shapiro Delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, General Relativistic Magnetohydrodynamic Simulations, and the Neutron Star Maximum Mass. Phys. Rev. D 2018, 97, 021501. [Google Scholar] [CrossRef]
- Shibata, M.; Zhou, E.; Kiuchi, K.; Fujibayashi, S. Constraint on the Maximum Mass of Neutron Stars Using GW170817 Event. Phys. Rev. D 2019, 100, 023015. [Google Scholar] [CrossRef]
- Nathanail, A.; Most, E.R.; Rezzolla, L. GW170817 and GW190814: Tension on the Maximum Mass. Astrophys. J. Lett. 2021, 908, L28. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for Quark-Matter Cores in Massive Neutron Stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Godzieba, D.A.; Gamba, R.; Radice, D.; Bernuzzi, S. Updated Universal Relations for Tidal Deformabilities of Neutron Stars from Phenomenological Equations of State. Phys. Rev. D 2021, 103, 063036. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration. Free Software (GPL). LIGO Algorithm Library—LALSuite. 2018. Available online: https://git.ligo.org/lscsoft/lalsuite (accessed on 20 January 2023).
- Bingham, E.; Chen, J.P.; Jankowiak, M.; Obermeyer, F.; Pradhan, N.; Karaletsos, T.; Singh, R.; Szerlip, P.A.; Horsfall, P.; Goodman, N.D. Pyro: Deep Universal Probabilistic Programming. J. Mach. Learn. Res. 2019, 20, 28:1–28:6. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. Neutron Star Radii, Universal Relations, and the Role of Prior Distributions. Eur. Phys. J. A 2016, 52, 18. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Riley, T.E.; Watts, A.L. A Pitfall of Piecewise-Polytropic Equation of State Inference. Mon. Not. R. Astron. Soc. 2018, 478, 2177–2192. [Google Scholar] [CrossRef]
- Endrizzi, A.; Ciolfi, R.; Giacomazzo, B.; Kastaun, W.; Kawamura, T. General Relativistic Magnetohydrodynamic Simulations of Binary Neutron Star Mergers with the APR4 Equation of State. Class. Quantum Gravity 2016, 33, 164001. [Google Scholar] [CrossRef]
- Maione, F.; Pietri, R.D.; Feo, A.; Löffler, F. Binary Neutron Star Merger Simulations with Different Initial Orbital Frequency and Equation of State. Class. Quantum Gravity 2016, 33, 175009. [Google Scholar] [CrossRef]
- Anderson, D.; Yunes, N. Scalar Charges and Scaling Relations in Massless Scalar—Tensor Theories. Class. Quantum Gravity 2019, 36, 165003. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Neutron Stars Phenomenology with Scalar—Tensor Inflationary Attractors. Phys. Dark Universe 2021, 32, 100805. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Riley, T.E.; Watts, A.L.; Greif, S.K.; Morsink, S.M.; Hebeler, K.; Schwenk, A.; Hinderer, T.; Nissanke, S.; Guillot, S.; et al. A NICER View of PSR J0030$\mathplus$0451: Implications for the Dense Matter Equation of State. Astrophys. J. 2019, 887, L22. [Google Scholar] [CrossRef]
- Miller, M.C.; Chirenti, C.; Lamb, F.K. Constraining the Equation of State of High-density Cold Matter Using Nuclear and Astronomical Measurements. Astrophys. J. 2019, 888, 12. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Riley, T.E.; Hinderer, T.; Hebeler, K.; Schwenk, A.; Watts, A.L.; Nissanke, S.; Guillot, S.; Lattimer, J.M.; et al. Constraining the Dense Matter Equation of State with Joint Analysis of NICER and LIGO/Virgo Measurements. Astrophys. J. Lett. 2020, 893, L21. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Hebeler, K.; Hinderer, T.; Nissanke, S.; Schwenk, A.; Riley, T.E.; Watts, A.L.; Lattimer, J.M.; Ho, W.C.G. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass—Radius Estimate of PSR J0740$\mathplus$6620 and Multimessenger Observations. Astrophys. J. Lett. 2021, 918, L29. [Google Scholar] [CrossRef]
- Lobato, R.; Chimanski, E.; Bertulani, C. Unsupervised Machine Learning Correlations in EoS of Neutron Stars. In Proceedings of the XV International Workshop on Hadron Physics—PoS(XVHadronPhysics), SISSA Medialab, Sao Jose dos Campos, Brazil, 13–17 September 2022; Volume 408, p. 062. [Google Scholar] [CrossRef]
- Lobato, R.V.; Chimanski, E.V.; Bertulani, C.A. Cluster Structures with Machine Learning Support in Neutron Star M-R Relations. J. Phys. Conf. Ser. 2022, 2340, 012014. [Google Scholar] [CrossRef]
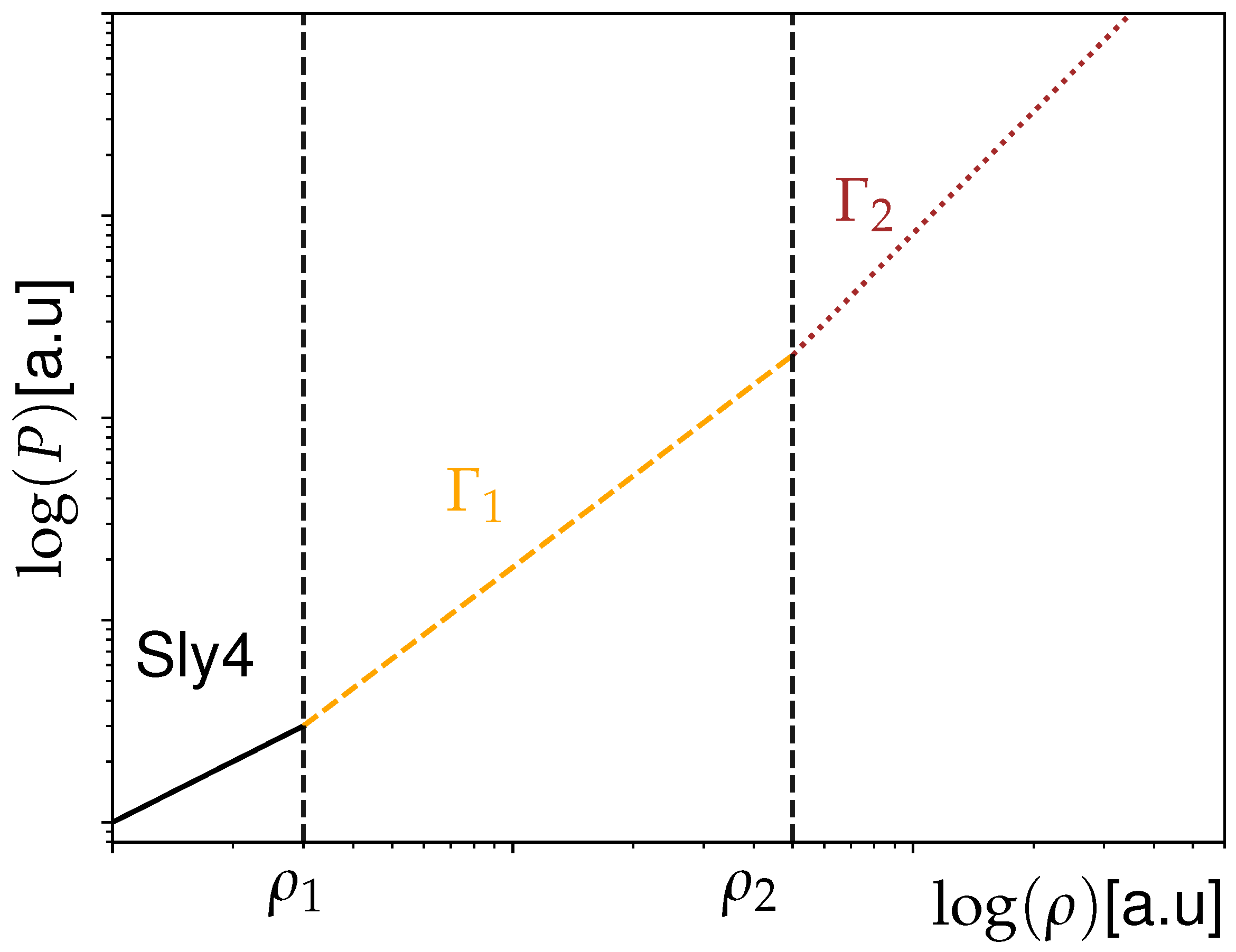



| Label | Color | ||||
|---|---|---|---|---|---|
| MD1 | 3.6 | 2.3 | purple | ||
| MD2 | 3.2 | 2.2 | blue | ||
| MD3 | 3.1 | 4.7 | green |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chimanski, E.V.; Lobato, R.V.; Goncalves, A.R.; Bertulani, C.A. Bayesian Exploration of Phenomenological EoS of Neutron/Hybrid Stars with Recent Observations. Particles 2023, 6, 198-216. https://doi.org/10.3390/particles6010011
Chimanski EV, Lobato RV, Goncalves AR, Bertulani CA. Bayesian Exploration of Phenomenological EoS of Neutron/Hybrid Stars with Recent Observations. Particles. 2023; 6(1):198-216. https://doi.org/10.3390/particles6010011
Chicago/Turabian StyleChimanski, Emanuel V., Ronaldo V. Lobato, Andre R. Goncalves, and Carlos A. Bertulani. 2023. "Bayesian Exploration of Phenomenological EoS of Neutron/Hybrid Stars with Recent Observations" Particles 6, no. 1: 198-216. https://doi.org/10.3390/particles6010011
APA StyleChimanski, E. V., Lobato, R. V., Goncalves, A. R., & Bertulani, C. A. (2023). Bayesian Exploration of Phenomenological EoS of Neutron/Hybrid Stars with Recent Observations. Particles, 6(1), 198-216. https://doi.org/10.3390/particles6010011







