Prediction of Construction-Induced Ground Vibrations Using Field Measurements and Bidirectional Gated Recurrent Unit Neural Network
Abstract
1. Introduction
2. Theory and Background
2.1. Ground Vibration Sources
2.2. Construction-Induced Ground Vibration Propagation
- = displacement amplitude at distance from the vibration source
- = displacement amplitude at distance from the vibration source
- = geometric damping coefficient
- = material damping coefficient
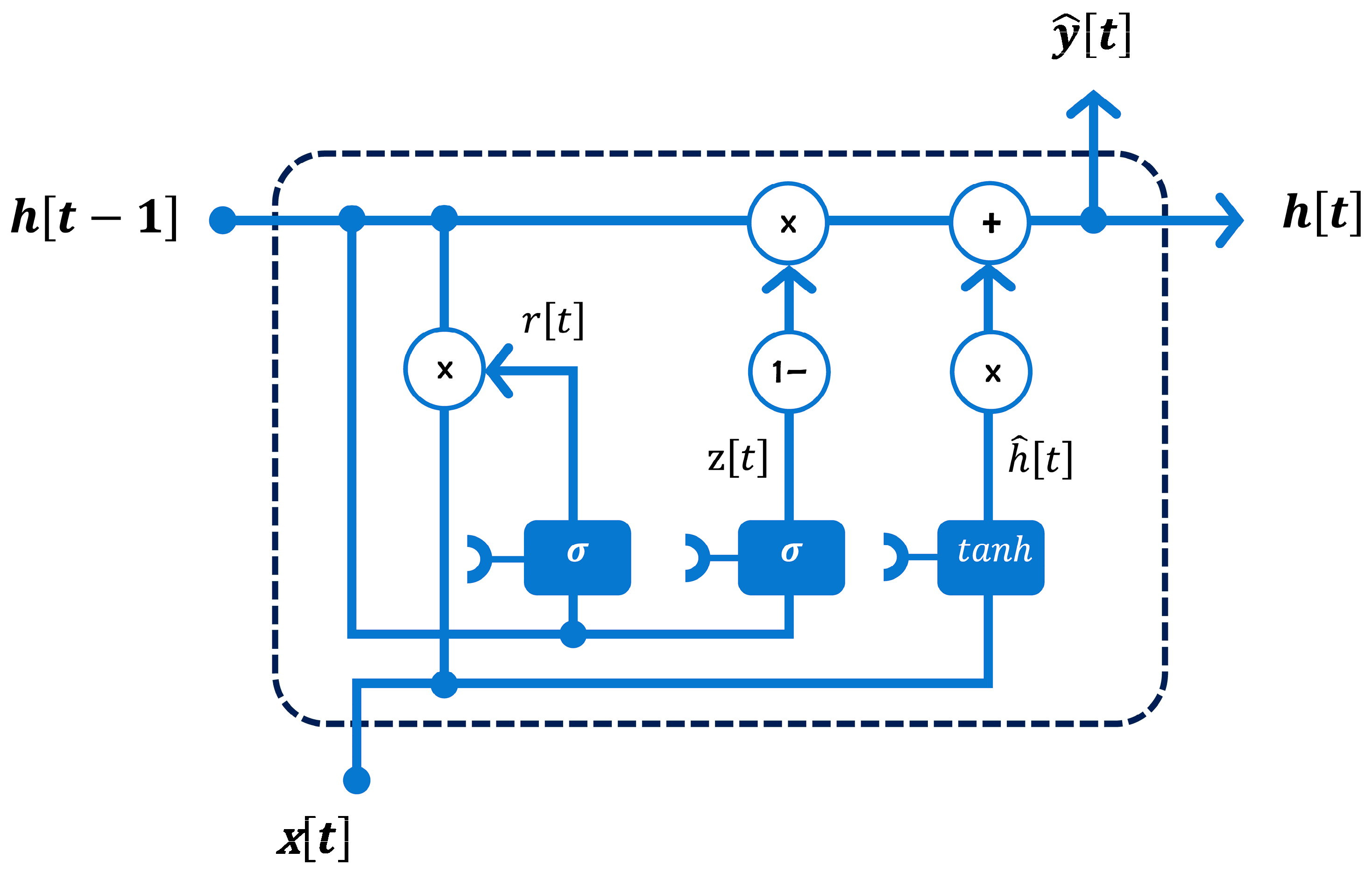
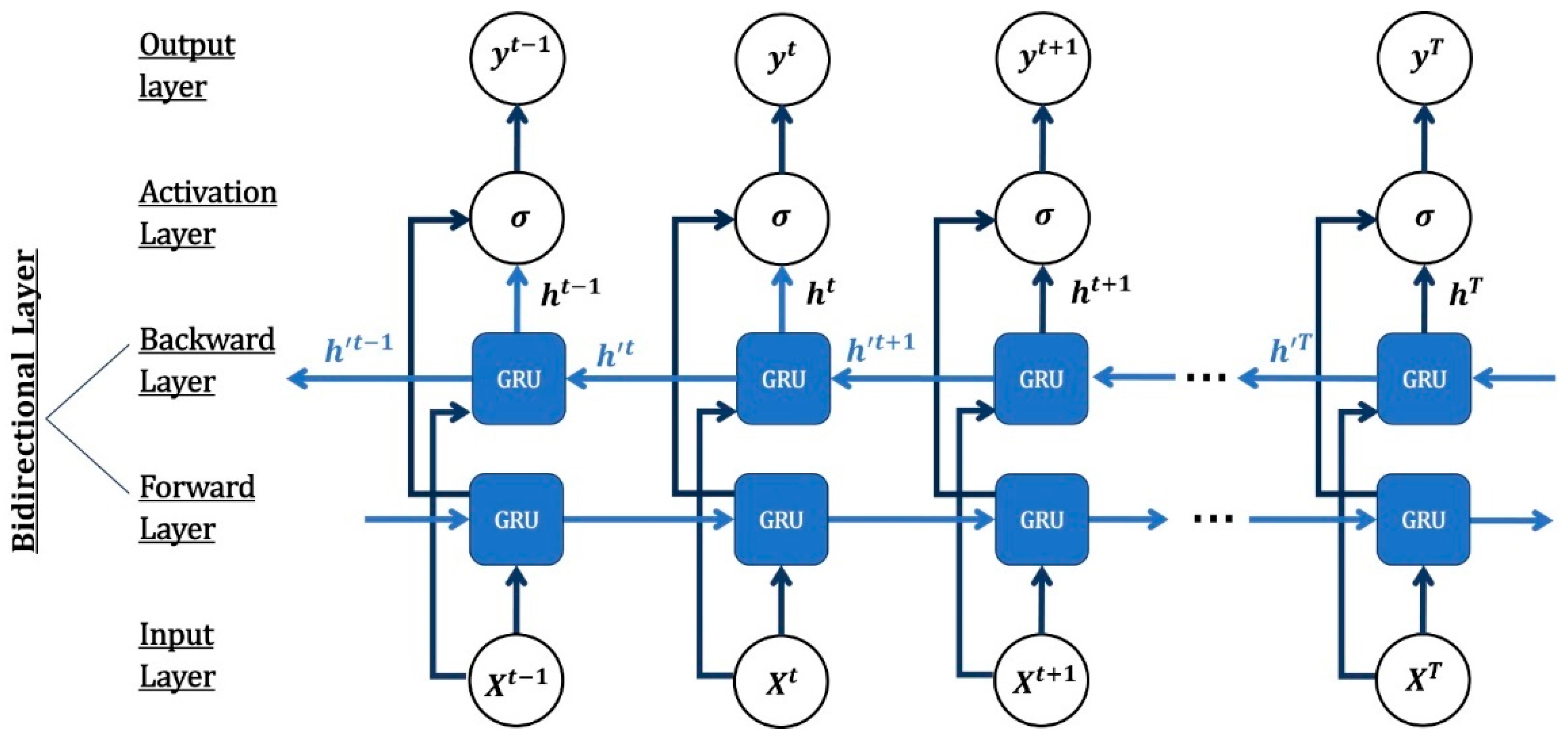
2.3. Recurrent Neural Network for Time Series Forecasting
- : input vector at time step t
- : output (hidden) state vector
- : candidate hidden state vector
- : update gate vector controlling the balance between past and new information
- : reset gate vector determining how much of the previous memory is forgotten
- : input weight matrices
- : recurrent weight matrices
- : bias vectors
- : element-wise (Hadamard) multiplication
- : sigmoid activation function, which maps its input to the range
- : hyperbolic tangent activation function, which maps its input to the range
2.4. Random Forest Method
2.5. ARIMA Method
2.6. Metrics for Model Evaluation
3. Vibration Data Acquisition
4. Problem Definition
- Maximum of vertical, horizontal longitudinal, and horizontal transverse components.
- Maximum value of the vector summation of the three particle velocity components at each time step.
- Vector summation of the maximum particle velocity components regardless of the time span in which the velocities are measured [44].
5. Results and Discussion
5.1. Random Forest Hyperparameters
- n_estimator: This parameter indicates the number of trees in the forest. More trees generally improve the model’s performance by reducing variance, but this also increases computational cost and memory usage. This parameter ranges between 100 and 1000 in this paper. Having at least 100 trees ensures that the model is robust, and going up to 1000 allows for finding the optimal balance between performance improvement and computational efficiency.
- max_depth: This parameter defines the maximum depth of the trees and controls how deep the tree can grow. The lower and upper bounds of max_depth are 10 and 100, respectively, with increments of 10. This range is sensible for exploring both shallow and deep trees, helping to prevent overfitting and underfitting.
- min_samples_split: This parameter controls the minimum number of samples required to split a node and helps prevent the model from creating nodes that only capture noise. A range of 2 to 20 for the minimum number of samples is considered in this paper. This range covers a variety of potential splits, ensuring that the model does not create overly specific trees while allowing for flexibility in how nodes are split.
- min_samples_leaf: This parameter specifies the minimum number of samples required to be present at a leaf node, ensuring that each leaf contains a sufficient number of observations. A range of 1 to 20 was selected for this hyperparameter to prevent the model from becoming overly specific to the training data. The min_samples_leaf parameter was optimized using a grid search approach, where its value was systematically varied within the defined range. For each trial, model performance was evaluated through cross-validation on the training dataset, and the value yielding the lowest validation error while minimizing overfitting was selected as the optimal setting for each project, as summarized in Table 4.
5.2. ARIMA Parameters
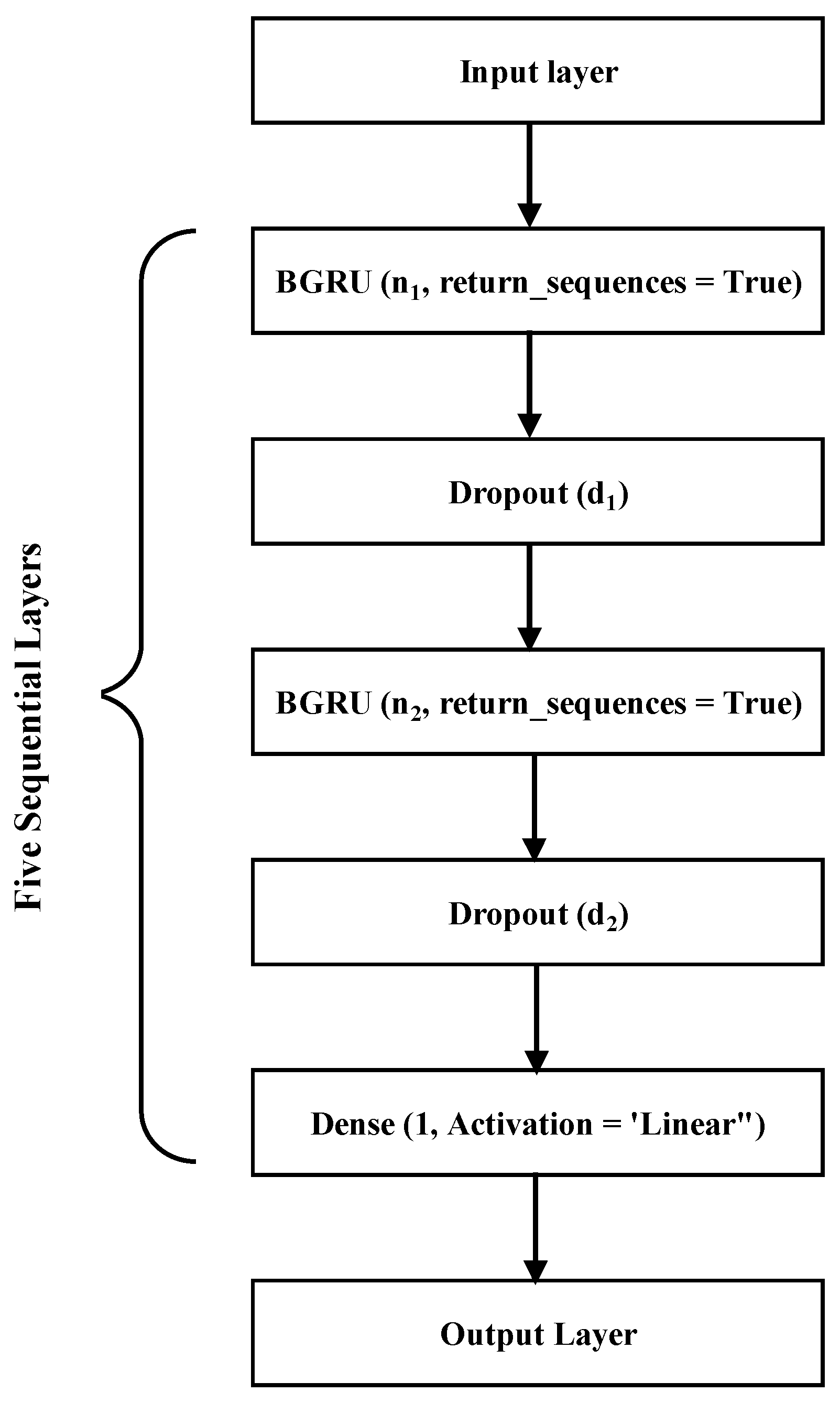
5.3. Details of the BGRU Model
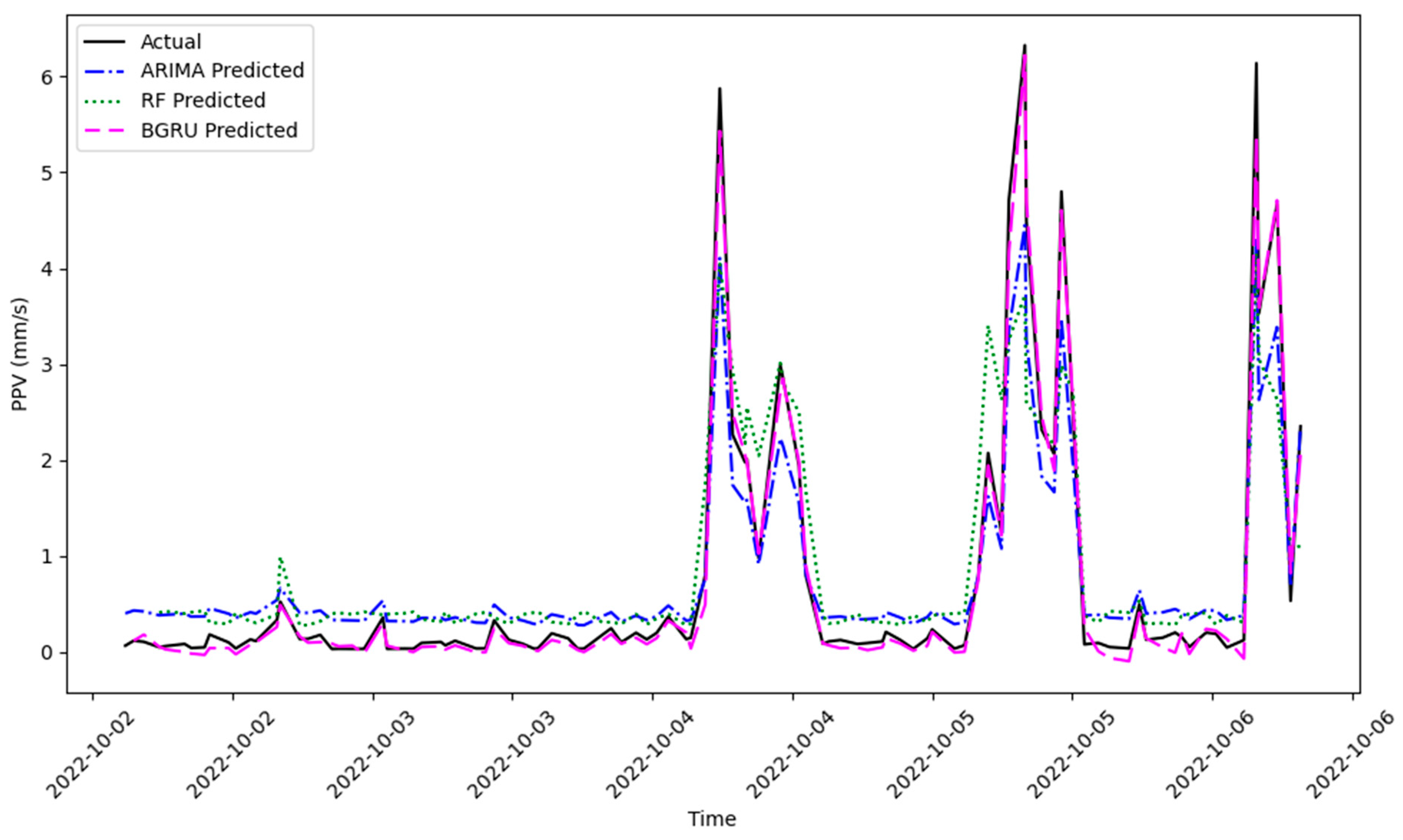
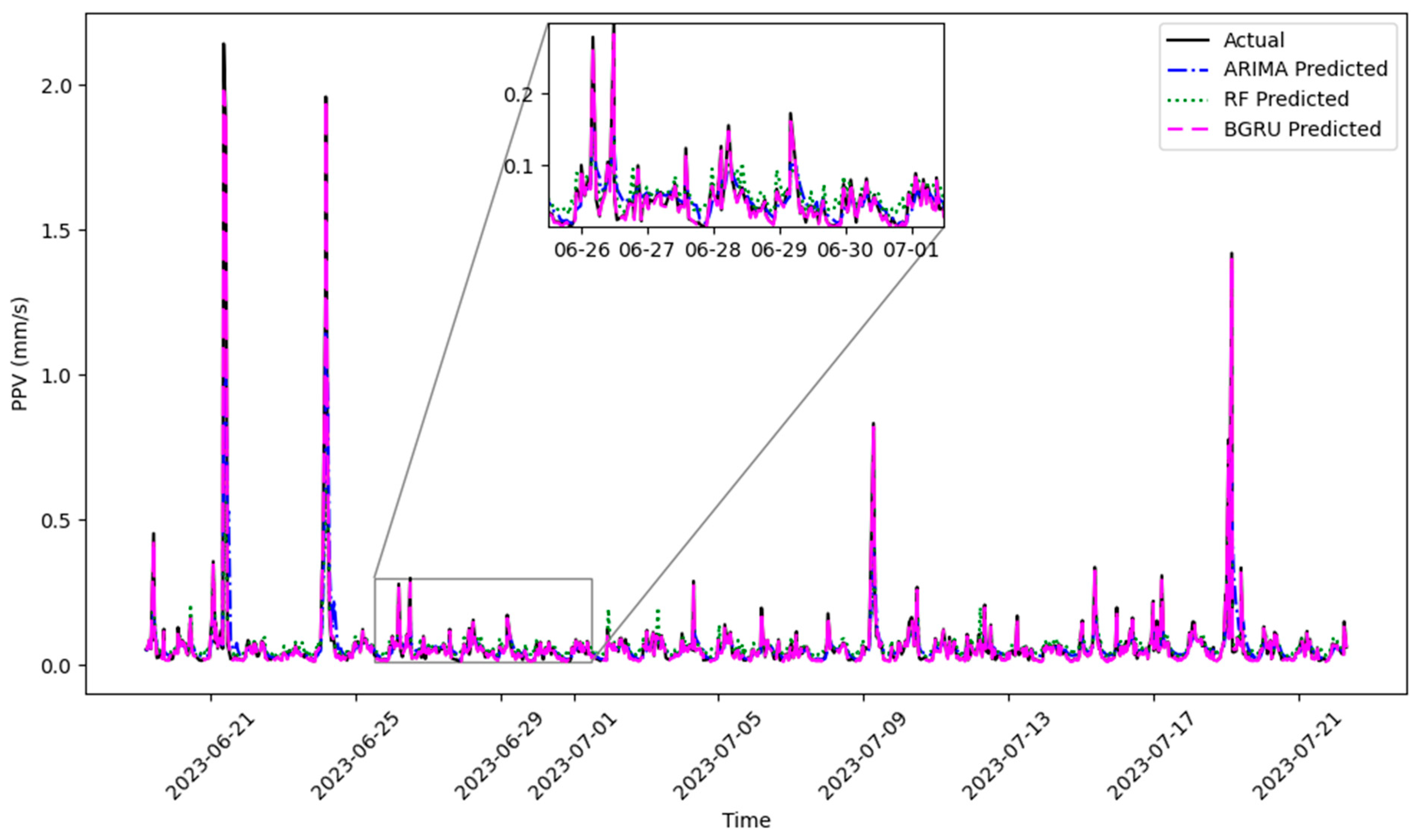
5.4. Discussions
5.5. Notes on the Optimization of Data and Methods
5.6. Frequency-Domain Considerations, Data Limitations, Feature Sensitivity
5.7. Practical Deployment Considerations
6. Conclusions
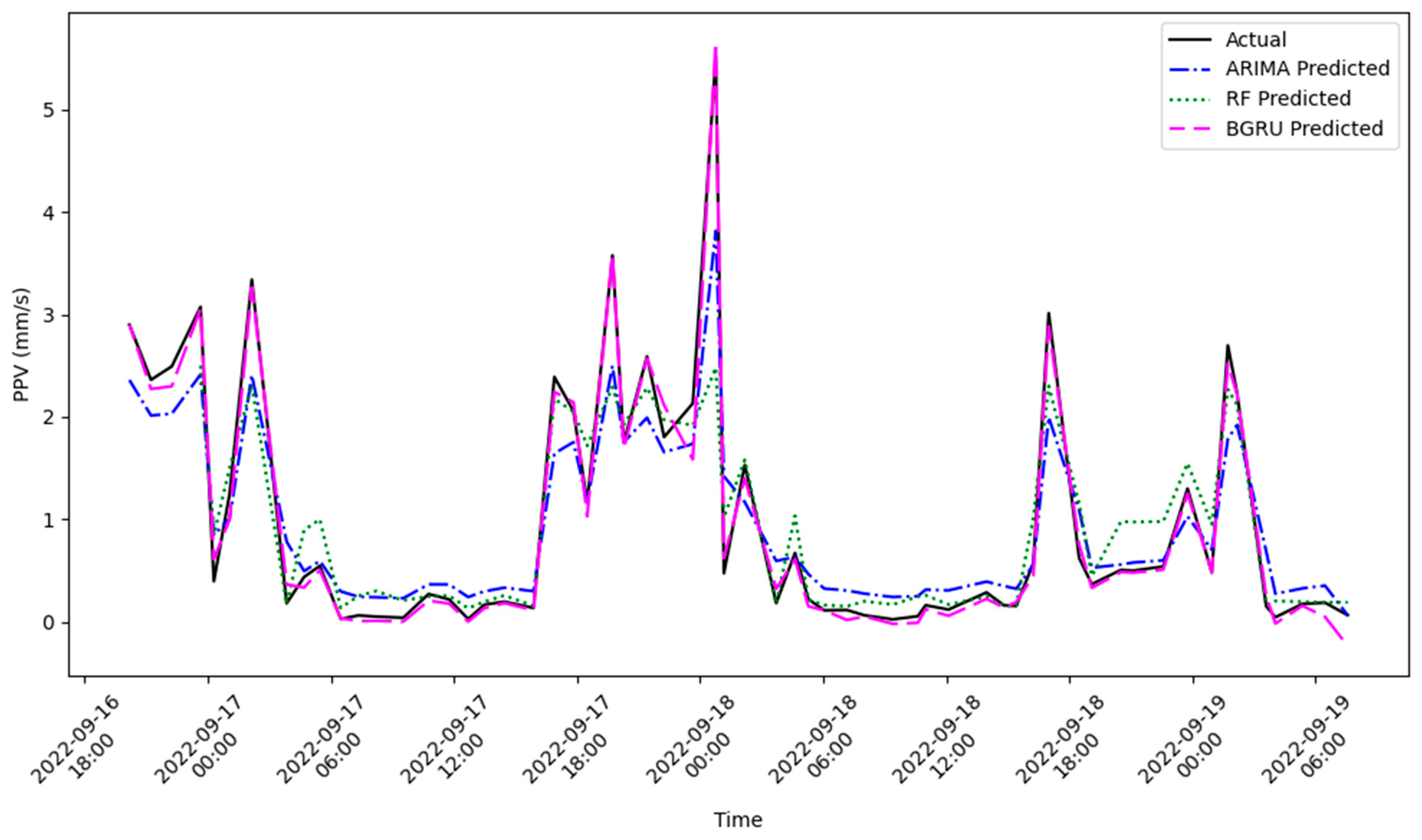
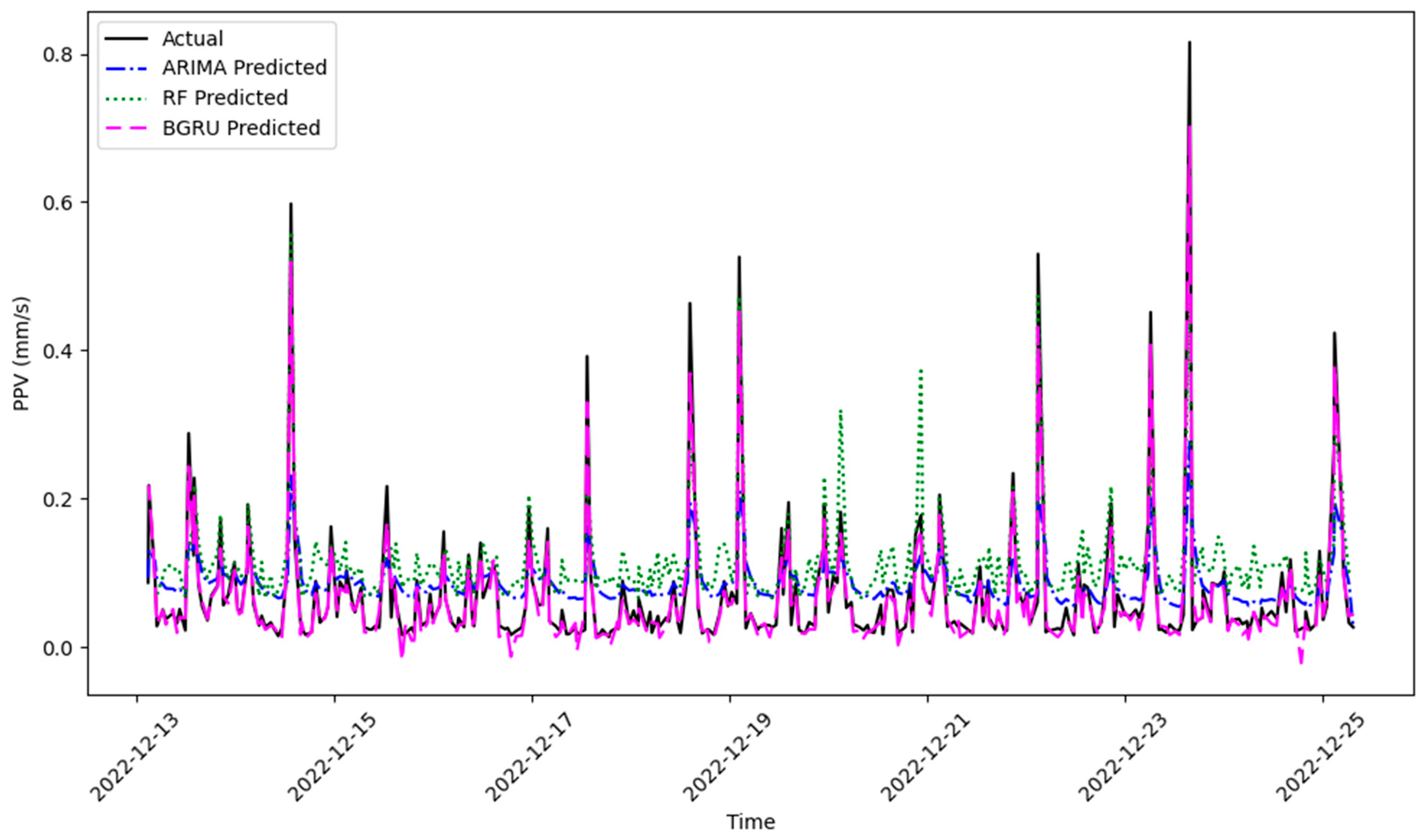
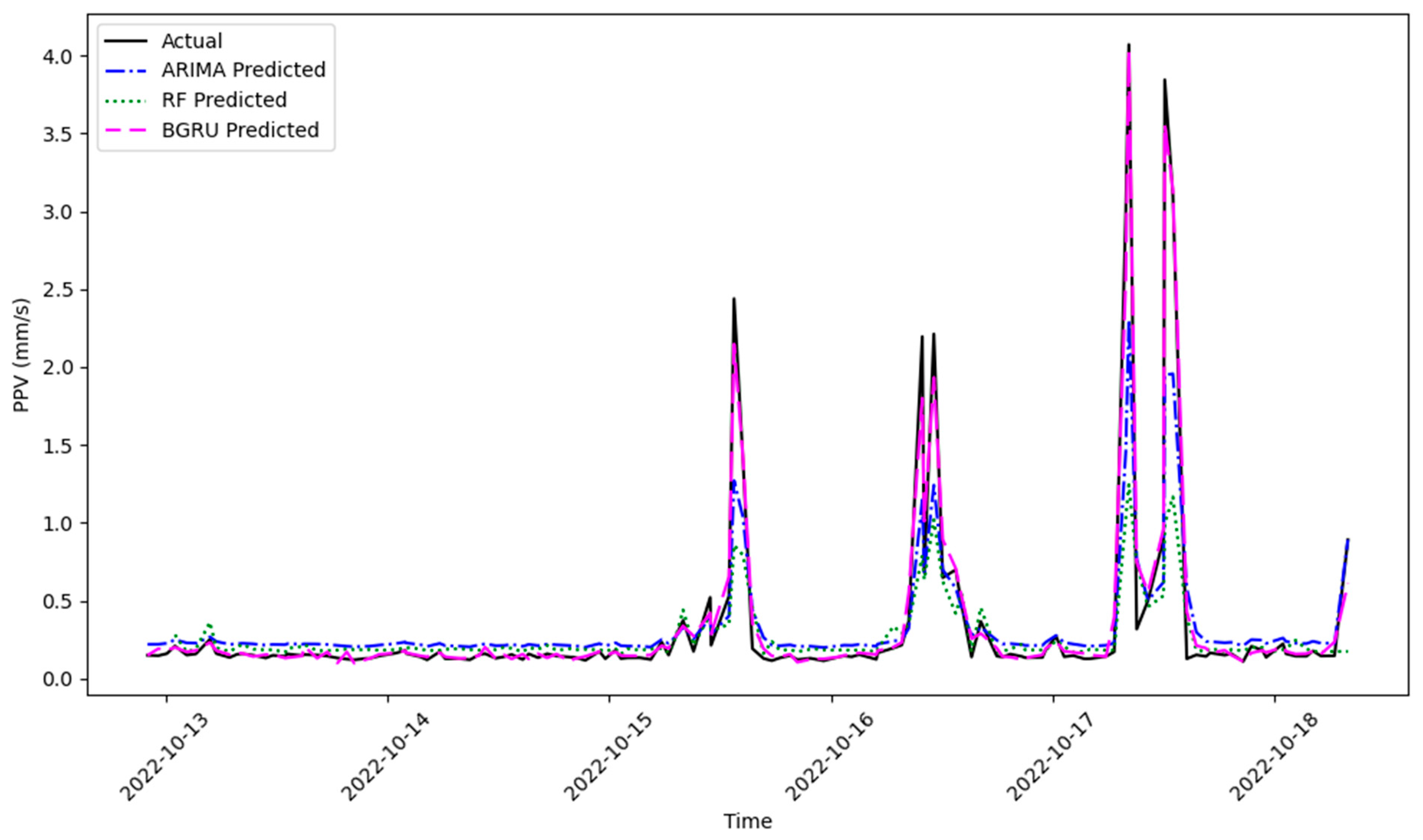
- The BGRU method’s superior performance not only outperforms the RF and ARIMA methods but also underscores the significance of our findings in predicting construction-induced ground vibrations.
- The BGRU method can distinguish between construction-induced and ambient vibration data in the training step. Therefore, it can predict either type of vibration data even if trained by a mixed type of database.
- The RF and ARIMA methods cannot distinguish between construction-induced and ambient vibration data in the training step. Therefore, they performed poorly (i.e., negative coefficient of determination) when the model was prepared using a mixed data type but was used to predict either ambient or construction-induced data.
- The BGRU method can well predict different types of construction-induced and ambient ground vibrations with various durations.
- The ARIMA method performs better than the RF method because it is based on the statistical concept of serial correlation, in which past data points affect future data points.
- The coefficient of determination for BGRU ranges from 83.5 to 99.8%, while its vmaximum value for RF and ARIMA methods is 78.9 and 88.1%, respectively.
- The coefficient of determination for the RF and ARIMA methods is negative in some projects because the nature of the testing and training data is different.
- In addition to the metric quantities, the predicted results’ visual inspection shows the obvious superiority of the BGRU method. This method predicts the amplitude of the peaks and the time of their occurrence very well.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Colaço, A.; Costa, P.A.; Parente, C.; Abouelmaty, A.M. Vibrations Induced by a Low Dynamic Loading on a Driven Pile: Numerical Prediction and Experimental Validation. Vibration 2022, 5, 829–845. [Google Scholar] [CrossRef]
- Abouelmaty, A.M.; Colaço, A.; Alves Costa, P. User-Friendly Tool for Expedited Ground Vibration Assessment Induced by Impact Pile Driving. Vibration 2025, 8, 17. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, S. Impact source localization and vibration intensity prediction on construction sites. Measurement 2021, 175, 109148. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Monjezi, M.; Shahnazar, A.; Armaghani, D.J.; Farazmand, A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Measurement 2015, 75, 289–297. [Google Scholar] [CrossRef]
- He, Y.; Peng, L.; He, K.; Guan, Q.; Han, J.; Xiao, X.; Sheng, X. Analysis of uncertainty and variation in underground train-induced vibration based on measured data. Measurement 2023, 222, 113600. [Google Scholar] [CrossRef]
- Wang, I.-T. Field experiments and numerical analysis of the ground vibration isolation of shock wave propagation under explosion shock loading. Vibration 2019, 2, 300–310. [Google Scholar] [CrossRef]
- Rajabi, A.M.; Vafaee, A. Prediction of blast-induced ground vibration using empirical models and artificial neural network (Bakhtiari Dam access tunnel, as a case study). J. Vib. Control 2020, 26, 520–531. [Google Scholar] [CrossRef]
- Kumar, R.; Choudhury, D.; Bhargava, K. Determination of blast-induced ground vibration equations for rocks using mechanical and geological properties. J. Rock Mech. Geotech. Eng. 2016, 8, 341–349. [Google Scholar] [CrossRef]
- Triepaischajonsak, N.; Thompson, D. A hybrid modelling approach for predicting ground vibration from trains. J. Sound Vib. 2015, 335, 147–173. [Google Scholar] [CrossRef]
- Faizan, A.A.; Kırtel, O.; Çelebi, E.; Zülfikar, A.C.; Göktepe, F. Experimental validation of a simplified numerical model to predict train-induced ground vibrations. Comput. Geotech. 2022, 141, 104547. [Google Scholar] [CrossRef]
- Esmaeili, M.H.; Haft-Cheshmeh, Y.M. Dynamic characteristics of elastomeric materials used as railway vibration mitigation measures considering the effect of shape factor. Measurement 2024, 236, 115058. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Li, Y.; Liu, G.; Zheng, Y.; Jiang, Z. Prediction and Control Method of Long-Term Vehicle-Induced Settlement of High-Speed Railway Tunnel in Diatomite Stratum. J. Vib. Eng. Technol. 2023, 11, 2297–2307. [Google Scholar] [CrossRef]
- Toygar, O.; Ulgen, D.; Fidan, N.B. Experimental Study on Reutilization of Waste Rubber Chips with Sheetpiles as a Coupled-Wave Barrier to Reduce Ground-Borne Vibrations. J. Vib. Eng. Technol. 2024, 12, 8451–8463. [Google Scholar] [CrossRef]
- Kedia, N.K.; Kumar, A.; Singh, Y. Prediction of underground metro train-induced ground vibration using hybrid PSO-ANN approach. Neural Comput. Appl. 2023, 35, 8171–8195. [Google Scholar] [CrossRef]
- Amiri, M.; Hasanipanah, M.; Bakhshandeh Amnieh, H. Predicting ground vibration induced by rock blasting using a novel hybrid of neural network and itemset mining. Neural Comput. Appl. 2020, 32, 14681–14699. [Google Scholar] [CrossRef]
- Ulgen, D.; Ertugrul, O.; Ozkan, M. Measurement of ground borne vibrations for foundation design and vibration isolation of a high-precision instrument. Measurement 2016, 93, 385–396. [Google Scholar] [CrossRef]
- Lurcock, D.; Thompson, D. A new empirical prediction approach for ground borne vibration in buildings. In Proceedings of the International Congress on Sound and Vibration, London, UK, 23–27 July 2017. [Google Scholar]
- Moghadam, A.E.; Rafiee-Dehkharghani, R. Optimal design of wave barriers in dry and saturated poroelastic grounds using covariance matrix adaptation evolution strategy. Comput. Geotech. 2021, 133, 104015. [Google Scholar] [CrossRef]
- Zhou, J.; Asteris, P.G.; Armaghani, D.J.; Pham, B.T. Prediction of ground vibration induced by blasting operations through the use of the Bayesian Network and random forest models. Soil Dyn. Earthq. Eng. 2020, 139, 106390. [Google Scholar] [CrossRef]
- Lu, Y. Underground blast induced ground shock and its modelling using artificial neural network. Comput. Geotech. 2005, 32, 164–178. [Google Scholar] [CrossRef]
- Khandelwal, M. Evaluation and prediction of blast-induced ground vibration using support vector machine. Int. J. Rock Mech. Min. Sci. 2010, 47, 509–516. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng. Comput. 2022, 38 (Suppl. S5), 4145–4162. [Google Scholar] [CrossRef]
- Bui, X.-N.; Nguyen, H.; Tran, Q.-H.; Nguyen, D.-A.; Bui, H.-B. Predicting blast-induced ground vibration in quarries using adaptive fuzzy inference neural network and Moth–Flame optimization. Nat. Resour. Res. 2021, 30, 4719–4734. [Google Scholar] [CrossRef]
- Yun, S.; Kang, J.-M.; Ha, J.; Lee, S.; Ryu, D.-W.; Kwon, J.; Kim, I.-M. Deep learning-based ground vibration monitoring: Reinforcement learning and RNN–CNN approach. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7502905. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar] [CrossRef]
- CDOT. Transportation and Construction Vibration Guidance Manual; CDOT: New Delhi, India, 2013. [Google Scholar]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice-Hall: Hoboken, NJ, USA, 1970. [Google Scholar]
- Amanat, S.; Gholami, K.; Rafiee-Dehkharghani, R.; Bansal, D. Modified non-dominated sorting genetic algorithm-II for the optimal design of soil-concrete periodic plane wave barriers. Comput. Geotech. 2024, 165, 105947. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Zhang, X.; Kuehnelt, H.; De Roeck, W. Traffic noise prediction applying multivariate bi-directional recurrent neural network. Appl. Sci. 2021, 11, 2714. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
- Chughtai, J.-u.-R.; Haq, I.u.; Islam, S.u.; Gani, A. A heterogeneous ensemble approach for travel time prediction using hybridized feature spaces and support vector regression. Sensors 2022, 22, 9735. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Talagala, T.S.; Hyndman, R.J.; Athanasopoulos, G. Meta-learning how to forecast time series. Monash Econom. Bus. Stat. Work. Pap. 2018, 6, 16. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Wei, W.W. Univariate and Multivariate Methods. Time Series Analysis; Greg Tobin: West Orange, NJ, USA, 2006. [Google Scholar]
- Terrapex Environmental Ltd. 2024. Available online: https://terrapex.com/ (accessed on 20 October 2024).
- Syscom. BARTEC SYSCOM. 2024. Available online: https://www.syscom.ch/documentation (accessed on 18 November 2024).
- Johnston, W. Chapter 363, Building Construction and Demolition. In Toronto Municipal Code; City of Toronto: Toronto, ON, Canada, 2023. [Google Scholar]
- Hiller, D.; Crabb, G. Groundborne Vibration Caused by Mechanised Construction Works; Transport Research Laboratory: Crowthorne, UK, 2000. [Google Scholar]
- Chollet, F. Keras. Available online: https://github.com/fchollet/keras (accessed on 15 December 2024).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems; Tensorflow: Mountain View, CA, USA, 2015. [Google Scholar]
- Chen, Z.; Zhang, Z.; Yan, J.; Zhong, M.; Lv, L.; Hou, Y. Neural Network–Based Reinforcement Iterative Learning Fault Estimation Scheme for Nonlinear Uncertain Manipulator Systems With Time-Delay. IEEE Trans. Ind. Inform. 2025, 21, 7287–7298. [Google Scholar] [CrossRef]
- Hou, Y.; Li, T.; Wang, J.; Ma, J.; Chen, Z. A lightweight transformer based on feature fusion and global–local parallel stacked self-activation unit for bearing fault diagnosis. Measurement 2024, 236, 115068. [Google Scholar] [CrossRef]

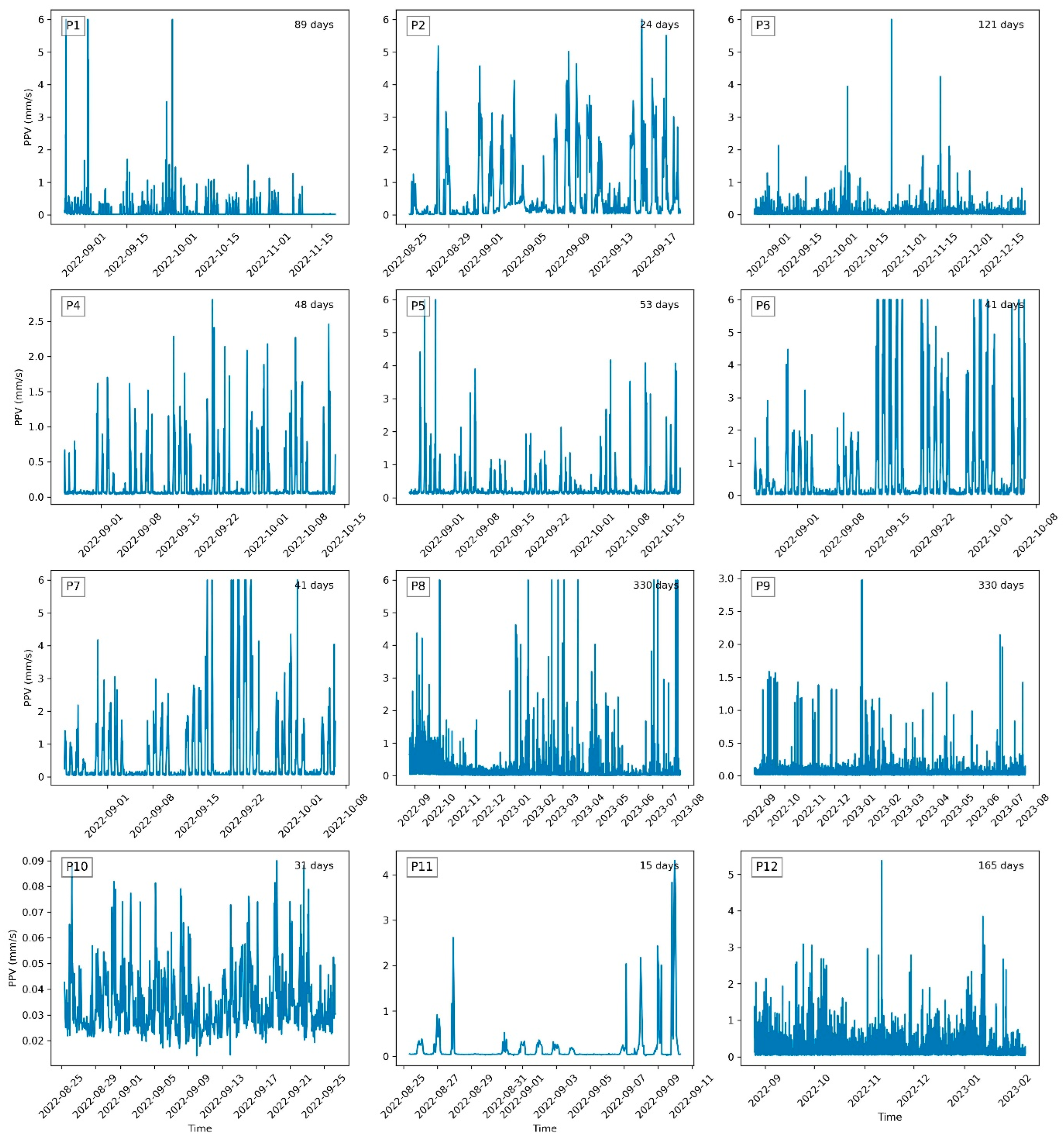









| Project No. | Duration (Days) | Location | Notes |
|---|---|---|---|
| 1 | 89 | Basement slab in a neighboring two-story house. | Events in the training data. |
| 2 | 24 | On the existing ground, on the boundary of a construction site. | Events in the whole data. |
| 3 | 121 | Basement slab in a neighboring two-story house | Events in the training data. |
| 4 | 48 | First floor slab in a neighboring convenience store | No event. Peaks are observed in the whole data. |
| 5 | 53 | Basement slab in a neighboring three-story industrial building. | Events in the training data. Other peaks in the whole data. |
| 6 | 41 | First floor slab in a neighboring one-story industrial building. | Events in the whole data. |
| 7 | 41 | Mounted on the midpoint of a wall in a neighboring one-story industrial building | Events in the training data. Some peaks in the testing data. |
| 8 | 330 | On the existing ground, on the boundary of a construction site. | Events in the whole data. |
| 9 | 330 | Mounted on the midpoint of a wall in a neighboring multi-story residential building | Peaks in the whole data. |
| 10 | 31 | Mounted on the midpoint of a wall in a neighboring church building tower | Very small ambient vibration. |
| 11 | 15 | On the existing ground, on the boundary of a construction site. | Peaks in the testing data. |
| 12 | 165 | First-floor slab in a neighboring one-story industrial building. | Peaks in the training data. |
| Project No. | Dominant Construction Equipment | Approximate Distance to the Source | General Construction Purpose |
|---|---|---|---|
| 1 | Loaded trucks; Vibratory roller | 10–25 m | Trail Extension |
| 2 | Small bulldozer; Vibratory roller | 0–10 m | Trail Extension |
| 3 | Loaded trucks; Large bulldozer; Hydraulic breaker | 0–10 m | Excavation; Foundation installation |
| 4 | Loaded trucks; Jackhammer; Small bulldozer | 0–10 m | Excavation; Grading |
| 5 | Loaded trucks, Vibratory roller, Excavator | 0–10 m | Site Remediation; Excavation; Backfilling |
| 6 | Vibratory roller; Large bulldozer | 0–10 m | Excavation; Building Construction |
| 7 | Vibratory roller; Loaded trucks | 10–25 m | Excavation; Building Construction |
| 8 | Loaded trucks; Small and large bulldozer | 0–10 m | Excavation; Foundation installation; Grading |
| 9 | Loaded trucks; Small and large bulldozer | 10–25 m | Excavation; Foundation installation; Grading |
| 10 | Not explicitly defined | 25–50 m | Underground subway development |
| 11 | Loaded trucks; Large bulldozer; Hydraulic breaker | 10–25 m | Excavation; Foundation installation |
| 12 | Loaded trucks; Large bulldozer; Hydraulic breaker | 0–10 m | Excavation; Shoring, Foundation installation |
| (Hz) | (mm/s) |
|---|---|
| 8 | |
| 15 | |
| 25 |
| Project No. | Max Depth | Min. Samples Leaf | Min. Samples Split | n_estimators |
|---|---|---|---|---|
| 1 | 80 | 5 | 18 | 401 |
| 2 | 60 | 18 | 9 | 740 |
| 3 | None * | 17 | 13 | 319 |
| 4 | 60 | 19 | 3 | 781 |
| 5 | 70 | 17 | 18 | 101 |
| 6 | 40 | 10 | 8 | 140 |
| 7 | None * | 4 | 10 | 300 |
| 8 | 60 | 19 | 18 | 791 |
| 9 | 40 | 12 | 13 | 104 |
| 10 | 100 | 19 | 18 | 49 |
| 11 | 30 | 11 | 8 | 289 |
| 12 | 10 | 4 | 10 | 300 |
| Project No. | p | q | d |
|---|---|---|---|
| 1 | 2 | 1 | 1 |
| 2 | 2 | 1 | 1 |
| 3 | 1 | 1 | 2 |
| 4 | 2 | 1 | 1 |
| 5 | 1 | 1 | 2 |
| 6 | 1 | 1 | 1 |
| 7 | 2 | 1 | 1 |
| 8 | 2 | 1 | 1 |
| 9 | 1 | 1 | 2 |
| 10 | 1 | 1 | 2 |
| 11 | 1 | 1 | 2 |
| 12 | 2 | 1 | 1 |
| Hyperparameter | Tuned Value |
|---|---|
| BGRU neuron numbers | , |
| Rate of dropout | , |
| Maximum number of epochs | 300 |
| Patience for early stopping | 10 |
| Optimizer | Adam |
| Learning rate | 0.0001 |
| Batch size | 48 |
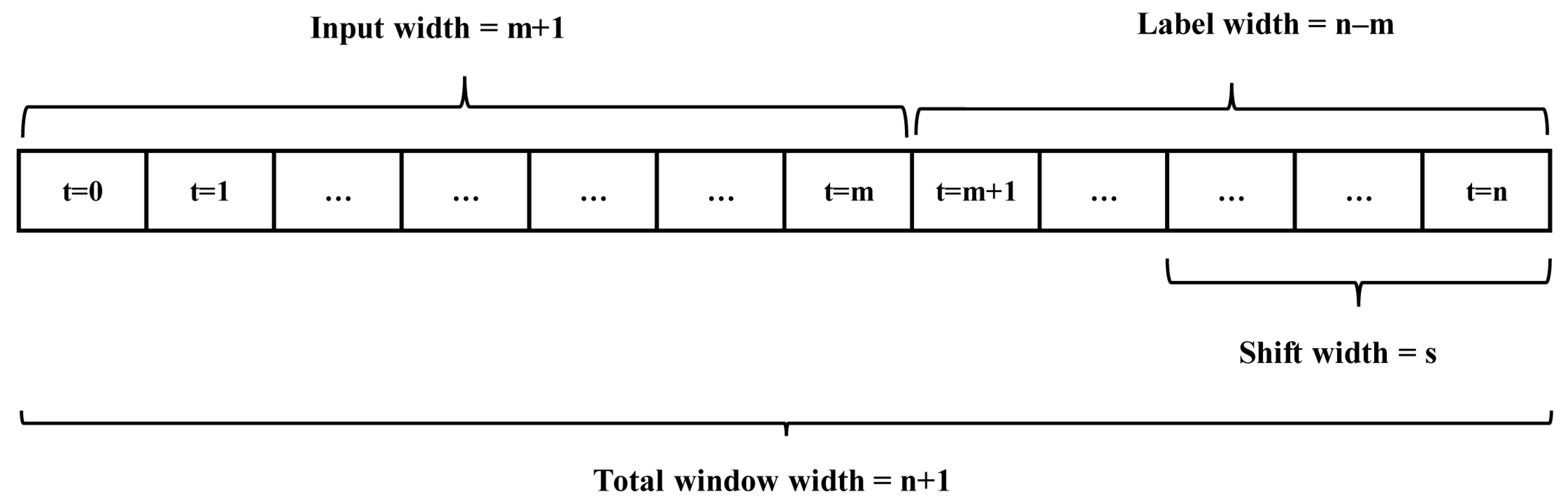
| Data window input length | 6 |
| Data window label length | 1 |
| Data window shift length | 1 |
| Training split ratio | 0.7 |
| Validation split ratio | 0.2 |
| Testing split ratio | 0.1 |
| Project No. | BGRU | RF | ARIMA | |||
|---|---|---|---|---|---|---|
| R-Squared | RMSE | R-Squared | RMSE | R-Squared | RMSE | |
| 1 | 83.5 | 0.0015 | NG * | 0.048 | NG | 0.0192 |
| 2 | 98.8 | 0.1281 | 78.9 | 0.5348 | 85.4 | 0.4548 |
| 3 | 95.4 | 0.0197 | 51.9 | 0.0642 | 43.4 | 0.0695 |
| 4 | 99.8 | 0.0152 | 71.0 | 0.1941 | 83.1 | 0.1465 |
| 5 | 97.6 | 0.1023 | 46.1 | 0.4969 | 74.0 | 0.3410 |
| 6 | 99.0 | 0.1421 | 79.7 | 0.6599 | 88.1 | 0.4988 |
| 7 | 98.1 | 0.0933 | NG | 0.7358 | 84.8 | 0.2676 |
| 8 | 99.8 | 0.0269 | 53.5 | 0.4114 | 67.2 | 0.3450 |
| 9 | 99.5 | 0.0103 | 46.0 | 0.1109 | 64.9 | 0.0892 |
| 10 | 99.3 | 0.0007 | 32.2 | 0.0056 | 57.9 | 0.0065 |
| 11 | 94.5 | 0.2814 | 8.1 | 1.1781 | 68.9 | 0.6655 |
| 12 | 99.8 | 0.0088 | 46.1 | 0.1659 | 64.4 | 0.1343 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiee-Dehkharghani, R.; Esmaeili, K.; Najari, M. Prediction of Construction-Induced Ground Vibrations Using Field Measurements and Bidirectional Gated Recurrent Unit Neural Network. Vibration 2025, 8, 70. https://doi.org/10.3390/vibration8040070
Rafiee-Dehkharghani R, Esmaeili K, Najari M. Prediction of Construction-Induced Ground Vibrations Using Field Measurements and Bidirectional Gated Recurrent Unit Neural Network. Vibration. 2025; 8(4):70. https://doi.org/10.3390/vibration8040070
Chicago/Turabian StyleRafiee-Dehkharghani, Reza, Kamran Esmaeili, and Meysam Najari. 2025. "Prediction of Construction-Induced Ground Vibrations Using Field Measurements and Bidirectional Gated Recurrent Unit Neural Network" Vibration 8, no. 4: 70. https://doi.org/10.3390/vibration8040070
APA StyleRafiee-Dehkharghani, R., Esmaeili, K., & Najari, M. (2025). Prediction of Construction-Induced Ground Vibrations Using Field Measurements and Bidirectional Gated Recurrent Unit Neural Network. Vibration, 8(4), 70. https://doi.org/10.3390/vibration8040070







