Enhancement of Inner Race Fault Features in Servo Motor Bearings via Servo Motor Encoder Signals
Abstract
1. Introduction
2. Theoretical Background
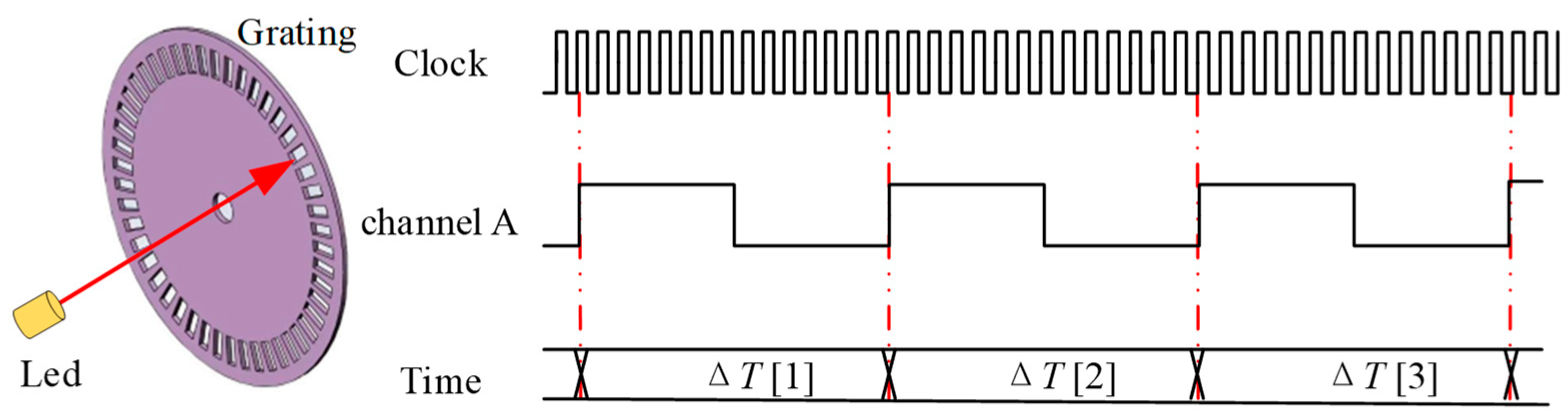
2.1. Measurement Principle of IAS
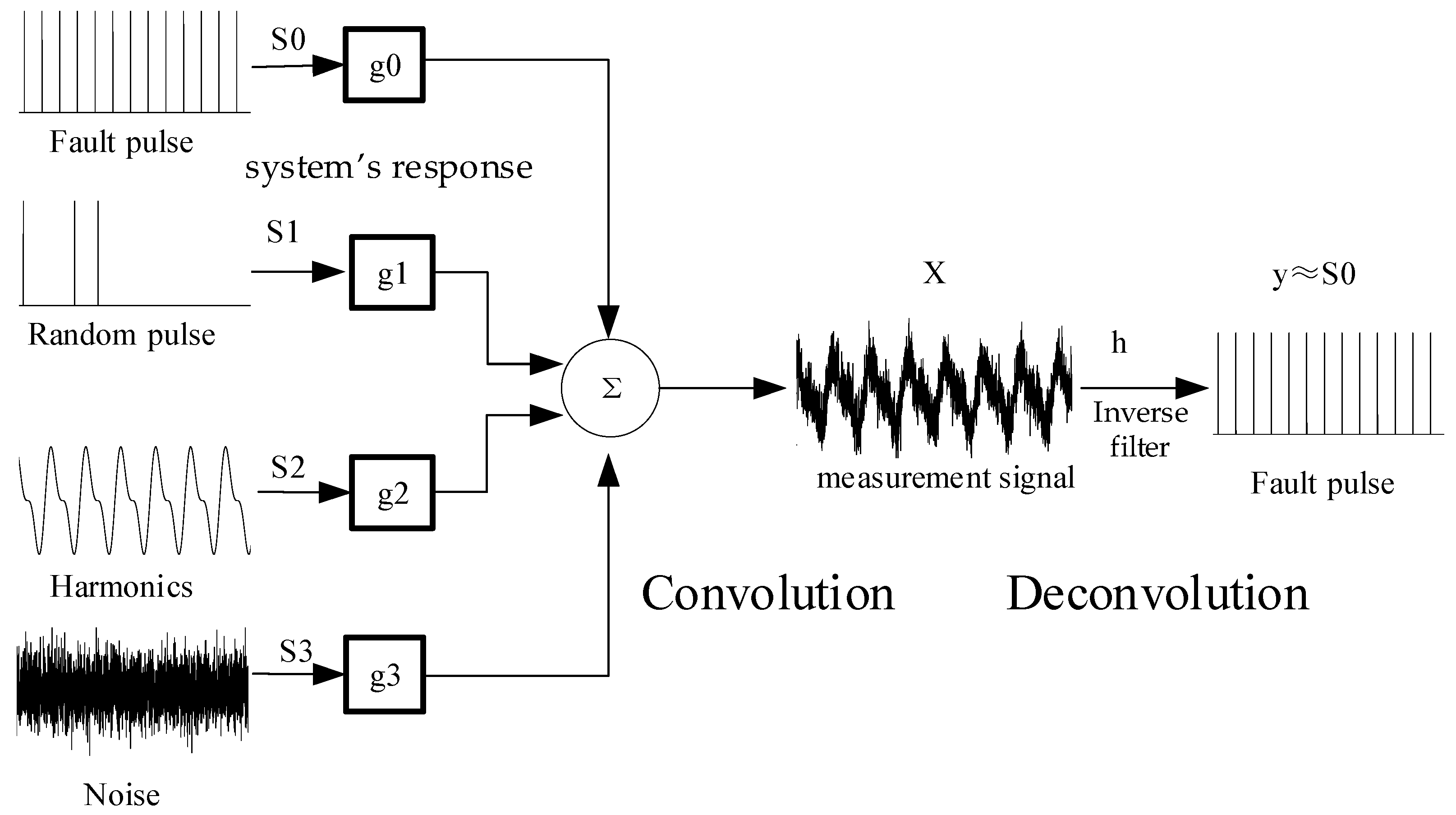
2.2. Brief on Cyclic Blind Deconvolution
2.3. Improved CYCBD
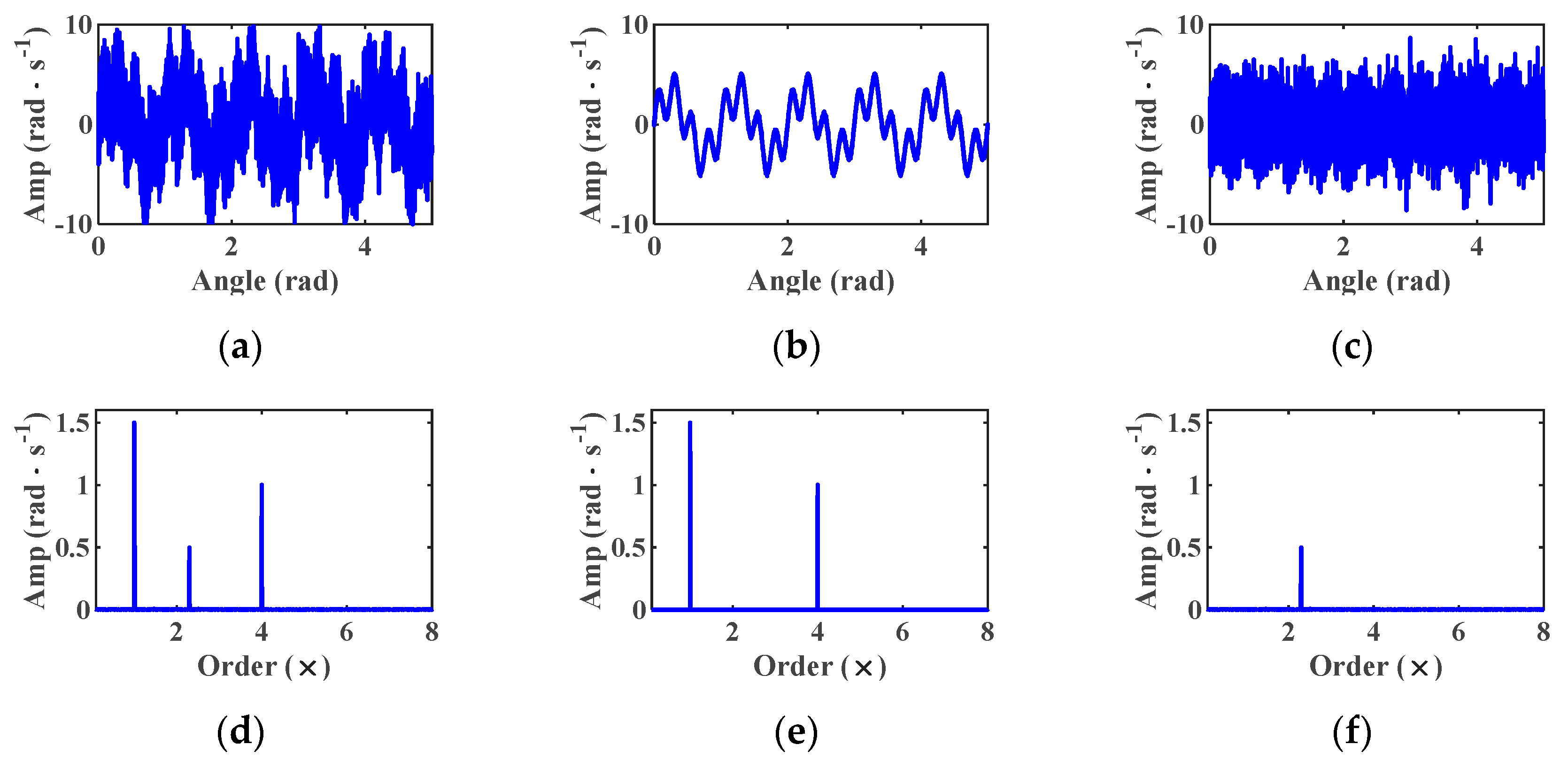
2.3.1. Comb-Notch Filtering Based on RDA
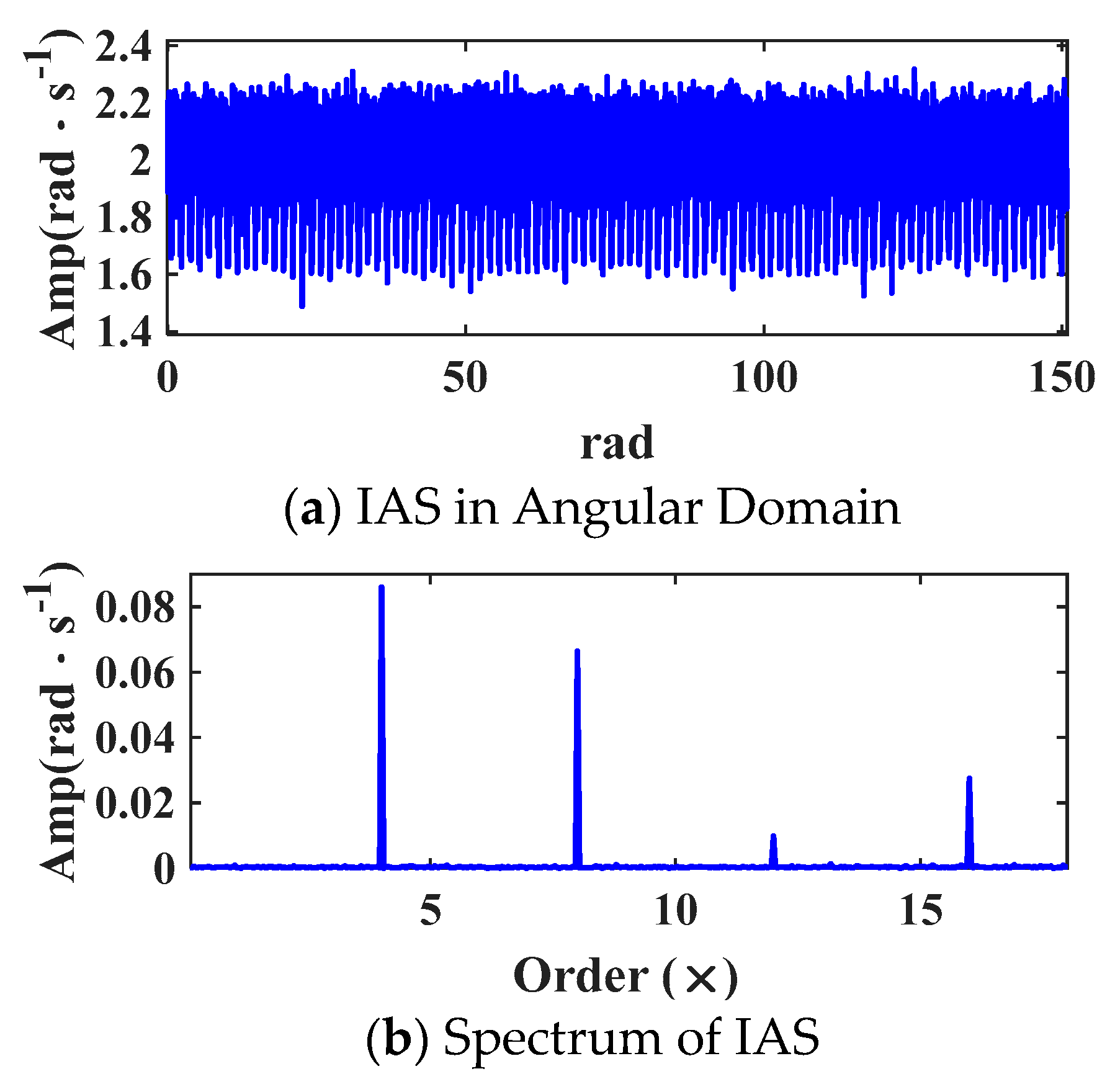
2.3.2. Adaptive Estimation of Fault Characteristic Order
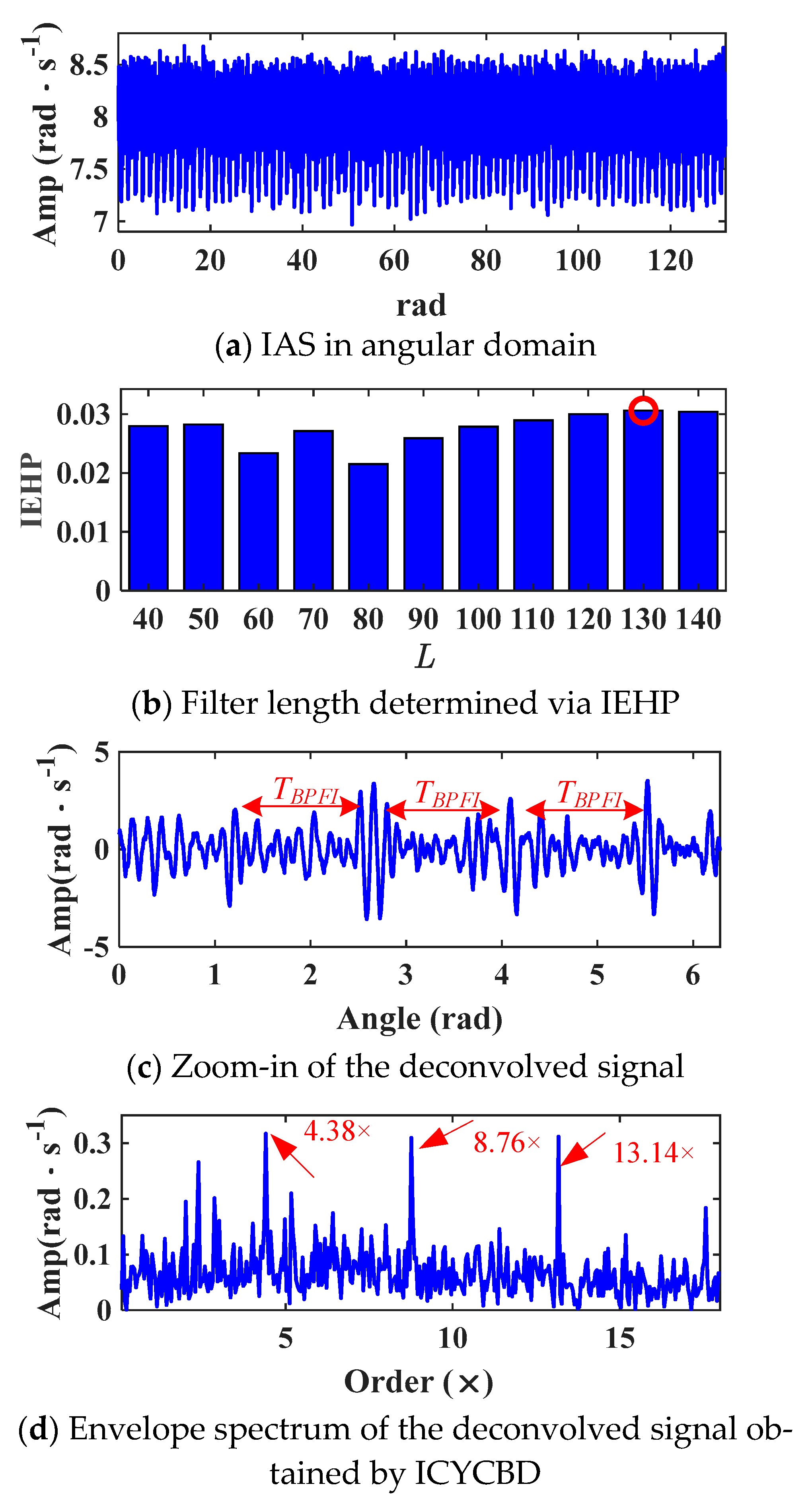
2.3.3. Adaptive Filter Length Tuning Using IEHP
3. Schematic of ICYCBD
- 1.
- IAS Signal AcquisitionThe pulse outputs from the servo motor encoders were recorded in this study using a high-speed counter based on FPGA technology. The time interval between adjacent pulses was calculated using Equation (2) and converted into an IAS signal sequence.
- 2.
- Signal PreprocessingThe IAS signal is segmented into data blocks, which correspond to integer complete cycles of the encoder. Equation (10) is used to perform the RDA. Subsequently, Equation (11) is utilized to obtain the residual IAS signal.
- 3.
- CYCBD-Based Weak Fault Feature ExtractionThe fault order is estimated from the residual IAS signal using Equation (13). A pre-whitening filter is initialized, and the inverse filter h is optimized to enhance cyclostationary at the target order. Convergence is evaluated using Equation (5), and the output is envelope-demodulated to reveal impulsive features.
- 4.
- Adaptive Filter Length OptimizationFor each candidate filter length L, the indicator defined in Equation (14) is calculated based on the estimated fault order Oopt. The filter length is adaptively adjusted by comparing the current IEHP value with its maximum to determine the optimal configuration.
- 5.
- Envelope Signal Calculation and Spectral Feature MatchingThe deconvolved signal obtained with optimal parameters is subjected to spectral analysis, and its features are compared with the estimated fault order to validate the fault diagnosis.
4. Experimental Results and Analysis
4.1. Experiment
4.1.1. Test Rig
4.1.2. Experimental Results
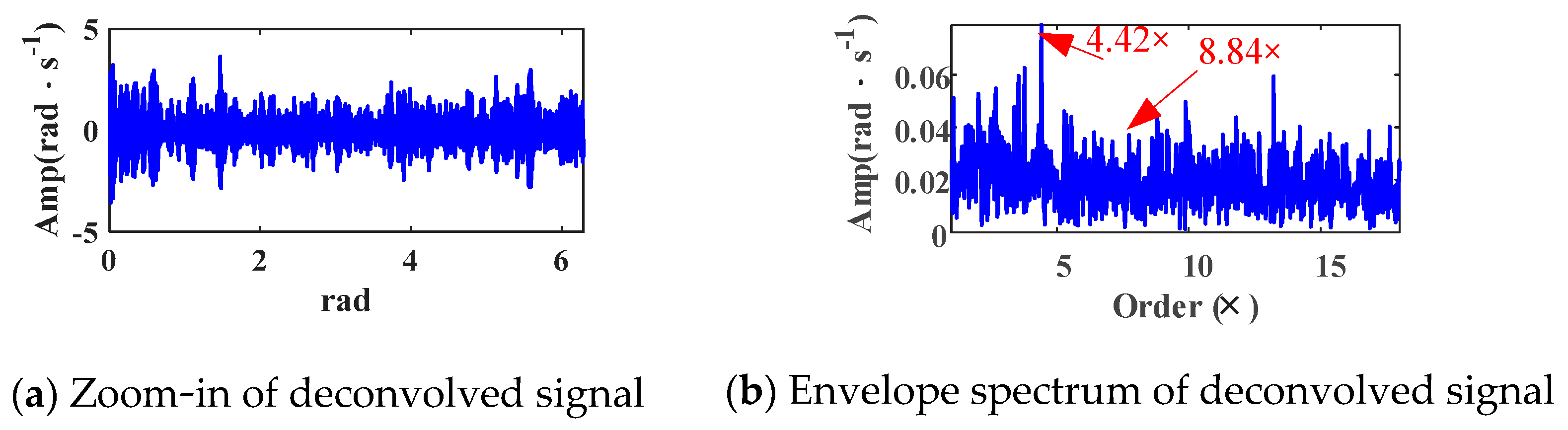
4.2. Comparison
4.3. Robustness Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IAS | Instantaneous Angular Speed |
| MED | Minimum Entropy Deconvolution |
| MCKD | Maximum Correlated Kurtosis Deconvolution |
| CYCBD | Cyclic Blind Deconvolution |
| ICYCBD | Improved Cyclic Blind Deconvolution |
| RDA | Rotary-domain Synchronous Averaging |
| SES | Squared Envelope Spectrum |
| FPGA | Field Programmable Gate Array |
References
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques in fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Ding, C.; Zhao, M.; Lin, J.; Jiao, J.; Liang, K. Sparsity-Based Algorithm for Condition Assessment of Rotating Machinery Using Internal Encoder Data. IEEE Trans. Ind. Electron. 2020, 67, 7982–7993. [Google Scholar] [CrossRef]
- Cristalli, C.; Paone, N.; Spinsante, S. Mechanical fault detection of electric motors by laser vibrometer and accelerometer measurements. Mech. Syst. Signal Process. 2006, 20, 1350–1361. [Google Scholar] [CrossRef]
- Adamczak, S.; Wrzochal, M.; Durakbasa, N.M. Evaluation of a Non-Contact Method for Measuring Vibration of Rolling Bearings in Industrial Conditions. Mechanik 2020, 93, 8–11. [Google Scholar] [CrossRef]
- Rothberg, S.J.; Allen, M.S.; Castellini, P.; Di Maio, D.; Dirckx, J.J.J.; Ewins, D.J.; Halkon, B.J.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An International Review of Laser Doppler Vibrometry: Making Light Work of Vibration Measurement. Opt. Lasers Eng. 2017, 99, 11–22. [Google Scholar] [CrossRef]
- Liu, H.Y.; Ji, D.C.; Lin, J. Non-contact torsional vibration measurement and residual vibration analysis methods for planetary gearbox fault diagnosis. J. Vib. Eng. 2025, 38, 1354–1362. [Google Scholar] [CrossRef]
- Liu, H.; Ji, D.; Lin, J. Residual angular speed analysis based on laser Doppler vibrometer and its application in planetary gearbox diagnosis. Measurement 2025, 250, 116987. [Google Scholar] [CrossRef]
- Renaudin, L.; Bonnardot, F.; Musy, O.; Doray, J.B.; Rémond, D. Natural roller bearing fault detection by angular measurement of true instantaneous angular speed. Mech. Syst. Signal Process. 2010, 24, 1998–2011. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, J.; Miao, Y. Application of an MAKD method via Dixon’s test for gearbox fault diagnosis based on built-in encoder signals. Meas. Sci. Technol. 2025, 36, 086115. [Google Scholar] [CrossRef]
- Stack, J.R.; Habetler, T.G.; Harley, R.G. Fault-signature modeling and detection of inner-race bearing faults. IEEE Trans. Ind. Appl. 2006, 42, 61–68. [Google Scholar] [CrossRef]
- Chen, X.; Guo, Y.; Na, J. Instantaneous-angular-speed-based synchronous averaging tool for bearing outer race fault diagnosis. IEEE Trans. Ind. Electron. 2023, 70, 6250–6260. [Google Scholar] [CrossRef]
- Wiggins, R.A. Minimum entropy deconvolution. Geoexploration 1978, 16, 21–35. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Buzzoni, M.; Antoni, J.; Borghesani, P. Cyclic blind deconvolution for bearing diagnostics. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Sun, H. Application of a novel improved adaptive CYCBD method in gearbox compound fault diagnosis. IEEE Access 2021, 9, 133835–133848. [Google Scholar] [CrossRef]
- Zhang, Q. Research on fault extraction method of CYCBD based on seagull optimization algorithm. Shock Vib. 2021, 2021, 8552024. [Google Scholar] [CrossRef]
- Huo, W.; Jiang, Z.; Sheng, Z.; Zhang, K.; Xu, Y. Cyclostationarity blind deconvolution via eigenvector screening and its applications to the condition monitoring of rotating machinery. Mech. Syst. Signal Process. 2025, 222, 111782. [Google Scholar] [CrossRef]
- Yin, X.; Guo, Y.; Na, J.; Fan, J. Incremental optical encoder error modeling and compensation for accurate speed acquisition in non-stationary conditions. IEEE Trans. Ind. Electron. 2025, 72, 1033–1042. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, L.; Wu, X.; Na, J. Tooth root crack detection of planet and sun gears based on resonance demodulation and vibration separation. IEEE Trans. Instrum. Meas. 2020, 69, 65–75. [Google Scholar] [CrossRef]
- Antoni, J.; Bonnardot, F.; Raad, A.; El Badaoui, M. Cyclostationary modelling of rotating machine vibration signals. Mech. Syst. Signal Process. 2004, 18, 1285–1314. [Google Scholar] [CrossRef]
- Zhang, B.; Miao, Y.; Lin, J.; Yi, Y. Adaptive maximum second-order cyclostationarity blind deconvolution and its application for locomotive bearing fault diagnosis. Mech. Syst. Signal Process. 2021, 158, 107736. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, J.; Du, W.; Lei, Y.; Wang, J. Bearing fault diagnosis method based on adaptive maximum cyclostationarity blind deconvolution. Mech. Syst. Signal Process. 2022, 162, 108018. [Google Scholar] [CrossRef]
- Qi, Y.; Shan, C.; Jia, S.; Liu, L.; Dong, C. A gearbox composite fault diagnosis based on enhanced CYCBD. Chin. Mech. Eng. 2022, 33, 2927–2941. [Google Scholar] [CrossRef]





| Bearing Parameter | Value |
|---|---|
| Pitch Diameter Dp (mm) | 43.5 |
| Rolling Element Diameter Db (mm) | 11.49 |
| Number of Rolling Elements Nb | 7 |
| Contact Angle α (°) | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Y.; Guo, Y.; Li, J.; Wang, H. Enhancement of Inner Race Fault Features in Servo Motor Bearings via Servo Motor Encoder Signals. Vibration 2025, 8, 59. https://doi.org/10.3390/vibration8040059
Lyu Y, Guo Y, Li J, Wang H. Enhancement of Inner Race Fault Features in Servo Motor Bearings via Servo Motor Encoder Signals. Vibration. 2025; 8(4):59. https://doi.org/10.3390/vibration8040059
Chicago/Turabian StyleLyu, Yubo, Yu Guo, Jiangbo Li, and Haipeng Wang. 2025. "Enhancement of Inner Race Fault Features in Servo Motor Bearings via Servo Motor Encoder Signals" Vibration 8, no. 4: 59. https://doi.org/10.3390/vibration8040059
APA StyleLyu, Y., Guo, Y., Li, J., & Wang, H. (2025). Enhancement of Inner Race Fault Features in Servo Motor Bearings via Servo Motor Encoder Signals. Vibration, 8(4), 59. https://doi.org/10.3390/vibration8040059





