Abstract
Traditional control strategies for vibration suppression primarily focus on reducing settling time. However, this approach may not adequately address situations where the initial peak response of the vibration poses a risk of damage. This paper presents a novel application of active disturbance rejection control (ADRC) for attenuating the first-cycle peak response of free vibration in flexible structures. Inspired by the sudden impact scenario of particle accelerator collimators, a smart beam was designed to investigate the percentage first-cycle peak attenuation (FCPA) achievable by the disturbance estimation-based controller, in comparison with a classical proportional–differential (PD) controller. This study examined the limitations of the controller in mitigating initial deviations caused by real-world factors, such as delay and noise, through experimental methods. Results indicate that the PD controller achieves a maximum attenuation of 18%, while the ADRC achieves 30% attenuation. Improving the collocation configuration of the smart beam further improves the ADRC attenuation to 46.5%. Experimental data was used to fine-tune the system model in a sensitivity analysis to determine the delay within the system. Additionally, a new tuning parameter, α, representing the ratio of the observer bandwidth to controller bandwidth, was introduced to investigate the impact of observer and controller gain choices. System noise was amplified by 20 to 30 times, depending on the α value, although no significant effect on the control of the beam was observed.
1. Introduction
Active vibration control (AVC) is an essential technology used to achieve lower levels of vibration often required for the optimal performance and longevity of machines and structures. Unlike passive control methods, which involve modifying the physical properties of a structure to absorb vibration, AVC can offer greater adaptability and effectiveness [1]. AVC operates on the principle of destructive interference by applying an identical counteractive force to the initial vibration caused by disturbances. When the amplitude and phase of this counteractive force closely matches the uncontrolled vibration, significant attenuation is often achieved [2]. The key components of an AVC system include the plant to be controlled, sensors to detect the vibration, actuators that provide the compensatory force, and a controller that executes the necessary algorithms [3].
A notable example of a system requiring active vibration control is the Adaptive Collimation System (ACS) [4] proposed for the CERN Large Hadron Collider (LHC). The ACS is designed to address slow deformations and vibratory responses that affect the collimators, which are critical for beam cleaning and concentration of circulating proton beams for optimal collision. In instances of excessive beam loss, a beam dump is triggered to extract the beam. Errors in this process can lead to direct beam impacts on the collimator jaws, resulting in significant vibratory responses. The proposed ACS aims to mitigate these issues using a closed-loop system, which integrates an intrinsic fibre-based interferometric strain measurement system and a series of high-powered piezo-ceramic (PZT) stack actuators. These piezo actuators effectively correct slow elastic deformations caused by gradual proton beam losses, ensuring the slow collimator jaw deflections remain within acceptable limits. However, the flexural oscillations induced by direct beam impacts from asynchronous beam dumps and beam injection errors remain uncompensated [5]. The initial deflection caused by these impulse impact scenarios can lead to plastic deformation of the collimator jaws, as demonstrated in several studies [6,7]. By reducing the first-cycle peak caused by beam impacts, the ACS can minimise the risk of plastic deformation and maintain the integrity of the collimation system.
The effectiveness of control measures for the CERN jaw active vibration challenge can be evaluated by the percentage of first-cycle peak attenuation (FCPA). Numerous studies in the literature explore active suppression of transversal free vibration in flexible smart structures. Various control strategies are used, different appraisal methods for control effectiveness are employed and, in some cases, the controlled vibration graphs show different levels of first-cycle peak suppression. Some of these efforts are based on modern control-state feedback methods. Kermani et al. investigated high-authority piezoelectric stack actuators for AVC of long-reach robotic manipulators. They compared a control law based on the Popov criterion with Linear Quadratic Regulator (LQR) control. The study found that the Popov criterion not only guarantees system stability but also enhances actuator performance in suppressing flexural modes. For initial displacement disturbances, the Popov criterion controller achieved 8% first-cycle peak attenuation [8]. Sethi and Song studied the suppression of free vibration in a smart beam and a model frame structure using pole placement and LQR control methods. These studies demonstrated vibration suppressed across multiple modes. Controller performance was evaluated using power spectrum plots without an investigation of first-cycle peak attenuation [9,10]. Martens and Waller presented practical results on cantilever beam vibration suppression using patch and stack-type piezo actuators. They employed the LQR method to attenuate impulsively excited vibrations, assessing suppression effectiveness in terms of the settling times of the uncontrolled beam, the stack actuator beam, and the bimorph patch actuator beam, where an 85% settling time reduction was achieved [11].
Soft computing fuzzy-based methods have also been applied for active suppression of free vibration. Li et al. applied the decentralised adaptive fuzzy control method to a large space truss structure under impulse excitation. While the resultant overall vibration suppression was effective, no attenuation of the first-cycle peak was observed [12]. Xu et al. developed a vibration control system for gossamer space structures using piezoelectric stack actuators. They compared decentralised adaptive fuzzy control with the traditional fuzzy control, focusing on settling time. Experimental results showed a 12.5% attenuation of the first-cycle peak of bending vibration for both control methods under initial displacement disturbances [13]. Additionally, Xu et al. developed an online learning fuzzy vibration controller for a smart truss structure. Although the reported evaluation parameter was the damping ratio, the experimental results showed that the fuzzy controller achieved a 7.5% first-cycle peak attenuation, while the online learning fuzzy controller achieved a reduction of 12.5% [14]. Alireza et al. applied fuzzy control to a smart beam subjected to initial displacement. They compared the time responses of the beam in the open loop, the proportional differential (PD), and the fuzzy controller, focusing on the root mean square (RMS) of the sensor output voltage. The fuzzy absorber reduced the magnitude of the first mode vibration by approximately 38% of the open-loop system; however, first peak response was not affected [15].
A variety of classical control and other advanced methods have been employed to suppress free vibration of flexible structures. Qui et al. developed a backpropagation neural network-based PD control algorithm for a piezoelectric beam, showing effectiveness in settling time reduction but no early attenuation [16]. Khot et al. presented active control of a cantilever beam using piezoelectric transducers with H-infinity and PD controllers designed in LabVIEW. Their experiments showed a reduction in settling time for initial displacement disturbances but no reduction in the initial peak. They also reported noise at the settling time due to spurious signals from the controller [17,18]. Takacs et al. implemented embedded explicit model predictive control on a piezoelectric smart beam, comparing their method with the classical positive position feedback control. The proposed method achieved similar vibration suppression with less control effort, but suppression only began from the third vibration cycle [19]. Song et al. investigated active vibration damping of a composite beam using positive position feedback and strain rate feedback methods, focusing on the power spectrum density reduction [20]. Malgaca and Karagulle implemented displacement feedback and direct velocity feedback control on laminated composite beams under step disturbance. Controller effectiveness was analysed using the damping ratios achieved using controller gain values. The maximum controller input peak voltage was presented; however, no FCPA of the response was observed [21,22]. In addition to structural and precision engineering applications, active vibration control methods are increasingly relevant to intelligent vehicle suspension systems, where road bumps or potholes can induce significant transient dynamics. Recent studies have explored active and semi-active strategies for suspension control [23,24] While these methods focus on improving ride comfort and road handling, our review of the literature revealed a limited emphasis on suppressing the first-cycle peak, which is the initial high-amplitude response following an impulse. This specific challenge has significant implications for ride quality and component fatigue.
Active disturbance rejection control (ADRC) compensates for disturbances by estimating them and applying corrective measures. Where it is not possible to directly measure the disturbance, ADRC combines the PID control error-driven approach with state observer techniques to address the shortcomings of classical and modern control, such as error computation and noise issues. This results in effective disturbance estimation and rejection using an extended state observer [25]. Gao advocates for ADRC due to the uncertainty of mathematical models representing real-life process dynamics, showing that the notion of disturbance can be generalised to represent any discrepancies between the physical system and the model [26]. He also proposed a scaling and bandwidth-parameterisation-based tuning method of linear ADRC. This method was used to quickly determine the maximum bandwidth by varying tuning parameters to make different trade-offs among different design considerations [27]. Herbst, Zhang et al., and Li et al. presented ADRC derivations and simulation results, relating key tuning parameters with control outcomes. The controller bandwidth was selected based on the desired system performance, particularly the settling time, and it was recommended to set the observer bandwidth between three and ten times the controller bandwidth for the optimal performance [28,29,30]. In the application of vibration control, Lee reported the use of an estimated disturbance input to compensate for vibrations of different structures. Early suppression of the vibratory response is observed as this method is applied [31,32]. A simulative study by Zhang et al. shows 33% and 42.6% attenuation in the first-cycle peak response for a smart beam under step disturbance. The tuning parameter produces larger observer gains, which shorten the rise time of the estimated disturbance, increase overshoot, and amplify noise in the system. However, the extent of noise amplification and its effects were not investigated [33]. Ostertag highlighted that a judicious choice of the observer gain facilitates a reduction in the effect of disturbance, particularly when certain conditions are met [34]. Zheng et al. implemented ADRC for reference tracking and vibration suppression of a piezoelectric beam, comparing its performance with observer-based state feedback with integral action (OBSFI) and PID controllers for the tracking of sinusoidal and square wave signals. While the vibration suppression experiment demonstrated a significant reduction in settling time, the reduction in the first-cycle peak was not quantified, nor was the effect of the tuning parameter ratio of the observer and controller bandwidths investigated [35].
The literature review identifies a gap in early suppression capabilities of controllers for the free vibration response, particularly first-cycle peak reduction. Most studies use the release test methodology rather than an impulse with a fixed amplitude and width. However, the vibrations of the collimator jaw are more closely related to the impact of an impulse. ADRC is the only algorithm that seems to deliver attenuation of the first-cycle peak by more than 30%; however, its experimental application needs further exploration, especially considering system uncertainties like delay, noise, and nonlinearities.
In this work, a smart cantilever beam is equipped with a piezo stack actuator for vibration suppression and a laser triangulation sensor for vibration measurement. The main contributions of this work are as follows:
- Introduction of the first-cycle peak attenuation as a novel and practical performance metric for evaluating the effectiveness of active vibration controllers under impulsive excitation. While previous studies often rely on RMS reduction, settling time, or frequency domain metrics, these do not capture the critical first-response amplitude, which is especially important in impact-sensitive applications.
- Implementing and experimentally validating the FCPA metric using a smart cantilever beam setup with a piezoelectric stack actuator and a laser triangulation sensor. The experimental platform allows for the precise measurement of transient responses, unlike some numerical-only studies in the literature.
- Investigating the impact of the actuator–sensor configuration (collocated vs. non-collocated) on ADRC performance. Although collocation effects have been studied in the general control literature, their specific influence on first-cycle peak suppression in piezo-based systems under impulse loads has not been addressed.
- Proposing and assessing a new tuning approach for ADRC based on the ratio between control bandwidth and observer bandwidth, denoted as a dimensionless tuning parameter α. Although it is acknowledged in the literature that increasing the controller bandwidth can amplify noise, the extent of this amplification and its impact on system behaviour have not been thoroughly investigated. Furthermore, while a ratio between the observer and controller bandwidths is often recommended, this guideline has not been tested on systems with high sensitivity to sensor noise, such as the one considered in this study.
- Model tuning and noise analysis using experimental data, revealing how measurement noise and system delay affect performance and observer behaviour. This adds a practical dimension to ADRC tuning and evaluation, which is often overlooked in simulation-based studies.
The outcome will provide insights into the achievable first-cycle peak response attenuation for a system with a specific delay and signal-to-noise ratio. A PD controller, widely considered the industry standard, is selected for a performance comparison with ADRC. Furthermore, control strategies reviewed, such as LQR and fuzzy logic, utilise output error and its first derivative to generate control efforts in a manner similar to PD control.
2. System Model
The piezoelectric beam used in this study is illustrated in Figure 1. The unidirectional piezoelectric actuator is attached at the root of the cantilever beam through an adapting mechanism. When voltage is applied to the actuator electrodes, the stack actuator expands in the axial direction and induces bending moments via the adapting mechanism. This causes transversal displacement of the beam tip relative to the optical sensor. A shaker is placed beside the beam to generate impulse disturbance.
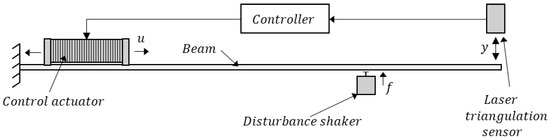
Figure 1.
Piezoelectric smart beam setup.
The system under investigation can be physically modelled as a distributed parameter system governed by the Euler–Bernoulli beam theory. For control design purposes, this is commonly reduced to a finite-degree-of-freedom approximation [13]. In this study, we adopt a second-order lumped parameter model, capturing the dominant vibration mode. The equation of motion for the reduced-order system is
where , , and k represent the modal mass, damping, and stiffness, respectively, is the displacement at the tip, is the disturbance force, and is the control force applied via the piezo actuator. The system model is described by a linear time-invariant (LTI) second-order state-space system according to
where the state vector contains the tip displacement and velocity as
The control input represents the voltage applied to the actuator, which generates a control force at the base of the beam. The disturbance input represents an external force applied to the beam tip, simulating an impulse excitation. The output is the measured displacement at the beam tip, obtained from the laser triangulation sensor. Matrices , , and are the state transition matrix, control input influence matrix, disturbance influence matrix, and output matrix, respectively. The linearised model capturing the dynamics of the beam between actuator voltage and tip displacement can be obtained by experimental means. A chirp signal with a frequency range of 1 Hz to 200 Hz and amplitude of 1 V peak to peak was applied over 300 s to the amplifier which drives the stack actuator. The system frequency response is shown in Figure 2. The figure shows three resonant frequencies in the frequency range of the test, located at , and . The impulse response of the disturbance from the shaker was recorded to deduce the disturbance model. The MATLAB v23.2 ‘ssest’ function, which uses a prediction error minimisation algorithm, was utilised to create the system model for the first bending mode in the observer canonical form given in Equation (4).
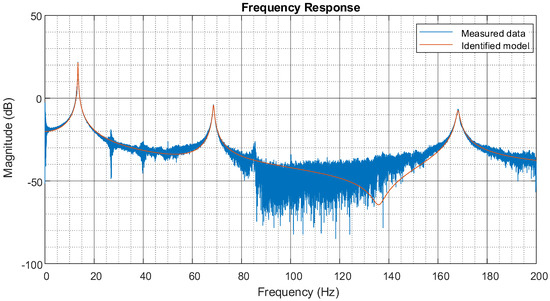
Figure 2.
Frequency domain model fit.
Although piezoelectric actuators can exhibit nonlinear behaviour such as hysteresis and creep, these effects are negligible in this case due to the use of low voltage excitation and the short-duration impulse nature of the disturbance. Hence, a linear time-invariant (LTI) model is considered sufficient to capture the dominant dynamics of the beam. Furthermore, nonlinear effects and unmodeled dynamics are treated as part of the lumped disturbance, for which the ADRC strategy is designed to estimate and compensate.
3. Active Suppression of Free Vibration
In disturbance estimation-based feedback control, the disturbance to the system is estimated and fed to the controller in a feedforward manner to respond proactively to disturbance. This feedforward method of control relies on the availability of a disturbance signal to generate a compensating signal early enough to contain the effects of the disturbance. In systems where the disturbance signal cannot be measured, observers are used to estimate this disturbance signal to generate compensation action.
3.1. ADRC Formulation
Consider a second-order process with input , output , DC gain , damping factor and time constant represented in the frequency domain as [28]
and in the time domain as
An input disturbance is entered into the process, such that
Setting
Equation (7) becomes
When substituting , where is the known part of and is the unknown part due to modelling error, Equation (9) becomes
The generalised disturbance is constructed as the difference between the actual system dynamics and the nominal second-order model assumed for the ADRC formulation. This includes the external disturbance and the model uncertainties captured in . By subtracting the expected nominal behaviour from the true system response, all residual effects are lumped into as
so that the process model becomes the following double integrator
which is represented in state space as
Equation (13) presents the disturbed process in an augmented state with state-space matrices
To employ a control law for vibration control, the Extended State Observer (ESO) in Figure 3 is required to provide an estimation for the three states, and . The ESO estimates the generalised disturbance in real time, enabling the control law to actively reject its effect and restore the desired system performance.
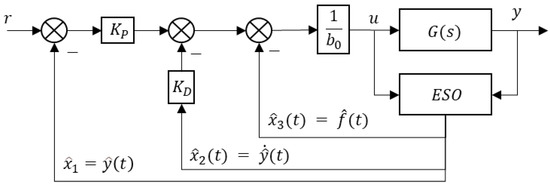
Figure 3.
ADRC control loop structure.
With the system states and total disturbance estimated by the observer, the dynamics are effectively simplified to that of a double integrator, allowing the output to be regulated using a conventional controller. A simplified PD controller, which uses only the output derivative in the derivative term and omits the derivative of the reference signal is used. This approach avoids the amplification of noise or unbounded values that can arise from differentiating sharp reference inputs such as steps or impulses. The resulting control law is an estimation-based state feedback controller:
where is a virtual control law based on estimated outputs, given as
Pole placement is used to compute the observer gain such that the estimation error dynamics of the following observer converge with the desired speed and stability
where
If the observer converges to deliver good estimates, Equation (17) can be substituted into Equation (12) to give
The control input is therefore obtained by
The tuning approach involves choosing and to derive a negative-real double pole according to the required settling time
The observer poles are placed at 3–10 times the closed loop poles to obtain the observer gain
and the critical gain is given by
3.2. Control Simulation
This section presents the results of control simulations for the active cantilever beam. FCPA capabilities are investigated for an arbitrary PD controller with a fixed proportional gain of 1 and varying derivative gain values (0, 0.1, 0.2, 0.3, and 0.4). The derivative term provides a damping effect by predicting the future behaviour of the error based on its rate of change. When the error changes rapidly, the derivative action generates a control signal that opposes this change, thereby dampening the oscillations. The ADRC tuning parameters are chosen to set the closed-loop system eigenvalues sufficiently far to the left of the system open-loop poles to increase damping, restricting the first-cycle peak. The closed-loop system poles are chosen as 20, 40, 60, 80, and 100 times the real component of the open-loop system poles. The observer poles are placed at six times the controller bandwidth . Simulation results are obtained using the MATLAB/Simulink PID and ADRC block, and the FCPA is calculated in percentages as
The results in Figure 4 and Figure 5, summarised in Table 1, show the FCPA achieved by the PD controller and ADRC in simulation.
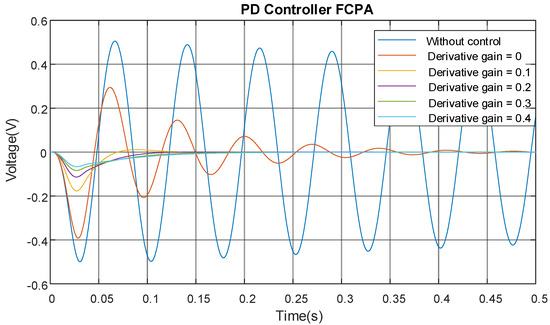
Figure 4.
Tip displacement response of PD vibration control simulation.
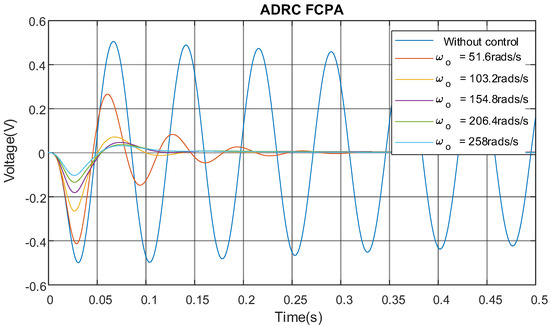
Figure 5.
Tip displacement response of ADRC vibration control simulation.

Table 1.
FCPA achieved by PD controller and ADRC through simulation.
Simulation results in Figure 4 and Figure 5, summarised in Table 1, show the capacity of the PD controller and ADRC to restrict the first-cycle peak for an ideal second-order LTI system. Similar levels of attenuation reaching up to 80% are achieved by both controllers for different tuning parameters.
4. Experiment
The proposed ADRC was implemented on the piezoelectric smart beam to demonstrate its FCPA control capability. Testing was performed for the non-collocated and collocated disturbance and sensor configurations using different tuning parameters to establish the peak attenuation, delay, and noise amplification due to changing tuning parameters. In the non-collocated configuration, the shaker is placed at a random point between the actuator and the sensor, while in the collocated configuration, the shaker is placed directly opposite the sensor.
4.1. Experimental Setup
The smart beam, constructed from aluminium alloy (Young’s modulus: , density: ), featured a piezoelectric stack-type actuator (Physik Instrumente, GmbH, model P-888.91) capable of generating a blocking force of 3800 N within a 0 to 100 V range. Actuators were controlled using a BCP303 Thorlabs amplifier with adjustable gain settings (7.5, 10, and 15). Beam tip deflection was non-contact measured via a Riftek RF603 laser triangulation sensor, providing a 0–10 V analogue signal indicative of deflection. Control algorithms were implemented using a Texas Instruments F28379D development board and MATLAB/Simulink. Signal conditioning circuits were designed to scale signals within the 0–3 V input–output range of the controller. Data acquisition utilised National Instruments hardware and software. Tip disturbance was induced by a simple electromagnetic shaker, driven by a pulse signal from a function generator. Figure 6 depicts the assembled setup.

Figure 6.
Experimental setup.
The presence of noise, delay, and nonlinearities can introduce significant deviations between experimental results and simulation outcomes, in terms of peak attenuation and system stability. The analogue-to-digital converter (ADC) of the control card contributes to noise, leading to spurious system outputs. Consequently, the response of the controller to this artificial disturbance inadvertently disrupts system behaviour. In controllers with high gain, this disturbance becomes pronounced, triggering free vibration. Attempts by the controller to mitigate this disturbance subsequently lead to spillover, manifesting as excitation of higher modes of vibration. While the system may remain marginally stable during spillover, damping of free vibration of the first mode is still achievable. However, in certain instances, amplification of the first-cycle peak occurs.
Figure 7 illustrates the contribution of ADC noise for varying sampling frequencies. Notably, while noise peaks occur at similar levels (approximately 0.1 V max) across different sampling frequencies, higher sampling frequencies exhibit more frequent spikes and a larger noise floor. Consequently, a sampling frequency of 1 kHz emerges as the optimal choice due to its superior performance in minimising the occurrence of spikes.
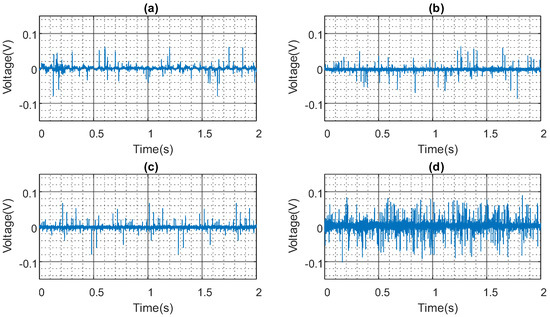
Figure 7.
ADC noise: (a) 1 kHz sampling frequency; (b) 2 kHz sampling frequency; (c) 5 kHz sampling frequency; (d) 10 kHz sampling frequency.
However, sampling at 1 kHz introduces a delay of 1 μs, which is a trade-off for reduced noise. Despite this sampling delay, it is considered a favourable compromise due to the significant noise reduction achieved. Furthermore, the overall delay within the system is compounded by delays arising from the actuator response and nonlinearities. These delays collectively contribute to the system response time, which is determined through an analysis of experimental results.
4.2. PD Controller vs. ADRC
In this part, the experimental results of non-collocated disturbance and the sensor PD controller and ADRC are presented and analysed. The control experiments were conducted with identical tuning parameters as those used in the simulations.
The results presented in Figure 8 and Figure 9, and summarised in Table 2, show the FCPA for the experimental beam. The PD controller achieves a maximum attenuation of 18.1% before the system experiences spillover, which occurs due to an increase in the derivative gain. The spillover excitation frequency observed was 340 Hz, higher than the third mode of vibration.
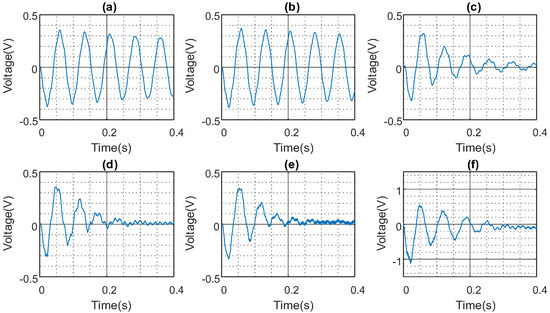
Figure 8.
PD controller FCPA of experimental beam. (a) Open loop response. (b) Derivative gain . (c) Derivative gain . (d) Derivative gain . (e) Derivative gain = . (f) Derivative gain .
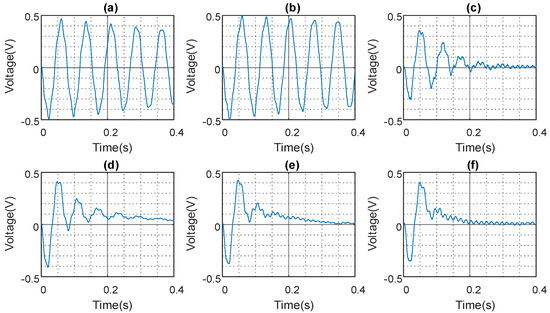
Figure 9.
ADRC controller FCPA of experimental beam. (a) Open loop response. (b). (c) . (d) . (e) = . (f) .

Table 2.
FCPA achieved by PD controller and ADRC through experiments.
With a derivative gain of 0.3, the vibration amplitude was 0.16 V, though an FCPA of 11.7% was achieved. The derivative gain of 0.4 resulted in a vibration amplitude of 0.2 V and amplification of the first-cycle peak by 200%, according to Figure 8f. In contrast, the ADRC achieved up to 30% FCPA when the observer bandwidth was set at 258 rad/s and the controller bandwidth at 43.03 rad/s.
4.3. Collocated Disturbance and Sensor ADRC
Control experiments were conducted repeatedly using the collocated sensor and disturbance configuration, with a varying ADRC tuning parameter . Multiple experiments with different settings and observer bandwidth values were performed to gather data for a parameter sensitivity analysis. This analysis involved systematically tuning the simulation model to better match experimental observations. By iteratively adjusting the delay in the simulation, the control effort was aligned with the experimental results, leading to a more accurate system characterisation.
The results presented in Figure 10, Figure 11 and Figure 12, and summarised in Table 3, show the FCPA for the experimental beam using the collocated disturbance and sensor configuration. The maximum FCPA achieved for the cases with , , and ranges from 44.8% to 48.4%.
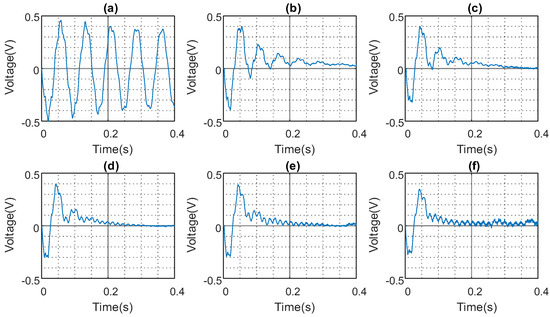
Figure 10.
ADRC controller FCPA of collocated beam . (a) Open loop response. (b) . (c) . (d) . (e) . (f) .
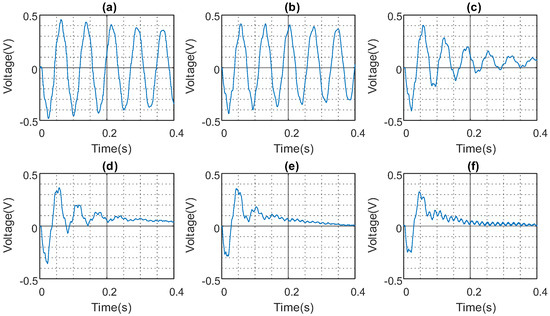
Figure 11.
ADRC controller FCPA of collocated beam . (a) Open loop response. (b) . (c) . (d) . (e) = . (f) .
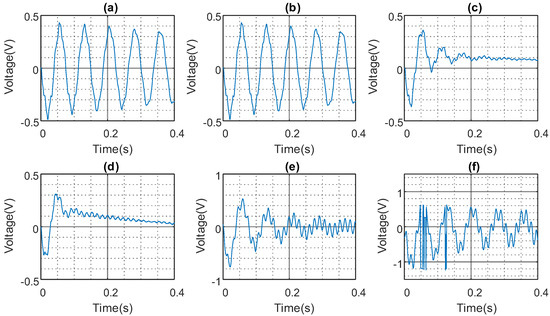
Figure 12.
ADRC controller FCPA of collocated beam case. (a) Open loop response. (b) . (c) . (d) . (e) = 34. (f) .For observer bandwidth values higher than 258 rad/s, the system experiences spillover at an excitation frequency of 67 Hz, which corresponds to the second mode of vibration.

Table 3.
FCPA achieved by ADRC using different values in experiment.
An observer bandwidth of 344 rad/s resulted in a spillover vibration amplitude of 0.28 V and first-cycle peak amplification of 56%, as observed in Figure 12e. An observer bandwidth of 430.3 rad/s resulted in a vibration amplitude of 0.7 V and amplification of the first-cycle peak by 150%, according to Figure 12f.
The profile of the control input signal which drives the actuator is shown in Figure 13. It is observed that the control input is a combination of the intended response to the impulse disturbance and a spurious response due to sensor noise, which is amplified based on the value. When these high-amplitude responses occur in succession, they combine with the system delay to cause spillover.
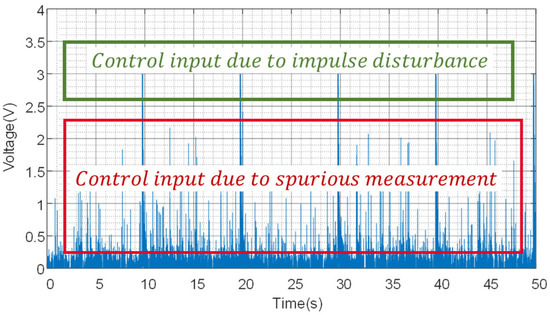
Figure 13.
Control input profile featuring amplified noise.
Figure 14 shows the noise amplification that results from FCPA across different controller gain settings. An analysis of the noise amplification in PID and non-collocated and collocated ADRCs reveals that the non-collocated ADRC achieved 12% more FCPA than the PID controller and the collocated ADRC achieved 18% more FCPA than the non-collocated ADRC. To investigate the recommended / ratio of between three and ten, the observer bandwidth was held at its optimal value of , while was varied to extract the control signal. The results are shown in Figure 15. Due to the 3 V control card saturation limit, it was not possible to deduce the mathematical relationship between and noise amplification. However, as this is an introductory investigation into the effect of this ratio, the results provide a springboard for further research.
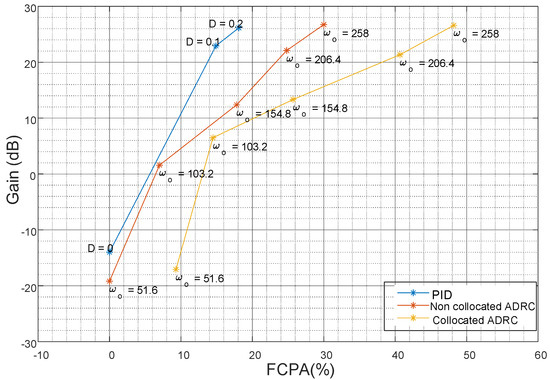
Figure 14.
FCPA vs. noise amplification.
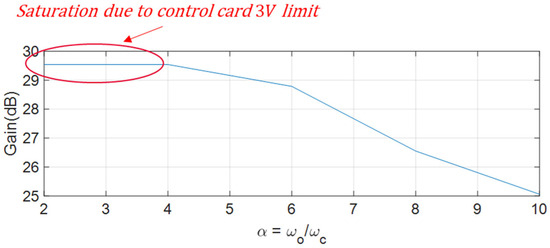
Figure 15.
Noise gain vs. observer and controller bandwidth ratio for fixed (collocated ADRC).
The graphs in Figure 16 present the results of the sensitivity analysis conducted to determine the system delay that affects the achieved FCPA for the experimental collocated disturbance and sensor beam. In addition to the sampling delay, other delays such as the output delay caused by energy transfer through the adapting mechanism of the actuator are expected. The sensitivity analysis indicated that a 10 delay was necessary to produce an initial peak in the control effort in simulation that matches the experimental results.
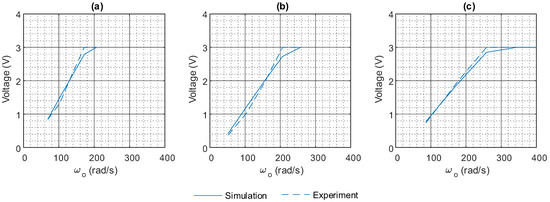
Figure 16.
Controller input voltage peak relationship in simulation and experiment for different values. (a) . (b) . (c) .
High values also result in controller effort peaks that exceed the 3 V limit allowable by the control card. According to Table 3 and Figure 16, when , the control input peak is saturated for . Similarly, when , the control input peak is saturated for , and when , the control input peak is saturated for . It is observed that for higher configurations, larger values are achieved before control input saturation, and this highlights the impact of the choice of on control signal amplification.
4.4. Noise Amplification
To investigate the effect of on noise amplification, experiments were conducted with fixed at 258 rad/s which has been determined to be the spillover limit of the controller. The values are set at 2, 4, 6, 8, and 10 in line with the 3–10 times recommendation given in [28]. Figure 14 presents the results of these tests. The findings show that for = 2, the control signal has a low noise floor with more frequent and higher-amplitude spikes, several reaching the control card maximum of 3 V. In contrast, the = 10 case results in a control signal with a higher noise floor of up to 0.5 V but with less frequent and lower-amplitude ADC noise spikes reaching up to 2 V.
The control signal reflects the plant output fed to the controller. As shown in Figure 17, the sensor signal can reach approximately 0.1 V. Therefore, with the controller output of the = 10 case reaching an amplitude of 2 V, the noise in the system is effectively amplified by a factor of 20. Similarly, with the controller output of the = 2 case reaching an amplitude of 3 V, the noise is amplified by a factor of 30. Despite this noise amplification, there was no significant effect on the excitation of the beam, as the beam did not experience spillover even at a high controller bandwidth, and the FCPA remained at an average of 46.5%.
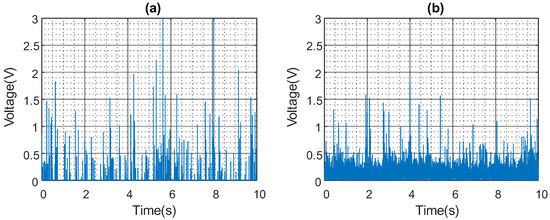
Figure 17.
Noise amplification for fixed and varying . (a) . (b) .
5. Conclusions
Application of ADRC to attenuate the first-cycle peak response of free vibration in flexible structures is presented. A smart cantilever beam equipped with a piezo stack actuator and a laser triangulation sensor was used in experiments to evaluate control effectiveness and investigate the influence of various parameters. The significant performance improvements offered by ADRC compared to the traditional PD controller are established, with ADRC providing 12% more FCPA than the PD controller in the non-collocated sensor and disturbance configuration of the smart beam. Additionally, collocating the disturbance with the displacement measurement achieved a further 16.5% attenuation of the first-cycle peak response. The introduction of a new tuning parameter, , allowed for a detailed investigation into delay and noise amplification effects.
In summary, the results demonstrate that for the flexible structure with a collocated sensor and disturbance and specific characteristics, including a first-mode natural frequency of 13.6 Hz, a damping coefficient of 0.43, and a signal-to-noise ratio of 5, an FCPA of 46% can be achieved using an observer bandwidth of 258 rad/s. These findings provide valuable insights into the design and implementation of ADRC for vibration control in flexible structures, particularly in applications similar to the studied smart beam. The demonstrated performance improvements highlight the potential for ADRC to enhance control strategies in engineering applications requiring precise vibration management. This includes compensating for the flexural oscillations in the ACS induced by direct beam impacts from asynchronous beam dumps and beam injection errors of the LHC.
Author Contributions
Conceptualization, A.J. and S.F.; methodology, A.J.; software, A.J.; validation, A.J., S.F. and A.L.; formal analysis, A.J.; investigation, A.J.; writing—original draft preparation, A.J.; writing—review and editing, S.F. and A.L.; supervision, S.F. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The results are provided within the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fuller, C.C.; Elliott, S.; Nelson, P.A. Active Control of Vibration; Elsevier Science: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Preumont, A.; Seto, K. Active Control of Structures; John Wiley: Chichester, UK, 2008. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 6th ed.; Pearson: Hoboken, NJ, USA, 2017. [Google Scholar]
- Furness, T.R.; Bertarelli, A.; Carra, F.; Fletcher, S.; Gentini, L.; Pasquali, M.; Redaelli, S.; Williamson, J.F. Adaptive Collimator Design for Future Particle Accelerators. In Proceedings of the International Beam Instrumentation Conference, Shanghai, China, 9–13 September 2018; pp. 240–244. [Google Scholar]
- Furness, T.; Fletcher, S.; Williamson, J.; Martin, H.; Redaelli, S.; Carra, F.; Bertarelli, A.; Pasquali, M. A closed loop system to control transverse deformations in LHC collimators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2023, 1050, 168128. [Google Scholar] [CrossRef]
- Bertarelli, A.; Aberle, O.; Assmann, R.; Dallocchio, A.; Kurtyka, T.; Magistris, M.; Mayer, M.; Leitner, M. Permanent deformation of the LHC collimator jaws induced by shock beam impact: An analytical and numerical interpretation. In Proceedings of the EPAC 2006, Edinburgh, UK, 26–30 June 2006. [Google Scholar]
- Cauchi, M.; Assmann, R.W.; Bertarelli, A.; Carra, F.; Cerutti, F.; Lari, L.; Redaelli, S.; Mollicone, P.; Sammut, N. Thermomechanical response of Large Hadron Collider collimators to proton and ion beam impacts. Phys. Rev. Spec. Top. Accel. Beams 2015, 18, 041002. [Google Scholar] [CrossRef]
- Kermani, M.R.; Patel, R.V.; Moallem, M. A High Authority Piezoelectric Stack Actuator for Structurally Flexible Mechanisms. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 229–234. [Google Scholar]
- Sethi, V.; Gangbing, S. Multimodal vibration control of a flexible structure using piezoceramics. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 851–856. [Google Scholar]
- Sethi, V.; Song, G. Optimal Vibration Control of a Model Frame Structure Using Piezoceramic Sensors and Actuators. J. Vib. Control 2005, 11, 671–684. [Google Scholar] [CrossRef]
- Martens, H.W.M. Vibration control of a mechanical structure with piezoelectric actuators—A comparison of bimorph and stack actuators. In Proceedings of the International Conference on New Actuators, Bremen, Germany, 17–19 June 1998. [Google Scholar]
- Li, D.; Liu, W.; Jiang, J.; Xu, R. Placement optimization of actuator and sensor and decentralized adaptive fuzzy vibration control for large space intelligent truss structure. Sci. China Technol. Sci. 2011, 54, 853–861. [Google Scholar] [CrossRef]
- Xu, R.; Li, D.; Jiang, J.; Zou, J. Decentralized adaptive fuzzy vibration control of smart gossamer space structure. J. Intell. Mater. Syst. Struct. 2017, 28, 1670–1681. [Google Scholar] [CrossRef]
- Xu, R.; Li, D.; Jiang, J. Online learning fuzzy vibration control of smart truss structure. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 231, 548–557. [Google Scholar] [CrossRef]
- Alireza, D.; Yousefi-Koma, A.; Behrouz, S.; Omid, R. Fuzzy control of flexible structure using piezoelements. Proc. SPIE 2008, 6926, 289–300. [Google Scholar]
- Qiu, Z.; Zhang, X.; Ye, C. Vibration suppression of a flexible piezoelectric beam using BP neural network controller. Acta Mech. Solida Sin. 2012, 25, 417–428. [Google Scholar] [CrossRef]
- Khot, S.M.; Yelve, N.P.; Kumar, P.; Purohit, G.A.; Singh, D. Implementation of H-infinity controller in experimental active vibration control of a cantilever beam. In Proceedings of the 2017 International Conference on Nascent Technologies in Engineering (ICNTE), Vashi, India, 27–28 January 2017; pp. 1–5. [Google Scholar]
- Khot, S.M.; Yelve, N.P.; Kumar, P. Investigation on Performances of Different types of Classical Controllers in Active Vibration Control. In Proceedings of the 2021 4th Biennial International Conference on Nascent Technologies in Engineering (ICNTE), Navi Mumbai, India, 15–16 January 2021; pp. 1–6. [Google Scholar]
- Takács, G.; Batista, G.; Gulan, M.; Rohaľ-Ilkiv, B. Embedded explicit model predictive vibration control. Mechatronics 2016, 36, 54–62. [Google Scholar] [CrossRef]
- Song, G.; Qiao, P.; Binienda, W.; Zou, G. Active Vibration Damping of Composite Beam using Smart Sensors and Actuators. J. Aerosp. Eng. 2002, 15, 97. [Google Scholar] [CrossRef]
- Malgaca, L. Integration of active vibration control methods with finite element models of smart laminated composite structures. Compos. Struct. 2010, 92, 1651–1663. [Google Scholar] [CrossRef]
- Malgaca, L.; Karagülle, H. Numerical and Experimental Study on Integration of Control Actions into the Finite Element Solutions in Smart Structures. Shock Vib. 2009, 16, 246419. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, B.L. Robust Static Output Feedback Control of a Semi-Active Vehicle Suspension Based on Magnetorheological Dampers. Appl. Sci. 2024, 14, 10336. [Google Scholar] [CrossRef]
- Suhail, S.A.; Bazaz, M.A.; Hussain, S. Adaptive sliding mode-based active disturbance rejection control for vehicle suspension control. Proc. Inst. Mech. Eng. Part I 2022, 236, 1523–1533. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Active Disturbance Rejection Control: A paradigm shift in feedback control system design. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; Volume 2006, p. 7. [Google Scholar]
- Zhiqiang, G. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Herbst, G. A Simulative Study on Active Disturbance Rejection Control (ADRC) as a Control Tool for Practitioners. Electronics 2013, 2, 246–279. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Wang, R.-X.; Zhang, S.-Q.; Wang, Z.-X.; Qin, X.-S.; Schmidt, R. Generalized-Disturbance Rejection Control for Vibration Suppression of Piezoelectric Laminated Flexible Structures. Shock Vib. 2018, 2018, 1538936. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Generalized Extended State Observer Based Control for Systems With Mismatched Uncertainties. IEEE Trans. Ind. Electron. 2012, 59, 4792–4802. [Google Scholar] [CrossRef]
- Lee, M.-H. Active vibration control of smart structural system using a novel control approach. J. Vibroengineering 2013, 15, 845–855. [Google Scholar]
- Lee, M.-H. Adaptive input estimation method and fuzzy robust controller combined for active cantilever beam structural system vibration control. J. Vibroengineering 2013, 15, 1230–1242. [Google Scholar]
- Zhang, S.Q.; Li, H.N.; Schmidt, R.; Müller, P.C. Disturbance rejection control for vibration suppression of piezoelectric laminated thin-walled structures. J. Sound Vib. 2014, 333, 1209–1223. [Google Scholar] [CrossRef]
- Ostertag, E.P. Mono- and Multivariable Control and Estimation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zheng, Q.; Richter, H.; Gao, Z. Active Disturbance Rejection Control for Piezoelectric Beam. Asian J. Control 2014, 16, 1612–1622. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).