Advancement in Intelligent Control for Dampening Structural Vibrations
Abstract
1. Introduction
2. Methodology
2.1. Motion Formulation of Intelligent Structures
2.2. Modeling with FEM Analysis
3. Results
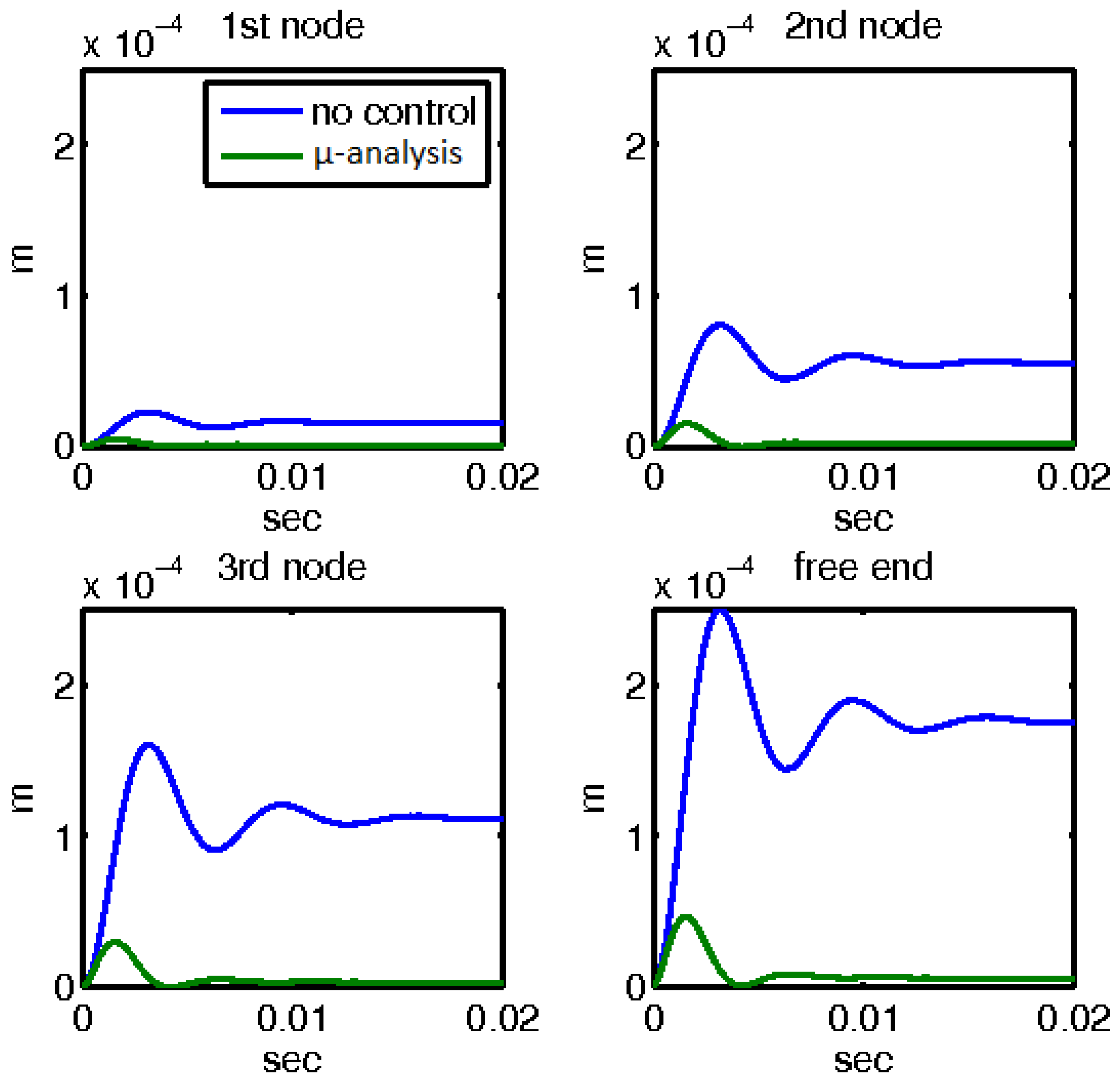
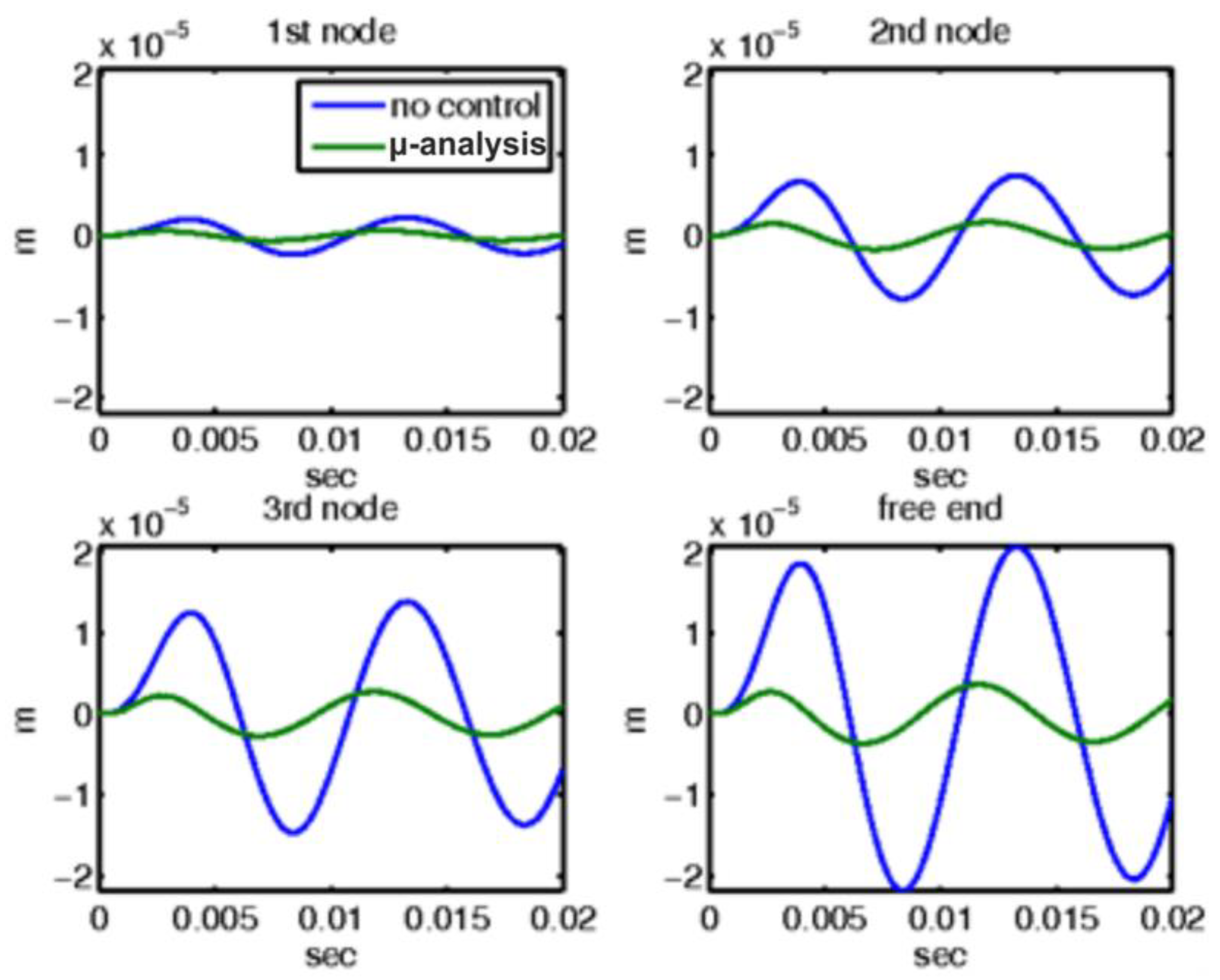
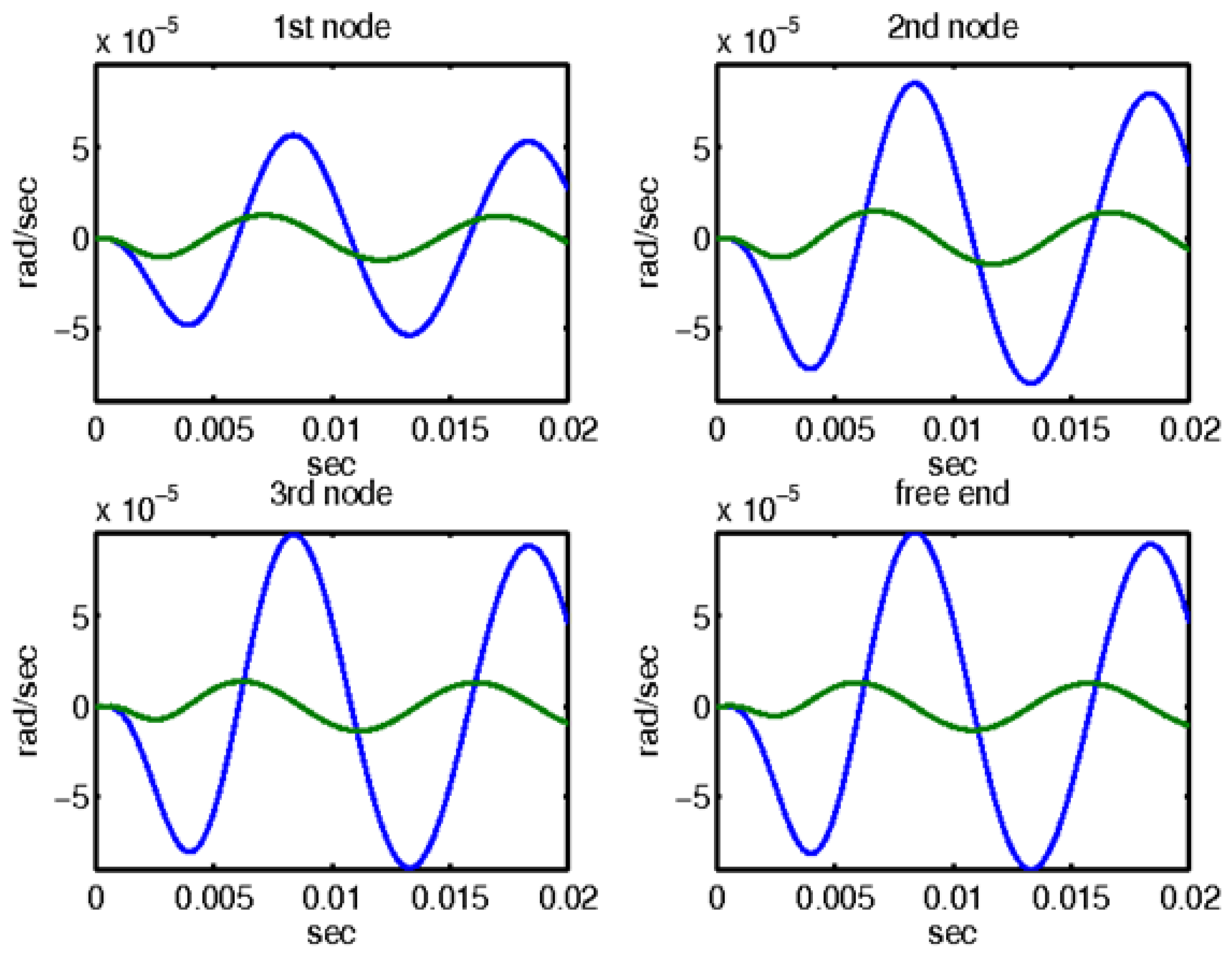
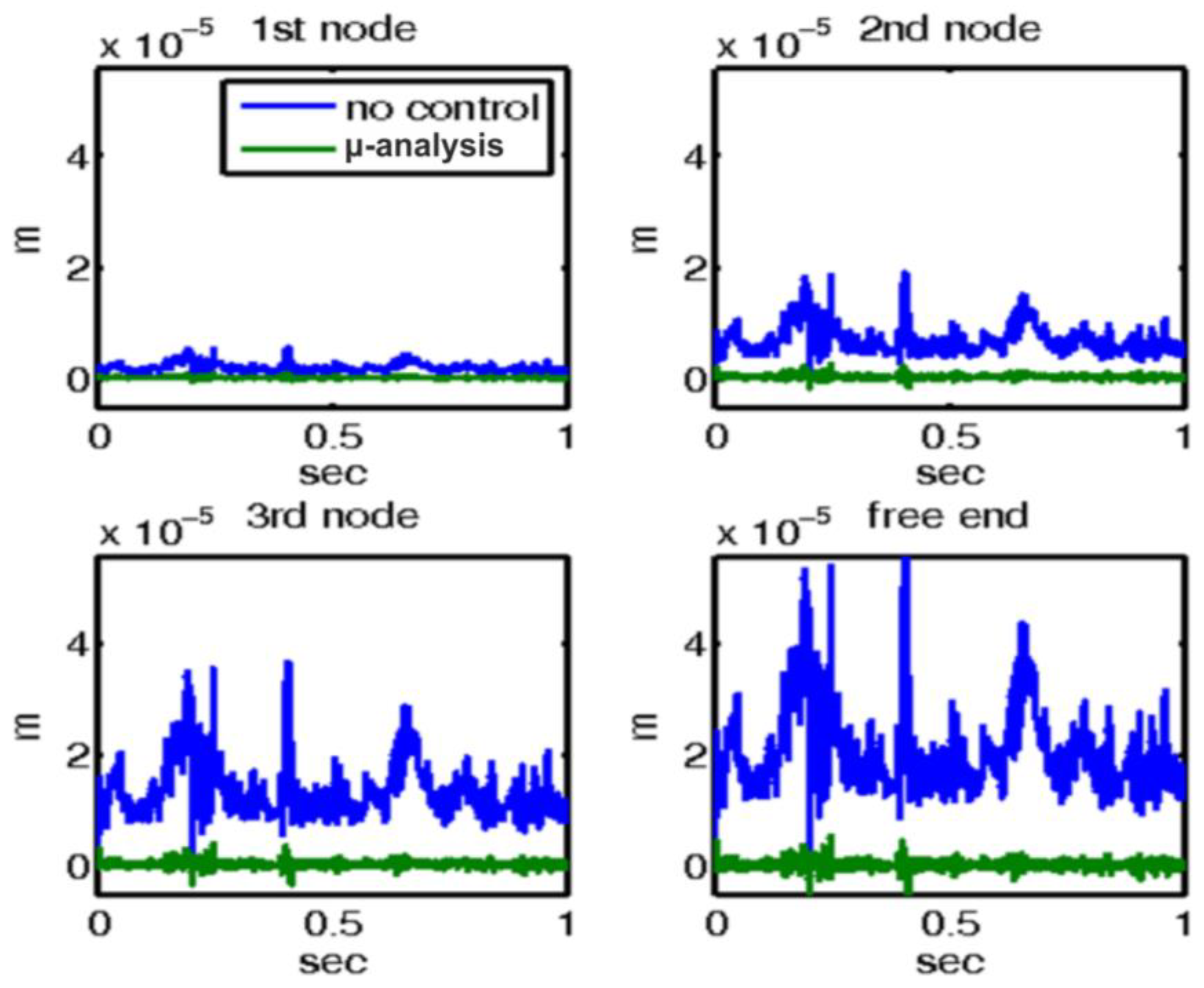
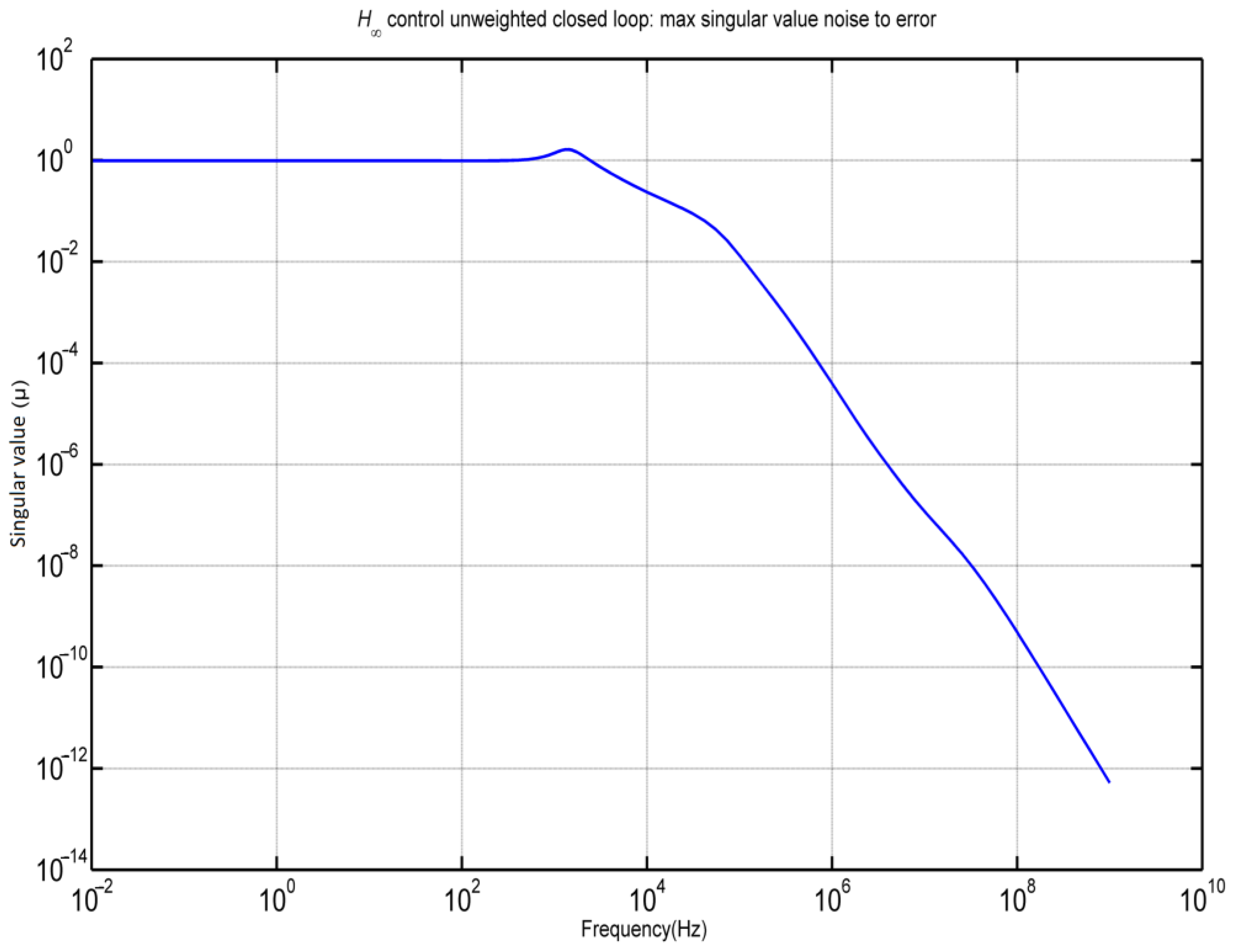
3.1. Controller Synthesis with (D, G-K) Iteration
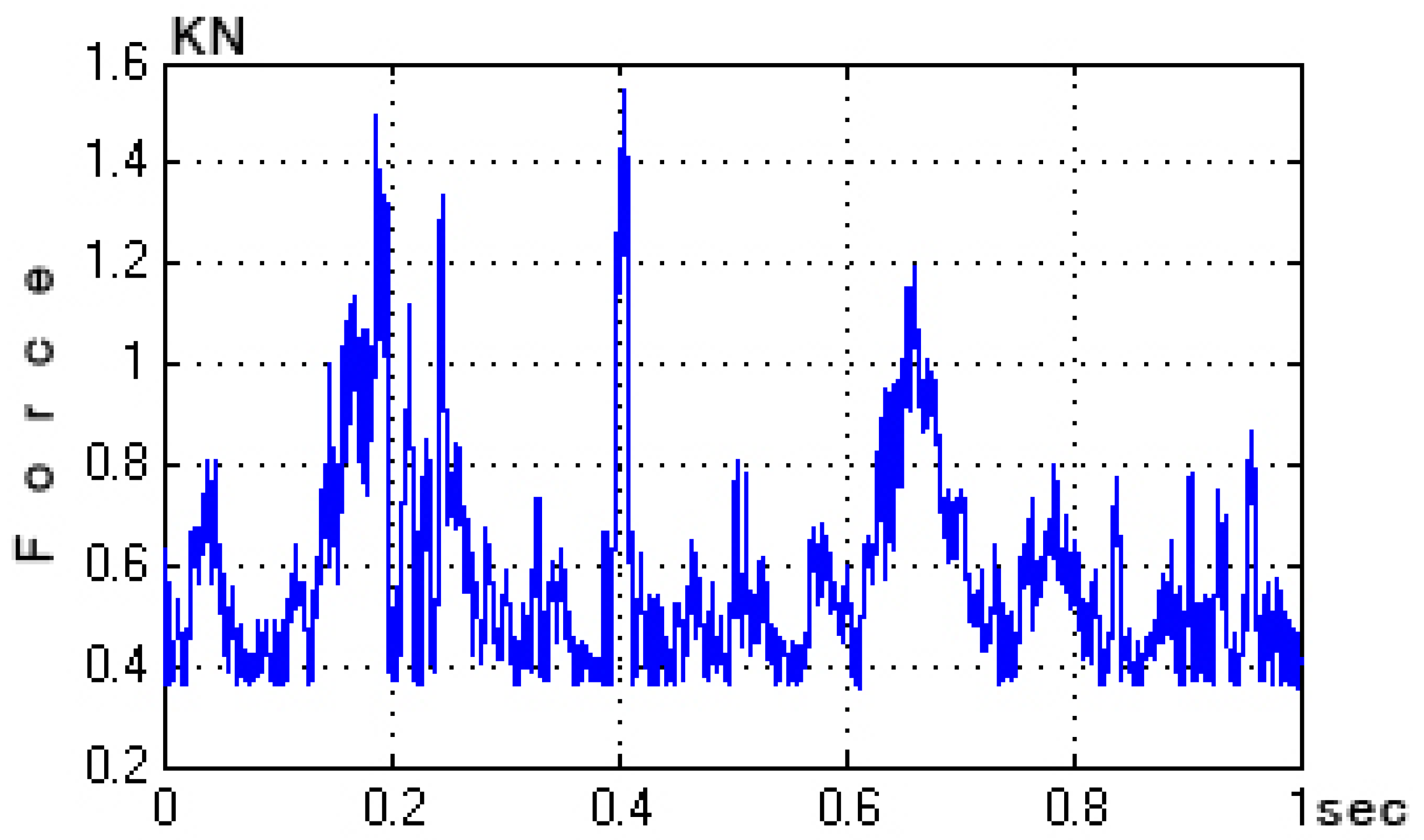
3.2. Mechanical External Disturbance (d = fm(t))
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benjeddou, A.; Trindade, M.A.; Ohayon, R. New Shear Actuated Smart Structure Beam Finite Element. AIAA J. 1999, 37, 378–383. [Google Scholar] [CrossRef]
- Bona, B.; Indri, M.; Tornambe, A. Flexible Piezoelectric Structures-Approximate Motion Equations and Control Algorithms. IEEE Trans. Autom. Contr. 1997, 42, 94–101. [Google Scholar] [CrossRef]
- Okko, B.; Kwakernaak, H.; Gjerrit, M. Design Methods for Control Systems. Course Notes Dutch Inst. Syst. Control 2001, 67. [Google Scholar]
- Burke, J.V.; Henrion, D.; Lewis, A.S.; Overton, M.L. Hifoo—A MATLAB Package for Fixed-Order Controller Design and H∞ Optimization. IFAC Proc. Vol. 2006, 39, 339–344. [Google Scholar] [CrossRef]
- Burke, J.V.; Henrion, D.; Lewis, A.S.; Overton, M.L. Stabilization via Nonsmooth, Nonconvex Optimization. IEEE Trans Autom. Contr. 2006, 51, 1760–1769. [Google Scholar] [CrossRef]
- Burke, J.V.; Lewis, A.S.; Overton, M.L. A Robust Gradient Sampling Algorithm for Nonsmooth, Nonconvex Optimization. SIAM J. Optim. 2005, 15, 751–779. [Google Scholar] [CrossRef]
- Burke, J.V.; Overton, M.L. Variational Analysis of Non-Lipschitz Spectral Functions. Math. Program. 2001, 90, 317–351. [Google Scholar] [CrossRef]
- Choi, S.-B.; Cheong, C.-C.; Lee, C.-H. Position Tracking Control of a Smart Flexible Structure Featuring a Piezofilm Actuator. J. Guid. Control. Dyn. 1996, 19, 1364–1369. [Google Scholar] [CrossRef]
- Culshaw, B. Smart Structures—A Concept or a Reality? Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1992, 206, 1–8. [Google Scholar] [CrossRef]
- Tzou, H.S.; Gabbert, U. Structronics—A New Discipline and Its Challenging Issues. Fortschr.-Berichte VDI Smart Mech. Syst. Adapt. Reihe 1997, 11, 245–250. [Google Scholar]
- Guran, A.; Tzou, H.-S.; Anderson, G.L.; Natori, M.; Gabbert, U.; Tani, J.; Breitbach, E. Structronic Systems: Smart Structures, Devices and Systems; World Scientific: Singapore, 1998; Volume 4, ISBN 978-981-02-2652-7. [Google Scholar]
- Doyle, J.; Glover, K.; Khargonekar, P.; Francis, B. State-Space Solutions to Standard H2 and H∞ Control Problems. In Proceedings of the 1988 American Control Conference, Atlanta, GA, USA, 15–17 June 1988; pp. 1691–1696. [Google Scholar]
- Tzou, H.S.; Anderson, G.L. Intelligent Structural Systems; Springer: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1992; ISBN 978-94-017-1903-2. [Google Scholar]
- Gabbert, U.; Tzou, H.S. IUTAM Symposium on Smart Structures and Structronic Systems. In Proceedings of the IUTAM Symposium, Magdeburg, Germany, 26–29 September 2000; Kluwer: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 2001. [Google Scholar]
- Tzou, H.S.; Natori, M.C. Piezoelectric Materials and Continua; Braun, S.B.T.-E.V., Ed.; Elsevier: Oxford, UK, 2001; pp. 1011–1018. ISBN 978-0-12-227085-7. [Google Scholar]
- Cady, W.G. Piezoelectricity: An Introduction to the Theory and Applications of Electromechanical Phenomena in Crystals; Dover Publication: New York, NY, USA, 1964. [Google Scholar]
- Tzou, H.S.; Bao, Y. A Theory on Anisotropic Piezothermoelastic Shell Laminates with Sensor/Actuator Applications. J. Sound Vib. 1995, 184, 453–473. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Mountakis, N.; Papadakis, V.; Moutsopoulou, A. Mechanical Strength Predictability of Full Factorial, Taguchi, and Box Behnken Designs: Optimization of Thermal Settings and Cellulose Nanofibers Content in PA12 for MEX AM. J. Mech. Behav. Biomed. Mater. 2023, 142, 105846. [Google Scholar] [CrossRef]
- Petousis, M.; Vidakis, N.; Mountakis, N.; Karapidakis, E.; Moutsopoulou, A. Functionality Versus Sustainability for PLA in MEX 3D Printing: The Impact of Generic Process Control Factors on Flexural Response and Energy Efficiency. Polymers 2023, 15, 1232. [Google Scholar] [CrossRef] [PubMed]
- David, C.; Sagris, D.; Petousis, M.; Nasikas, N.K.; Moutsopoulou, A.; Sfakiotakis, E.; Mountakis, N.; Charou, C.; Vidakis, N. Operational Performance and Energy Efficiency of MEX 3D Printing with Polyamide 6 (PA6): Multi-Objective Optimization of Seven Control Settings Supported by L27 Robust Design. Appl. Sci. 2023, 13, 8819. [Google Scholar] [CrossRef]
- Moutsopoulou, A.; Stavroulakis, G.E.; Petousis, M.; Vidakis, N.; Pouliezos, A. Smart Structures Innovations Using Robust Control Methods. Appl. Mech. 2023, 4, 856–869. [Google Scholar] [CrossRef]
- Cen, S.; Soh, A.-K.; Long, Y.-Q.; Yao, Z.-H. A New 4-Node Quadrilateral FE Model with Variable Electrical Degrees of Freedom for the Analysis of Piezoelectric Laminated Composite Plates. Compos. Struct. 2002, 58, 583–599. [Google Scholar] [CrossRef]
- Yang, S.M.; Lee, Y.J. Optimization of Noncollocated Sensor/Actuator Location and Feedback Gain in Control Systems. Smart Mater. Struct. 1993, 2, 96. [Google Scholar] [CrossRef]
- Kumar, K.R.; Narayanan, S. Active Vibration Control of Beams with Optimal Placement of Piezoelectric Sensor/Actuator Pairs. Smart Mater. Struct. 2008, 17, 55008. [Google Scholar] [CrossRef]
- Hanagud, S.; Obal, M.W.; Calise, A.J. Optimal Vibration Control by the Use of Piezoceramic Sensors and Actuators. J. Guid. Control. Dyn. 1992, 15, 1199–1206. [Google Scholar] [CrossRef]
- Song, G.; Sethi, V.; Li, H.-N. Vibration Control of Civil Structures Using Piezoceramic Smart Materials: A Review. Eng. Struct. 2006, 28, 1513–1524. [Google Scholar] [CrossRef]
- Kimura, H. Robust Stabilizability for a Class of Transfer Functions. IEEE Trans. Autom. Contr. 1984, 29, 788–793. [Google Scholar] [CrossRef]
- Francis, B.A. A Course in H∞ Control Theory; Springer: Berlin/Heidelberg, Germany, 1987; ISBN 978-3-540-17069-3. [Google Scholar]
- Kwakernaak, H. Robust Control and H∞-Optimization—Tutorial Paper. Automatica 1993, 29, 255–273. [Google Scholar] [CrossRef]
- Chandrashekhara, K.; Varadarajan, S. Adaptive Shape Control of Composite Beams with Piezoelectric Actuators. J. Intell. Mater. Syst. Struct. 1997, 8, 112–124. [Google Scholar] [CrossRef]
- Blondel, V.D.; Tsitsiklis, J.N. A Survey of Computational Complexity Results in Systems and Control. Automatica 2000, 36, 1249–1274. [Google Scholar] [CrossRef]
- Moutsopoulou, A.; Stavroulakis, G.E.; Pouliezos, A.; Petousis, M.; Vidakis, N. Robust Control and Active Vibration Suppression in Dynamics of Smart Systems. Inventions 2023, 8, 47. [Google Scholar] [CrossRef]
- Zhang, N.; Kirpitchenko, I. Modelling Dynamics of a Continuous Structure with a Piezoelectric Sensoractuator for Passive Structural Control. J. Sound Vib. 2002, 249, 251–261. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, C.; Li, S.; Xu, D.; Erdman, A.G. Robust H∞ Vibration Control for Flexible Linkage Mechanism Systems With Piezoelectric Sensors And Actuators. J. Sound Vib. 2001, 243, 145–155. [Google Scholar] [CrossRef]
- Packard, A.; Doyle, J.; Balas, G. Linear, Multivariable Robust Control With a μ Perspective. J. Dyn. Syst. Meas. Control. 1993, 115, 426–438. [Google Scholar] [CrossRef]
- Karatzas, I.; Lehoczky, J.P.; Shreve, S.E.; Xu, G.-L. Modeling, Control and Implementation of Smart Structures: A FEM-State Space Approach; Springer: Berlin/Heidelberg, Germany, 1990; ISBN 9783540483939. [Google Scholar]
- Miara, B.; Stavroulakis, G.E.; Valente, V. Topics on Mathematics for Smart Systems. In Proceedings of the European Conference, Rome, Italy, 26–28 October 2006; World Scientific: Singapore, 2007. [Google Scholar] [CrossRef]









| Beam Parameter | Value |
|---|---|
| L is the length of the beam | 1.40 m |
| b is the width of the beam | 0.07 m |
| h is the thickness of the beam | 0.02 m |
| ρ is the density of the beam | 1700.0 kg/m3 |
| E is the modulus of elasticity of the beam | 1.8 × 1011 N/m2 |
| hp, hs, and ha are the Pzt thickness | 0.003 m |
| d31 is the piezoelectric constant | 230 × 10−12 m/V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moutsopoulou, A.; Petousis, M.; Vidakis, N.; Pouliezos, A.; Stavroulakis, G.E. Advancement in Intelligent Control for Dampening Structural Vibrations. Vibration 2024, 7, 844-862. https://doi.org/10.3390/vibration7030045
Moutsopoulou A, Petousis M, Vidakis N, Pouliezos A, Stavroulakis GE. Advancement in Intelligent Control for Dampening Structural Vibrations. Vibration. 2024; 7(3):844-862. https://doi.org/10.3390/vibration7030045
Chicago/Turabian StyleMoutsopoulou, Amalia, Markos Petousis, Nectarios Vidakis, Anastasios Pouliezos, and Georgios E. Stavroulakis. 2024. "Advancement in Intelligent Control for Dampening Structural Vibrations" Vibration 7, no. 3: 844-862. https://doi.org/10.3390/vibration7030045
APA StyleMoutsopoulou, A., Petousis, M., Vidakis, N., Pouliezos, A., & Stavroulakis, G. E. (2024). Advancement in Intelligent Control for Dampening Structural Vibrations. Vibration, 7(3), 844-862. https://doi.org/10.3390/vibration7030045







