Unsteady Aerodynamic Lift Force on a Pitching Wing: Experimental Measurement and Data Processing
Abstract
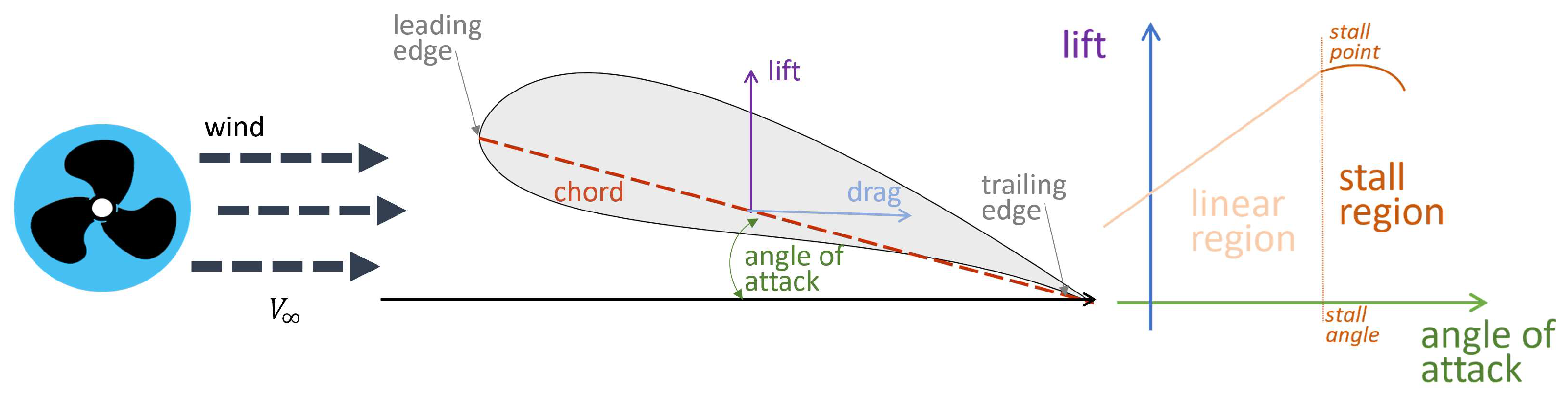
1. Introduction
2. Experimental Setup
2.1. Wind Tunnel
2.2. Position Control Setup
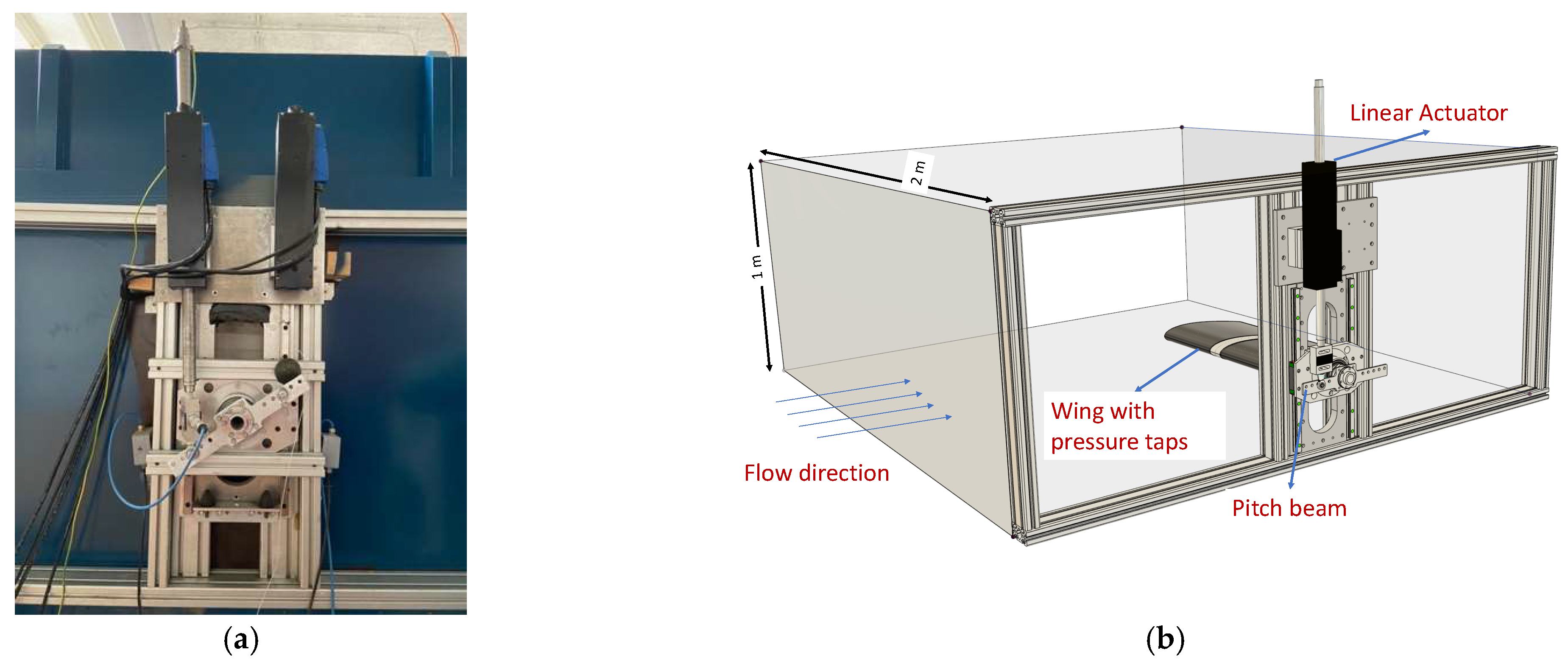
2.3. Pressure Measurement Setup


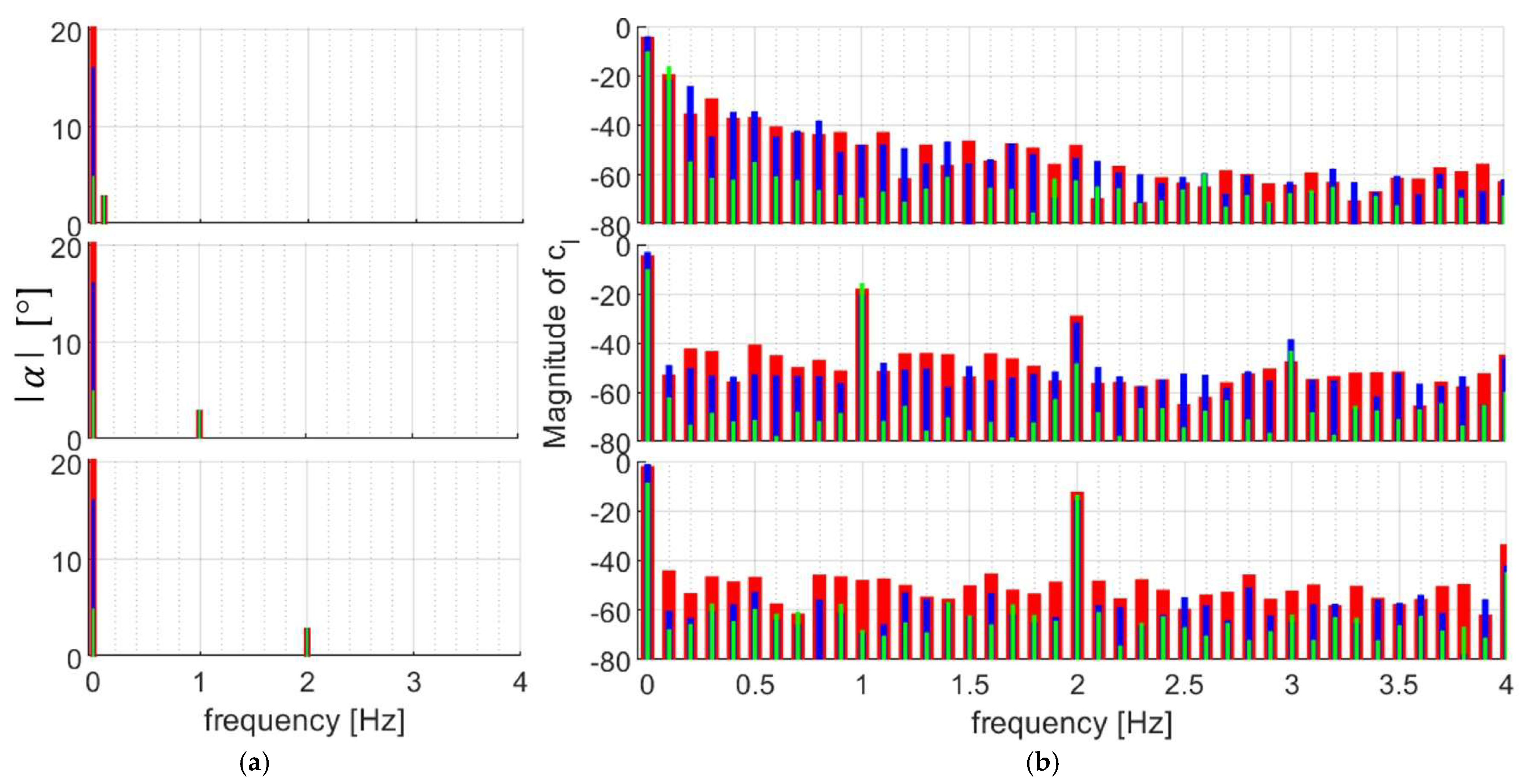
3. Post-Processing of the Experimental Data
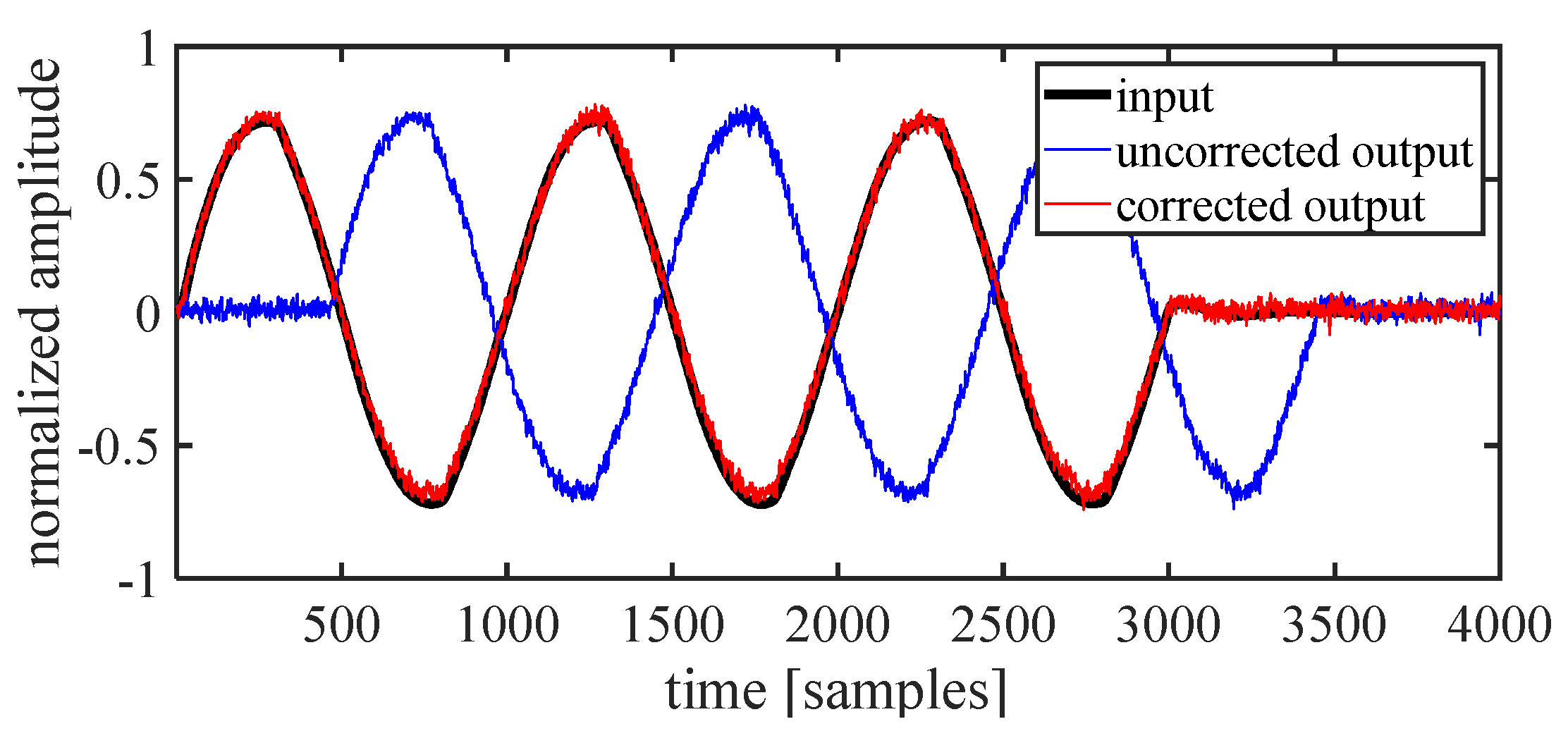
3.1. Synchronization of the Input and Output Data
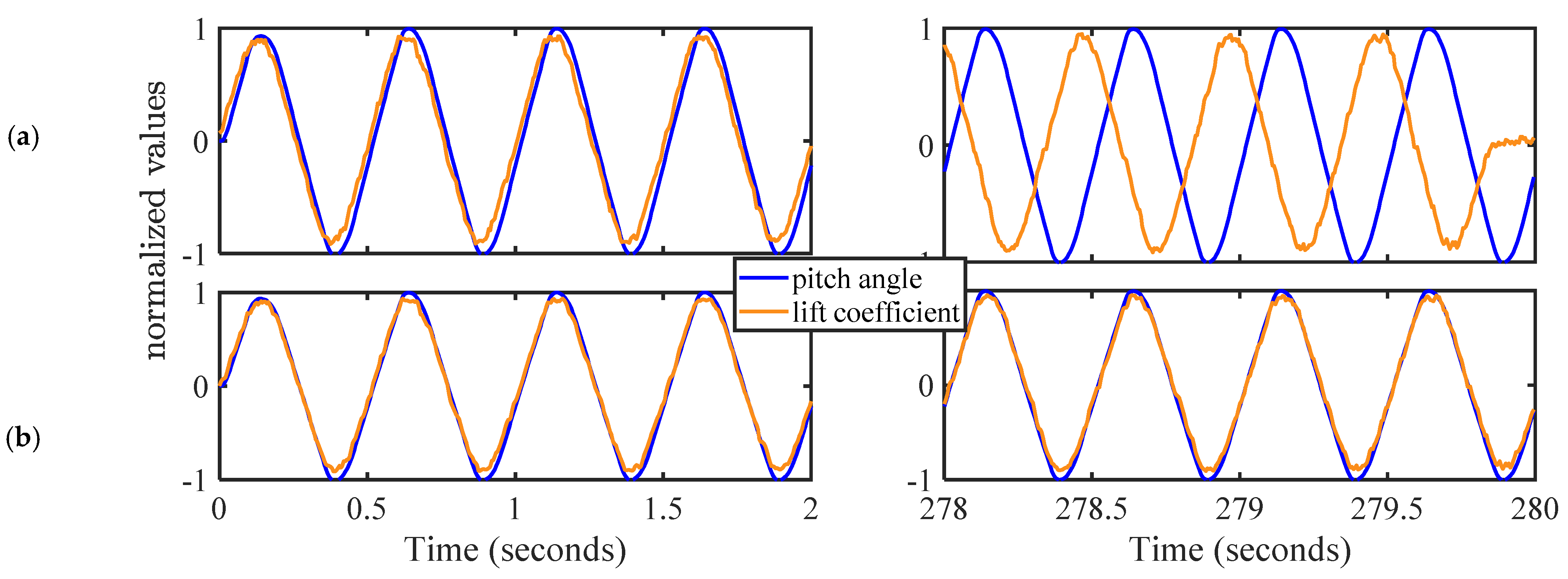
3.2. Angle of Attack Correction
3.3. Sampling Frequency Correction of the Pressure Signal
3.4. Aerodynamic Force Calculation
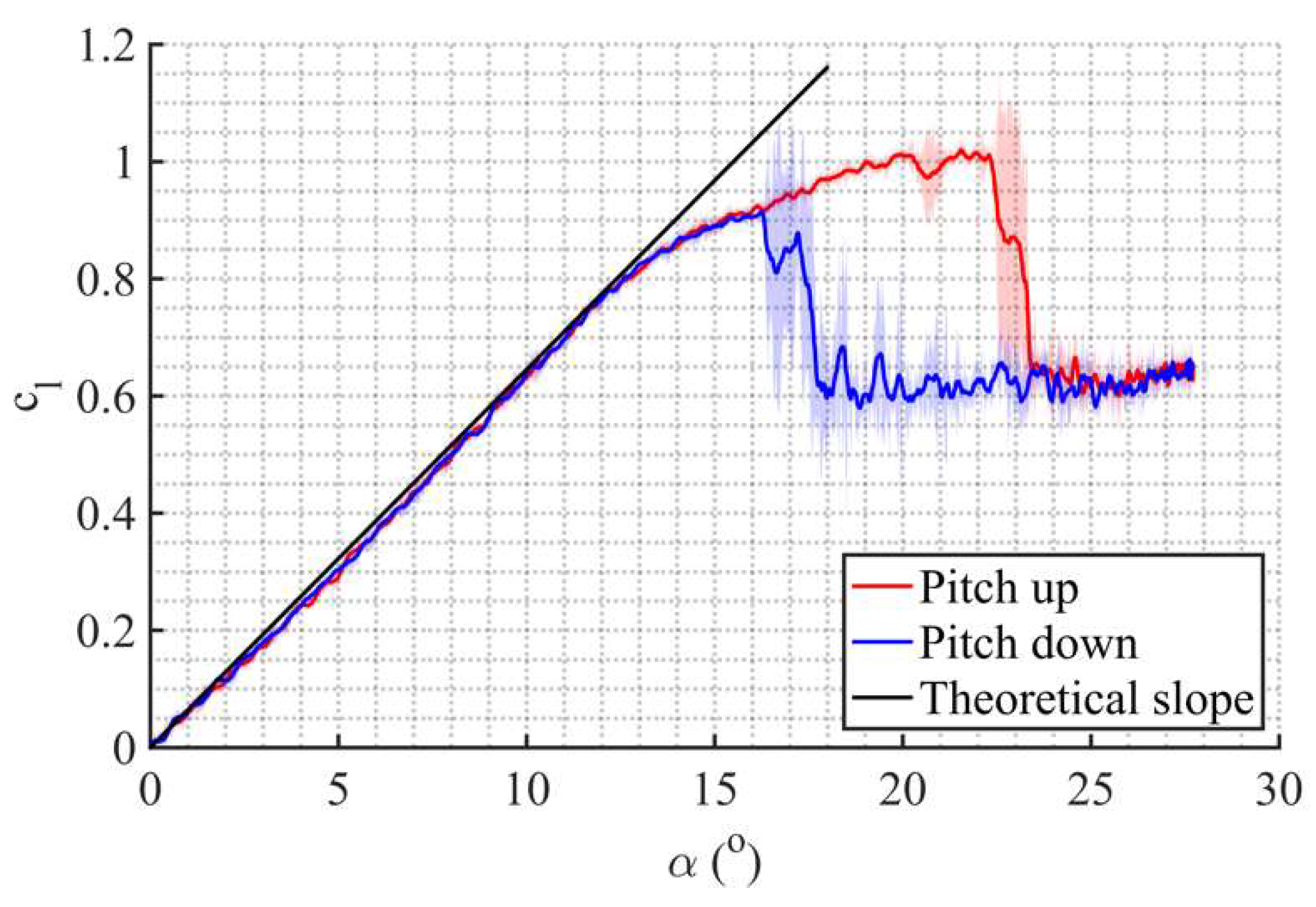
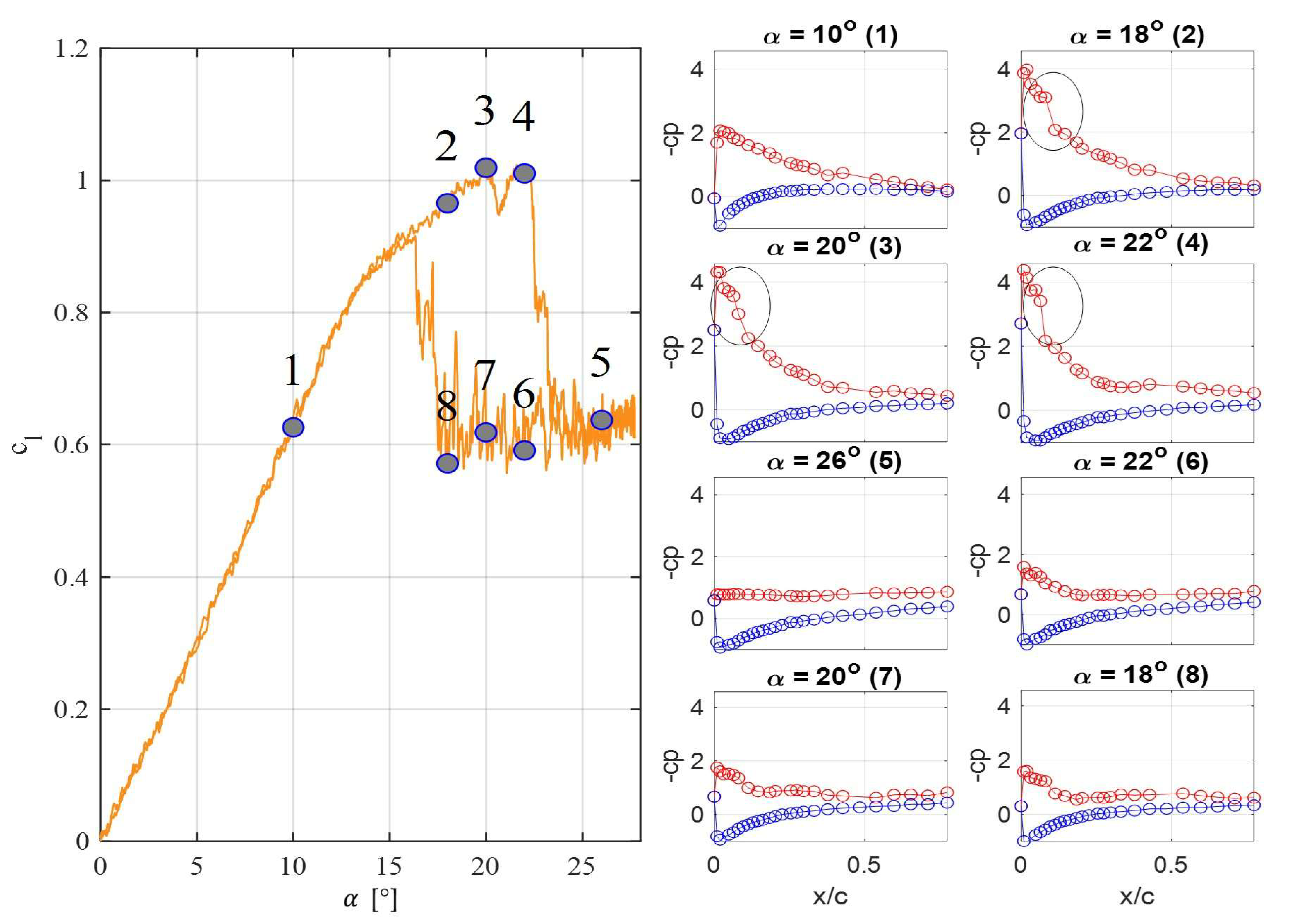
4. Quasi-Static Experiments
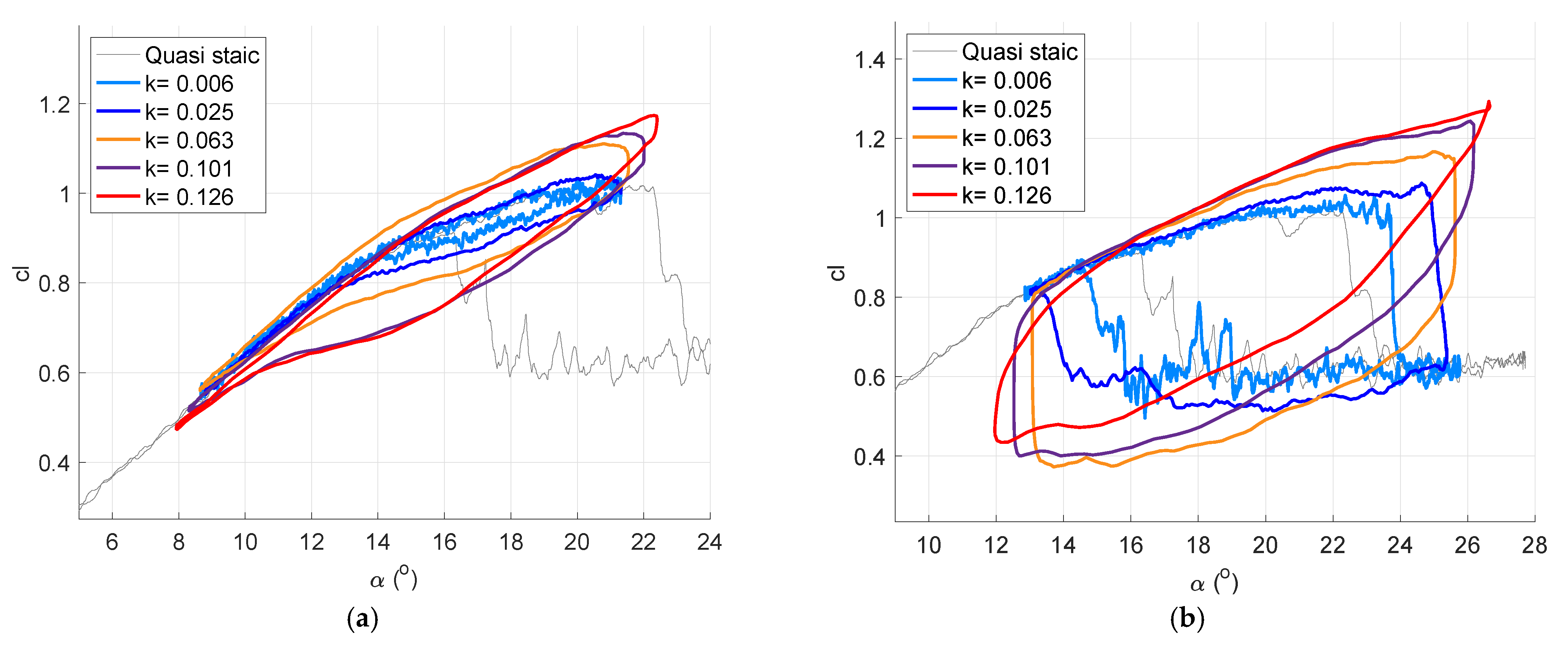
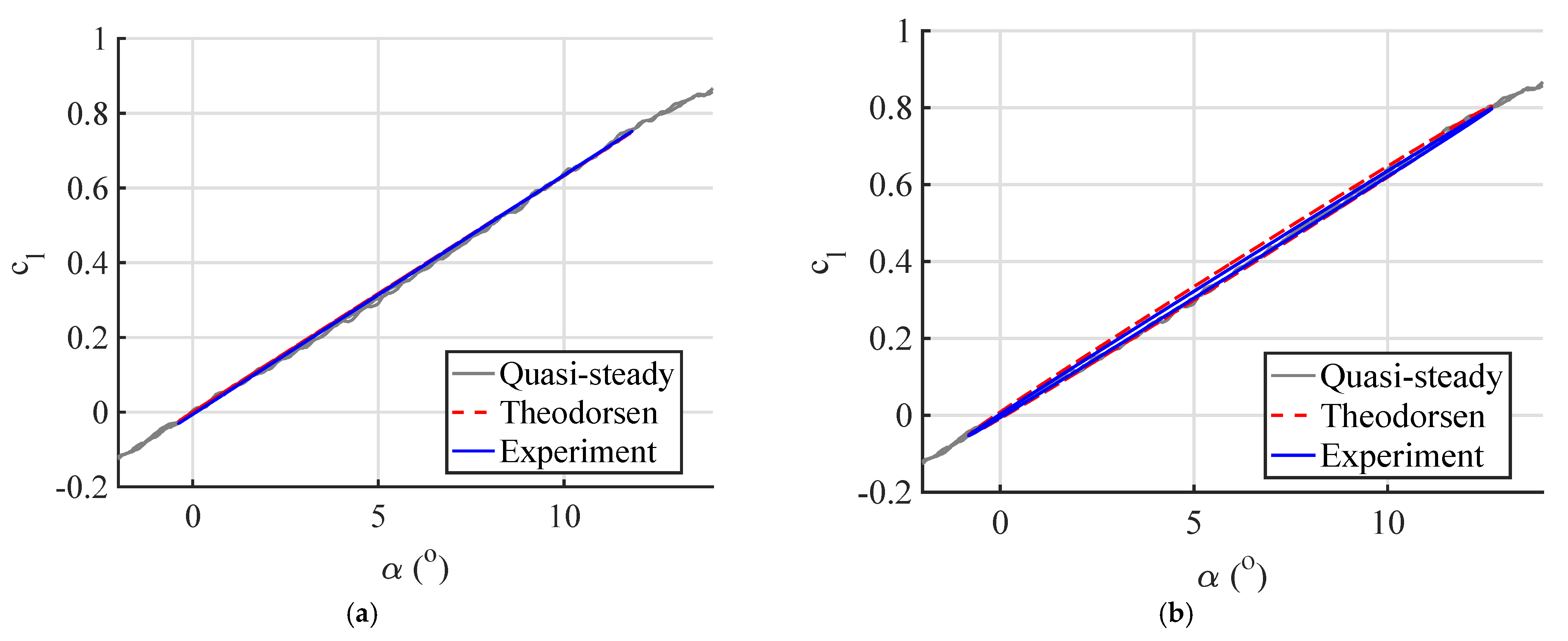
5. Monosine Experiments
5.1. Aerodynamic Viewpoint
5.2. Vibro-Acoustic Viewpoint
6. Conclusions
- The lack of synchronization was solved through a so-called starting signal specifically constructed for the proper synchronization of the pitch angle and lift force data. This allowed for synchronization of the two datasets with an accuracy of <5 ms.
- The faulty clock frequency of the pressure measurement DAQ was determined through a fully automated spectral analysis tool that estimates the period time of a periodic signal for a given sampling frequency. The analysis revealed that the correct sampling frequency of the DAQ was 199.88 Hz instead of 200 Hz.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mueller, T.J. Fixed and Flapping Wing Aerodynamics for Micro Air Vehicle Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar]
- Ansari, S.A.; Żbikowski, R.; Knowles, K. Non-linear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 2: Implementation and validation. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 169–186. [Google Scholar] [CrossRef]
- Leishman, J.G. Challenges in modelling the unsteady aerodynamics of wind turbines. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2002, 5, 85–132. [Google Scholar] [CrossRef]
- De Troyer, T.; Hasin, D.; Keisar, D.; Santra, S.; Greenblatt, D. Plasma-Based Dynamic Stall Control and Modeling on an Aspect-Ratio-One Wing. AIAA J. 2022, 60, 2905–2915. [Google Scholar] [CrossRef]
- Siddiqui, M.; De Troyer, T.; Decuyper, J.; Csurcsia, P.; Schoukens, J.; Runacres, M. A data-driven nonlinear state-space model of the unsteady lift force on a pitching wing. J. Fluids Struct. 2022, 114, 103706. [Google Scholar] [CrossRef]
- De Troyer, T.; Csurcsia, P.Z.; Siddiqui, M.F.; Runacres, M. Using a broadband multisine excitation signal for the data-driven modeling of the unsteady lift force on a pitching wing. In Proceedings of the 2022 ISMA International Conference on Noise and Vibration Engineering, Leuven, Belgium, 12–14 September 2022. [Google Scholar]
- Balajewicz, M.; Dowell, E. Reduced-order modeling of flutter and limit-cycle oscillations using the sparse Volterra series. J. Aircr. 2012, 49, 1803–1812. [Google Scholar] [CrossRef]
- Beddoes, T.S. A Qualitative Discussion of Dynamic Stall; AGARD Special Course on Unsteady Aerodynamics, AGARD Report 679; Advisory Group for Aerospace Research and Development: London, UK, 1979. [Google Scholar]
- Patil, M.J.; Hodges, D.H. On the importance of aerodynamic and structural geometrical nonlinearities in aeroelastic behavior of high-aspect-ratio wings. J. Fluids Struct. 2004, 19, 905–915. [Google Scholar] [CrossRef]
- Rockwood, M.; Medina, A.; Garmann, D.J.; Visbal, M.R. Dynamic Stall of a Swept Finite Wing for a Range of Reduced Frequencies. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Ertveldt, J.; Pintelon, R.; Vanlanduit, S. Identification of Unsteady Aerodynamic Forces from Forced Motion Wind Tunnel Experiments. AIAA J. 2016, 54, 3265–3273. [Google Scholar] [CrossRef]
- Ertveldt, J.; Lataire, J.; Pintelon, R.; Vanlanduit, S. Frequency-domain identification of time-varying systems for analysis and prediction of aeroelastic flutter. Mech. Syst. Signal Process. 2014, 47, 225–242. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; National Advisory Committee for Aeronautics: Washington, WA, USA, 1979. [Google Scholar]
- Razak, N.A.; Andrianne, T.; Dimitriadis, G. Flutter and Stall Flutter of a Rectangular Wing in a Wind Tunnel. AIAA J. 2011, 49, 2258–2271. [Google Scholar] [CrossRef]
- Dimitriadis, G.; Li, J. Bifurcation Behavior of Airfoil Undergoing Stall Flutter Oscillations in Low-Speed Wind Tunnel. AIAA J. 2009, 47, 2577–2596. [Google Scholar] [CrossRef]
- Dimitriadis, G. Introduction to Nonlinear Aeroelasticity; Wiley: New York, NY, USA, 2017. [Google Scholar]
- Deparday, J.; Mulleners, K. Modeling the interplay between the shear layer and leading edge suction during dynamic stall. Phys. Fluids 2019, 31, 107104. [Google Scholar] [CrossRef]
- Schreck, S.J.; Hellin, H.E. Unsteady vortex dynamics and surface pressure topologies on a finite pitching wing. J. Aircr. 1994, 31, 899–907. [Google Scholar] [CrossRef]
- Wernert, P.; Geissler, W.; Raffel, M.; Kompenhans, J. Experimental and numerical investigations of dynamic stall on a pitching airfoil. AIAA J. 1996, 34, 982–989. [Google Scholar] [CrossRef]
- Okamoto, M.; Azuma, A. Experimental Study on Aerodynamic Characteristics of Unsteady Wings at Low Reynolds Number. AIAA J. 2005, 43, 2526–2536. [Google Scholar] [CrossRef]
- Kaufmann, K.; Merz, C.B.; Gardner, A.D. Dynamic stall simulations on a pitching finite wing. J. Aircr. 2017, 54, 1303–1316. [Google Scholar] [CrossRef]
- Angulo, I.A.; Ansell, P.J. Influence of Aspect Ratio on Dynamic Stall of a Finite Wing. AIAA J. 2019, 57, 2722–2733. [Google Scholar] [CrossRef]
- Visbal, M. Flow Structure and Unsteady Loading over a Pitching and Perching Low-Aspect-Ratio Wing. In Proceedings of the 42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, LA, USA, 25 June 2012. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. Effect of Sweep on Dynamic Stall of a Pitching Finite-Aspect-Ratio Wing. AIAA J. 2019, 57, 3274–3289. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. Dynamic stall of a finite-aspect-ratio wing. AIAA J. 2019, 57, 962–977. [Google Scholar] [CrossRef]
- Spentzos, A.; Barakos, G.; Badcock, K.; Richards, B.; Wernert, P.; Schreck, S.; Raffel, M. Investigation of Three-Dimensional Dynamic Stall Using Computational Fluid Dynamics. AIAA J. 2005, 43, 1023–1033. [Google Scholar] [CrossRef]
- Spentzos, A.; Barakos, G.N.; Badcock, K.J.; Richards, B.E.; Coton, F.N.; Galbraith, R.M.; Berton, E.; Favier, D. Computational fluid dynamics study of three-dimensional dynamic stall of various planform shapes. J. Aircr. 2007, 44, 1118–1128. [Google Scholar] [CrossRef]
- Hoerner, S.F.; Borst, H.V. Fluid-Dynamic Lift: Practical Information on Aerodynamic and Hydrodynamic Lift; LA Hoerner: New York, NY, USA, 1985. [Google Scholar]
- Chinwicharnam, K.; Ariza, D.G.; Moschetta, J.-M.; Thipyopas, C. Aerodynamic Characteristics of a Low Aspect Ratio Wing and Propeller Interaction for a Tilt-Body MAV. Int. J. Micro Air Veh. 2013, 5, 245–260. [Google Scholar] [CrossRef]
- Aboelezz, A.; Hassanalian, M.; Desoki, A.; Elhadidi, B.; El-Bayoumi, G. Design, experimental investigation, and nonlinear flight dynamics with atmospheric disturbances of a fixed-wing micro air vehicle. Aerosp. Sci. Technol. 2020, 97, 105636. [Google Scholar] [CrossRef]
- Timmer, W. Two-dimensional low-Reynolds number wind tunnel results for airfoil NACA 0018. Wind Eng. 2008, 32, 525–537. [Google Scholar] [CrossRef]
- Bhandari, P.; Csurcsia, P.Z. Digital implementation of the PID controller. Softw. Impacts 2022, 13, 100306. [Google Scholar] [CrossRef]
- Bergh, H.; Tijdeman, H. Theoretical and Experimental Results for the Dynamic Response of Pressure Measuring Systems; National Aero and Astronautical Research Institute: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Csurcsia, P.Z.; Lataire, J. Nonparametric estimation of time-varying systems using 2-D regularization. IEEE Trans. Instrum. Meas. 2016, 65, 1259–1270. [Google Scholar] [CrossRef]
- Csurcsia, P.Z.; Peeters, B.; Schoukens, J. User-friendly nonlinear nonparametric estimation framework for vibro-acoustic industrial measurements with multiple inputs. Mech. Syst. Signal Process. 2020, 145, 106926. [Google Scholar] [CrossRef]
- Csurcsia, P.Z.; Peeters, B.; Schoukens, J.; De Troyer, T. Simplified analysis for multiple input systems: A toolbox study illustrated on F-16 measurements. Vibration 2020, 3, 70–84. [Google Scholar] [CrossRef]
- Csurcsia, P.Z.; Peeters, B.; Schoukens, J. The best linear approximation of MIMO systems: Simplified nonlinearity assessment using a toolbox. In Proceedings of the International Conference on Noise and Vibration Engineering 2020, Leuven, Belgium, 12–14 September 2022; pp. 2239–2252. [Google Scholar]
- Schoukens, J.; Rolain, Y.; Simon, G.; Pintelon, R. Fully automated spectral analysis of periodic signals. IEEE Trans. Instrum. Meas. 2003, 52, 1021–1024. [Google Scholar] [CrossRef]
- Wickens, R. Wind Tunnel Investigation of Dynamic Stall of an NACA 0018 Airfoil Oscillating in Pitch (Etude en Soufflerie du Decrochage Aerodynamique d’un Profil NACA 0018 Oscillant en Tangage); National Aeronautical Establishment: Ottawa, ON, Canada, 1985. [Google Scholar]
- Stengel, R.F. Flight Dynamics; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Gudmundsson, S. General Aviation Aircraft Design: Applied Methods and Procedures; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Arena, A.V.; Mueller, T.J. Laminar Separation, Transition, and Turbulent Reattachment near the Leading Edge of Airfoils. AIAA J. 1980, 18, 747–753. [Google Scholar] [CrossRef]
- Coton, F.; Galbraith, R. An examination of dynamic stall on an oscillating rectangular wing. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA; 2003; p. 3675. [Google Scholar]
- Ullah, A.H.; Tomek, K.L.; Fabijanic, C.; Estevadeordal, J. Dynamic Stall Characteristics of Pitching Swept Finite-Aspect-Ratio Wings. Fluids 2021, 6, 457. [Google Scholar] [CrossRef]
- Brunton, S.L.; Rowley, C.W. Empirical state-space representations for Theodorsen’s lift model. J. Fluids Struct. 2013, 38, 174–186. [Google Scholar] [CrossRef]
- Csurcsia, P.Z. User-Friendly Method to Split Up the Multiple Coherence Function Into Noise, Nonlinearity and Transient Components Illustrated on Ground Vibration Testing of an F-16 Fighting Falcon. J. Vib. Eng. Technol. 2022, 10, 2577–2591. [Google Scholar] [CrossRef]
- Siddiqui, M.F.; Decuyper, J.; Csurcsia, P.Z.; Ertveldt, J.; De Troyer, T.; Schoukens, J.; Runacres, M.C. Estimating a nonparametric data-driven model of the lift on a pitching wing. J. Phys. Conf. Ser. 2020, 1618, 05201. [Google Scholar] [CrossRef]



| System accuracy | 0.08 % FS or better, accordingly to the used pressure scanner |
| A/D resolution | 16 bit |
| Scan rate | Ethernet data transfer: up to 500 S/ch/s with 64 ch ZOC |
| Motion Type | Pitch Amplitude | Pitch Offset | k |
|---|---|---|---|
| Single sine | 6 | 6, 9, 11, 13, 15, 17, 19, 21 | 0.006, 0.025, 0.063, 0.101, 0.126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csurcsia, P.Z.; Siddiqui, M.F.; Runacres, M.C.; De Troyer, T. Unsteady Aerodynamic Lift Force on a Pitching Wing: Experimental Measurement and Data Processing. Vibration 2023, 6, 29-44. https://doi.org/10.3390/vibration6010003
Csurcsia PZ, Siddiqui MF, Runacres MC, De Troyer T. Unsteady Aerodynamic Lift Force on a Pitching Wing: Experimental Measurement and Data Processing. Vibration. 2023; 6(1):29-44. https://doi.org/10.3390/vibration6010003
Chicago/Turabian StyleCsurcsia, Péter Zoltán, Muhammad Faheem Siddiqui, Mark Charles Runacres, and Tim De Troyer. 2023. "Unsteady Aerodynamic Lift Force on a Pitching Wing: Experimental Measurement and Data Processing" Vibration 6, no. 1: 29-44. https://doi.org/10.3390/vibration6010003
APA StyleCsurcsia, P. Z., Siddiqui, M. F., Runacres, M. C., & De Troyer, T. (2023). Unsteady Aerodynamic Lift Force on a Pitching Wing: Experimental Measurement and Data Processing. Vibration, 6(1), 29-44. https://doi.org/10.3390/vibration6010003






