Nonlinear Piezoelectric Energy Harvester: Experimental Output Power Mapping
Abstract
1. Introduction
2. Materials and Methods
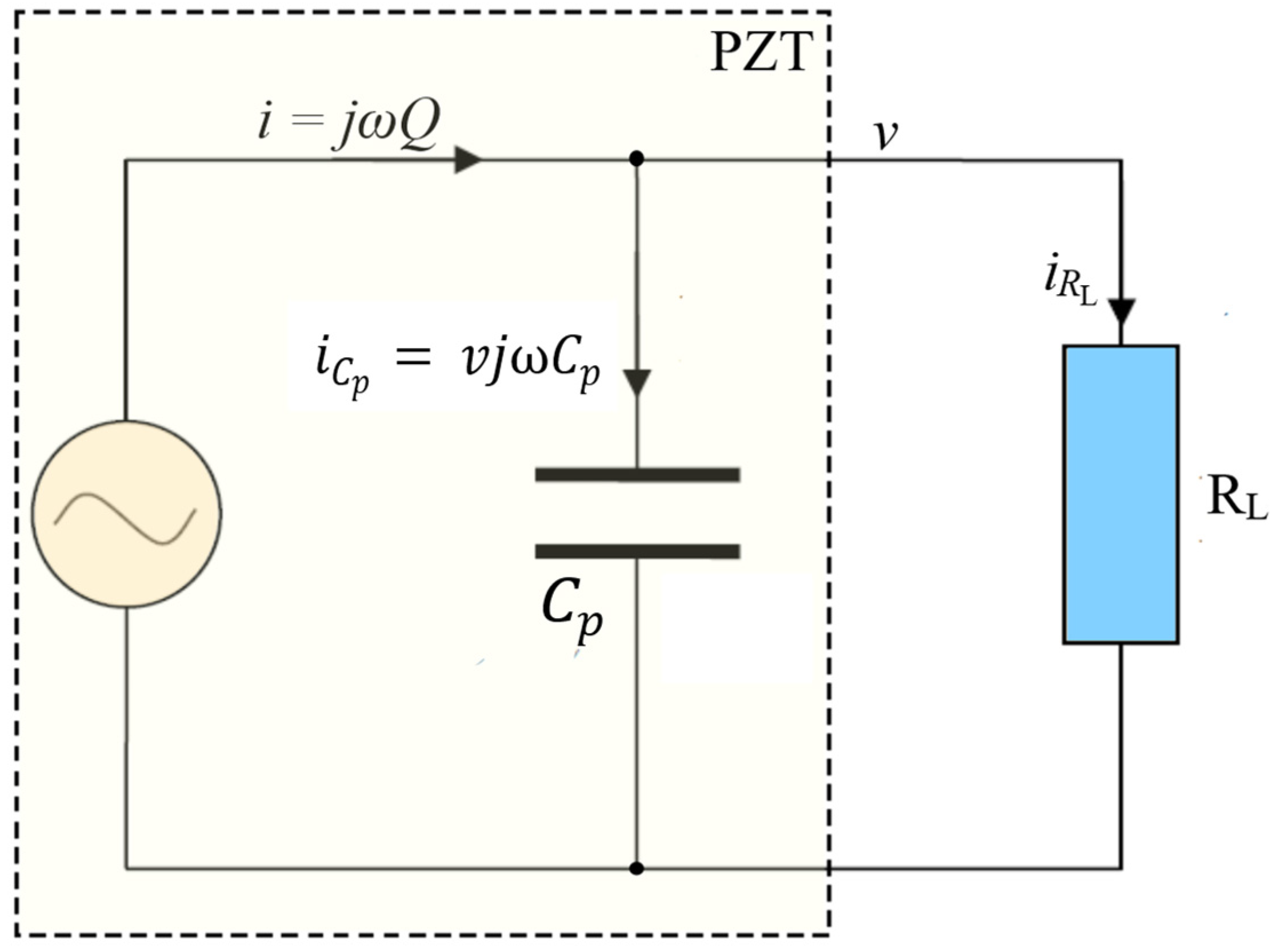
2.1. Basic Principles of the Nonlinear Piezoelectric Energy Harvester
2.2. Mechanical Setup
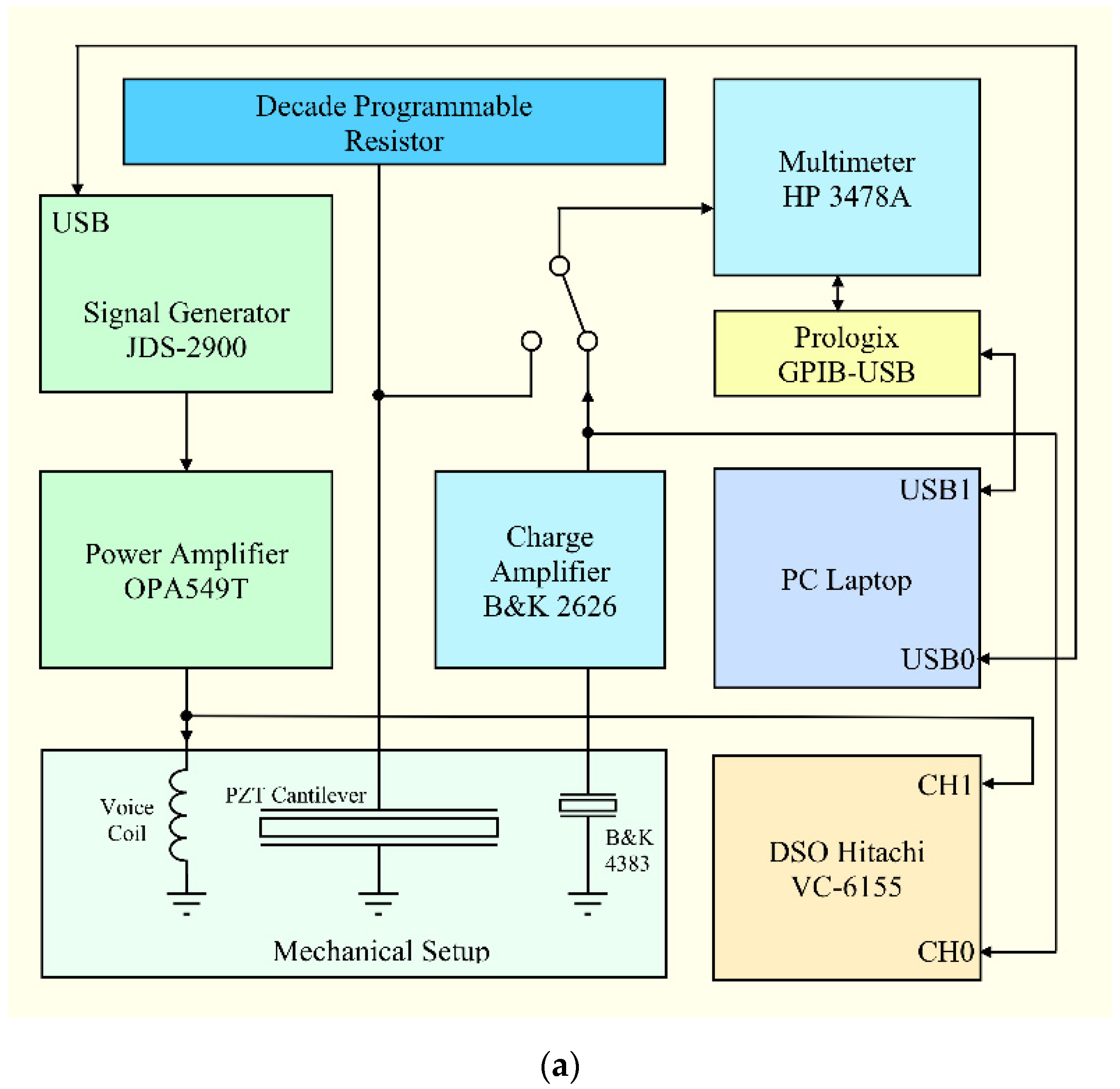
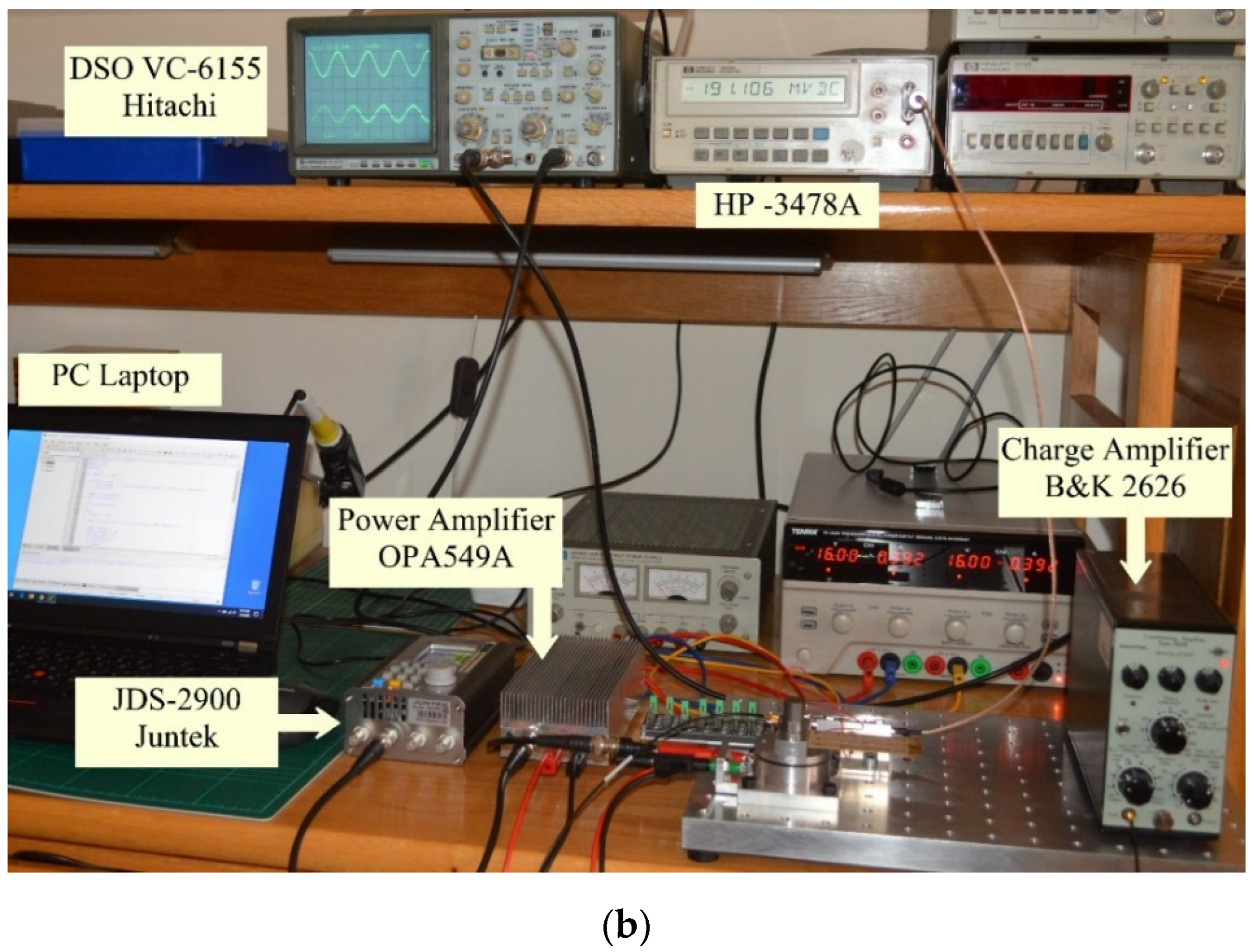
2.3. Experimental Setup
3. Results
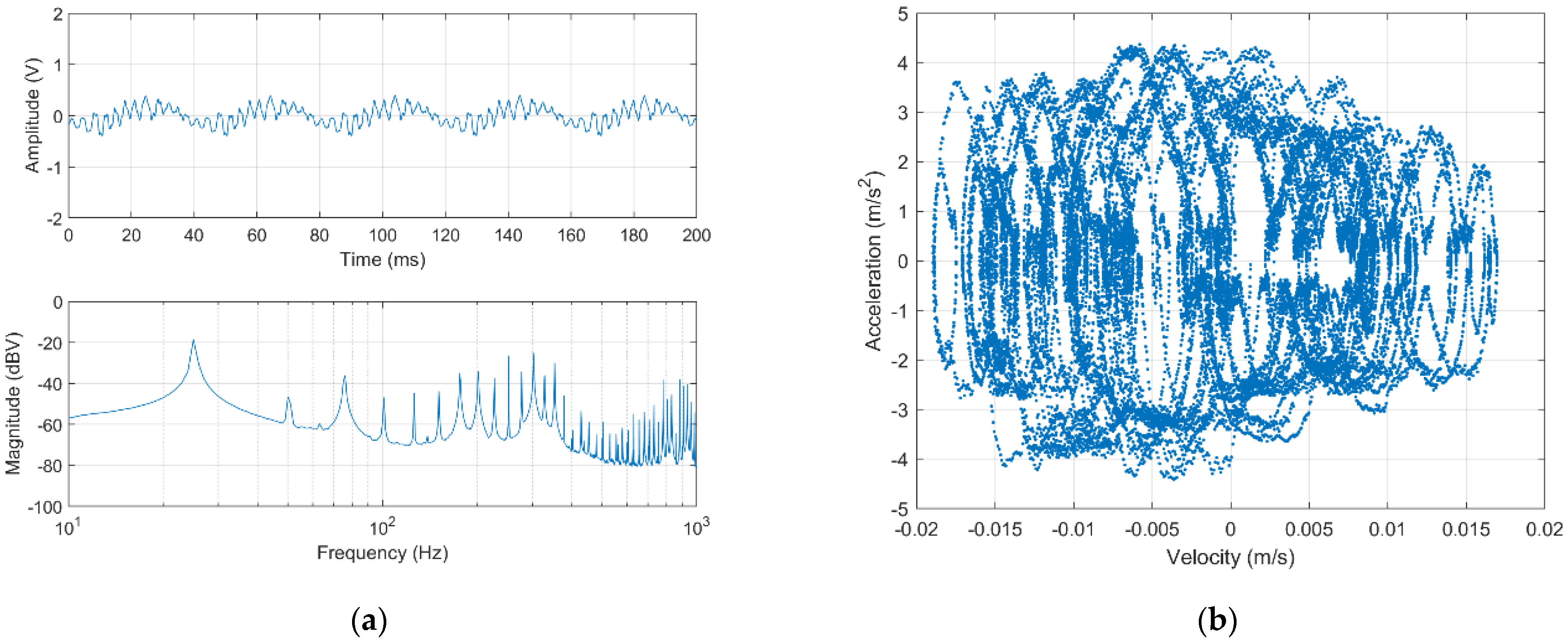
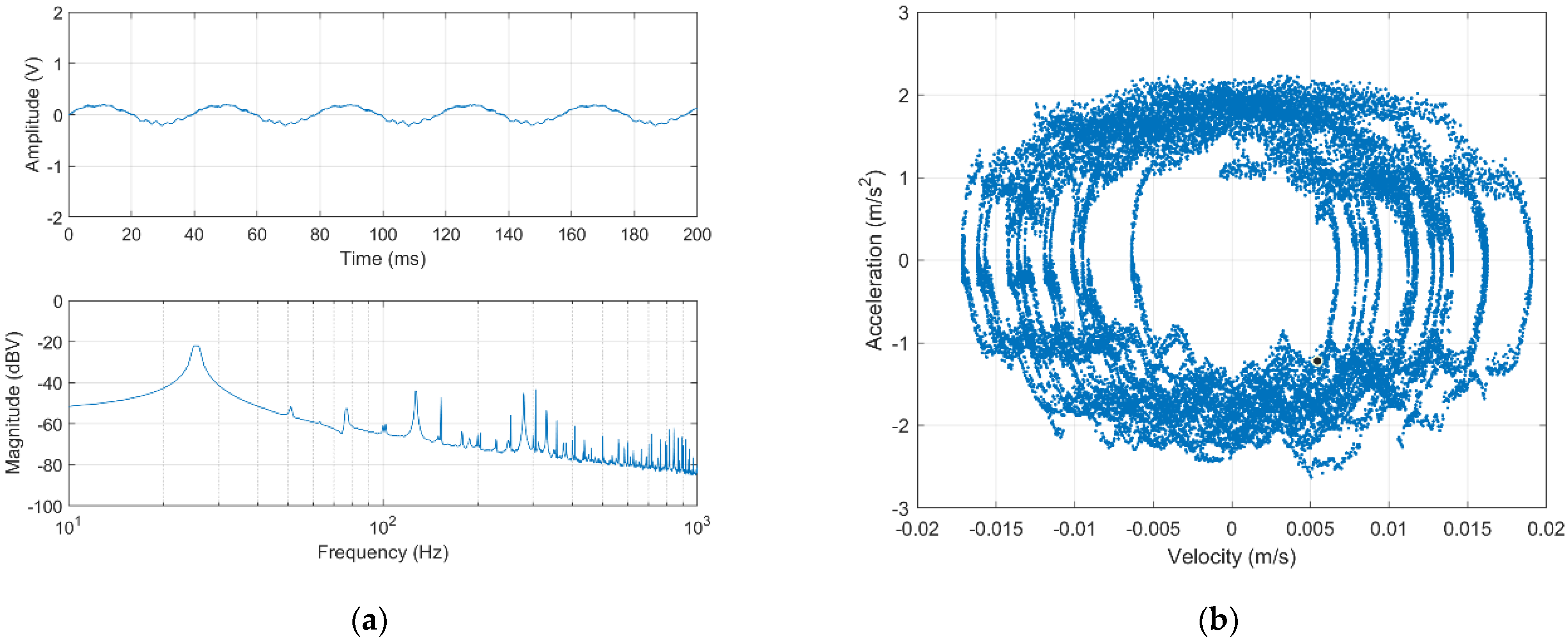
3.1. Dynamic Characterization of the Nonlinear Piezoelectric Energy Harvester
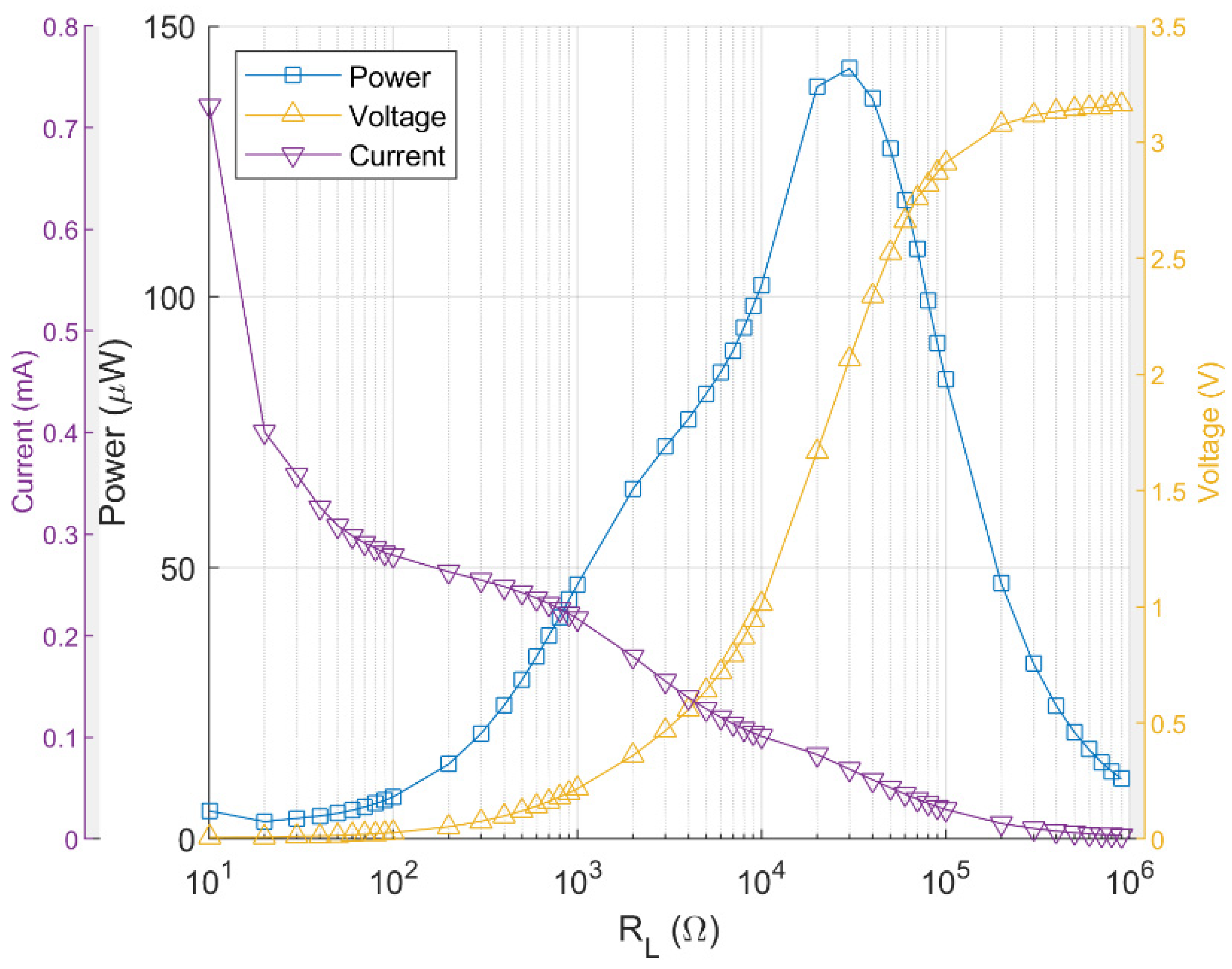
3.2. Output Power of a Nonlinear Piezoelectric Electrical Harvester
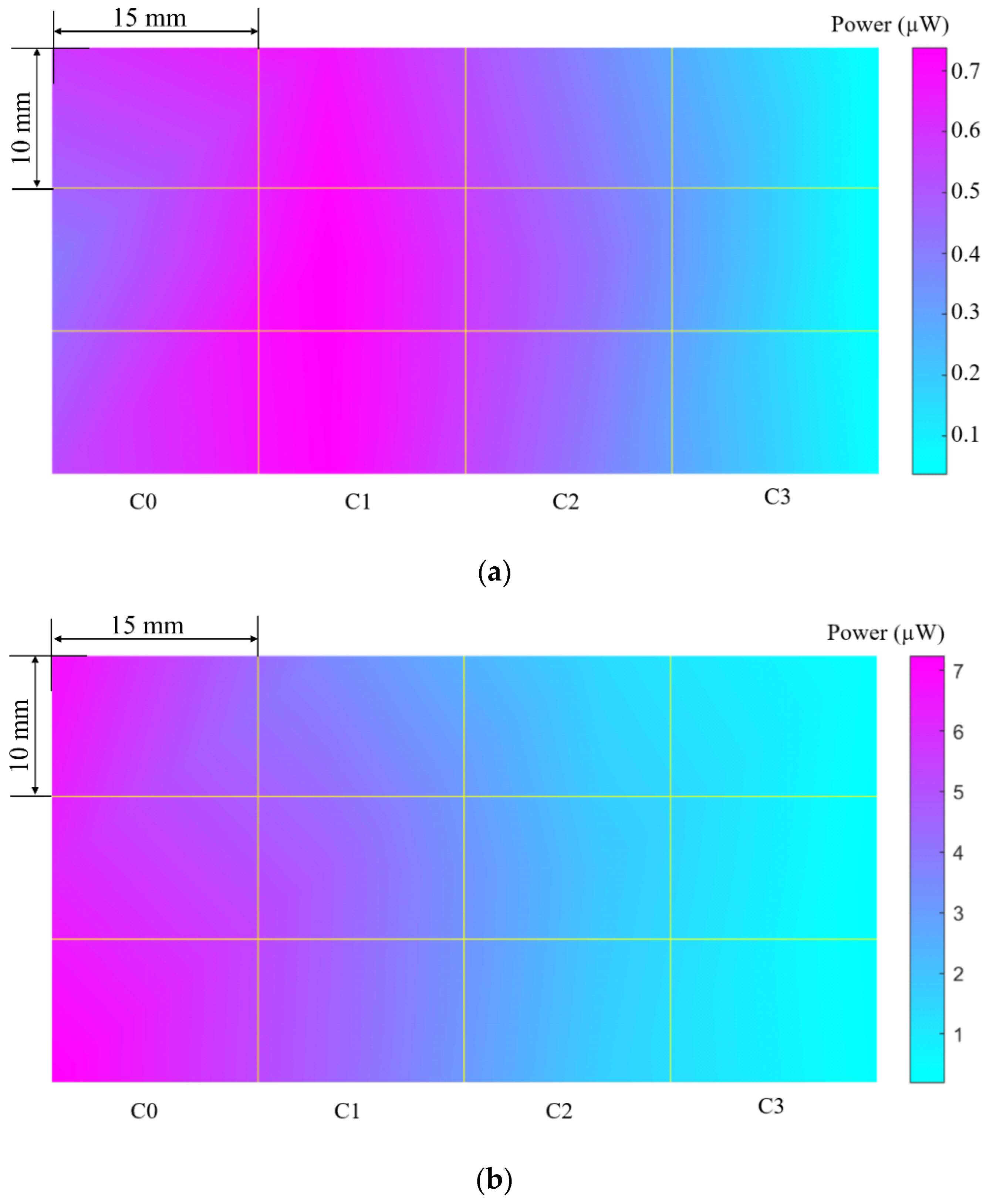
3.3. Experimental Output Power Mapping
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Liang, H.; Hao, G.; Olszewski, O.Z. A review on vibration-based piezoelectric energy harvesting from the aspect of compliant mechanisms. Sens. Actuators A Phys. 2021, 331, 112743. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric Energy Harvesting Solutions: A Review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Bogue, R. Energy harvesting and wireless sensors: A review of recent developments. Sens. Rev. 2009, 29, 194–199. [Google Scholar] [CrossRef]
- Harb, A. Energy harvesting: State-of-the-art. Renew. Energy 2011, 36, 2641–2654. [Google Scholar] [CrossRef]
- Khaligh, A.; Zeng, P.; Zheng, C. Kinetic Energy Harvesting Using Piezoelectric and Electromagnetic Technologies—State of the Art. IEEE Trans. Ind. Electron. 2010, 57, 850–860. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Zhu, D.; Tudor, M.J.; Beeby, S.P. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2009, 21, 022001. [Google Scholar] [CrossRef]
- Williams, C.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Keshmiri, A.; Wu, N. A Wideband Piezoelectric Energy Harvester Design by Using Multiple Non-Uniform Bimorphs. Vibration 2018, 1, 93–104. [Google Scholar] [CrossRef]
- Edwards, B.; Aw, K.C.; Hu, A.P. Mechanical frequency up-conversion for sub-resonance, low-frequency vibration harvesting. J. Intell. Mater. Syst. Struct. 2016, 27, 2145–2159. [Google Scholar] [CrossRef]
- Kathpalia, B.; Tan, D.; Stern, I.; Erturk, A. An experimentally validated model for geometrically nonlinear plucking-based frequency up-conversion in energy harvesting. Smart Mater. Struct. 2017, 27, 015024. [Google Scholar] [CrossRef]
- Ramlan, R.; Brennan, M.J.; Mace, B.R.; Kovacic, I. Potential benefits of a nonlinear stiffness in an energy harvesting device. Nonlinear Dyn. 2010, 59, 545–558. [Google Scholar] [CrossRef]
- Friswell, M.I.; Ali, S.F.; Adhikari, S.; Lees, A.W.; Bilgen, O.; Litak, G. Nonlinear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electroelastic energy harvesters: Modeling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed]
- Mann, B.; Owens, B. Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- Triplett, A.; Quinn, D.D. The Effect of Non-linear Piezoelectric Coupling on Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2009, 20, 1959–1967. [Google Scholar] [CrossRef]
- Gebrel, I.F.; Wang, L.; Asokanthan, S.F. Dynamic Analysis and Design of a Novel Ring-Based Vibratory Energy Harvester. Vibration 2019, 2, 271–284. [Google Scholar] [CrossRef]
- Sato, T.; Watanabe, K.; Igarashi, H. Coupled analysis of electromagnetic vibration energy harvester with nonlinear oscillation. IEEE Trans. Magn. 2014, 50, 313–316. [Google Scholar] [CrossRef][Green Version]
- Xie, Z.; Wang, T.; Kwuimy, C.K.; Shao, Y.; Huang, W. Design, analysis and experimental study of a T-shaped piezoelectric energy harvester with internal resonance. Smart Mater. Struct. 2019, 28, 085027. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, L.; Mace, B.R. Internal resonance with commensurability induced by an auxiliary oscillator for broadband energy harvesting. Appl. Phys. Lett. 2016, 108, 203901. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, L.; Mace, B.R. A comprehensive study of 2:1 internal-resonance-based piezoelectric vibration energy harvesting. Nonlinear Dyn. 2018, 91, 1817–1834. [Google Scholar] [CrossRef]
- Saint-Martin, C.; Morel, A.; Charleux, L.; Roux, E.; Benhemou, A.; Badel, A. Power expectation as a unified metric for the evaluation of vibration energy harvesters. Mech. Syst. Signal. Process. 2022, 181, 109482. [Google Scholar] [CrossRef]
- Liao, Y.; Liang, J. Unified modeling, analysis and comparison of piezoelectric vibration energy harvesters. Mech. Syst. Signal. Process. 2019, 123, 403–425. [Google Scholar] [CrossRef]
- Zaghari, B.; Rustighi, E.; Ghandchi Tehrani, M. Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation. Vibration 2018, 1, 157–171. [Google Scholar] [CrossRef]
- Arroyo, E.; Badel, A.; Formosa, F.; Wu, Y.; Qiu, J. Comparison of electromagnetic and piezoelectric vibration energy harvesters: Model and experiments. Sens. Actuators A Phys. 2012, 183, 148–156. [Google Scholar] [CrossRef]
- Le, C.P.; Halvorsen, E.; Søråsen, O.; Yeatman, E.M. Wideband Excitation of an Electrostatic Vibration Energy Harvester with Power-Extracting End-Stops. Smart Mater. Struct. 2013, 22, 075020. [Google Scholar] [CrossRef]
- Janphuang, P.; Lockhart, R.; Uffer, N.; Briand, D.; de Rooij, N.F. Vibrational Piezoelectric Energy Harvesters Based on Thinned Bulk PZT Sheets Fabricated at the Wafer Level. Sens. Actuators A Phys. 2014, 210, 1–9. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Z.; Liu, W. Systematic adjustment strategy of a nonlinear beam generator for high-energy orbit. Mech. Syst. Signal. Process. 2022, 166, 108444. [Google Scholar] [CrossRef]
- Morel, A.; Brenes, A.; Gibus, D.; Lefeuvre, E.; Gasnier, P.; Pillonnet, G.; Badel, A. A comparative study of electrical interfaces for tunable piezoelectric vibration energy harvesting. Smart Mater. Struct. 2022, 31, 045016. [Google Scholar] [CrossRef]
- Masana, R.; Daqaq, M.F. Response of duffing-type harvesters to band-limited noise. J. Sound Vib. 2013, 332, 6755–6767. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.; Marletta, V.A. Bistable buckled beam based approach for vibrational energy harvesting. Sens. Actuators A Phys. 2014, 211, 153–161. [Google Scholar] [CrossRef]
- Zayed, A.A.; Assal, S.F.; Nakano, K.; Kaizuka, T.; El-Bab, F.; Ahmed, M. Design procedure and experimental verification of a broadband quad-sTable 2-DOF vibration energy harvester. Sensors 2019, 19, 2893. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, S.; Liu, H.; Jin, L. Nonlinear Hybrid Piezoelectric and Electromagnetic Energy Harvesting Driven by Colored Excitation. Energies 2018, 11, 498. [Google Scholar] [CrossRef]
- Hajati, A.; Kim, S.G. Ultra-wide bandwidth piezoelectric energy harvesting. Appl. Phys. Lett. 2011, 99, 083105. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Litak, G. Theoretical analysis of multi-stable energy harvesters with high-order stiffness terms. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 270–286. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal. Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Ando, B. How can energy be scavenged from wideband vibrations? IEEE Instrum. Meas. Mag. 2015, 18, 40–44. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burda, I. Nonlinear Piezoelectric Energy Harvester: Experimental Output Power Mapping. Vibration 2022, 5, 483-496. https://doi.org/10.3390/vibration5030027
Burda I. Nonlinear Piezoelectric Energy Harvester: Experimental Output Power Mapping. Vibration. 2022; 5(3):483-496. https://doi.org/10.3390/vibration5030027
Chicago/Turabian StyleBurda, Ioan. 2022. "Nonlinear Piezoelectric Energy Harvester: Experimental Output Power Mapping" Vibration 5, no. 3: 483-496. https://doi.org/10.3390/vibration5030027
APA StyleBurda, I. (2022). Nonlinear Piezoelectric Energy Harvester: Experimental Output Power Mapping. Vibration, 5(3), 483-496. https://doi.org/10.3390/vibration5030027





