Data-Informed Decomposition for Localized Uncertainty Quantification of Dynamical Systems
Abstract
:1. Introduction
2. Methodology
2.1. Bayesian Inference
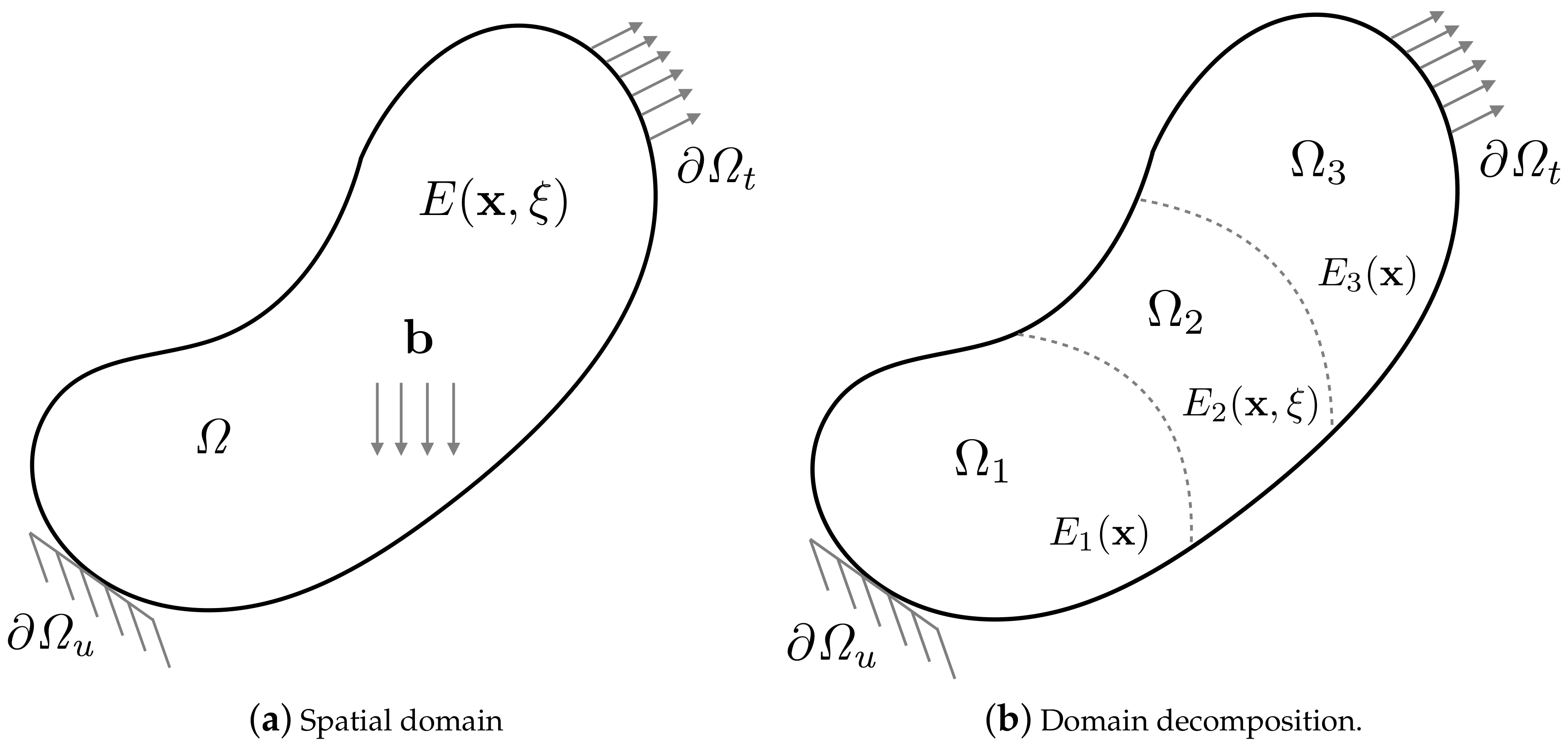
2.2. The Forward Problem
Spatial and Temporal Discretizations
2.3. Surrogate Modeling
2.4. Polynomial Chaos
3. Numerical Example
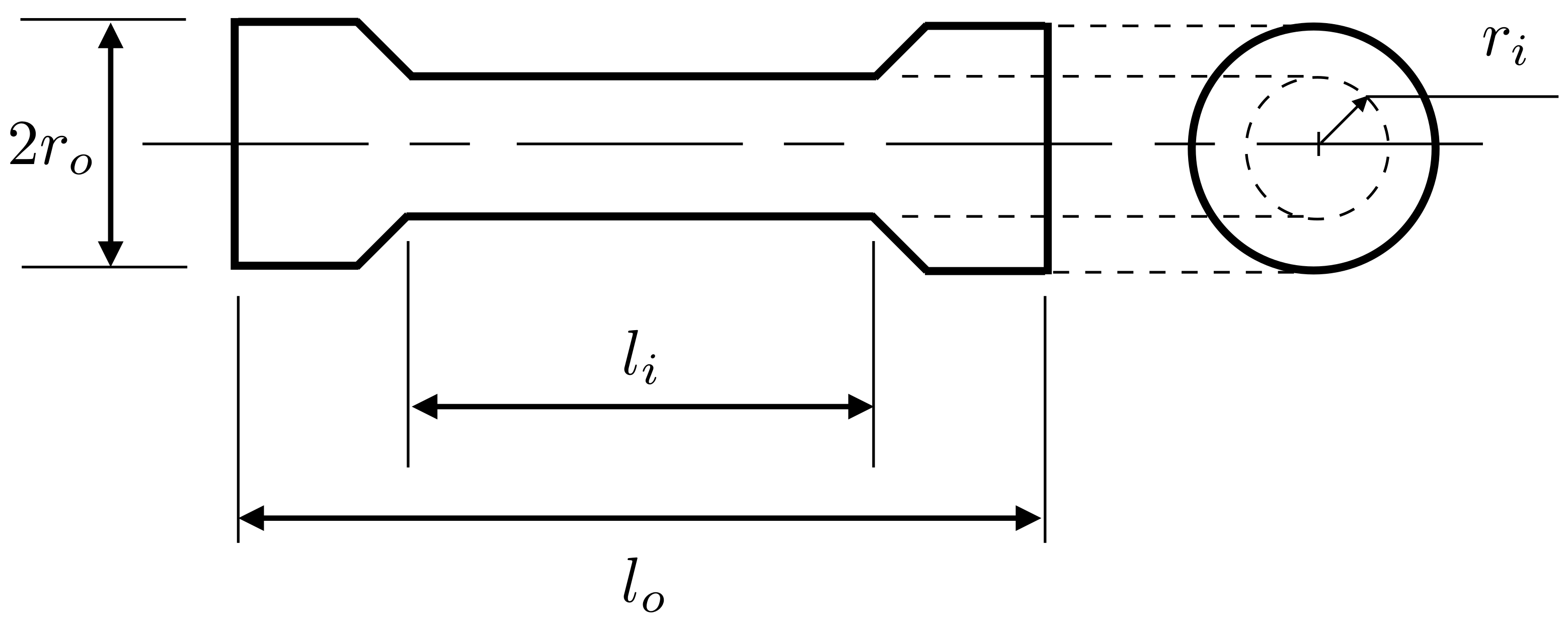
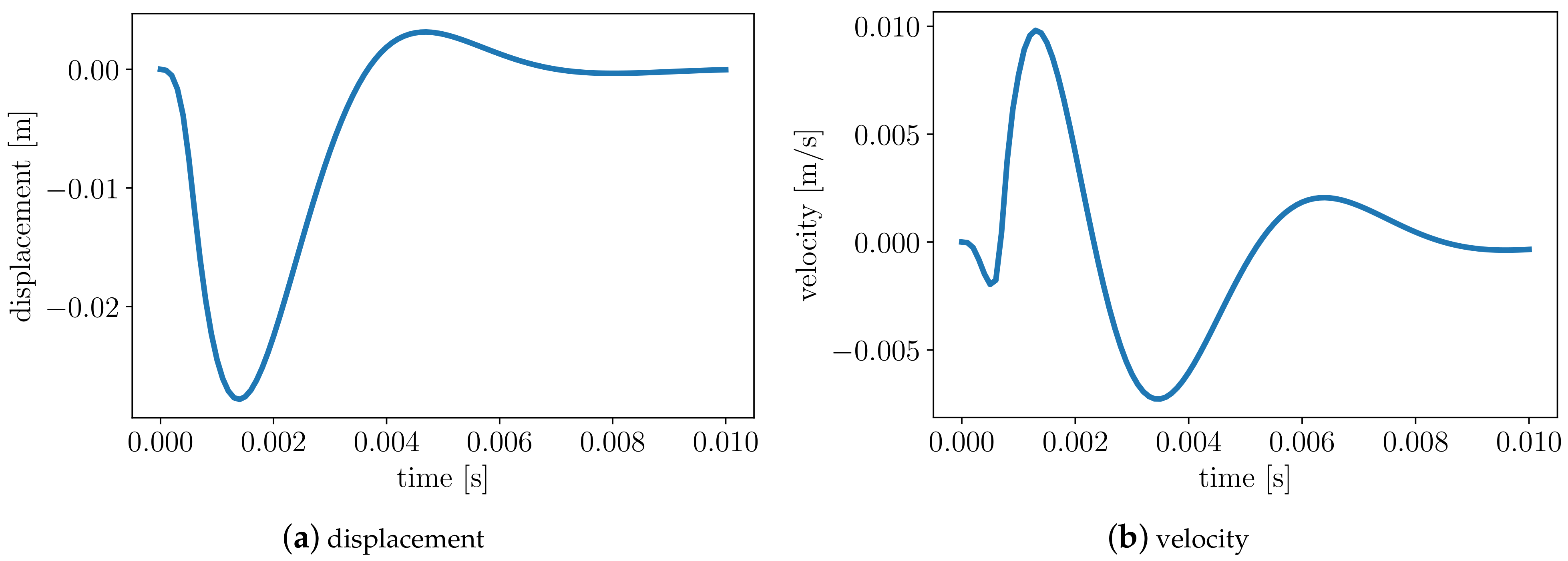
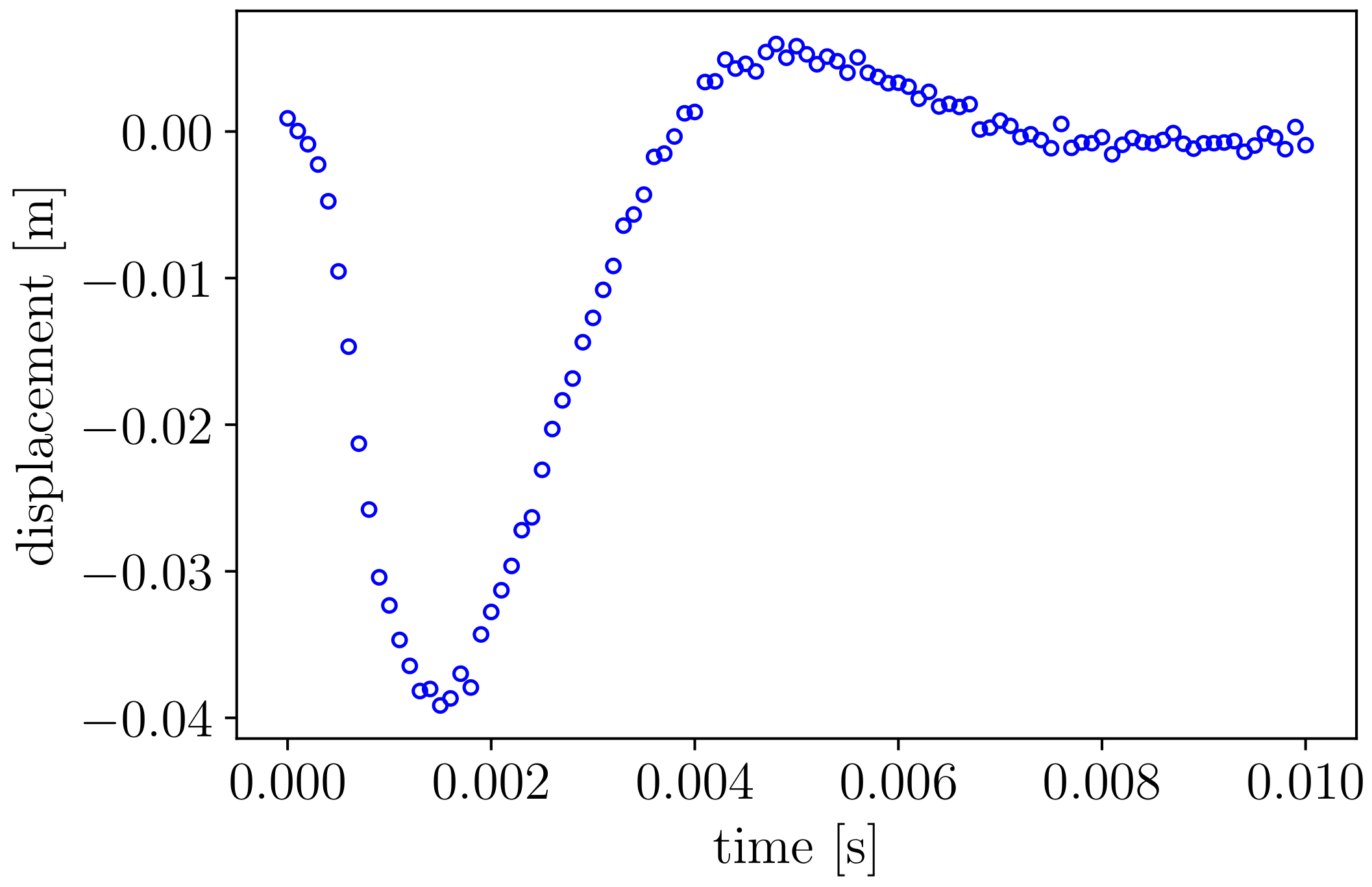
3.1. The Forward Problem
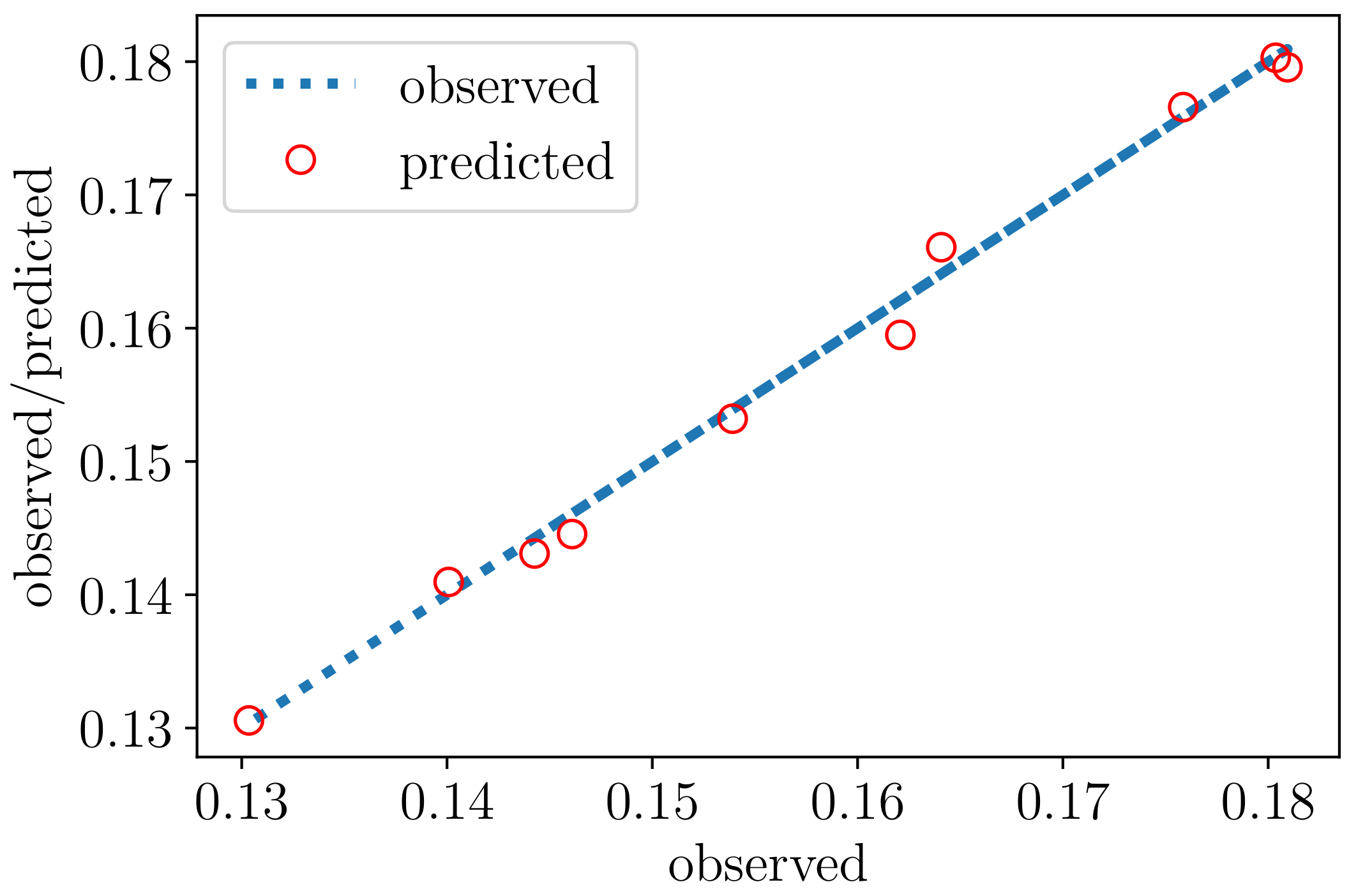
3.2. The Surrogate Model
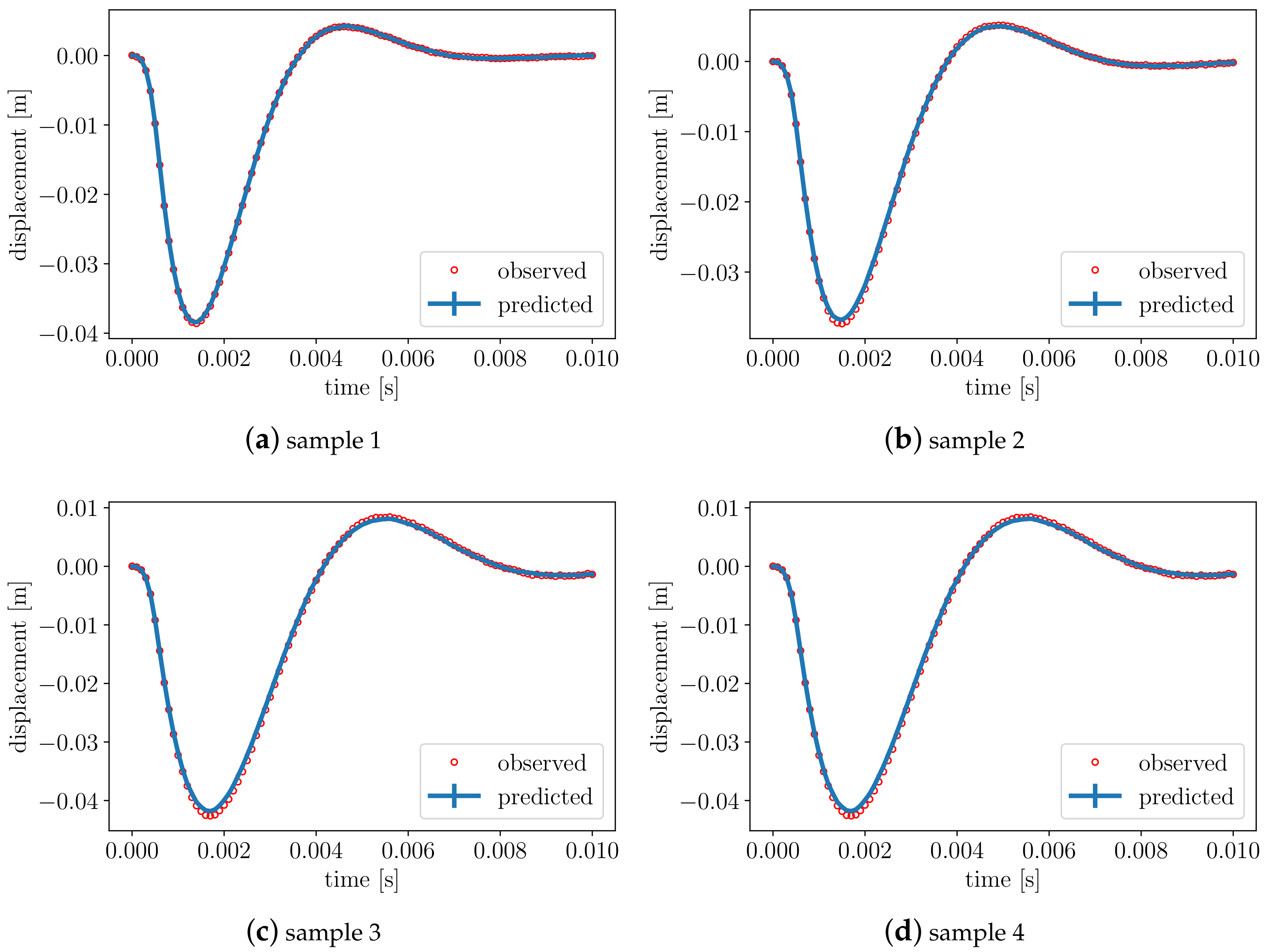
3.3. The Backward Problem
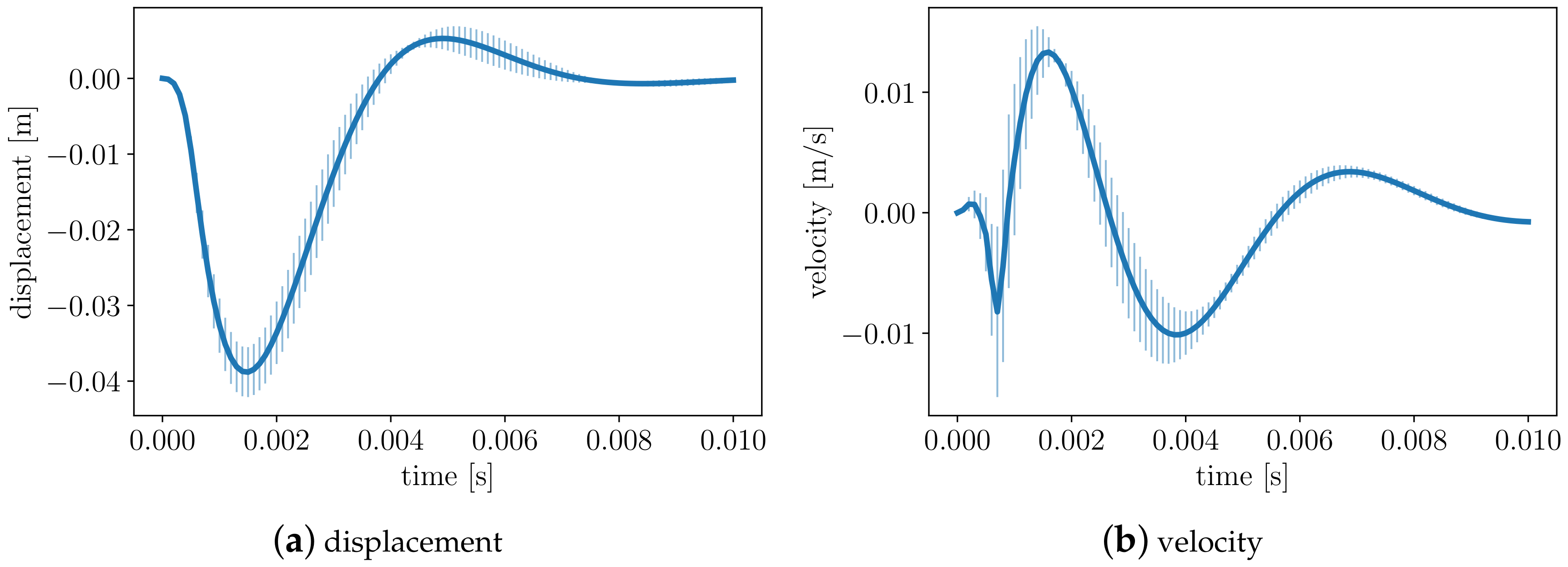
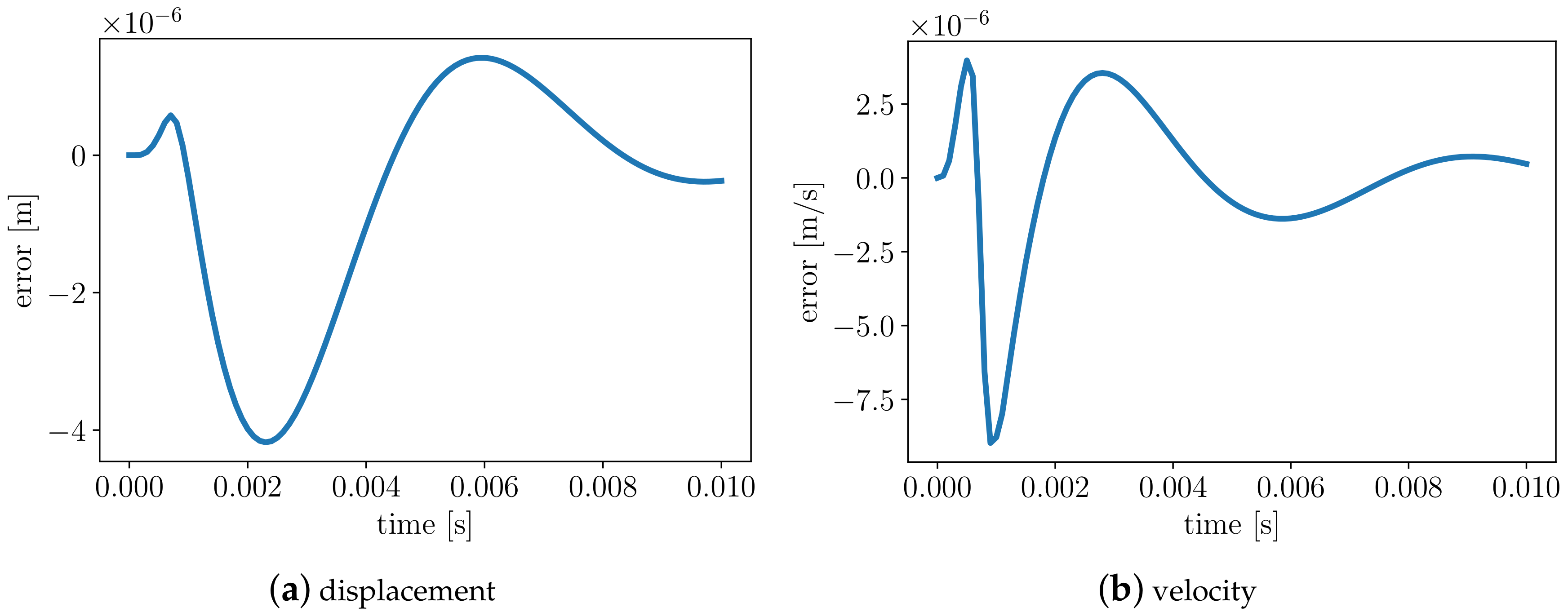
3.4. Localized Uncertainty Propagation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dutton, S.; Kelly, D.; Baker, A. Composite Materials for Aircraft Structures; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Mrazova, M. Advanced composite materials of the future in aerospace industry. Incas Bull. 2013, 5, 139. [Google Scholar]
- Pettit, C.L. Uncertainty quantification in aeroelasticity: Recent results and research challenges. J. Aircr. 2004, 41, 1217–1229. [Google Scholar] [CrossRef]
- Munk, C.L.; Nelson, P.E.; Strand, D.E. Determinant Wing Assembly. U.S. Patent 6,808,143, 26 November 2004. [Google Scholar]
- Katunin, A.; Dragan, K.; Dziendzikowski, M. Damage identification in aircraft composite structures: A case study using various non-destructive testing techniques. Compos. Struct. 2015, 127, 1–9. [Google Scholar] [CrossRef]
- Diamanti, K.; Soutis, C. Structural health monitoring techniques for aircraft composite structures. Prog. Aerosp. Sci. 2010, 46, 342–352. [Google Scholar] [CrossRef]
- Subber, W.; Matouš, K. Asynchronous space-time domain decomposition method with localized uncertainty quantification. Comput. Methods Appl. Mech. Eng. 2017, 325, 369–394. [Google Scholar] [CrossRef]
- Subber, W.; Salvadori, A.; Lee, S.; Matouš, K. Uncertainty quantification of the reverse Taylor impact test and localized asynchronous space-time algorithm. In AIP Conference Proceedings, St. Louis, MO, USA, 9–14 July 2017; AIP Publishing LLC: Melville, NY, USA, 2018; Volume 1979, p. 140005. [Google Scholar]
- Subber, W.; Matouš, K. Asynchronous space-time algorithm based on a domain decomposition method for structural dynamics problems on non-matching meshes. Comput. Mech. 2016, 57, 211–235. [Google Scholar] [CrossRef]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM: Philadelphia, PA, USA, 2013; Volume 12. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman & Hall/CRC: Boca Raton, FL, USA, 2014; Volume 2. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Courier Corporation: North Chelmsford, MA, USA, 2003. [Google Scholar]
- Le Maître, O.; Knio, O.M. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Miles, P.R. pymcmcstat: A Python Package for Bayesian Inference Using Delayed Rejection Adaptive Metropolis. J. Open Source Softw. 2019, 4, 1417. [Google Scholar] [CrossRef]
- Babuška, I.; Nobile, F.; Tempone, R. A stochastic collocation method for elliptic partial differential equations with random input data. SIAM J. Numer. Anal. 2007, 45, 1005–1034. [Google Scholar] [CrossRef]
- Hughes, T.J. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Ghosh, S.; Pandita, P.; Subber, W.; Zhang, Y.; Wang, L. Efficient bayesian inverse method using robust gaussian processes for design under uncertainty. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1877. [Google Scholar]
- Ghosh, S.; Pandita, P.; Atkinson, S.; Subber, W.; Zhang, Y.; Kumar, N.C.; Chakrabarti, S.; Wang, L. Advances in Bayesian Probabilistic Modeling for Industrial Applications. ASCE-ASME J. Risk Uncert. Eng. Syst. Part B Mech. Eng. 2020, 6. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ghosh, S.; Pandita, P.; Subber, W.; Khan, G.; Wang, L. Remarks for scaling up a general gaussian process to model large dataset with sub-models. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0678. [Google Scholar]
- Shabouei, M.; Subber, W.; Williams, C.W.; Matouš, K.; Powers, J.M. Chemo-thermal model and gaussian process emulator for combustion synthesis of ni/al composites. Combust. Flame 2019, 207, 153–170. [Google Scholar] [CrossRef]
- Feinberg, J.; Langtangen, H.P. Chaospy: An open source tool for designing methods of uncertainty quantification. J. Comput. Sci. 2015, 11, 46–57. [Google Scholar] [CrossRef] [Green Version]
- Logg, A.; Mardal, K.A.; Wells, G. Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 84. [Google Scholar]
- Kristensen, J.; Subber, W.; Zhang, Y.; Ghosh, S.; Kumar, N.C.; Khan, G.; Wang, L. Industrial applications of intelligent adaptive sampling methods for multi-objective optimization. In Design Engineering and Manufacturing; IntechOpen: London, UK, 2019. [Google Scholar]
- Kristensen, J.; Bilionis, I.; Zabaras, N. Adaptive simulation selection for the discovery of the ground state line of binary alloys with a limited computational budget. In Recent Progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science; Springer: Berlin/Heidelberg, Germany, 2017; pp. 185–211. [Google Scholar]
- Pronzato, L.; Müller, W.G. Design of computer experiments: Space filling and beyond. Stat. Comput. 2012, 22, 681–701. [Google Scholar] [CrossRef]
- Ghosh, S.; Kristensen, J.; Zhang, Y.; Subber, W.; Wang, L. A Strategy for Adaptive Sampling of Multi-Fidelity Gaussian Processes to Reduce Predictive Uncertainty. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59193, p. V02BT03A024. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subber, W.; Ghosh, S.; Pandita, P.; Zhang, Y.; Wang, L. Data-Informed Decomposition for Localized Uncertainty Quantification of Dynamical Systems. Vibration 2021, 4, 49-63. https://doi.org/10.3390/vibration4010004
Subber W, Ghosh S, Pandita P, Zhang Y, Wang L. Data-Informed Decomposition for Localized Uncertainty Quantification of Dynamical Systems. Vibration. 2021; 4(1):49-63. https://doi.org/10.3390/vibration4010004
Chicago/Turabian StyleSubber, Waad, Sayan Ghosh, Piyush Pandita, Yiming Zhang, and Liping Wang. 2021. "Data-Informed Decomposition for Localized Uncertainty Quantification of Dynamical Systems" Vibration 4, no. 1: 49-63. https://doi.org/10.3390/vibration4010004
APA StyleSubber, W., Ghosh, S., Pandita, P., Zhang, Y., & Wang, L. (2021). Data-Informed Decomposition for Localized Uncertainty Quantification of Dynamical Systems. Vibration, 4(1), 49-63. https://doi.org/10.3390/vibration4010004



