Characterizing the Frequency Response of Compliant Materials by Laser Döppler Vibrometry Coupled Acoustic Excitation
Abstract
1. Introduction
2. Methodology
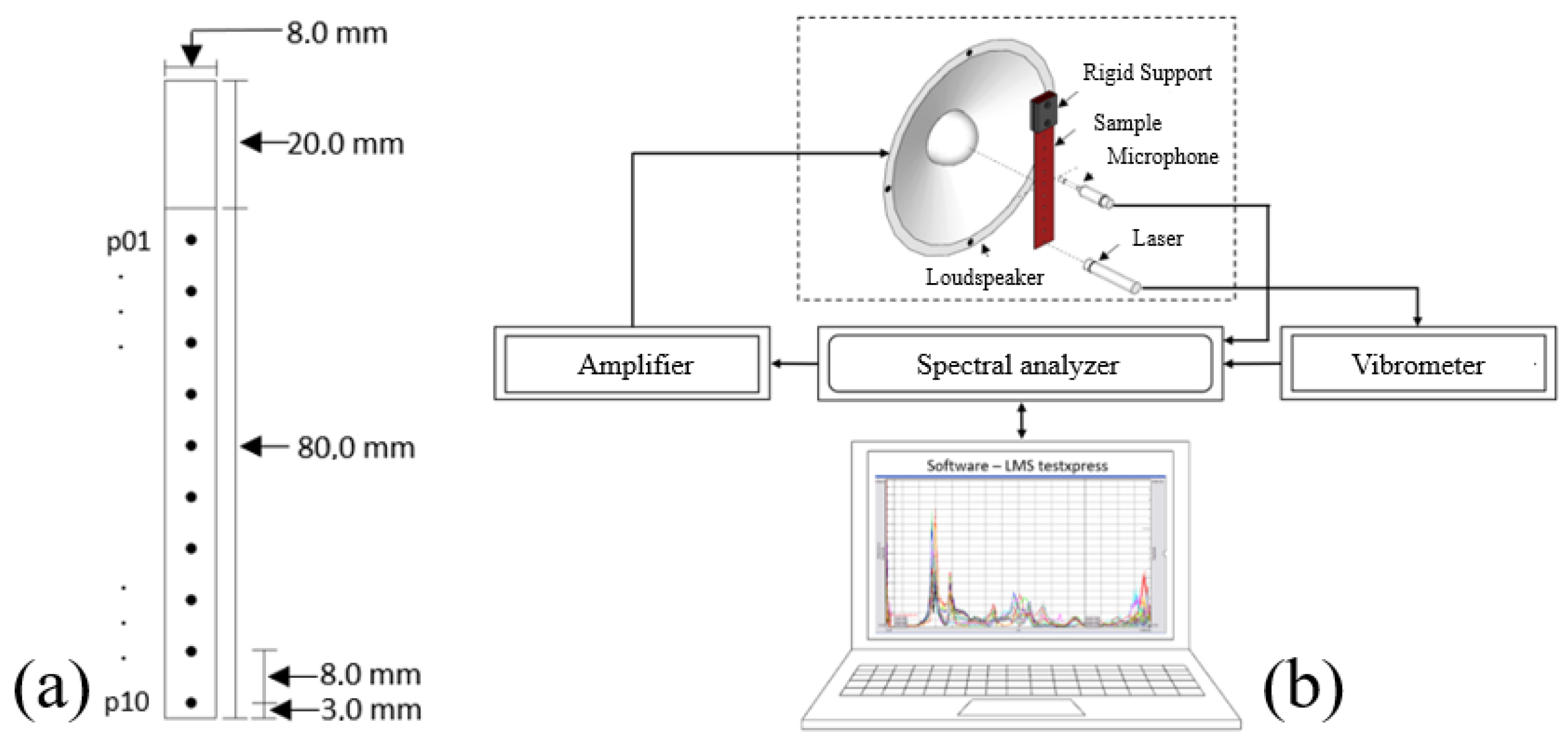
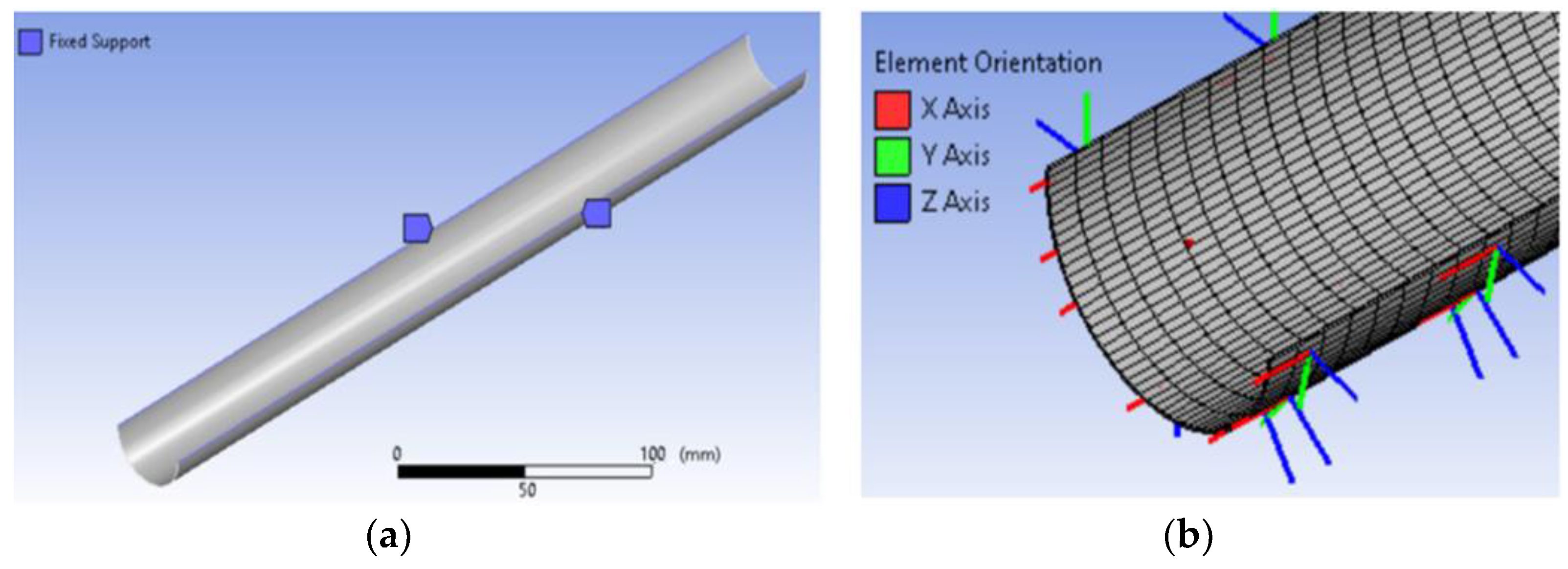
2.1. Modal Analysis—Cantilever Beam Approach
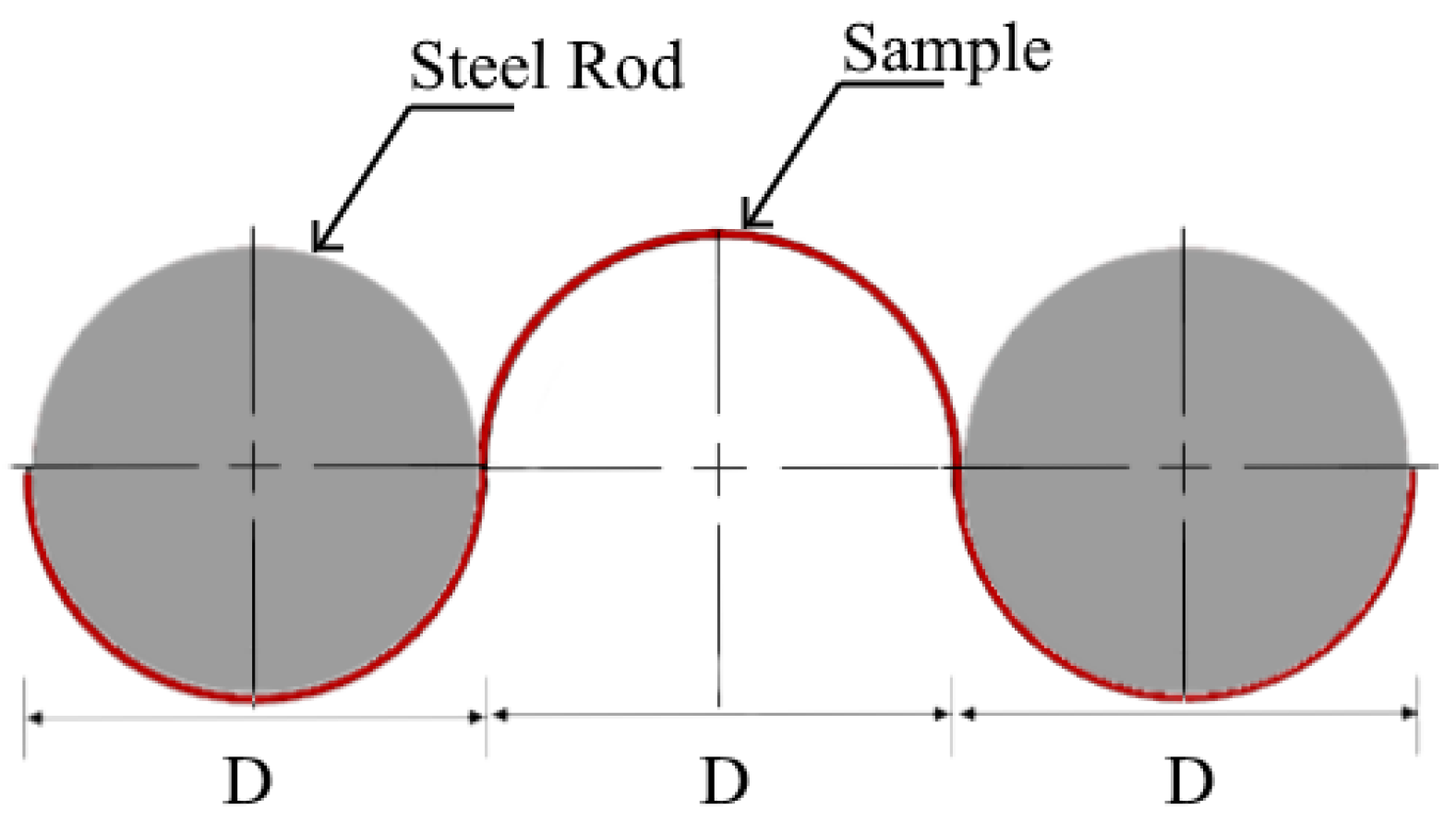
2.2. Modal Analysis—Optimized Half-Cane Sample
3. Results and Discussion
3.1. Cantilever Beam Approach
3.2. Optimized Half-Cane Sample Approach
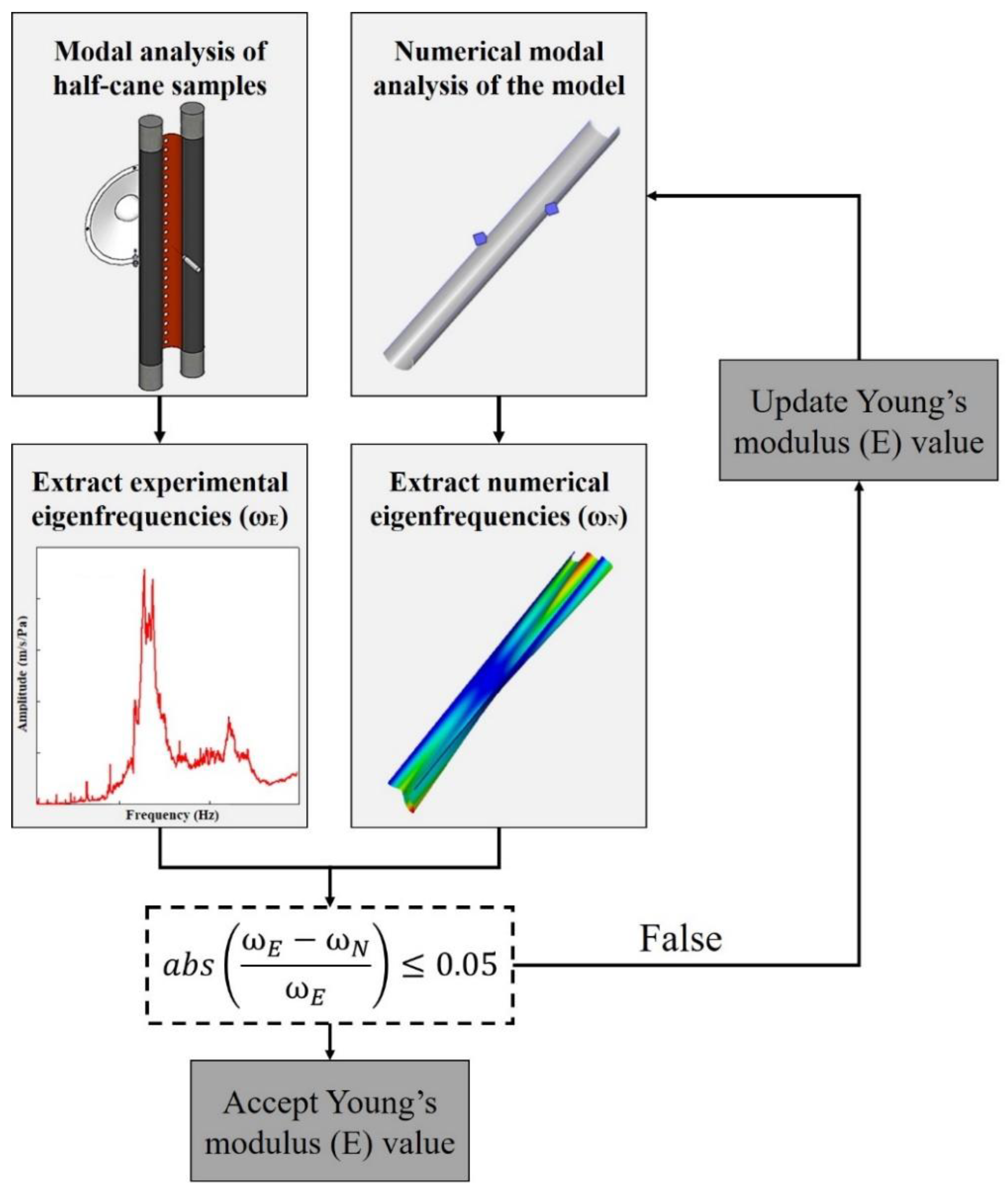
3.3. Considerations on the Method for the Determination of Dynamic Young’s Modulus
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, W.; Xu, Z.; Bian, H.; Li, Z. Lightweight Heavy-Duty CNC Horizontal Lathe Based on Particle Damping Materials. Mech. Syst. Signal Process. 2021, 147, 107127. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Yang, Y.; Wang, J.; Yuan, J. Active Control of Low-Frequency Vibrations in Ultra-Precision Machining with Blended Infinite and Zero Stiffness. Int. J. Mach. Tools Manuf. 2019, 139, 64–74. [Google Scholar] [CrossRef]
- Gharaibeh, M.A. A Numerical Study on the Effect of the Fixation Methods on the Vibration Fatigue of Electronic Packages. Microelectron. Reliab. 2020, 115, 113967. [Google Scholar] [CrossRef]
- Nadkarni, I.; Bhardwaj, R.; Ninan, S.; Chippa, S.P. Experimental Modal Parameter Identification and Validation of Cantilever Beam. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Pereira, D.A.; Guimarães, T.A.M.; Resende, H.B.; Rade, D.A. Numerical and Experimental Analyses of Modal Frequency and Damping in Tow-Steered CFRP Laminates. Compos. Struct. 2020, 244, 112190. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Puga, H. Temperature Variability of Poisson’s Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis. Technologies 2018, 6, 81. [Google Scholar] [CrossRef]
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction; CRC Press: Boca Raton, FL, USA, 2008; ISBN 1-4200-5313-2. [Google Scholar]
- Pandiripalli, B. Repeatability and Reproducibility Studies: A Comparison of Techniques; Wichita State University: Wichita, KS, USA, 2010. [Google Scholar]
- Witos, M. Modal Analysis as a High Sensitive NDT Method of Compressor Blades; NDT: Prague, Czech Republic, 2015; pp. 12–14. [Google Scholar]
- Hu, H.; He, Z.; Zhang, Y.; Gao, S. Modal Frequency Sensitivity Analysis and Application Using Complex Nodal Matrix. IEEE Trans. Power Deliv. 2013, 29, 969–971. [Google Scholar] [CrossRef]
- Ege, K.; Boutillon, X.; David, B. High-Resolution Modal Analysis. J. Sound Vib. 2009, 325, 852–869. [Google Scholar] [CrossRef]
- Amraoui, Y.M.; Lieven, N.A.J. Noncontacting Excitation and Measurement of Light Structures. J. Vib. Acoust. 2003, 125, 114–119. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; Wiley Online Library: Hoboken, NJ, USA, 2007; Volume 464. [Google Scholar]
- Carneiro, V.H.; Lopes, D.; Puga, H.; Meireles, J. Numerical Inverse Engineering as a Route to Determine the Dynamic Mechanical Properties of Metallic Cellular Solids. Mater. Sci. Eng. A 2020, 140428. [Google Scholar] [CrossRef]
- Chomette, B.; Le Carrou, J.-L. Operational Modal Analysis Applied to the Concert Harp. Mech. Syst. Signal Process. 2015, 56–57, 81–91. [Google Scholar] [CrossRef]
- Lafleur, F.; Thomas, M.; Laville, F. Modal Analysis of Structures Using Acoustical Excitation; Internoise: Nice, France, 2000. [Google Scholar]
- Bokil, V.B.; Shirahatti, U.S. A Technique for the Modal Analysis of Sound-Structure Interaction Problems. J. Sound Vib. 1994, 173, 23–41. [Google Scholar] [CrossRef]
- Wu, J.; Moslehy, F.A. On Modal Testing Using Speaker for Excitation; SPIE: Bellingham, WA, USA, 1995; Volume 2460, p. 24. [Google Scholar]
- Xu, Y.F.; Zhu, W.D. Operational Modal Analysis of a Rectangular Plate Using Non-Contact Excitation and Measurement. J. Sound Vib. 2013, 332, 4927–4939. [Google Scholar] [CrossRef]
- Roozen, N.B.; Leclère, Q.; Urbán, D.; Kritly, L.; Glorieux, C. Assessment of the Sound Reduction Index of Building Elements by near Field Excitation through an Array of Loudspeakers and Structural Response Measurements by Laser Doppler Vibrometry. Appl. Acoust. 2018, 140, 225–235. [Google Scholar] [CrossRef]
- Urbán, D.; Roozen, N.B.; Muellner, H.; Zaťko, P.; Niemczanowski, A.; Rychtáriková, M.; Glorieux, C. Vibrometry Assessment of the External Thermal Composite Insulation Systems Influence on the Façade Airborne Sound Insulation. Appl. Sci. 2018, 8, 703. [Google Scholar] [CrossRef]
- Satthiyaraju, M.; Ramesh, T. Modal Analysis of Microcantilever Using Vibration Speaker. In Proceedings of the 2016 COMSOL Conference, Munich, Germany, 12–14 October 2016. [Google Scholar]
- Bukhari, S.A.; Goswami, A.; McGee, R.; Abraham, R.; Hume, D.; Chung, H.J.; Thundat, T. Bidirectional Frequency Tuning of Vanadium Dioxide (VO 2) Microstring Resonator by Optothermal Excitation; IEEE: New York, NY, USA, 2020; pp. 961–964. [Google Scholar]
- Adriana, G.; Jussi, L.; Robert, S.; Franz, S. Humidity Response of Kraft Papers Determined by Dynamic Mechanical Analysis. Thermochim. Acta 2013, 570, 33–40. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Ho, L.V.; Bui-Tien, T.; De Roeck, G.; Wahab, M.A. Damage Evaluation of Free-Free Beam Based on Vibration Testing. Appl. Mech. 2020, 1, 10. [Google Scholar] [CrossRef]
- Standard, A. Standard Test Method for Measuring Vibration-Damping Properties of Materials; E756-05; ASTM: West Conshohocken, PA, USA, 2010. [Google Scholar]





| Eigenmode | Experimental Eigenfrequency (Hz) | Shape | |
|---|---|---|---|
| Experimental | Analytical | ||
| 1 | N.A. | N.A. | 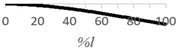 |
| 2 | 59 ± 2 | 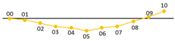 |  |
| 3 | 161 ± 3 |  |  |
| 4 | 321 ± 4 |  |  |
| Eigenmode | Dynamic Young’s Modulus (MPa) |
|---|---|
| 2 | 0.782 ± 0.003 |
| 3 | 0.813 ± 0.002 |
| 4 | 0.821 ± 0.005 |
| Eigenmode | Eigenfrequency (Hz) | |||
|---|---|---|---|---|
| Experimental | Numerical | Δ—Variation (%) | Dynamic Young’s Modulus (MPa) | |
| 1 | 635 ± 3 | 683 | −4.6 | 0.832 |
| 2 | 675 ± 3 | 710 | −5.2 | 0.837 |
| 3 | 1118 ± 14 | 1047 | 6.4 | 0.842 |
| 4 | 1664 ± 22 | 1656 | 0.5 | 0.861 |
| Eigenmode | Shape | |
|---|---|---|
| Experimental | Numerical | |
| 1 |  | 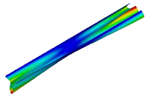 |
| 2 | 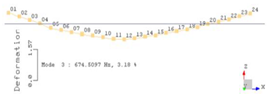 | 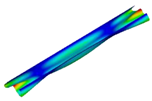 |
| 3 | 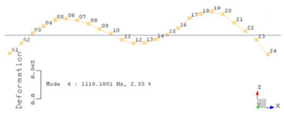 |  |
| 4 | 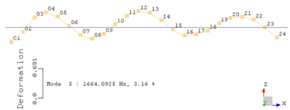 | 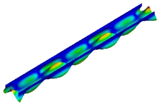 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricarte, A.; Meireles, J.; Inácio, O. Characterizing the Frequency Response of Compliant Materials by Laser Döppler Vibrometry Coupled Acoustic Excitation. Vibration 2021, 4, 64-74. https://doi.org/10.3390/vibration4010005
Ricarte A, Meireles J, Inácio O. Characterizing the Frequency Response of Compliant Materials by Laser Döppler Vibrometry Coupled Acoustic Excitation. Vibration. 2021; 4(1):64-74. https://doi.org/10.3390/vibration4010005
Chicago/Turabian StyleRicarte, Arlindo, José Meireles, and Octávio Inácio. 2021. "Characterizing the Frequency Response of Compliant Materials by Laser Döppler Vibrometry Coupled Acoustic Excitation" Vibration 4, no. 1: 64-74. https://doi.org/10.3390/vibration4010005
APA StyleRicarte, A., Meireles, J., & Inácio, O. (2021). Characterizing the Frequency Response of Compliant Materials by Laser Döppler Vibrometry Coupled Acoustic Excitation. Vibration, 4(1), 64-74. https://doi.org/10.3390/vibration4010005





