Experimental Study on Impact Force Identification on a Multi-Storey Tower Structure Using Different Transducers
Abstract
1. Introduction
2. Problem Formulation
2.1. Single Impact Force Reconstruction
- one impact is being applied at a time,
- structural responses are linear,
- the impact location is known.
2.2. Transfer Function
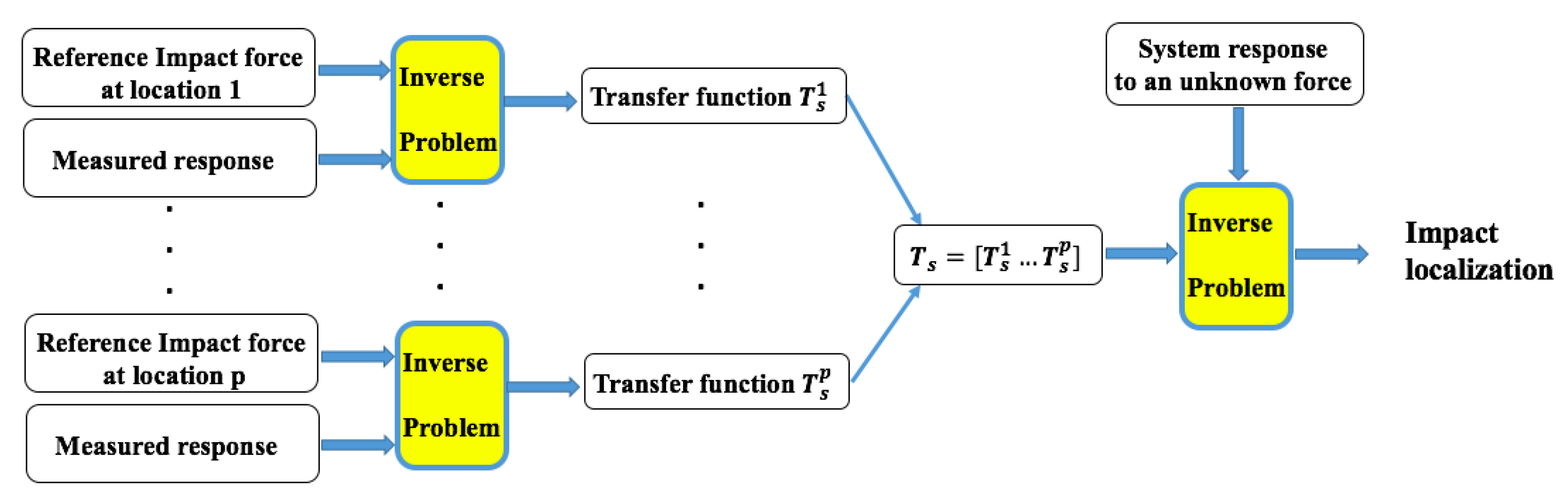
2.3. Impact Force Location
3. Experimental Set-Up
4. Results and Discussion
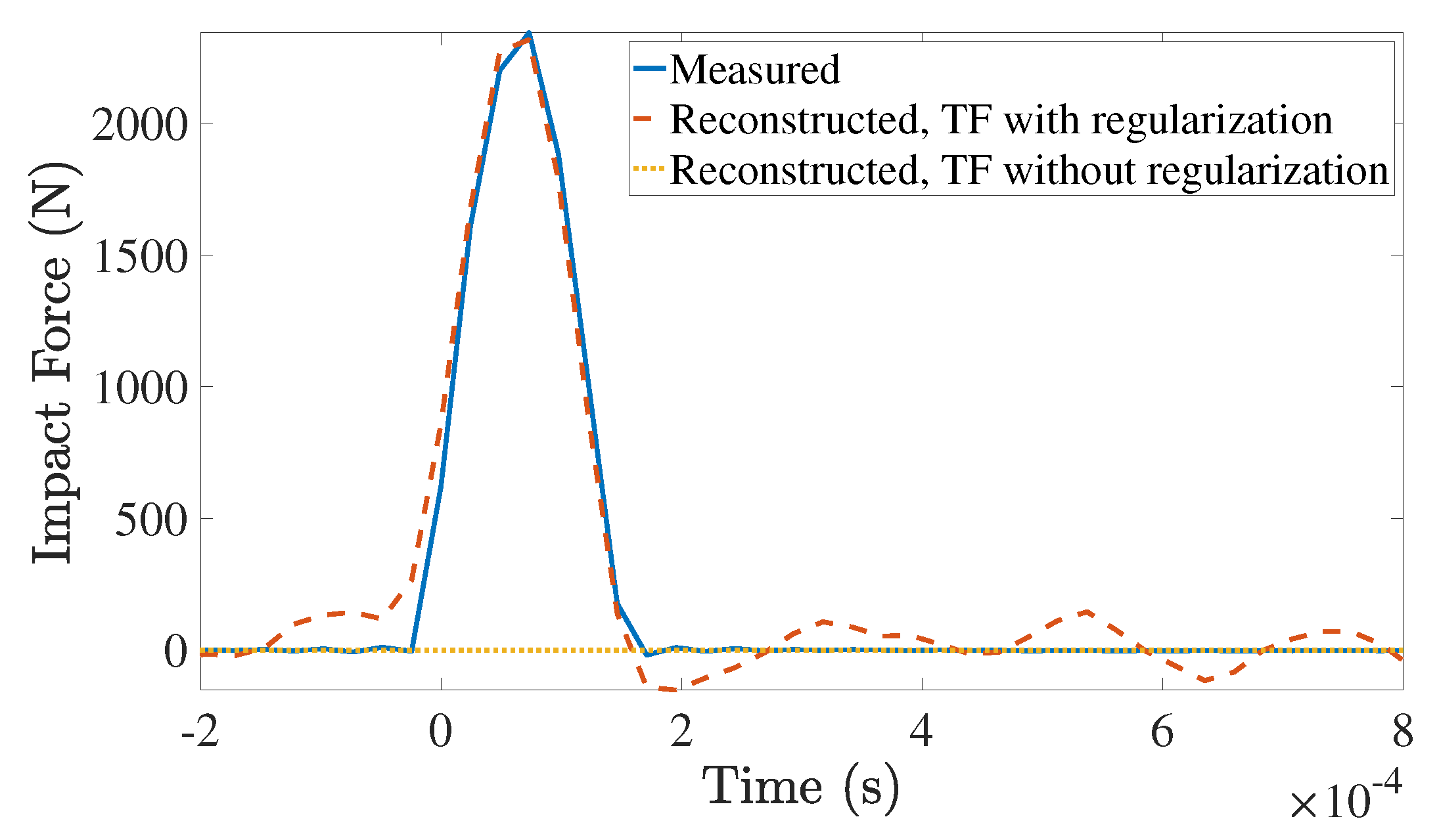
4.1. Effect of Regularization
4.2. Establishing the Transfer Function
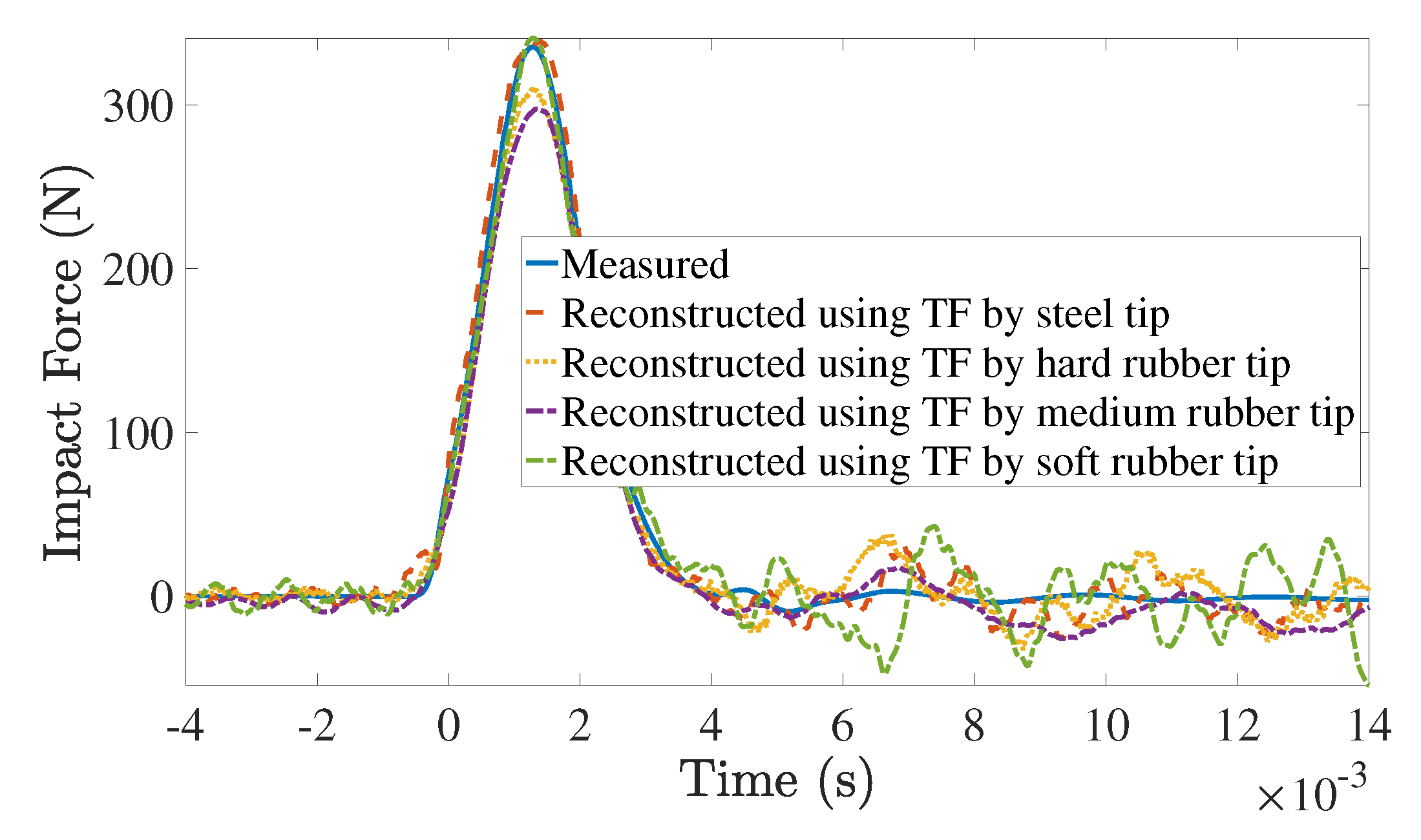
4.3. Influence of Sensor Type and Location
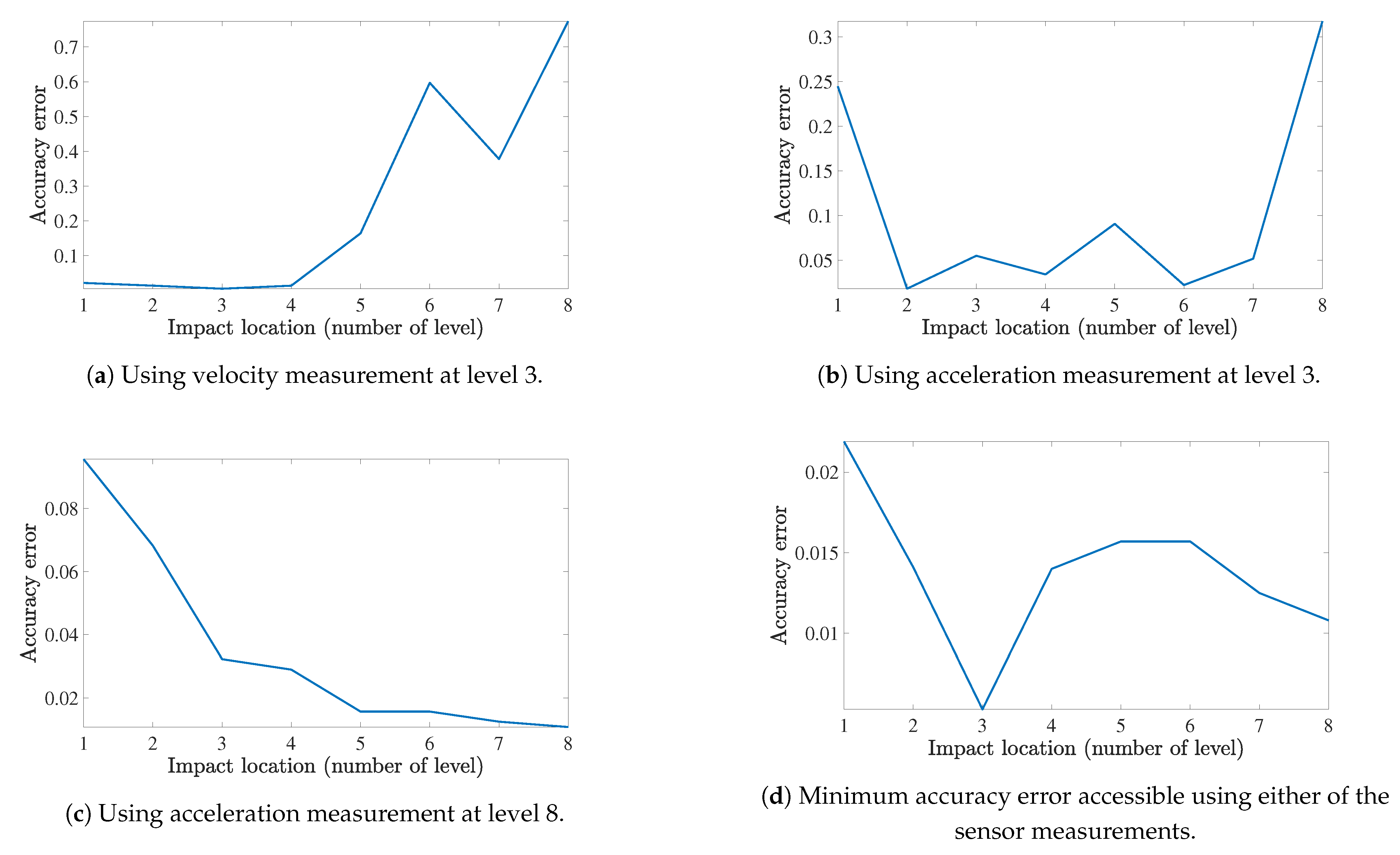
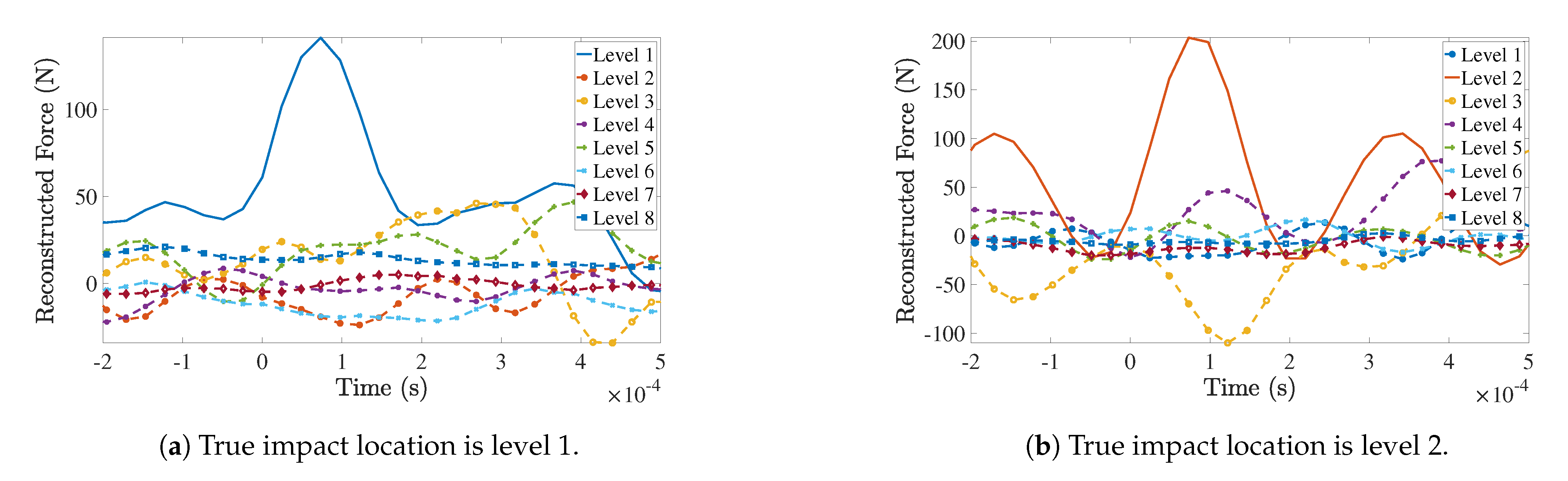
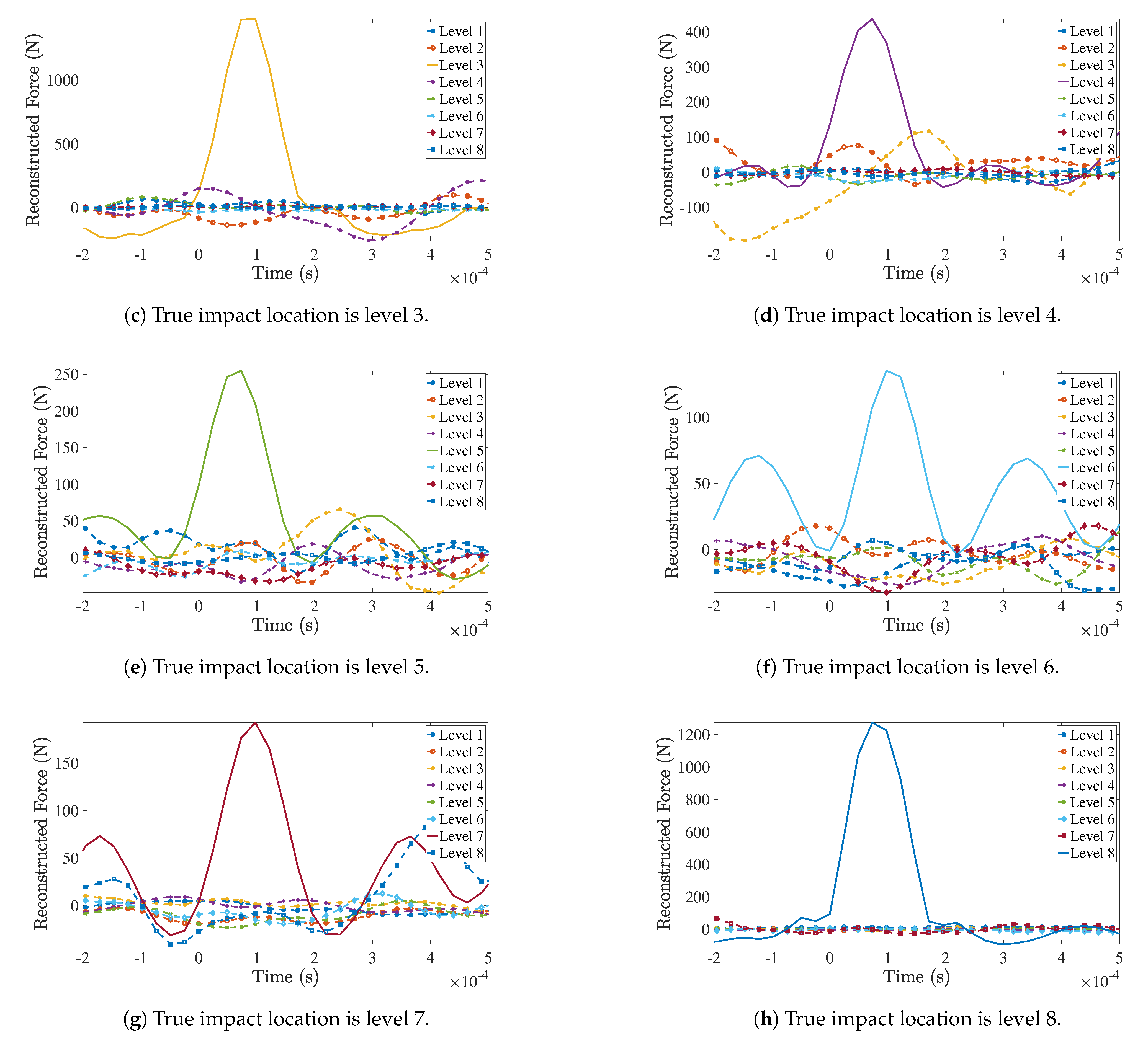
4.4. Impact Force Location
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Qiao, B.; Mao, Z.; Liu, J.; Zhao, Z.; Chen, X. Group sparse regularization for impact force identification in time domain. J. Sound Vib. 2019, 445, 44–63. [Google Scholar] [CrossRef]
- Qiu, B.; Zhang, M.; Li, X.; Qu, X.; Tong, F. Unknown impact force localisation and reconstruction in experimental plate structure using time-series analysis and pattern recognition. Int. J. Mech. Sci. 2020, 166, 105231. [Google Scholar] [CrossRef]
- Sung, D.U.; Oh, J.H.; Kim, C.G.; Hong, C.S. Impact monitoring of smart composite laminates using neural network and wavelet analysis. J. Intell. Mater. Syst. Struct. 2000, 11, 180–190. [Google Scholar] [CrossRef]
- LeClerc, J.; Worden, K.; Staszewski, W.J.; Haywood, J. Impact detection in an aircraft composite panel—A neural-network approach. J. Sound Vib. 2007, 299, 672–682. [Google Scholar] [CrossRef]
- Sarego, G.; Zaccariotto, M.; Galvanetto, U. Artificial neural networks for impact force reconstruction on composite plates. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 211–216. [Google Scholar]
- Sarego, G.; Zaccariotto, M.; Galvanetto, U. Artificial neural networks for impact force reconstruction on composite plates and relevant uncertainty propagation. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 38–47. [Google Scholar] [CrossRef]
- Jacquelin, E.; Bennani, A.; Hamelin, P. Force reconstruction: Analysis and regularization of a deconvolution problem. J. Sound Vib. 2003, 265, 81–107. [Google Scholar] [CrossRef]
- Kalhori, H.; Ye, L.; Mustapha, S.; Li, J. Impact force reconstruction on a concrete deck using a deconvolution approach. In Proceedings of the 8th Australasian Congress on Applied Mechanics: ACAM 8, Engineers Australia, Melbourne, Australia, 23–26 November 2014; p. 763. [Google Scholar]
- Kalhori, H.; Ye, L.; Mustapha, S.; Li, J.; Li, B. Reconstruction and analysis of impact forces on a steel-beam-reinforced concrete deck. Exp. Mech. 2016, 56, 1547–1558. [Google Scholar] [CrossRef]
- Kalhori, H.; Ye, L.; Mustapha, S. Inverse estimation of impact force on a composite panel using a single piezoelectric sensor. J. Intell. Mater. Syst. Struct. 2017, 28, 799–810. [Google Scholar] [CrossRef]
- Qiao, B.; Zhang, X.; Gao, J.; Liu, R.; Chen, X. Sparse deconvolution for the large-scale ill-posed inverse problem of impact force reconstruction. Mech. Syst. Signal Process. 2017, 83, 93–115. [Google Scholar]
- Kalhori, H.; Alamdari, M.M.; Ye, L. Automated algorithm for impact force identification using cosine similarity searching. Measurement 2018, 122, 648–657. [Google Scholar] [CrossRef]
- Tran, H.; Inoue, H. Development of wavelet deconvolution technique for impact force reconstruction: Application to reconstruction of impact force acting on a load-cell. Int. J. Impact Eng. 2018, 122, 137–147. [Google Scholar] [CrossRef]
- Kalhori, H.; Alamdari, M.M.; Li, B.; Halkon, B.; Hosseini, S.M.; Ye, L.; Li, Z. Concurrent Identification of Impact Location and Force Magnitude on a Composite Panel. Int. J. Struct. Stab. Dyn. 2020, 20, 2042004. [Google Scholar] [CrossRef]
- Hollandsworth, P.; Busby, H. Impact force identification using the general inverse technique. Int. J. Impact Eng. 1989, 8, 315–322. [Google Scholar] [CrossRef]
- Law, S.S.; Fang, Y. Moving force identification: Optimal state estimation approach. J. Sound Vib. 2001, 239, 233–254. [Google Scholar] [CrossRef]
- Lourens, E.; Reynders, E.; De Roeck, G.; Degrande, G.; Lombaert, G. An augmented Kalman filter for force identification in structural dynamics. Mech. Syst. Signal Process. 2012, 27, 446–460. [Google Scholar]
- Ding, Y.; Law, S.; Wu, B.; Xu, G.; Lin, Q.; Jiang, H.; Miao, Q. Average acceleration discrete algorithm for force identification in state space. Eng. Struct. 2013, 56, 1880–1892. [Google Scholar]
- Wang, T.; Wan, Z.; Wang, X.; Hu, Y. A novel state space method for force identification based on the Galerkin weak formulation. Comput. Struct. 2015, 157, 132–141. [Google Scholar] [CrossRef]
- Liu, J.; Xie, J.; Li, B.; Hu, B. Regularized Cubic B-Spline Collocation Method With Modified L-Curve Criterion for Impact Force Identification. IEEE Access 2020, 8, 36337–36349. [Google Scholar] [CrossRef]
- Kreitinger, T.; Wang, M.; Schreyer, H. Non-parametric force identification from structural response. Soil Dyn. Earthq. Eng. 1992, 11, 269–277. [Google Scholar]
- Carne, T.G.; Mayes, R.L.; Bateman, V.I. Force Reconstruction Using the Sum of Weighted Accelerations Technique—Max-Flat Procedure; Technical Report; Sandia National Labs.: Albuquerque, NM, USA, 1993. [Google Scholar]
- Allen, M.; Carne, T. Comparison of inverse structural filter (ISF) and sum of weighted accelerations (SWAT) time domain force identification methods. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 14th AIAA/ASME/AHS Adaptive Structures Conference 7th, Newport, RI, USA, 1–4 May 2006; p. 1885. [Google Scholar]
- Shiozaki, H.; Geluk, T.; Daenen, F.; Iwanaga, Y.; Van Herbruggen, J. Time-Domain Transfer Path Analysis for Transient Phenomena Applied to Tip-In/Tip-Out (Shock & Jerk); Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Yan, G.; Sun, H. A non-negative Bayesian learning method for impact force reconstruction. J. Sound Vib. 2019, 457, 354–367. [Google Scholar] [CrossRef]
- Liu, Y.; Shepard, W.S., Jr. Dynamic force identification based on enhanced least squares and total least-squares schemes in the frequency domain. J. Sound Vib. 2005, 282, 37–60. [Google Scholar] [CrossRef]
- Thite, A.; Thompson, D. The quantification of structure-borne transmission paths by inverse methods. Part 2: Use of regularization techniques. J. Sound Vib. 2003, 264, 433–451. [Google Scholar] [CrossRef]
- Nordström, L.J. A dynamic programming algorithm for input estimation on linear time-variant systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 6407–6427. [Google Scholar] [CrossRef]
- Ronasi, H.; Johansson, H.; Larsson, F. A numerical framework for load identification and regularization with application to rolling disc problem. Comput. Struct. 2011, 89, 38–47. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Identification of structural stiffness and excitation forces in time domain using noncontact vision-based displacement measurement. J. Sound Vib. 2017, 406, 15–28. [Google Scholar] [CrossRef]
- Pan, C.D.; Yu, L.; Liu, H.L. Identification of moving vehicle forces on bridge structures via moving average Tikhonov regularization. Smart Mater. Struct. 2017, 26, 085041. [Google Scholar] [CrossRef]
- Leclere, Q.; Pezerat, C.; Laulagnet, B.; Polac, L. Indirect measurement of main bearing loads in an operating diesel engine. J. Sound Vib. 2005, 286, 341–361. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Han, X.; Jiang, C.; Yu, D. A novel computational inverse technique for load identification using the shape function method of moving least square fitting. Comput. Struct. 2014, 144, 127–137. [Google Scholar] [CrossRef]
- Miao, B.; Zhou, F.; Jiang, C.; Chen, X.; Yang, S. A comparative study of regularization method in structure load identification. Shock Vib. 2018, 2018. [Google Scholar] [CrossRef]
- Uhl, T. The inverse identification problem and its technical application. Arch. Appl. Mech. 2007, 77, 325–337. [Google Scholar] [CrossRef]
- Nordberg, T.P.; Gustafsson, I. Using QR factorization and SVD to solve input estimation problems in structural dynamics. Comput. Methods Appl. Mech. Eng. 2006, 195, 5891–5908. [Google Scholar] [CrossRef]
- Nordberg, T.P.; Gustafsson, I. Dynamic regularization of input estimation problems by explicit block inversion. Comput. Methods Appl. Mech. Eng. 2006, 195, 5877–5890. [Google Scholar] [CrossRef]
- Feng, D.; Sun, H.; Feng, M.Q. Simultaneous identification of bridge structural parameters and vehicle loads. Comput. Struct. 2015, 157, 76–88. [Google Scholar] [CrossRef]
- Liu, J.; Meng, X.; Jiang, C.; Han, X.; Zhang, D. Time-domain Galerkin method for dynamic load identification. Int. J. Numer. Methods Eng. 2016, 105, 620–640. [Google Scholar] [CrossRef]
- Qiao, B.; Zhang, X.; Wang, C.; Zhang, H.; Chen, X. Sparse regularization for force identification using dictionaries. J. Sound Vib. 2016, 368, 71–86. [Google Scholar] [CrossRef]
- Liu, J.; Qiao, B.; He, W.; Yang, Z.; Chen, X. Impact force identification via sparse regularization with generalized minimax-concave penalty. J. Sound Vib. 2020, 484, 115530. [Google Scholar] [CrossRef]
- Samagassi, S.; Jacquelin, E.; Khamlichi, A.; Sylla, M. Bayesian sparse regularization for multiple force identification and location in time domain. Inverse Probl. Sci. Eng. 2019, 27, 1221–1262. [Google Scholar] [CrossRef]
- Pan, C.; Ye, X.; Zhou, J.; Sun, Z. Matrix regularization-based method for large-scale inverse problem of force identification. Mech. Syst. Signal Process. 2020, 140, 106698. [Google Scholar] [CrossRef]
- Chen, Z.; Chan, T.H.; Yu, L. Comparison of regularization methods for moving force identification with ill-posed problems. J. Sound Vib. 2020, 478, 115349. [Google Scholar] [CrossRef]
- Boukria, Z.; Perrotin, P.; Bennani, A. Experimental impact force location and identification using inverse problems: Application for a circular plate. Int. J. Mech. 2011, 5, 48–55. [Google Scholar]
- Hundhausen, R.J.; Adams, D.E.; Derriso, M. Impact loads identification in standoff metallic thermal protection system panels. J. Intell. Mater. Syst. Struct. 2007, 18, 531–541. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Beam length | 2 m |
| Beam cross-section | 65.3 × 35 mm |
| Beam thickness | 2.5 mm |
| Lumped masses dimension | 128× 98 × 50 mm |
| Lumped masses weight | 4 kg |
| Lumped masses distances | 250 mm |
| Impact Location | Measured Response | ||
|---|---|---|---|
| Vel. at Level 3 | Acc. at Level 3 | Acc. at Level 8 | |
| Level 1 | 0.0219 | 0.2448 | 0.0956 |
| Level 2 | 0.0141 | 0.0182 | 0.0682 |
| Level 3 | 0.0053 | 0.0551 | 0.0323 |
| Level 4 | 0.0140 | 0.0342 | 0.0290 |
| Level 5 | 0.1644 | 0.0908 | 0.0157 |
| Level 6 | 0.5969 | 0.0223 | 0.0157 |
| Level 7 | 0.3779 | 0.0518 | 0.0125 |
| Level 8 | 0.7738 | 0.3177 | 0.0108 |
| Hammer Tip | Impact Location | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Soft rubber | 0.0974 | 0.0516 | 0.0339 | 0.0576 | 0.0482 | 0.0642 | 0.0563 | 0.0604 |
| Medium rubber | 0.0863 | 0.0502 | 0.0590 | 0.0563 | 0.0967 | 0.0902 | 0.1031 | 0.0932 |
| Hard rubber | 0.0472 | 0.0239 | 0.0558 | 0.0404 | 0.0558 | 0.3282 | 0.0464 | 0.0421 |
| Measured Response | Impact Location | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Vel. at level 3 | 0.9581 | 0.9370 | 0.2522 | 0.9395 | 0.9608 | 1.0389 | 0.9821 | 1.0117 |
| Acc. at level 3 | 0.9303 | 0.8922 | 0.4225 | 0.8439 | 0.9145 | 0.9701 | 0.9706 | 0.9883 |
| Acc. at level 8 | 1.0055 | 0.9861 | 0.9868 | 1.0233 | 0.9899 | 0.9831 | 0.9164 | 0.1559 |
| Vel. at l3 and Acc. at l8 | 1.0093 | 0.9842 | 0.9934 | 1.0149 | 0.9992 | 1.0375 | 0.9067 | 0.1163 |
| Acc. at l3 and Acc. at l8 | 0.8947 | 0.8839 | 0.3038 | 0.7664 | 0.8968 | 0.9948 | 0.8844 | 0.0991 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalhori, H.; Tashakori, S.; Halkon, B. Experimental Study on Impact Force Identification on a Multi-Storey Tower Structure Using Different Transducers. Vibration 2021, 4, 101-116. https://doi.org/10.3390/vibration4010009
Kalhori H, Tashakori S, Halkon B. Experimental Study on Impact Force Identification on a Multi-Storey Tower Structure Using Different Transducers. Vibration. 2021; 4(1):101-116. https://doi.org/10.3390/vibration4010009
Chicago/Turabian StyleKalhori, Hamed, Shabnam Tashakori, and Benjamin Halkon. 2021. "Experimental Study on Impact Force Identification on a Multi-Storey Tower Structure Using Different Transducers" Vibration 4, no. 1: 101-116. https://doi.org/10.3390/vibration4010009
APA StyleKalhori, H., Tashakori, S., & Halkon, B. (2021). Experimental Study on Impact Force Identification on a Multi-Storey Tower Structure Using Different Transducers. Vibration, 4(1), 101-116. https://doi.org/10.3390/vibration4010009






