Simultaneous Regression and Selection in Nonlinear Modal Model Identification
Abstract
1. Introduction
2. Theory
2.1. Nonlinear Dynamic Equations of Motion
2.2. Generating Static Force-Displacement Data
2.3. Estimating the Nonlinear Stiffness Terms
2.3.1. Least Squares Estimator
2.3.2. Least Absolute Shrinkage and Selection Operator (LASSO)
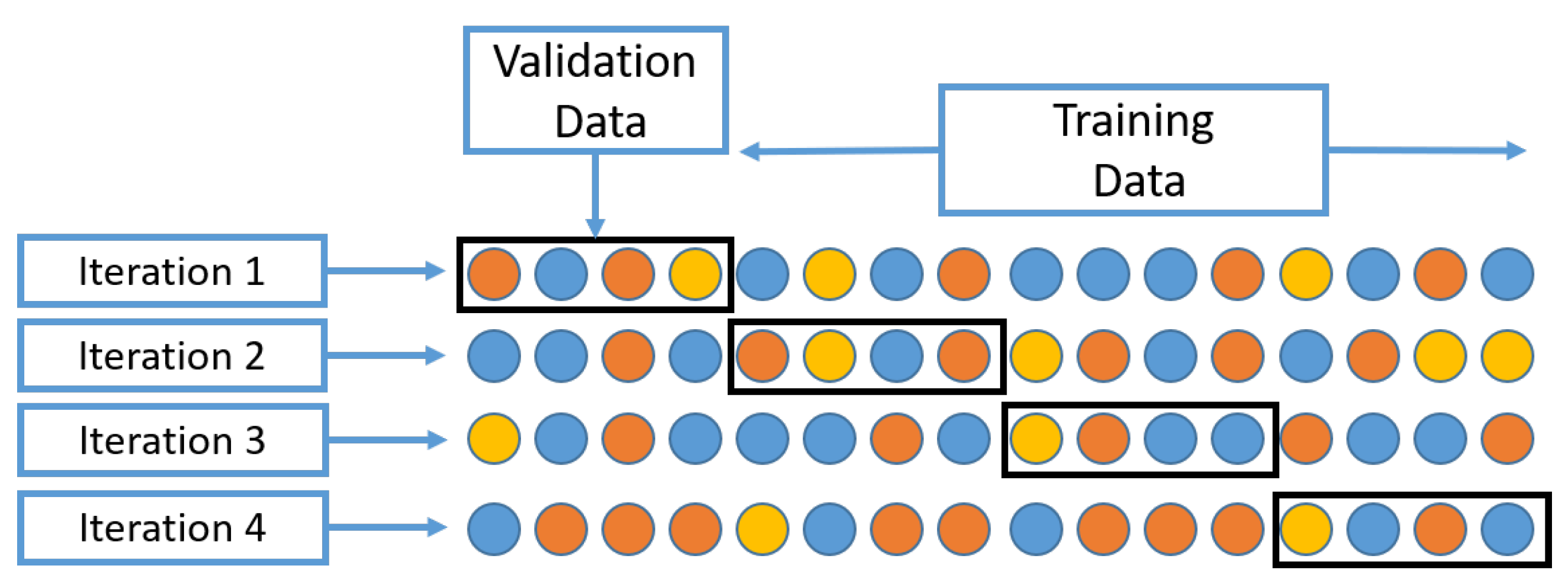
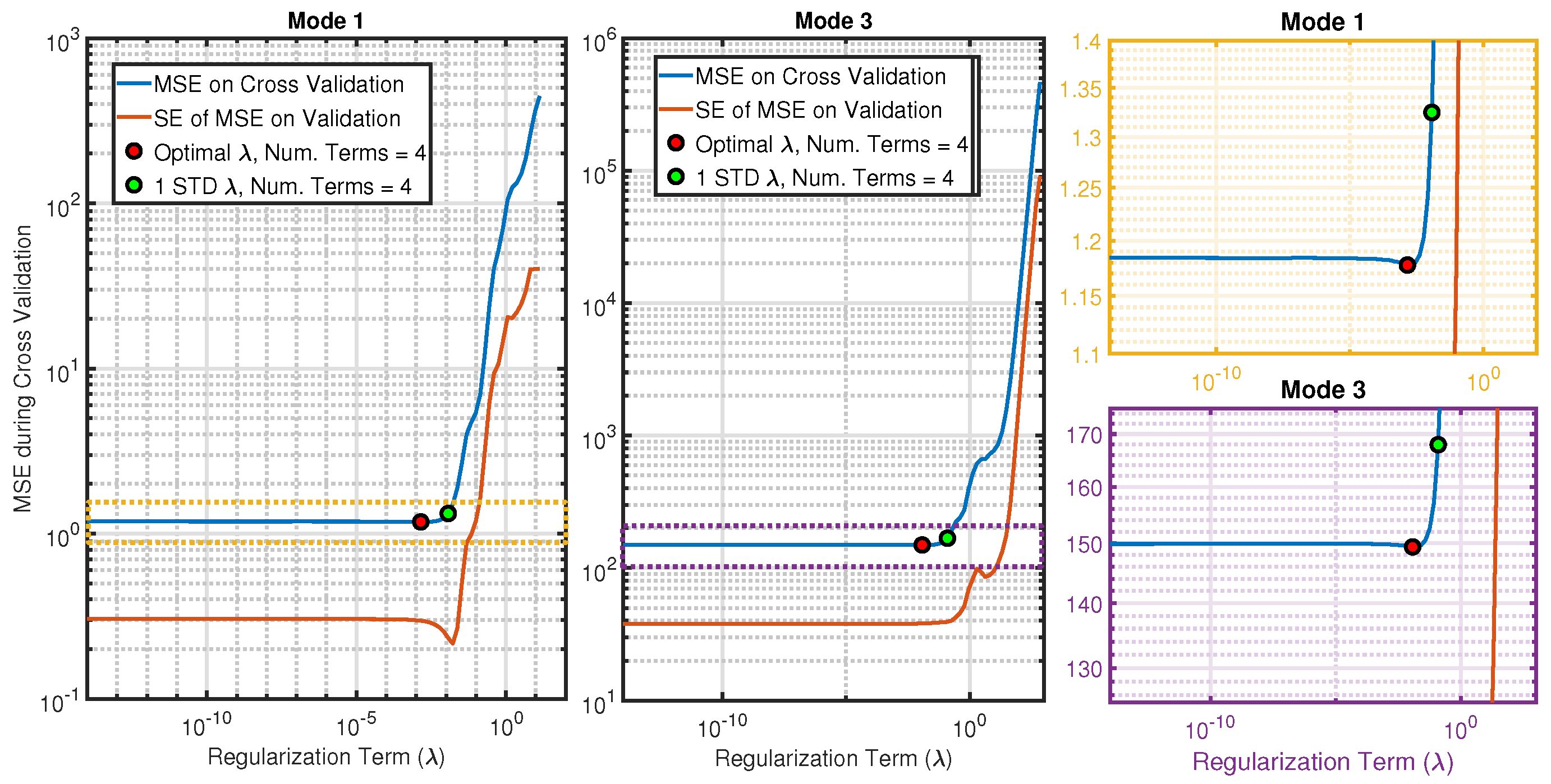
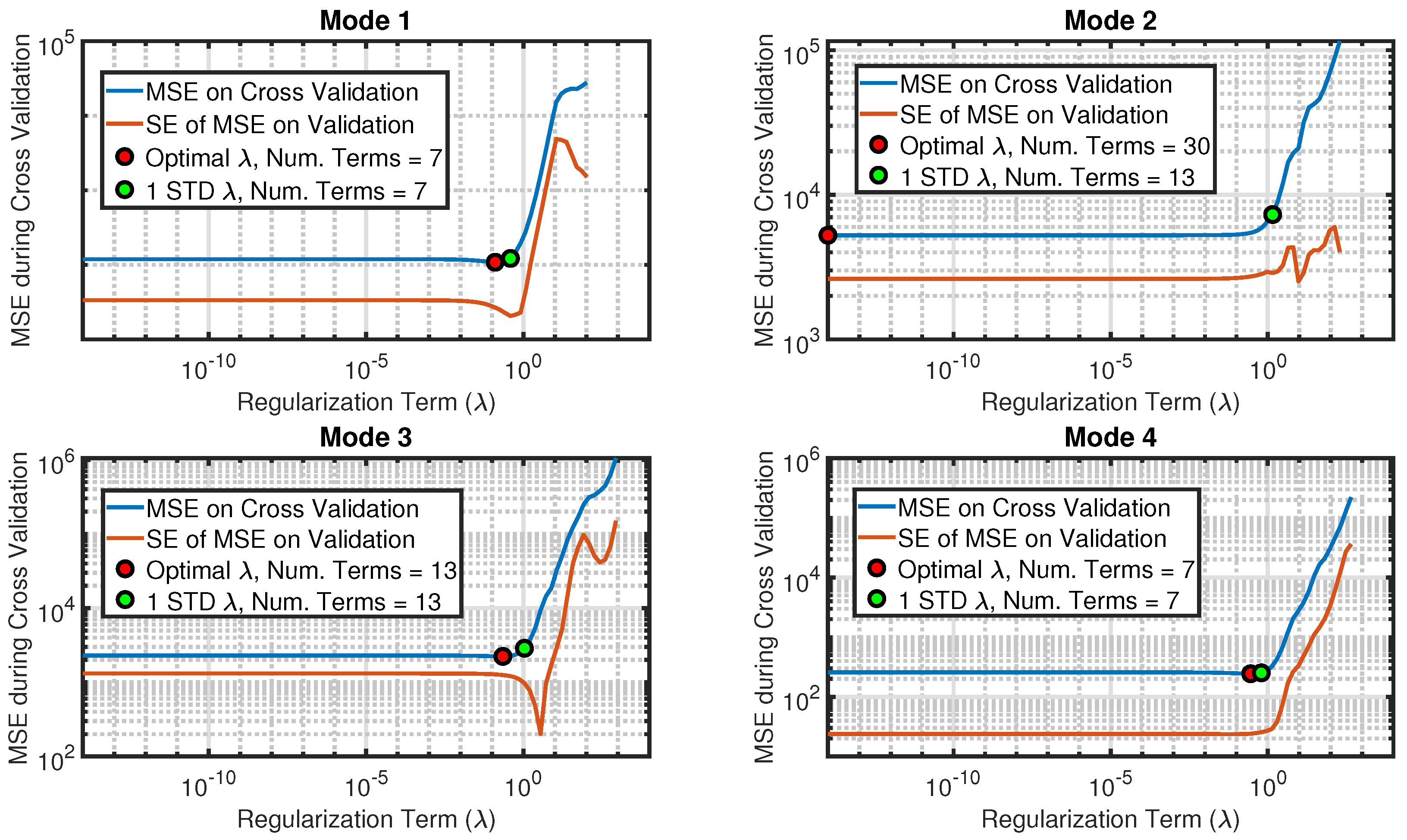
2.3.3. Repeated K-Fold Cross-Validation and Hyper-Parameter Selection
2.3.4. Discussion on Computational Cost
3. Numerical Examples
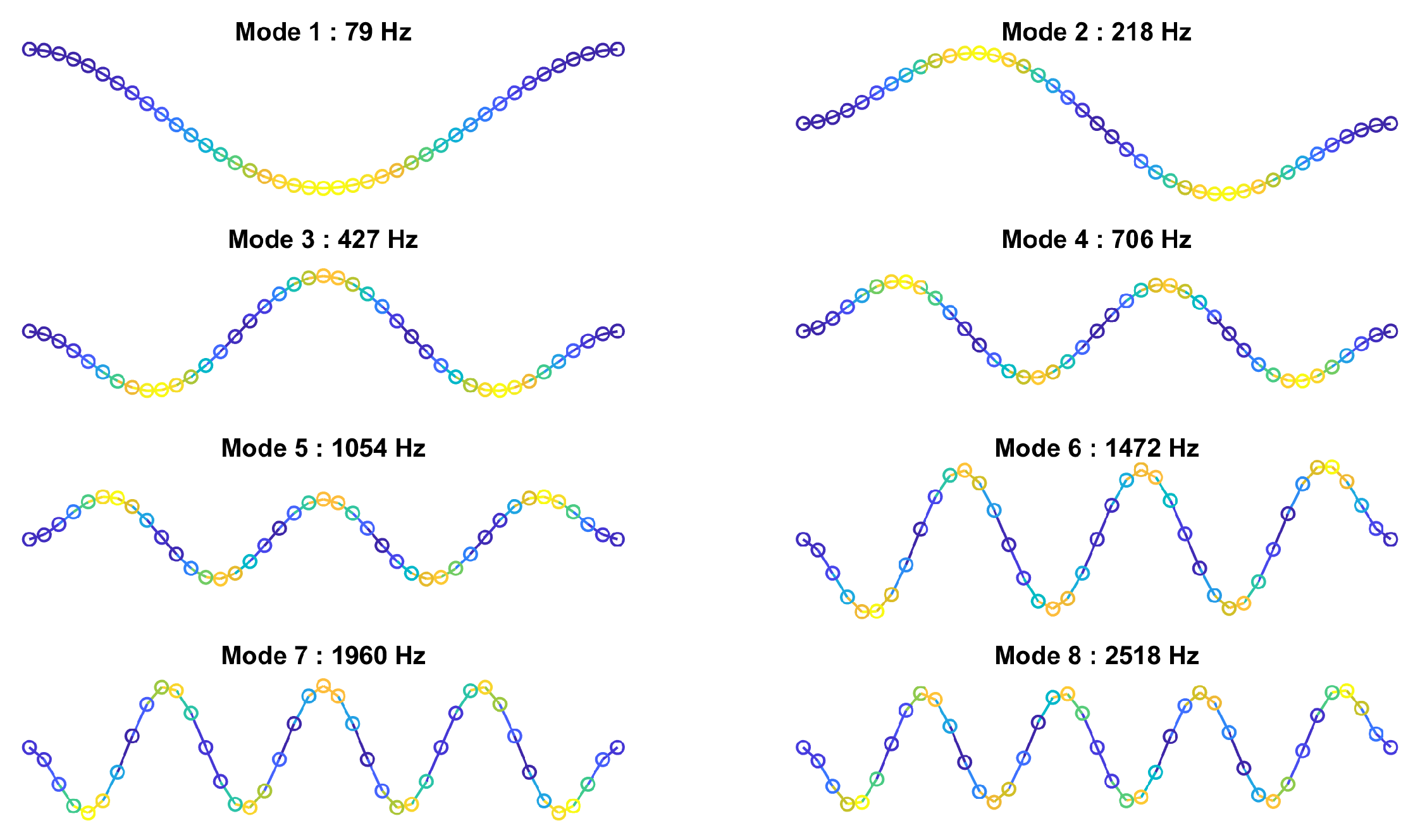
3.1. Flat Beam
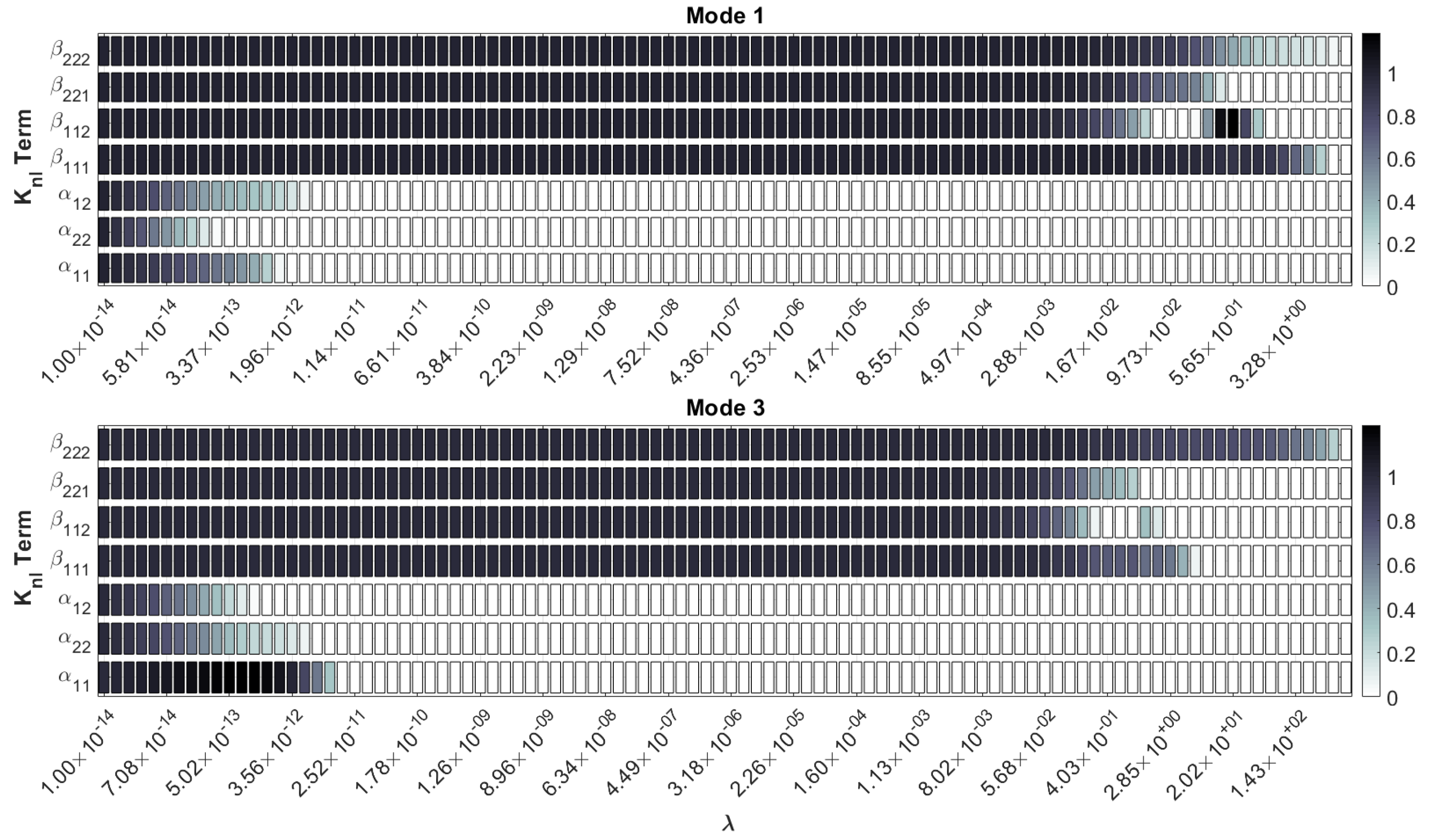
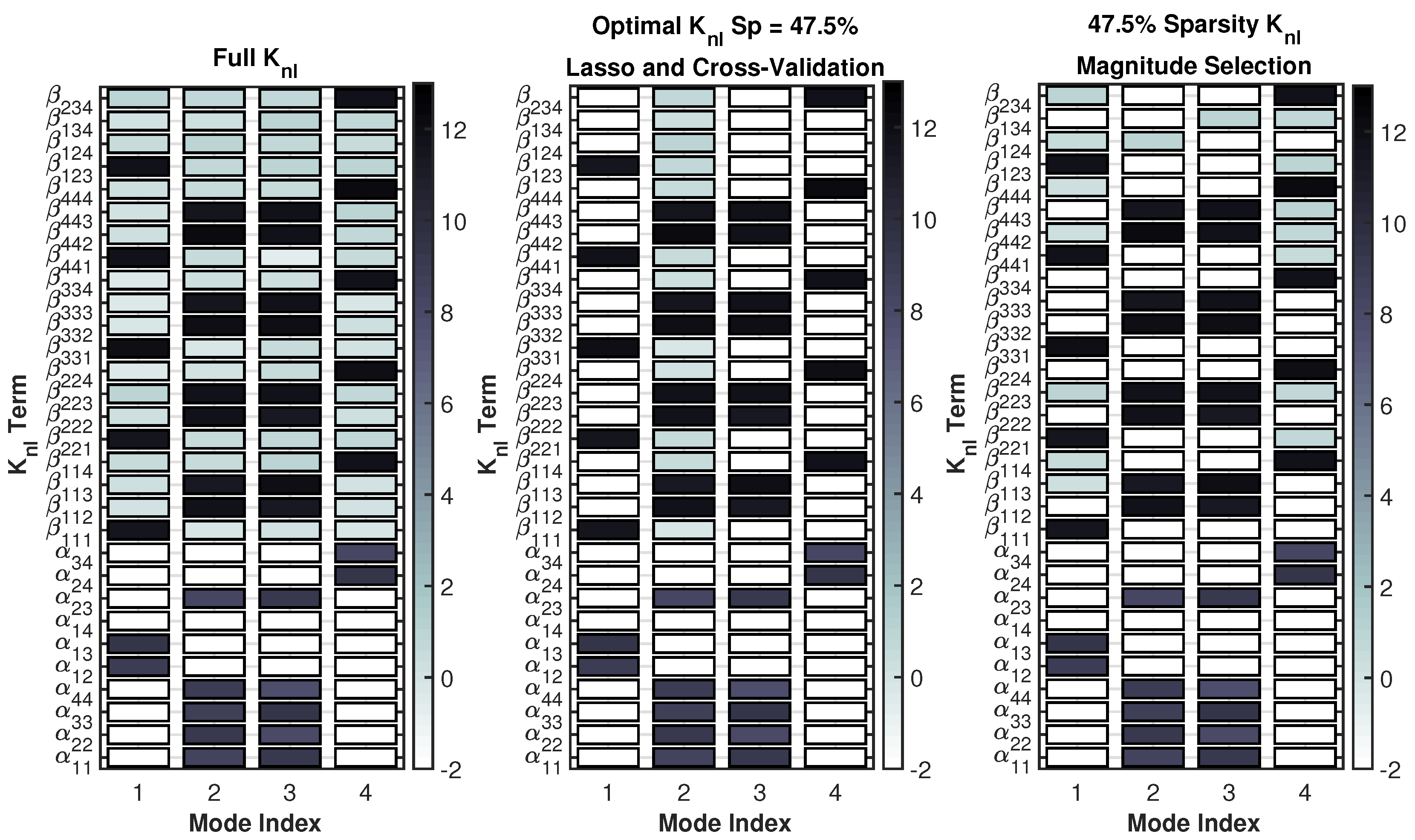
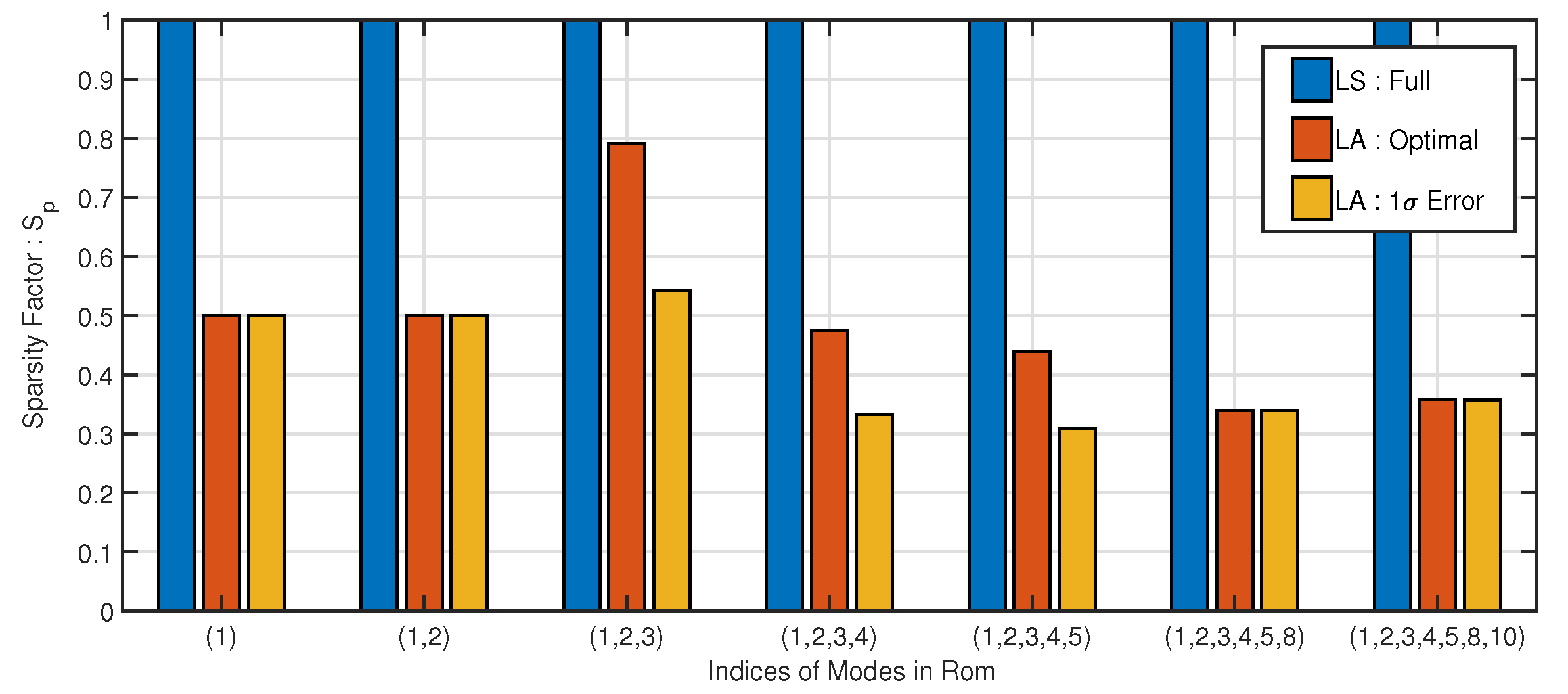
3.1.1. ROM Training and Nonlinear Stiffness Terms
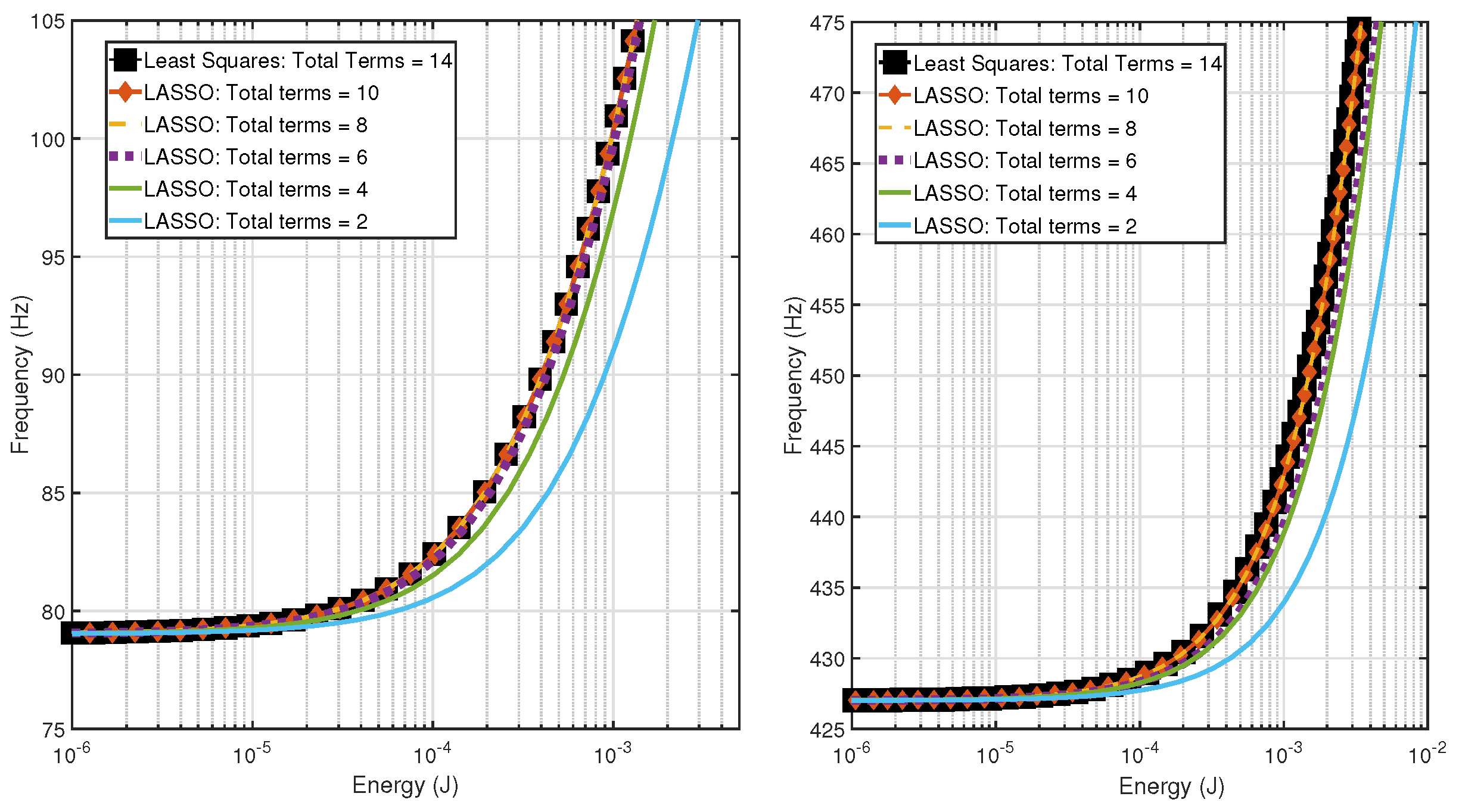
3.1.2. Evaluation of Accuracy
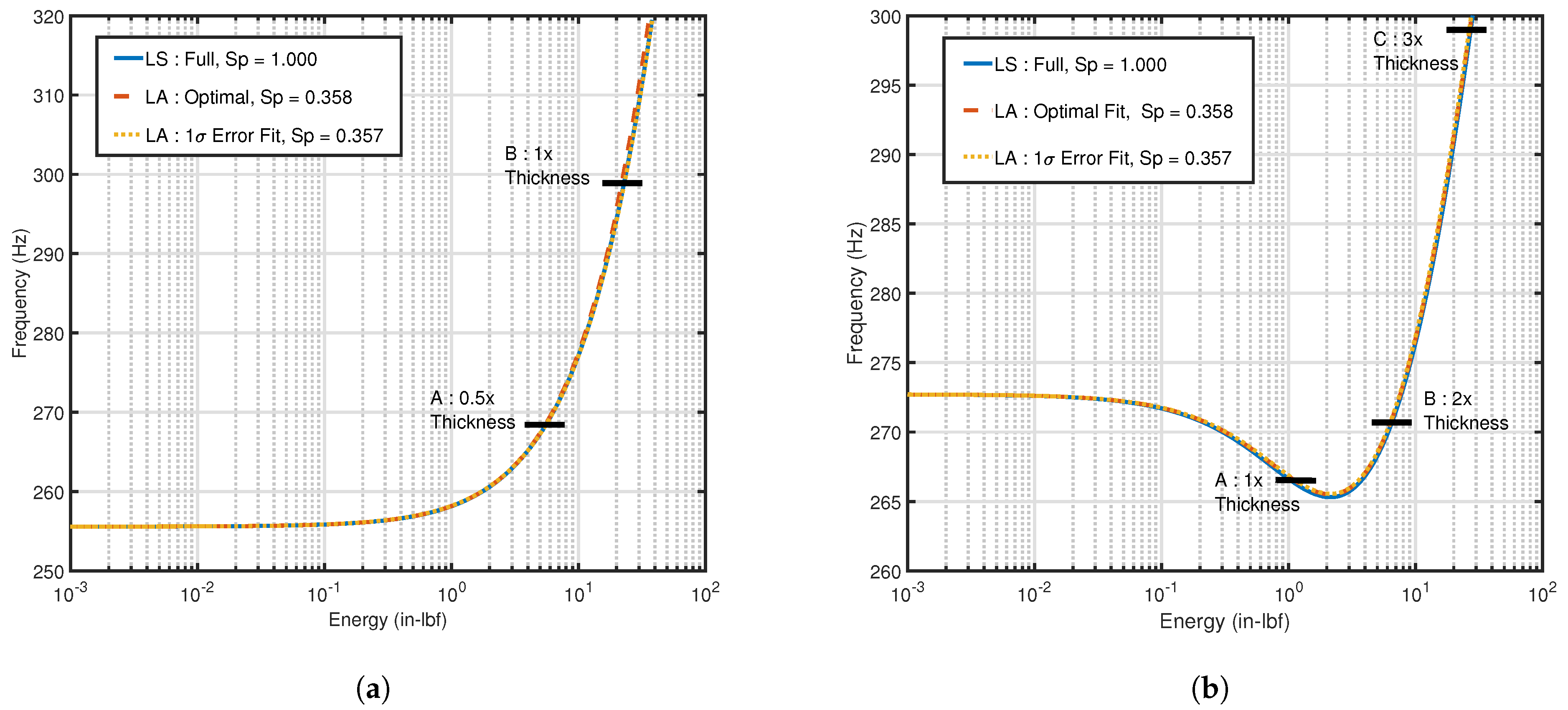
3.2. Curved Panel
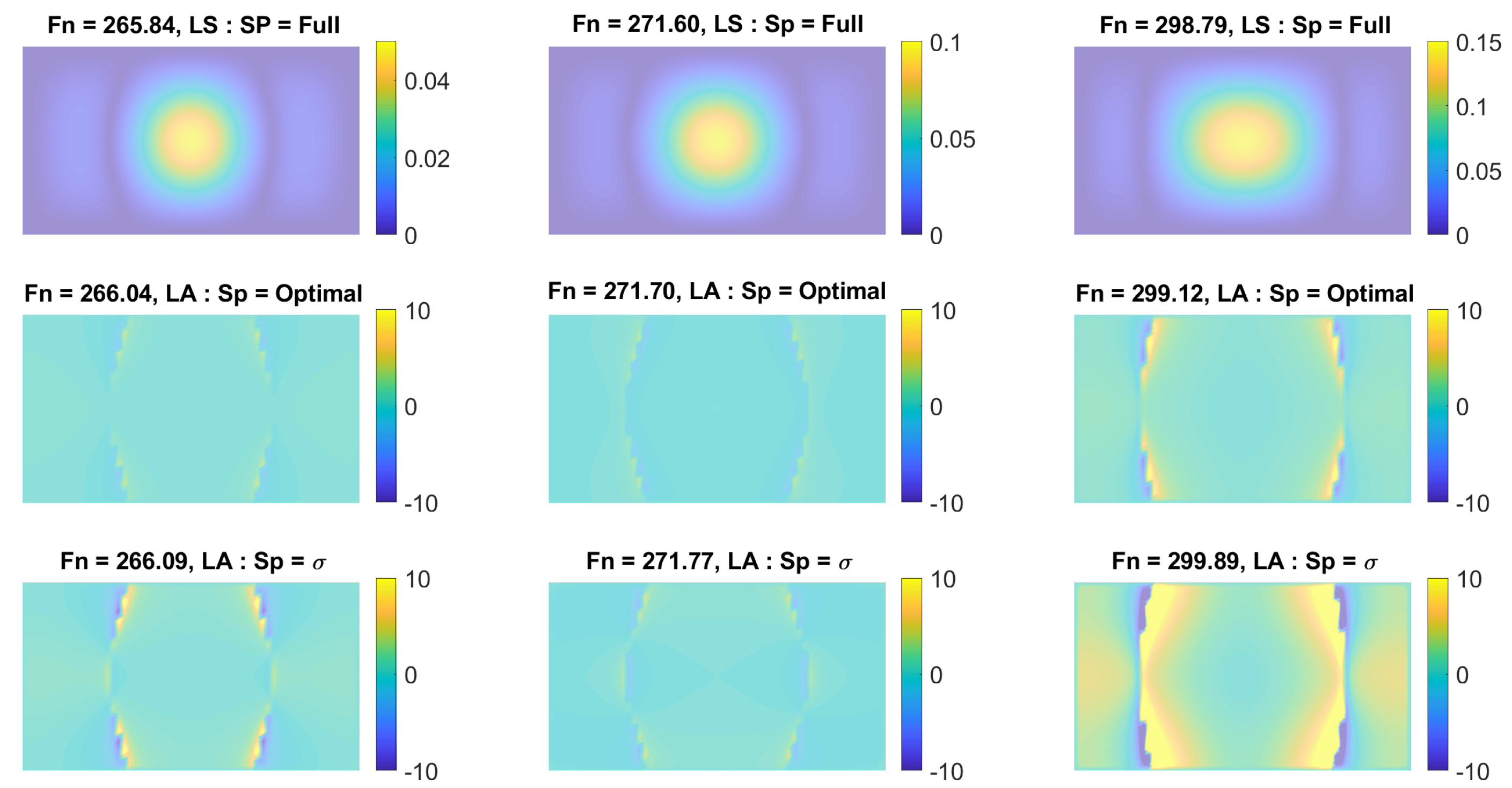
3.2.1. Training and Nonlinear Stiffness Identification
3.2.2. Dynamic Accuracy Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis; Wiley: New York, NY, USA, 1974; Volume 4. [Google Scholar]
- Shi, Y.; Mei, C. A Finite Element Time Domain Modal Formulation for Large Amplitude Free Vibrations of Beams and Plates. J. Sound Vib. 1996, 193, 453–464. [Google Scholar] [CrossRef]
- Muravyov, A.A.; Rizzi, S.A. Determination of nonlinear stiffness with application to random vibration of geometrically nonlinear structures. Comput. Struct. 2003, 81, 1513–1523. [Google Scholar] [CrossRef]
- Perez, R.; Wang, X.Q.; Mignolet, M.P. Nonintrusive structural dynamic reduced order modeling for large deformations: Enhancements for complex structures. J. Comput. Nonlinear Dyn. 2014. [Google Scholar] [CrossRef]
- Mignolet, M.; Przekop, A.; Rizzi, S.; Spottswood, M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometricstructures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- McEwan, M.; Wright, J.; Cooper, J.; Leung, A. Combined Modal/Finite Element Analysis Technique for the Dynamic Response of a Non-linear Beam to Harmonic Excitation. J. Sound Vib. 2001, 243, 601–624. [Google Scholar] [CrossRef]
- McEwan, M.; Wright, J.; Cooper, J.; Leung, A. A finite element/modal technique for nonlinear plate and stiffened panel response prediction. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 1595. [Google Scholar]
- Hollkamp, J.J.; Spottswood, M.S.; Gordon, R.W. Nonlinear modal models for sonic fatigue response prediction: A comparison of methods. Sound Vib. 2005, 284, 1145–1163. [Google Scholar] [CrossRef]
- Hollkamp, J.J.; Gordon, R.W. Modeling Membrane Displacements in the Sonic Fatigue Response Prediction Problem. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005. [Google Scholar]
- Rizzi, S.A.; Przekop, A. System identification-guided basis selection for reduced-order nonlinear response analysis. J. Sound Vib. 2008, 315, 467–485. [Google Scholar] [CrossRef]
- Gordon, R.W.; Hollkamp, J.J. Reduced-Order Models for Acoustic Response Prediction; Technical, Tech Report: AFRL-RB-WP-TR-2011-3040; Air Force Research Laboratory, Wright-Patterson AFB: Dayton, OH, USA, 2011. [Google Scholar]
- Nicolaidou, E.; Melanthuru, V.R.; Hill, T.L.; Neild, S.A. Accounting for Quasi-Static Coupling in Nonlinear Dynamic Reduced-Order Models. J. Comput. Nonlinear Dyn. 2020, 15. [Google Scholar] [CrossRef]
- Shen, Y.; Béreux, N.; Frangi, A.; Touzé, C. Reduced order models for geometrically nonlinear structures: Assessment of implicit condensation in comparison with invariant manifold approach. Eur. J. Mech. A/Solids 2021, 86, 104165. [Google Scholar] [CrossRef]
- Wang, X.; Mignolet, M.P. Uncertainty Quantification of Nonlinear Stiffness Coefficients in Non-Intrusive Reduced Order Models. In Proceedings of the 38th International Modal Analysis Conference (IMAC XXXVIII), Orlando, FL, USA, 10–13 February 2020. [Google Scholar]
- Dong, H.; Chen, K.; Linderoth, J. Regularization vs. Relaxation: A conic optimization perspective of statistical variable selection. arXiv 2015, arXiv:1510.06083. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Kuether, R.J.; Deaner, B.; Hollkamp, J.J.; Allen, M.S. Evaluation of Geometrically Nonlinear Reduced-Order Models with Nonlinear Normal Modes. AIAA J. 2015, 53, 3273–3285. [Google Scholar] [CrossRef]
- VanDamme, C.I.; Allen, M.S. Using nnms to evaluate reduced order models of curved beam. In Rotating Machinery, Hybrid Test Methods, Vibro-Acoustics & Laser Vibrometry, Volume 8; Springer: Berlin/Heidelberg, Germany, 2016; pp. 457–469. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef] [PubMed]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Boston, MA, USA, 2009; pp. 532–538. [Google Scholar]
- Gordon, R.; Hollkamp, J. Reduced-Order Models for Acoustic Response Prediction of a Curved Panel. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Structures, Structural Dynamics, and Materials and Co-located Conferences, Denver, CO, USA, 4–7 April 2011. [Google Scholar] [CrossRef]
- Kuether, R.J.; Allen, M.S. Validation of Nonlinear Reduced Order Models with Time Integration Targeted at Nonlinear Normal Modes. In Nonlinear Dynamics, Volume 1; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Kerschen, G.; Peeters, M.; Vakakis, A.F.; Golinval, J.C. Nonlinear normal modes, Part I: A useful framework for the structural dynamicist. Mech. Syst. Signal Process. 2009, 23, 170–194. [Google Scholar] [CrossRef]
- VanDamme, C.I.; Moldenhauer, B.; Allen, M.S.; Hollkamp, J.J. Computing Nonlinear Normal Modes of Aerospace Structures Using the Multi-harmonic Balance Method. In Nonlinear Dynamics, Volume 1; Springer: Berlin/Heidelberg, Germany, 2018; pp. 247–259. [Google Scholar]
- Kuether, R.J.; Allen, M.S. A numerical approach to directly compute nonlinear normal modes of geometrically nonlinear finite element models. Mech. Syst. Signal Process. 2014, 46, 1–15. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Damme, C.; Madrid, A.; Allen, M.; Hollkamp, J. Simultaneous Regression and Selection in Nonlinear Modal Model Identification. Vibration 2021, 4, 232-247. https://doi.org/10.3390/vibration4010016
Van Damme C, Madrid A, Allen M, Hollkamp J. Simultaneous Regression and Selection in Nonlinear Modal Model Identification. Vibration. 2021; 4(1):232-247. https://doi.org/10.3390/vibration4010016
Chicago/Turabian StyleVan Damme, Christopher, Alecio Madrid, Matthew Allen, and Joseph Hollkamp. 2021. "Simultaneous Regression and Selection in Nonlinear Modal Model Identification" Vibration 4, no. 1: 232-247. https://doi.org/10.3390/vibration4010016
APA StyleVan Damme, C., Madrid, A., Allen, M., & Hollkamp, J. (2021). Simultaneous Regression and Selection in Nonlinear Modal Model Identification. Vibration, 4(1), 232-247. https://doi.org/10.3390/vibration4010016





