Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions
Abstract
1. Introduction
2. Nonlocal Elasticity Theory
Hamilton’s Principle
3. Analytical Solution
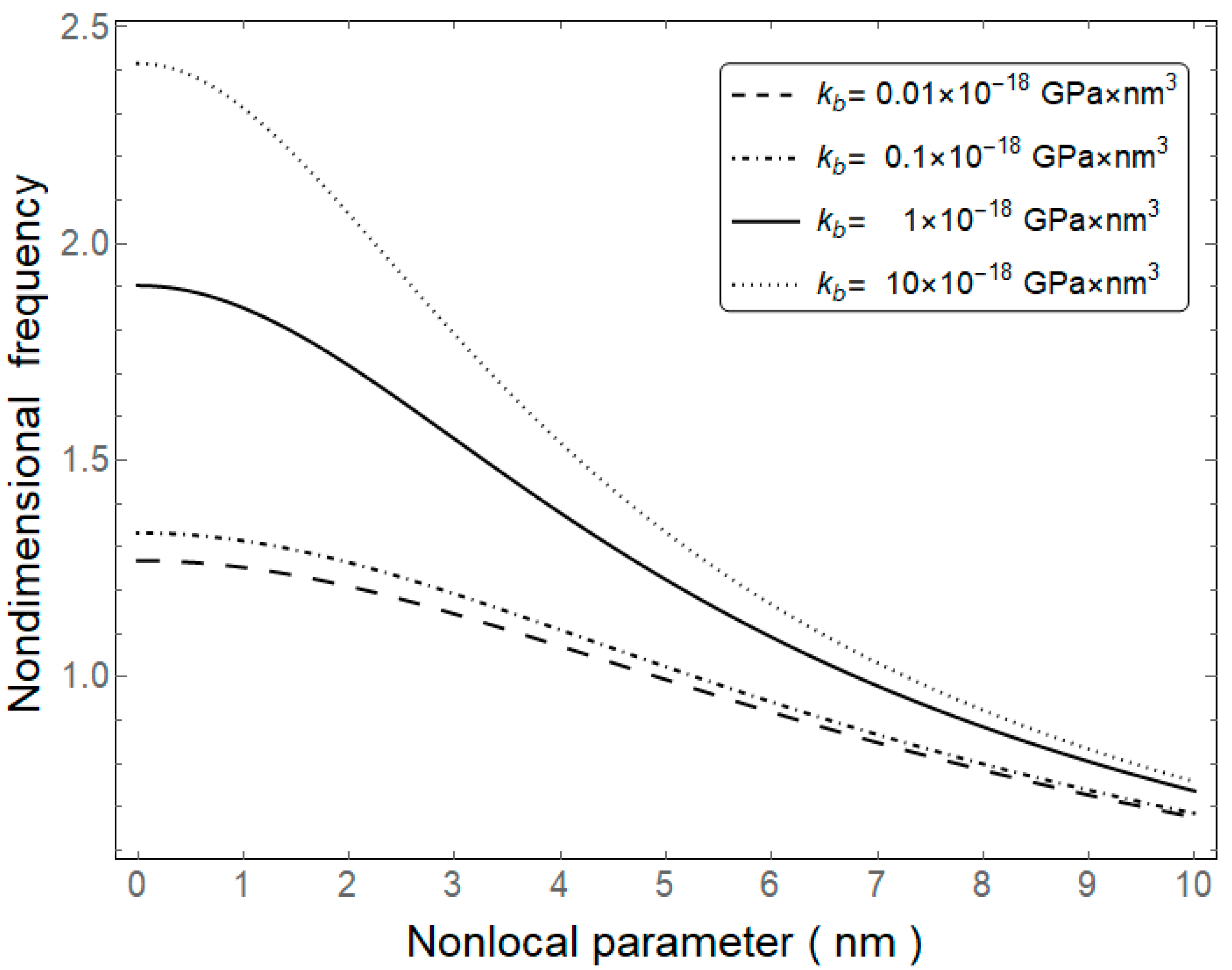
4. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Chopra, N.G.; Zettl, A. Measurement of the elastic modulus of a multi-wall boron nitride nanotube. Solid State Commun. 1998, 105, 297–300. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Tang, C.; Golberg, D. Engineering of electronic structure of boron-nitride nanotubes by covalent functionalization. Phys. Rev. B 2006, 74, 153413. [Google Scholar] [CrossRef]
- Wang, Z.L.; Dai, Z.R.; Gao, R.P.; Ba, Z.G. Side-by-side silicon carbide–silica biaxial nanowires: Synthesis, structure, and mechanical properties. Appl. Phys. Lett. 2000, 77, 3349. [Google Scholar] [CrossRef]
- Latu-Romain, L.; Ollivier, M. Silicon carbide based one-dimensional nanostructure growth: Towards electronics and biology perspectives. J. Phys. D. Appl. Phys. 2014, 47, 203001. [Google Scholar] [CrossRef]
- Krasavin, S.E.; Osipov, V.A. Vacancy-induced enhancement of thermal conductivity in grapheme. EPL (Europhys. Lett.) 2016, 113, 66002. [Google Scholar] [CrossRef]
- Korobeynikov, S.N.; Alyokhin, V.V.; Babichev, A.V. On the molecular mechanics of single layer graphene sheets. Int. J. Eng. Sci. 2018, 133, 109–131. [Google Scholar] [CrossRef]
- Salvetat, J.P.; Bonard, J.M.; Thomson, N.H.; Kulik, A.J.; Forrò, L.; Benoit, W.; Zuppiroli, L. Mechanical properties of carbon nanotubes. Appl. Phys. A 1999, 69, 255–260. [Google Scholar] [CrossRef]
- Song, Y.W. Single-walled carbon nanotubes for high-energy optical pulse formation. Appl. Phys. Lett. 2008, 92, 021115. [Google Scholar] [CrossRef]
- Kinoshita, Y.; Murashima, M.; Kawachi, M.; Ohno, N. First-principles study of mechanical properties of one-dimensional carbon nanotube intramolecular junctions. Comput. Mater. Sci. 2013, 70, 1–7. [Google Scholar] [CrossRef]
- Férec, J.; Bertevas, E.; Khoo, B.C.; Ausias, G.; Phan-Thien, N. Thermal or electrical bulk properties of rod-filled composites. Int. J. Eng. Sci. 2018, 133, 219–230. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Baughman, R.H.; Cui, C.; Zakhidov, A.A.; Iqbal, Z.; Barisci, J.N.; Spinks, G.M.; Wallace, G.G.; Mazzoldi, A.; de Rossi, D.; Rinzler, A.G.; et al. Carbon nanotube actuators. Science 1999, 284, 1340–1344. [Google Scholar] [CrossRef]
- Saito, Y.; Hta, K.; Tkakura, A.; Yotani, J.; Uemura, S. Field emission of carbon nanotubes and its application as electron sources of ultra-high luminance light-source devices. Physica B 2002, 323, 30–37. [Google Scholar] [CrossRef]
- Wang, J. Carbon-nanotube based electrochemical biosensors: A review. Electroanal. An Int J. Dev. Fundam. Pract. Asp. Electroanal. 2005, 17, 7–14. [Google Scholar] [CrossRef]
- Arnold, M.S.; Green, A.A.; Hulvat, J.F.; Stupp, I.S.; Hersam, M.C. Sorting carbon nanotubes by electronic structure using density differentiation. Nat. Nanotech 2006, 1, 60–65. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, H.; Yu, P. Rational functionalization of carbon nanotubes leading to electrochemical devices with striking applications. Adv. Mater. 2008, 20, 2899–2906. [Google Scholar] [CrossRef]
- Eatemadi, A.; Daraee, H.; Karimkhanloo, H.; Kouhi, M.; Zarghami, N.; Akbarzadeh, A.; Abasi, M.; Hanifehpour, Y.; Joo, S.W. Carbon nanotubes: Properties, synthesis, purification, and medical applications. Nanoscale Res. Lett. 2014, 9, 393. [Google Scholar] [CrossRef] [PubMed]
- Bianco, A.; Kostarelos, K.; Partidos, C.D.; Prato, M. Biomedical applications of functionalised carbon nanotubes. Chem. Commun. 2005, 5, 571–577. [Google Scholar] [CrossRef] [PubMed]
- Miyako, E.; Hosokawa, C.; Kojima, M.; Yudasaka, M.; Funahashi, R.; Oishi, I.; Hagihara, Y.; Shichiri, M.; Takashima, M.; Nishio, K.; et al. A Photo-Thermal-Electrical Converter Based On Carbon Nanotubes for Bioelectronic Applications. Angew. Chem. Int. Ed. 2011, 50, 12266–12270. [Google Scholar] [CrossRef] [PubMed]
- Gooding, J.J. Nanostructuring electrodes with carbon nanotubes: A review on electrochemistry and applications for sensing. Electrochim. Acta 2005, 50, 3049–3060. [Google Scholar] [CrossRef]
- Paradise, M.; Goswami, T. Carbon nanotubes–production and industrial applications. Mat. Des. 2007, 28, 1477–1489. [Google Scholar] [CrossRef]
- He, H.; Pham-Huy, L.A.; Dramou, P.; Xiao, D.; Zuo, P.; Pham-Huy, C. Carbon nanotubes: Applications in pharmacy and medicine. BioMed Res. Int. 2013, 578290. [Google Scholar] [CrossRef]
- Braun, M.; Aranda-Ruiz, J.; Rodriguez-Millan, M.; Loya, J.A. On the bulk modulus and natural frequency of fullerene and nanotube carbon structures obtained with a beam based method. Compos. Struct. 2018, 187, 10–17. [Google Scholar] [CrossRef]
- Avouris, P.; Hertel, T.; Martel, R.; Schmidt, T.; Shea, H.R.; Walkup, R.E. Carbon nanotubes: Nanomechanics, manipulation, and electronic devices. Appl. Surf. Sci. 1999, 141, 201–209. [Google Scholar] [CrossRef]
- Dai, H.; Hafner, J.H.; Rinzler, A.G.; Colbert, D.T.; Smalley, R.E. Nanotubes as nanoprobes in scanning probe microscopy. Nature 1996, 384, 147–150. [Google Scholar] [CrossRef]
- Lau, A.K.T.; Hui, D. The revolutionary creation of new advanced materials-carbon nanotube composites. Compos. Part B Eng. 2002, 33, 263–277. [Google Scholar] [CrossRef]
- Sun, C.H.; Li, F.; Cheng, H.M. Axial Young’s modulus prediction of single-walled carbon nanotube arrays with diameters from nanometer to meter scales. Appl. Phys. Lett. 2005, 87, 193101. [Google Scholar] [CrossRef]
- De Volder, M.F.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J. Carbon nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef]
- Hibbeler, R.C. Statics and Mechanics of Materials, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Flügge, W. Tatik und Dynamik der Schalen; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Danesh, M.; Farajpour, A.; Mohammadi, M. Axial vibration analysis of a tapered nanorod based on nonlocal elasticity theory and differential quadrature method. Mech. Res. Commun. 2012, 39, 23–27. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Farajpour, A. Axisymmetric free and forced vibrations of initially stressed circular nanoplates embedded in an elastic medium. Acta Mech. 2012, 223, 2311–2330. [Google Scholar] [CrossRef]
- Mohammadi, M.; Moradi, A.; Ghayour, M.; Farajpour, A. Exact solution for thermo-mechanical vibration of orthotropic mono-layer graphene sheet embedded in an elastic medium. Lat. Am. J. Solids Struct. 2014, 11, 437–458. [Google Scholar] [CrossRef][Green Version]
- Mohammadi, M.; Farajpour, A.; Goodarzi, M.; Dinari, F. Thermo-mechanical vibration analysis of annular and circular graphene sheet embedded in an elastic medium. Lat. Am. J. Solids Struct. 2014, 11, 659–682. [Google Scholar] [CrossRef][Green Version]
- Farajpour, A.; Rastgoo, A. Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results Phys. 2017, 7, 1367–1375. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes. Int. J. Mech. Sci. 2019, 150, 510–525. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Plane waves in nonlocal micropolar elasticity. Int. J. Eng. Sci. 1984, 22, 1113–1121. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Sudak, L.J. Column buckling of multiwalled carbon nanotubes using nonlocal continuum mechanics. J. Appl. Phys. 2003, 94, 7281–7287. [Google Scholar] [CrossRef]
- Li, C.Y.; Chou, T.W. Vibrational behaviors of multi-walled carbon nanotube-based nanomechancial resonators. Appl. Phys. Lett. 2004, 84, 121–123. [Google Scholar] [CrossRef]
- He, X.Q.; Kitipornchai, S.; Liew, K.M. Buckling analysis of multi-walled carbon nanotubes: A continuum model accounting for van der Waals interaction. J. Mech. Phys. Solid 2005, 53, 303–326. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liu, G.R.; Xie, X.Y. Free transverse vibrations of double-walled carbon nanotubes using a theory of nonlocal elasticity. Phys. Rev. B 2005, 71, 195404. [Google Scholar] [CrossRef]
- Wang, Q.; Varadan, V.K. Vibration of carbon nanotubes studied using nonlocal continuum mechanics. Smart Mat. Struct. 2006, 15, 659–666. [Google Scholar] [CrossRef]
- Aranda-Ruiz, J.; Loya, J.A.; Fernández-Sáez, J. Bending vibrations of rotating nonuniform nanocantilevers using the Eringen nonlocal elasticity theory. Compos. Struct. 2012, 94, 2990–3001. [Google Scholar] [CrossRef]
- Numanoğlu, H.M.; Akgöz, B.; Civalek, Ö. On dynamic analysis of nanorods. Int. J. Eng. Sci. 2018, 130, 33–50. [Google Scholar] [CrossRef]
- Malikan, M.; Dimitri, R.; Tornabene, F. Transient response of oscillated carbon nanotubes with an internal and external damping. Compos. Part B-Eng. 2019, 158, 198–205. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Civalek, Ö. On dynamic instability of magnetically embedded viscoelastic porous FG nanobeam. Int. J. Eng. Sci. 2019, 143, 14–32. [Google Scholar] [CrossRef]
- Numanoğlu, H.M.; Civalek, Ö. On the dynamics of small-sized structures. Int. J. Eng. Sci. 2019, 145, 103164. [Google Scholar] [CrossRef]
- Lim, C.W. Equilibrium and static deflection for bending of a nonlocal nanobeam. Adv. Vib. Eng. 2009, 8, 277–300. [Google Scholar]
- Kiani, K.; Mehri, B. Assessment of nanotube structures under a moving nanoparticle using nonlocal beam theories. J. Sound Vib. 2010, 329, 2241–2264. [Google Scholar] [CrossRef]
- Lim, C.W.; Niu, J.C.; Yu, Y.M. Nonlocal stress theory for buckling instability of nanotubes: New predictions on stiffness strengthening effects of nanoscales. J. Comput. Theor. Nanosci. 2010, 7, 2104–2111. [Google Scholar] [CrossRef]
- Li, C.; Lim, C.W.; Yu, J.L. Dynamics and stability of transverse vibrations of nonlocal nanobeams with a variable axial load. Smart Mat. Struct. 2011, 20, 015023. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Demir, Ç.; Civalek, Ö. On the analysis of microbeams. Int. J. Eng. Sci. 2017, 121, 14–33. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nanoplatelets. Compos. Part B Eng. 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Pinnola, F.P.; Faghidian, S.A.; Barretta, R.; de Sciarra, F.M. Variationally consistent dynamics of nonlocal gradient elastic beams. Int. J. Eng. Sci. 2020, 149, 103220. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory. Nanotechnology 2007, 18, 385704. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Vibration analysis of nanoplates under uniaxial prestressed conditions via nonlocal elasticity. J. Appl. Phys. 2009, 106, 104301. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Srividhya, S.; Raghu, P.; Rajagopal, A.; Reddy, J.N. Nonlocal nonlinear analysis of functionally graded plates using third-order shear deformation theory. Int. J. Eng. Sci. 2018, 125, 1–22. [Google Scholar] [CrossRef]
- Dindarloo, M.H.; Li, L.; Dimitri, R.; Tornabene, F. Nonlocal elasticity response of doubly-curved nanoshells. Symmetry 2020, 12, 466. [Google Scholar] [CrossRef]
- Malikan, M.; Krasheninnikov, M.; Eremeyev, V.A. Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int. J. Eng. Sci. 2020, 148, 103210. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. Free Vibration of Flexomagnetic Nanostructured Tubes Based on Stress-Driven Nonlocal Elasticity, In Analysis of Shells, Plates, and Beams; Springer: Berlin/Heidelberg, Germany, 2020; pp. 215–226, Chapter 12. [Google Scholar]
- Ansari, R.; Gholami, R.; Ajori, S. Torsional vibration analysis of carbon nanotubes based on the strain gradient theory and molecular dynamic simulations. J. Vib. Acoustic. 2013, 135, 051016. [Google Scholar] [CrossRef]
- Fatahi-Vajari, A.; Imam, A. Torsional vibration of single-walled carbon nanotubes using doublet mechanics. Z. Angew. Math. Phys. 2016, 67, 81. [Google Scholar] [CrossRef]
- Arda, M.; Aydogdu, M. Torsional vibration of double CNT system embedded in an elastic medium. Noise Theory Pract. 2018, 4, 4. [Google Scholar]
- Li, C. Torsional vibration of carbon nanotubes: Comparison of two nonlocal models and a semi-continuum model. Int. J. Eng. Sci. 2014, 82, 25–31. [Google Scholar] [CrossRef]
- Aydogdu, M.; Arda, M. Torsional vibration analysis of double walled carbon nanotubes using nonlocal elasticity. Int. J. Mech. Mater. Design 2016, 12, 71–84. [Google Scholar] [CrossRef]
- Demir, C.; Civalek, Ö. Torsional and longitudinal frequency and wave response of microtubules based on the nonlocal continuum and nonlocal discrete models. Appl. Math. Model. 2013, 37, 9355–9367. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S.; Wang, C. Torsional vibration of carbon nanotube–buckyball systems based on nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2011, 43, 1276–1280. [Google Scholar] [CrossRef]
- Suzuki, N.; Yokoi, H.; Shamoto, E. Micro/nano sculpturing of hardened steel by controlling vibration amplitude in elliptical vibration cutting. Precis. Eng. 2011, 35, 44–50. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, T.; Ge, C.; Sui, Y.; Yang, H. Review of micro/nano machining by utilizing elliptical vibration cutting. Int. J. Mach. Tool Manufact. 2016, 196, 109–126. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, Y.; Guo, P. Structural coloration of metallic surfaces with micro/nano-structures induced by elliptical vibration texturing. Appl. Surf. Sci. 2017, 402, 400–409. [Google Scholar] [CrossRef]
- Mikeš, K.; Jirásek, M. Free warping analysis and numerical implementation. Appl. Mech. Mat. 2016, 825, 141–148. [Google Scholar] [CrossRef]
- Barr, A. Torsional waves in uniform rods of non-circular section. J. Mech. Eng. Sci. 1962, 4, 127–135. [Google Scholar] [CrossRef]
- Stephen, N. Comparison of dynamic torsion theories for beams of elliptical cross-section. J. Sound Vib. 1985, 100, 1–6. [Google Scholar] [CrossRef]
- Francu, J.; Novácková, P.; Janicek, P. Torsion of a non-circular bar. Eng. Mech. 2012, 19, 45–60. [Google Scholar]
- Christides, S.; Barr, A. Torsional vibration of cracked beams of non-circular cross-section. Int. J. Mech. Sci. 1986, 28, 473–490. [Google Scholar] [CrossRef]
- Loya, J.A.; Aranda-Ruiz, J.; Fernández-Sáez, J.F. Torsion of cracked nanorods using a nonlocal elasticity model. J. Phys. D Appl. Phys. 2014, 47, 115304. [Google Scholar] [CrossRef]
- Loya, J.; López-Puente, J.; Zaera, R.; Fernández-Sáez, J. Free transverse vibrations of cracked nanobeams using a nonlocal elasticity model. J. Appl. Phys. 2009, 105, 044309. [Google Scholar] [CrossRef]
- Loya, J.A.; Rubio, L.; Fernández-Sáez, J. Natural frequencies for bending vibrations of Timoshenko cracked beams. J. Sound Vib. 2006, 290, 640–653. [Google Scholar] [CrossRef]
- Ogata, Y.; Mizutani, G. Control of cross-sections and optical nonlinearity of Pt Nanowires and the Roughness Effect. Phys. Res. Int. 2012, 2012, 969835. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; Wiley Online Library: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mir, M.; Hosseini, A.; Majzoobi, G. A numerical study of vibrational properties of single-walled carbon nanotubes. Comp. Mater. Sci. 2008, 43, 540–548. [Google Scholar] [CrossRef]
- Ruoff, R.S.; Qian, D.; Liu, W.K. Mechanical properties of carbon nanotubes: Theoretical predictions and experimental measurements. Comptes. Rendus. Phys. 2003, 4, 993–1008. [Google Scholar] [CrossRef]
- El Khoury, E.; Messager, T.; Cartraud, P. Derivation of the Young’s and shear moduli of single-walled carbon nanotubes through a computational homogenization approach. Int. J. Multisc. Comput. Eng. 2011, 9, 97–118. [Google Scholar] [CrossRef]
- Khosravi, F.; Hosseini, S.A.; Tounsi, A. Torsional dynamic response of viscoelastic SWCNT subjected to linear and harmonic torques with general boundary conditions via Eringen’s nonlocal differential model. Eur. Phys. J. Plus 2020, 135, 183. [Google Scholar] [CrossRef]

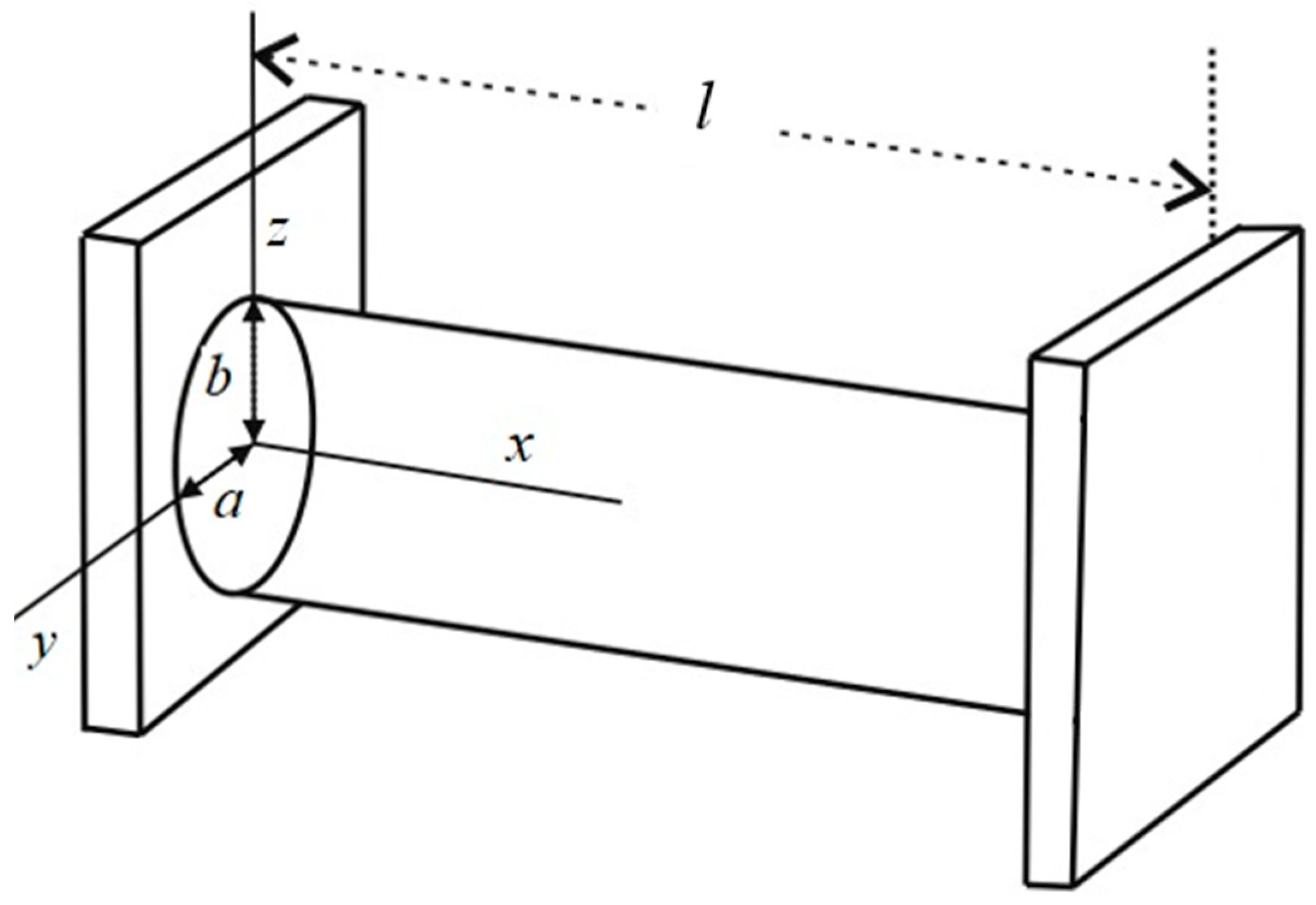
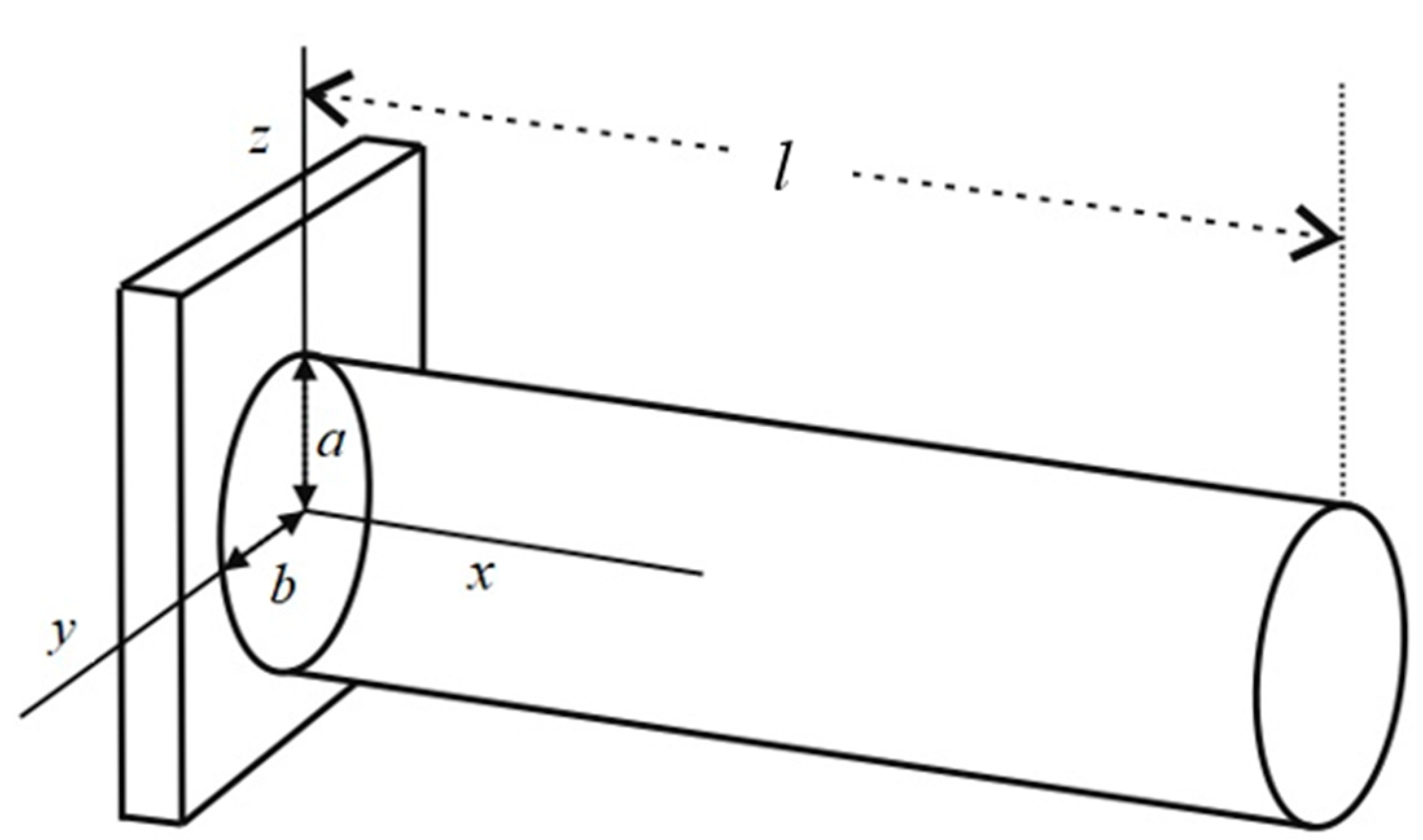
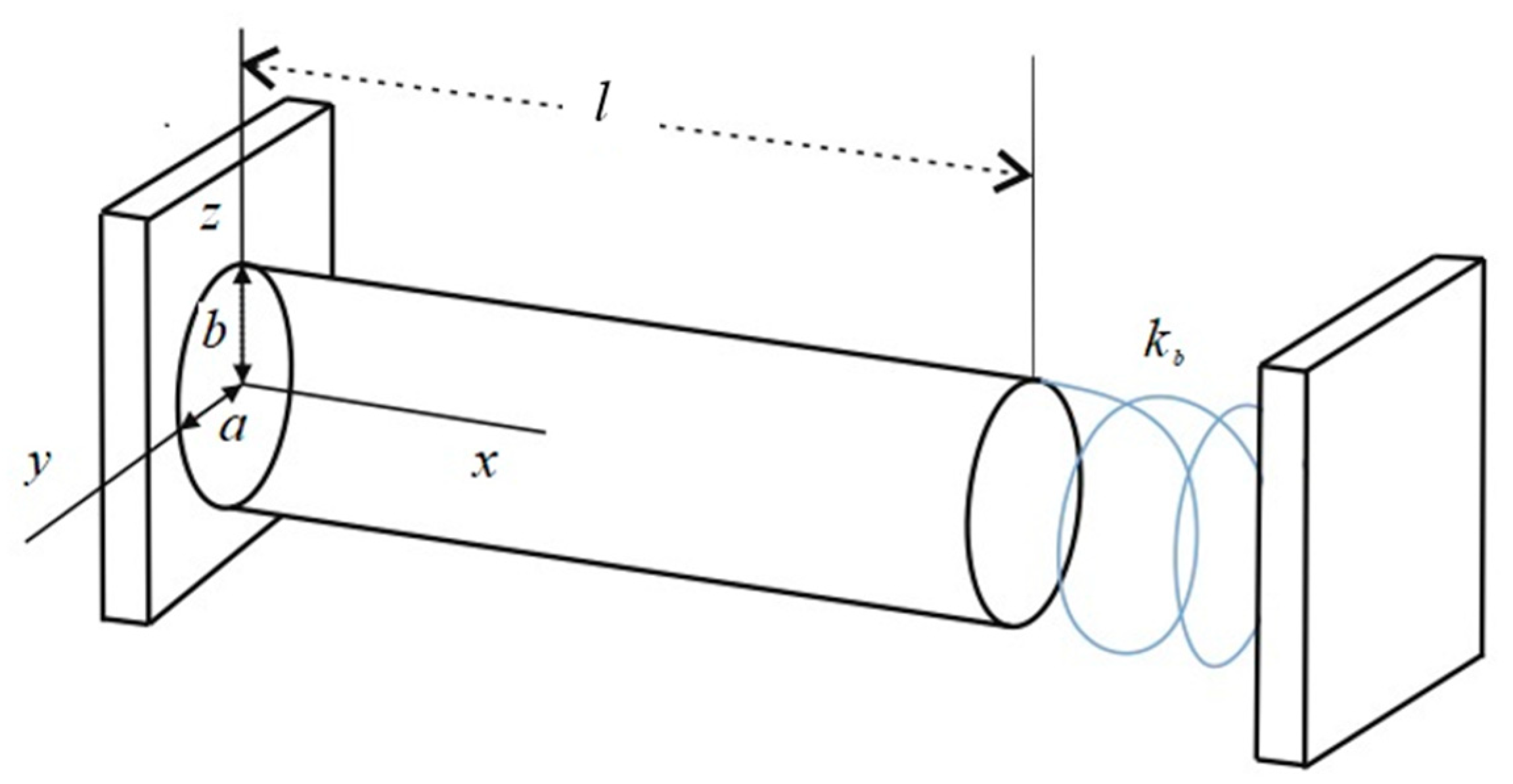
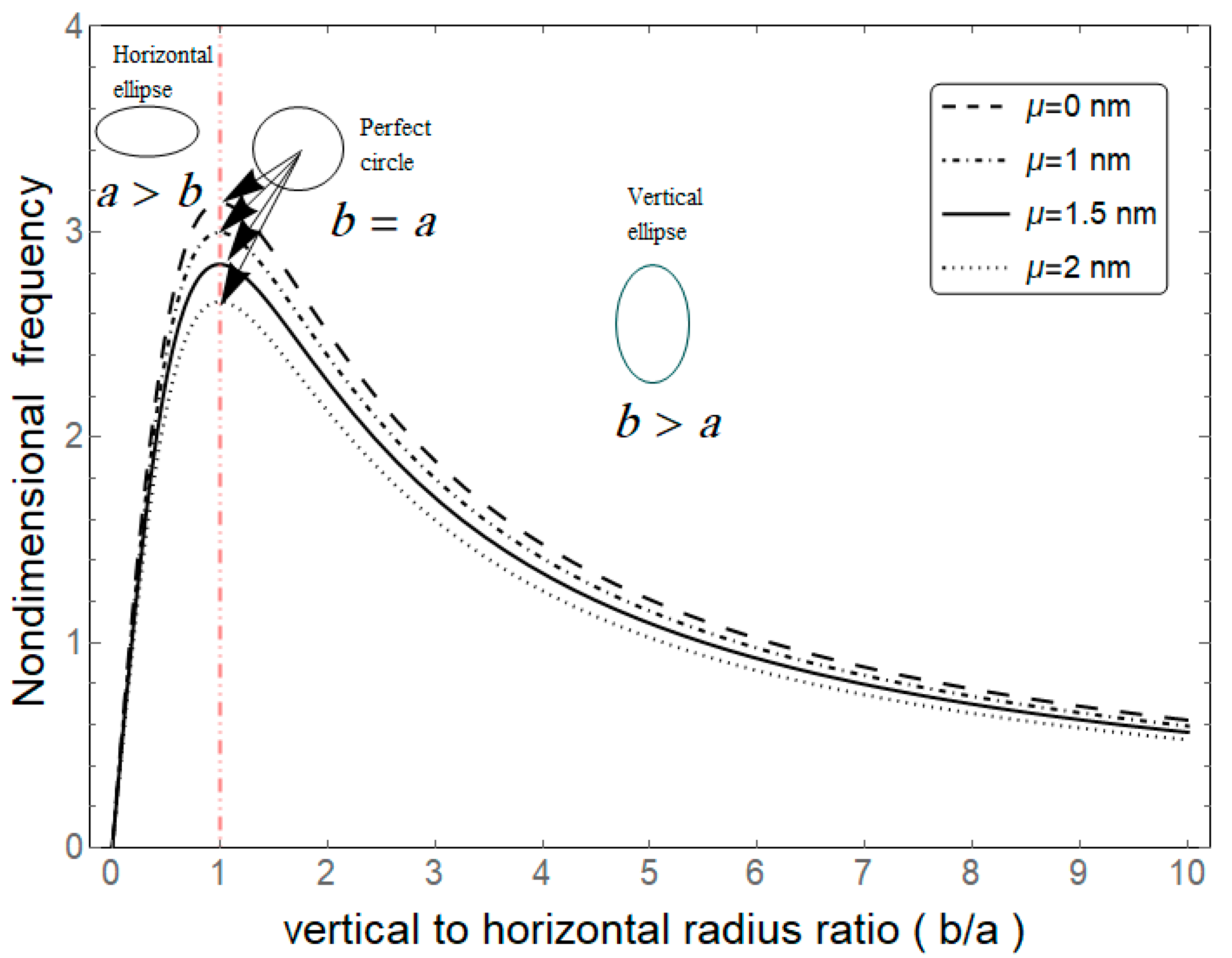

| n = 1 | n = 2 | n = 3 | n = 4 | |
|---|---|---|---|---|
| Present | 2.9971 | 5.3201 | 6.8586 | 7.8247 |
| Ref. [95] | 2.9971 | 5.3201 | 6.8586 | 7.8247 |
| 0 | 0.6220 | 1.2082 | 3.1415 | 1.2062 | 0.6208 |
| 1 | 0.6145 | 1.1935 | 3.1035 | 1.1916 | 0.6133 |
| 1.5 | 0.6055 | 1.1760 | 3.0578 | 1.1741 | 0.6043 |
| 2 | 0.5934 | 1.1526 | 2.9971 | 1.1508 | 0.5923 |
| 0 | 0.3110 | 1.2565 | 1.5708 | 1.2564 | 0.3108 |
| 1 | 0.3100 | 1.2527 | 1.5659 | 1.2525 | 0.3099 |
| 1.5 | 0.3089 | 1.2479 | 1.5600 | 1.2478 | 0.3087 |
| 2 | 0.3072 | 1.2413 | 1.5517 | 1.2412 | 0.3071 |
| 0 | 1 | 1.5 | 2 | |
|---|---|---|---|---|
| 0.01 | 1.2815 | 1.2774 | 1.2723 | 1.2653 |
| 0.1 | 1.4690 | 1.4628 | 1.4552 | 1.4448 |
| 1 | 2.1225 | 2.1040 | 2.0817 | 2.0515 |
| 10 | 2.4638 | 2.4351 | 2.4006 | 2.3547 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosravi, F.; Hosseini, S.A.; Hamidi, B.A.; Dimitri, R.; Tornabene, F. Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions. Vibration 2020, 3, 189-203. https://doi.org/10.3390/vibration3030015
Khosravi F, Hosseini SA, Hamidi BA, Dimitri R, Tornabene F. Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions. Vibration. 2020; 3(3):189-203. https://doi.org/10.3390/vibration3030015
Chicago/Turabian StyleKhosravi, Farshad, Seyyed Amirhosein Hosseini, Babak Alizadeh Hamidi, Rossana Dimitri, and Francesco Tornabene. 2020. "Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions" Vibration 3, no. 3: 189-203. https://doi.org/10.3390/vibration3030015
APA StyleKhosravi, F., Hosseini, S. A., Hamidi, B. A., Dimitri, R., & Tornabene, F. (2020). Nonlocal Torsional Vibration of Elliptical Nanorods with Different Boundary Conditions. Vibration, 3(3), 189-203. https://doi.org/10.3390/vibration3030015







