Experimental and Numerical Investigations into Dynamic Modal Parameters of Fiber-Reinforced Foamed Urethane Composite Beams in Railway Switches and Crossings
Abstract
1. Introduction
2. Materials and Methods
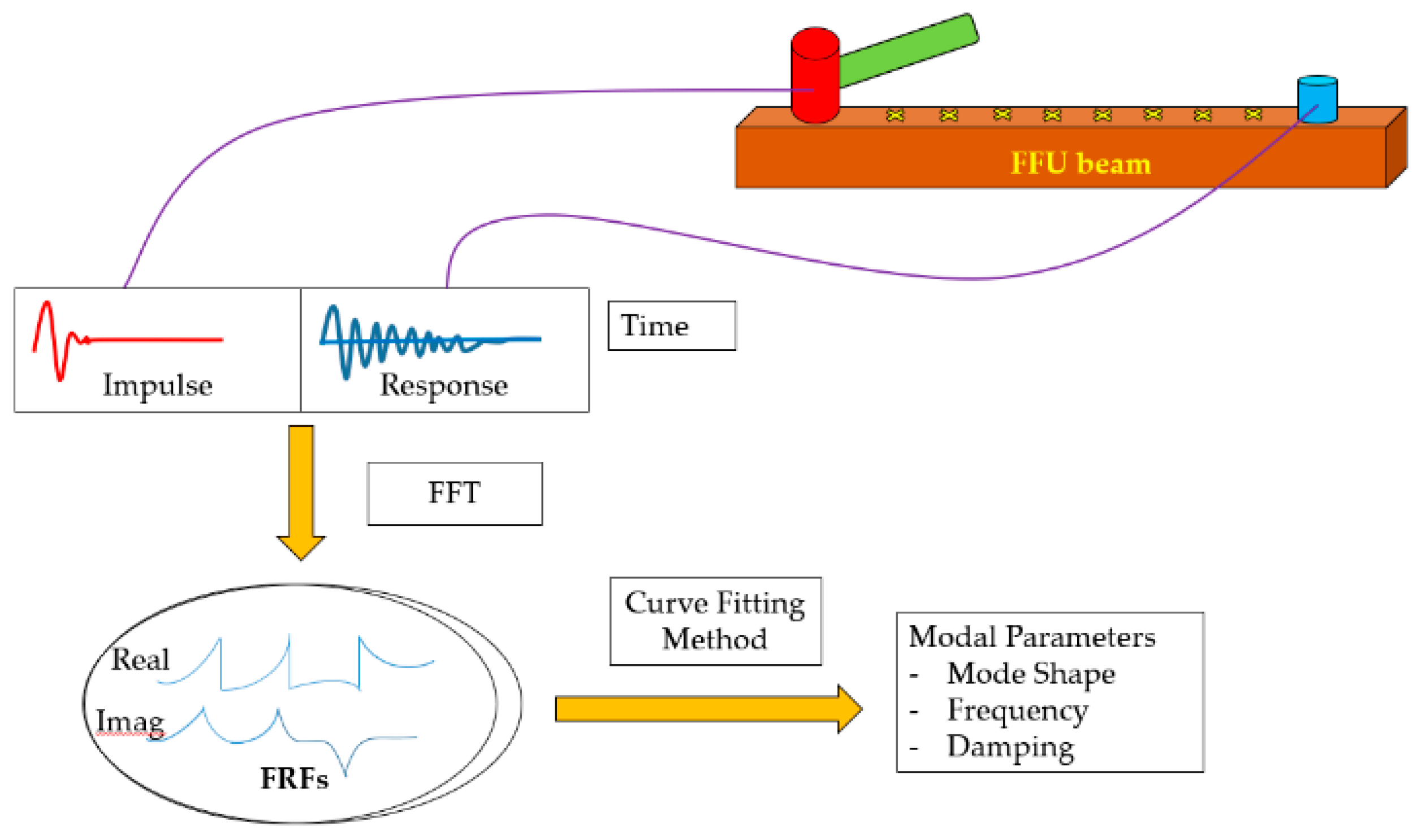
2.1. Modal Equipment
2.2. Experimental Overview
2.2.1. Modal Testing
2.2.2. Three-Point Bending Tests
2.3. Determination of Dynamic Elastic Modulus
2.4. A Finite-Element (FE) Model
3. Results
3.1. Experimental Results
3.2. Numerical Results
4. Conclusions
- The first bending mode in a vertical plane obviously dominates the first resonant mode of vibration under a free-free condition;
- The dynamic modal parameters of full-scale FFU composite beams reduce when damages occur. Thus, they decrease with damage severity;
- The highest dynamic Young’s modulus of FFU composite beams is found in the resonant frequency of the first bending mode and also reduces when the second and third bending modes appear.
Author Contributions
Funding
Conflicts of Interest
References
- Van Erp, G.; McKay, M. Recent Australian Developments in Fibre Composite Railway Sleepers. Electron. J. Struct. Eng. 2013, 13, 62–66. [Google Scholar]
- Manalo, A. Behaviour of Fibre Composite Sandwich Structures: A Case Study on Railway Sleeper Application. Ph.D. Thesis, Centre of Excellence in Engineered Fibre Composites Faculty of Engineering and Surveying University of Southern Queensland Toowoomba, Toowoomba, Australia, 2011. [Google Scholar]
- Ngamkhanong, C.; Kaewunruen, S.; Costa, B.J.A. State-of-the-Art Review of Railway Track Resilience Monitoring. Infrastructures 2018, 3, 3. [Google Scholar] [CrossRef]
- Gamage, E.K.; Kaewunruen, S.; Remennikov, A.M.; Ishida, T. Toughness of Railroad Concrete Crossties with Holes and Web Openings. Infrastructures 2017, 2, 3. [Google Scholar] [CrossRef]
- Kaewunruen, S. Monitoring in-service performance of fibre-reinforced foamed urethane material as timber-replacement sleepers/bearers in railway urban turnout systems. Struct. Monit. Maint. 2014, 1, 131–157. [Google Scholar]
- Kaewunruen, S. In situ performance of a complex urban turnout grillage system using fibre-reinforced foamed urethane (FFU) bearers. In Proceedings of the 10th World Congress on Rail Research, Sydney, Australia, 25–28 November 2013. [Google Scholar]
- Kaewunruen, S. Monitoring structural deterioration of railway turnout systems via dynamic wheel/rail interaction. Case Stud. Nondestr. Test. Eval. 2014, 1, 19–24. [Google Scholar] [CrossRef]
- Indraratna, B.; Salim, W.; Rujikiatkamjorn, C. Advanced Rail Geotechnology—Ballasted Track; CRC Press/Balkema: Leiden, The Netherlands, 2011. [Google Scholar]
- RailCorp. Timber Sleepers & Bearers; Engineering Specification SPC 231; RailCorp: Sydney, Australia, 2012.
- Kaewunruen, S.; Remennikov, A.M. Dynamic flexural influence on a railway concrete sleeper in track system due to a single wheel impact. Eng. Fail. Anal. 2009, 16, 705–712. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Kaewunruen, S. A review of loading conditions for railway track structures due to train and track vertical interaction. Struct. Control. Health Monit. 2008, 15, 207–234. [Google Scholar] [CrossRef]
- Standards Australia. Australian Standards: AS3818.2 Timber; Standards Australia: Sydney, Australia, 2001. [Google Scholar]
- Dindar, S.; Kaewunruen, S.; An, M. Identification of Appropriate Risk Analysis Techniques for Railway Turnout Systems. J. Risk Res. 2016, 21, 974–995. [Google Scholar] [CrossRef]
- Pen, L.L. Track Behaviour: The Importance of the Sleeper to the Ballast Interface. Ph.D. Thesis, University of Southampton, Southampton, UK, 2008. [Google Scholar]
- Griffin, D.W.P.; Mirza, O.; Kwok, K.; Kaewunruen, S. Finite element modelling of modular precast composites for railway track support structure: A battle to save Sydney Harbour Bridge. Aust. J. Struct. Eng. 2015, 16, 150–168. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sengsri, P.; de Melo, A.L.O. Experimental and Numerical Investigations of Flexural Behaviour of Composite Bearers in Railway Switches and Crossings. In Sustainable Issues in Transportation Engineering; Mohammad, L., Abd El-Hakim, R., Eds.; Sustainable Civil Infrastructures; GeoMEast; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Silva, E.A.; Pokropski, D.; You, R.; Kaewunruen, S. Comparison of structural design methods for railway composites and plastic sleepers and bearers. Aust. J. Struct. Eng. 2017, 18, 160–177. [Google Scholar] [CrossRef]
- Kaewunruen, S. Discussion of “Evaluation of an Innovative Composite Railway Sleeper for a Narrow-Gauge Track under Static Load” by Wahid Ferdous, Allan Manalo, Gerard Van Erp, Thiru Aravinthan, and Kazem Ghabraie. J. Compos. Constr. 2019, 23, 07018001. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A.M.; Murray, M.H. Introducing a new limit states design concept to railway concrete sleepers: An Australian experience. Front. Mater. 2014, 1, 8. [Google Scholar] [CrossRef]
- Crystal Instruments. Basics of Structural Vibration Testing and Analysis. Available online: https://www.crystalinstruments.com/basics-of-modal-testing-and-analysis (accessed on 12 January 2020).
- Kaewunruen, S. Experimental and Numerical Studies for Evaluating Dynamic Behaviour of Prestressed Concrete Sleepers Subject to Severe Impact Loading. The University of Wollongong. Available online: http://ro.uow.edu.au/theses/277 (accessed on 8 January 2020).
- Remennikov, A.; Kaewunruen, S. Experimental Investigation on Dynamic Railway Sleeper/Ballast Interaction. Exp. Mech. 2006, 46, 57–66. [Google Scholar] [CrossRef]
- Pickett, G. Equations for computing elastic constants from flexural and torsional resonant frequencies of vibrating prisms and cylinders. ASTM Proc. 1945, 45, 846–865. [Google Scholar]
- Spinner, S.; Reichard, T.W.; Tefft, W.E. A Comparison of Experimental and Theoretical Relations Between Young’s Modulus and the Flexural and Longitudinal Resonance Frequencies of Uniform Bars. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1960, 64, 2–147. [Google Scholar] [CrossRef] [PubMed]
- Spinner, S.; Tefft, W.E. A Method for Determining Mechanical Resonance Frequencies and for Calculating Elastic Moduli from These Frequencies. ASTM Proc. 1961, 61, 1221–1238. [Google Scholar]
- ASTM Standard E 1876–07. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 1876. [Google Scholar]
- Wesolowski, M.; Barkanov, E.; Rucevskis, S.; Chate, A.; La Delfa, G. Characterisation of elastic properties of laminated composites by non-destructive techniques. In Proceedings of the 17th International Conference on Composite Materials, Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Yu, L.; Wang, J.; Xia, D. Vibration Method for Elastic Modulus of Glued Laminated Beams. In Proceedings of the 3rd International Conference on Material, Mechanical and Manufacturing Engineering, IC3ME 2015, Guangzhou, China, 27–28 June 2015; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 1603–1606. [Google Scholar]
- Giaccu, G.F.; Meloni, D.; Valdès, M.; Fragiacomo, M. Dynamic determination of the modulus of elasticity of maritime pine cross-laminated panels using vibration methods. WIT Trans. Ecol. Environ. 2017, 226, 571–579. [Google Scholar]
- Ivanova, Y.; Partalin, T.; Georgiev, I. Characterisation of elastic properties of laminated composites by ultrasound and vibration. Sci. Proc. Sci. Tech. Union Mech. Eng. 2016, 1, 418–425. [Google Scholar]
- Gillich, G.R.; Samoilescu, G.; Berinde, F.; Chioncel, C.P. Experimental determination of the rubber dynamic rigidity and elasticity module by time-frequency measurements. Mater. Plast. 2007, 44, 18–21. [Google Scholar]
- Iancu, V.; Vasile, O.; Gillich, G.R. Modelling and Characterization of Hybrid Rubber-Based Earthquake Isolation Systems. Mater. Plast. 2012, 49, 237–241. [Google Scholar]
- Nedelcu, D.; Gillich, G.R.; Cziple, F.; Ciuca, I.; Padurean, I. Considerations about using polymers in adaptive guardrails construction. Mater. Plast. 2008, 45, 47–52. [Google Scholar]
- Roohnia, M. An Estimation of Dynamic Modulus of Elasticity in Cantilever Flexural Timber Beams. Drv. Ind. 2014, 65, 1–10. [Google Scholar] [CrossRef]
- Kubojima, Y.; Tonosaki, M.; Yoshihara, H. Young’s modulus obtained by flexural vibration test of a wooden beam with inhomogeneity of density. J. Wood Sci. 2006, 52, 20–24. [Google Scholar] [CrossRef]
- Lee, K.M.; Kim, D.S.; Kim, J.S. Determination of Dynamic Young’s Modulus of Concrete at Early Ages by Impact Resonance Test. KSCE J. Civ. Eng. 1997, 1, 11–18. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Lewandrowski, T.; Chamniprasart, K. Dynamic responses of interspersed railway tracks to moving train loads. Int. J. Struct. Stab. Dyn. 2017, 18, 1850011. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ngamkhanong, C.; Papaelias, M.; Roberts, C. Wet/dry influence on behaviors of closed-cell polymeric cross-linked foams under static, dynamic and impact loads. Constr. Build. Mater. 2018, 187, 1092–1102. [Google Scholar] [CrossRef]
- Krezo, S.; Mirza, O.; Kaewunruen, S.; Sussman, J.M. Evaluation of CO2 emissions from railway resurfacing maintenance activities. Transp. Res. Part. D Transp. Environ. 2018, 65, 458–465. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Lopes, L.M.C.; Papaelias, M.P. Georisks in railway systems under climate uncertainties by different types of sleeper/crosstie materials. Lowl. Technol. Int. 2018, 20, 77–86. [Google Scholar]
- BSI. BSI Standards Publication Railway Applications—Track—Concrete Sleepers and Bearers Part 2: Prestressed Monoblock Sleepers; BSI: London, UK, 2016. [Google Scholar]
- Kaewunruen, S. Systemic values of enhanced dynamic damping in concrete sleepers – Comments on the paper: Ahn S, Kwon S, Hwang Y-T, Koh H-I, Kim H-S, Park J. Complex structured polymer concrete sleeper for rolling noise reduction of high-speed train system. Comp, Struct. 2020, 234, 111711. [Google Scholar] [CrossRef]
- Resonance, S. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration 1; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Stokey, W.F. Chapter 7 Vibration of Systems Having Distributed Mass and Elasticity. In Shock and Vibration Handbook. 22 October 2001. Available online: https://www.globalspec.com/reference/64452/203279/chapter-7-vibration-of-systems-having-distributed-mass-and-elasticity (accessed on 1 February 2020).
- Kaewunruen, S.; Janeliukstis, R.; Ngamkhanong, C. Dynamic properties of fibre reinforced foamed urethane composites in wet and dry conditions. Mat. Today. Procs. 2020, 5, 690. [Google Scholar] [CrossRef]
- G+D Computing. Using Strand7 Introduction to the Strand7 Finite Element Analysis System; G+D Computing Pty Ltd.: Sydney, Australia, 2002. [Google Scholar]
- Kaewunruen, S.; Goto, K.; Xie, L. Failure modes of fibre reinforced foamed urethane composite beams: Full-scale experimental determination. Mat. Today. Procs. 2020, 5, 691. [Google Scholar] [CrossRef]
- Kaewunruen, S.; You, R.; Ishida, M. Composites for Timber-Replacement Bearers in Railway Switches and Crossings. Infrastructures 2017, 2, 13. [Google Scholar] [CrossRef]
- Sengsri, P.; Ngamkhanong, C.; Melo, A.L.O.; Papaelias, M.; Kaewunruen, S. Damage Detection in Fiber-Reinforced Foamed Urethane Composite Railway Bearers Using Acoustic Emissions. Infrastructures 2020, 5, 50. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sussman, J.M.; Matsumoto, A. Grand Challenges in Transportation and Transit Systems. Front. Built Environ. 2016, 2, 4. [Google Scholar] [CrossRef]






| Properties [37] | Units | FFU Sleepers and Bearers [6] | |||
|---|---|---|---|---|---|
| New | After 10 Years Used | After 15 Years Used | After 30 Years Used | ||
| Elastic Modulus | GPa | 8.10 | 8.04 | 8.79 | 8.41 |
| Bending Strength | GPa | 0.142 | 0.125 | 0.131 | 0.116 |
| Shear Strength | MPa | 10 | 9.5 | 9.6 | 7 |
| Vertical Compressive Strength | MPa | 58 | 66 | 63 | 55 |
| Density | kg/m3 | 740 | 740 | 740 | 740 |
| Service Life | Years | 50 | 40 | 35 | 20 |
| Hardness | MPa | 28 | 25 | 17 | - |
| Mode No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0 (Translation) | 4.730 | 7.853 | 10.996 | 14.137 |
| Parameter lists | Values | Units |
|---|---|---|
| Density | 740 | kg/m3 |
| Length | 3.3 | m |
| Cross-section area | 0.16 × 0.26 = 0.042 | m2 |
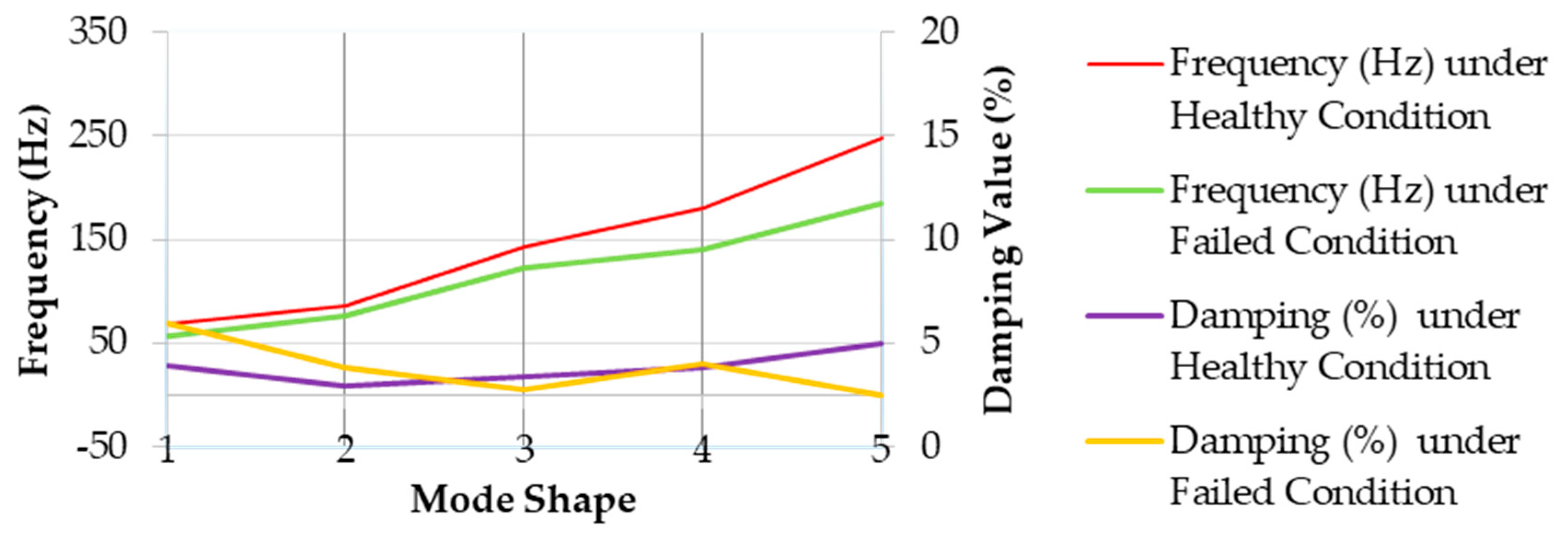
| Healthy Condition | Failed Condition | Difference | |||
|---|---|---|---|---|---|
| Frequency (Hz) | Damping (%) | Frequency (Hz) | Damping (%) | Frequency (Hz) | Damping (%) |
| Mode 1 (1st bending)  68.23 | 3.96 |  56.92 | 5.9 | 11.31 | 1.94 |
| Mode 2 (1st twisting)  85.78 | 2.98 |  75.94 | 3.83 | 9.84 | 0.85 |
| Mode 3 (2nd bending)  143.61 | 3.37 |  121.87 | 2.8 | 21.74 | 0.57 |
| Mode 4 (2nd twisting)  180.14 | 3.85 |  139.68 | 3.99 | 40.46 | 0.14 |
| Mode 5 (3rd bending)  247.96 | 4.96 | 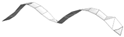 185.28 | 2.53 | 62.68 | 2.43 |
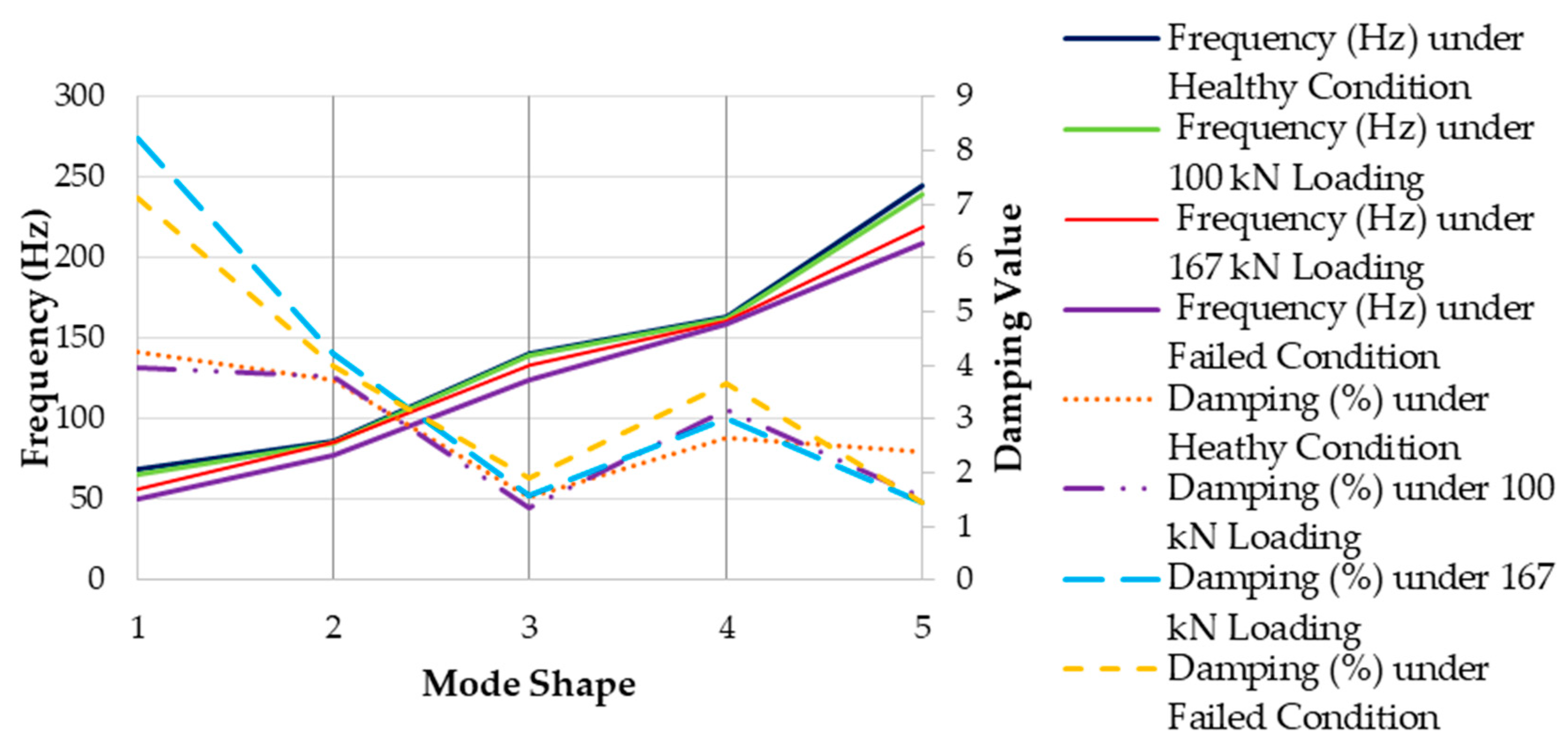
| Healthy | 67 kN | 100 kN | 167 kN | 170 kN (Failed) |
|---|---|---|---|---|
| Frequency (Hz)/Damping (%) | ||||
| Mode 1 (1st bending) | ||||
 |  |  |  |  |
| 69.2/4.23 | 68.03/5.04 | 65.84/3.94 | 55.99/8.24 | 50.44/7.12 |
| Mode 2 (1st twisting) | ||||
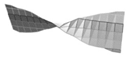 |  |  |  | 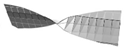 |
| 85.63/1.55 | 84.8/3.84 | 85.24/3.78 | 85.54/4.22 | 77.31/3.97 |
| Mode 3 (2nd bending) | ||||
 |  |  |  |  |
| 140.09/1.55 | 139.88/1.6 | 139.04/1.35 | 132.98/1.58 | 124.08/1.9 |
| Mode 4 (2nd twisting) | ||||
 |  |  |  | 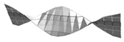 |
| 163.3/2.66 | 162.43/3.16 | 162.13/3.16 | 160.82/3.00 | 159.07/3.66 |
| Mode 5 (3rd bending) | ||||
 |  |  |  |  |
| 244.77/2.39 | 241.69/1.53 | 239.30/1.54 | 219.40/1.44 | 209.17/1.44 |
| Difference in Frequencies (Hz)/Damping (%) | ||||
|---|---|---|---|---|
| No. Mode | 67 kN | 100 kN | 167 kN | 170 kN (Failed) |
| 1 | 1.17/0.81 | 3.36/0.29 | 13.21/4.01 | 18.76/2.89 |
| 2 | 0.83/2.29 | 0.39/2.23 | 0.09/2.67 | 8.32/2.42 |
| 3 | 0.21/0.05 | 1.05/0.20 | 7.11/0.03 | 16.01/0.35 |
| 4 | 0.87/0.50 | 1.17/0.50 | 2.48/0.34 | 4.23/1.00 |
| 5 | 3.08/0.86 | 5.47/0.85 | 25.37/0.95 | 35.60/0.95 |
| Mode No. | Experimental Frequency (Hz) | Dynamic Young’s Modulus, E (GPa) |
|---|---|---|
| 1 (bending) | 68.23 | 15.34 |
| 2 (twisting) | 85.78 | - |
| 3 (bending) | 143.61 | 8.81 |
| 4 (twisting) | 180.14 | - |
| 5 (bending) | 247.96 | 6.83 |
| Mode No. | Mode Shape | Numerical (Hz) | Experimental (Hz) | Difference (%) |
|---|---|---|---|---|
| 1 (First Bending) | 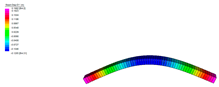 | 68.70 | 68.23 | 0.69 |
| 2 (First Twisting) |  | 86.82 | 85.78 | 1.21 |
| 3 (Second Bending) |  | 143.44 | 143.61 | 0.12 |
| 4 (Second Twisting) |  | 173.58 | 180.14 | 3.64 |
| 5 (Third Bending) | 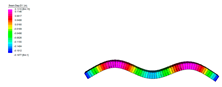 | 247.44 | 247.96 | 0.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sengsri, P.; Ngamkhanong, C.; de Melo, A.L.O.; Kaewunruen, S. Experimental and Numerical Investigations into Dynamic Modal Parameters of Fiber-Reinforced Foamed Urethane Composite Beams in Railway Switches and Crossings. Vibration 2020, 3, 174-188. https://doi.org/10.3390/vibration3030014
Sengsri P, Ngamkhanong C, de Melo ALO, Kaewunruen S. Experimental and Numerical Investigations into Dynamic Modal Parameters of Fiber-Reinforced Foamed Urethane Composite Beams in Railway Switches and Crossings. Vibration. 2020; 3(3):174-188. https://doi.org/10.3390/vibration3030014
Chicago/Turabian StyleSengsri, Pasakorn, Chayut Ngamkhanong, Andre Luis Oliveira de Melo, and Sakdirat Kaewunruen. 2020. "Experimental and Numerical Investigations into Dynamic Modal Parameters of Fiber-Reinforced Foamed Urethane Composite Beams in Railway Switches and Crossings" Vibration 3, no. 3: 174-188. https://doi.org/10.3390/vibration3030014
APA StyleSengsri, P., Ngamkhanong, C., de Melo, A. L. O., & Kaewunruen, S. (2020). Experimental and Numerical Investigations into Dynamic Modal Parameters of Fiber-Reinforced Foamed Urethane Composite Beams in Railway Switches and Crossings. Vibration, 3(3), 174-188. https://doi.org/10.3390/vibration3030014








