A Vibrometer Based on Magnetorheological Optical Resonators
Abstract
1. Introduction
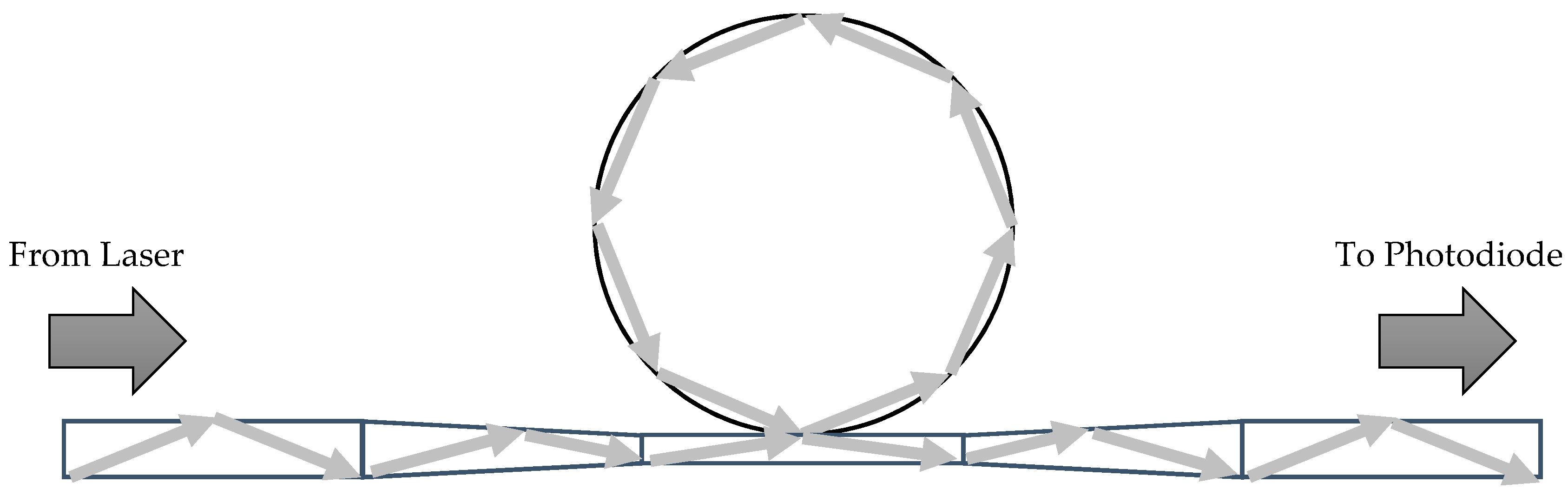
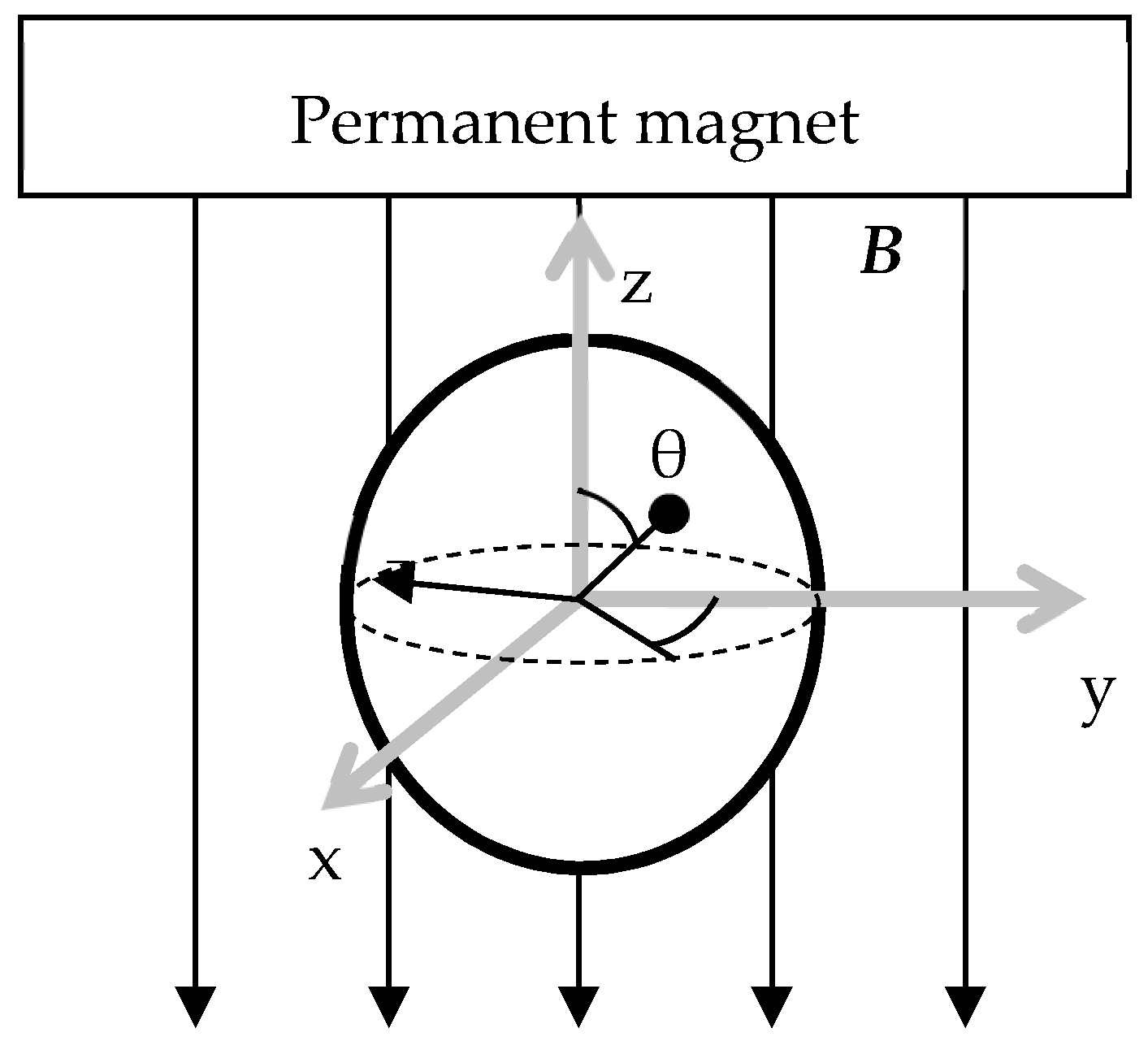
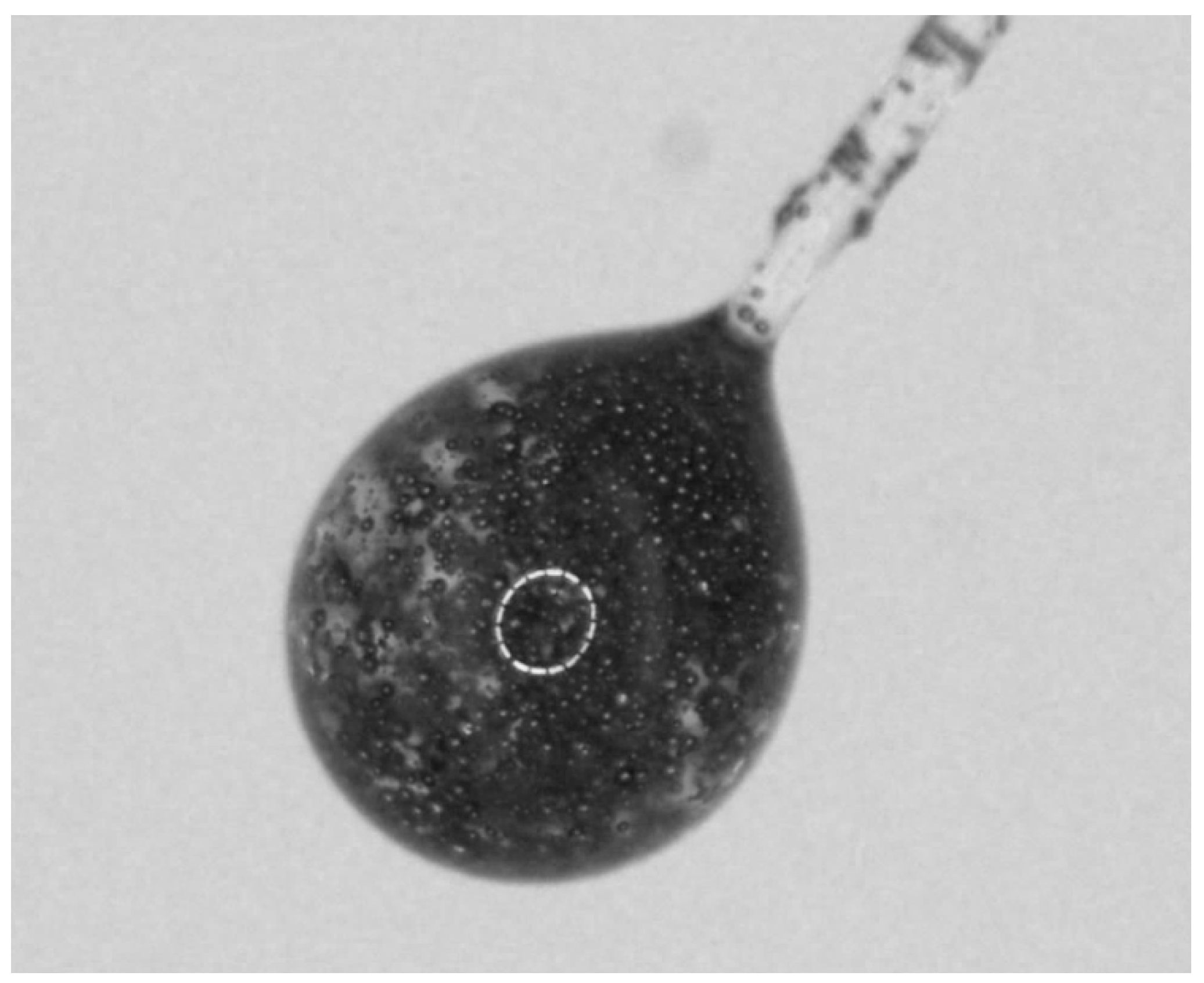
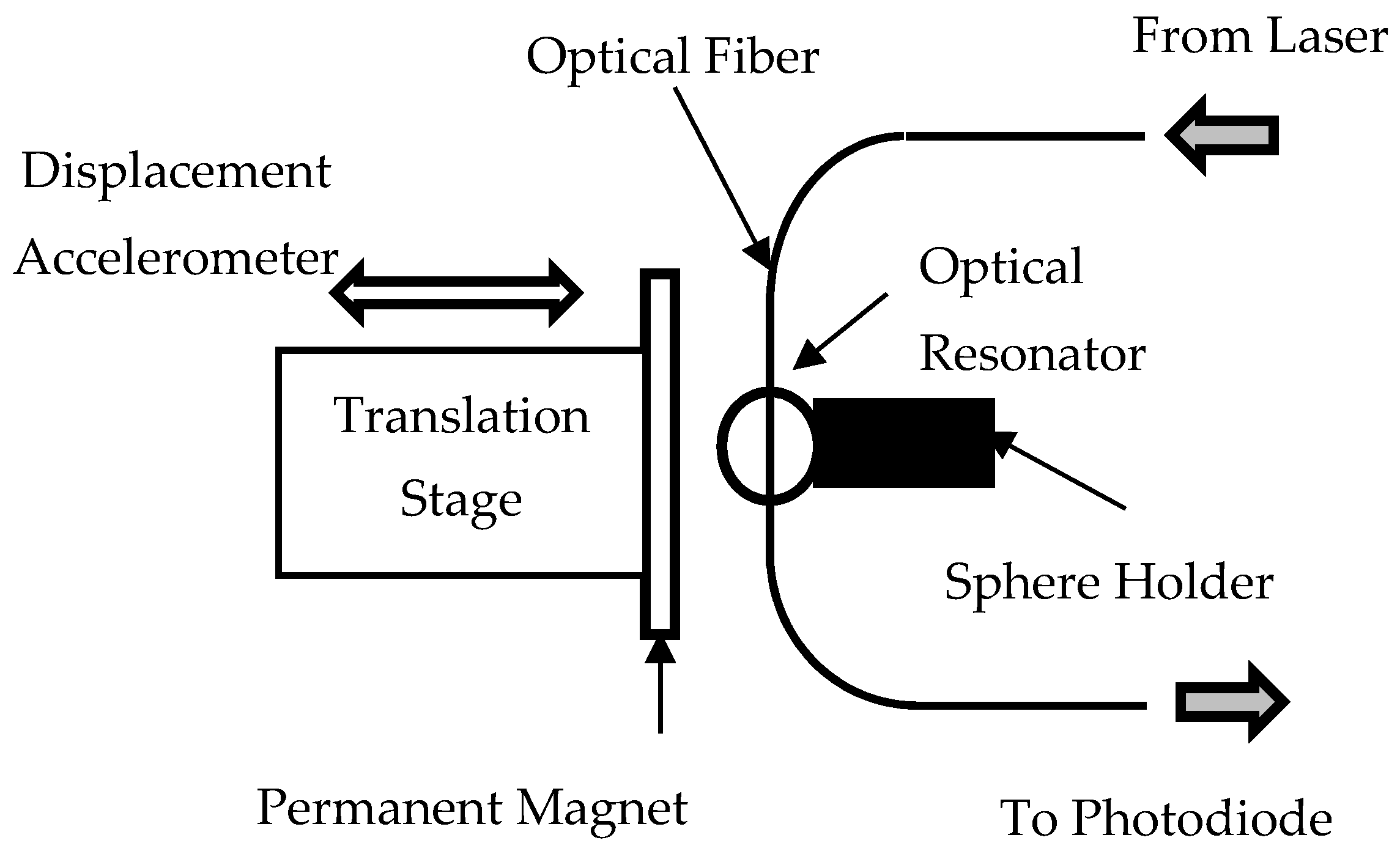
2. Sensor Concept
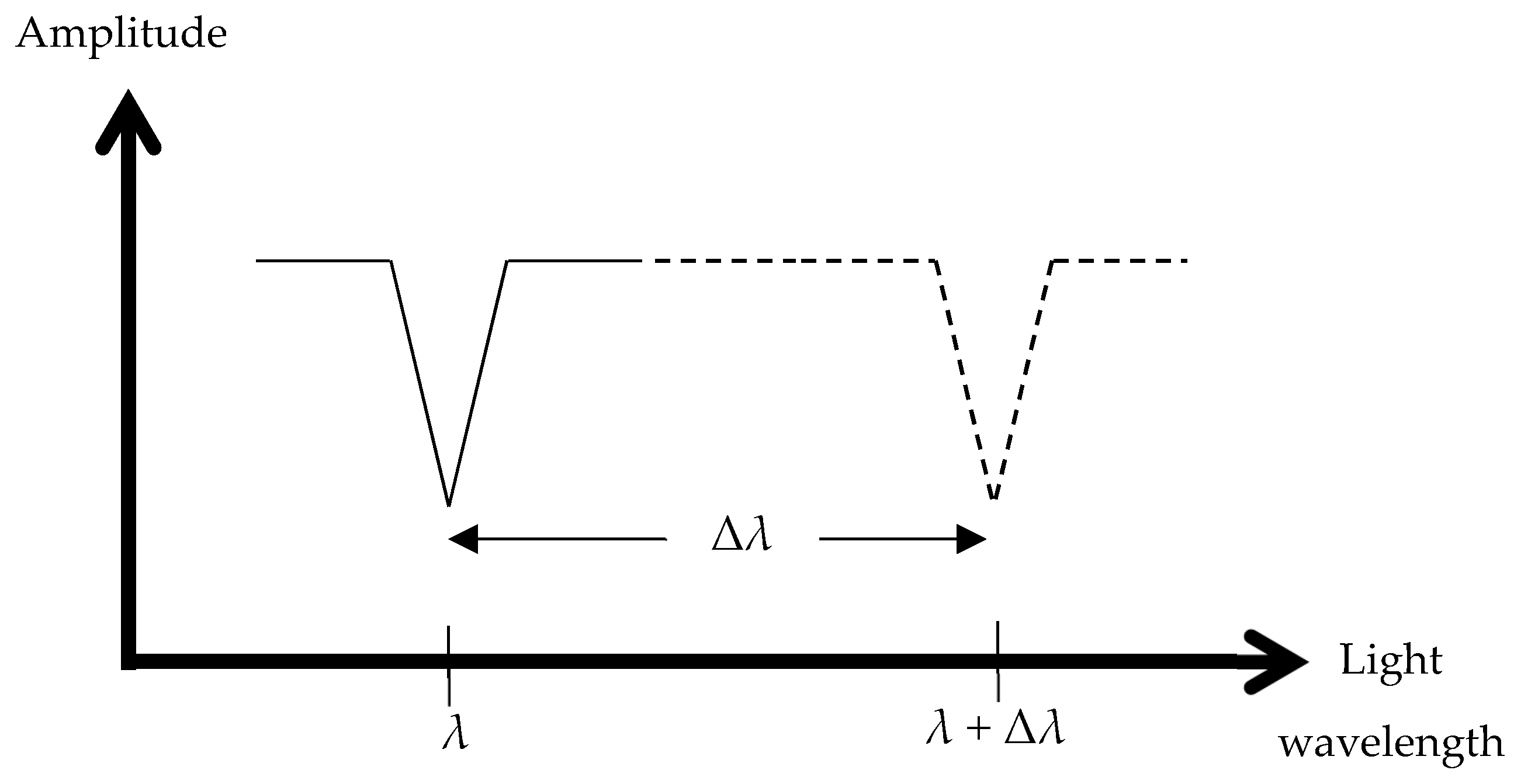
3. Analysis
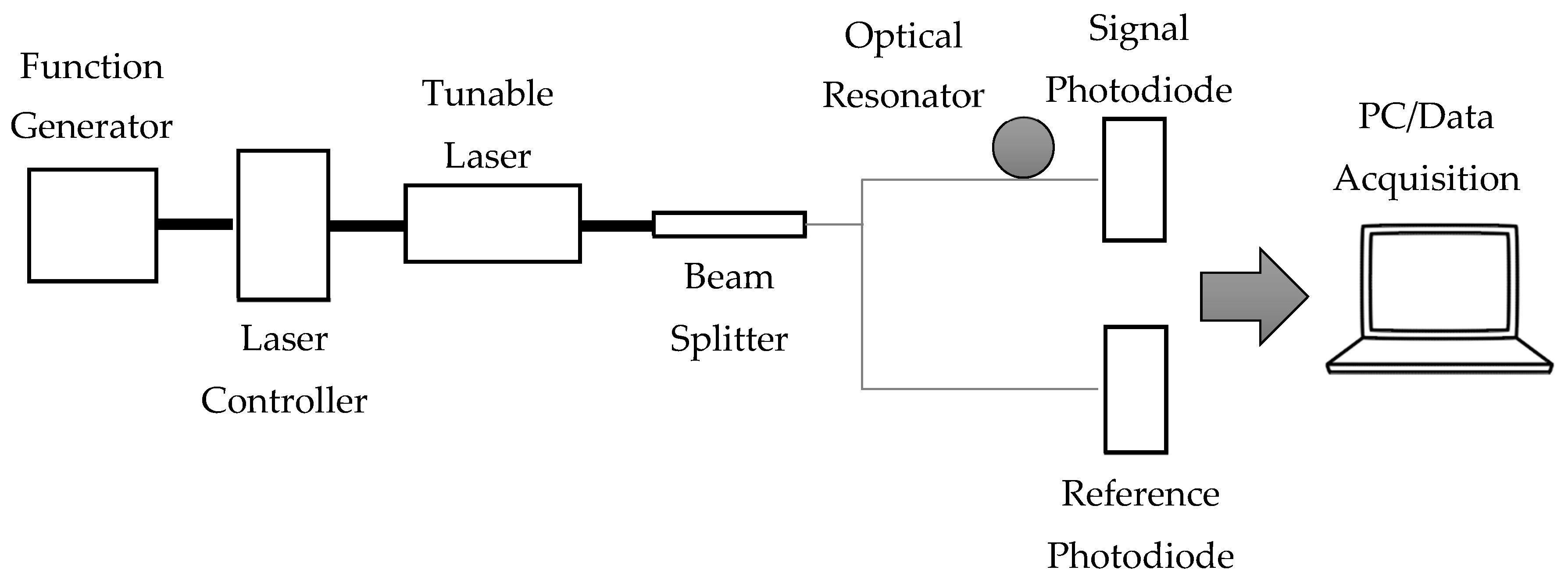
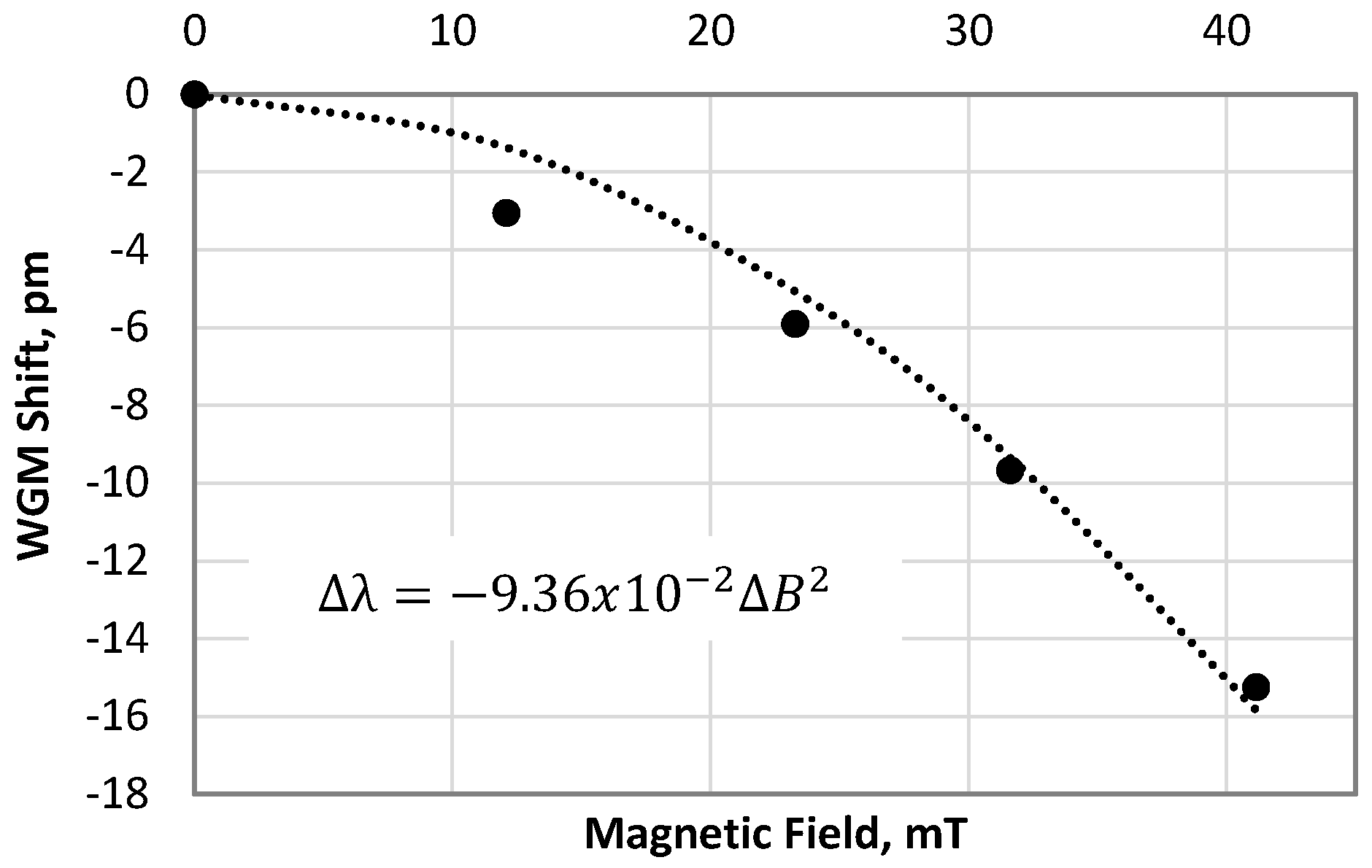
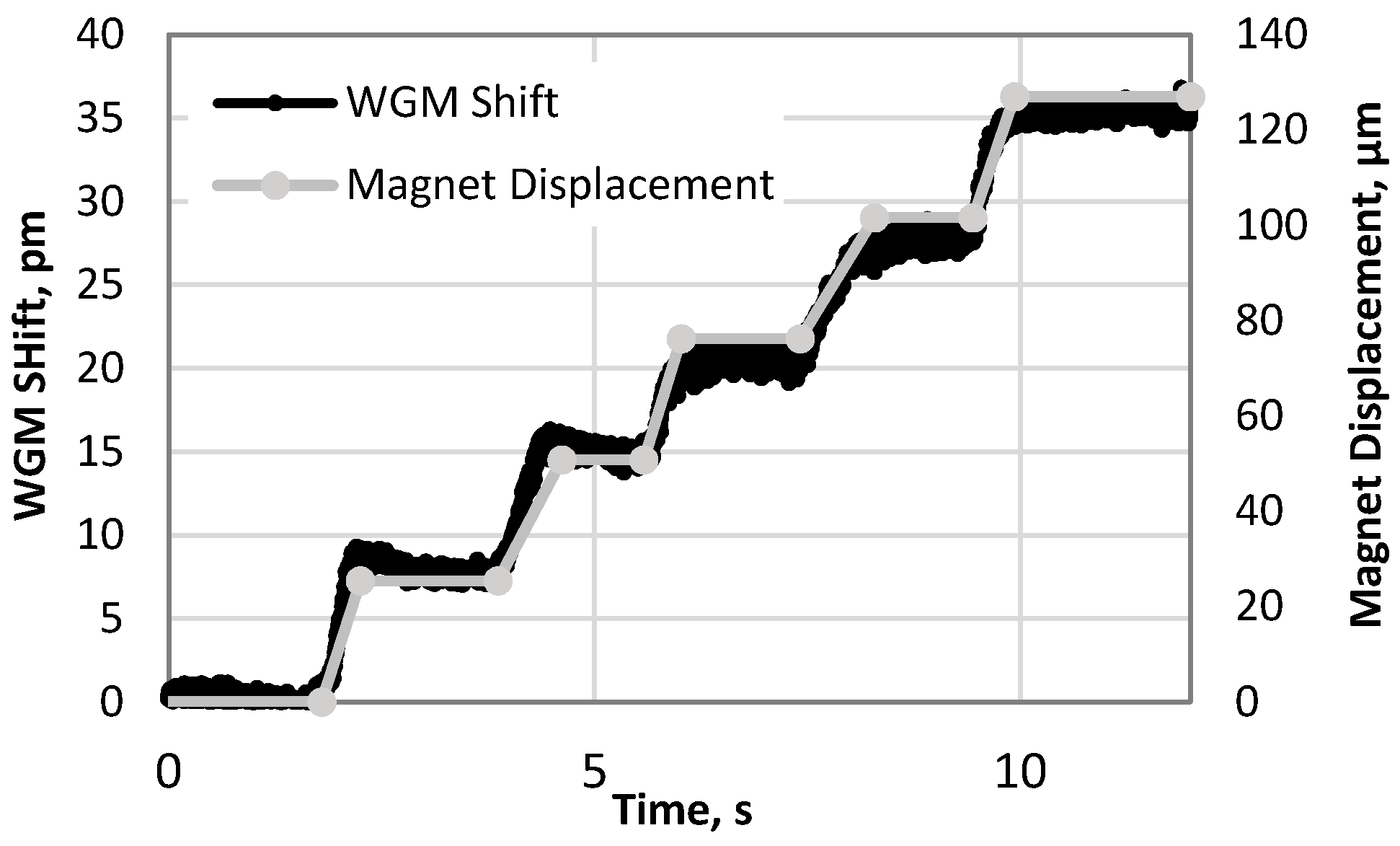
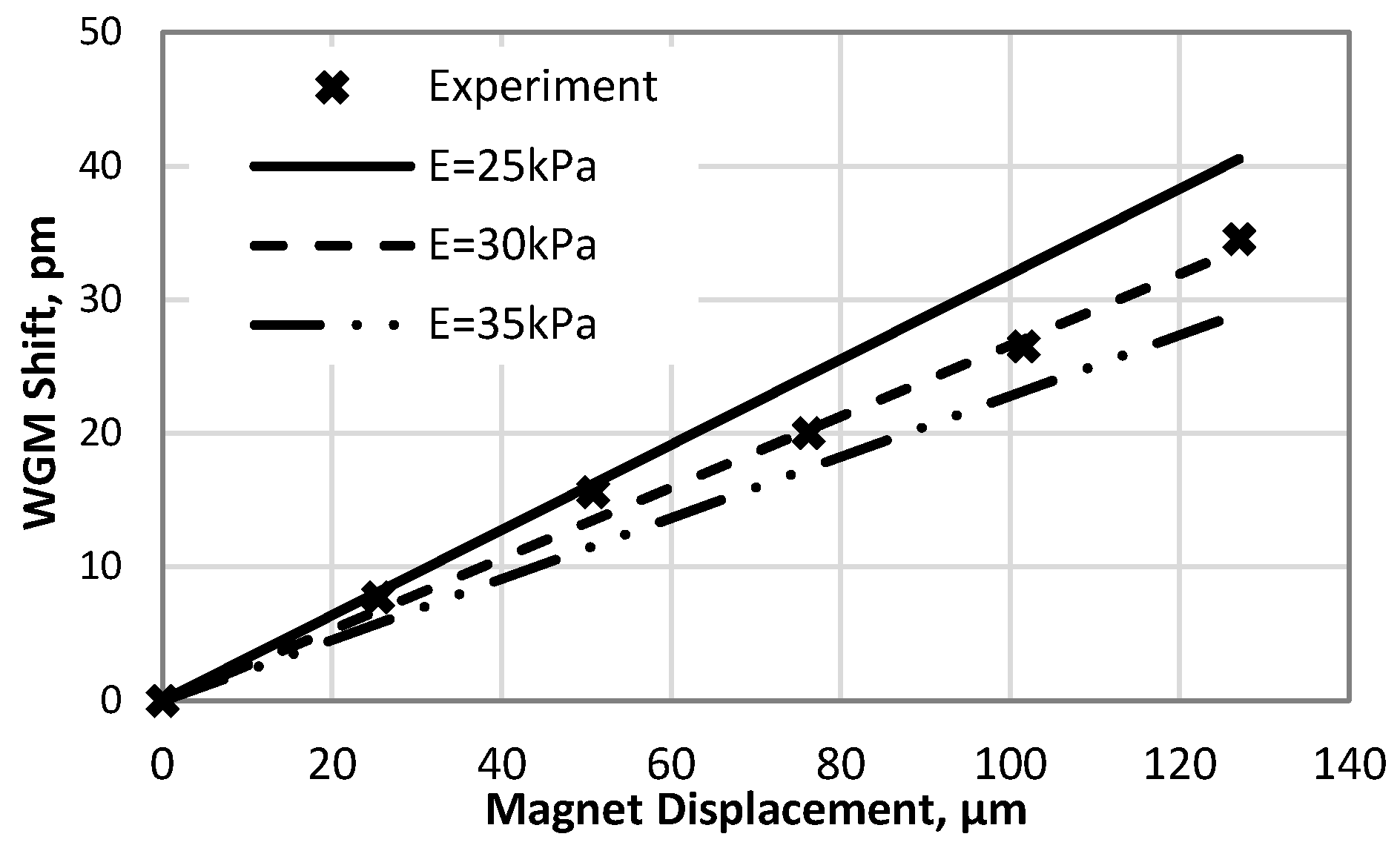
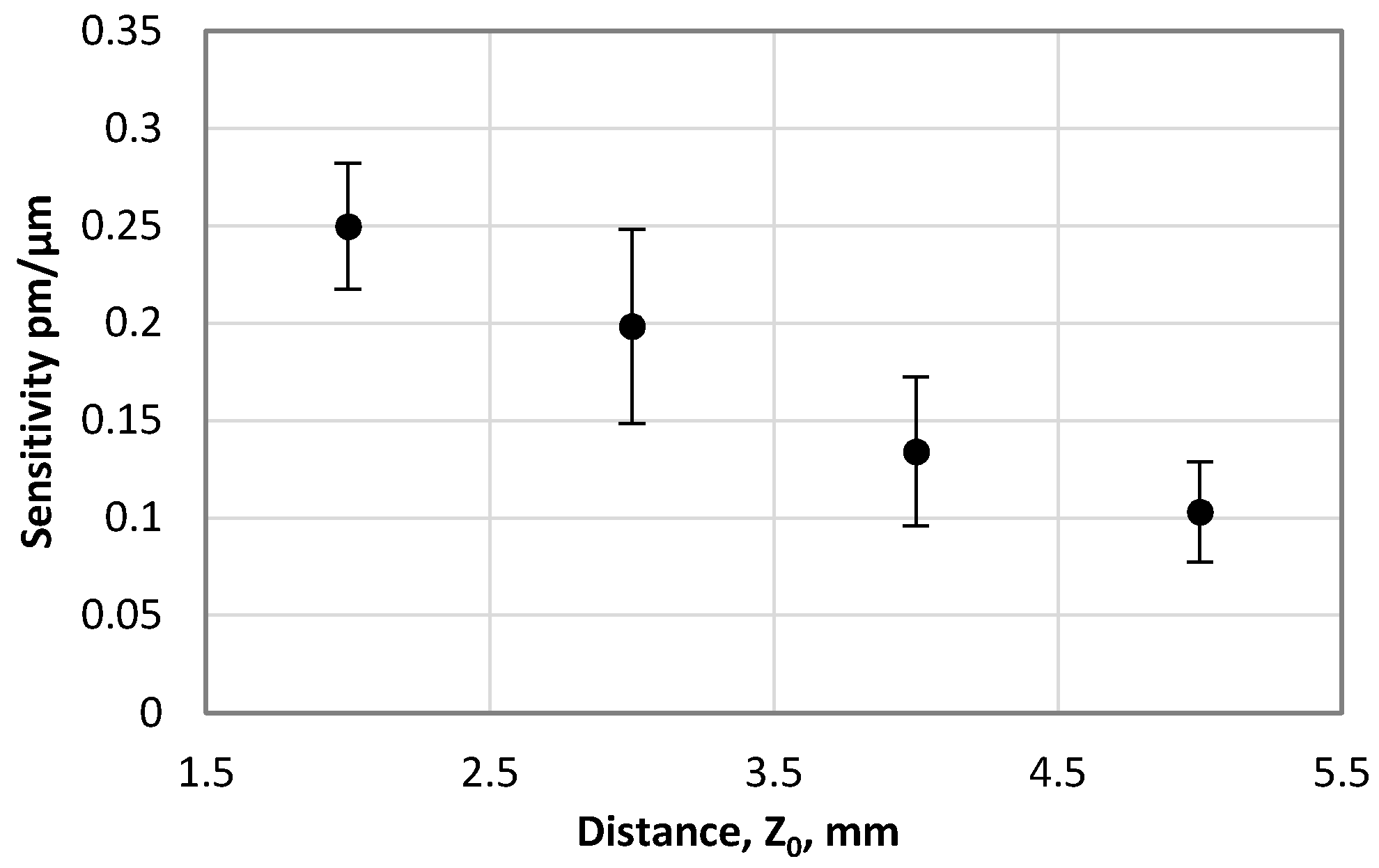
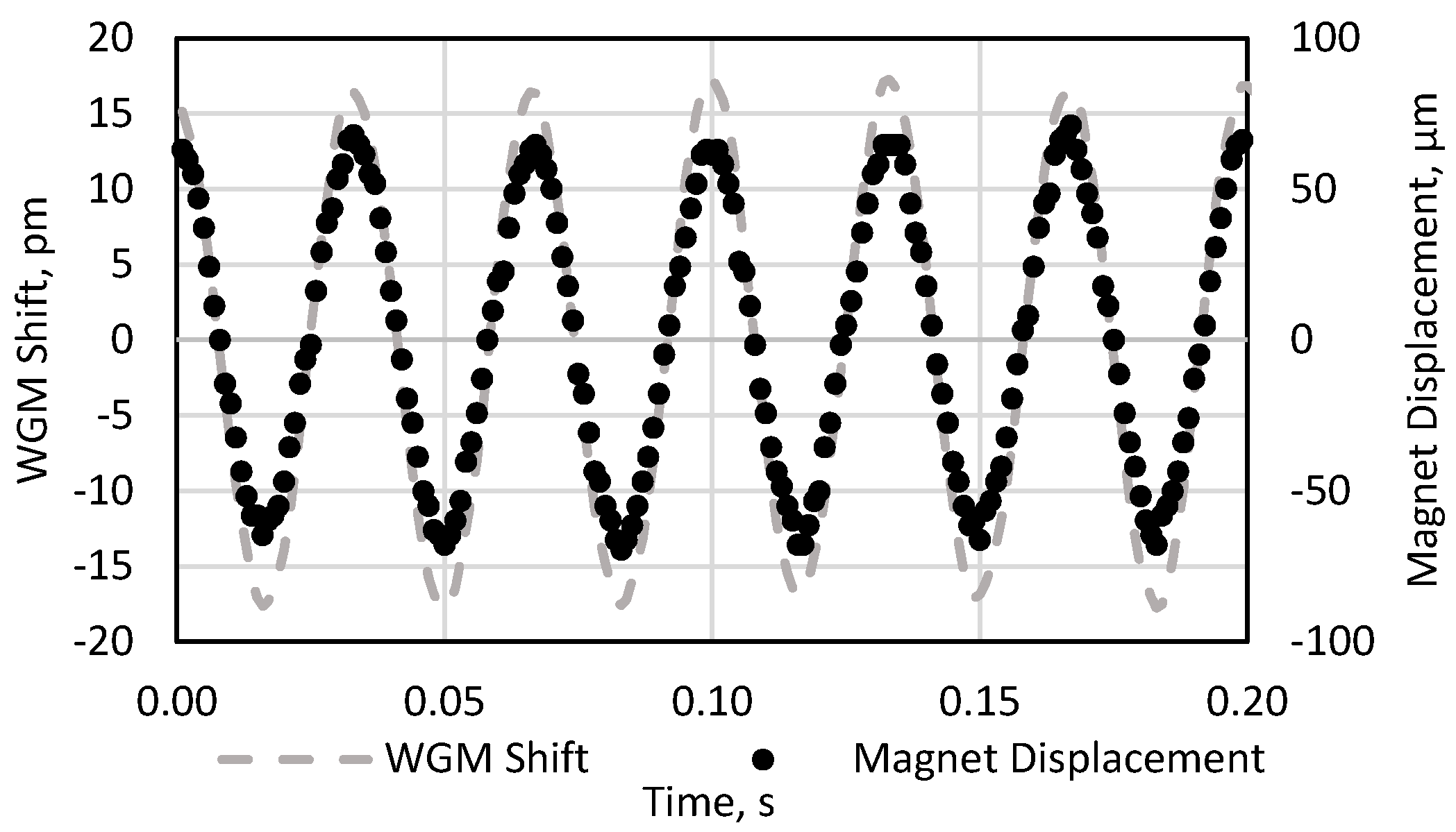
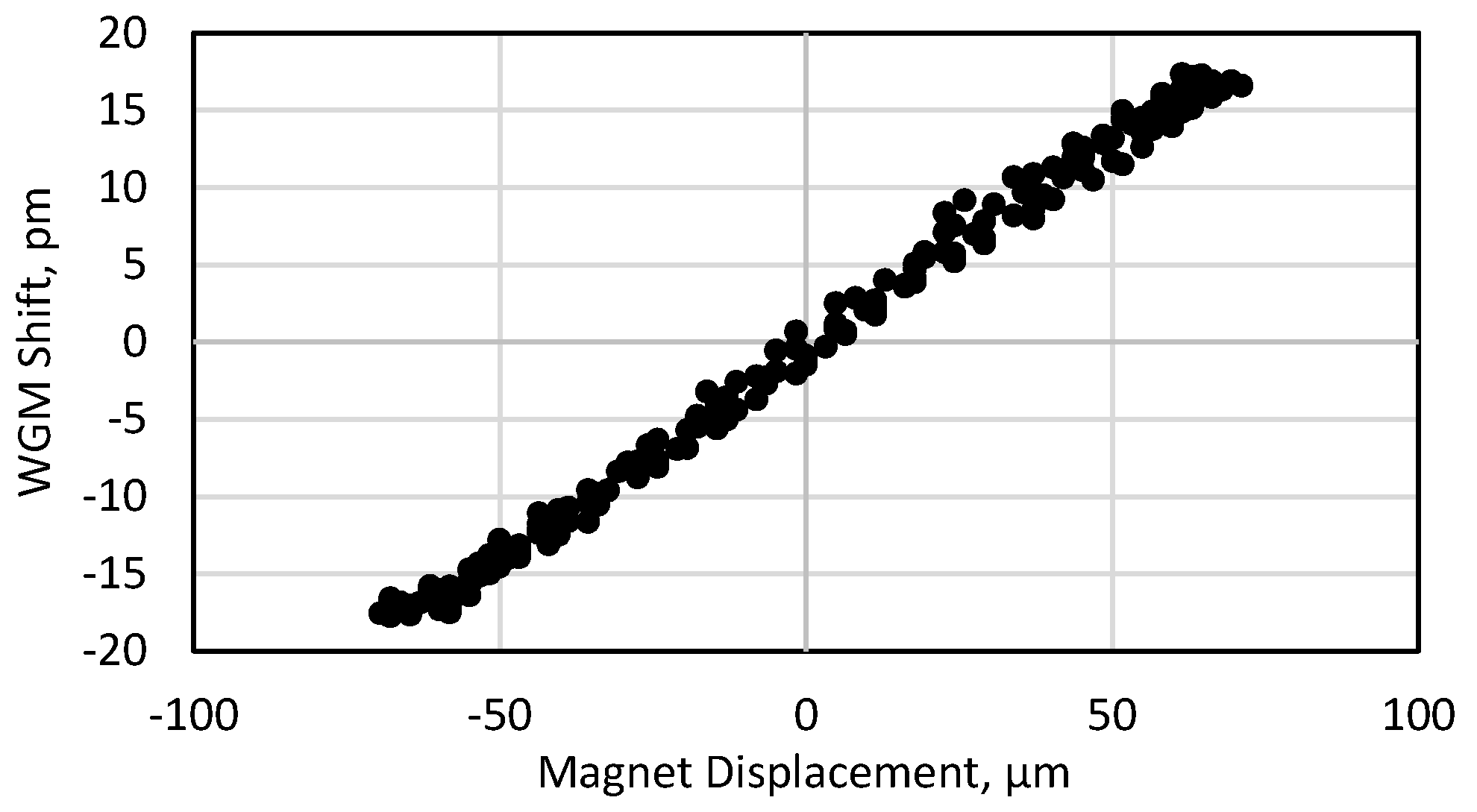
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Donati, S.; Norgia, M.; Giuliani, G. Self-mixing differential vibrometer based on electronic channel subtraction. Appl. Opt. 2006, 45, 7264. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, G.; Bozzi-Pietra, S.; Donati, S. Self-mixing laser diode vibrometer. Meas. Sci. Technol. 2003, 14, 24–32. [Google Scholar] [CrossRef]
- Stanbridge, A.B.; Ewins, D.J. Measurement of translational and angular vibration using a scanning laser Doppler vibrometer. In Proceedings of the First International Conference on Vibration Measurements by Laser Techniques: Advances and Applications, Ancona, Italy, 3–5 October 1994; Volume 2358, pp. 37–47. [Google Scholar] [CrossRef]
- Rothberg, S.J.; Allen, M.S.; Castellini, P.; Di Maio, D.; Dirckx, J.J.J.; Ewins, D.J.; Halkon, B.J.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2017, 99, 11–22. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y. Experimental study of laser Doppler vibrometer and ambient vibration for vibration-based damage detection. Eng. Struct. 2006, 28, 1803–1815. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y. Noncontact operational modal analysis of structural members by laser doppler vibrometer. Comput. Civ. Infrastruct. Eng. 2009, 24, 249–265. [Google Scholar] [CrossRef]
- Muramatsu, N.; Sakurai, N.; Wada, N.; Yamamoto, R.; Tanaka, K.; Asakura, T.; Ishikawa-Takano, Y.; Nevins, D.J. Critical comparison of an accelerometer and a laser Doppler vibrometer for measuring fruit firmness. Horttechnology 1997, 7, 434–438. [Google Scholar]
- Muramatsu, N.; Sakurai, N.; Wada, N.; Yamamoto, R.; Tanaka, K.; Asakura, T.; Ishikawa-Takano, Y.; Nevins, D.J. Remote sensing of fruit textural changes with a laser doppler vibrometer. J. Am. Soc. Hort. Sci. 1999, 125, 120–127. [Google Scholar]
- Rembe, C.; Kadner, L.; Giesen, M. Approaching attometer laser vibrometry. Rev. Sci. Instrum. 2016, 87. [Google Scholar] [CrossRef] [PubMed]
- Maekawa, A.; Noda, M.; Shintani, M.; Suzuki, M. Development of noncontact measurement methods using multiple laser displacement sensors for bending and torsional vibration stresses in piping systems. Int. J. Press. Vessel Pip. 2016, 137, 38–45. [Google Scholar] [CrossRef]
- Maekawa, A.; Noda, M.; Shintani, M. Experimental study on a noncontact method using laser displacement sensors to measure vibration stress in piping systems. Measurements 2016, 79, 101–111. [Google Scholar] [CrossRef]
- Maekawa, A.; Takahashi, T.; Tsuji, T.; Noda, M. Experimental validation of non-contacting measurement method using LED-optical displacement sensors for vibration stress of small-bore piping. Measurement 2015, 71, 1–10. [Google Scholar] [CrossRef]
- Lee, J.J.; Shinozuka, M. Real-time displacement measurement of a flexible bridge using digital image processing techniques. Exp. Mech. 2006, 46, 105–114. [Google Scholar] [CrossRef]
- Yasin, M.; Harun, S.W.; Ahmad, H. The performance of a fiber optic displacement sensor. Laser Phys. Lett. 2008, 58, 55–58. [Google Scholar] [CrossRef]
- Binu, S.; Pillai, V.P.M.; Chandrasekaran, N. Fibre optic displacement sensor for the measurement of amplitude and frequency of vibration. Opt. Laser Technol. 2007, 39, 1537–1543. [Google Scholar] [CrossRef]
- Perrone, G.; Vallan, A. A low-cost optical sensor for noncontact vibration measurements. IEEE Trans. Instrum. Meas. 2009, 58, 1650–1656. [Google Scholar] [CrossRef]
- Wu, N.; Yang, L.; Zhang, H.; Wang, X. Optical excitation and detection of a quartz crystal resonator. In Proceedings of the Smart Sensor Phenomena, Technology, Networks, and Systems Integration, San Diego, CA, USA, 8–12 March 2012; Volume 9436. [Google Scholar]
- Milewska, D.; Karpienko, K.; Jędrzejewska-Szczerska, M. Application of thin diamond films in low-coherence fiber-optic Fabry Pérot displacement sensor. Diam. Relat. Mater. 2016, 64, 169–176. [Google Scholar] [CrossRef]
- Li, J.; Neumann, H.; Ramalingam, R. Design, fabrication, and testing of fiber Bragg grating sensors for cryogenic long-range displacement measurement. Cryogenics 2015, 68, 36–43. [Google Scholar] [CrossRef]
- Gokhale, V.J.; Gorman, J.J. Optical Knife-Edge Displacement Measurement with Sub-Picometer Resolution for RF-MEMS. J. Microelectromech. Syst. 2018, 27, 910–920. [Google Scholar] [CrossRef]
- Tapalian, H.C.; Laine, J.P.; Lane, P.A. Thermooptical switches using coated microsphere resonators. IEEE Photonics Technol. Lett. 2002, 14, 1118–1120. [Google Scholar] [CrossRef]
- Little, B.E.; Chu, S.T.; Haus, H.A.; Foresi, J.; Laine, J.P. Microring resonator channel dropping filters. J. Lightw. Technol. 1997, 15, 998–1005. [Google Scholar] [CrossRef]
- Ilchenko, V.; Volikov, P.; Velichansky, V.; Treussart, F.; Lefèvre-Seguin, V.; Raimond, J.-M.; Haroche, S. Strain-tunable high-Q optical microsphere resonator. Opt. Commun. 1998, 145, 86–90. [Google Scholar] [CrossRef]
- Monifi, F.; Ozdemir, S.K.; Yang, L. Tunable add-drop filter using an active whispering gallery mode microcavity. Appl. Phys. Lett. 2013, 103, 181103. [Google Scholar] [CrossRef]
- Rubino, E.; Ioppolo, T. Electrostrictive optical resonators for non-contact displacement measurement. Appl. Opt. 2017, 56, 229–233. [Google Scholar] [CrossRef] [PubMed]
- Ioppolo, T. Whispering Gallery Mode-Based Micro Optical Sensors for Aerospace Applications; Polytechnic University: New York, NY, USA, 2008. [Google Scholar]
- Rubino, E.; Ioppolo, T. Non-contact photonic displacement sensor based on the morphology dependent resonances. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; pp. 2–6. [Google Scholar]
- Rubino, E. Magnetic Field and Electric Field Effect on Magnetostrictive and Electrostrictive Photonic Resonators; Southern Methodist University: Dallas, TX, USA, 2016. [Google Scholar]
- Ciminelli, C.; Dell’Olio, F.; Campanella, C.; Armenise, M.N. Photonic technologies for angular velocity sensing. Adv. Opt. Photonics 2010, 2, 370–404. [Google Scholar] [CrossRef]
- Matsko, A.B.; Savchenkov, A.; Ilchenko, V.S.; Maleki, L. Optical gyroscope with whispering gallery mode optical cavities. Opt. Commun. 2004, 233, 107–112. [Google Scholar] [CrossRef]
- Quang, N.; Gupta, N.; Ioppolo, T.; Otugen, V. Whispering gallery mode-based micro-optical sensors for structural health monitoring of composite materials. J. Mater. Sci. 2009, 1560–1571. [Google Scholar] [CrossRef]
- Rubino, E.; Ioppolo, T. Magnetic field detection using magnetorheological optical resonators. In Proceedings of the SPIE OPTO 2018, San Francisco, CA, USA, 2–7 February 2018. [Google Scholar] [CrossRef]
- Guan, G.; Arnold, S.; Otugen, V. Temperature measurements using a microoptical sensor based on whispering gallery modes. AIAA J. 2006, 44, 2385–2389. [Google Scholar] [CrossRef]
- Ioppolo, T.; Manzo, M. Dome-shaped whispering gallery mode laser for remote wall temperature sensing. Appl. Opt. 2014, 53, 5065–5069. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, M.; Avellan, M.; Guo, Z. Whispering-gallery mode composite sensors for on-chip dynamic temperature monitoring. Meas. Sci. Technol. 2013, 24. [Google Scholar] [CrossRef]
- Dong, C.-H.; He, L.; Xiao, Y.-F.; Gaddam, V.R.; Ozdemir, S.K.; Han, Z.-F.; Guo, G.-C.; Yang, L. Fabrication of high-Q polydimethylsiloxane optical microspheres for thermal sensing. Appl. Phys. Lett. 2009, 94, 231119. [Google Scholar] [CrossRef]
- Ioppolo, T.; Das, N.; Ötügen, M.V. Whispering gallery modes of microspheres in the presence of a changing surrounding medium: A new ray-tracing analysis and sensor experiment. J. Appl. Phys. 2010, 107, 103105. [Google Scholar] [CrossRef]
- Vollmer, F.; Braun, D.; Libchaber, A.; Khoshsima, M.; Teraoka, I.; Arnold, S. Protein detection by optical shift of a resonant microcavity. Appl. Phys. Lett. 2002, 80, 4057–4059. [Google Scholar] [CrossRef]
- Arnold, S.; Khoshsima, M.; Teraoka, I.; Holler, S.; Vollmer, F. Shift of whispering-gallery modes in microspheres by protein adsorption. Opt. Lett. 2003, 28, 272–274. [Google Scholar] [CrossRef] [PubMed]
- Armani, A.M.; Vahala, K.J. Heavy water detection using ultra-high-Q microcavities. Opt. Lett. 2006, 31, 1896–1898. [Google Scholar] [CrossRef] [PubMed]
- Chistiakova, M.V.; Armani, A.M. Optical detection of CO and CO2 temperature dependent desorption from carbon nanotube clusters. Nanotechnology 2014, 25, 395201. [Google Scholar] [CrossRef] [PubMed]
- Cicek, K.; Eryürek, M.; Kiraz, A. Single-slot hybrid microring resonator hydrogen sensor. J. Opt. Soc. Am. B 2017, 34, 1465. [Google Scholar] [CrossRef]
- Ioppolo, T.; Ötügen, M.V. Magnetorheological polydimethylsiloxane micro-optical resonator. Opt. Lett. 2010, 35, 2037–2039. [Google Scholar] [CrossRef] [PubMed]
- Ioppolo, T.; Otugen, V.; Marcis, K. Magnetic field-induced excitation and optical detection of mechanical modes of microspheres. J. Appl. Phys. 2010, 107, 123115. [Google Scholar] [CrossRef]
- Ioppolo, T.; Kozhevnikov, M.; Stepaniuk, V.; Ötügen, M.V.; Sheverev, V. Micro-optical force sensor concept based on whispering gallery mode resonators. Appl. Opt. 2008, 47, 3009–3014. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubino, E.; Ioppolo, T. A Vibrometer Based on Magnetorheological Optical Resonators. Vibration 2018, 1, 239-249. https://doi.org/10.3390/vibration1020017
Rubino E, Ioppolo T. A Vibrometer Based on Magnetorheological Optical Resonators. Vibration. 2018; 1(2):239-249. https://doi.org/10.3390/vibration1020017
Chicago/Turabian StyleRubino, Edoardo, and Tindaro Ioppolo. 2018. "A Vibrometer Based on Magnetorheological Optical Resonators" Vibration 1, no. 2: 239-249. https://doi.org/10.3390/vibration1020017
APA StyleRubino, E., & Ioppolo, T. (2018). A Vibrometer Based on Magnetorheological Optical Resonators. Vibration, 1(2), 239-249. https://doi.org/10.3390/vibration1020017





