A Robust Methodology for the Reconstruction of the Vertical Pedestrian-Induced Load from the Registered Body Motion
Abstract
1. Introduction
2. Experimental Data
3. Initial Approximation: Newton’s Second Law
4. New Approach: Combining the Experimentally Identified Time-Variant Pacing Rate with a Single-Step Load Model
4.1. Numerical Investigations
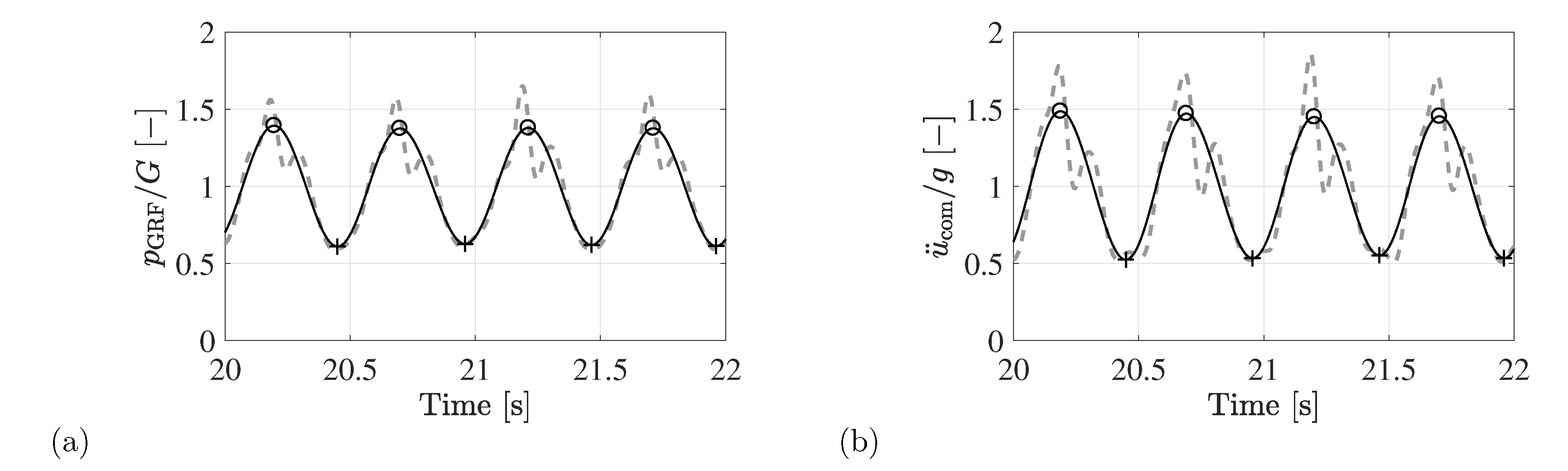
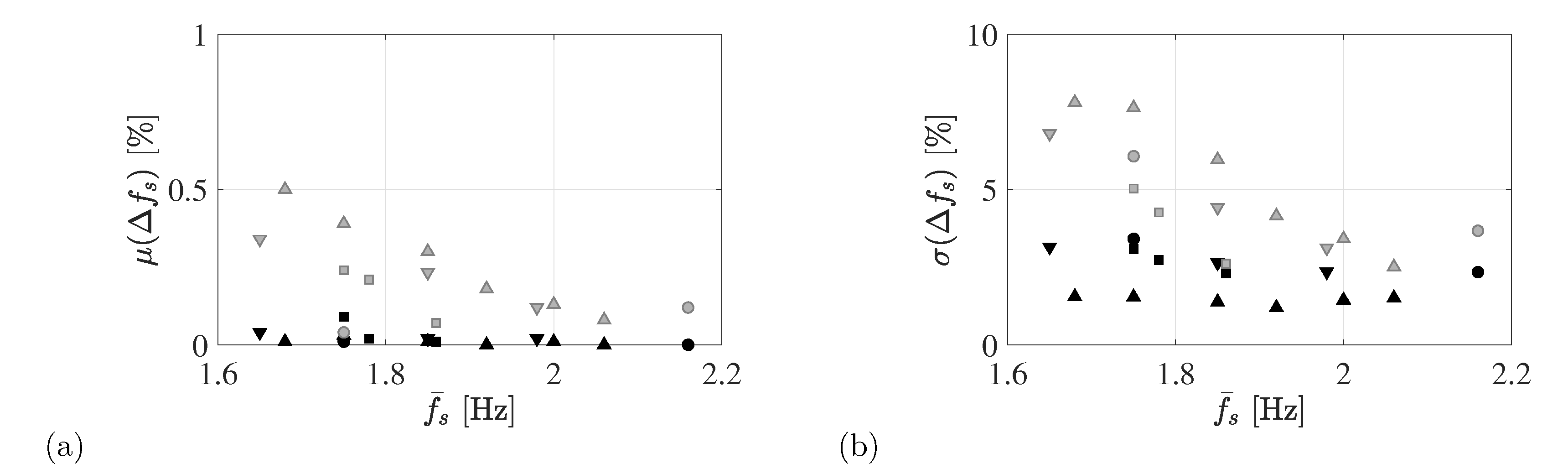
4.1.1. Identification of the Time-Variant Pacing Rate
4.1.2. Influence of a Cut-off Frequency at or
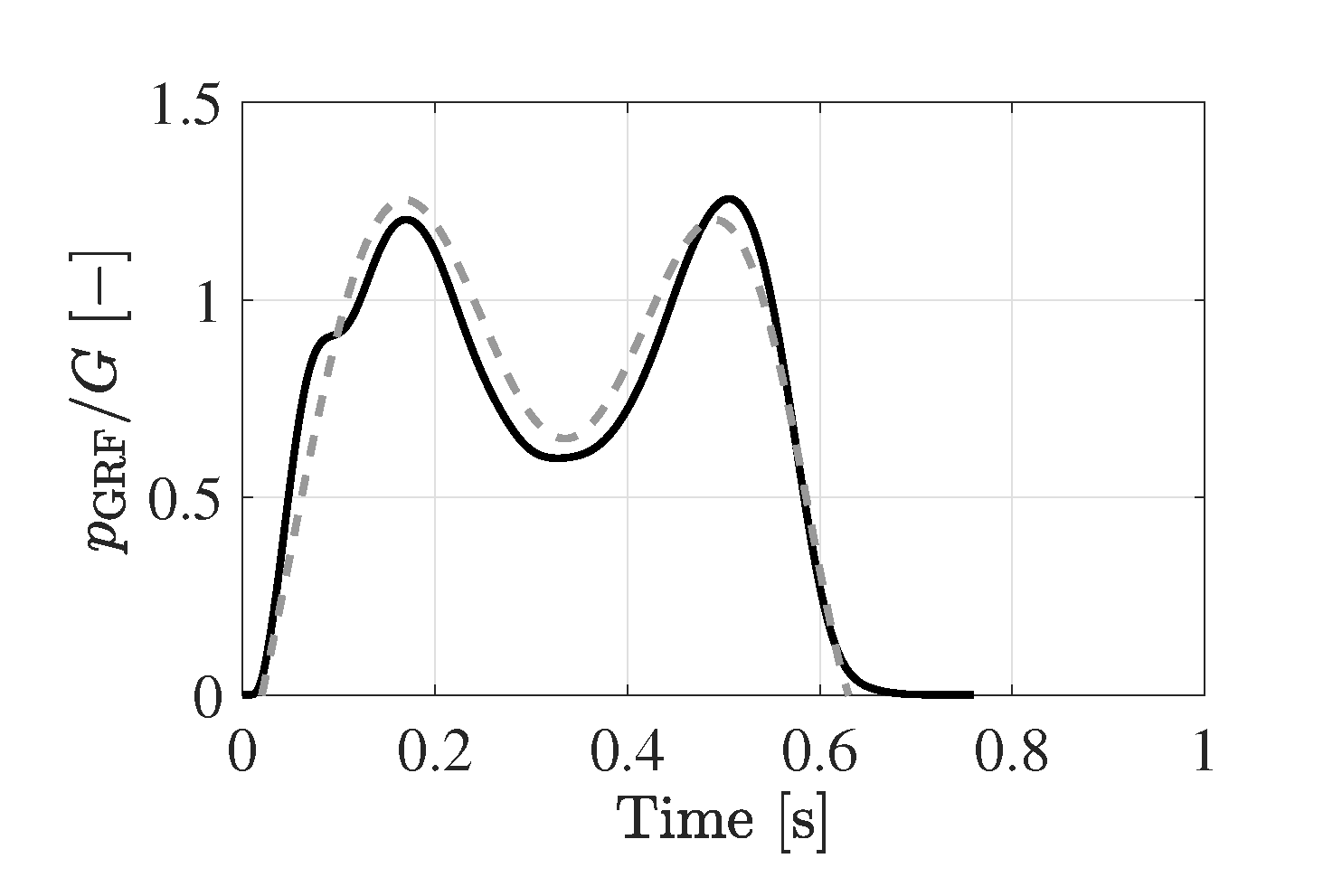
4.1.3. Influence of the Single-Step Load Model
- The coefficient on average reduces with 10%,
- The coefficient on average reduces with 5%.
4.2. Application to the Experimentally Registered Body Motion
4.3. Summary
- An experiment is performed where the body motion of the pedestrian is registered, e.g., the acceleration levels close to the BCoM.
- The registered body motion data is preprocessed:
- the data is resampled at at least 500 Hz: Given the accuracy that has to be attained when identifying the time-variant pacing rate (), a resolution in time domain of 0.002 s is recommend. This resolution corresponds to 0.5% of the smallest period of the walking cycle that reasonably can be expected, i.e., corresponding to a step frequency of 2.5 Hz;
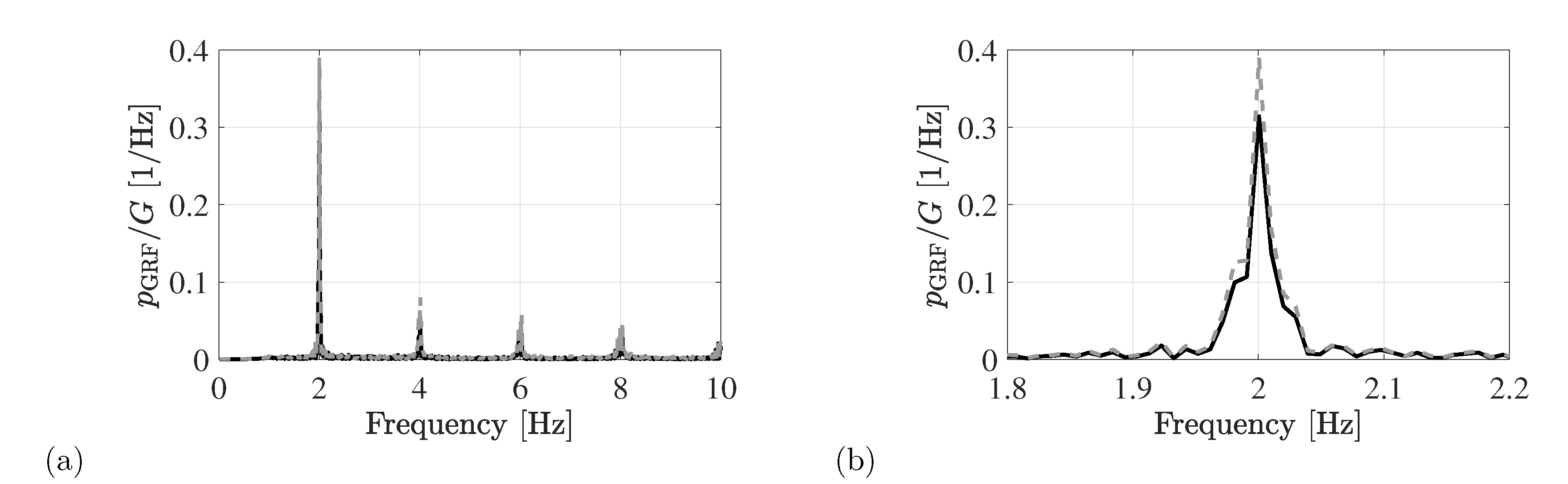
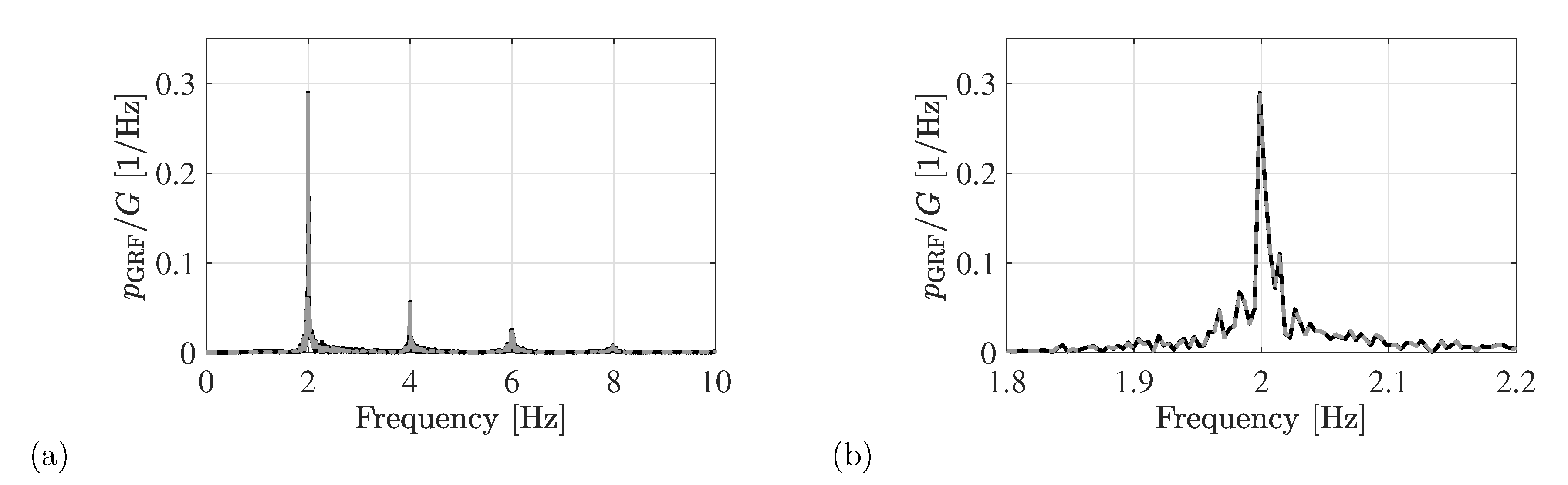
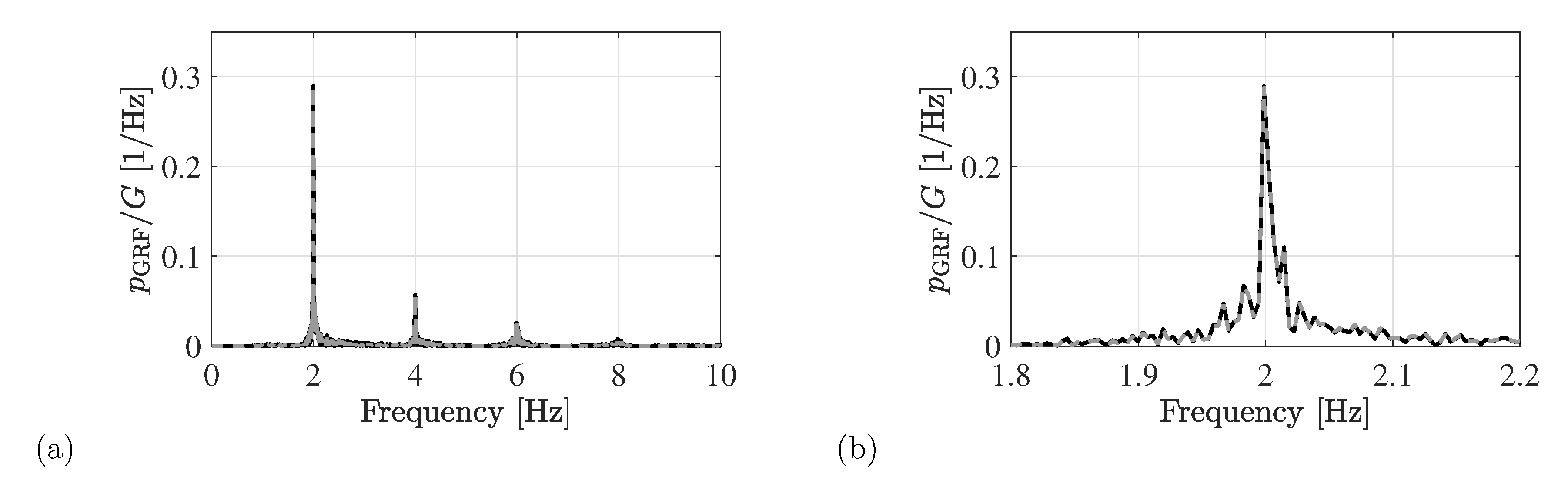
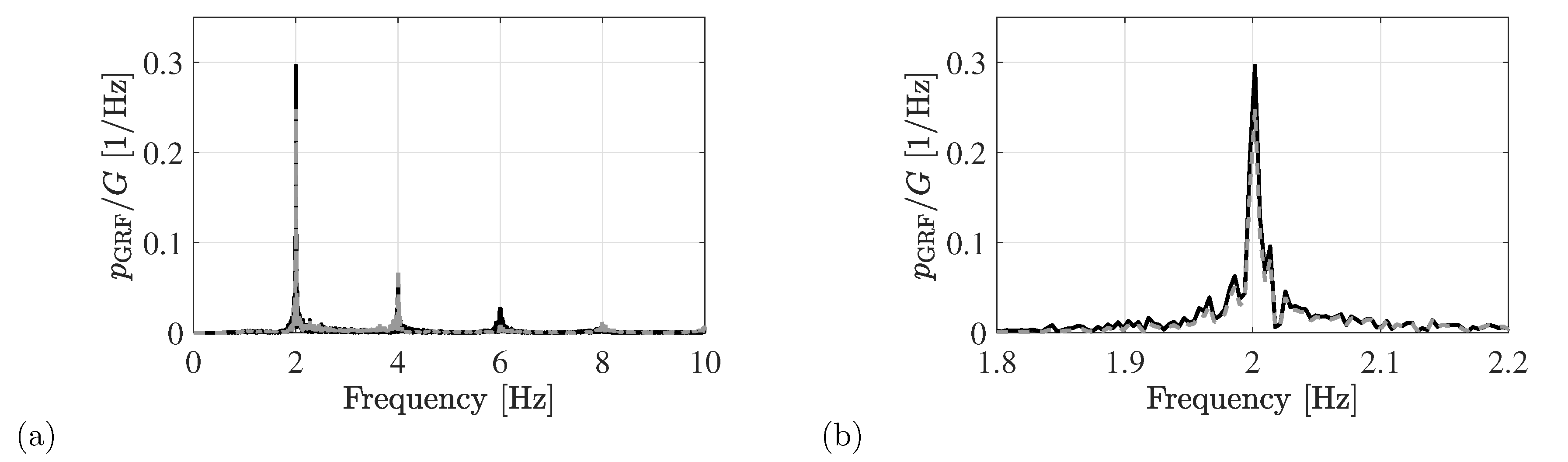
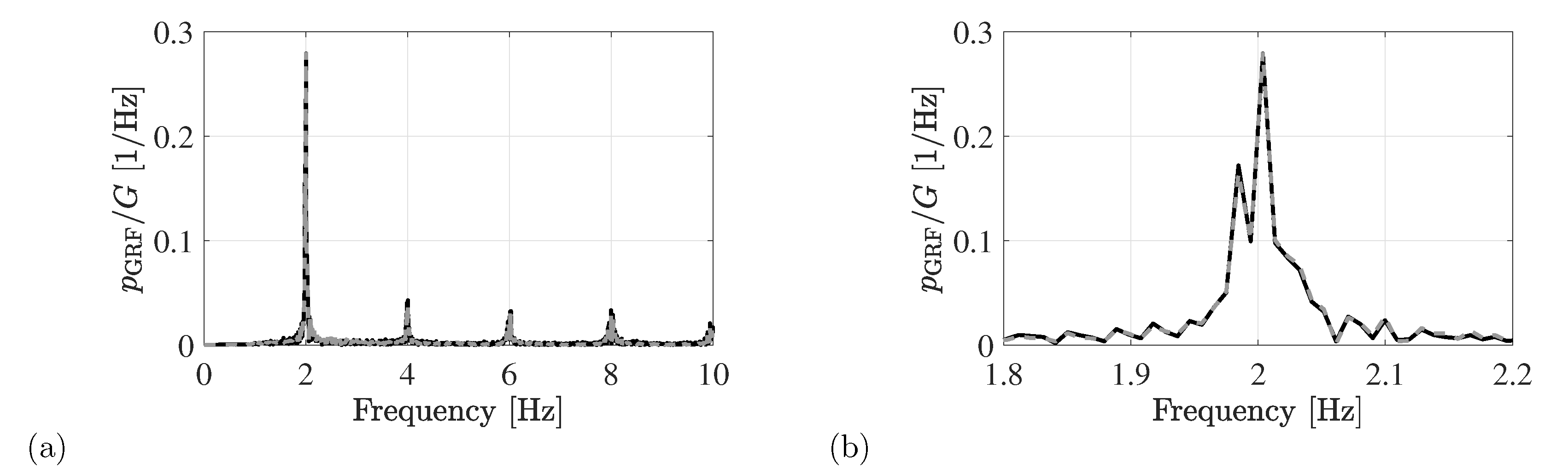
- the mean step frequency is estimated as the dominant contribution in the PSD of the registered body motion in the relevant frequency range [1.0–2.5] Hz. A frequency resolution of at least 0.05 Hz is recommended;
- the data is lowpass filtered with a cut-off frequency at .
- The preprocessed data is used to identify the time-variant pacing rate using the method detailed in Section 4.1.1, preferably based on the double-stance peaks. If necessary, apply the appropriate time shift to arrive at an estimate of the actual onset of each step.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BCoM | Body Centre of Mass |
| CoM | Centre of Mass |
| GRFs | Ground Reaction Forces |
| HSI | Human–Structure Interaction |
| PSD | Power Spectral Density |
References
- Živanović, S.; Pavić, A.; Reynolds, P. Vibration serviceability of footbridges under human-induced excitation: A literature review. J. Sound Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef]
- Association Française de Génie Civil, Sétra/AFGC. Sétra: Evaluation du Comportement Vibratoire des Passerelles Piétonnes Sous L’action des Piétons (Assessment of Vibrational Behaviour of Footbridges Under Pedestrian Loading); AFGC: Paris, France, 2006. [Google Scholar]
- Heinemeyer, C.; Butz, C.; Keil, A.; Schlaich, M.; Goldack, A.; Lukić, M.; Chabrolin, B.; Lemaire, A.; Martin, P.; Cunha, A.; Caetano, E. Design of Lightweight Footbridges for Human Induced Vibrations—Background Document in Support to the Implementation, Harmonization and Further Development of the Eurocodes; JRC-ECCS 2009; EU Publications: Luxembourg, 2009. [Google Scholar]
- Georgakis, C.T.; Ingólfsson, E. Recent advances in our understanding of vertical and lateral footbridge vibrations. In Proceedings of the 5th International Footbridge Conference, London, UK, 6–18 July 2014. [Google Scholar]
- Venuti, F.; Racic, V.; Corbetta, A. Modelling framework for dynamic interaction between multiple pedestrians and vertical vibrations of footbridges. J. Sound Vib. 2016, 379, 245–263. [Google Scholar] [CrossRef]
- Zang, M.; Georgakis, C.; Chen, J. Biomechanically Excited SMD Model of a Walking Pedestrian. J. Bridge Eng. 2016, 21. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavić, A.; Racić, V. Interaction between Walking Humans and Structures in Vertical Direction: A Literature Review. Shock Vib. 2016, 12–17. [Google Scholar] [CrossRef]
- Dang, H.; Živanović, S. Influence of Low-Frequency Vertical Vibration on Walking Locomotion. J. Struct. Eng. 2016. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. The impact of vertical human–structure interaction on the response of footbridges to pedestrian excitation. J. Sound Vib. 2017, 402, 104–121. [Google Scholar] [CrossRef]
- Živanović, S. Benchmark footbridge for vibration serviceability assessment under vertical component of pedestrian load. J. Struct. Eng. 2012, 138, 1193–1202. [Google Scholar] [CrossRef]
- McDonald, M.; Živanović, S. Measuring ground reaction force and quantifying variability in jumping and bobbing actions. J. Struct. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Racić, V.; Brownjohn, J.M.W.; Pavić, A. Reproduction and application of human bouncing and jumping forces from visual marker data. J. Sound Vib. 2010, 329, 3397–3416. [Google Scholar] [CrossRef]
- Carroll, S.P.; Owen, J.S.; Hussein, M.F.M. Reproduction of lateral ground reaction forces from visual marker data and analysis of balance response while walking on a laterally oscillating deck. Eng. Struct. 2013, 49, 1034–1047. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; Jonkers, I.; De Roeck, G.; Van den Broeck, P. Characterisation of walking loads by 3D inertial motion tracking. J. Sound Vib. 2014, 333, 5212–5226. [Google Scholar] [CrossRef]
- Toso, M.; Gomes, H.; da Silva, F.; Pimentel, R. Experimentally fitted biodynamic models for pedestrian-structure interaction in walking situations. Mech. Syst. Signal Process. 2015, 72–73, 590–606. [Google Scholar] [CrossRef]
- Bocian, M.; Brownjohn, J.; Racic, V.; Hester, D.; Quattrone, A.; Monnickendam, R. A framework for experimental determination of localised vertical pedestrian forces on full-scale sturctures using wireless attitude and heading reference systems. J. Sound Vib. 2016, 376, 217–243. [Google Scholar] [CrossRef]
- Brownjohn, J.; Bocian, M.; Hester, D.; Quattrone, A.; Hudson, W.; Moore, D.; Goh, S.; Lim, M. Footbridge system identification using wireless inertial measurement units for force and response measurements. J. Sound Vib. 2016, 384, 339–355. [Google Scholar] [CrossRef]
- Bocian, M.; Brownjoh, J.; Racić, V.; Hester, D.; Quattrone, A.; Gilbert, L.; Beasley, R. Time-dependent spectral analysis of interactions within groups of walking pedestrians and vertical structural motion using wavelets. Mech. Syst. Signal Process. 2018, 105, 502–523. [Google Scholar] [CrossRef]
- Brownjoh, J.; Chen, J.; Bocian, M.; Racić, V.; Shahabpoor, E. Using inertial measurement units to identify medio-lateral ground reaction forces due to walking and swaying. J. Sound Vib. 2018, 426, 90–110. [Google Scholar] [CrossRef]
- Dang, H.; Živanović, S. Experimental characterisation of walking locomotion on rigid level surfaces using motion capture system. Eng. Struct. 2015, 91, 141–154. [Google Scholar] [CrossRef]
- Nigg, B.M.; Herzog, W. Biomechanics of the Musculo-Skeletal System, 3rd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Shahabpoor, E.; Pavic, A.; Brownjohn, J.; Billings, S.; Guo, L.; Bocian, M. Real-life measurement of tri-axial walking ground reaction forces using optimal network of wearable inertial measurement units. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1243–1253. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Butz, C. Beutrag zur Berechnung Fussgängerinduzierter Brückenschwingungen—Shaker Verlag (Contribution to the Determination of Pedestrian Induced Bridge Vibrations). Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2006. [Google Scholar]
- Middleton, C. Dynamic Performance of High Frequency Floors. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2009. [Google Scholar]
- Duysens, J.; Jonkers, I.; Verschueren, S. MALL: Movement & Posture Analysis Laboratory Leuven; Interdepartmental Research Laboratory at the Faculty of Kinisiology and Rehabilitation Sciences: Leuven, Belgium.
- Racić, V.; Pavić, A.; Reynolds, P. Experimental identification and analytical modelling of walking forces: A literature review. J. Sound Vib. 2009, 326, 1–49. [Google Scholar] [CrossRef]
- Paolini, G.; Croce, U.; Riley, P.; Neuwton, F.; Kerrigan, D. Testing of a tri-instrumented-treadmill unit for kinetic analysis of locomotion tasks in static and dynamic loading conditions. Med. Eng. Phys. 2007, 29, 404–411. [Google Scholar] [CrossRef]
- MATLAB. R2015b, The MathWorks Inc.: Natick, MA, USA, 2015.
- Van den Bogert, A.; Read, L.; Nogg, B. A method for inverse dynamic analysis using accelerometry. J. Biomech. 1996, 29, 949–954. [Google Scholar] [CrossRef]
- Liikavainio, T.; Bragge, T.; Hakkarainen, M.; Jurvelin, J.; Karjalainen, P.; Arokoski, J. Reproducibility of loading measurements with skin-mounted accelerometers during walking. Arch. Phys. Med. Rehabil. 2007, 88, 907–915. [Google Scholar] [CrossRef]
- Vicon Motion Systems. Vicon Motion Systems Product Manuals; Vicon Motion Systems: Oxford, UK.
- CODAmotion. Technical Data Sheet; Charnwood Dynamics: Rothley, UK, 2012. [Google Scholar]
- Xsens Technologies B.V. MTw User Manual; Xsens: Enschede, The Netherlands, 2010. [Google Scholar]
- Draper, N.; Smith, H. Applied Regression Analysis; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Denoth, J. Chapter: Load on the locomotor system and modelling. In Biomechanics of Running Shoes; Nigg, B., Ed.; Human Kinetics Publishers: Champaign, IL, USA, 1986; pp. 63–116. [Google Scholar]
- Silva, F.; Pimentel, R. Biodynamic walking model for vibration serviceability of footbridges in vertical direction. In Proceedings of the 8th International Conference on Structural Dynamics of EURODYN, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Silva, F.; Brito, H.; Pimentel, R. Modeling of crowd load in vertical direction using biodynamic model of pedestrians crossing footbridges. Can. J. Civ. Eng. 2014, 41, 1196–1204. [Google Scholar] [CrossRef]
- Racić, V.; Pavić, A. Mathematical model to generate near-periodic human jumping force signals. Mech. Syst. Signal Process. 2010, 24, 138–152. [Google Scholar] [CrossRef]
- Young, P. Improved floor vibration prediction methodologies. ARUP Vibration Seminar, 2001. [Google Scholar]
- Willford, M.R.; Field, C.; Young, P. Improved methodologies for the prediction of footfall-induced vibration. In Proceedings of the SPIE 2005, San Diego, CA, USA; pp. 1–15.
- Butz, C.; Feldmann, M.; Heinemeyer, C.; Sedlacek, G. SYNPEX: Advanced Load Models for Synchronous Pedestrian Excitation and Optimised Design Guidelines for Steel Footbridges; Technical Report, Research Fund for Coal and Steel; EU Publications: Luxembourg, 2008. [Google Scholar]

| Participant | Sex | Age | Height [m] | Mass [kg] | Considered Treadmill Speeds [m/s] |
|---|---|---|---|---|---|
| 1 | female | 26 | 1.65 | 52 | [0.97, 1.11, 1.25, 1.39, 1.53, 1.67] |
| 2 | male | 23 | 1.81 | 72 | [1.11, 1.25, 1.39] |
| 3 | male | 27 | 1.75 | 66 | [1.1, 1.7] |
| 4 | male | 24 | 1.80 | 72 | [1.0, 1.3, 1.6] |
| [-] | [-] | |||||
|---|---|---|---|---|---|---|
| [Hz] | [-] | m | m | |||
| 3.5 | 1.68 | 0.78 | 0.861 | 0.942 | 0.903 | 0.973 |
| 4.0 | 1.75 | 0.76 | 0.857 | 0.955 | 0.893 | 0.981 |
| 4.5 | 1.85 | 0.76 | 0.864 | 0.962 | 0.896 | 0.986 |
| 5.0 | 1.92 | 0.76 | 0.869 | 0.959 | 0.900 | 0.982 |
| 5.5 | 2.00 | 0.74 | 0.863 | 0.962 | 0.890 | 0.982 |
| 6.0 | 2.06 | 0.74 | 0.872 | 0.963 | 0.896 | 0.981 |
| Average | 0.860 | 0.951 | 0.895 | 0.976 | ||
| [%] | [%] | [-] | [-] | |||||
|---|---|---|---|---|---|---|---|---|
| 1.5 | 0.02 | 1.05 | 0 | 0 | 0.988 | 1 | 0.997 | 1 |
| 1.6 | 0.01 | 1.09 | 0 | 0 | 0.989 | 1 | 0.997 | 1 |
| 1.7 | 0.02 | 1.02 | 0 | 0 | 0.992 | 1 | 0.998 | 1 |
| 1.8 | 0.01 | 0.97 | 0 | 0 | 0.994 | 1 | 0.998 | 1 |
| 1.9 | 0.02 | 1.00 | 0 | 0 | 0.994 | 1 | 0.998 | 1 |
| 2 | 0.02 | 0.87 | 0 | 0 | 0.995 | 1 | 0.998 | 1 |
| 2.1 | 0.01 | 1.01 | 0 | 0 | 0.994 | 1 | 0.998 | 1 |
| Average | 0.016 | 1.001 | 0 | 0 | 0.992 | 1 | 0.998 | 1 |
| Influence of a cut-off frequency at | ||||||||
| 1.5 | 0.02 | 0.74 | 0.11 | 2.35 | 0.994 | 0.949 | 0.998 | 0.974 |
| 1.6 | 0.01 | 0.68 | 0.13 | 2.47 | 0.996 | 0.958 | 0.999 | 0.975 |
| 1.7 | 0.01 | 0.66 | 0.09 | 1.93 | 0.997 | 0.978 | 0.999 | 0.986 |
| 1.8 | 0.01 | 0.61 | 0.09 | 1.78 | 0.998 | 0.984 | 0.999 | 0.989 |
| 1.9 | 0.01 | 0.62 | 0.07 | 1.54 | 0.998 | 0.989 | 0.999 | 0.993 |
| 2 | 0.01 | 0.57 | 0.05 | 1.23 | 0.998 | 0.993 | 0.999 | 0.996 |
| 2.1 | 0.02 | 0.74 | 0.05 | 1.20 | 0.997 | 0.994 | 0.999 | 0.996 |
| Average | 0.01 | 0.66 | 0.08 | 1.79 | 0.999 | 0.98 | 0.999 | 0.990 |
| Influence of a cut-off frequency at | ||||||||
| 1.5 | 0.01 | 0.84 | 0.01 | 0.71 | 0.993 | 0.995 | 0.999 | 0.998 |
| 1.6 | 0.01 | 0.81 | 0.01 | 0.64 | 0.994 | 0.996 | 0.999 | 0.999 |
| 1.7 | 0.01 | 0.83 | 0.01 | 0.61 | 0.995 | 0.997 | 0.999 | 0.999 |
| 1.8 | 0.01 | 0.73 | 0.01 | 0.61 | 0.996 | 0.997 | 0.999 | 0.999 |
| 1.9 | 0.01 | 0.75 | 0.01 | 0.57 | 0.997 | 0.998 | 0.999 | 0.999 |
| 2 | 0.02 | 1.10 | 0.01 | 0.55 | 0.993 | 0.998 | 0.998 | 0.999 |
| 2.1 | 0.02 | 1.03 | 0.01 | 0.51 | 0.994 | 0.998 | 0.999 | 0.999 |
| Average | 0.01 | 0.87 | 0.01 | 0.60 | 0.995 | 0.997 | 0.999 | 0.999 |
| Influence of the single-step load model | ||||||||
| 1.5 | = | = | = | = | 0.903 | 0.905 | 0.949 | 0.951 |
| 1.6 | = | = | = | = | 0.9 | 0.903 | 0.951 | 0.952 |
| 1.7 | = | = | = | = | 0.919 | 0.92 | 0.954 | 0.955 |
| 1.8 | = | = | = | = | 0.915 | 0.915 | 0.951 | 0.951 |
| 1.9 | = | = | = | = | 0.891 | 0.889 | 0.951 | 0.952 |
| 2 | = | = | = | = | 0.853 | 0.858 | 0.948 | 0.95 |
| 2.1 | = | = | = | = | 0.859 | 0.857 | 0.955 | 0.956 |
| Average | 0.891 | 0.892 | 0.951 | 0.952 | ||||
| [%] | [%] | [-] | [-] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [Hz] | |||||||||
| 3.5 | 1.68 | 0.01 | 1.55 | 0.50 | 7.80 | 0.824 | 0.855 | 0.945 | 0.930 |
| 4 | 1.75 | 0.03 | 1.54 | 0.39 | 7.63 | 0.922 | 0.894 | 0.971 | 0.958 |
| 4.5 | 1.85 | 0.01 | 1.38 | 0.30 | 5.96 | 0.914 | 0.923 | 0.976 | 0.970 |
| 5 | 1.92 | 0.00 | 1.20 | 0.18 | 4.15 | 0.943 | 0.954 | 0.982 | 0.980 |
| 5.5 | 2.00 | 0.01 | 1.44 | 0.13 | 3.41 | 0.966 | 0.963 | 0.990 | 0.988 |
| 6 | 2.06 | 0.00 | 1.51 | 0.08 | 2.51 | 0.970 | 0.953 | 0.992 | 0.980 |
| Average | 0.01 | 1.44 | 0.26 | 5.24 | 0.923 | 0.924 | 0.976 | 0.968 | |
| 3.5 | 1.68 | = | = | = | = | 0.614 | 0.645 | 0.865 | 0.837 |
| 4 | 1.75 | = | = | = | = | 0.682 | 0.713 | 0.900 | 0.887 |
| 4.5 | 1.85 | = | = | = | = | 0.770 | 0.780 | 0.927 | 0.917 |
| 5 | 1.92 | = | = | = | = | 0.814 | 0.827 | 0.924 | 0.921 |
| 5.5 | 2.00 | = | = | = | = | 0.847 | 0.843 | 0.922 | 0.919 |
| 6 | 2.06 | = | = | = | = | 0.846 | 0.828 | 0.905 | 0.912 |
| Average | = | = | = | = | 0.762 | 0.773 | 0.907 | 0.899 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Nimmen, K.; Zhao, G.; Seyfarth, A.; Van den Broeck, P. A Robust Methodology for the Reconstruction of the Vertical Pedestrian-Induced Load from the Registered Body Motion. Vibration 2018, 1, 250-268. https://doi.org/10.3390/vibration1020018
Van Nimmen K, Zhao G, Seyfarth A, Van den Broeck P. A Robust Methodology for the Reconstruction of the Vertical Pedestrian-Induced Load from the Registered Body Motion. Vibration. 2018; 1(2):250-268. https://doi.org/10.3390/vibration1020018
Chicago/Turabian StyleVan Nimmen, Katrien, Guoping Zhao, André Seyfarth, and Peter Van den Broeck. 2018. "A Robust Methodology for the Reconstruction of the Vertical Pedestrian-Induced Load from the Registered Body Motion" Vibration 1, no. 2: 250-268. https://doi.org/10.3390/vibration1020018
APA StyleVan Nimmen, K., Zhao, G., Seyfarth, A., & Van den Broeck, P. (2018). A Robust Methodology for the Reconstruction of the Vertical Pedestrian-Induced Load from the Registered Body Motion. Vibration, 1(2), 250-268. https://doi.org/10.3390/vibration1020018





