An Automated Cropland Burned-Area Detection Algorithm Based on Landsat Time Series Coupled with Optimized Outliers and Thresholds
Abstract
1. Introduction
2. Materials and Methods
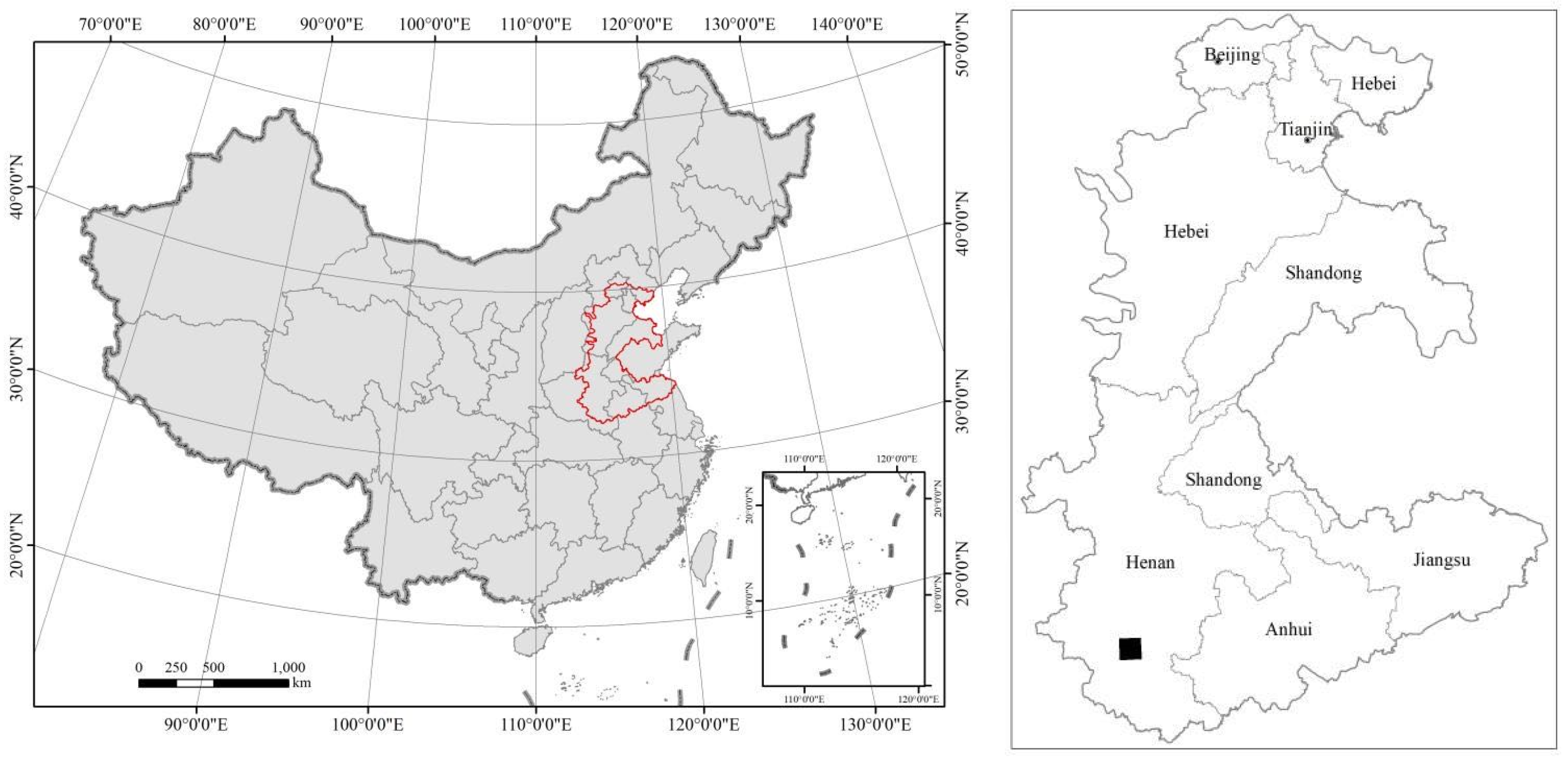
2.1. Study Area
2.2. Workflow of Burned-Area Mapping
- (1)
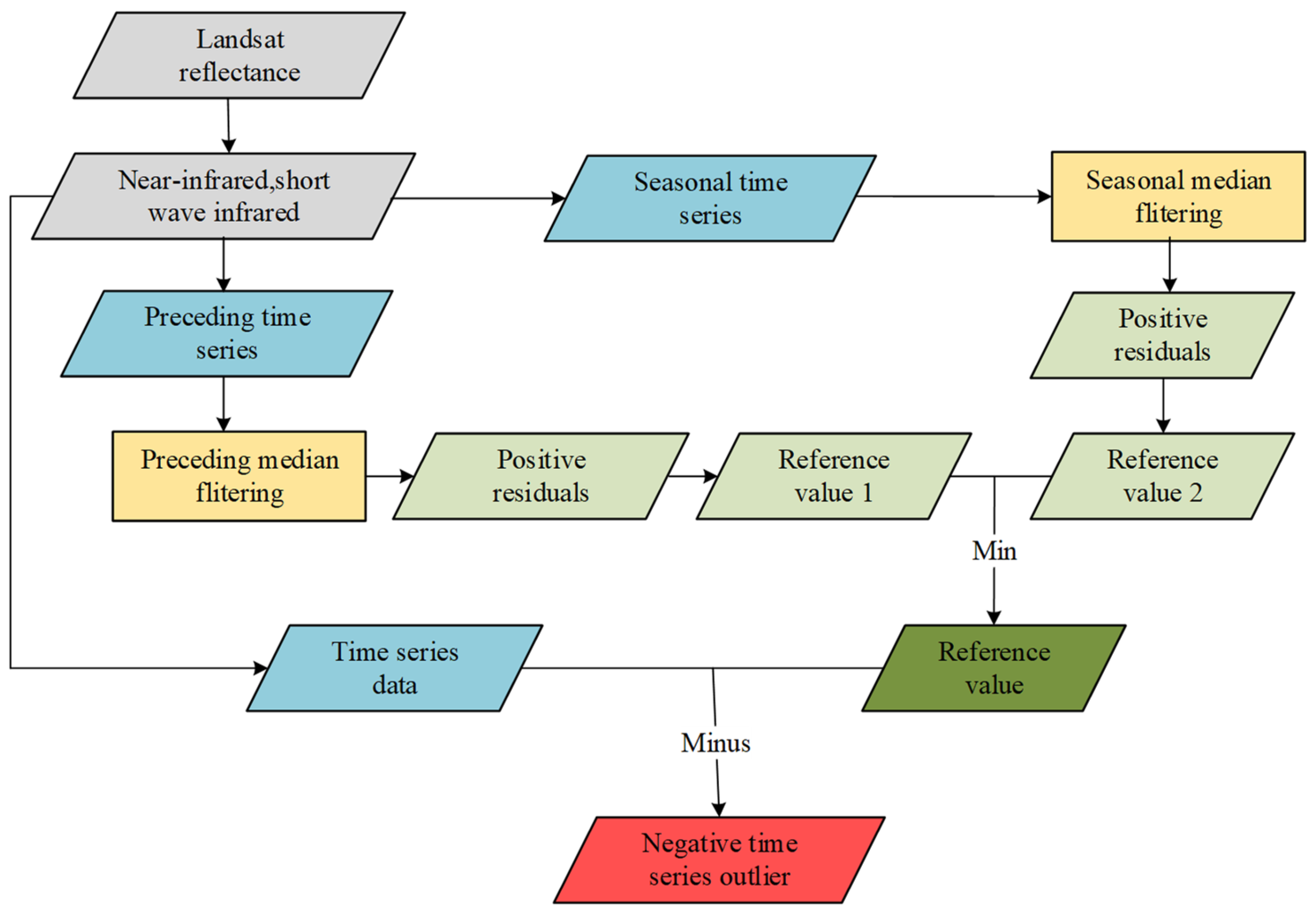
- Construction of preceding and seasonal time series: Time-series data were organized to capture the temporal variation in reflectance. This involved constructing the preceding time series, which reflects changes before and after burning events, and the seasonal time series, which captures seasonal variations.
- (2)
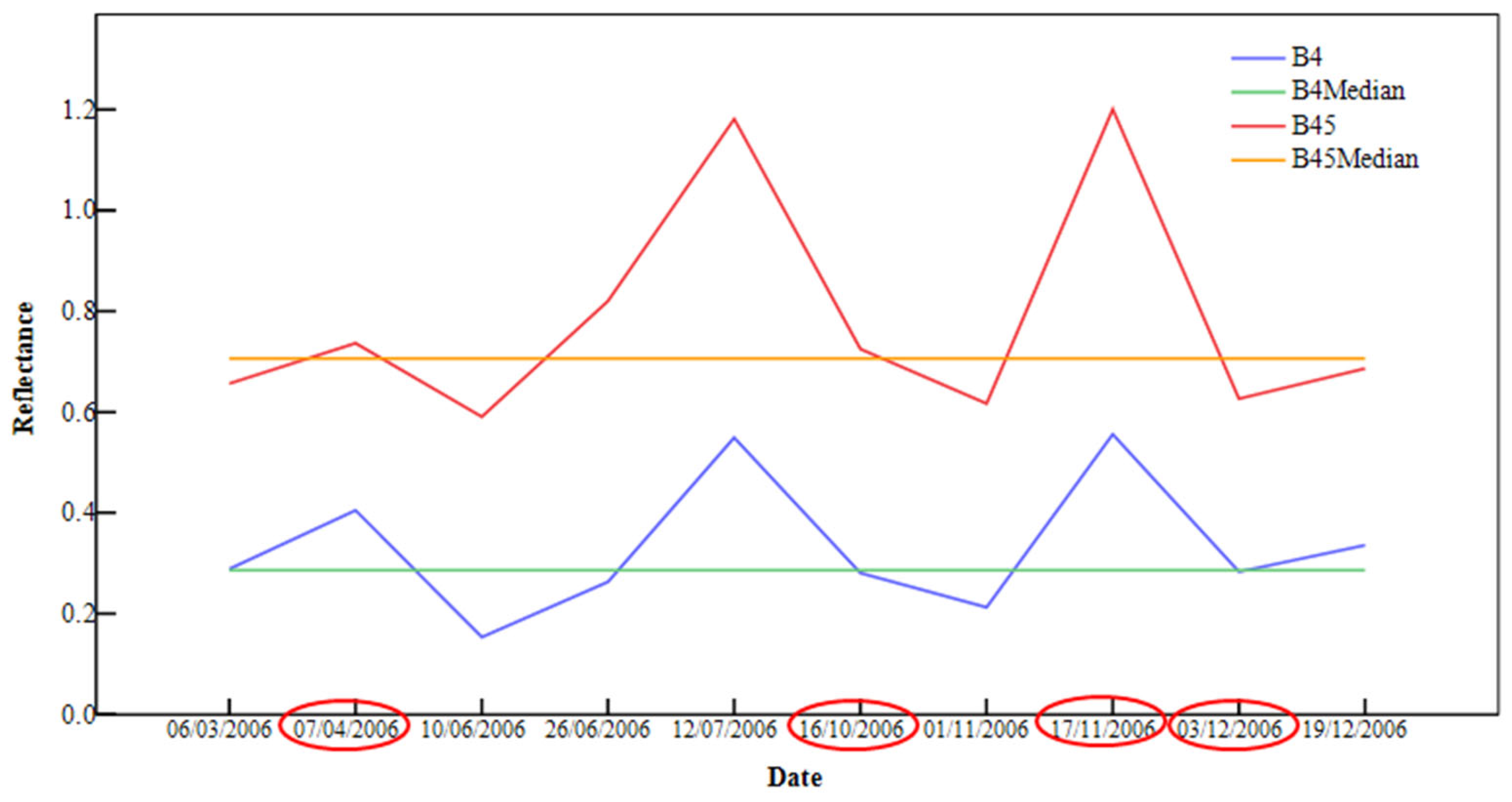
- Calculation of time-series outliers: Outliers in the time series were determined by calculating two reference values through the application of median filtering to each of the constructed time series.
- (3)
- Determination of the optimal threshold: An iterative procedure was implemented to determine the optimal threshold. This involved systematic iteration through various threshold combinations to identify the threshold value yielding the best results.
- (4)
- Extraction of cropland burned pixels: The logical relationship between the outliers and optimal threshold was used to extract cropland burned pixels.
2.2.1. Time-Series Construction
- (1)
- The solar azimuth angle and solar altitude angle of the target image were denoted as Azimuth0 and Zenith0, respectively.
- (2)
- Images were selected based on the criteria that the solar azimuth angle must fall within the interval range [Azimuth0 −15°, Azimuth0 −3°] and [Azimuth0 +3°, Azimuth0 +15°], while the solar altitude angle must be within the range [Zenith0 −15°, Zenith0 −3°] and [Zenith0 +3°, Zenith0 +15°]. Additionally, care was taken to avoid selecting images that were too similar to the target image in terms of seasonal characteristics. Therefore, the selected image and the target image must be within a 60-day interval to capture the desired seasonal spectral changes. This sampling strategy aims to include as many time-series datasets as possible to reflect the variation in surface reflectance.
2.2.2. Time-Series Outlier Detection
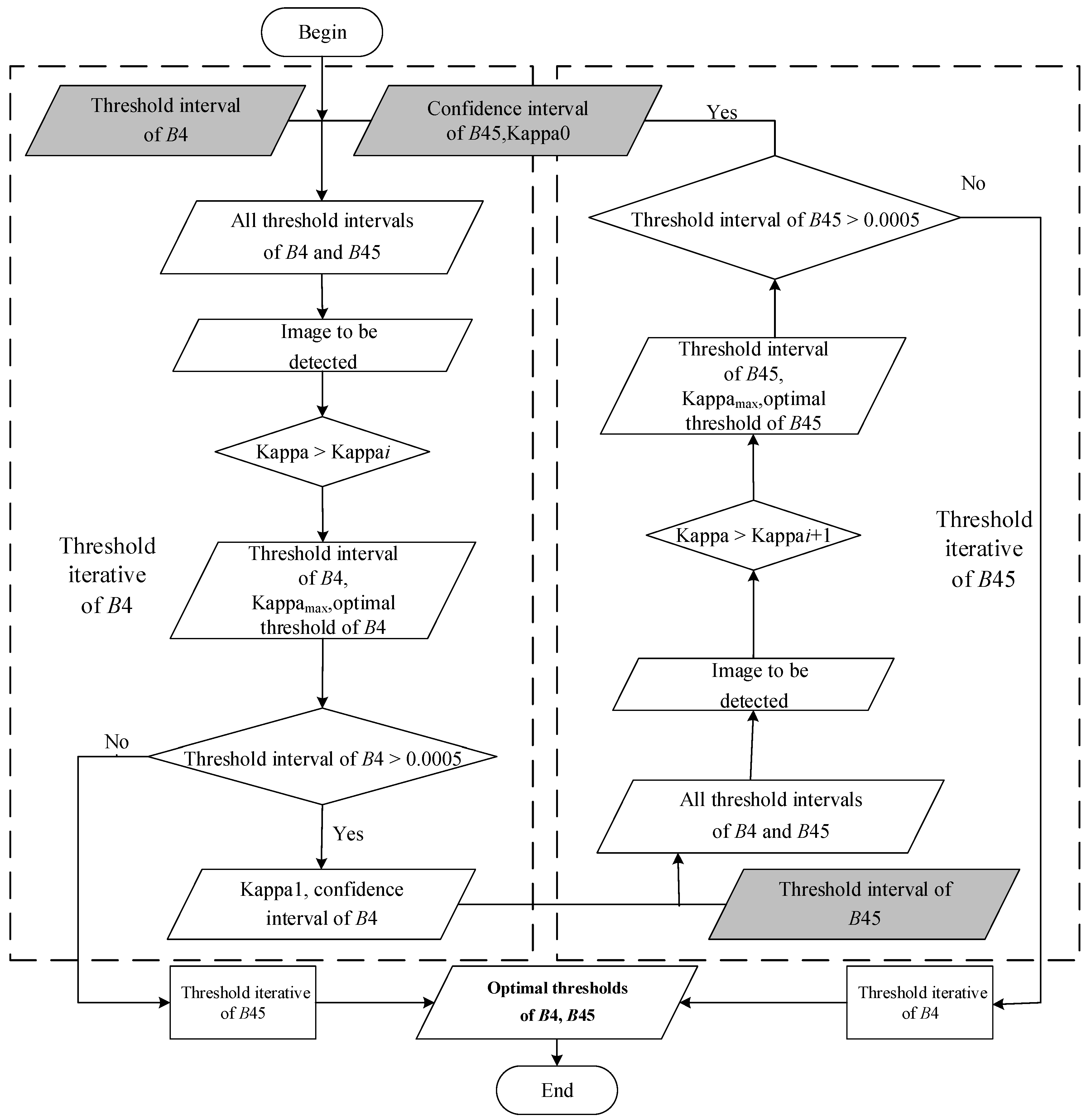
2.2.3. Optimal Threshold Determination and Burned-Area Detection
- (1)
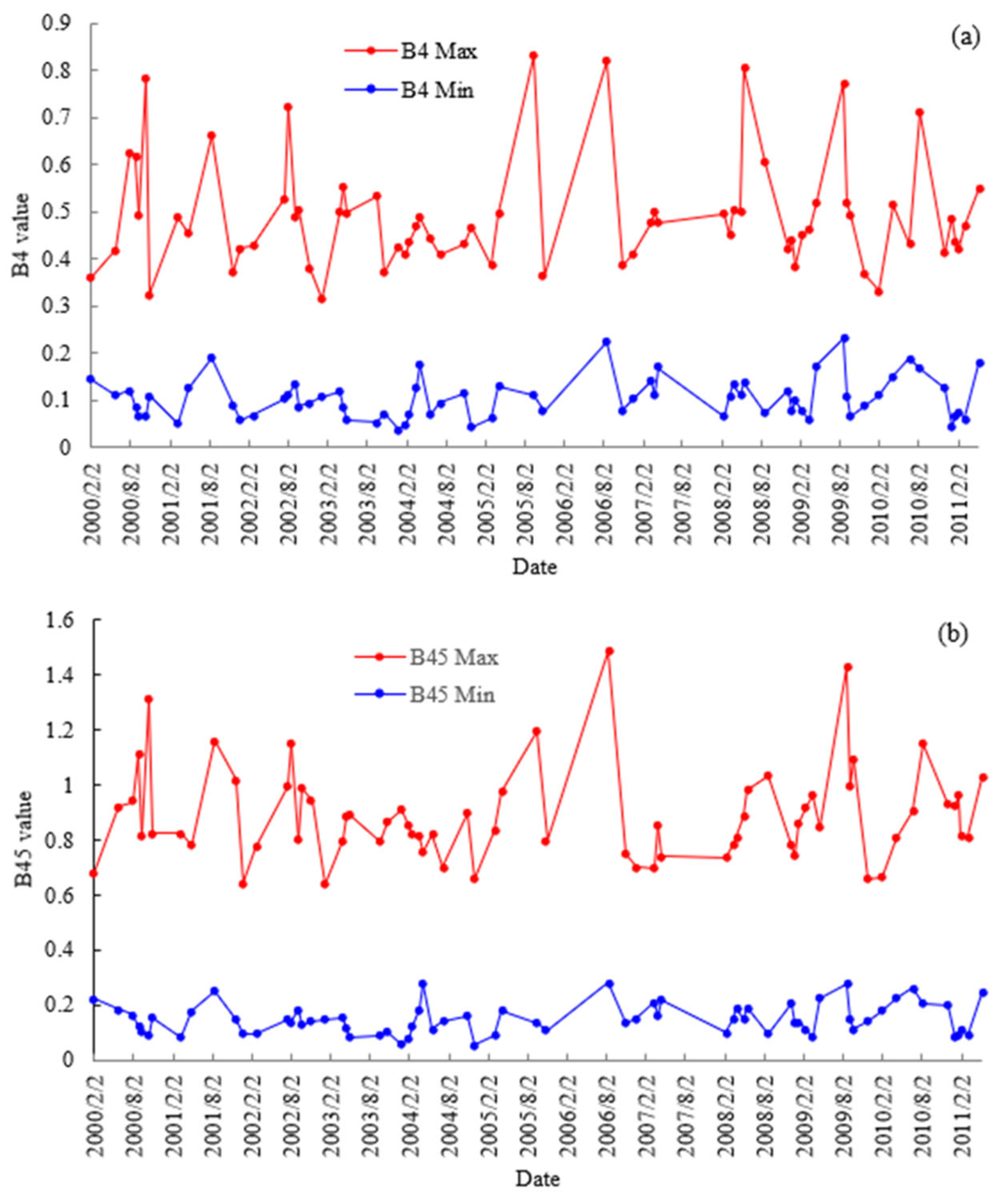
- We determined the threshold interval, i.e., the upper and lower bounds of the threshold, through analysis of the time series and calculation of the range. Specifically, the reflectance change curves (maximum and minimum values) for all B4 and B45 images within the time series were plotted, and reasonable upper and lower thresholds were set based on the distribution of these values. Changes in the minimum and maximum values were used to determine the lower and upper thresholds, respectively.
- (2)
- We initialized six parameters for the iteration, including threshold lower bound, threshold upper bound (for both B45 and B4), kappa coefficient (kappa), and confidence threshold corresponding to the dark gray area in Figure 3. Each iteration required four input parameters: threshold lower bound, threshold upper bound, kappa, and confidence threshold. The output included the updated threshold lower bound, threshold upper bound, kappa, and optimal threshold.
- (3)
- The kappa and optimal threshold values obtained in each iteration were used as input parameters for the next iteration. Except for the first and second iterations, the threshold interval in the input parameters of the 2nd *i iteration corresponded to the threshold interval in the output parameters of the 2nd *i − 2 iteration. Similarly, the threshold interval in the input parameters of the 2nd *i − 1 iteration corresponded to the threshold interval in the output parameters of the 2nd *i − 3 iteration, where i is a natural number ≥2.
- (4)
- Kappa was recalculated in each iteration. If the calculated kappa was larger than the reference kappa, the corresponding threshold interval was retained. Simultaneously, this kappa and optimal threshold were retained as input parameters for the next iteration. The range of the threshold interval was gradually reduced if the current kappa was >Kappai. The iteration continued until the range of the threshold interval was <0.0005. It is important to note that the entire iteration procedure was completed by an extra B4 or B45 threshold iteration.
3. Results
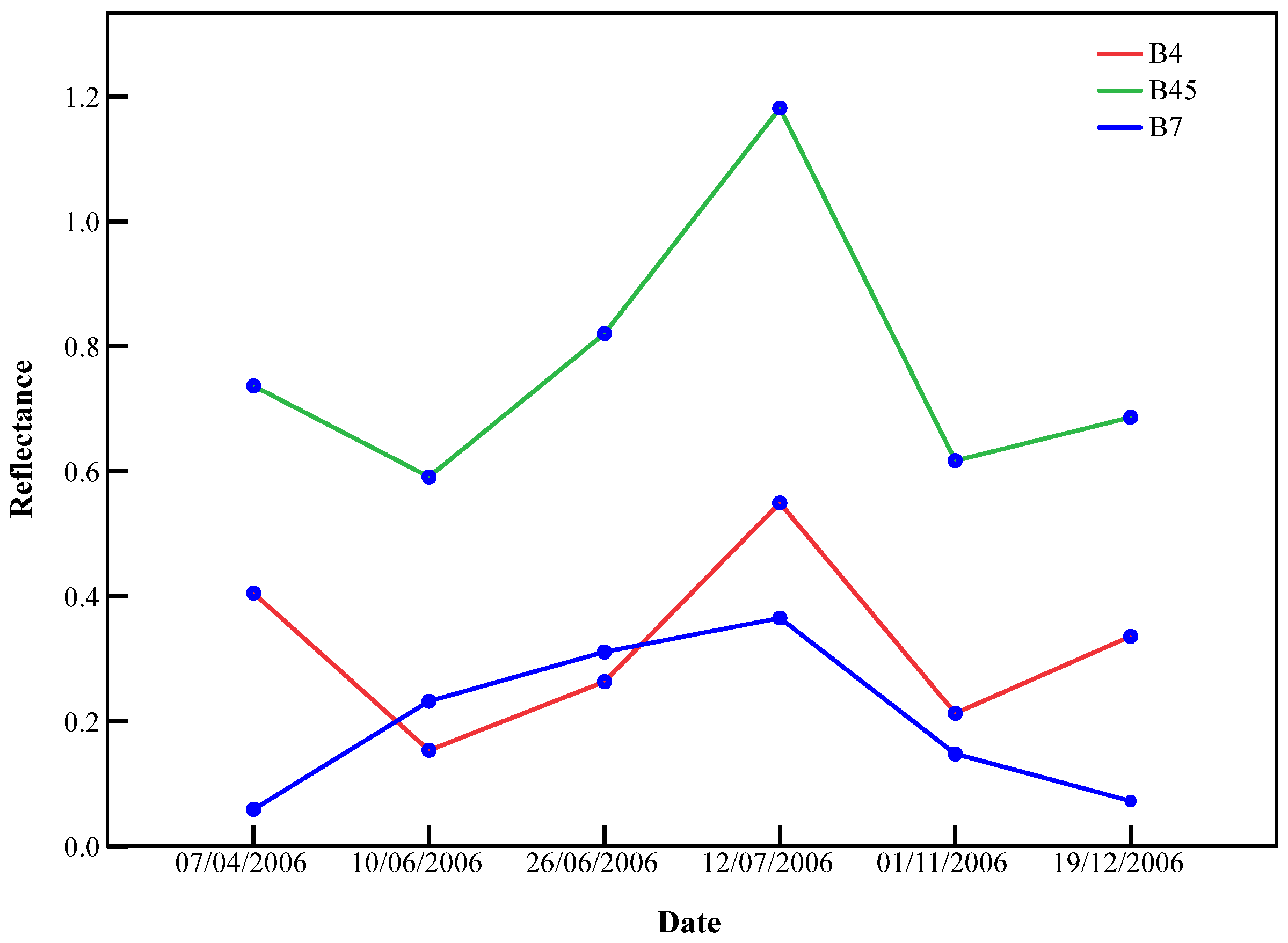
3.1. Time-Series Outliers
3.2. Optimal Threshold
3.2.1. Threshold Interval Determination
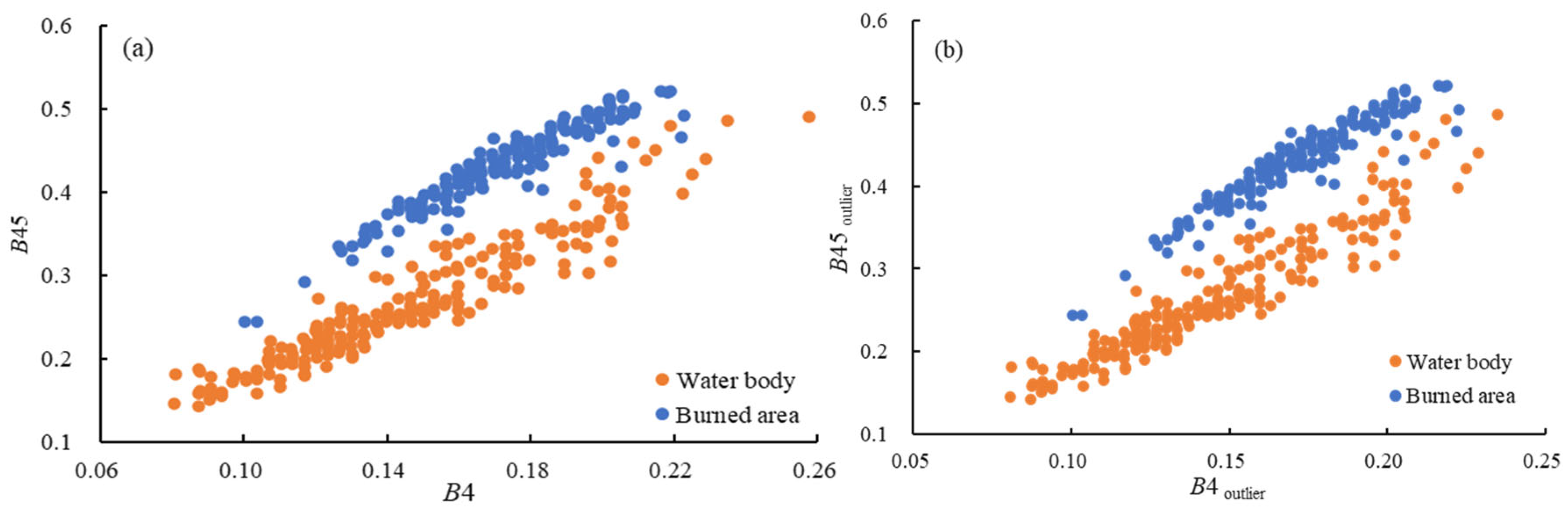
3.2.2. Sampling Points for Threshold Optimization
3.2.3. Optimal Threshold Iteration
3.2.4. Optimal Threshold Validation
3.3. Intercomparison of Burned Area and MCD64A1
4. Discussion
4.1. Advantages of the Algorithm
4.2. Limitations of the Algorithm
4.3. Future Directions and Recommendations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, C.H.; Liu, C.C.; Tseng, P.Y. Emissions Inventory for Rice Straw Open Burning in Taiwan Based on Burned Area Classification and Mapping Using Formosat-2 Satellite Imagery. Aerosol Air Qual. Res. 2013, 13, 474–487. [Google Scholar] [CrossRef]
- Chen, D.; Loboda, T.V.; He, T.; Zhang, Y.; Liang, S. Strong cooling induced by stand-replacing fires through albedo in Siberian larch forests. Sci. Rep. 2018, 8, 4821. [Google Scholar] [CrossRef] [PubMed]
- López-Saldaña, G.; Bistinas, I.; Pereira, J.M.C. Global analysis of radiative forcing from fire-induced shortwave albedo change. Biogeosciences 2015, 12, 557–565. [Google Scholar] [CrossRef]
- Ward, D.S.; Kloster, S.; Mahowald, N.M.; Rogers, B.M.; Randerson, J.T.; Hess, P.G. The changing radiative forcing of fires: Global model estimates for past, present and future. Atmos. Chem. Phys. 2012, 12, 10857–10886. [Google Scholar] [CrossRef]
- Stavrakoudis, D.; Katagis, T.; Minakou, C.; Gitas, I.Z. Towards a fully automatic processing chain for operationally mapping burned areas countrywide exploiting Sentinel-2 imagery. In Proceedings of the Seventh International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2019), International Society for Optics and Photonics, Paphos, Cyprus, 18–21 March 2019; Volume 11174, p. 1117405. [Google Scholar]
- van Dijk, D.; Shoaie, S.; Leeuwen, T.V.; Veraverbekea, S. Spectral signature analysis of false positive burned area detection from agricultural harvests using Sentinel-2 data. Int. J. Appl. Earth. Obs. Geoinf. 2021, 97, 102296. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Y.; Guo, X.; Zhao, W.; Wu, H.; Xu, W. Burned area detection and mapping using time series Sentinel-2 multispectral images. Remote Sens. Environ. 2023, 296, 113753. [Google Scholar] [CrossRef]
- Bastarrika, A.; Chuvieco, E.; Martín, M.P. Automatic burned land mapping from MODIS time series images: Assessment in Mediterranean ecosystems. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3401–3413. [Google Scholar] [CrossRef]
- Chuvieco, E.; Roteta, E.; Sali, M.; Stroppiana, D.; Boettcher, M.; Kirches, G.; Storm, T.; Khairoun, A.; Pettinari, M.L.; Franquesa, M.; et al. Building a small fire database for Sub-Saharan Africa from Sentinel-2 high-resolution images. Sci. Total Environ. 2022, 845, 157139. [Google Scholar] [CrossRef]
- Ramo, R.; Roteta, E.; Bistinas, I.; Van Wees, D.; Bastarrika, A.; Chuvieco, E.; Van der Werf, G.R. African burned area and fire carbon emissions are strongly impacted by small fires undetected by coarse resolution satellite data. Proc. Natl. Acad. Sci. USA 2021, 118, e2011160118. [Google Scholar] [CrossRef]
- Pinto, M.M.; Libonati, R.; Trigo, R.M.; Trigo, I.F.; DaCamara, C.C. A deep learning approach for mapping and dating burned areas using temporal sequences of satellite images. ISPRS J. Photogramm. Remote Sens. 2020, 160, 260–274. [Google Scholar] [CrossRef]
- Roteta, E.; Bastarrika, A.; Ibisate, A.; Chuvieco, E. A preliminary global automatic burned-area algorithm at medium resolution in Google Earth Engine. Remote Sens. 2021, 13, 4298. [Google Scholar] [CrossRef]
- Libonati, R.; DaCamara, C.C.; Setzer, A.W.; Morelli, F.; Melchiori, A.E. An algorithm for burned area detection in the Brazilian Cerrado using 4 µm MODIS imagery. Remote Sens. 2015, 7, 15782–15803. [Google Scholar] [CrossRef]
- Zhu, C.; Kobayashi, H.; Kanaya, Y.; Saito, M. Size-dependent validation of MODIS MCD64A1 burned area over six vegetation types in boreal Eurasia: Large underestimation in croplands. Sci. Rep. 2017, 7, 4181. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xin, L.; Zhang, H.; Li, Y. An estimation of the extent of rent-free farmland transfer and its driving forces in rural China: A multilevel logit model analysis. Sustainability 2019, 11, 3161. [Google Scholar] [CrossRef]
- Long, T.; Zhang, Z.; He, G.; Jiao, W.; Tang, C.; Wu, B.; Zhang, X.; Wang, G.; Yin, R. 30 m resolution global annual burned area mapping based on Landsat Images and Google Earth Engine. Remote Sens. 2019, 11, 489. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Vanderhoof, M.K.; Schmidt, G.L.; Beal, Y.J.; Picotte, J.J.; Takacs, J.D.; Falgout, J.T.; Dwyer, J.L. The Landsat Burned Area algorithm and products for the conterminous United States. Remote Sens. Environ. 2020, 244, 111801. [Google Scholar] [CrossRef]
- Boschetti, L.; Flasse, S.; Trigg, S.; de Dixmude, A.J. A multitemporal change-detection algorithm for the monitoring of burnt areas with SPOT-Vegetation data. In Analysis of Multi-Temporal Remote Sensing Images; World Scientific Publishing: Singapore, 2002; pp. 75–82. [Google Scholar]
- Schroeder, W.; Oliva, P.; Giglio, L.; Quayle, B.; Lorenz, E.; Morelli, F. Active fire detection using Landsat-8/OLI data. Remote Sens. Environ. 2016, 185, 210–220. [Google Scholar] [CrossRef]
- Lizundia-Loiola, J.; Otón, G.; Ramo, R.; Chuvieco, E. A spatio-temporal active-fire clustering approach for global burned area mapping at 250 m from MODIS data. Remote Sens. Environ. 2020, 236, 111493. [Google Scholar] [CrossRef]
- Bastarrika, A.; Alvarado, M.; Artano, K.; Martinez, M.P.; Mesanza, A.; Torre, L.; Ramo, R.; Chuvieco, E. BAMS: A tool for supervised burned area mapping using Landsat data. Remote Sens. 2014, 6, 12360–12380. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Vanderhoof, M.K.; Beal, Y.J.; Takacs, J.D.; Schmidt, G.L.; Falgout, J.T.; Williams, B.; Fairau, N.M.; Caldwell, M.K.; Picotte, J.J.; et al. Mapping burned areas using dense time-series of Landsat data. Remote Sens. Environ. 2017, 198, 504–522. [Google Scholar] [CrossRef]
- Liu, J.; Heiskanen, J.; Maeda, E.E.; Pellikka, P.K.E. Burned area detection based on Landsat time series in savannas of southern Burkina Faso. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 210–220. [Google Scholar] [CrossRef]
- Ruscalleda-Alvarez, J.; Moro, D.; Van Dongen, R. A multi-scale assessment of fire scar mapping in the Great Victoria Desert of Western Australia. Int. J. Wildland Fire 2021, 30, 886–898. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, Z.; Long, T.; He, G.; Wang, G. Monitoring Landsat based burned area as an indicator of Sustainable Development Goals. Earth’s Future 2021, 9, e2020EF001960. [Google Scholar] [CrossRef]
- Pereira, M.C.; Setzer, A.W. Spectral characteristics of fire scars in Landsat-5 TM images of Amazonia. Remote Sens. 1993, 14, 2061–2078. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Collett, L.J. Development of an automated method for mapping fire history captured in Landsat TM and ETM+ time series across Queensland, Australia. Remote Sens. Environ. 2014, 148, 206–221. [Google Scholar] [CrossRef]
- Mor, S.; Singh, T.; Bishnoi, N.R.; Bhukal, S.; Ravindra, K. Understanding seasonal variation in ambient air quality and its relationship with crop residue burning activities in an agrarian state of India. Environ. Sci. Pollut. Res. 2022, 29, 4145–4158. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Moriya, K.; Sakai, T.; Koyama, L.; Cao, C.X. Mapping a burned forest area from Landsat TM data by multiple methods. Geomat. Nat. Hazards Risk 2014, 7, 384–402. [Google Scholar] [CrossRef]
- Woźniak, E.; Aleksandrowicz, S. Self-Adjusting Thresholding for Burnt Area Detection Based on Optical Images. Remote Sens. 2019, 11, 2669. [Google Scholar] [CrossRef]
- Filipponi, F. Exploitation of Sentinel-2 Time Series to Map Burned Areas at the National Level: A Case Study on the 2017 Italy Wildfires. Remote Sens. 2019, 11, 622. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Zhao, H. Integration of Multiple Spectral Data via a Logistic Regression Algorithm for Detection of Crop Residue Burned Areas: A Case Study of Songnen Plain, Northeast Chin. Chin. Geogr. Sci. 2024, 34, 548–563. [Google Scholar] [CrossRef]
- Stroppiana, D.; Bordogna, G.; Carrara, P.; Boschetti, M.; Boschetti, L.; Brivio, P.A. A method for extracting burned areas from Landsat TM/ETM+ images by soft aggregation of multiple Spectral Indices and a region growing algorith. ISPRS J. Photogramm. Remote Sens. 2012, 69, 88–102. [Google Scholar] [CrossRef]
- Storey, E.A.; Lee West, K.R.; Stow, D.A. Utility and optimization of LANDSAT-derived burned area maps for southern California. Int. J. Remote Sens. 2021, 42, 486–505. [Google Scholar] [CrossRef]
- Koutsias, N.; Pleniou, M.; Mallinis, G.; Nioti, F.; Sifakis, N.I. A rule-based semi-automatic method to map burned areas: Exploring the USGS historical Landsat archives to reconstruct recent fire history. Int. J. Remote Sens. 2013, 34, 7049–7068. [Google Scholar] [CrossRef]
- Zhang, Y.; Dore, A.J.; Ma, L.; Liu, X.J.; Ma, W.Q.; Cape, J.N.; Zhang, F.S. Agricultural ammonia emissions inventory and spatial distribution in the North China Plain. Environ. Pollut. 2010, 158, 490–501. [Google Scholar] [CrossRef] [PubMed]
- Key, C.H.; Benson, N.C. Measuring and remote sensing of burn severity: The CBI and NBR. In Proceedings of the Joint Fire Science Conference and Workshop, Boise, ID, USA, 15–17 June 1999; Volume 2000, pp. 284–285. [Google Scholar]
- Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar]
- Pereira, J.M.; Sá, A.C.; Sousa, A.M.; Silva, J.M.; Santos, T.N.; Carreiras, J.M. Spectral characterisation and discrimination of burnt areas. In Remote Sensing of Large Wildfires; Springer: Berlin/Heidelberg, Germany, 1999; pp. 123–138. [Google Scholar]
- He, Y.; Yang, J.; Ma, Y.; Liu, J.B.; Chen, F.; Li, X.P.; Yang, Y.F. A method for fire detection using Landsat 8 data. J. Infrared Millim. Waves 2016, 35, 600–609. [Google Scholar]


| ID | Threshold Lower Bound | Threshold Upper Bound | Kappai | Confidence Threshold | Threshold Lower Bound | Threshold Upper Bound | Kappai + 1 | Optimal Threshold |
|---|---|---|---|---|---|---|---|---|
| 1 | B4min | B4max | Kappa0 | B45T0 | B4min1 | B4max1 | Kappa1 | B4T1 |
| 2 | B45min | B45max | Kappa1 | B4T1 | B45min2 | B45max2 | Kappa2 | B45T2 |
| 3 | B4min1 | B4max1 | Kappa2 | B45T2 | B4min3 | B4max3 | Kappa3 | B4T3 |
| 4 | B45min2 | B45max2 | Kappa3 | B4T3 | B45min4 | B45max4 | Kappa4 | B45T4 |
| 5 | B4min3 | B4max3 | Kappa4 | B45T4 | B4min5 | Band4max5 | Kappa5 | B4T5 |
| ID | Threshold Lower Bound | Threshold Upper Bound | Kappai | Confidence Threshold | Threshold Lower Bound | Threshold Upper Bound | Kappai + 1 | Optimal Threshold |
|---|---|---|---|---|---|---|---|---|
| 1 | 1000 | 6000 | 0 | 5000 | 1000 | 6000 | 0.785 | 2020.408 |
| 2 | 2000 | 10,000 | 0.785 | 2020.408 | 5102.041 | 10,000 | 0.811 | 5561.224 |
| 3 | 1000 | 6000 | 0.811 | 5561.224 | 2020.408 | 2122.449 | 0.812 | 2122.449 |
| 4 | 5102.041 | 10,000 | 0.812 | 2122.449 | 5501.874 | 5501.874 | 0.812 | 5501.874 |
| 5 | 2020.408 | 2122.449 | 0.812 | 5501.874 | 2022.491 | 2122.449 | 0.820 | 2030.820 |
| ID | Threshold Lower Limit | Threshold Upper Limit | Kappai | Confidence Threshold | Threshold Lower Limit | Threshold Upper Limit | Kappai + 1 | Optimal Threshold |
|---|---|---|---|---|---|---|---|---|
| 1 | 1000 | 6000 | 0 | 5000 | 1000 | 6000 | 0.939 | 1816.327 |
| 2 | 2000 | 10,000 | 0.939 | 1816.327 | 4183.673 | 10,000 | 0.939 | 4183.673 |
| 3 | 1000 | 6000 | 0.939 | 4183.673 | 1816.327 | 2020.408 | 0.939 | 1816.327 |
| 4 | 4183.673 | 10,000 | 0.939 | 1816.327 | 4183.673 | 10,000 | 0.939 | 4183.673 |
| 5 | 1816.327 | 2020.408 | 0.939 | 4183.673 | 1816.327 | 2020.408 | 0.939 | 1816.327 |
| Overall Accuracy | Kappa | Burned Pixel | Unburned Pixel | ||
|---|---|---|---|---|---|
| Commission Error | Omission Error | Commission Error | Omission Error | ||
| 93.0% | 0.84 | 13.85% | 8.2% | 3.7% | 6.48% |
| Overall Accuracy | Kappa | Burned | Unburned | |||
|---|---|---|---|---|---|---|
| Commission Error | Omission Error | Commission Error | Omission Error | |||
| MCD64A1 | 76.5% | 0.24 | 50.90% | 69.90% | 19.00% | 9.45% |
| Burned area in this paper | 93.25% | 0.82 | 18.90% | 7.53% | 2.38% | 6.51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, H.; Zhao, H. An Automated Cropland Burned-Area Detection Algorithm Based on Landsat Time Series Coupled with Optimized Outliers and Thresholds. Fire 2024, 7, 257. https://doi.org/10.3390/fire7070257
Zhang S, Li H, Zhao H. An Automated Cropland Burned-Area Detection Algorithm Based on Landsat Time Series Coupled with Optimized Outliers and Thresholds. Fire. 2024; 7(7):257. https://doi.org/10.3390/fire7070257
Chicago/Turabian StyleZhang, Sumei, Huijuan Li, and Hongmei Zhao. 2024. "An Automated Cropland Burned-Area Detection Algorithm Based on Landsat Time Series Coupled with Optimized Outliers and Thresholds" Fire 7, no. 7: 257. https://doi.org/10.3390/fire7070257
APA StyleZhang, S., Li, H., & Zhao, H. (2024). An Automated Cropland Burned-Area Detection Algorithm Based on Landsat Time Series Coupled with Optimized Outliers and Thresholds. Fire, 7(7), 257. https://doi.org/10.3390/fire7070257





