Abstract
The hydrocarbon temperature–time curve is widely used instead of the standard curve to describe the temperature in the environment of structural surfaces exposed to fire in oil and gas chemical facilities and tunnels. This paper presents calculations of the ratio of time to reach critical temperatures at different nominal fire curves for steel structures such as bulkheads and columns with different types of fireproofing. The thermophysical properties of the fireproofing materials were obtained by solving the inverse heat conduction problem using computer simulation. It was found that the time interval for reaching critical temperatures in structures with different types of fireproofing in a hydrocarbon fire decreased, on average, by a factor of 1.2–1.7 compared to the results of standard fire tests. For example, for decks and bulkheads with mineral wool fireproofing, the K-factor of the ratio of the time for reaching the critical temperature of steel under the standard curve to the hydrocarbon curve was 1.30–1.62; for plaster, it was 1.56; for cement boards, it was 1.34; for non-combustible coatings, it was 1.38–2.0; and, for epoxy paints, it was 1.71. The recommended values of the K-factor for fire resistance up to 180 min (incl.) were 1.7 and, after 180 min, 1.2. The obtained dependencies would allow fireproofing manufacturers to predict the insulation thickness for expensive hydrocarbon fire experiments if the results of fire tests under standard (cellulosic) conditions are known.
1. Introduction
The fire safety of oil and gas complex production facilities (O&GC) is one of the most important parts in the safety concept of industrial facilities and provides the protection of people and the environment from threats of technogenic and environmental nature in case of emergencies [1,2,3]. At the same time, the stability of structural systems of O&GC in the case of fire and ensuring their required fire resistance play one of the most important roles. As a rule, fires in industry have a large-scale character and last for a long time [4].
It is important to note that fires in industrial areas are typically large-scale and long-lasting [4]. This article focuses on bearing and enclosing structures that are used in different process of O&GC, including transportation, storage, and processing. These will include the decks and bulkheads of tankers, offshore oil production and processing platforms, and metal structures of onshore buildings and structures (Figure 1).

Figure 1.
Platforms and trestles with structural fire protection at gas facilities. Author’s photo.
1.1. The Nominal Temperature–Time Curves and Fire Protection
The standard temperature–time curve (hereinafter referred to as “S-curve”) has been used effectively for many years to determine the fire resistance of building constructions. The temperature–time relationship is set out in European standard EN 1363 [5] and international ISO 834 [6] (the main world standard for fire resistance tests). However, in most cases, it is hydrocarbons that burn at oil and gas facilities, so, to justify the fire resistance of structures and equipment, it is recommended to provide the hydrocarbon temperature–time curve (hereinafter referred to as “H-curve”) regulated by European EN 1363 [6] and American UL 1709 [7]. Modern software complexes that implement the computational fluid dynamics (CFD) model also simulate the “real” or “parametric” fire curves determined on the basis of the combustible load and specific conditions on the object [8,9,10,11].
Both curves are also used to test the decks and bulkheads of tankers transporting hydrocarbons. Fire protection structures on ships are categorized into “A”, “B”, and “C” types when tested under the standard and “H” under the hydrocarbon fire conditions. The test methods outlined in the “Resolution” in [12] are also based on [6]. The difference in the “temperature–time” between the two curves is represented by dependencies in the national and international standards. For the S-mode, these can be found in references [6,13,14,15,16], while, for the H-mode, they can be found in references [7,14,17] (see Figure 2).
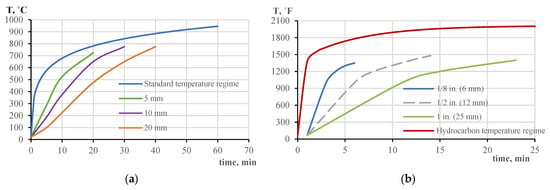
Figure 2.
Temperature–time curves and rate of temperature increase for unprotected steel plates of different thicknesses exposed to an open gasoline fire according to the standard [16] (a) and the hydrocarbon curve [17] (b).
Figure 2 shows a sharp increase in the hydrocarbon fire curve within 5 min. The heat flux is 205 kW/m2 ± 15 kW/m2, compared to the standard one of 50 kW/m2 [7]. Without passive fire protection (PFP), steel structures have a fire resistance of only 25 min at a critical temperature of 500 °C for steel according to the S-fire curve [16] and 10 min according to the H-fire curve [17]. Therefore, PFP is typically used to protect steel structures [17,18,19,20,21,22,23]. Figure 3 shows the types of fire protection coatings used at O&GC facilities.
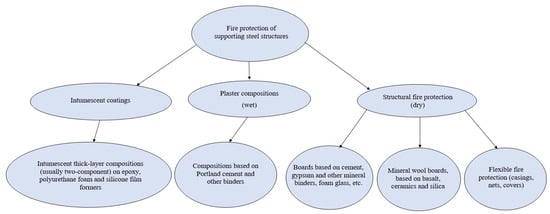
Figure 3.
Scheme of fire protection coatings applied at O&GC facilities.
Passive fire protection often contains water-saturated fillers such as gypsum, vermiculite, and perlite. The intensive evaporation of this water slows down the heating of the metal element. Protective materials can also undergo endothermic decomposition reactions. The following classification was developed prior to the publication of European Design Codes, as noted in [24], and defines three types of fire protection:
- “dry” substances as structural protection with boards;
- “wet” substances as plasters, impregnations, and flame retardants;
- intumescent substances such as paints and coatings.
The calculation and modeling of wet protection is divided into two stages: before water evaporation and after. The use of intumescent coatings makes the mechanism of reaction in the heating process very complex [25,26], because the process is often divided into three stages: growth of the foam-coke, its stabilization, and then burnout [27,28]. However, when it comes to the coatings used on O&GC, the foam-coke is extremely rigid and remains fixed throughout almost the entire testing process [29,30,31]. Therefore, it is possible to model two sites: the growth of the foam-coke and its stabilization as a thermal insulating layer.
1.2. Limit States of Structures and Predictive Model with Fire Protection
Fire resistance is the ability of a specified structure (material, geometry) to fulfil its required (load-bearing and/or fire-separating) functions for a specified load level, fire exposure, and period of time. The load bearing function is determined by the loss of strength (R) that occurs for steel at 450–500 °C, according to [14,16], or at 538 °C, according to [7]. The fire-separating function depends on the loss of thermal insulating ability (I), which is defined as the attainment of an average temperature of 140 °C on the unheated surface according to thermocouple readings and the loss of integrity (E), which involves the formation of cracks and the falling out of pieces of building material from the structure, making it difficult to calculate [6,15]. The fire resistance limit is the total of one or more parameters for the required time or the actual onset of one of the factors (R, E, I) simultaneously or each separately.
The fire resistance limits of steel structures without fire protection can be calculated analytically based on the section factor Ap/V (the ratio of the heated area to the structure volume, according to [14]) or its inverse value, known as the specific metal thickness [18]. The equations of thermal physics enable the calculation of heat transfer (convection, radiation, thermal conductivity) based on the given fire curve, while taking into account the change in the thermophysical properties of the fire protection material [14].
where
Δt—the time interval, s; Δt ≤ 30 s;
Δθa t, Δθg t—the temperature increase for the steel and ambient gas (respectively) during the time interval , K;
Ap—the appropriate area of the fire protection material per unit length of the member, m2/m;
V—volume of the member per unit length, m3/m;
λp—the thermal conductivity of the fire protection system, W/(m·K);
dp—the thickness of the fire protection material, m;
ca, cp—the specific heat of steel (temperature dependent) and fire protection material (temperature independent), respectively, J/(kg·K);
ρa, ρp—the unit mass of steel and fire protection material, respectively, kg/m3;
θa t, θg t—the temperature of steel and ambient gas (respectively) at time , °C;
φ—additional parameter;
It is important to note that Formula (1) does not take into account the influence of water contained in wet fire-retardant materials, as well as the type of protective material and the method of its application [24].
1.3. Concept for Optimization of Fire Protection
The objective of this study was to formulate the problem of substantiating the characteristics (layer thickness, thermal conductivity, density, heat capacity) that ensure the required fire protection performance of the considered structure at a minimum total cost of the material and its installation. To achieve this, a forecast model of the temperature increase in the construction at each moment during the specified period is required. The model should also take into account the technical characteristics of the protective material. The problem can be mathematically described as follows:
where CΣ is the total cost of the protective material and its installation (taking into account the area of the structure), price; and pj is the unknown variable value of the technical characteristic of the protective material with index j (j = 1, 2, …, n), MUj.
Taking into account the previously introduced designations,
MUj is the unit of measurement for the technical characteristic of the protective material with index j.
n represents the total number of technical characteristics taken into account for the protective material, measured in units.
pjmin and pjmax, respectively, represent the minimum and maximum values of the technical characteristic of the protective material with index j, measured in MUj.
treq is the normative time interval for preserving the serviceable state of the structure under thermal influence, measured in minutes.
θa is the temperature of the material determined by the technical characteristics of the material and the time factor, measured in degrees Celsius.
θamax represents the maximum temperature that the structural material can withstand while still being able to perform its intended functions, measured in degrees Celsius.
The optimal values of the unknown variables {pj} can be determined by the implementation of the mathematical model described by Expressions (3)–(5), with known dependencies CΣ({pj}) and θa({pj}, treq), using appropriate computational algorithms.
The practical significance of the mathematical model is determined by the following factors:
- ▪
- adequacy of dependencies CΣ({pj}) and θa({pj}, treq) (formed for various categories of protective materials), determined by the completeness and quality of the statistical and/or experimental data used;
- ▪
- effectiveness of the computational algorithm assigned to implement the model in accordance with the structure of the generated dependencies.
The structure of the dependence CΣ({pj}) of the total cost of the protective material and its installation on the technical characteristics of the material in the general case assumes a superposition of individual components, each of which represents a monotonic linear or nonlinear function of a certain technical characteristic of the material (in some cases, a non-monotonic dependence is possible, for the formation of which it is advisable to use existing tools, including the models proposed in [32,33]).
The dependence CΣ ({pj}) of the total cost of the protective material and its installation on the technical characteristics of the material can be determined by analyzing various instances of protective materials available for mass application in the market. To create an accurate forecast model for determining the temperature of the material based on technical characteristics and time factor θa ({pj}, treq), a significant number of experiments and fire tests must be performed. This involves significant amounts of labor, money, and other resources, especially in the case of H-regime modeling.
The similarity in the thermodynamic processes between the S- and H-curves and the relatively lower costs associated with conducting experiments with S-curve fires (compared to the H-curve) make it possible to establish a correlation between the temperature ratio values for these modes and the time factor. It is of interest to find a numerical relationship between the fire resistance limits of structures exposed to S- and H-curve fires.
1.4. Review of Research on Predicting the Fire Resistance of Structures under Different Fire Exposure
Global Asset Protection Services LLC (GAPS), USA [34] and AXA Insurance Company, France [35] conducted a study on fire protection products. They presented test reports (the tests are the same, but the revision of the report has been updated) that compared the thicknesses of a passive fire protection material using ASTM E-119 (S-curve) [13] and UL 1709 (H-curve) [7] (Table 1). The study applied this material on the 10 W × 49 steel columns of 2.7 m length that are commonly used in independent stack-frames, equipment supports, and utility bridges.

Table 1.
Comparisons of ASTM E-119 [13] and UL 1709 [7] ratings.
As it can be seen from Table 1, the standard fire resistance of materials is clearly reduced in the case of the hydrocarbon fire test. Thus, two intumescent coatings—No. 1 and No. 2—with a fire resistance of 90 min under standard conditions only have 52 and 62 min when hydrocarbon fire is applied. The fire resistance of cement panels is reduced from 180 min to 148 min.
The article by [36] focuses on the computational evaluation of the fire resistance of unprotected steel structures. It presents a fire dynamic simulation (FDS)-based mathematical equation that determines the ratio of fire resistance limits for S- and H-curves of a steel frame with an Ap/V = 261 m−1. The coefficient K = 3.6 for unprotected steel structures is obtained, but the comparison with experimental data is not performed.
The study by [37] aimed to verify and summarize the computational coefficient presented in [36] regarding steel structures with fire protection. The calculations of the fire resistance under S- and H-curve heating were conducted for samples with different thicknesses of mineral wool and section factor Ap/V. The results showed that the relation proposed in [36] was not fulfilled. The relative coefficient K = S/H was 1.0–1.3 for steel structures with a critical temperature of 500 °C and mineral wool thickness in the range of 40 to 60 mm. The coefficient tended towards 1 as the section factor Ap/V (critical temperature increased from 450 °C to 600 °C) and thermal insulator thickness increased. It is important to consider the possibility of areas where this relationship may not be applicable.
1.5. Aims and Objectives of this Study
The purpose of this study is to obtain the ratio between the fire resistance obtained under standard (cellulose) and hydrocarbon (for objects of on O&GC) fire temperature-time curves. This ratio will be based on experimental studies, calculations, and modeling. This dependence will make it possible to approximate the fire resistance limit of structures under H-curve fire conditions based on the known value of the fire resistance limit under S-curve fire conditions, taking into account different types of fire protection.
For the above purpose, models were built in a software package implementing the finite element method on the basis of experiments previously conducted by the authors or provided by them and published data. The simulation of fire exposure under different fire curves was carried out, and the corresponding coefficients were obtained.
2. Materials and Methods
The authors independently conducted or used the results of previously conducted experiments to determine the fire resistance of steel structures of offshore platforms, tankers, steel columns with fireproof plaster, epoxy compositions, cement boards, and non-combustible covers under standard and hydrocarbon fire conditions. The aim of this study was also to obtain the thermophysical characteristics and ratio coefficients for critical temperatures of 500 °C for R-resistance and 140 °C for EI-resistance. In this work, the behavior of structures with fire protection was modeled by the finite element method, verified on prototypes, and used to predict the results for cases not realized in the experimental part. The ratio of K = S/H coefficients was determined.
2.1. Experimental Studies
The ambient temperature under hydrocarbon fire conditions is dependent on the time, as described below [5]:
The ambient temperature under standard fire conditions is dependent on the time, as described according to ISO 834 [6]:
where
T, T0—ambient temperature at the current and initial moment, °C;
t—time, min.
2.1.1. Decks and Bulkheads
The specific test conditions and procedures were applied for decks and bulkheads according to IMO Resolution A.754 [12]. The paper by [38] presents experimental studies for a number of decks and bulkheads. A-60 and H-60 bulkheads were selected for the current study. Figure 4 shows the arrangement of thermocouples on the unheated surface of the A-60 and H-60 bulkheads.
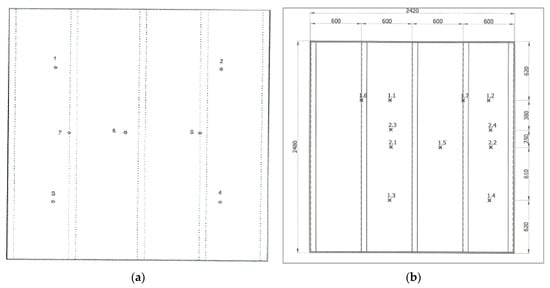
Figure 4.
Location of thermocouples on the unheated surface of bulkheads A-60 (a) and H-60 (b).
Class-H bulkhead prototypes were tested under hydrocarbon fire conditions. Class-A bulkhead prototypes were tested under standard fire conditions. The following structures were tested under relevant fire conditions (Table 2).

Table 2.
Tested samples of decks and bulkheads.
The critical (maximum allowable) temperature on the unheated surface (side) of the structure for the bulkhead was 140 °C [12].
2.1.2. Columns
Test conditions and procedures were applied to column specimens of different cross-sections with fire protection according to [18] (Figure 5). Experimental studies for epoxy paints, plaster compositions, non-combustible covers PROMIZOL MIX PROPLATE and cement boards are presented in [31,39,40,41]. The cross sections of I-columns for different samples, as well as thermocouple locations are shown in Figure 6.
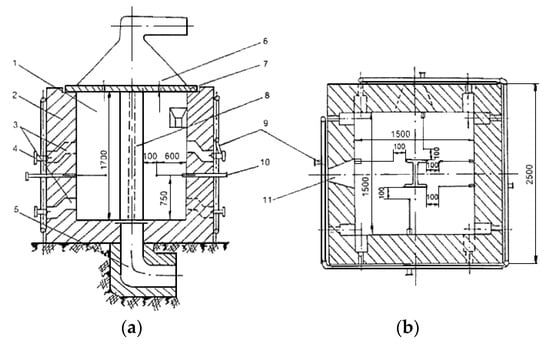
Figure 5.
The furnace according to [18]: (a) main view and (b) top view, where (1) is a fire chamber, (2) is a furnace masonry, (3) is a nozzle-heating channel, (4) is a nozzle, (5) is a smoke duct, (6) is an exhaust umbrella, (7) is a furnace vault, (8) is a test sample, (9) is an air duct, (10) is a thermocouple, and (11) is an inspection hatch.
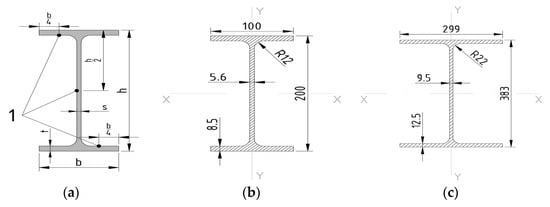
Figure 6.
I-beam: (a) general view, 1-thermocouple location; (b) I-beam profile IB20, and (c) I-beam profile IK40.
In Figure 6, the cross-sections of the I-columns for different samples as well as locations of thermocouple installation are shown.
Table 3 shows the characteristics of the cross-sections of the I-columns.

Table 3.
Cross-section characteristics of the IB20, I30K1, and I40K columns.

Table 4.
Types of samples and thickness of plaster coating for different types of experiments.

Table 5.
Main parameters of samples with intumescent coatings.

Table 6.
Main parameters of samples with fire protection non-combustible covers.

Table 7.
Main parameters of samples with fire protection boards on cement binder.
The limit state of the specimen during the fire test was considered to have been reached when the temperature of the specimen material reached 500 °C.
2.2. Modeling Method
The QuickField, Tera Analysis Ltd., Denmark, (in another version, ELCUT, LLC Tor, Russia) software was used to build thermodynamical finite element models, taking into account heat sources in blocks, edges, or individual vertices of the model [42]. QuickField packages can be applied to various aspects of thermal model design—heat transfer, temperature distribution, evaluation of local overheating, transient heating processes—and to solve thermophysical problems with the purpose of verifying experimental data [38,39,40,41].
The heat transfer module was used to analyze the temperature distribution in static and transient heat transfer processes. The heat sources in the heat transfer module can be specified directly and/or imported from other QuickField problems (coupled problems) as Joule Losses. Steady-state heat transfer analysis is possible not only in 2D Plane-Parallel and 2D axisymmetrical formulations but also as a 3D Extrusion and a 3D Import.
Mathematical models of the heat conduction process were applied, and the method of solving inverse problems by heat conduction was used according to the system of Equations (9)–(13) [43,44]:
- -
- equation of heat conduction
- -
- initial condition
- -
- boundary condition on the surface of the inverse heat conduction task at x ≤ dp
- -
- boundary condition on the inner surface of the fireproof coating at x = 0
x—coordinate in the fire protection coating (x = 0 corresponds to the point of contact between the coating and the metal where the sample is measured, temperature θa = θp (0, t));
cp—specific heat capacity, J/(kg∙K);
ρp—density, kg/m3;
Ap/V—section ratio, mm−1;
λp—heat conductivity coefficient, W/(m∙K);
t—time, s;
c0—calculation parameter; c0 = 0.57;
dp—thickness of fireproof coating, mm;
tmax—the maximum heating time of the sample, s;
αc—heat transfer coefficient on the outer surface of the fireproof coating, W/(m2∙K);
ε = 0.7—the degree of blackness of the surface of the mineral coating [43];
θ0—initial temperature of the sample, °C;
θt—temperature in the firing furnace, °C.
The initial characteristics of steel were as follows: grade C245 [44]; density 7800 kg/m3; and thermal conductivity and heat capacity variable depending on temperature (values taken from the default program reference book). The boundary conditions are presented in Table 8.

Table 8.
Boundary conditions defined in SP QuickField.
For the boundary solutions of the third kind, material density was assumed to be independent of temperature. To solve the problem with boundary conditions of the first kind, then the temperature should be set according to Equations (9) and (10) for the corresponding mode. To determine the characteristics of the fire resistance of structures, mathematical models of the heat conduction process were applied, and the method of solving inverse problems of heat conduction was used, defined by the system of Equations (11)–(13).
Heat transfer coefficients were determined for different types of fire protection in accordance with test protocols by solving the inverse heat conduction problem. The boundary conditions and model verification for structures with fire protection were provided in similar articles on this topic [30,31,32,33,34,35,36,37,38,39,40].
3. Discussion and Results
3.1. The Analysis of the GAPS Report [33,34] and Data Provided in the Standards
The data presented in Figure 7 can be used to perform first analyses of the fire resistance for unprotected steel constructions under temperature conditions in accordance with S- and H-curves and calculate the ratio of fire resistance, which we denote as the K-factor. The corresponding calculations can be performed using the procedures and dependencies provided in EN 1993-1-2 [14] (Figure 7a). Figure 7b presents the graph of the dependence of the K-factor on the temperature for different plate thicknesses. Based on the approximations of the aforementioned dependencies, the K-factor for a 5 mm thick plate at 500 °C is 3.3. This value is consistent with the findings of a previous study [36,37], which reported a coefficient of 3.6 for a for sections with a lower volume factor.
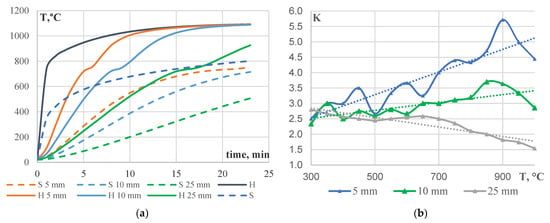
Figure 7.
Dependences of the steel temperature on the value of the time factor for S- [13,16] and H-curves [7,14] (a), as well as the value of the K-factor (fire resistance ratio) on the chosen critical temperatures (b).
The reports by GAPS [34] and AXA XL Risk Consulting [35] do not provide sufficient details on material thickness, density, effective thermal conductivity, and other relevant factors. This lack of information makes it challenging to draw conclusions about the relationship between the value of the ratio of fire resistance limits for S- and H-fire curves (K-factor) and the values of these factors. However, based on our data-processing results, we can conclude that there is a monotonically decreasing relationship between the value of the K-factor and the fire resistance limit. This relationship has a horizontal asymptote at a value of 1 on the vertical axis. Based on the graph in Figure 5, the K-factor ranges from 1.0 to 1.7 and has an average K = 1.6 for fire resistance limits of 90 min or less. For fire resistance limits exceeding 90 min, K is approximately 1.2. The described relationships are a result of the significant differences in the growth dynamics between the temperature curves (see Figure 8) for test durations of up to 90 min.
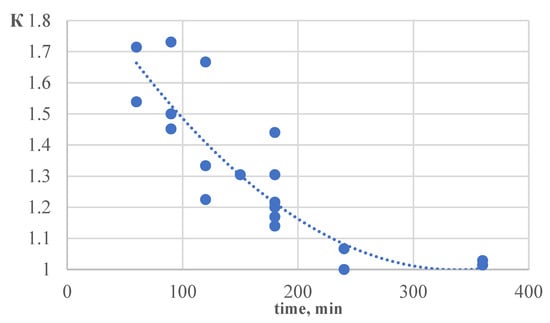
Figure 8.
Ratio S/H (K-factor) of the fire resistance limit under hydrocarbon fire conditions to the results of standard tests according to data from [34,35].
However, for test durations exceeding 170 min, the temperature described by the S-curve is higher compared to the H-curve. It should be noted that the provided values for the K-factor are only accurate for smaller structures (with a section factor Ap/V of less than 200 m−1). Additionally, the K-factor decreases as the structure becomes bigger. Therefore, it may be necessary to generalize the data, including previously published materials by the authors.
3.2. Steel Decks and Bulkheads with Mineral Wool Fire Protection
The study by [38] presents the thermophysical characteristics of mineral wool as a fire protection material for various types of steel decks and bulkheads.
In the research, the authors used validated finite element models from QuickField that were based on laboratory experiments to describe the dependence of the heating process under different test conditions. The results were compared for bulkheads A-60 and H-60. Figure 9 and Figure 10 show a graphical description of the modeling. Proceeding, for the purpose of this work, the models of bulkhead H-60 were predicted to obtain indicators of temperature reaching 140 °C on the unheated surface for bulkhead A-80 (K-factor of 1.7–1.8 according to Figure 8); the A-60 model was predicted to obtain the H-30 bulkhead.
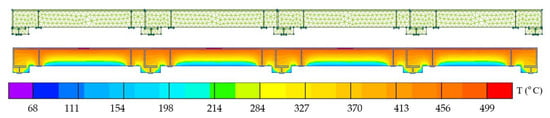
Figure 9.
Fire exposure simulation for the A-60 bulkhead.
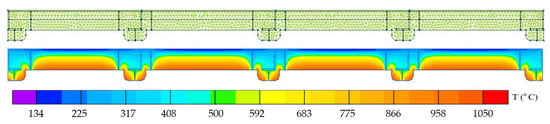
Figure 10.
Fire exposure simulation for the H-60 bulkhead.
A general view of the bulkhead corresponding to the H-60 variant used in the laboratory experiments is shown in Figure 11.

Figure 11.
Bulkhead H-60 after testing on the heated (a) and unheated (b) side.
The temperature on the unheated surface was measured during laboratory experiments using thermocouples placed at specific points. Based on these data, the relationship between temperature and time is established and presented graphically in Figure 12. The authors set the task of predicting the time for reaching 140 °C in the H-60 bulkhead structure when subjected to the standard mode, trying to determine what fire resistance limit could be obtained. Similarly, the authors tried to determine what parameter for H would be most predicted if the A-60 bulkhead was to be subjected to a hydrocarbon regime.
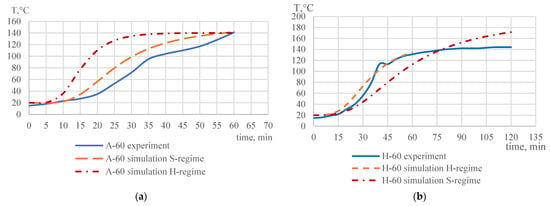
Figure 12.
Dependences of the temperature on the unheated surface for bulkheads A-60 (a) and H-60 (b) for S- and H-curve fire conditions.
The laboratory experiments were also conducted for the following design variants:
- -
- H-60 bulkhead: two layers of mineral wool, each 60/125 mm thick, density 150 kg/m3
- -
- A-60 bulkhead: two layers of mineral wool, each 60/85 mm thick, density 100 kg/m3.
Based on the results obtained, we calculated the average value of the K-factor (Table 9).

Table 9.
K-factor for bulkheads A-60 and H-60.
Figure 13 presents a graphical representation of the relationship between the coefficient K-factor and the time for bulkheads A-60 and H-60, as obtained from the laboratory experiments.
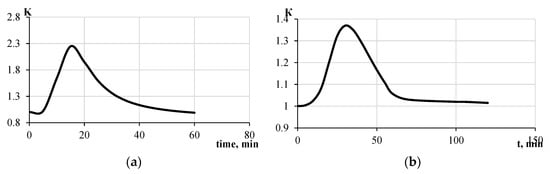
Figure 13.
Dependence of K-factor on time for bulkheads A-60 (a) and H-60 (b).
Thus, the simulation results for bulkhead H-60 were predicted to produce A-80, resulting in values typical of bulkhead A-78. H-30 was predicted for bulkhead A-60, resulting in structural heating values characteristic of H-37. The lower K-factor was explained by the fact that, in the experiment, lower density values were used for bulkhead A.
3.3. Fire-Retardant Plasters and Epoxy Coatings
Fire-retardant plaster compositions were tested to determine their thermophysical properties based on the data provided in [39]. Table 10 shows the test results of I-beams (height 2700 mm, section factor Ap/V = 135 m−1) covered with a 32 mm thick plaster layer on a base of cement and vermiculite with density 300 kg/m3 for a critical temperature value of 500 °C, as well as the calculated value of the K-factor.

Table 10.
Test results of I-column with plaster coating.
The K-factor was obtained during laboratory experiments using sensors (thermocouples) installed on the surface of the tested samples. The results show a smooth extremum (maximum) in the plots of K coefficients plotted as a function of the time factor (see Figure 14). This extremum is due to the evaporation of water from the plaster layer within 25–50 min. At this time, the time of water evaporation on the graphs looks like flat areas, and the temperatures are equalized [24]. Thus, the K-factor is equal to 1. During the test, the surface temperature of the original sample reached the critical value of 500 °C between 120 and 160 min. In the quasi-stationary regime, the K-factor decreased monotonically and approached the asymptotic value of 1 between 150 and 300 min. The temperature of the standard regime exceeded those of the hydrocarbon regime (Figure 2), so the K-factor decreased.
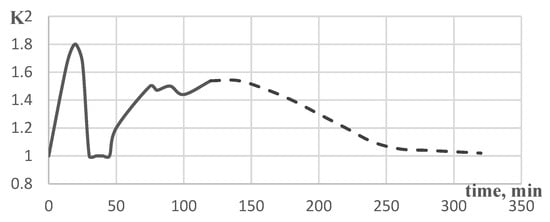
Figure 14.
Dependence of the K-factor for plaster-coated I-beam on the time.
Laboratory experiments were also conducted to determine the thermophysical properties of epoxy intumescent coating. The experiments considered prototypes of steel columns covered with a dry layer of epoxy intumescent compound of varying thicknesses. In the QuickField PC model, the thickness of the fireproofing coating was assumed to be equal to the thickness of the dry layer before the formation of foam-coke. After the formation of foam-coke, the average thickness of the fireproofing coating was taken as 40 mm in the calculation [31].
Table 11 shows the test results of samples 2.1–2.2 of I-beams I50B2 (Ap/V = 172 m−1) and samples 2.3–2.6 of I-beams I14B1 (Ap/V = 408 m−1) with a height of 1700 mm. All the samples were coated with a layer of epoxy coating of various thicknesses. To obtain the average coefficient, the value was interpolated depending on the thickness.

Table 11.
Test results of I-columns with epoxy coating.
The value for sample 2.3 turned out to have been underestimated due to the fact that the sample was cracked. Modeling of epoxy intumescent coatings in different modes depends on the thickness and thermal conductivity of the foam-coke (density, cell size). Such data are not available from manufacturers, so the K-factor is calculated only from experimental data. In the calculation of the value of the K-factor, the difference in coating thicknesses was taken into account as a weighted average value of the ratio of fire resistance limits.
Figure 15 shows the dependence of the K-factor on time when modeling the heating of samples under different fire regimes. The graph indicates that the highest value of the K-factor corresponds to a test duration of 15 min during the process of coke formation in the epoxy coating.
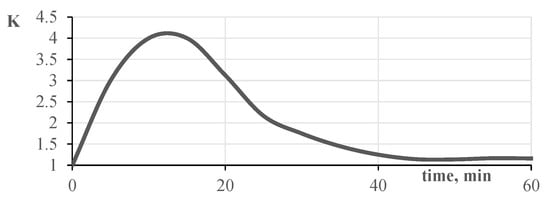
Figure 15.
Dependence of the K-factor for an epoxy-coated steel column on time.
This high value of the K-factor can be explained by the chemical reaction of foam-coke growth for epoxy paints and its different growth rate depending on the fire regime.
3.4. Fire Protection System with Basalt and Ceramic Fibers (Non-Combustible Covers)
The PROMIZOL-MIX PROPLATE system, developed by LLC “RPC PROMIZOL” (Russia), is a flexible rolled-sheet material made of non-combustible glass fiber and silica. It is installed on structures using special straps and fasteners, as shown in Figure 16.

Figure 16.
Non-combustible PROMIZOL-MIX PROPLATE system before, during, and after fire exposure (180 min) according to an S-curve fire.
The thermophysical properties of a protective material were determined through laboratory experiments based on five samples [40]. The results of the laboratory experiments as well as the calculated value of the K-factor (for the critical temperature of 500 °C) are summarized in Table 12. The K-factor corresponds to the results of laboratory experiments performed in relation to the 20B1 beam (Ap/V = 294 m−1), taking into account the fire protection system (density—130 kg/m3).

Table 12.
Test results of steel columns covered with non-combustible PROMIZOL-MIX PROPLATE system.
Figure 17 shows the graphical representation of dependencies of the K-factor for samples No. 2 and No. 3 of the fireproofing material.
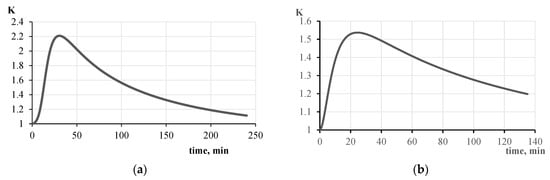
Figure 17.
Dependence of K-factor on time for steel columns covered with non-combustible PROMIZOL-MIX PROPLATE samples No. 2 (a) and No. 3 (b).
Figure 17 shows that, for sample No. 3, the highest value of the K-factor (2.2) corresponds to a test duration of 30 min. For sample No. 5, the highest value of the K-factor (1.57) is observed at a test duration of 20 min.
3.5. Portland Cement-Based Fireproofing Boards
The article by [41] presents the results of experiments on assessing the fire resistance of steel structures using Portland cement-based fire protection (Figure 18a–c). Additionally, it includes the results of the modeling temperature of construction under different fire exposures (Figure 18d,e). Thermophysical characteristics of flame retardant boards were determined by the authors on the basis of modeling and results of works in [46,47,48].

Figure 18.
The columns with structural fire protection before fire exposure (a), after fire exposure S- curves, 240 min (b), after fire exposure H- curves, 180 min (c) and the results of fire exposure modeling at a test duration of 25 min with S- (d) and H-curves (e) of fire.
It is important to note that it is difficult to conduct laboratory experiments to determine the thermal conductivity of the considered coatings at temperatures above 300 °C. In this case, it is recommended to conduct fire tests using the S-curve model with the subsequent determination of the thermophysical characteristics of the materials by solving the inverse problem of thermal conductivity. In [47,48], the characteristics of similar slabs consisting of Portland cement reinforced on both sides with glass mesh and one-sided protective coating are given. According to [47,48], the thermal conductivity of the slab at 25 °C is 0.3 W/(m-K), with a specific heat capacity of 1444 J/(kg-K) and a density of 1100 kg/m3. «Pyrosafe-Austover T» slabs have half the density of 650 kg/m3. The following characteristics were obtained during modeling (Table 13).

Table 13.
Thermal and physical properties of cement plates «Pyrosafe-Austover T».
The calculated values of the K-factor obtained on the basis of the results of laboratory experiments performed in relation to the considered structures are presented in Table 14. The K-factor corresponds to the results of a laboratory test performed in relation to the 30K1 beam (Ap/V = 157 m−1)-protected boards on cement binder “Pyrosafe-Austover T” (density 650 kg/m3).

Table 14.
Experimental results of fire protection “Pyrosafe-Austover T”.
The fire model was built for a steel column with fireproofing plates on cement binder “Pyrosafe-Austover T”. The K-factor was found to depend on the thickness and density of the fireproofing layer, the initial heat capacity and thermal conductivity of the fireproofing material, and the rate of change in thermal conductivity and heat capacity with the increasing temperature of the material used. The graphs in Figure 19, Figure 20 and Figure 21 demonstrate that the thickness of the fireproofing material, the rate of change in its thermal conductivity depending on the heating, and the density have the greatest influence on the K value.
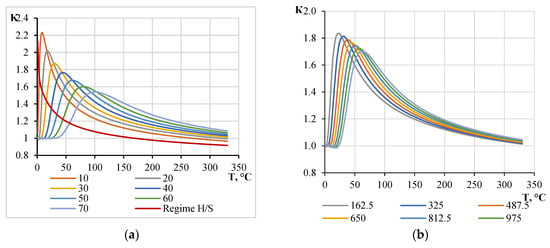
Figure 19.
Dependence of the K-factor on the value of the temperature of the material of the structure at different parameters of fire protection: (a) thickness of the s, mm; and (b) density ρ, kg/m3.
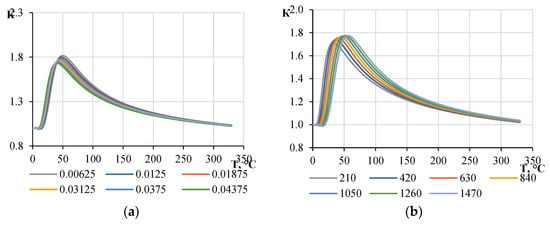
Figure 20.
Dependence of the K-factor on the value of the temperature of the material of the structure at different parameters of fire protection: (a) initial thermal conductivity λ, W/kg-K; and (b) initial heat capacity c, J/kg-K.
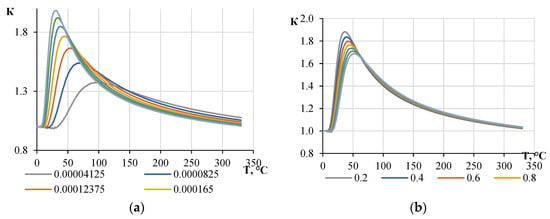
Figure 21.
Dependence of the K-factor on the value of the temperature of the material of the structure at different parameters of fire protection: (a) rate of change of thermal conductivity δλ, W/kg-K2; and (b) rate of change of heat capacity δc, J/kg-K2.
The maximum value of the K-factor is observed in the temperature range of 0–100 °C, which corresponds to the beginning of the fire test. With a further increase in temperature (100 °C and above), the K-factor decreases monotonically and asymptotically approaches a value of 1. This effect occurs because, under long fire exposure, the temperature difference between the material in S- and H-fires tends to zero, resulting in a quasi-stationary state.
Figure 22 summarizes the experimentally substantiated values of fire resistance under fire conditions in accordance to S- and H-curves, as well as the calculated values of the K-factors for all the variants of fire-protected structures considered in this paper.
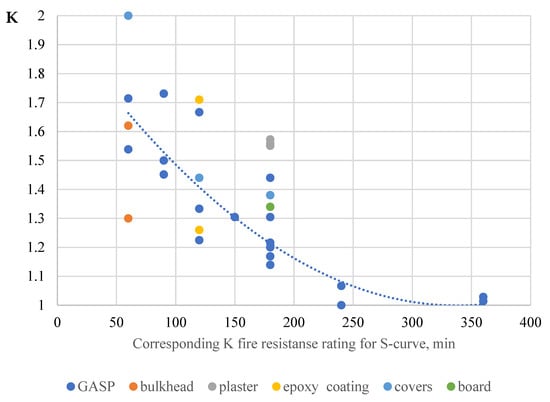
Figure 22.
K-factor of the fire resistance limit under hydrocarbon fire conditions to the results of standard tests: experimental and literature data [34,35].
The critical temperature value is 140 °C for the unheated surface of bulkheads and 500 °C for other types of fire protection.
Based on the obtained results, it is possible to objectively divide the ratio of fire resistance limits into three groups: up to 90 min (inclusive), it is approximately equal to 1.7; in the range from 90 to 180 min, it is 1.5; and starting from 180 min, it tends to 1. Due to the great uncertainty and the need to consider each of the values from individual experiments, we recommend taking values up to 180 min as 1.7 (rounding up) and after 180 min as 1.2.
4. Conclusions
In construction practice worldwide, building structures are typically standardized based on their fire resistance relative to cellulose fire, which is determined by the combustion of wood.
However, the local standards of the major and largest corporations in the petrochemical, oil, and gas industries prescribe the use of design curves where the temperature is determined by burning hydrocarbons. The idealized cellulose and hydrocarbon curves differ in the temperature increase during the first twenty minutes, but then level off.
The temperature rise is dependent on the section factor of the steel structure and the thickness of the fire protection material. This research presents new experimental data on the fire resistance of steel structures with various types of fire protection in hydrocarbon fires. The types of fire protection analyzed include intumescent coatings, plaster compositions, structural protection based on basalt superfine fiber, and protection based on a composition of cement binder.
This study shows that the fire resistance of a structure in a hydrocarbon fire is reduced by a factor of 1.3–1.6 compared to the results obtained in a standard fire resistance test. These K-factor values were obtained for temperatures of 140 °C in the case of flat surfaces (decks, bulkheads, possibly walls, partitions, curtains). In addition, values were obtained for temperatures of 500 °C in the case of vertical structures (columns). In the general trend, in the region of the first 20 min of K exposure, the difference is 2.2–2.0 times, and then K tends to 1.
It is important to note that this decrease can be mitigated through various fire protection options. The ratio can be influenced by the characteristics of the insulation material: density, effective thermal conductivity, and heat capacity. Also, the location of the material, the methods of fixing, and installation affect this coefficient. The recommended values for the K-factor for fire resistance up to 180 min (incl.) are 1.7 and, after 180 min, 1.2.
The practical relevance of this study is that the vast majority of fire protection manufacturers, for improving the fire resistance of structures, first test structures in the cellulose regime. For example, this is the case for fire curtains, coatings, and most fire protection formulations for structures that are tested in the standard regime. However, such structures may also be operated in a hydrocarbon fire regime in oil and gas facilities. Thus, predicting the required material consumption for the required fire resistance time in a hydrocarbon regime will provide savings in the resources available for the required number of experiments.
Author Contributions
Conceptualization, M.G.; methodology, M.G.; software, N.S.; validation, N.S. and I.D.; formal analysis, A.R.; investigation, I.D.; data curation, N.S. and I.D.; supervision, M.G; writing—original draft, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation (RSF) under grant no. 23-29-00618. URL: https://rscf.ru/project/23-29-00618/ (accessed on 19 May 2024).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within this article.
Acknowledgments
We are grateful for the help and support of PROZASK Ltd. and LLC “RPC PROMIZOL” (Russia).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nolan, D.P. Handbook of Fire and Explosion Protection Engineering Principles for Oil, Gas, Chemical, and Related Facilities, 4th ed; Gulf Professional Publishing: Houston, TX, USA, 2018; p. 522. ISBN 978-0-12-816002-2. [Google Scholar]
- Matyushin, A.V.; Kondashov, A.A.; Matyushin, Y.A.; Sibirko, V.I. Analytical Methodology for Substantiating the Optimal Frequency of Scheduled Inspections of the Fire-fighting Condition of Industrial and Warehouse Buildings. Occup. Saf. Ind. 2023, 9, 32–38. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Probability Analysis and Prevention of Offshore Oil and Gas Accidents: Fire as a Cause and a Consequence. Fire 2021, 4, 71. [Google Scholar] [CrossRef]
- Hosseinnia Davatgar, B.; Paltrinieri, N.; Bubbico, R. Safety Barrier Management: Risk-Based Approach for the Oil and Gas Sector. J. Mar. Sci. Eng. 2021, 9, 722. [Google Scholar] [CrossRef]
- EN 1363-2:1999; Fire Resistance Tests—Part 2: Alternative and Additional Procedures. CEN (European Committee for Standardization): Brussels, Belgium, 2001. Available online: https://nd.gostinfo.ru/document/6239985.aspx (accessed on 2 September 2023).
- ISO 834-1:1999/Amd 2; 2021 Fire-Resistance Tests. Elements of Building Construction. Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 2012. Available online: https://cdn.standards.iteh.ai/samples/81661/75243e089adb4a66b90d236c28cc55da/ISO-834-1-1999-Amd-2-2021.pdf (accessed on 18 May 2024).
- UL 1709-2017; Standard for Safety Rapid Rise Fire Tests of Protection Materials for Structural Steel. Underwriters Laboratories Inc. (UL): Northbrook, IL, USA, 2017. Available online: https://docs.cntd.ru/document/550713257 (accessed on 29 January 2024).
- Abdulkareem, B.F.; Izzet, A.F.; Oukaili, N. Post-Fire Behavior of Non-Prismatic Beams with Multiple Rectangular Openings Monotonically Loaded. Eng. Technol. Appl. Sci. Res. 2021, 11, 7763–7769. [Google Scholar] [CrossRef]
- Mahmood, E.M.; Allawi, A.A.; El-Zohairy, A. Analysis and Residual Behavior of Encased Pultruded GFRP I-Beam under Fire Loading. Sustainability 2022, 14, 13337. [Google Scholar] [CrossRef]
- Chen, L.; Tong, H.; Liu, Z.; Zhang, Z.; Mou, P. Research on Quantitative Calculation Method of Accident Scope of Gathering and Transportation Station. Energies 2022, 15, 9476. [Google Scholar] [CrossRef]
- Li, N.; Zhang, B.; Liu, X.; Wang, K.; Wang, H. Experimental Research and Numerical Analysis of Marine Oil Leakage and Accidental Ignition in Fishing Vessels. Appl. Sci. 2023, 13, 11510. [Google Scholar] [CrossRef]
- IMO Resolution A.754 (18); Recommendation for Testing Fire Resistance of Class “A”, “B” and “F” Slabs. International Maritime Organization: London, UK, 1993. Available online: https://wwwcdn.imo.org/localresources/en/KnowledgeCentre/IndexofIMOResolutions/AssemblyDocuments/A.754(18).pdf (accessed on 18 May 2024).
- ASTM E119; Standard Test Methods for Fire Tests of Building Construction and Materials. ASTM International: West Conshohocken, PA, USA, 2022. Available online: https://www.astm.org/e0119-00a.html (accessed on 29 January 2024).
- EN 1991-1-2; Eurocode 1: Actions on Structures—Part 1–2: General Actions—Actions on Structures Exposed to Fire. CEN (European Committee for Standardization): Brussels, Belgium, 2002. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.2.2002.pdf (accessed on 25 October 2023).
- GOST 30247.1-94; Elements of Building Constructions. Fire-Resistance Test Methods. Loadbearing and Separating Constructions. IPK Izdatelstvo Standartov: Moscow, Russia, 1995. Available online: https://docs.cntd.ru/document/9055247 (accessed on 20 November 2023).
- Standard of the Organization of the Russian Association for the Development of Steel Construction “Design of Fire Protection of Load-Bearing Steel Structures with the Use of Various Types of Coatings”. Izdatelstvo: Development Association Steel Construction. Available online: https://steel-development.ru/en/for-designers/ntd-kategoriya/sto-arss (accessed on 7 May 2024).
- API RP 2218; Fireproofing Practices in Petroleum and Petrochemical Processing Plants. API Publishing Services: Washington, DC, USA, 2013; p. 68. Available online: https://www.apiwebstore.org/standards/2218 (accessed on 7 May 2024).
- GOST 53295-2009; Fire Retardant Compositions for Steel Constructions. General Requirement. Method for Determining Fire Retardant Efficiency. IPK Izdatelstvo Standartov: Moscow, Russia, 2009. Available online: https://docs.cntd.ru/document/1200071913 (accessed on 7 May 2024).
- Eremina, T.; Korolchenko, D. Fire Protection of Building Constructions with the Use of Fire-Retardant Intumescent Compositions. Buildings 2020, 10, 185. [Google Scholar] [CrossRef]
- Häßler, D.; Hothan, S. Performance of intumescent fire protection coatings applied to structural steel tension members with circular solid and hollow sections. Fire Saf. J. 2022, 131, 103605. [Google Scholar] [CrossRef]
- Randaxhe, J.; Popa, N.; Vassart, O.; Tondini, N. Development of a plug-and-play fire protection system for steel columns. Fire Saf. J. 2021, 121, 103272. [Google Scholar] [CrossRef]
- Al-Jadiri, M.S.F.; Said, A.M.I. Reinforced Concrete Columns Insulated by Different Gypsum Layers Exposed to 900 °C One Side Fire Flame. Eng. Technol. Appl. Sci. Res. 2023, 13, 11586–11592. [Google Scholar] [CrossRef]
- Diaconu, B.; Cruceru, M.; Anghelescu, L. Fire Retardance Methods and Materials for Phase Change Materials: Performance, Integration Methods, and Applications—A Literature Review. Fire 2023, 6, 175. [Google Scholar] [CrossRef]
- Barthelemy, B.; Kruppa, J. Fire Resistance of Building Structures/Transl.; Predtechensky, M.V., Zhukov, V.V., Zhukov, V., Eds.; Stroyizdat: Moscow, Russia, 1985; 216 c.-Translation from: Resistance au feu des structures beton-asier-bois/V. Barthelemy, J. Kruppa. [Google Scholar]
- Bogdanova, V.V.; Kobets, O.I.; Buraya, O.N.; Ustinov, A.A.; Zybina, O.A. Intumescent compounds for fireproofing of polymer pipelines. Mag. Civ. Eng. 2022, 116, 11607. [Google Scholar] [CrossRef]
- Ustinov, A.; Babikova, A.; Zybina, O.; Lobov, D.; Printseva, M.; Klaptyuk, I.; Shkitronov, M. Improvement of Methodology for Assessing Fire-Protective Efficiency of Intumescent Coatings Applied on Metal Constructions. E3S Web Conf. 2021, 320, 02009. [Google Scholar] [CrossRef]
- Wang, X.; Weinell, C.E.; Ring, L.; Kiil, S. Thermal insulation performance and char formation and degradation mechanisms of boron-containing hydrocarbon intumescent coatings. Fire Saf. J. 2021, 123, 103369. [Google Scholar] [CrossRef]
- Häßler, D.; Mund, M.; Daus, L.; Hothan, S.; Schaumann, P.; Schartel, B. Durability of intumescent coatings and recommendations for test concepts for a working life of more than 10 years. Fire Saf. J. 2024, 146, 104173. [Google Scholar] [CrossRef]
- Strakhov, V.L.; Kuz’min, I.A.; Bakulin, V.N. Complex mathematical modeling of thermal protection made of highly extended elastomers. High Temp. 2019, 57, 250–255. [Google Scholar] [CrossRef]
- Polevoda, I.I.; Ivanitskiy, A.G.; Zhamoydik, S.M.; Prorovsky, V.M. Software Tool for Calculating the Dynamics of Heating of Steel Structures with Structural Fire Protection//Fire Safety: Problems and Prospects. 2010. N°1 (1). Available online: https://cyberleninka.ru/article/n/programmnoe-sredstvo-dlya-rascheta-dinamiki-progreva-stalnyh-konstruktsiy-s-konstruktivnoy-ognezaschitoy (accessed on 10 November 2023).
- Gravit, M.; Shabunina, D.; Shcheglov, N. Thermal Characteristics of Epoxy Fire-Retardant Coatings under Different Fire Regimes. Fire 2023, 6, 420. [Google Scholar] [CrossRef]
- Wang, S.; Hou, X.; Wang, Y.; Chen, Y.; Xu, D.; Liu, C.; Huang, Q. Design and Validation of Lifetime Prediction Model for Lithium-Thiocarbonyl Chloride Batteries Based on Accelerated Aging Experiments. Metals 2023, 13, 1579. [Google Scholar] [CrossRef]
- Cheng, S.; Yuan, Z.; Ye, X.; Zhang, F.; Liu, J. Empirical prediction model for Li/SOCl2 cells based on the accelerated degradation test. Microelectron. Reliab. 2015, 55, 101–106. [Google Scholar] [CrossRef]
- Fireproofing for Hydrocarbon Fire Exposures//GAPS Guidelines. Publication of Global Asset Protection Services LLC. 2000. Available online: https://www.appliedbuildingtech.com/system/files/gap2.5.1.fireproofingforhydrocarbonexposures.pdf (accessed on 24 August 2021).
- AXA XL Risk Consulting. GAPS© 2020. Available online: https://axaxl.com/-/media/axaxl/files/pdfs/prc-guidelines/prc-2/prc251fireproofingforhydrocarbonfireexposuresv1.pdf (accessed on 7 May 2024).
- Shebeko, Y.N.; Zuban, A.V.; Shebeko, A.Y. An evaluation of an actual fire resistance limit of non-protected steel structures for different temperature regimes of fires. Pozharovzryvobezopasnost/Fire Explos. Saf. 2019, 28, 29–34. (In Russian) [Google Scholar] [CrossRef]
- Cherkasov, E.Y.; Voroncova, A.A.; Mit’ko, A.V. Fire resistance of steel structures exposed to standard and hydrocarbon fire regimes. Neftegaz.RU. 2021, 12, 100–102. (In Russian). Available online: https://magazine.neftegaz.ru/articles/prombezopasnost/714005-ognestoykost-stalnykh-konstruktsiy-pri-vozdeystvii-standartnogo-i-uglevodorodnogo-rezhimov-pozhara/ (accessed on 7 May 2024).
- Gravit, M.; Shabunina, D. Numerical and Experimental Analysis of Fire Resistance for Steel Structures of Ships and Offshore Platforms. Fire 2022, 5, 9. [Google Scholar] [CrossRef]
- Gravit, M.; Shabunina, D.; Antonov, S.; Danilov, A. Thermal Characteristics of Fireproof Plaster Compositions in Exposure to Various Regimes of Fire. Buildings 2022, 12, 630. [Google Scholar] [CrossRef]
- Gravit, M.; Prusakov, V.; Shcheglov, N.; Kotlyarskaya, I. Fire Protection of Steel Structures of Oil and Gas Facilities: Multilayer, Removable, Non-Combustible Covers. Fire 2024, 7, 86. [Google Scholar] [CrossRef]
- Gravit, M.; Golub, E.; Klementev, B.; Dmitriev, I. Fire Protective Glass Fiber Reinforced Concrete Plates for Steel Structures under Different Types of Fire Exposure. Buildings 2021, 11, 187. [Google Scholar] [CrossRef]
- QuickField. Modeling of Two-Dimensional Fields by the Finite Element Method. Available online: https://quickfield.com/ (accessed on 17 December 2023).
- Kung, F.; Yang, M.C. Improvement of the Heat-Dissipating Performance of Powder Coating with Graphene. Polymer 2020, 12, 1321. [Google Scholar] [CrossRef] [PubMed]
- GOST 26020-83; Russian State Standard, Hot-Rolled Steel I-Beam with Parallel Flange Edges. Dimensions. IPK Izdatelstvo Standartov: Moscow, Russia, 2003. Available online: https://internet-law.ru/gosts/gost/21141/ (accessed on 29 January 2024).
- Markus, E.S.; Snegirev, A.Y.; Kuznetsov, E.A. Numerical Simulation of a Fire Using Fire Dynamics; St. Petersburg Polytech-Press: St. Petersburg, Russia, 2021. [Google Scholar]
- Palevoda, I.I.; Zhamoydik, S.M.; Zaynudinova, N.V.; Nekhan, D.S. Regulation of the fire resistance of modern building structures of reinforced concrete. J. Civ. Prot. 2023, 7, 144–163. [Google Scholar] [CrossRef]
- Garashchenko, A.N.; Antonov, S.P.; Vinogradov, A.V. Studying the thermal characteristics and effectiveness of structural fire proofing made of PROSASK Firepanel cement boards by means of reproducing the high-temperature effect. Pozharovzryvobezopasnost/Fire Explos. Saf. 2022, 31, 13–29. (In Russian) [Google Scholar] [CrossRef]
- Garashchenko, A.N.; Danilov, A.I.; Antonov, S.P.; Marchenkova, S.V.; Pavlov, V.V. The thermal analysis of fire test results obtained for loaded cast iron tubing used to line subway tunnels, their rational fire protection and pre-set fire resistance. Pozharovzryvobezopasnost/Fire Explos. Saf. 2022, 31, 21–39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).