A Quasi-Spherical Fusion Reactor Burning Boron-11 Fuel

Abstract

In this study, particle-in-cell (PIC) simulation was used to validate a conceptual design for a quasi-spherical, net power, hydrogen-plus-boron-11-fueled fusion reactor incorporating high-temperature superconducting (HTS) magnets. By burning a fully thermalized plasma, our proposed MET6 reactor uses the principles of the 1980 magneto-electrostatic trap design of Yushmanov to improve the classic Polywell design. Because the input power consumed by the reactor will barely balance the waste bremsstrahlung radiation, future research must focus on reducing the bremsstrahlung losses to reach practical net power levels. The first step to reducing bremsstrahlung, explored in this paper, is to tune the reactor parameters to reduce the energies of trapped electrons. We assume the quality factor Q can be approximated as the ratio of fusion power output divided by bremsstrahlung power loss. Thus, assuming the particles’ power loss is negligible compared to bremsstrahlung power loss, the resulting quality factor is estimated to be Q ≈ 1.3.

1. Introduction

This paper reports on a conceptual design process aimed at producing a net power fusion reactor constructed with six high-temperature superconducting (HTS) electromagnets. The computer simulation results were analyzed using Yushmanov’s magneto-electrostatic trap (MET) theory [1]. Our spherical design, which we named MET6, has a more efficient shape for plasma confinement than cylindrical designs. Yushmanov showed that, considering only particle losses, quality factor (Q) scales linearly with the volume-to-surface ratio of a confined plasma core. Since a sphere has a bigger volume-to-surface ratio than a cylinder of the same volume, our spherical design might be expected to produce larger Q-values than recent cylindrical ones [2,3] but only if its electron boron bremsstrahlung loss can be kept to manageable levels.

In addition to bremsstrahlung loss, a second potential source of radiation loss has also been considered and found negligible. Synchrotron radiation will be emitted from any magnetized portions of the plasma volume. But due to diamagnetic cancelation inside the plasma, a magnetic field with plasma may exist only in a relatively thin sheath layer at the surface of a trapped plasma ball [1]. Not only does the sheath occupy a small portion of the reactor volume, but any synchrotron radiation emitted from it is in the infrared/microwave region of the optical spectrum, making it possible to absorb the synchrotron radiation inside the reactor, thereby preventing its loss [4]. For these reasons, namely limited volume and low photon energy, the loss of energy via synchrotron radiation can be justifiably ignored compared to the losses due to the higher-energy bremsstrahlung radiation.

Yushmanov’s analysis was specialized to reactors burning deuterium plus tritium (DT) fuel. Because of concerns about the long-term availability of the rare isotope tritium [5,6], we chose to design a reactor burning hydrogen plus boron-11 (pB11) fuel. Compared to tritium, terrestrial B11 is so plentiful that supplying it to future generations will not substantially increase the operational costs of the MET6 reactor. Natural boron is 80% composed of the isotope boron-11. In our analysis, we compute the reactor quality factor to serve as a figure of merit in comparing various reactor designs. The quality factor is defined as the ratio of usable power output to the drive power input. Drive power input is what is needed to confine and heat the fuel plus what is needed to compensate for the heat lost to bremsstrahlung radiation. Because of the relatively high 5+ charge state of the boron-11 in the fuel, our power output is dominated by useless bremsstrahlung radiation overpowering fusion power output. For this reason, the quest for a practical pB11 reactor design shifts to the need to reduce bremsstrahlung losses as opposed to a DT reactor focusing on reducing particle losses.

Reactors burning DT fuel are little troubled by bremsstrahlung radiation. It is largely ignored in the analysis of Yushmanov [1]. On the contrary, in our case, we can approximate the minimum input power requirement to be just that needed to balance the bremsstrahlung losses. This simplifies the calculation of power input which can now be computed from a textbook formula for bremsstrahlung power. The resulting quality factor is predicted to be 1.3, just barely in the break-even range.

The design still holds promise as a contender for commercial power because the predicted quality factor depends on the reactor’s many design parameters, most of which have not been systematically explored. For example, the best footprint for the HTS magnets is unknown, pending future development by HTS magnet designers, e.g., Commonwealth Fusion Systems of Massachusetts. In lieu of a specification for a workable HTS magnet, we chose to adopt the footprint of a commercially available resistive magnet [7]. The simulated footprint of the magnet affects the design’s performance in a complex way. The surfaces of the four magnets mounted on the four side-faces of the cube intersect the simulation plane in the eight square boxes shown in each panel of Figure 1a–c. The bias voltage applied to the magnets creates a complicated equipotential surface determining the E-field throughout the simulated plane. The shape of a resistive magnet is normally optimized to facilitate water-cooling through hollow wires wound on a cylindrical central spool. HTS magnets would be optimized differently, producing a different E-field from the resistive design. The design of our HTS magnets would include features chosen to maximize the quality factor via computer simulation.

MET6 evolved naturally from its predecessor, the hexahedral Polywell reactor, invented by Robert Bussard in 1989 [8]. Bussard’s Polywell design was effectively criticized by Rider in 1997 [9] and again in the 2018 Jason Report [10], summarizing the U.S. Department of Energy’s ARPAE funding program. The Jason Report concluded that Polywell was “unlikely to reach scientific break-even”, referencing Rider [9] and Rostoker et al. [11]. Rostoker et al. had convincingly shown that Rider had wrongly assumed impossible operating conditions, making his conclusions inapplicable for practical reactor design.

The design of our MET6 sidesteps this controversy [9,11] over Polywell’s claim to a non-thermal energy distribution. In contrast to Polywell, the plasma in our MET6 reactor is predicted to have a Maxwellian (i.e., thermal) energy distribution, with only a slight departure predicted due to the extreme high-energy tail of electrons up-scattering to energies exceeding the height of the trapping potential. This minor departure from the Maxwellian distribution was ignored by Yushmanov [1], Dolan [2] and Sporer [3] and likewise in this paper. Pure Maxwellian energy distribution is a specified feature of the MET6 design.

We chose the particle-in-cell (PIC) simulation technique as the most reliable and convenient method for plasma simulation. The simulation software was developed over many years by Prof. Charles Birdsall’s group at UC Berkeley [12] and sold to Tech-X Corporation of Boulder, Colorado. We licensed a software package, named OOPIC Pro (for Object Oriented PIC), from Tech-X.

2. Hardware Design

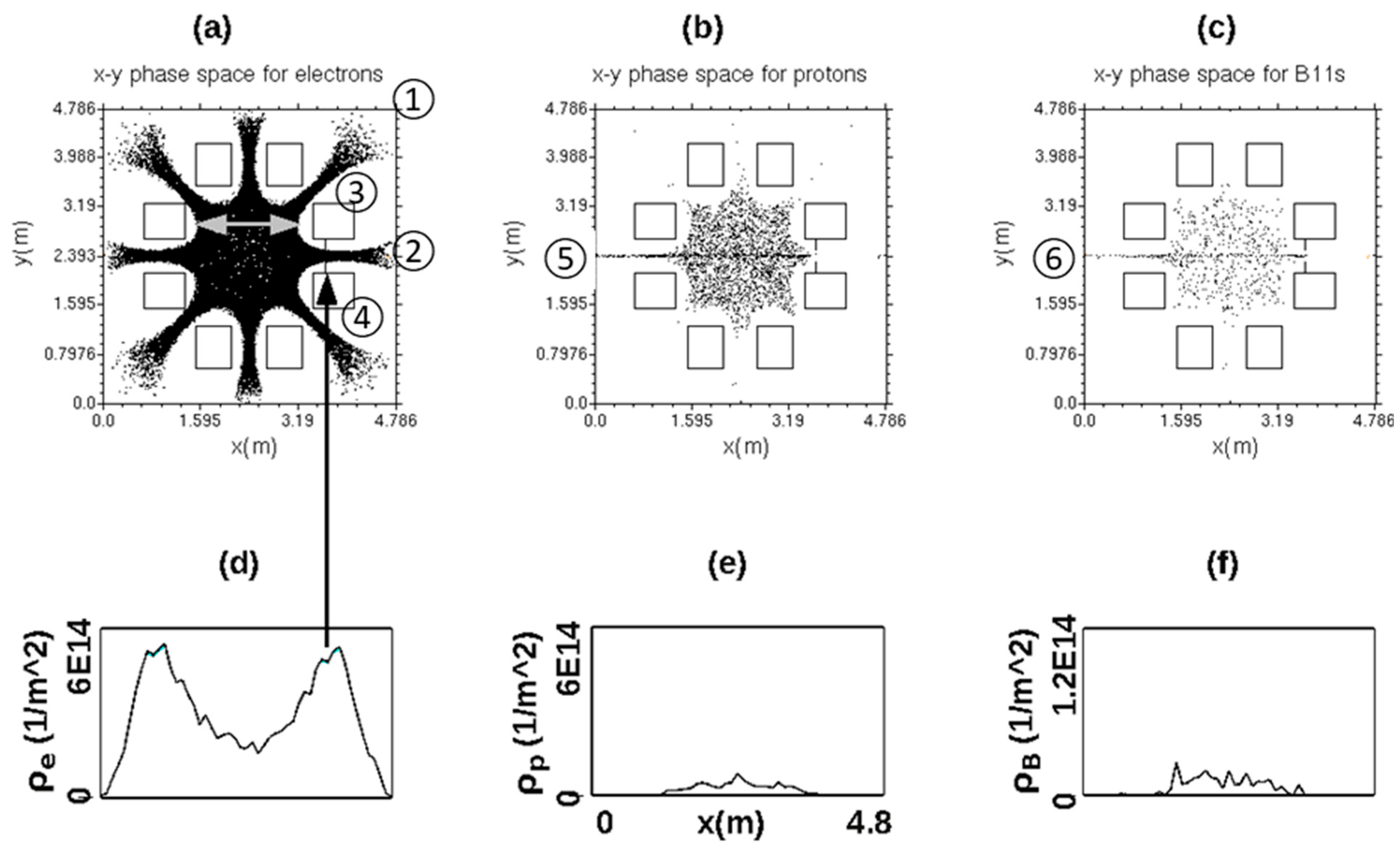
MET6 is a fusion reactor designed around six cylindrical, HTS coil magnets mounted on the faces of a regular hexahedron (i.e., cube). Figure 1a–c show PIC [13]-simulated snapshots of the plasma in the central plane of the cube. The positions of individual macroparticles are plotted as black dots, electrons in (a), protons in (b) and boron-11 ions in (c). When the simulation program runs, it displays a new snapshot of the particle positions at each time step, i.e., every 73 picoseconds of plasma time. An analysis of the particle movements guided our optimization of the design. The most important parameter of the design is the size of the magnets, which determines the resulting size of the cubic vacuum tank and the diameter of the plasma ball enclosed by the magnets. The fusion power scales with this size in proportion to the volume of the vacuum tank, labeled as ① in Figure 1a. The tank is required to be big enough to leave clearance outside the ring of magnets to accommodate insulating, hollow legs supporting the magnets from the tank. Clear spaces are left to accommodate the legs without causing plasma losses. The invention of hollow, insulating support legs and clear space to accommodate them is the subject of a 2015 patent on a proposed Polywell reactor [14]. Although our MET6 reactor does not function like Polywell was supposed to [8], the support legs would be the same as described in the patent. The magnets in Figure 1 appear to be floating in space, but eight areas clear of plasma are predicted by the simulation to occur between the magnets and the nearest tank wall. These clear spaces were designed to accommodate non-intercepting support legs which would reach from the tank wall to each of the eight magnet boxes shown.

Figure 1a–c show the major internal components of the reactor labeled with circled integers as follows: ① indicates the square cross-section of the cubic vacuum tank, of diameter 4.79 m and shown with tick marks. The metal tank is simulated as an electrical conductor held at zero volts. The tank serves as a grounded cathode for injecting electrons, protons and boron fuel ions. ② indicates the location of an electron emitter, envisioned as a hot filament biased to the same zero voltage as the tank. Starting at time t = 0, 15 amps(A) of zero-energy electrons was simulated from the point source depicted as an orange dot located 1 cell width (=9.57 cm) inside the right-hand tank wall in panels (a–c). Electrons are accelerated inward by an electric field formed by applying a 2.4-megavolt (MV) DC voltage to eight conducting magnet boxes serving as an electrical anode. The square boxes labeled ③ and ④ represent one of the four magnet coils mounted on the four side-faces of the cube. Three other pairs of boxes represent the other three magnets surrounding the central plane of the cube. Each coil intersects the central plane in two areas, outlined by square boxes. At the approximate center of each box, a long straight HTS wire is simulated carrying the current appropriate for generating the magnetic field required to confine electrons, as shown in Figure 1a. The location of each of the eight wires was adjusted to be no less than one-half a cell width from the geometrical center of its nearest magnet box. Such adjustment was necessary to avoid calculating the field too near a singularity in the field expression when evaluated at zero distance from a wire.

Choosing to locate the eight wires near but not too near the centers of the boxes is a simplification made to facilitate the tabulation of B-field values for each cell. The x- and y-coordinates of the static B-field were computed separately and stored as two 50 × 50 arrays in memory. A real-world superconducting coil would have wires filling the area inside each box. The quality factor from a reactor with such real coils will differ by an unknown amount from the one calculated from our simulated coils. This difference is the main uncertainty in the simulation.

Starting at time t = 0, electrons flow continuously into the center of the tank through the open bore of the right-hand magnet coil, i.e., between the squares labeled ③ and ④. The trapped electrons’ density increased with time until it reached the spatially uniform density shown in snapshot (a), made at a plasma time of t = 0.38 ms. This time was chosen as a stopping point for the simulation. It is the earliest time that the plasma density reached a stable, steady-state condition. As long as the electron drive current was held at 15 A, the plasma density was constant, independent of time.

The duty factor of MET6 is naturally unity.

This density is still many orders of magnitude too low to produce net power. In real-world startup, the electron drive current and matching ion injection currents would be increased over time to raise plasma density to net power levels. In the simulation, the diagnostics at this early time are enough to predict the net power conditions, making it unnecessary to explicitly simulate beyond t = 0.38 ms. A key finding is that the shape of the plasma core is constant in simulated time, so the net power density could be determined by the β = 1 condition that defines the same surface at net power, as we see in Figure 1. From the Plasma Formulary [15], the formula for β = (4 × 10⁻¹¹) nT/B is a function of electron density n, temperature T and magnetic field B, all evaluated at the surface of the plasma core. The β = 1 equation was inverted to find the surface electron density n, which also must equal the surface fuel density due to the requirement for quasi-neutrality. Figure 1b,c show the fuel density to be uniform inside the surface. The fuel density determines the reactor’s power output and, when dividing it by the drive power, the quality factor, which is the key measure of reactor performance.

In a real reactor, the magnetic field internal to the plasma sheath would become zero as the density rises to β = 1. In the simulation, at the time shown in Figure 1, the plasma density was still too low to generate any significant diamagnetic field. To help speed up the calculation, the OOPIC simulation was run using the “electrostatic” mode, in which the magnetic field is static in time and initialized cell by cell from programmed expressions. To simulate diamagnetism, the t = 0 field from the HTS wires was replaced cell by cell with a zero value for all cells inside a square region of cells spanning the center of the tank. Outside the region, the field was computed from the textbook formula for fields from eight infinitely long wires. The width of the field-free region is indicated by the double-headed arrow in Figure 1a. The diameter of the region was used as an adjustable parameter, adjusted to match the width of the recirculating electron beam to just fill an aperture at the position of the vertical arrow in Figure 1a. The wider the field-free region selected, the wider the beam width at the aperture. The wider the beam at the aperture, the greater the current of electrons scraped off by the aperture.

Ions enter the tank from point sources, protons from a source located at position ⑤ in Figure 1b and boron ions from a source at position ⑥ in Figure 1c. The positions of the point sources were fixed at the center of the left-hand tank wall and the velocities/currents of the ions specified by adjustable parameters in the input file. The velocities were adjusted by trial and error for the ions to pass freely into the core of the reactor along the cusp line through the bore of the left-hand magnet. The currents were adjusted to stabilize the densities of the two species of ions to form charge densities equal to each other and each matching half the electrons’ charge density.

The design of ion sources for tokamaks is the subject of some of our other papers [16,17]. Injection into tokamaks is more demanding than that into MET6 due to the tokamak’s transverse magnetic field, which tends to deflect charged particle beams. To avoid such deflection, tokamaks require neutral or neutralized beams whereas MET6’s cusp injection works well with simpler charged particle beams, i.e., those simulated here. As seen in Figure 1b,c, the ions incoming from sources ⑤ and ⑥ are focused into narrow beams by the cusp field in the left-hand magnet.

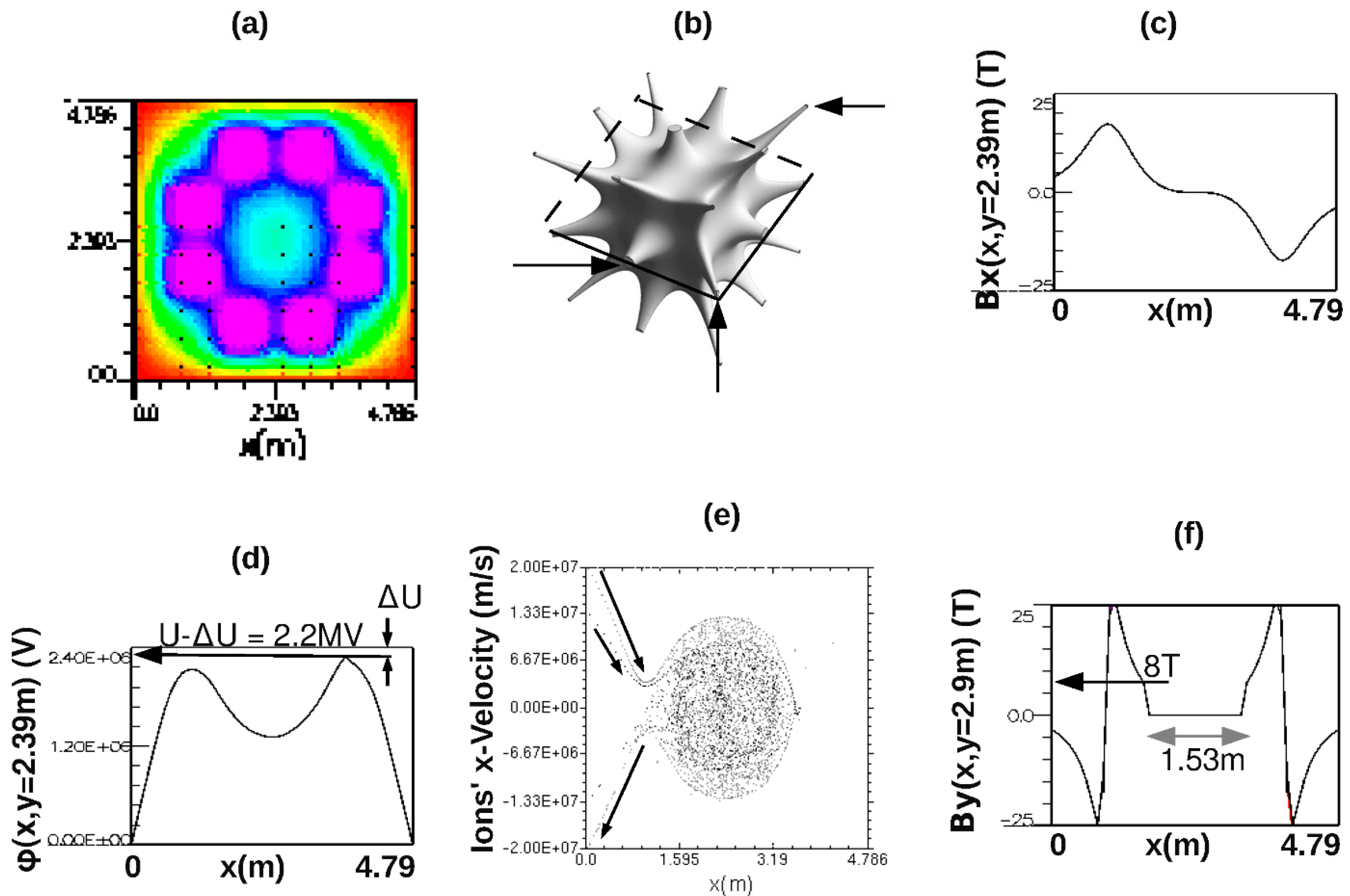
On entering the tank, newborn ions travel through the open bore of the left-hand magnet. The initial energies of the ions, selectively imparted by the sources, were chosen to just exceed the peak of the decelerating potential they will find on entry. Figure 2d shows a graph of the steady-state potential function along the horizontal midline of the reactor, the path followed by ions on their first pass through center. The shape of this potential function is crucial to the functioning of the reactor. It determines the temperatures of the electrons’ and ions’ plasma. Yushmanov [1] presented a similar potential function for his hypothetical toroidal multipole with 10 anode gaps. Yushmanov identified its main characteristics as a central potential minimum at half the bias voltage U and the trapping of electrons in the potential wells represented by the inversion of the two peaks. The trapped electrons depress the maximum potential voltage by an amount Yushmanov called ΔU. He divided the remaining potential equally to produce equal electron and ion temperatures. In our design, the temperatures of electrons and ions may be unequal and manipulated to reduce the level of bremsstrahlung losses.

The force on a newborn ion is proportional to the negative gradient of the potential shown. The ions’ initial velocities are slowed by the rising slope of the potential until they reach the left-hand peak of the potential, where the force is zero. The residual momentum of the ions carries them into the core, down the falling slope of the potential well. They accelerate to the tank center, where the force is again zero. To the right of the center, they decelerate until they reach the right-hand peak, marked “U − ΔU = 2.2 MV” in Figure 2d. At this point, they reverse direction and turn back to the left. To avoid the loss of newborn ions to the right-hand tank wall, their initial kinetic energies were chosen to be slightly less than the potential energy e(U − ΔU), which is subtracted from their kinetic energy at the top of the right-hand peak.

To visualize the ions’ early history, their positions in velocity–position phase space are displayed in Figure 2e; here, gray dots represent protons, and black dots represent boron ions. The upper arrow marks the incoming paths of protons, and the middle arrow marks the incoming path of the boron ions. Due to their different charge-to-mass ratios, boron ions follow a different path than protons of the same energy. Due to their higher charge state, boron ions scatter more and become trapped more often than the protons on their first pass. Most protons are seen to reflect from the rising potential they experience in the right-hand magnet and then exit the tank to the left after a single pass forward and back through center. The bottom arrow shows the exit path of protons; it is more densely populated than the boron ions’ exit path just above it because more protons survive trapping on their first pass than boron ions.

The stopping conditions of the simulation leading to the diagnostics at this time t = 0.38 ms were determined by the condition that the particles’ densities stabilized in time and the ions’ positive charge density approximately cancel the electrons’ negative charge density at the center of the reactor. The ion injection currents were adjusted to make the sum of the two ions’ central density values, shown in Figure 1e,f, approximately equal to the electrons’ central density value, shown in Figure 1d. This condition made the central plasma approximately charge-neutral, with only a slight excess of negative charge. The visible discrepancy between the level of the proton charge density in (e) and boron charge density in (f) is accidental, due to random statistical variations in cell counts. The curves in (e) and (f) are subject to relatively large statistical noise because they represent charges in a horizontal row of cells only one cell wide in the vertical direction. For this reason, each cell contains only a few macroparticles, and consequentially the exact number is subject to relatively large statistical uncertainty. The apparent discrepancy between proton and boron densities does not affect the predicted quality factor of the reactor, which is determined by the ratio of bremsstrahlung power to fusion power at the final electron temperature. Making the proton and boron charge densities equal was adopted for simplicity, later found to be non-optimum for the quality factor, as described in the discussion of Equations (1) and (2) in the next section of this paper.

The electrons formed the 2D electrostatic potential color-coded in Figure 2a. The colors (published online) code the potential voltage; magenta codes the applied voltage of 2.4 MV, found uniformly inside the eight magnet boxes. Light blue codes the tank central value of potential, 1.2 MV, half the applied voltage. Red codes voltages near zero, outside the ring of magnet boxes and extending to the tank walls. Figure 2d shows a 1D graph of the potential voltage seen along the horizontal midline of the 2D plot (a). The central value is half the applied voltage, a feature found in the original MET reactor concept [1]. In our simulation, the depth of the potential well was found to vary with the selected electron injection current. We initially adjusted the electron injection current to be 15A, to produce a potential well depth equal to half the drive voltage and to agree with Yushmanov’s analysis [1]. This 15A drive current produced equal ion and electron temperatures, a restriction adopted by Yushmanov as a simplifying assumption. The restriction to equal temperatures was relaxed in our later analysis. We reduced electrons’ temperature below ion temperature as a means to reduce bremsstrahlung losses and thereby increase the quality factor. Although the individual electrons in Figure 1a are in constant motion, the potential they form is static in time from t = 0.38 ms onwards. The stopping condition of the simulation was chosen to make the ions’ positive charge density to be slightly less than the negative charge density of the electrons. This made the central potential nearly the same with or without ions injected. In the steady state, the electrons’ charge density was partially neutralized by the trapped ions, but a slight negative charge was intentionally left to keep the attractive potential approximately the same as it was before injected ions began to accumulate.

The magnetic field from our six-magnet reactor is dominated by cusps. Figure 2b shows a rendering of the magnetic field’s equal-magnitude surface in a six-magnet Polywell constructed at the University of Sydney [18]. The size of our simulated reactor is bigger than the Sydney one, but the shape of the magnetic field is the same. The shape is dominated by 26 cusp lines, a selected 3 of which are marked by arrows in (b). Charged plasma particles travel freely along the cusp lines, undeflected by the parallel magnetic field vector. This feature allows for the controlled injection of charged particles from the electron, proton and boron sources mounted at either ends of the horizontal cusp line.

Unfortunately, the 26 cusp lines also provide 26 paths for hot plasma particles to escape the core and (some of which) become lost by hitting the tank walls. The simulation software is, by design, two-dimensional, which requires the selection of a plane through the cube in which to simulate the features also relevant to a 3D plasma. The plane selected is the cube’s central plane, outlined by a square of solid and dashed lines in Figure 2b. This plane contains face and edge cusps, typical ones of which are indicated by the two lower arrows in (b), but none of the cube corner vertices, a typical one of which is indicated by the upper left-pointing arrow. The cube’s eight corner vertices are out of the central plane, and therefore their losses are not simulated. By this omission, the simulation ignores the losses through the cube corner vertices but includes the losses through the more lossy face and edge cusps. Luckily, the rate of loss of these omitted cusps, proportional to the area of the circle at the head of the left-pointing arrow, are smaller than those of the in-plane cusps, proportional to the areas of the cusps pointed to by the lower two arrows. By including the more lossy face and edge cusps in the simulation, while omitting the less lossy cube corner vertex cusps, we expect to overestimate the total cusp losses compared to what they would be in a more realistic, e.g., 3D, simulation. Because the bremsstrahlung losses are believed to overpower the cusp losses, the differences between loss rates through the face, edge and corner cusps do not add to the uncertainty of our estimated quality factor.

Our simplified magnetic field is simulated as if generated by electric currents in eight straight wires oriented perpendicular to the simulated plane and located near the centers of the eight magnet boxes. The magnet boxes are simulated as metal conductors biased to 2.4 MV. The biased, conducting surfaces of the eight boxes provide the electric field, which combines with the magnetic field from the wires to confine particles.

The polarity of the currents in the wires is arranged to generate magnetic field vectors pointing inward at the center bores of each of the four side-facing coil magnets. The magnitude of the bore field was adjusted to be 25 Teslas (T) at the center of an isolated magnet. The 25 T field capability is the only HTS feature adopted from the specifications of commercially available HTS magnet coils [19]. When four magnets are assembled into a square, opposing fields from adjacent coils partially cancel to reduce the bore field in each magnet to 18 T. The spacing of the magnets was varied by trial and error to produce the same field magnitude in the corners between the coils as in the bores. This made the recirculating electron current the same through the face and corner cusps. The static magnetic field at each PIC location inside the tank was computed from the textbook formula [20] for the in-plane component fields from eight infinitely long straight wires. Horizontal and vertical field components were computed and stored in two 50 × 50 arrays, one for the x-field and one for the y-field. The eight biased, conducting magnet boxes shown, plus eight HTS wires simulated at the centers of the boxes combine to simulate the electric and magnetic fields from the four superconducting coils mounted on the side-faces of the hexahedral reactor.

Figure 2c shows the x-component of the magnetic field from the eight wires, plotted along the horizontal midline of the tank. As expected, the magnitude of the field is the maximum (18 T) in the bores of the two magnets on the midline and zero at the center of the tank. The field shown is the applied field which would exist prior to the injection of plasma. In the steady state, the plasma modifies the central field by adding a diamagnetic current which suppresses the applied field in the central region, expanding the B = 0 volume that contains the fusion fuel.

To verify that the top and bottom coils could realistically be omitted from the 2D simulation, a separate simulation of the applied magnetic field was made with the public domain 3D simulation packages WarpX [21] and Magpylib [22]. The 3D simulation included six circular coil magnets on the six faces of the cube, including top and bottom coils that are the same size and have the same field strength as those in the MET6 design. In the simulation plane, the magnetic field from the 3D simulation was found to be qualitatively the same as the field from the eight straight wires, approximately matching the midline field shown in Figure 2c. This gives us confidence that our simulated magnetic field from the eight wires captures the essential details of the magnetic field that would be found in a real cubic reactor. Although the WarpX simulation contained a realistic magnetic field, the results have not yet progressed to a level that could be used for further quantitative analysis. Our WarpX simulation so far lacks the essential biased anode, which forms an electric field that recirculates most of the escaping electrons back into the core whenever they happen to exit the central region through a cusp. Without this bias potential, the plasma would have excessive losses.

Figure 1d shows a graph of the electron’s particle density plotted along the midline of the 2D distribution in (a). The units of the vertical axis are electrons per square meter. Two peaks of concentrated density appear, centered in the bores of the left-hand and right-hand magnets. The right-hand peak is marked by an arrow. The peaks are concentrations of deviant electrons which have down-scattered in energy to become trapped in the local minima of the electric potential formed by the bias voltage. The concentration of these trapped electrons is detrimental to the efficient operation of the reactor. By their negative charge concentration, they repel and rob energy from the newborn electrons entering from the source at position ②. To reduce the trapped electrons’ concentration, a special electrode was simulated in the bore of the right-hand magnet, as shown at the head of the arrow in (a). This electrode was simulated to describe a thin metal disk with a circular hole drilled in its center. The electrode was invented to extract a portion of the trapped electrons. The current of electrons hitting the electrode is adjusted to halt the growth of the peaks before the latest time simulated.

The current of electrons hitting the extra electrode was adjusted by varying the width of the B = 0 imposed field-free region. The electron beams through the cusps are found to be broadened after crossing the field-free region. The larger the width of the region, the larger the beam widths and the larger the extracted current. Increasing the current of electrons hitting the aperture was found to reduce the height of the peaks in (d). The larger the current selected, the smaller the concentration of trapped electrons populating the peaks in Figure 1d. The extra electrode provides an adjustable mechanism for “pumping-out” trapped electrons, identified as necessary by Yushmanov in the following quote from his 1981 paper [23]:

“To keep the gaps ‘empty’ it is necessary to create in them an artificial pumping-out mechanism which has a number of specific characteristics including selectivity with respect to the trapped electrons and a carefully adjusted intensity within fixed narrow limits. No specific technical ideas for methods of creating such a pumping-out mechanism have as yet been put forward.”

Our placement of the aperture in the right-hand magnet satisfies the need to actively pump low-energy electrons, perhaps the first proposed solution since it was recognized as a need in 1981. The steady and uniform density of trapped electrons and ions in Figure 1 shows that this solution works well enough. Little effort was made to optimize the adjusted electron current loss on the aperture. Adjusting the current and power lost by the electrons hitting the electrode would impact the predicted quality factor Q but only slightly compared to the power consumed by compensating for the bremsstrahlung losses. Such optimization of the pumping current is a detail of the design we chose to leave for the future fine tuning of the design parameters. Such fine tuning was not possible using our simulation, as discussed further in the Discussion of Results Section of this paper.

In addition to providing for the pumping out of slow electrons, the extra electrode has a second important function. It shapes the potential along the path of the newborn ions to increase their probability of being trapped on their first passage through the core. The potential function shown in Figure 2d exhibits two peaks. The difference in the heights of the peaks defines a range of injection energies suitable to choose for the incoming ions. Their injected energies need to be in a range higher than the eU value at the left-hand peak and lower than the eU value at the right-hand peak. Ions in this energy range pass freely in through the left-hand cusp and then are reflected by the potential at the right-hand cusp. This gives each ion the maximum probability of being trapped in passing twice through the bulk of the trapped plasma. The ions not trapped on their round-trip passage exit the core to the left to be lost on the left-hand tank wall. The bottom-most of the three arrows in Figure 2e marks the exit path of the (gray-colored) protons just above the arrow. The density of protons along the bottom-most arrow in Figure 2e differs from the density of boron ions on the path just above it. This is due to the different probabilities of the capture of ions on their first pass forward and back through center. Because most of the newborn ions exit after a single pass, the efficiency of trapping ions from the sources mounted on the left-hand wall will improve as the central plasma density grows with time. At this early time (t = 0.38 ms), the injected currents of protons and boron ions were adjusted to be 2.5 A and 2.75 A, respectively. These currents were set by trial and error to just equilibrate the densities of newborn ions in Figure 1e,f.

The ion heating power injected by these ion currents replaces the lost power carried away by ions hitting the tank walls. This level of injected power is just enough to maintain a constant plasma temperature. Each escaping ion exits the trap starting with near-zero kinetic energy at the peak of the potential energy function, marked by the arrow in Figure 2d. This amount of potential energy is converted to an equal amount of kinetic energy as the escaping ion accelerates to the left down the potential hill, along the path marked by the bottom-most arrow in Figure 2e. The total power lost by this process is the average kinetic energy of the ions, 2.2 MeV, from Figure 2d, times their combined current, 5.25 A, from the previous paragraph. This product, (2.2 MeV) (5.25 A), is 11.6 megawatts. We considered this to be small enough to be ignored in computing a rough estimate of the quality factor from the bremsstrahlung power loss P_brem, computed as 116 megawatts in Equation (5) below.

The distribution of the ions in Figure 2e reflects the history of fueling the reactor over the first 0.38 ms after time zero. As simulated time increases beyond this early time, the fueling process fills in the central region of Figure 2e, and the thermalization process degrades the ions’ initial velocities to smaller values than those shown in Figure 2e. After many milliseconds, the dots accumulate densely near the center of the phase space (velocity vs. position) distribution, providing a direct measure of the final temperature of the plasma after it reaches thermal equilibrium. Rather than undertaking such an impractically long OOPIC simulation run to estimate this temperature, we relied on the analysis of Yushmanov [1], which found that thermalization lowered the plasma temperature from the applied eU to an equilibrium temperature equal to “about 1/16 of e(U − ΔU)”, where ΔU is the potential depression in the gaps due to electrons’ space charge accumulating in the gaps. From the horizontal arrow in Figure 2d and the results of Yushmanov, the temperature of the thermalized plasma can be estimated as T = e(2.2 MV)/16 = 140 keV. The effects of thermalization lower the plasma temperature by a factor of 16. This estimate of thermalization loss is the main contribution of Yushmanov’s theory, which distinguishes our MET6 reactor design from the earlier Polywell designs. In Polywell theory, ions were mistakenly assumed to maintain their original eU temperature until they fused. In MET theory they are found to be 16 times colder.

3. Estimating the Quality Factor Q from PIC Diagnostics

The standard definition of the quality factor is the ratio of fusion power output to drive power input. The fusion power output is calculated from the textbook [24] formula:

P_pB = n_p n_B <σv> E_pB V,

(1)

where n_p is the protons’ particle density; n_B is the B11-ions’ particle density; <σv> is the fusion reactivity averaged over the thermal velocities (v) of the T = 140 keV thermal plasma; E_pB = 8.7 MeV, the energy yield of one pB11 fusion event ([15] pg. 44); and V is the volume of the fusing plasma. From the diameter of the cubic plasma core shown in Figure 2f, V = (1.53 m)³ = 3.6 m³ = 3.6 × 10⁶ cm³. The densities, n_p and n_B, were found by our simulation to be approximately constant inside the volume V, the volume indicated by the double-headed arrows in Figure 1a and 2f.

To simulate the plasma’s natural quasi-neutrality, the magnitude of the charge density of the ions must approximately equal the magnitude of the charge density of the electrons. We initially chose the particle densities n_p and n_B to divide the positive charge density equally between protons and boron ions. (This choice was subsequently adjusted to reduce the bremsstrahlung contribution to the quality factor as simulated.) To make equal contributions from protons and boron ions, the 5+ charge state of the fully stripped boron ions implies particle densities n_B = n_p/5 = n/10, where n is the electrons’ density derived from the β = 1 condition at the surface of the plasma core. This density was calculated by inverting the equation β = 1 (from the Plasma Formulary [15] pg 29] to yield the following expression for the electron density at the surface:

n = B_s²/[(4 × 10⁻¹¹) T_s],

(2)

where B_s is the magnitude of the magnetic field vector at the surface of the plasma core and T_s the electron energy at the same point, both expressed in cgs units. The resulting units of n are also in cgs units, cm⁻³. (This analysis uses the interpretation of β as a ratio of pressures at a chosen point, as discussed in Glasstone and Lovberg’s textbook [24], especially in the final footnote on p. 52).

In Figure 1a, the double-headed, gray arrow points to selected points on the surface of the plasma core. These points were selected to be where the surface of the plasma core is parallel to the y-axis of the simulation plane. In the online version of Figure 1a, electrons at these points were seen to move parallel to the y-axis, indicating that the magnetic vector points parallel to the y-axis at these points. Thus, the B_y component of the field is the only non-zero component of the field’s three-vector. As one of its standard diagnostic displays, the simulation software displays the cell-by-cell values of the three components of the magnetic field, including B_y as a 2D array. Figure 2f shows a graph of B_y as a function of x, extracted from the 2D array along the line marked by the double-headed, gray arrow. This arrow from Figure 1a is reproduced in Figure 2f and marked “1.53 m”. A second, left-pointing arrow in (f) marks the value of B_y at the tip of the double-headed arrow, i.e., at the surface of the plasma core. This surface value is B_s = B_y = 8 T, which equals 80 kilogauss (8 × 10⁴) in cgs units. The electron energy at the surface is taken to be the most probable energy of the thermal distribution, given by the plasmas’ temperature, 140 keV. Inserting these values into Equation (2) yields our estimate of electron density:

n = B_s²/[4 × 10⁻¹¹ T] = (8 × 10⁴)²/[(4 × 10⁻¹¹) (1.4 × 10⁵)] cm⁻³ = 1.3 × 10¹⁵ cm⁻³.

(3)

The remaining factor needed to evaluate the fusion power from Equation (1) is the average reactivity, <σv>, evaluated at the plasma temperature of T = 140 keV. Ref. [25] shows graphs of experimental <σv> values as functions of temperature for different fuels. From the applicable curve for p+B11 fuel (colored red online) our temperature 140 keV corresponds to reactivity <σv> of 1.0 × 10⁻¹⁶ cm⁻³s⁻¹. Substituting this into Equation (1) yields our estimate of the reactor’s nuclear fusion output:

P_pB = n_p n_B <σv> E_pB V = (n/2) (n/10) <σv> E_pB V = [(1.3 × 10¹⁵)²/20)] (1.0 × 10⁻¹⁶) (8.7 × 10⁶) (3.6 × 10⁶) eV/s = 2.6 × 10²⁶ eV/s = 42 megawatts,

(4)

where the symbols are those defined previously in the introductions of Equations (1) and (2). This fusion power output forms the numerator of the quality factor ratio.

The denominator is the bremsstrahlung power loss, which we assume equals the required drive power input. Drive power is supplied by the electron source on the right-hand tank wall plus the ion/proton sources on the left-hand tank wall. The power supplied by these sources is required to balance bremsstrahlung losses plus a smaller fraction which goes to balance the particle losses. Particle losses occur whenever a tracked particle’s path intersects one of the reactor’s solid components, e.g., magnet box, collimator or tank wall, shown by solid lines in Figure 1a–c. Omitting the power required to confine/heat the electrons and ions is a necessary simplification of our analysis. Only the power required to compensate for bremsstrahlung radiation is known quantitatively. The power consumed by particle losses is arguably omitted from analysis because it is believed to be much smaller than for the bremsstrahlung loss.

The formula for bremsstrahlung power is the following from Glasstone and Lovberg [24]:

P_brem = 5.35 × 10³¹ n (n_p + Z²n_B) (T_keV)^1/2 V =
5.35 × 10³¹ n (n/2 + 25n/10) V =
5.35 × 10³¹ (1.3 × 10¹⁵)² (0.5 + 2.5) (140)^1/2 (3.6 × 10⁶) =
116 megawatts,

(5)

where n, n_p, n_B and V are as in Equation (4) above; Z = 5 is the charge of the fully stripped boron ions; and T_keV = 140 is the electrons’ thermal energy in units of keV. This drive power exceeds the fusion power output in Equation (4), leading to the following estimate for the quality factor:

Q₀ = 42 MW/116 MW = 0.36.

(6)

From the structure of Equation (5), bremsstrahlung power can be reduced by changing the fuel mixture from the previous mixture with equal proton and boron charge densities to a modified mixture having a reduced percentage of boron relative to hydrogen. To explore this feature, we repeated the simulation with boron density reduced from n/10 to n/25. Maintaining quasi-neutrality (n = n_p + 5n_b) requires the proton density rise to balance the loss of charge density from declining boron density. Thus, n_p rises from n/2 to 0.8n, and as a result, the n_pn_B factor increases the numerator by a ratio of n²/20 to (0.8)(0.05)n², a factor of 0.05/(0.04) = 1.2. In addition to the change in the numerator, the (n_p + Z²n_B) factor in the denominator of Q decreases from (n/2 + 25n/10) to 0.8n + n, a relative factor of 0.75/1.8 = 0.42. The overall quality factor changes by a factor equal to the quotient of the factors in numerator and denominator, 1.2/0.42 = 2.9, yielding the new quality factor as the following:

Q₁ = 2.9 × Q₀ = 2.9 × 0.36 = 1.02,

(7)

which is improved over Q₀ but still too small for practical net power.

Another method of reducing the power wasted in bremsstrahlung losses is to reduce the temperature of the trapped plasma’s electrons. The bremsstrahlung formula in Equation (5) contains the square root of electron temperature, T_keV^1/2, which can be reduced by changing the operational parameters of the reactor. We found that this energy decreases if we raise the injection current of electrons from the source, at ② in Figure 1a. Keeping the remaining parameters the same as in the latest design, Figure 3 shows the results of a simulation with this modification. Central electron potential and proportional central electron energy are reduced from 1.27 megavolts to 0.74 megavolts, a factor of 0.58. The square root of this factor multiplies the new bremsstrahlung expression in the denominator of the quality factor. The final estimate of the quality factor is as follows:

Q₂ = Q₁/(0.58)^1/2 = 1.02/0.76 = 1.3.

(8)

A further reduction in electron energy is theoretically possible by varying the reactor’s many other operational parameters, for instance, the shape and spacing of the magnets. Such variations were deemed beyond the scope of this paper because our analysis relies on the bremsstrahlung loss dominating the losses. If the bremsstrahlung losses were made much smaller by further reducing the central electron energies, our analysis method would break down.

4. Discussion of Results

A reliable PIC simulation was coupled to the classic MET analysis method of Yushmanov [1] to design a compact, quasi-spherical reactor, MET6.

Table 1. Comparison of Sporer’s HTS reactor with our MET6 reactor.

Reactor Parameter	HTS Ref. [3]	MET6
B-field in anode cusps B (Teslas)	16	18
Applied voltage U (kV)	500	2400
Anode gap spacing b (mm)	4	80
Plasma electron density n (m−3)	2.9 × 1020	1.3 × 1021
Plasma temperature T (keV)	25	140
Coil/cusp radius R (cm)	83	57
Plasma length L (m)	10	5
Fuel species	D+T	p+B11
Quality factor Q	10	1.3

shows the final simulation parameters of MET6 compared to Sporer’s cylindrical design [3].

The two reactors tabulated have very different quality factors Q, the main metric for performance. Although our MET6 design is predicted to have a poorer quality factor than Sporer’s design, it burns a more plentiful fuel, giving it an advantage in sustainability. Plus, it does not produce many neutrons. MET6 burns hydrogen plus boron fuel, economically available from terrestrial sources. Sporer’s design, like most of the many tokamak designs (ITER, SPARC, EAST, etc.), burns tritium, scarcely available from a few aging Candu reactors [6]

As the plasma density rises during startup, the electrons’ space charge builds up in the cusps unless they are suppressed by some artificial means [23]. If not checked, the accumulation of space charge would be fatal, leading to the loss of the potential well due to the reduced energy of incoming electrons after plowing through the trapped charge. A major discovery of this work is that scraping the exterior surface of the bounding sheath can eliminate this loss of the potential well. In the reactor’s final configuration, as shown in Figure 3, the suppression of the space charge trapped in the cusps required only 17% of the incoming electrons’ current to be lost by hitting the gap-confining aperture. Thus, the power consumed by electron pump out is found to be a small fraction of the injected power in the electron beam. The remainder of the injected beam power is available to heat the plasma to compensate for bremsstrahlung losses. The surface layer of the sheath was scraped off by the edges of the aperture. The current of electrons scraped was minimized by trial and error, adjusting the diameter of the diamagnetic region, which was about 15 cells wide. In a real reactor, adjusting the diameter of the aperture’s gap would be a more direct way to adjust the amount of current scraped. In simulation, the aperture ’s width was held at its minimum legal value of 2 PIC cells wide.

Varying the width of the diamagnetic region to adjust the amount of scraping utilizes a defocusing effect, which increases with the length of the beam’s transit through the field-free region. The passage of the recirculating electron beam through a wider or narrower B = 0 region defocused the beam more or less depending on the width of the region. A defocused beam resulted in a greater loss of electrons at the point of the arrow in Figure 1a. The larger the diameter of the exclusion region, the larger the current scraped. The amount of scraping was adjusted using the feedback from the simulation’s diagnostics in Figure 1d. Here the trapped electrons form two peaks located inside the left-hand and right-hand magnets’ bores. With no scraping, the peak-to-valley ratio continued to grow with simulated time, gradually reducing the depth of the potential well in Figure 2d. This reduced depth would eventually release the trapped ions. When the amount of scraping was adjusted to be above a certain current, the ratio of the peak height to the central density became constant in time. In other words, the scraping halted the build-up of trapped electrons, in effect pumping out low-energy electrons from the cusp traps at the same rate they are trapped.

The amount of power required for scraping depends on the detailed structure of the plasma inside the thin sheath marking the boundary between the field-free interior and the plasma-free exterior of the central ball of plasma. The details of the spatial structure in the sheath are not well simulated by our choice of PIC size much larger than the electron gyroradius. A PIC technique with better resolution was established by Park et al. [26], which reports a massive PIC simulation consuming more than a million CPU hours to run. The device simulated by Park et al. is a picket fence device, not a candidate for a net power reactor because it lacks the essential blocking electric field required to return electrons that leak out through the cusps. In our design, the essential blocking electrode is the grounded tank. The grounded tank plus the positive magnet bias voltage create an electric field that repels electrons as they approach the tank from inside. Without such repulsion, all the electrons that leak out of the cusps would hit the tank and be lost, which would ruin the quality factor. Although Park et al. [26] did not claim to present a workable reactor design, they did demonstrate that resolving the detailed structure of the simulated sheath would require choosing our PIC size to be as small as the electron gyroradius in the sheath.

With our relatively large cell size, we do not resolve the detailed spatial structure inside the sheath. But such good resolution was not required to validate the MET6 reactor’s design using our simulation. Our simulations describe a surface layer thicker than the real-world layer would be. This may affect the level of the current required to pump out the trapped electrons from the cusps but not the quality factor. The sufficient level of the pumping current was set by the trial-and-error adjustment of the density of trapped electrons in Figure 1d. The chosen current was the minimum that produced a stable, time-invariant electron density. Because bremsstrahlung dominates the power requirement, the level of power invested in electron pumping has a negligible effect on the reactor’s predicted quality factor.

To verify that the simulated quality factor does not depend on PIC size, a separate simulation run was made with the same device parameters shown in Table 1 but with a PIC size one-half of the cell size used so far. The higher resolution produced the same confining potential (U − ΔU), the same electron temperature T and the same electron density n as the lower-resolution simulation. With these factors held constant, repeating the above analysis would produce the same quality factor estimate as predicted with the lower resolution.

5. Conclusions

The simulated quality factor of Q = 1.3 is too small to ensure usable net power. The question of how big the simulated quality factor needs to be to be practical has different answers depending on whether the reactor will operate as an ignition device or as a power amplifier. As a power amplifier, the conversion of gross power into net power is subject to efficiency factors for converting nuclear energy into electrical energy outside the reactor and then back to heat the plasma inside the reactor. The limited efficiency of the conversion of nuclear energy to and from electrical energy would require a quality factor on the order of Q = 5–10 [23]. On the other hand, as an ignition device, the inefficiencies of electrical conversion are avoided. In this case, a quality factor as small as Q = 2 might be useful to obtain ignition. To operate as an ignition device, the kinetic energy of the three final-state alpha particles must be converted to heat by dE/dx energy loss conversion in the plasma. This process would be lossless if the alpha particles have a short enough range to stop in the plasma. The lossless conversion of fusion energy into plasma heating is the essential advantage of ignition devices over power amplifiers.

Not all fusion power is available for such lossless heating. Fusion energy is carried by three final-state alpha particles which have an average energy of 4 MeV at birth [27]. Alpha particles of this energy are not confined by the potential well, shown to have a depth of less than 1 MV in Figure 3d. Due to dE/dx energy loss in traversing the confined plasma, the alphas have a characteristic range which allows most of the reaction products to escape the reactor. These escaping alphas are essential for energy generation outside the reactor, either by the Rankine Cycle or by direct conversion [28]. The fraction of alphas that escape depends on the relative size of the alphas’ range in plasma vs. the size of the confined plasma ball, shown to be 1.53 m in Figure 2f. If the range is much greater than the diameter of the plasma ball, the alphas escape, taking the fusion energy with them.

Regarding the range of the alphas in plasma, we estimate it to be the measured 3 cm range of alphas in air [29] multiplied by the ratio of electron densities, air to plasma. From Table 1, the electron density of our plasma is n = 1.3 × 10²¹ m⁻³. We estimate the electron density of air from the ideal gas law, n_a = (14)N_o/(0.0224 m³), where N_o is Avogadro’s number (=6.02 × 10²³), 0.0224 m³ is the volume of a mole of ideal gas and 14 g is the mass of a mole of diatomic nitrogen, the main component of air. The factor of 14 in the formula for n_a is also the number of electrons in one diatomic nitrogen molecule. Substituting these quantities yields our estimate of the electron density of air to be the following:

n_a = (14)(6.02 × 10²³)/(0.0224) m⁻³ = 3.7 × 10²⁶ m⁻³,

(9)

which is vastly greater than the 1.3 × 10²¹ m⁻³ electron density of our plasma. The range of alphas in plasma is their measured 3 cm range in air multiplied by the air density just computed in Equation (9) and then divided by the electron density of plasma. Substituting these values, the range R_ap of alphas in plasma is therefore as follows:

R_ap = (0.03 m) (3.7 × 10²⁶)/(1.3 × 10²¹) = 8.5 × 10³ m >> 1.53 m.

(10)

The relatively small density of the plasma allows all the fusion alphas to escape the reactor. The range of the alphas in the reactor’s plasma, R_ap = 8.5 km, is thousands of times larger than the 1.53 m diameter of the MET6 plasma ball. Ignition is not possible in such a small reactor. Yushmanov’s [1] states the required quality factor of MET reactors, in general, to be Q = 5–10, which must still remain the target for our MET6 reactor’s development. At the present level of design effort, our Q = 1.3 estimate falls far short of Yushmanov’s desired Q = 5–10 [23]. Yushmanov’s goal must be considered an order-of-magnitude figure not worth refining until the simulation results approach it more closely.

The path to simulating an improved quality factor in MET6 is the subject of ongoing research by our group using various simulation techniques. Moreover, any practical concept such as ours that can attain a near-unity quality factor will also have the effect of stimulating new scrutiny, especially related to improved methods of analysis and design.

The ultimate proof of our conceptual design will require continuing investigations, hopefully leading to constructing and testing a prototype reactor of the MET6 design.