Abstract
A pioneering detailed comparative study of the dynamics of plasma flows generated by high-power nanosecond and high-intensity femtosecond laser pulses with similar fluences of up to J/cm2 is presented. The experiments were conducted on the petawatt laser facility PEARL using two types of high-power laser radiation: femtosecond pulses with energy exceeding 10 J and a duration less than 60 fs, and nanosecond pulses with energy exceeding 10 J and a duration on the order of 1 ns. In the experiments, high-velocity (>100 km/s) flows of «femtosecond» (created by femtosecond laser pulses) and «nanosecond» plasmas propagated in a vacuum across a uniform magnetic field with a strength over 14 T. A significant difference in the dynamics of «femtosecond» and «nanosecond» plasma flows was observed: (i) The «femtosecond» plasma initially propagated in a vacuum (no B-field) as a collimated flow, while the «nanosecond» flow diverged. (ii) The «nanosecond» plasma interacting with external magnetic field formed a quasi-spherical cavity with Rayleigh–Taylor instability flutes. In the case of «femtosecond» plasma, such flutes were not observed, and the flow was immediately redirected into a narrow plasma sheet (or «tongue») propagating across the magnetic field at an approximately constant velocity. (iii) Elongated «nanosecond» and «femtosecond» plasma slabs interacting with a transverse magnetic field broke up into Rayleigh–Taylor «tongues». (iv) The ends of these «tongues» in the femtosecond case twisted into vortex structures aligned with the ion motion in the external magnetic field, whereas the «tongues» in the nanosecond case were randomly oriented. It was suggested that the twisting of femtosecond «tongues» is related to Hall effects. The experimental results are complemented by and consistent with numerical 3D magnetohydrodynamic simulations. The potential applications of these findings for astrophysical objects, such as short bursts in active galactic nuclei, are discussed.
1. Introduction
Laser plasma generated by irradiating solid targets with nanosecond pulses has been actively studied since the 1960s, when it was first proposed to use only the newly invented lasers for heating and compressing thermonuclear plasma [1]. Particular attention has been paid to issues of hydrodynamic instabilities of plasma in external and self-generated magnetic fields [2]. After the invention of chirped pulse amplification (CPA) technology [3] in 1985, the first studies of «femtosecond» plasma, i.e., plasma generated by short ( 1 picosecond) laser pulses, began to appear.
The physics of laser–plasma interaction, despite the significant attention of the scientific community, remains an incompletely studied field. An adequate theoretical description of the evolution of laser plasma is an extremely complex task, as it requires the comprehensive consideration of processes such as heating, ionization, vaporization of solid matter, and the generation of energetic particles, which can be relativistic in the case of ultra-powerful femtosecond pulses. Moreover, the processes occurring during laser ablation and the properties of the resulting plasma depend substantially on the laser pulse parameters, such as the wavelength, the energy, the pulse duration, and the intensity of the laser radiation. Therefore, numerical simulations and codes are actively used to study the evolution of laser plasma and its interaction with magnetic fields. Each code operates under certain approximations—for example, magnetohydrodynamics (fluid), hybrid (PIC-fluid), or fully kinetic (PIC, Vlasov). To reliably validate these codes, experimental studies are conducted in simplified model geometries—for instance, classical investigations of plasma expansion (not only laser-produced) into an external quasi-uniform magnetic field [4,5,6,7]. In such simplified geometries, it is easier to study plasma dynamics experimentally and compare the results with numerical calculations. The knowledge and approaches gained from this experimental «modeling» can then be applied to solve other problems with more complex geometries.
The dynamics of plasma flows induced by nanosecond laser pulses was actively studied in a number of scientific problems, ranging from controlled thermonuclear fusion [2,8,9] to laboratory astrophysics research [10,11,12]. Indeed, «nanosecond» laser plasma flows are used to model astrophysical phenomena, such as accretion [11,13,14], jet collimation [10,15], shock wave generation and interaction [12,16], and others. Despite a significant difference between the temporal and spatial scales of astrophysical and laboratory plasmas, the equivalence of the dynamics of both systems can be demonstrated under certain similarity criteria. Such scaling is feasible, for example, within the magnetohydrodynamic (MHD) approximation, when the key dimensionless parameters determining plasma evolution—such as plasma beta (magnetization), Euler number, Mach number, and Alfvén Mach number—coincide for both systems [17,18,19].
The evolution of plasma induced by ultra-powerful short laser pulses was studied, for example, for fast ignition (FI) [20,21], where spherically compressed deuterium–tritium fuel was irradiated by a beam of relativistic electrons accelerated by laser pulses (usually of picosecond duration) with an intensity of to W/cm2. Applications in which plasma irradiated by ultra-powerful laser pulses is used to generate relativistic electrons, accelerate protons and neutrons [22,23,24,25], generate X-ray [26] and terahertz radiation [27,28], and produce electron–positron pairs [29] have been actively developing.
Laser ablation of targets by nanosecond and femtosecond pulses is widely used for substance composition analysis [30,31]. Traditionally, these methods employed nanosecond pulses from Nd:YAG lasers (1054 nm). However, due to the widespread adoption of powerful femtosecond Ti:Sa lasers, a new research direction has emerged related to femtosecond laser spark emission spectroscopy [32].
When irradiating solid targets with short ultra-intense pulses, several significant differences from nanosecond ablation are observed [32]. Under nanosecond pulse irradiation, the ionization and heating of the solid target occur primarily through collisions [33]. In contrast, femtosecond intense irradiation gives rise to a substantial fraction of accelerated collisionless electrons, whose oscillatory energy can range from several hundred keV to hundreds of MeV [22,34]. These energetic electrons can escape and move away from the heated region [35], resulting in the formation of an electric field that pulls electrons back and accelerates ions, sometimes up to tens of MeV [36,37]. Moreover, the direct and reverse oscillating electron flows contribute to magnetic field generation—for example, large-scale fountain magnetic fields [38,39,40,41,42]—as well as small-scale filamentary fields arising from the development of beam-type current instabilities (Weibel-type instability) [43,44,45,46]. Such self-generated magnetic fields in plasma can significantly exceed the Biermann fields [47], observed during nanosecond ablation and can reach several hundred Tesla [40,41,42].
To describe the dynamics of nanosecond plasma flows, approaches based on MHD equations are often employed [6,15,18,19,48,49,50,51]. The question of applying MHD approaches to describe the large-scale dynamics of «femtosecond» plasma flows remains open. To the best of our knowledge, the influence of kinetic effects on the large-scale dynamics of «femtosecond» plasma flows has not yet been investigated in the literature. In this work, we aim to determine whether the kinetic effects observed in «femtosecond» plasma constitute a significant limitation for the application of MHD approaches. For this purpose, we conducted experiments with plasma generated by nanosecond and femtosecond laser pulses with similar fluences of approximately J/cm2. To investigate the features of the evolution of «nanosecond» and «femtosecond» plasma flows, an external magnetic field of approximately 14 T was applied. A detailed comparative study of the dynamics of plasma flows created by high-intensity femtosecond and high-power nanosecond laser pulses in an external magnetic field is of fundamental importance for plasma physics and astrophysics, as well as for thermonuclear fusion, laser spark emission spectroscopy, and mass spectrometry.
2. Methods
In the experiment at the PEARL complex (IAP RAS, Nizhny Novgorod) [10,11,14,23,52,53,54,55], targets made of polytetrafluoroethylene () or polymethyl methacrylate () were irradiated with nanosecond ( = 1 ns) or intense femtosecond ( = 60 fs) laser pulses, hereafter referred to as pump pulses, with energies of 6 to 10 J. The basic scheme is shown in Figure 1. As a result of irradiation, target ionization occurred along with the formation of high-velocity plasma flows propagating at speeds of approximately 100–150 km/s for femtosecond pumping and 300–400 km/s for nanosecond pumping.
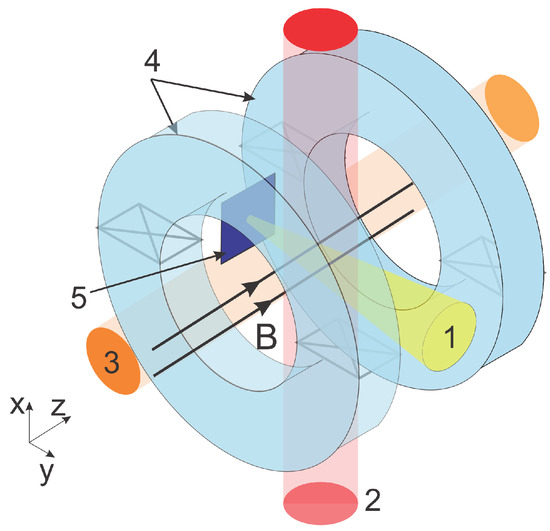
Figure 1.
Experimental setup: (1) femtosecond or nanosecond pump pulse, (2) diagnostic femtosecond laser pulse probing plasma across magnetic field, (3) pulse probing plasma along magnetic field, (4) coils, and (5) solid target placed inside magnetic system.
Flexible adjustment of the spatial profile of the laser spot on the targets allowed changing the conditions for plasma generation and obtaining various topologies of diverging plasma flows. In the first case, the laser radiation was focused on the target surface into a circular spot with a diameter of 100–300 m. In this scenario, the radiation intensity on the target was approximately W/cm2 for nanosecond pulses and approximately W/cm2 for femtosecond pulses, respectively, and the plasma source was quasi-point-like. The guaranteed pre-pulse level of the intense laser pulse did not exceed of the main pulse intensity.
In the second case, the laser spot on the target had a rectangular shape measuring 200 m by 3000–8000 m, with an intensity of approximately W/cm2 for nanosecond pulses and approximately W/cm2 for femtosecond pulses. Irradiation with such a laser pulse enabled the generation of an elongated plasma flow or slab. The studies on the interaction of this flow with an external magnetic field represent unique conditions for laboratory modeling, similar to those encountered in astrophysical objects, such as accretion disks or intense gamma-ray bursts from active galactic nuclei [56]. Moreover, by comparing the evolution of instabilities in an elongated slab and a quasi-point-like plasma flow, we can understand how the initial scale and geometry of the flow influence the development of flute-like instabilities, as well as the transition to the nonlinear stage and subsequent relaxation of such instabilities.
In the experiments aimed at studying the influence of an external magnetic field on the evolution of plasma flows, the target was placed in a quasi-uniform magnetic field with a strength of approximately 14 T, generated by a pulsed magnetic system (see Figure 1). The target surface was positioned along the magnetic field lines. The magnetic system consisted of a pair of Helmholtz coils. Details about the magnetic system can be found in the work [57]. For diagnostics of the plasma structure and density, we used a Mach–Zehnder interferometer based on probing femtosecond laser pulses with an energy of about 1–10 J precisely synchronized with the pump pulse. The interferometry scheme employed provided a spatial resolution of approximately 50 m.
3. Results
The irradiation of the target with a laser pulse, which we will collectively refer to as «pumping», led to the ablation of material from the target surface and the formation of a supersonic plasma flow propagating normally to the target surface. The plasma temperature generated by the nanosecond pulse was measured in earlier experiments using X-ray spectral diagnostics, specifically a focusing spectrometer with spatial resolution (FSSR) [58,59], and was found to be approximately 100–200 eV near the target and about 30 eV at a distance of several centimeters from the surface. During femtosecond heating, a large portion of the laser energy was deposited into a hot electron fraction. Consequently, the electron energy distribution function within several tens of picoseconds after irradiation can differ substantially from Maxwellian values [34,35]. For hot electrons, an effective temperature can be introduced, which may reach 10–100 keV on picosecond timescales, but the characteristic time between Coulomb collisions of hot and cold electrons in the target with density ∼ cm−3 shows that these hot electrons relax on timescales of about 10 ps. Meanwhile, the temperature of cold and quasi-equilibrium plasma studied tens of nanoseconds after the irradiation is estimated to be in the range of 15–30 eV [34,35]. The key parameters characterizing the plasma are summarized in Table 1.

Table 1.
Calculated values of some parameters.
3.1. Expansion of Femtosecond and Nanosecond Flows into Vacuum
The two-dimensional distributions of the linear plasma density for nanosecond and femtosecond ablation are presented in Figure 2a,b for 18 and 15 ns after irradiation, respectively. The density distribution was obtained by analyzing experimental interferograms using the IDEA software package [60]. Details on the interferometric approach to reconstructing the plasma density distribution can be found in the works [23,61]. The comparison of Figure 2a,b reveals differences in the structure of «nanosecond» and «femtosecond» plasma flows. The «nanosecond» plasma exhibits a quasi-uniform conical flow structure with a divergence angle of 40°. The «femtosecond» plasma flow has a collimated structure with a divergence angle close to zero. This collimation of the «femtosecond» plasma is most likely due to large-scale fountain magnetic fields generated by hot accelerated electrons [38,39,40,41,42]. Fountain self-generated magnetic fields in the «femtosecond» plasma can significantly exceed Biermann fields [47] observed in «nanosecond» plasma flows, reaching several hundred Tesla [40,41,42,62,63]. Such strong magnetic fields can exert a constraining influence on the radial expansion of the plasma [38]. We provide an energy-based estimate to address the collimation criterion: the magnetic pressure must exceed the plasma ram pressure of 0.5 V2. For our experimental parameters, this requires B ≳ 25 T—a value well below the peak fountain fields, which could reach several hundred Teslas, measured in both experiments and simulations [38,40,41,42,62,63]. A comprehensive simulation of the fountain magnetic field from its generation by relativistic electrons to its nanosecond-scale relaxation is an extremely challenging task that lies beyond the scope of this study and will be addressed in future work.
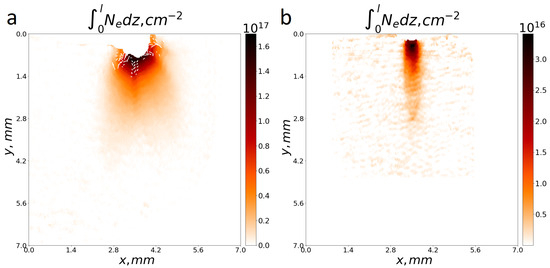
Figure 2.
Comparison of morphology of «nanosecond» (a) and «femtosecond» (b) plasma expanding into vacuum: (a) linear plasma density profile 18 ns after irradiation with nanosecond pulse; (b) linear plasma density profile 15 ns after irradiation with 60 fs femtosecond pulse of similar energy.
By integrating the linear electron density shown in Figure 2a,b one can obtain the total number of particles in the «nanosecond» and «femtosecond» plasmas. For comparable laser pulse energies, nanosecond ablation injects approximately four times more particles into space than femtosecond ablation. This is explained by the fact that the absorbed portion of laser energy deposited into the plasma during irradiation with nanosecond pulses exceeds by several times the energy absorbed during femtosecond irradiation. Direct measurements indicate that, for nanosecond pulses, the energy contribution to the plasma can reach 80–90%, whereas for femtosecond pulses it is about 30–50%. It is also worth noting that a significant portion of the laser energy during femtosecond heating is transferred to hot collisionless electrons, which leave the near-surface volume of the target much faster.
3.2. Features of the Expansion of «Femtosecond» and «Nanosecond» Plasma Flows into an External Transverse Magnetic Field of 14 T
The plasma created by both nanosecond and femtosecond pulses is a conducting ionized gas. Therefore, the dynamics of such plasma in a strong magnetic field will differ significantly from Figure 2. The expansion of «nanosecond» plasma in a transverse magnetic field is described in detail in our previous works [6,14,55,64,65] and in other studies [4,66,67]. We will briefly outline the main stages of «nanosecond» flow dynamics, some of which are demonstrated in Figure 3a,b. At the initial stage, the ram pressure V2 of the plasma greatly exceeds the magnetic pressure, so it pushes apart and compresses the external magnetic field. At a certain point, the plasma pressure drops and equalizes with the magnetic pressure. At this stage, the so-called plasma diamagnetic cavity is formed [4,6,55] (Figure 3a) with the characteristic size described by the classical plasma stopping radius [4,66]. As a result of magnetic deceleration, the boundary of the cavity experiences an effective acceleration counterdirected to the density gradient. This leads to the development of the flute instability at the plasma front [4], which in some cases is referred to as magnetic Rayleigh–Taylor instability [6]. Further, the cavity starts to collapse and plasma is pressed-out of it, thus facilitating the development of Richtmyer–Meshkov-type instability [68]. At that stage, already in a quasi-hydrostatic regime, flutes develop and elongate, as shown in Figure 3b, while the cavity compresses into a thin plasma sheet moving across the magnetic field at an approximately constant velocity of 300–400 km/s. The detailed dynamics of such «nanosecond» cavity collapse is described in the works [6,64].
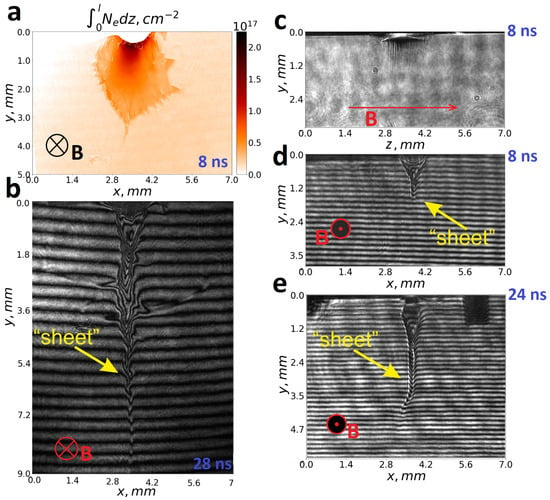
Figure 3.
Dynamics of «nanosecond» (a,b) and «femtosecond» (c–e) plasma flows injected from quasi-point source into external magnetic field with a strength of 14 T. (a) Linear density of plasma 8 ns after irradiation with a nanosecond pulse. (b) Interferogram obtained 28 ns after irradiation with a nanosecond pulse. (c) Shadow photograph and (d) interferogram of plasma 8 ns after irradiation with a femtosecond pulse, acquired in projections normal to and along magnetic field, respectively. (e) Interferogram of plasma 24 ns after irradiation with a femtosecond pulse. All figures are on the same scale.
The detailed dynamics of «femtosecond» plasma in a transverse magnetic field, as far as the authors know, has not been studied before. As seen in Figure 3, the dynamics of «femtosecond» plasma significantly differ from that of «nanosecond» plasma. Firstly, there is no pronounced quasi-spherical cavity, as the one in the case of «nanosecond» plasma formed when the plasma pressure and the magnetic pressure were close. A likely explanation is that the femtosecond flow was initially collimated, so the radial components of the ram pressure tensor were minimal and unable to oppose magnetic forces, which redirected the plasma flow into a narrow «sheet» from the very early stages (the dynamics were studied from 0.5 ns). At the same time, no instability flutes were observed at the cavity boundary, which may also have the same cause, i.e., collimation of the flow. The magnitude of the projection of the effective acceleration at the lateral boundary separating the plasma and the magnetic field is small and cannot lead to Rayleigh–Taylor instability flutes. The plasma flow is first redirected into a narrow sheet, which, as in the case of «nanosecond» plasma, propagates with a quasi-constant velocity across the external magnetic field. More differences in the dynamics of the sheets (or «tongues») appear at ns (Figure 3e), when the bending at the tip of the «femtosecond» plasma «tongue» is observed. The direction of bending of the «femtosecond» plasma «tongue» depends on the magnetic field direction. By changing the direction of the external magnetic field in the experiment and observing the rotation of the plasma flow, it was found that the «femtosecond tongue» rotates toward the direction of ion motion in the external magnetic field (see Figure 4). Such an effect was not observed in the studies of «nanosecond» flows, where bending of the plasma «tongue» had a random direction.

Figure 4.
Flows of «femtosecond» plasma interacting with transverse magnetic field at times (a) 39 ns and (b) 49 ns after target irradiation. In panel (a), the magnetic field is directed toward observer; in panel (b), the shot is shown for which the direction (indicated by the cross) of external magnetic field was changed relative to the shot in panel (a). The figure demonstrates that the twist of the «tongue» tip depends on the direction of external magnetic field. The direction of the twist is determined by ion motion in magnetic field.
3.3. Interaction of Elongated Laser Plasma Slab with Transverse Magnetic Field
The morphology of the plasma flow and the nature of instabilities that arise during propagation in a transverse magnetic field significantly depend on its initial topology. When the transverse scale L of the flow increases to the values exceeding the classical radius , cavity formation is not observed [11], and the character of the developing instabilities may change. Therefore, experiments were conducted with a distributed elongated plasma flow (we will call it a slab), whose maximum size exceeds the radius by several times for spherical expansion. To generate such a flow, the laser beam was spatially profiled and had a rectangular shape on the target surface. Thus, the largest dimension of the flow was on the order of and reached 10 mm, while the plasma size along the external magnetic field at the initial stages did not exceed 1 mm. The dynamics of the interaction of such a «nanosecond» plasma flow with a magnetic field was studied in our earlier work [11]. It was demonstrated that the plasma flow breaks into separate sub-flows or «tongues» as a result of Rayleigh–Taylor instability development.
Figure 5 shows two-dimensional images of linear density for «nanosecond» (a, b) and «femtosecond» (c, d) plasmas. The stage where elongated, initially quasi-uniform «nanosecond» and «femtosecond» slabs break up into separate «tongues» as a result of instability development is presented in Figure 5a,c. At this stage, differences in the structure of the plasma tongues under nanosecond and femtosecond irradiation are insignificant. However, at later stages (t > 40 ns), some features of the dynamics of the «nanosecond» and «femtosecond» flows appear (see Figure 5b,d).
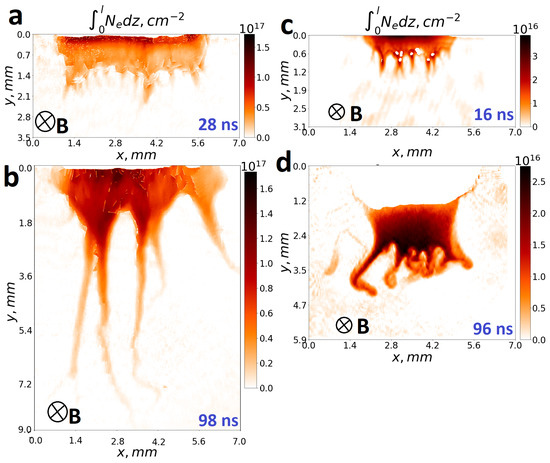
Figure 5.
Dynamics of «nanosecond» (a,b) and «femtosecond» (c,d) plasma flows injected during irradiation with elongated laser beam in external magnetic field of 14 T. (a,b) Images of linear plasma density at 28 and 98 ns after irradiation with nanosecond pulses. (c,d) Images of plasma linear density at 16 and 96 ns after irradiation with femtosecond pulses. Experimental images of «nanosecond» plasma similar to panel (a,b) are published in our previous work [11]. All images are scaled identically.
In the case of the nanosecond flow, the «tongues» move at a constant velocity, while the base of the flow where the tongues begin to form remains almost stationary. At the same time, chaotic redirection of the ends of the «tongues» is observed (see Figure 5b).
Contrariwise, the «femtosecond» flows have the following features: (i) The base where the flow splits into «tongues» does not stop but moves at a speed of about 30–40 km/s, comparable to the «tongues» velocity of 100 km/s. (ii) The maximum plasma density is observed in the region where the flow splits into «tongues». (iii) At times exceeding 50 ns, leaks of neutral gas with a refractive index > 1 are observed near the target, while plasma has a refractive index <1. As a result, in the interferograms in Figure 4, near the target, the interference fringes bend in different directions: downward in the plasma region and upward in the neutral gas region. To avoid confusion, the neutral gas area near the target is masked in Figure 5d, so the density near the target is zero. (iv) For the «femtosecond» flows, the ends of the «tongues» are markedly redirected. As in the case of a single «tongue» in Section 3.2, the twisting of the «tongues» is determined by ion motion and varies depending on the direction of external magnetic field. Thus, in Figure 5d, all tongues twist in the same direction, which differs significantly from the chaotic dynamics of the «tongues» shown in Figure 5b for «nanosecond» plasma.
Table 1 presents estimates of the key parameters characterizing plasma flows for nanosecond («Ns flow») and femtosecond («Fs flow») ablation. The initial parameters obtained from experiments, observations, and modeling are highlighted in bold. Unless otherwise specified, the parameter estimates are calculated using the expressions from [69]. The kinematic viscosity is computed according to the formula from the work [17], p. 825, and the magnetic diffusivity according to the formula on p. 467 of [18]. These parameters are used to estimate the Reynolds number and the magnetic Reynolds number , where L is the characteristic spatial scale of the plasma flow, and V is the flow velocity. The Reynolds numbers in both cases, «femtosecond» and «nanosecond» plasma, are significantly above 1, indicating that the viscosity effects are negligible. The magnetic Reynolds number exceeds unity in both cases so that «femtosecond» and «nanosecond» plasma flows can be considered as conducting fluids capable of advecting and being slowed by magnetic fields. However, the role of magnetic field diffusion at for the evolution of «femtosecond» plasma is more significant than for «nanosecond» plasma with . It is also worth noting that in both cases, the plasma is substantially collisional; the mean free paths for e-e, e-i, and i-i collisions do not exceed the ion cyclotron radius. At the same time, the electrons are magnetized.
It should be noted that dimensionless parameters, such as the Mach-Alfvén number , are estimated based on the parameters of the flow itself, including density and pressure, as well as external magnetic field. Thus, this parameter is used not quite in the classical sense, where it characterizes the regime of expansion into an external environment. In this context, the considered expansion into the vacuum is significantly sub-Alfvénic and subsonic. Here, the parameter characterizes an important ratio between the magnetic field energy and the energy stored in the plasma in the form of kinetic energy within the same volume during the deceleration stage of the plasma flow. It is worth noting that the plasma beta in both cases—«femtosecond» and «nanosecond» plasma—is less than one, indicating that magnetic pressure dominates over thermal pressure. The Euler number Eu = > 1, meaning that the kinetic energy of the plasma exceeds its thermal energy in both cases. At the same time, in the nanosecond case, the Mach–Alfvén number exceeds 1, indicating that the plasma kinetic energy surpasses the magnetic field energy. Conversely, in the femtosecond case, , which suggests magnetic field dominance. Of course, these simple estimates do not account for the effects such as local magnetic field amplification and/or temperature increase in the deceleration region caused by magnetic fields. A comprehensive treatment requires 3D calculations that consider laser heating processes—two types in our case—as well as nonlocal heat and radiation transfer, finite plasma conductivity, and other effects. Such detailed calculations are not yet fully available. Nonetheless, these simple estimates hint at significant differences between the expansion regimes of «nanosecond» and «femtosecond» plasmas.
4. Simulation
To investigate the nonlinear dynamics of the plasma described in Section 3.2, specifically the processes of diamagnetic cavity formation, the development of flute instability, and the formation and evolution of a plasma sheet («tongue»), simulations were performed using the 3D MHD code FLASH [70]. FLASH is a highly modular, finite-volume Eulerian Godunov-type code that operates on a block-structured adaptive mesh (AMR) capable of simulating a wide range of astrophysical and high-energy-density physics phenomena. For the current simulation, we employed a uniform grid configuration (without AMR) and utilized several key physics modules, including a laser module that describes radiation propagation in the geometric optics approximation and absorption via the inverse bremsstrahlung mechanism, as well as a «three-temperature» (3T) module, which allows an electron–ion fluid to have two effective temperatures ( and ) and also enables the fluid to emit and absorb radiation, described by a third temperature .
In the modeling, a laser pulse with an energy of 10 J and a duration of 1 ns was incident on a solid polyethylene target initially at rest and with a temperature of 300 K. For the proper description of thermodynamic processes in the plasma, tabulated equations of state and opacity data for polyethylene at high temperatures were applied to correctly describe its properties under such conditions [71]. To accurately account for the physics of laser–target interaction, models of collisional ionization and radiative diffusion transfer were employed [71,72]. To account for dissipative effects on plasma dynamics, the «Spitzer» module was used, which self-consistently calculates the components of conductivity and based on the classical expressions from Braginskii (1965) [73]. Hall effects were not considered in this model. The target was placed in a uniform magnetic field . The space outside the target was filled with helium gas at a density more than times lower than that of the target. The external gas had no significant impact on the plasma dynamics and was added to stabilize the numerical scheme. The simulation box dimensions were 4 mm (x) × 8 mm (y) × 8 mm (z) with grid step less 20 m. Magnetic field boundaries used Neumann conditions, while fluid boundaries applied outflow conditions.
The results of simulating the experiment on a «nanosecond» plasma interacting with a transverse magnetic field are shown in Figure 6. Figure 6 presents central slices () of plasma density, ram pressure, and magnetic pressure in a plane perpendicular to the external magnetic field. Three distinct stages characterizing the plasma dynamics are shown 20, 40, and 80 ns after the start of irradiation. The detailed dynamics of the instability at the cavity boundary were studied in our previous works [6,64]. In this work, we focus on the subsequent evolution of the plasma sheet. Therefore, we do not consider the details of flute instability formation but directly present slices showing the developed instability and further evolution of the sheet or «tongue».
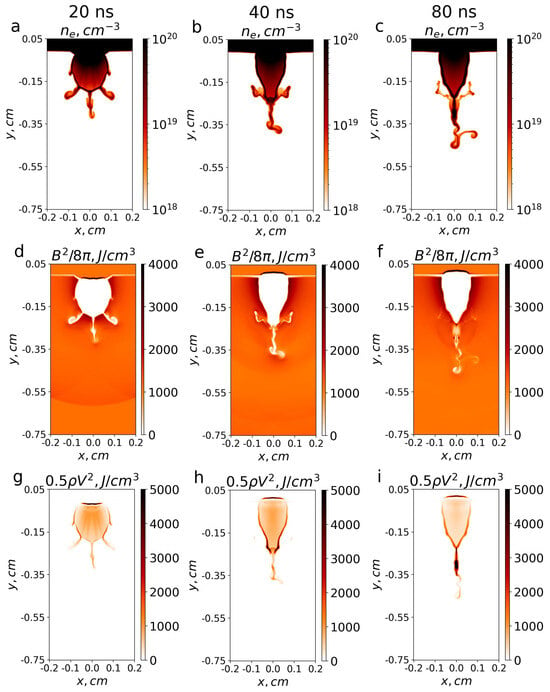
Figure 6.
Simulations performed with three-dimensional MHD code FLASH. All images show slices at : (a–c) plasma density, (d–f) magnetic field pressure, and (g–i) dynamic plasma pressure 20, 40, and 80 ns after the start of irradiation.
The most important conclusions that can be drawn from the modeling are as follows. (i) In the MHD approximation with dissipation (finite conductivity), significant diamagnetism is observed in the plasma «tongue» region. This observation demonstrates that the propagation of the «tongue» across the external magnetic field is not just ion drift but fluid-like MHD behavior of conducting plasma. (ii) In the ideal MHD approximation without Hall effects, the twist (vortex) of the plasma «tongue» does not depend on the direction of the external magnetic field and has a random character, similar to the experimentally observed «tongues» in the nanosecond cases (see Figure 3 and Figure 5). The plasma was laser heated to temperatures exceeding 100 eV, consistent with our experiments involving nanosecond laser pulses.
5. Discussion
Several possible candidates for the observed flute instability can be identified: the lower hybrid drift instability (LHDI) [74,75], the electron–ion hybrid instability (EIH) [76], the Rayleigh–Taylor instability (RTI) [77,78], and its variations: large Larmor radius instability (LLRI) [4,5,79,80,81] (or unmagnetized ion Rayleigh–Taylor instability [82,83]); and the Hall-modified Rayleigh–Taylor instability (HRTI) [81,84]. The LHDI and EIH types of instabilities may be excluded from consideration because their growth times are on the order of < 0.1 ns, and their wavelengths are orders of magnitude smaller [6] than those detectable under our conditions. However, microturbulence associated with instabilities such as LHDI can lead to anomalously reduced conductivity and thus influence the evolution of large-scale instabilities [6,74]. Large Larmor Radius instability at plays an important role in the evolution of flute instabilities and cavity collapse in weakly collisional plasmas [4,7,85]. In our case, however, the ion mean free path lengths and (see Table 1) are significantly smaller than the ion Larmor radius , and the effect of ion unmagnetization is not relevant under the observed conditions. Therefore, we will consider only RTI and HRTI instabilities in our further analysis.
Instabilities similar to RTI, HRTI, and LLRI can occur when acceleration is counterdirected to the density gradient at the interface between the media. In our experiments, the plasma flow, which initially possesses a significant density of kinetic energy (; ), is decelerated by an external magnetic field. In a reference frame associated with the plasma shell, the flow deceleration can be regarded as the effect of an effective acceleration [84,86], always directed opposite to the density gradient . Thus, the experimentally studied conditions of plasma expansion into an external magnetic field are favorable for the development of these instabilities. Moreover, as noted above, the absence of lateral flutes at the cavity boundary in the femtosecond case (see Figure 3d) can be naturally explained by the fact that the projection on the lateral boundary normal is close to zero due to the initial collimation of the «femtosecond» plasma flow.
We will investigate the instabilities arising in the elongated slabs (Figure 5) of «femtosecond» and «nanosecond» plasmas interacting with a transverse magnetic field. We will derive an expression for the effective acceleration following the work [86], but modifying the total energy conservation Equation (4) of spherical expansion from [86] to an equation describing quasi-cylindrical plasma expansion with the angle of divergence :
where in the right-hand side is the total laser energy deposited into the plasma, is the initial kinetic energy of the plasma, is the kinetic energy of the plasma at time t, is the magnetic field energy in the volume occupied by the plasma at time t, is plasma divergence angle, is the cylindrical radius of the plasma at time t, and L is its length along the cylindrical z coordinate. By expressing and taking the derivative with respect to time, we obtain an expression for the effective acceleration:
where is the Alfvén speed calculated based on the external undisturbed magnetic field and plasma flow density, and is the radius of plasma stopping for cylindrical expansion [84]. It can be estimated that for a «nanosecond» flow, m/s2, and in the case of a «femtosecond» flow, m/s2.
According to the linear theory, in the small dissipation approximation, the RTI growth rate (see, for example, p. 466 of [77]) and the HRTI [81,84] can be written as and , respectively, where is the scale length of the plasma density gradient, is the effective acceleration, and k is the instability wave number. Assuming mm in both nanosecond and femtosecond cases, we can obtain preliminary estimates of the instability increments: ns−1, ns−1 and ns−1, ns−1. It is noteworthy that, due to the lower density of the «femtosecond» plasma, the instability increments are several times larger than in the case of the «nanosecond» plasma. The maximum value of the increment without dissipation is observed for the HRTI in the femtosecond case.
It should be noted that the mean free paths in both cases for ion–ion and ion–electron collisions are on the order of or less than 10 m, which is significantly smaller than the ion Larmor radius (see Table 1). Therefore, dissipative terms cannot be neglected in the linear analysis, as they can, for example, lead to stabilization of short-wavelength perturbations. This is confirmed by the theory [86] and MHD calculations [6], which show the best agreement with experiment when accounting for increased resistivity. When including dissipative effects related to finite conductivity and isotropic viscosity included, the linear dispersion equation can be rewritten as follows [67,87]:
where k is the instability wave vector, is the magnetic diffusion coefficient, is the kinematic viscosity coefficient, and is the growth rate neglecting dissipation, which differs for RTI and HRTI. According to the experimental data, the linear stage of instability evolution occurs over time from 5 to 15 ns. During these times, «femtosecond» plasma can be characterized by the temperature 20 eV, while «nanosecond» plasma has a temperature of 100 eV (values are given in Table 1). These values are consistent with the direct measurements of plasma temperature using an X-ray focusing spectrometer with spatial resolution (FFSR) [88,89] made in our previous works under similar conditions [6,11,14,36,64]. From the classical Spitzer expressions for plasma conductivity (for example, from [18]) and the classical Braginskii expression for ion dynamic viscosity (for example, p. 825 [17]), it can be found that the magnetic diffusion coefficient m2/s for T1 = 20 eV and 5.4 m2/s for T2 = 100 eV. Meanwhile, the kinematic viscosity coefficient is several orders of magnitude smaller and can be neglected, as well as the term in the expression (1). We will consider purely unstable modes with and then derive an expression for the growth rate:
The dissipative term in the growth rate (2) has comparable values with the growth rates and , indicating the crucial role of dissipation in the observed flute instability. It is straightforward to derive expressions for the wavelengths of the most rapidly growing modes for RTI, , and for HRTI, , analogous to the expression (1) from the work [6]. In Figure 7a, the points represent the time evolution of the instability wavelength, averaged over a shot, observed experimentally during expansion for «femtosecond» (blue circles) and for «nanosecond» (red triangles) elongated plasma slabs (Figure 5). The horizontal lines in Figure 7a indicate the wavelengths of the most rapidly growing modes obtained in the linear approximation for RTI (red) and HRTI (blue). In Figure 7b, the points show the length of the flutes, averaged over a single shot, observed experimentally during expansion of elongated plasma slabs: «femtosecond» (blue circles) and «nanosecond» (red triangles), as well as the predictions from the expression (4) of the linear theory for RTI (blue lines) and HMRTI (red lines) at two characteristic temperatures 20 eV and 100 eV. The graphs in Figure 7 demonstrate that the RTI gives a better description of the elongated tongues observed in the nanosecond case, while the HRTI provides a better agreement with the observed wavelengths in the femtosecond case. The discrepancy between the experiment and the linear theory for times exceeding 30 ns can be naturally explained by the nonlinear nature of the instability at later times.
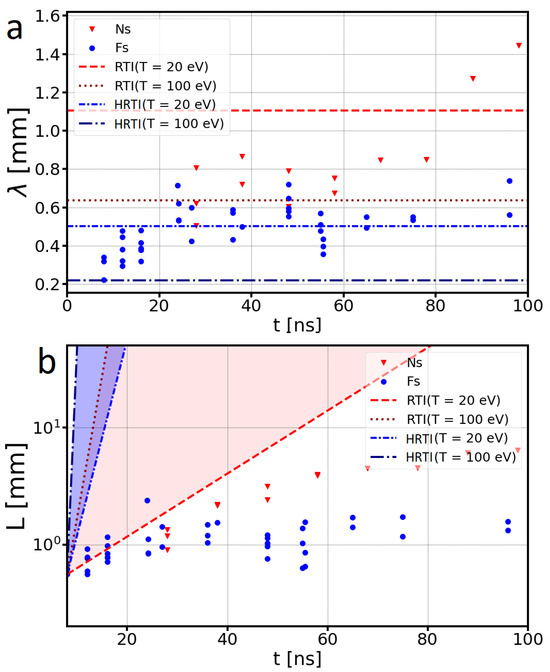
Figure 7.
Comparison of experimental results with the linear theory of Rayleigh–Taylor instability (RTI) and Hall-modified Rayleigh–Taylor instability (HRTI). (a) Average wavelength of instability in experiments with elongated flows (Figure 5) for «nanosecond» (red triangles) and «femtosecond» (blue circles) plasmas. Horizontal lines indicate wavelengths obtained from the linear approximation of (RTI) and (HRTI) for temperatures of 20 and 100 eV. (b) «Tongue» lengths in experiments with elongated plasma flows (Figure 5) for nanosecond (red triangles) and femtosecond (blue dots) laser pumping. In the linear approximation, RTI (red lines) and HRTI (blue lines), the instability amplitudes () are plotted for two characteristic temperatures, T1 = 20 eV and T2 = 100 eV.
The physical reasons for the emergence of (HRTI) can be understood by referring to the theory of Hall magnetohydrodynamics, that is, to an approximation in which the physical system is described by classical MHD with an added electric field term in the generalized Ohm’s law, associated with the Hall effect . This approximation, unlike the classical MHD, is applicable to the phenomena occurring on spatial scales shorter than or on the order of the ion inertial length and on temporal scales shorter than or on the order of the ion cyclotron period [84]. To estimate the influence of Hall effects under our conditions, consider the magnetic induction equation with Hall corrections, neglecting dissipative terms at this stage:
where the first term on the right-hand side describes convection, while the last term represents the Hall effect, is the plasma (ion) flow velocity, is the electron density of the plasma, and e is the elementary positive charge (electron charge). The other MHD equations do not require modifications related to the Hall effects and are therefore not presented here. To determine the conditions under which Hall effects significantly influence the dynamics, we compare the last term in Equation (5) with the convective term, which dominates under our conditions. First, in the approximation (Table 1), the Hall term can be rewritten as [90]
where accounts for the spatial scales. Estimating the convective term as , we find that the Hall effects are significant for processes with temporal scales . This condition can be interpreted as the influence of unbalanced ion inertia during cyclotron rotation against the background magnetized electron fluid. For the instability under study, this condition is expressed as , which is satisfied in our conditions in both «nanosecond» and «femtosecond» cases (Table 1). However, as noted above, in the considered plasma, the ion–ion and ion–electron collisions with frequencies (Table 1) are quite significant, which prevents Hall effects from having a significant influence on the flow dynamics near the target, where the plasma density is highest. Nevertheless, Hall effects may be important at the leading edge of plasma «tongues», which have lower densities <1017 cm−3, fewer collisions and sharper gradients in comparison with the mean free path lengths .
To estimate the influence of the Hall term at the front of the plasma flow, assume that . Then, the ratio of the Hall term to the convective term is expressed by the parameter [91,92]:
This parameter demonstrates that the Hall effects are significant at the front of the plasma flow at lower density gradients and lower densities, which is expressed by a larger ion inertial length , as well as at lower velocities, which, perhaps counterintuitively, is characterized by a smaller Larmor radius compared to the same ion inertial length . The values of the parameter for «nanosecond» and «femtosecond» plasma cases, assuming a conservative estimate of the inhomogeneity scale , are given in Table 1. The estimates in Table 1 show that the value for «nanosecond» flows is less than unity, while for «femtosecond» flows, it is noticeably larger than unity. This indicates that for «femtosecond» flows the Hall effects at the «tongues» front play a more significant role.
Measuring Hall currents and fields in experiments is an extremely challenging task. The most common methods used for diagnosing magnetic and electric fields in laser plasma, such as optical diagnostics (Faraday effect) or proton radiography, are integral techniques and do not ensure the required accuracy of localized measurement of Hall fields. Measurement methods based on probes are not applicable on our plasma scales , but such methods are actively used in experiments with plasmas having significantly larger spatial scales () [65,93,94]. However, these experiments typically involve lower particle densities, pressures, and magnetic fields. For example, detailed probe measurements of currents during plasma propagation across external magnetic field were performed in the works [95,96]. In [97], a correlation was found between the emergence of Hall azimuthal magnetic fields and large-scale flute instability and diamagnetic cavity collapse.
The hypothesis of a significant influence of Hall effects on the dynamics of the«tongues» front is supported by the RTI modeling in slab geometry using Hall MHD and hybrid codes [98,99], which implement a kinetic approach for ion dynamics and a fluid approach for electrons, as well as fully kinetic Vlasov simulations [100]. In these studies, when Hall effects were «turned on», the plasma dynamics is modified such that, instead of the classical RTI manifested as «tongues», twisted «tongues» are observed. The topology of these «tongues» remarkably coincides with the topology of the «femtosecond» plasma «tongues» in our experiment. It has been demonstrated that the physical cause of the twisting of the «tongues» into vortices is the Hall electric field, amplified by diamagnetic currents in the presence of a sharp pressure gradient at the tip of the «tongues», leading to asymmetric ion motion at the flow front [100]. Macroscopically, this effect can be viewed as an emergence of a Kelvin–Helmholtz-type instability [98,99,100].
Astrophysical Implication
The laboratory study conducted here can be used for modeling one of the most interesting and enigmatic phenomena in the universe—bright and short flares in active galactic nuclei [101,102]. One of the most plausible causes of these events is the interaction of dense clouds or red giants with jets of active galactic nuclei [103,104,105]. An intriguing feature of these powerful flares is the presence of several distinct peaks, which are most likely associated with the fragmentation of the cloud interacting with the jet. The individual «tongues» observed in the experiments with nanosecond laser pulses caused by RTI probably form these separate peaks on the brightness curves in the GeV and TeV ranges. Future 3D MHD simulations of such phenomena could confirm this hypothesis.
The parameters of astrophysical clouds are given in Table 1 (Astro). The scaling between astrophysical and laboratory systems is based on dimensionless parameters characterizing plasma evolution within the MHD approximation: the Euler number , the Alfvén–Mach number , and the plasma beta [17,18,19]. It is evident that these parameters for the astrophysical system match those for «nanosecond» plasma but are noticeably less consistent with «femtosecond» plasma. Additionally, for scaling within the MHD approximation, dissipative effects and non-ideal effects of the system must be small [17,18,19]. In the case of astrophysical and laboratory «nanosecond» plasmas, dissipative effects such as viscosity and magnetic field diffusion are approximately negligible since Re and . In «femtosecond» plasma, viscosity can be neglected; however, magnetic diffusion may significantly influence plasma dynamics ( 10). Also, non-ideal effects related to Hall effects are absolutely insignificant for astrophysical objects with large spatial scales L, since . Therefore, «nanosecond» plasma flows like those in our experiments are more suitable than «femtosecond» ones for modeling astrophysical objects in laboratory conditions and have been actively used in our previous works to model accretion and jet collimation in Young stars [10,11,14].
6. Conclusions
A detailed comparative study of the dynamics of plasma flows generated by high-intensity femtosecond and nanosecond laser pulses with similar fluences on the order of has been conducted for the first time. The interaction of such plasma flows with a transverse, uniform magnetic field with strength exceeding 14 T has been investigated. The dynamics and three-dimensional morphology of two types of plasma flows have been studied using femtosecond optical diagnostics.
A substantial difference in the dynamics of «femtosecond» and «nanosecond» plasma flows was observed in vacuum with and without an external magnetic field. The «femtosecond» plasma flow initially propagates, being collimated in vacuum, whereas the «nanosecond» flow diverges with a finite divergence angle of approximately 40°. The investigation of the cause of this collimation is beyond the scope of the present work and will be addressed in future studies.
The main features of «femtosecond» plasma dynamics in an external magnetic field have been described using a qualitative and quantitative comparison with «nanosecond» plasma. Unlike «nanosecond» plasma, there are no quasi-spherical cavities in «femtosecond» plasma. Furthermore, side flutes are not observed in the femtosecond plasma. Instead, the flow is immediately redirected into a narrow plasma sheet («tongue») propagating across the magnetic field at a constant velocity, similarly to the «nanosecond» case. Furthermore, the dynamics of the «femtosecond tongue» at significantly differ from that of the «nanosecond» one. The end of the «femtosecond tongue» twists in the direction of ion motion in the external magnetic field, whereas «nanosecond tongues» are randomly oriented.
The instability in the unique geometry of the plasma flow in the form of an elongated plasma slab has been investigated. Using the linear theory, we have demonstrated that, similarly to the «nanosecond» plasma, the «femtosecond» plasma flow interacts with a transverse magnetic field and breaks up into «tongues» due to the development of Rayleigh–Taylor instability. However, a significant difference lies in the behavior at the tips of the «tongues». In the femtosecond case, the «tongues» twist in the direction of ion motion in the magnetic field, whereas in «nanosecond» flows, the «tongues» are oriented randomly. Numerical magnetohydrodynamic simulations using the FLASH code confirmed that this random behavior of the «tongues», independent of the external magnetic field, is characteristic of the classical MHD Rayleigh–Taylor instability. The estimates of Hall effects from simulations indicate that the behavior of the «femtosecond» «tongues» may be influenced by Hall effects at their tips. It was shown that the influence of Hall effects on «femtosecond» «tongues» is enhanced due to lower density and reduced flow velocity. These conclusions agree well with the previous laboratory measurements of Hall fields [97] in plasmas with larger spatial scales (L ∼ 1 m) and are consistent with the numerical studies [98,99,100], where topologically similar twisted «tongues» caused by Hall currents were observed. The ion kinetic-type effects (Hall effects) in a large-scale «femtosecond» plasma depend on the characteristic values of parameters, such as density, temperature, and velocity, rather than on hot accelerated electrons produced during interaction with an intense femtosecond pulse.
Author Contributions
Conceptualization, R.S.Z., M.V.B., A.A.S. (Alexander A. Soloviev) and M.V.S.; methodology, R.S.Z., K.F.B., A.V.K., S.E.P., J.F. and A.A.S. (Alexander A. Soloviev); software, R.S.Z.; validation, R.S.Z., M.V.B., K.F.B., J.F. and M.V.S.; formal analysis, R.S.Z., K.F.B., E.S.B., S.E.P. and A.V.K.; investigation, R.S.Z., K.F.B., S.E.P., A.V.K., J.F. and A.A.S. (Alexander A. Soloviev); resources, V.N.G., A.A.K. (Alexey A. Kuzmin), A.A.K. (Anton A. Kochetkov), I.A.S., S.E.S., I.V.Y., M.V.S., A.A.S. (Andrey A. Shaykin) and E.A.K.; data curation, R.S.Z.; writing—original draft preparation, R.S.Z. and M.V.B.; writing—review and editing, R.S.Z., M.V.B. and M.V.S.; visualization, R.S.Z.; supervision, A.A.S. (Alexander A. Soloviev), M.V.S.; project administration, A.A.S. (Alexander A. Soloviev), A.A.S. (Andrey A. Shaykin), E.A.K. and M.V.S.; funding acquisition, A.A.S. (Andrey A. Shaykin) and M.V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, project No. 24-62-00032.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available upon request.
Acknowledgments
During the preparation of this manuscript/study, the author(s) used FLASH code 4.6 for the numerical simulations. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Basov, N.; Krokhin, O. Conditions for heating up of a plasma by the radiation from an optical generator. Sov. Phys. JETP 1964, 19, 123–126. [Google Scholar]
- Chang, P.; Fiksel, G.; Hohenberger, M.; Knauer, J.; Betti, R.; Marshall, F.; Meyerhofer, D.; Séguin, F.; Petrasso, R. Fusion yield enhancement in magnetized laser-driven implosions. Phys. Rev. Lett. 2011, 107, 035006. [Google Scholar] [CrossRef] [PubMed]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 55, 447–449. [Google Scholar] [CrossRef]
- Zakharov, Y.; Antonov, V.; Boyarintsev, E.; Melekhov, A.; Posukh, V.; Shaikhislamov, I.; Pickalov, V. Role of the Hall flute instability in the interaction of laser and space plasmas with a magnetic field. Plasma Phys. Rep. 2006, 32, 183–204. [Google Scholar] [CrossRef]
- Ripin, B.; McLean, E.; Manka, C.; Pawley, C.; Stamper, J.; Peyser, T.; Mostovych, A.; Grun, J.; Hassam, A.; Huba, J. Large-Larmor-radius interchange instability. Phys. Rev. Lett. 1987, 59, 2299. [Google Scholar] [CrossRef] [PubMed]
- Khiar, B.; Revet, G.; Ciardi, A.; Burdonov, K.; Filippov, E.; Béard, J.; Cerchez, M.; Chen, S.; Gangolf, T.; Makarov, S.; et al. Laser-produced magnetic-Rayleigh-Taylor unstable plasma slabs in a 20 T magnetic field. Phys. Rev. Lett. 2019, 123, 205001. [Google Scholar] [CrossRef]
- Hassam, A.; Huba, J. Structuring of the AMPTE magnetotail barium releases. Geophys. Res. Lett. 1987, 14, 60–63. [Google Scholar] [CrossRef]
- Fujioka, S.; Zhang, Z.; Ishihara, K.; Shigemori, K.; Hironaka, Y.; Johzaki, T.; Sunahara, A.; Yamamoto, N.; Nakashima, H.; Watanabe, T.; et al. Kilotesla magnetic field due to a capacitor-coil target driven by high power laser. Sci. Rep. 2013, 3, 1170. [Google Scholar] [CrossRef]
- Froula, D.; Ross, J.; Pollock, B.; Davis, P.; James, A.; Divol, L.; Edwards, M.; Offenberger, A.; Price, D.; Town, R.; et al. Quenching of the Nonlocal Electron Heat Transport by Large External Magnetic Fields in a Laser-Produced Plasma Measured with Imaging Thomson Scattering. Phys. Rev. Lett. 2007, 98, 135001. [Google Scholar]
- Zemskov, R.; Burdonov, K.; Soloviev, A.; Sladkov, A.; Korzhimanov, A.; Fuchs, J.; Bisikalo, D.; Zhilkin, A.; Barkov, M.; Ciardi, A.; et al. Laboratory modeling of YSO jets collimation by a large-scale divergent interstellar magnetic field. Astron. Astrophys. 2024, 681, A37. [Google Scholar] [CrossRef]
- Burdonov, K.; Yao, W.; Sladkov, A.; Bonito, R.; Chen, S.; Ciardi, A.; Korzhimanov, A.; Soloviev, A.; Starodubtsev, M.; Zemskov, R.; et al. Laboratory modelling of equatorial ‘tongue’accretion channels in young stellar objects caused by the Rayleigh-Taylor instability. Astron. Astrophys. 2022, 657, A112. [Google Scholar] [CrossRef]
- Fazzini, A.; Yao, W.; Burdonov, K.; Beard, J.; Chen, S.; Ciardi, A.; d’Humieres, E.; Diab, R.; Filippov, E.; Kisyov, S.; et al. Particle energization in colliding subcritical collisionless shocks investigated in the laboratory. Astron. Astrophys. 2022, 665, A87. [Google Scholar] [CrossRef]
- Burdonov, K.; Revet, G.; Bonito, R.; Argiroffi, C.; Béard, J.; Bolanõs, S.; Cerchez, M.; Chen, S.N.; Ciardi, A.; Espinosa, G.; et al. Laboratory evidence for an asymmetric accretion structure upon slanted matter impact in young stars. Astron. Astrophys. 2020, 642, A38. [Google Scholar] [CrossRef]
- Burdonov, K.; Bonito, R.; Giannini, T.; Aidakina, N.; Argiroffi, C.; Béard, J.; Chen, S.; Ciardi, A.; Ginzburg, V.; Gubskiy, K.; et al. Inferring possible magnetic field strength of accreting inflows in EXor-type objects from scaled laboratory experiments. Astron. Astrophys. 2021, 648, A81. [Google Scholar] [CrossRef]
- Albertazzi, B.; Ciardi, A.; Nakatsutsumi, M.; Vinci, T.; Beard, J.; Bonito, R.; Billette, J.; Borghesi, M.; Burkley, Z.; Chen, S.N.; et al. Laboratory formation of a scaled protostellar jet by coaligned poloidal magnetic field. Science 2014, 346, 325–328. [Google Scholar] [CrossRef]
- Yao, W.; Fazzini, A.; Chen, S.; Burdonov, K.; Antici, P.; Beard, J.; Bolanos, S.; Ciardi, A.; Diab, R.; Filippov, E.; et al. Laboratory evidence for proton energization by collisionless shock surfing. Nat. Phys. 2021, 17, 1177–1182. [Google Scholar] [CrossRef]
- Ryutov, D.; Drake, R.P.; Kane, J.; Liang, E.; Remington, B.A.; Wood-Vasey, W.M. Similarity Criteria for the Laboratory Simulation of Supernova Hydrodynamics. Astrophys. J. 1999, 518, 821–832. [Google Scholar] [CrossRef]
- Ryutov, D.D.; Drake, R.P.; Remington, B.A. Criteria for Scaled Laboratory Simulations of Astrophysical MHD Phenomena. Astrophys. J. Suppl. Ser. 2000, 127, 465–468. [Google Scholar] [CrossRef]
- Ryutov, D.D. Scaling laws for dynamical plasma phenomena. Phys. Plasmas 2018, 25, 100501. [Google Scholar] [CrossRef]
- Roth, M.; Cowan, T.; Key, M.; Hatchett, S.; Brown, C.; Fountain, W.; Johnson, J.; Pennington, D.; Snavely, R.; Wilks, S.; et al. Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 2001, 86, 436. [Google Scholar] [CrossRef]
- Tabak, M.; Clark, D.; Hatchett, S.; Key, M.; Lasinski, B.; Snavely, R.; Wilks, S.; Town, R.; Stephens, R.; Campbell, E.; et al. Review of progress in fast ignition. Phys. Plasmas 2005, 12. [Google Scholar] [CrossRef]
- Albert, F.; Thomas, A.G. Applications of laser wakefield accelerator-based light sources. Plasma Phys. Control. Fusion 2016, 58, 103001. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Burdonov, K.F.; Ginzburg, V.N.; Glyavin, M.Y.; Zemskov, R.S.; Kotov, A.V.; Kochetkov, A.A.; Kuzmin, A.A.; Murzanev, A.A.; Mukhin, I.B.; et al. Research in plasma physics and particle acceleration using the PEARL petawatt laser. Uspekhi Fiz. Nauk. 2024, 194, 313–335. [Google Scholar] [CrossRef]
- Perevalov, S.E.; Kotov, A.V.; Zemskov, R.S.; Burdonov, K.F.; Ginzburg, V.N.; Kuzmin, A.A.; Stukachev, S.E.; Yakovlev, I.V.; Shaykin, A.; Lopatin, A.Y.; et al. Acceleration of Electrons upon Interaction of Laser Pulses with Solid Targets in the Laser Peeler Regime. Bull. Lebedev Phys. Inst. 2024, 51, S305–S315. [Google Scholar] [CrossRef]
- Perevalov, S.; Burdonov, K.; Kotov, A.; Romanovskiy, D.; Soloviev, A.; Starodubtsev, M.; Golovanov, A.; Ginzburg, V.; Kochetkov, A.; Korobeinikova, A.; et al. Experimental study of strongly mismatched regime of laser-driven wakefield acceleration. Plasma Phys. Control. Fusion 2020, 62, 094004. [Google Scholar] [CrossRef]
- Schoenlein, R.; Elsaesser, T.; Holldack, K.; Huang, Z.; Kapteyn, H.; Murnane, M.; Woerner, M. Recent advances in ultrafast X-ray sources. Philos. Trans. R. Soc. 2019, 377, 20180384. [Google Scholar] [CrossRef]
- Liao, G.Q.; Li, Y.T. Review of intense terahertz radiation from relativistic laser-produced plasmas. IEEE Trans. Plasma Sci. 2019, 47, 3002–3008. [Google Scholar] [CrossRef]
- Zemskov, R.; Perevalov, S.; Kotov, A.; Bodrov, S.; Stepanov, A.; Solov’ev, A.; Bakunov, M.; Luchinin, A.; Ginzburg, V.; Kuz’min, A.; et al. Experimental Study of Terahertz Radiation Generation in the Interaction of Ultrashort Laser Pulse with Gas Targets. Radiophys. Quantum Electron. 2023, 65, 877–887. [Google Scholar] [CrossRef]
- Chen, H.; Fiuza, F. Perspectives on relativistic electron–positron pair plasma experiments of astrophysical relevance using high-power lasers. Phys. Plasmas 2023, 30, 020601. [Google Scholar] [CrossRef]
- Gurevich, E.; Hergenröder, R. Femtosecond laser-induced breakdown spectroscopy: Physics, applications, and perspectives. Appl. Spectrosc. 2007, 61, 233A–242A. [Google Scholar] [CrossRef]
- Singh, J.P.; Thakur, S.N. Laser-Induced Breakdown Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Harilal, S.S.; Freeman, J.R.; Diwakar, P.K.; Hassanein, A. Femtosecond laser ablation: Fundamentals and applications. In Laser-Induced Breakdown Spectroscopy: Theory and Applications; Springer: New York, NY, USA, 2014; pp. 143–166. [Google Scholar]
- Amoruso, S.; Bruzzese, R.; Spinelli, N.; Velotta, R. Characterization of laser-ablation plasmas. J. Phys. At. Mol. Opt. Phys. 1999, 32, R131. [Google Scholar] [CrossRef]
- Antici, P.; Gremillet, L.; Grismayer, T.; Mora, P.; Audebert, P.; Borghesi, M.; Cecchetti, C.; Mančic, A.; Fuchs, J. Modeling target bulk heating resulting from ultra-intense short pulse laser irradiation of solid density targets. Phys. Plasmas 2013, 20, 123116. [Google Scholar] [CrossRef]
- Dubois, J.L.; Lubrano-Lavaderci, F.; Raffestin, D.; Ribolzi, J.; Gazave, J.; Fontaine, A.C.L.; d’Humières, E.; Hulin, S.; Nicolaï, P.; Poyé, A.; et al. Target charging in short-pulse-laser–plasma experiments. Phys. Rev. E 2014, 89, 013102. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, A.; Burdonov, K.; Chen, S.; Eremeev, A.; Korzhimanov, A.; Pokrovskiy, G.; Pikuz, T.; Revet, G.; Sladkov, A.; Ginzburg, V.; et al. Experimental evidence for short-pulse laser heating of solid-density target to high bulk temperatures. Sci. Rep. 2017, 7, 12144. [Google Scholar] [CrossRef]
- Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 2012, 75, 056401. [Google Scholar] [CrossRef]
- Sarri, G.; Macchi, A.; Cecchetti, C.; Kar, S.; Liseykina, T.; Yang, X.; Dieckmann, M.E.; Fuchs, J.; Galimberti, M.; Gizzi, L.; et al. Dynamics of Self-Generated, Large Amplitude Magnetic Fields Following High-Intensity Laser Matter Interaction. Phys. Rev. Lett. 2012, 109, 205002. [Google Scholar] [CrossRef]
- Albertazzi, B.; Chen, S.; Antici, P.; Böker, J.; Borghesi, M.; Breil, J.; Dervieux, V.; Feugeas, J.; Lancia, L.; Nakatsutsumi, M.; et al. Dynamics and structure of self-generated magnetics fields on solids following high contrast, high intensity laser irradiation. Phys. Plasmas 2015, 22, 123108. [Google Scholar] [CrossRef]
- Shaikh, M.; Lad, A.D.; Jana, K.; Sarkar, D.; Dey, I.; Kumar, G.R. Megagauss magnetic fields in ultra-intense laser generated dense plasmas. Plasma Phys. Control. Fusion 2016, 59, 014007. [Google Scholar] [CrossRef]
- Borghesi, M.; Mackinnon, A.; Gaillard, R.; Willi, O.; Pukhov, A.; Meyer-ter Vehn, J. Large quasistatic magnetic fields generated by a relativistically intense laser pulse propagating in a preionized plasma. Phys. Rev. Lett. 1998, 80, 5137. [Google Scholar] [CrossRef]
- Gopal, A.; Tatarakis, M.; Beg, F.; Clark, E.; Dangor, A.; Evans, R.; Norreys, P.; Wei, M.; Zepf, M.; Krushelnick, K. Temporally and spatially resolved measurements of multi-megagauss magnetic fields in high intensity laser-produced plasmas. Phys. Plasmas 2008, 15, 122701. [Google Scholar] [CrossRef]
- Weibel, E.S. Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys. Rev. Lett. 1959, 2, 83. [Google Scholar] [CrossRef]
- Ruyer, C.; Bolaños, S.; Albertazzi, B.; Chen, S.; Antici, P.; Böker, J.; Dervieux, V.; Lancia, L.; Nakatsutsumi, M.; Romagnani, L.; et al. Growth of concomitant laser-driven collisionless and resistive electron filamentation instabilities over large spatiotemporal scales. Nat. Phys. 2020, 16, 983–988. [Google Scholar] [CrossRef]
- Krishnamurthy, S.; Makur, K.; Ramakrishna, B. Observation of resistive Weibel instability in intense laser plasma. Laser Part. Beams 2020, 38, 152–158. [Google Scholar] [CrossRef]
- Quinn, K.; Romagnani, L.; Ramakrishna, B.; Sarri, G.; Dieckmann, M.E.; Wilson, P.; Fuchs, J.; Lancia, L.; Pipahl, A.; Toncian, T.; et al. Weibel-induced filamentation during an ultrafast laser-driven plasma expansion. Phys. Rev. Lett. 2012, 108, 135001. [Google Scholar] [CrossRef] [PubMed]
- Biermann, L. Über den Ursprung der Magnetfelder auf Sternen und im interstellaren Raum (miteinem Anhang von A. Schlüter). Z. Naturforschung Teil A 1950, 5, 65. [Google Scholar]
- Ciardi, A.; Vinci, T.; Fuchs, J.; Albertazzi, B.; Riconda, C.; Pépin, H.; Portugall, O. Astrophysics of Magnetically Collimated Jets Generated from Laser-Produced Plasmas. Phys. Rev. Lett. 2013, 110, 025002. [Google Scholar] [CrossRef]
- Ciardi, A.; Lebedev, S.; Frank, A.; Blackman, E.; Chittenden, J.; Jennings, C.; Ampleford, D.; Bland, S.; Bott, S.; Rapley, J.; et al. The evolution of magnetic tower jets in the laboratory. Phys. Plasmas 2007, 14, 056501. [Google Scholar] [CrossRef]
- Ryu, D.; Schleicher, D.R.; Treumann, R.A.; Tsagas, C.G.; Widrow, L.M. Magnetic fields in the large-scale structure of the universe. Space Sci. Rev. 2012, 166, 1–35. [Google Scholar] [CrossRef]
- Ryutov, D.; Kugland, N.; Park, H.; Plechaty, C.; Remington, B.; Ross, J. Basic scalings for collisionless-shock experiments in a plasma without pre-imposed magnetic field. Plasma Phys. Control. Fusion 2012, 54, 105021. [Google Scholar] [CrossRef]
- Lozhkarev, V.; Freidman, G.; Ginzburg, V.; Katin, E.; Khazanov, E.; Kirsanov, A.; Luchinin, G.; Mal’Shakov, A.; Martyanov, M.; Palashov, O.; et al. Compact 0.56 petawatt laser system based on optical parametric chirped pulse amplification in KD* P crystals. Laser Phys. Lett. 2007, 4, 421. [Google Scholar] [CrossRef]
- Ginzburg, V.; Yakovlev, I.; Kochetkov, A.; Kuzmin, A.; Mironov, S.; Shaikin, I.; Shaykin, A.; Khazanov, E. 11 fs, 1.5 PW laser with nonlinear pulse compression. Opt. Express 2021, 29, 28297–28306. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, A.; Kotov, A.; Martyanov, M.; Perevalov, S.; Zemskov, R.; Starodubtsev, M.; Alexandrov, A.; Galaktionov, I.; Samarkin, V.; Kudryashov, A.; et al. Improving focusability of post-compressed PW laser pulses using a deformable mirror. Opt. Express 2022, 30, 40584–40591. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, A.; Burdonov, K.; Kotov, A.; Perevalov, S.; Zemskov, R.; Ginzburg, V.; Kochetkov, A.; Kuzmin, A.; Shaikin, A.; Shaikin, I.; et al. Experimental study of the interaction of a laser plasma flow with a transverse magnetic field. Radiophys. Quantum Electron. 2021, 63, 876–886. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Barkov, M.V.; Khangulyan, D. Scenarios for Ultrafast Gamma-Ray Variability in AGN. Astrophys. J. 2017, 841, 61. [Google Scholar] [CrossRef]
- Luchinin, A.; Malyshev, V.; Kopelovich, E.; Burdonov, K.; Gushchin, M.; Morozkin, M.; Proyavin, M.; Rozental, R.; Soloviev, A.; Starodubtsev, M.; et al. Pulsed magnetic field generation system for laser-plasma research. Rev. Sci. Instrum. 2021, 92, 123506. [Google Scholar] [CrossRef]
- Faenov, A.Y.; Colgan, J.; Hansen, S.; Zhidkov, A.; Pikuz, T.; Nishiuchi, M.; Pikuz, S.; Skobelev, I.Y.; Abdallah, J.; Sakaki, H.; et al. Nonlinear increase of X-ray intensities from thin foils irradiated with a 200 TW femtosecond laser. Sci. Rep. 2015, 5, 13436. [Google Scholar] [CrossRef]
- Faenov, A.Y. X-ray spectroscopic methods for measuring the parameters of high-temperature dense plasma. Meas. Tech. 1997, 40, 94–100. [Google Scholar] [CrossRef]
- Hipp, M.; Woisetschlager, J.; Reiterer, P.; Neger, T. Digital evaluation of interferograms. Measurement 2004, 36, 53–66. [Google Scholar] [CrossRef]
- Basov, N.; Zakharenkov, Y.A.; Rupasov, A.; Sklizkov, G.; Shikanov, A. Diagnostics of Dense Plasma. Nauka Mosc. 1989, 11, 9. [Google Scholar]
- Tatarakis, M.; Gopal, A.; Watts, I.; Beg, F.; Dangor, A.; Krushelnick, K.; Wagner, U.; Norreys, P.; Clark, E.; Zepf, M.; et al. Measurements of ultrastrong magnetic fields during relativistic laser–plasma interactions. Phys. Plasmas 2002, 9, 2244–2250. [Google Scholar] [CrossRef]
- Tatarakis, M.; Watts, I.; Beg, F.; Clark, E.; Dangor, A.; Gopal, A.; Haines, M.; Norreys, P.; Wagner, U.; Wei, M.S.; et al. Measuring huge magnetic fields. Nature 2002, 415, 280. [Google Scholar] [CrossRef]
- Zemskov, R.; Burdonov, K.; Kuzmin, A.; Shaikin, I.A.; Ginsburg, V.N.; Yakovlev, I.V.; Kochetkov, A.A.; Perevalov, S.E.; Kotov, A.V.; Solovyov, A.A.; et al. Laboratory study of Rayleigh-Taylor instability in laser plasma interacting with an external magnetic field. Radiophys. Quantum Electron. 2024, 67, 1029–1037. [Google Scholar] [CrossRef]
- Korobkov, S.; Nikolenko, A.; Gushchin, M.; Strikovsky, A.; Zudin, I.Y.; Aidakina, N.; Shaikhislamov, I.; Rumenskikh, M.; Zemskov, R.; Starodubtsev, M. Features of Dynamics and Instability of Plasma Jets Expanding into an External Magnetic Field in Laboratory Experiments with Compact Coaxial Plasma Generators on a Large-Scale “Krot” Stand. Astron. Rep. 2023, 67, 93–103. [Google Scholar] [CrossRef]
- Winske, D.; Huba, J.D.; Niemann, C.; Le, A. Recalling and updating research on diamagnetic cavities: Experiments, theory, simulations. Front. Astron. Space Sci. 2019, 5, 51. [Google Scholar] [CrossRef]
- Tang, H.b.; Hu, G.y.; Liang, Y.h.; Wang, Y.l.; Tao, T.; Hu, P.; Yuan, P.; Zhu, P.; Zuo, Y.; Zhao, B.; et al. Observation of large Larmor radius instability in laser plasma expanding into a 10 T external magnetic field. Phys. Plasmas 2020, 27, 022108. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 1969, 4, 101–104. [Google Scholar] [CrossRef]
- Richardson, A.S. 2019 NRL Plasma Formulary; Naval Research Laboratory: Washington, DC, USA, 2019.
- Fryxell, B.; Olson, K.; Ricker, P.; Timmes, F.X.; Zingale, M.; Lamb, D.; MacNeice, P.; Rosner, R.; Truran, J.; Tufo, H. FLASH: An Adaptive Mesh Hydrodynamics Code for ModelingAstrophysical Thermonuclear Flashes. Astrophys. J. Suppl. Ser. 2000, 131, 273. [Google Scholar] [CrossRef]
- Wollaeger, R.T.; Van Rossum, D.R. Radiation transport for explosive outflows: Opacity regrouping. Astrophys. J. Suppl. Ser. 2014, 214, 28. [Google Scholar] [CrossRef][Green Version]
- Chatzopoulos, E.; Weide, K. Gray radiation hydrodynamics with the FLASH code for astrophysical applications. Astrophys. J. 2019, 876, 148. [Google Scholar] [CrossRef]
- Braginskii, S. Transport processes in a plasma. Rev. Plasma Phys. 1965, 1, 205. [Google Scholar]
- Huba, J.; Gladd, N.; Papadopoulos, K. The lower-hybrid-drift instability as a source of anomalous resistivity for magnetic field line reconnection. Geophys. Res. Lett. 1977, 4, 125–128. [Google Scholar] [CrossRef]
- Okada, S.; Sato, K.; Sekiguchi, T. Possibility of lower-hybrid-drift instability in laser produced plasma in a uniform magnetic field. J. Phys. Soc. Jpn. 1979, 46, 355–356. [Google Scholar] [CrossRef]
- Peyser, T.; Manka, C.; Ripin, B.; Ganguli, G. Electron–ion hybrid instability in laser-produced plasma expansions across magnetic fields. Phys. Fluids Plasma Phys. 1992, 4, 2448–2458. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Sharp, D.H. Overview of Rayleigh-Taylor Instability; Technical Report; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 1983.
- Winske, D. Short-wavelength modes on expanding plasma clouds. J. Geophys. Res. Space Phys. 1988, 93, 2539–2552. [Google Scholar] [CrossRef]
- Zakharov, Y.P. Collisionless laboratory astrophysics with lasers. IEEE Trans. Plasma Sci. 2003, 31, 1243–1251. [Google Scholar] [CrossRef]
- Huba, J.; Lyon, J.; Hassam, A. Theory and simulation of the Rayleigh-Taylor instability in the limit of large Larmor radius. Phys. Rev. Lett. 1987, 59, 2971. [Google Scholar] [CrossRef]
- Huba, J.; Hassam, A.; Satyanarayana, P. Nonlocal theory of the Rayleigh–Taylor instability in the limit of unmagnetized ions. Phys. Fluids Plasma Phys. 1989, 1, 931–941. [Google Scholar] [CrossRef]
- Hassam, A.; Huba, J. Nonlinear evolution of the unmagnetized ion Rayleigh–Taylor instability. Phys. Fluids Plasma Phys. 1990, 2, 2001–2006. [Google Scholar] [CrossRef]
- Huba, J. Hall magnetohydrodynamics in space and laboratory plasmas. Phys. Plasmas 1995, 2, 2504–2513. [Google Scholar] [CrossRef]
- Bernhardt, P.; Roussel-Dupre, R.; Pongratz, M.; Haerendel, G.; Valenzuela, A.; Gurnett, D.; Anderson, R. Observations and theory of the AMPTE magnetotail barium releases. J. Geophys. Res. Space Phys. 1987, 92, 5777–5794. [Google Scholar] [CrossRef]
- Huba, J.; Hassam, A.; Winske, D. Stability of sub-Alfvénic plasma expansions. Phys. Fluids Plasma Phys. 1990, 2, 1676–1697. [Google Scholar] [CrossRef]
- Zhu, P.; Sovinec, C.; Hegna, C. The formation of blobs from a pure interchange process. Phys. Plasmas 2015, 22, 022311. [Google Scholar] [CrossRef]
- Faenov, A.Y.; Pikuz, S.; Erko, A.; Bryunetkin, B.; Dyakin, V.; Ivanenkov, G.; Mingaleev, A.; Pikuz, T.; Romanova, V.; Shelkovenko, T. High-performance x-ray spectroscopic devices for plasma microsources investigations. Phys. Scr. 1994, 50, 333. [Google Scholar] [CrossRef]
- Filippov, E.D.; Makarov, S.S.; Burdonov, K.F.; Yao, W.; Revet, G.; Béard, J.; Bolaños, S.; Chen, S.N.; Guediche, A.; Hare, J.; et al. Enhanced X-ray emission arising from laser-plasma confinement by a strong transverse magnetic field. Sci. Rep. 2021, 11, 8180. [Google Scholar] [CrossRef] [PubMed]
- Hassam, A.; Huba, J. Magnetohydrodynamic equations for systems with large Larmor radius. Phys. Fluids 1988, 31, 318–325. [Google Scholar] [CrossRef]
- Ryutov, D.; Kugland, N.; Levy, M.; Plechaty, C.; Ross, J.; Park, H. Magnetic field advection in two interpenetrating plasma streams. Phys. Plasmas 2013, 20, 032703. [Google Scholar] [CrossRef]
- Gordeev, A.V.; Kingsep, A.S.; Rudakov, L.I. Electron magnetohydrodynamics. Phys. Rep. 1994, 243, 215–315. [Google Scholar] [CrossRef]
- Gushchin, M.E.; Korobkov, S.V.; Terekhin, V.A.; Strikovskiy, A.; Gundorin, V.I.; Zudin, I.Y.; Aidakina, N.A.; Nikolenko, A. Laboratory simulation of the dynamics of a dense plasma cloud expanding in a magnetized background plasma on a Krot large-scale device. JETP Lett. 2018, 108, 391–395. [Google Scholar] [CrossRef]
- Nikolenko, A.; Gushchin, M.; Korobkov, S.; Zudin, I.Y.; Aidakina, N.; Strikovskiy, A.; Loskutov, K. Dynamics of a Plasma Cloud Generated by a Compact Coaxial Gun upon Expansion into Vacuum and Large-Volume Background Plasma in an External Magnetic Field. Plasma Phys. Rep. 2023, 49, 1284–1299. [Google Scholar] [CrossRef]
- Collette, A.; Gekelman, W. Structure of an exploding laser-produced plasma. Phys. Rev. Lett. 2010, 105, 195003. [Google Scholar] [CrossRef]
- Collette, A.; Gekelman, W. Structure of an exploding laser-produced plasma. Phys. Plasmas 2011, 18, 055705. [Google Scholar] [CrossRef]
- Chibranov, A.; Shaikhislamov, I.; Berezutskiy, A.; Posukh, V.; Trushin, P.; Zakharov, Y.P.; Miroshnichenko, I.; Rumenskikh, M.; Terekhin, V. Hall Effects and Diamagnetic Cavity Collapse during a Laser Plasma Cloud Expansion into a Vacuum Magnetic Field. Astron. Rep. 2024, 68, 418–428. [Google Scholar] [CrossRef]
- Winske, D. Regimes of the magnetized Rayleigh–Taylor instability. Phys. Plasmas 1996, 3, 3966–3974. [Google Scholar] [CrossRef]
- Huba, J.; Winske, D. Rayleigh–Taylor instability: Comparison of hybrid and nonideal magnetohydrodynamic simulations. Phys. Plasmas 1998, 5, 2305–2316. [Google Scholar] [CrossRef]
- Umeda, T.; Wada, Y. Non-MHD effects in the nonlinear development of the MHD-scale Rayleigh-Taylor instability. Phys. Plasmas 2017, 24, 072307. [Google Scholar] [CrossRef]
- Aliu, E.; Arlen, T.; Aune, T.; Beilicke, M.; Benbow, W.; Bouvier, A.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; Byrum, K.; et al. VERITAS Observations of Day-scale Flaring of M 87 in 2010 April. Astrophys. J. 2012, 746, 141. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berenji, B.; et al. Fermi Gamma-ray Space Telescope Observations of the Gamma-ray Outburst from 3C454.3 in November 2010. Astrophys. J. Lett. 2011, 733, L26. [Google Scholar] [CrossRef]
- Barkov, M.V.; Aharonian, F.A.; Bosch-Ramon, V. Gamma-ray Flares from Red Giant/Jet Interactions in Active Galactic Nuclei. Astrophys. J. 2010, 724, 1517–1523. [Google Scholar] [CrossRef]
- Barkov, M.V.; Aharonian, F.A.; Bogovalov, S.V.; Kelner, S.R.; Khangulyan, D. Rapid TeV Variability in Blazars as a Result of Jet-Star Interaction. Astrophys. J. 2012, 749, 119. [Google Scholar] [CrossRef]
- Bosch-Ramon, V.; Perucho, M.; Barkov, M.V. Clouds and red giants interacting with the base of AGN jets. Astron. Astrophys. 2012, 539, A69. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).