What Machine Learning Can and Cannot Do for Inertial Confinement Fusion
Abstract
1. Introduction
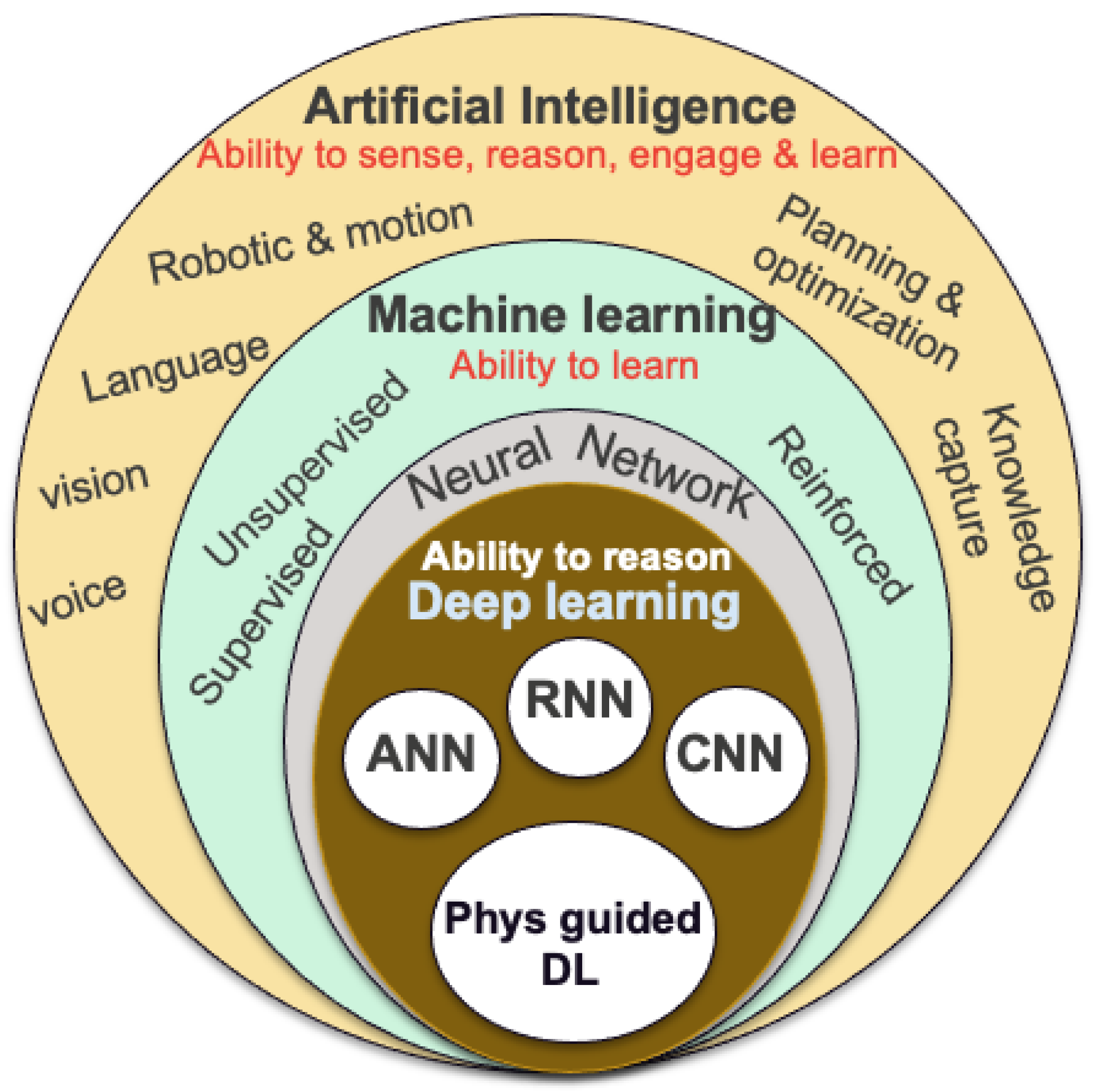
2. Machine Learning and Limitations
3. Inertial Confinement Fusion
4. Tasks Good for Machine Learning
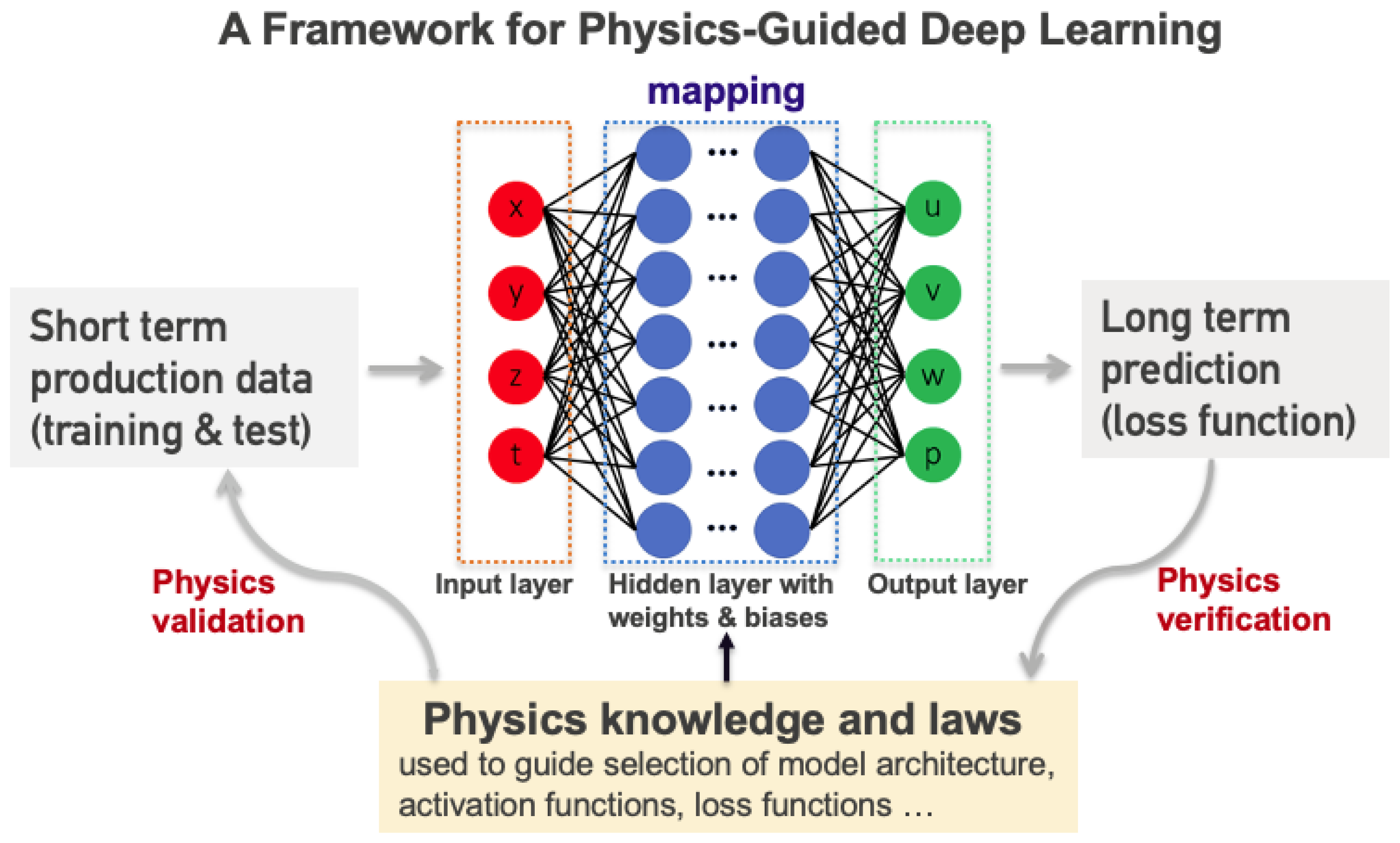
5. Physics-Guided Deep Learning
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mitchell, T. Machine Learning; McGraw Hill: New York, NY, USA, 1997; ISBN 0–07-042807-7. [Google Scholar]
- Bengio, Y.; LeCun, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Udrescu, S.-M.; Tegmark, M. AI Feynman: A physics-inspired method for symbolic regression. Sci. Adv. 2020, 6, eaay2531. [Google Scholar] [CrossRef] [PubMed]
- Ng, A. How Artificial Intelligence Is Transforming the Industry. 2021. Available online: https://www.bosch.com/stories/artificial-intelligence-in-industry/ (accessed on 29 July 2022).
- Hatfield, P.W.; Gaffney, J.A.; Anderson, G.J.; Ali, S.; Antonelli, L.; Başeğmez du Pree, S.; Citrin, J.; Fajardo, M.; Knapp, P.; Kettle, B.; et al. The data-driven future of high-energy-density physics. Nature 2021, 593, 351–361. [Google Scholar] [CrossRef]
- Humphreys, D.; Kupresanin, A.; Boyer, M.D.; Canik, J.; Chang, C.S.; Cyr, E.C.; Granetz, R.; Hittinger, J.; Kolemen, E.; Lawrence, E.; et al. Advancing Fusion with Machine Learning Research Needs Workshop Report. J. Fusion Energy 2020, 39, 123–155. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.J.; Brunner, R.J. Star–galaxy classification using deep convolutional neural networks. MNRAS 2017, 464, 4463–4475. [Google Scholar] [CrossRef]
- Iten, R.; Metger, T.; Wilming, H.; del Rio, L.; Renner, R. Discovering Physical Concepts with Neural Networks. Phys. Rev. Lett. 2020, 124, 010508. [Google Scholar] [CrossRef]
- Keshavan, A.; Yeatman, J.D.; Rokem, A. Combining Citizen Science and Deep Learning to Amplify Expertise in Neuroimaging. Front. Neuroinform. 2019, 13, 29. [Google Scholar] [CrossRef]
- Beck, M.R.; Scarlata, C.; Fortson, L.F.; Lintott, C.J.; Simmons, B.D.; Galloway, M.A.; Willett, K.W.; Dickinson, H.; Masters, K.L.; Marshall, P.J.; et al. Integrating human and machine intelligence in galaxy morphology classification tasks. MNRAS 2018, 476, 5516–5534. [Google Scholar] [CrossRef]
- Atzeni, S.; Meyer-ter Vehn, J. 2004 The Physics of Inertial Fusion: BeamPlasma Interaction, Hydrodynamics, Hot Dense Matter International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Lindl, J. Inertial Confinement Fusion: The Quest for Ignition and Energy Gain Using Indirect Drive; AIP Press: College Park, MD, USA, 1998. [Google Scholar]
- Mehta, P.; Bukov, M.; Wang, C.-H.; Day, A.G.R.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to Machine Learning, for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. 2006 Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Pearson, K. On Lines and Planes of Closest Fit to Systems of Points in Space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Atwell, J.A.; King, B.B. Proper orthogonal decomposition for reduced basis feedback controllers for parabolic equations. Math. Comput. Model. 2001, 33, 1–19. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Kates-Harbeck, J.; Svyatkovskiy, A.; Tang, W. Predicting disruptive instabilities in controlled fusion plasmas through deep learning. Nature 2019, 568, 526. [Google Scholar] [CrossRef]
- Lee, K.; Carlberg, K. Model Reduction of Dynamical Systems on Nonlinear Manifolds Using Deep Convolutional Autoencoders. arXiv 2018, arXiv:1812.08373. [Google Scholar] [CrossRef]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter Optimization: Comparing Genetic Algorithm against Grid Search and Bayesian Optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021. [Google Scholar]
- Andrieu, C.; De Freitas, N.; Doucet, A.; Jordan, M.I. An Introduction to MCMC for Machine Learning. Mach. Learn. 2003, 50, 5–43. [Google Scholar] [CrossRef]
- Feurer, M.; Hutter, F. Automated Machine Learning: Methods, Systems, Challenges; The Springer Series on Challenges in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Moonen, M.; Moor, B.D.; Vandenberghe, L.; Vandewalle, J. On- and Off-Line Identification of Linear State Space Models. Int. J. Control 1989, 49, 219–232. [Google Scholar] [CrossRef]
- Viberg, M. Subspace-based Methods for the Identification of Linear Time-invariant Systems. Automatica 1995, 31, 1835–1851. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Dupond, S. A thorough review on the current advance of neural network structures. Annu. Rev. Control 2019, 14, 200–230. [Google Scholar]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Gaffney, J.A.; Brandon, S.T.; Humbird, K.D.; Kruse, M.K.G.; Nora, R.C.; Peterson, J.L.; Spears, B.K. Making inertial confinement fusion models more predictive. Phys. Plasmas 2019, 26, 082704. [Google Scholar] [CrossRef]
- Spears, B.K.; Brase, J.; Bremer, P.-T.; Chen, B.; Field, J.; Gaffney, J.; Kruse, M.; Langer, S.; Lewis, K.; Nora, R.; et al. Deep learning: A guide for practitioners in the physical sciences. Phys. Plasmas 2018, 25, 080901. [Google Scholar] [CrossRef]
- Kritcher, A.L.; Young, C.V.; Robey, H.F.; Weber, C.R.; Zylstra, A.B.; Hurricane, O.A.; Callahan, D.A.; Ralph, J.E.; Ross, J.S.; Baker, K.L.; et al. Design of inertial fusion implosions reaching the burning plasma regime. Nat. Phys. 2022, 18, 251–258. [Google Scholar] [CrossRef]
- Zylstra, A.B.; Hurricane, O.A.; Callahan, D.A.; Kritcher, A.; Ralph, J.E.; Robey, H.F.; Ross, J.S.; Young, C.V.; Baker, K.L.; Casey, D.T.; et al. Burning plasma achieved in inertial fusion. Nature 2022, 601, 542–548. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Merrill, F.E.; Cerjan, C.J.; Batha, S.H. Analysis of NIF experiments with the minimal energy implosion model. Phys. Plasmas 2015, 22, 082704. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Batha, S.H. On Thermonuclear ignition criterion at the National Ignition Facility. Phys. Plasmas 2014, 21, 102707. [Google Scholar] [CrossRef]
- Cheng, B.; Bradley, P.A.; Finnagan, S.A.; Thomas, C.A. Fundamental factors affecting thermonuclear ignition. Nucl. Fusion 2020, 61, 096010. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Batha, S.H. Scaling laws for ignition at the National Ignition Facility from first principles. Phys. Rev. E 2013, 88, 041101. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Yi, S.A.; Batha, S.H.; Wysocki, F.J. Ignition and pusher adiabat. Phys. Control. Fusion 2018, 60, 074011. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Yi, S.A.; Batha, S.H.; Wysocki, F.J. Effects of preheat and mix on the fuel adiabat of an imploding capsule. Phys. Plasmas 2016, 23, 120702. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Yi, S.A.; Landen, O.L.; Wang, Y.-M.; Cerjan, C.J.; Batha, S.H.; Wysocki, F.J. Effects of asymmetry and hot-spot shape on ignition capsules. Phys. Rev. E 2018, 98, 023203. [Google Scholar] [CrossRef] [PubMed]
- Edwards, M.J.; Patel, P.K.; Lindl, J.D.; Atherton, L.J.; Glenzer, S.H.; Haan, S.W.; Kilkenny, J.D.; Landen, O.L.; Moses, E.I.; Nikrooet, A.; et al. Progress towards ignition on the national ignition facility. Phys. Plasmas 2013, 20, 070501. [Google Scholar] [CrossRef]
- Nakhleh, J.B.; Fernández-Godino, M.G.; Grosskopf, M.J.; Wilson, B.M.; Kline, J.; Srinivasan, G. Exploring Sensitivity of ICF Outputs to Design Parameters in Experiments Using Machine Learning. IEEE Trans. Plasma Sci. 2021, 49, 2238–2246. [Google Scholar] [CrossRef]
- Vazirani, N.N.; Grosskopf, M.J.; Stark, D.J.; Bradley, P.A.; Haines, B.M.; Loomis, E.; England, S.L.; Scales, W.A. Coupling 1D xRAGE simulations with machine learning for graded inner shell design optimization in double shell capsules. Phys. Plasmas 2021, 28, 122709. [Google Scholar] [CrossRef]
- Peterson, J.L.; Humbird, K.D.; Field, J.E.; Brandon, S.T.; Langer, S.H.; Nora, R.C.; Spears, B.K.; Springer, P.T. Zonal flow generation in inertial confinement fusion implosions. Phys. Plasmas 2017, 24, 032702. [Google Scholar] [CrossRef]
- Melvin, J.; Lim, H.; Rana, V.; Cheng, B.; Glimm, J.; Sharp, D.H.; Wilson, D.C. Sensitivity of inertial confinement fusion hot spot properties to the deuterium-tritium fuel adiabat. Phys. Plasmas 2015, 22, 022708. [Google Scholar] [CrossRef]
- Vander Wal, M.D.; McClarren, R.G.; Humbird, K.D. Transfer learning of hight-fidelity opacity spectra in autoencoders and surrogate models. arXiv 2022, arXiv:2203.00853. [Google Scholar]
- Michoski, C.; Milosavljevic, M.; Oliver, T.; Hatch, D. Solving Irregular and Data-Enriched Differential Equations Using Deep Neural Networks. arXiv 2019, arXiv:1905.04351. [Google Scholar]
- Humbird, K.D.; Peterson, J.L.; Salmonson, J.; Spears, B.K. Cognitive simulation models for inertial confinement fusion: Combining simulation and experimental data. Phys. Plasmas 2021, 28, 042709. [Google Scholar] [CrossRef]
- Gopalaswamy, V.; Betti, R.; Knauer, J.P.; Luciani, N.; Patel, D.; Woo, K.M.; Bose, A.; Igumenshchev, I.V.; Campbell, E.M.; Anderson, K.S.; et al. Tripled yield in direct-drive laser fusion through statistical modelling. Nature 2019, 565, 581–586. [Google Scholar] [CrossRef]
- Ross, J.S.; Ralph, J.E.; Zylstra, J.E.A.B.; Kritcher, A.L.; Robey, H.F.; Young, C.V.; Hurricane, O.A.; Callahan, D.A.; Baker, K.L.; Casey, D.T.; et al. Experiments conducted in the burning plasma regime with inertial fusion implosions. arXiv 2021, arXiv:2111.04640. [Google Scholar]
- Abu-Shawared, H.; Acree, R.; Adams, P.; Adams, J.; Addis, B.; Aden, R.; Adrian, P.; Afeyan, B.B.; Aggleton, M.; Indirect Drive ICF Collaboration; et al. Lawson’s criteria for ignition exceeded in an inertial fusion experiment. Phys. Rev. Lett. 2022, 129, 075001. [Google Scholar] [CrossRef] [PubMed]
- Hsu, A.; Cheng, B.; Bradley, P.A. Analysis of NIF scaling using physics informed machine learning. Phys. Plasmas 2020, 27, 012703. [Google Scholar] [CrossRef]
- Kramer, O. K-Nearest Neighbors. Dimensionality Reduction with Unsupervised Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–23. [Google Scholar]
- Liu, W.; Principe, J.C.; Haykin, S.S. Kernel Adaptive Filtering: A Comprehensive Introduction, 1st ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Humbird, K.D.; Peterson, J.L.; Mcclarren, R.G. Deep Neural Network Initialization With Decision Trees. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 1286. [Google Scholar] [CrossRef]
| Successful areas | Pattern recognition, image classification, cancer diagnosis, and systems with the following features: (a) large digital datasets (inputs, outputs), clear goals, and metrics; (b) not dominated by a long chain of logic and reasoning; (c) no requirement for diverse background knowledge and explanation of decision process; (d) high tolerance for errors and no requirement for provably correct or optimal solutions. |
| Inherent limitations | Unable to (a) achieve reasoning; (b) incorporate physics constraints in the framework of machine learning. |
| Deep learning features | (a) Input data based on multi-step learning process; (b) Advanced neural network; (c) Able to discover new patterns, requires a new mindset, and can potentially distinguish between causation and correlation; (d) Does not work well for problems with limited data and data with complex hierarchical structures, no mechanism for learning abstractions. |
| Specialized methods | (1) Flexible regression method (artificial neural network and Gaussian process regression) for static and low-dimension systems; (2) Principal component analysis, autoencoder, and convolutional neural network methods for high-dimension systems; (3) Hyperparameter-tuning approach for optimization and model accuracy; (4) Linear-star-space system identification method and recurrent neural networks for identifying models. |
| Desired tools | Combining physics knowledge with human analysis and deep learning algorithms. |
| Required for AI | Cognitive computing algorithms that enable the extraction of information from unstructured data by sorting concepts and relationships into a knowledge base. |
| ICF systems | Limited data, requiring a long chain of logical, multi-scale, and multi-dimensional physics; sensitivity to small perturbations; low-error tolerance level. |
| Required ML | Physics-informed and human analysis incorporated into deep learning and transfer learning algorithms. |
| Suitable problems | (1) Study of sensitivity of outputs to design parameters; (2) Integration of simulations and experimental data into a common framework; (3) Exploration of general correlations among the variables buried in the experimental data and between the measured and simulated data; (4) Optimization of implosion symmetry, pusher mass/thickness/materials, and laser-pulse shape; (5) Advanced neutron image analysis and reconstruction. |
| Successful examples | (a) NIF high-yield Hybrid E series ignition target design and optimization guided by the LLNL transfer learning model; (b) OMEGA trip-alpha experiment driven by combining machine learning with human analysis and physics knowledge. |
| Future plans | (1) Optimizing energy-coupling coefficients; designing parameter space of implosion (symmetry, pusher mass/thickness/materials, and laser-pulse shape); (2) Minimizing hydrodynamic instabilities using optimized spectrum of perturbations; (3) Quantifying uncertainties for both methods and experimental data; (4) Improving 3D neutron image reconstruction using 2D projection and autocoded features; (5) Combining physics knowledge, human analysis, data, and deep learning algorithms in each step of a design. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Bradley, P.A. What Machine Learning Can and Cannot Do for Inertial Confinement Fusion. Plasma 2023, 6, 334-344. https://doi.org/10.3390/plasma6020023
Cheng B, Bradley PA. What Machine Learning Can and Cannot Do for Inertial Confinement Fusion. Plasma. 2023; 6(2):334-344. https://doi.org/10.3390/plasma6020023
Chicago/Turabian StyleCheng, Baolian, and Paul A. Bradley. 2023. "What Machine Learning Can and Cannot Do for Inertial Confinement Fusion" Plasma 6, no. 2: 334-344. https://doi.org/10.3390/plasma6020023
APA StyleCheng, B., & Bradley, P. A. (2023). What Machine Learning Can and Cannot Do for Inertial Confinement Fusion. Plasma, 6(2), 334-344. https://doi.org/10.3390/plasma6020023






