Abstract
Concepts of dynamic oscillations of positive and negative ions to enhance fusion reactions are examined in this paper. Collective oscillations of positive and negative ions produce large oscillating electrostatic fields and could provide a significant reduction of the Coulomb potential barrier between the two interacting species (such as hydrogen anion H− and B+ in the hydrogen-boron fusion reaction). The negative hydrogen ions can be produced by populating low-temperature electrons around the neutral hydrogen atoms in a rotation chamber. The existence of H− ensures the stability of the plasma and the effectiveness of fusion interactions between H− and B+. In this paper, theoretical analyses of such oscillations systems will be presented and the conditions for fusion enhancement are discussed.
1. Introduction
The main problem of achieving efficient fusion reactions is the issue of bringing two participating species, usually two ions, close enough to each other such that the probability of tunneling through the Coulomb barrier is greatly enhanced. For thermal nuclear fusion, this is generally achieved through heating up the ions to hundreds of millions of degrees so that they collide with each other at an energy in the range of tens or hundreds of keV [1,2]. This is easier said than done, since the ions at such energy are extremely difficult to confine. The other method is to accelerate the ions to tens of keV and direct the beam at the target ions to induce the fusion reactions [3]. This technique makes it easier to control the ions. However, it suffers from the low beam density and the low efficiency since most of the beam energy will be lost and ions cannot be reused. To overcome this drawback, we propose a dynamic concept of fusion interactions between anions and cations instead of cations with cations. In particular, the anions and the cations are brought together to oscillate with each other. Due to the overall neutrality of charges, the oscillations are more stable than a single-component plasma. The oscillations also mean that anions and cations, both traveling back and forth out of phase, will meet with each other repeatedly, which increases the probability of fusion reactions. In Section 2, the analytical method of calculating the potential reduction for general fusion enhancement is described; together in the same section the coaxial chamber set-up for creating plasma rotations and generating negative ions is also described. In Section 3 the results of plasma oscillations involving opposite-charge species and how the process benefits the fusion reactions are presented. In Section 4 side effects of our concept are discussed. In Section 5 our conclusions are presented.
2. Methods
2.1. Effects of Electric Potential on Fusion Cross Section
One of the key factors in calculating fusion reaction rates is the cross section, which is usually exceedingly small at low energy due to the extremely low penetration factor through the Coulomb barrier around the nucleus. The tunneling through the Coulomb barrier is purely a quantum mechanical phenomenon and can be described by the Coulomb scattering process based on the Schrodinger equation,
Here is the Coulomb potential between particles of charges and . Equation (1) can be solved for the Coulomb wave function around the nucleus [4]. Since the nuclear radius (~10−15 m) is much smaller than the Coulomb radius (~10−10 m), the penetration probability P is related closely to the wave function near r = 0 and obtained as,
where α = e2/ℏc is the fine structure constant, v is the particle velocity, and c is the light velocity in vacuum. The Sommerfeld constant η can be expressed in terms of the particle energy E [5],
where EG is the Gamow energy equivalent to the Coulomb potential at the Bohr nuclear radius. EG is proportional to the nuclear charges squared, making it much more difficult to get fusion going between high-Z nuclei. Since the reaction rate is proportional to the penetration factor, the fusion cross section is customarily written as [5]
where S(E) is the astrophysical factor, which represents the probability of nuclear reaction after penetration. Usually, S(E) has a weak dependence on E and can be expanded in power of and the coefficients of expansion are determined from experiments.
When the penetration probability is small, the fusion cross section can also be calculated from the WKB method. Under this approximation, the barrier penetration factor P can be found as
where the integral covers the radial range where the argument of the square root is positive (i.e., E < (r)). For unscreened Coulomb potential, , the integral can be carried out exactly and
and is the peak potential barrier. In the case of small E, is negligible and
Here P has the same exponential dependence on energy E as given in (2) when E is much smaller than EG (generally valid for most cases).
If an external negative potential is created besides the positive Coulomb potential, the height and width of the overall Coulomb barrier to be penetrated will become smaller. Usually, this external potential comes from the electrons around the nuclei and typically has a characteristic distance longer than the separation between nuclei. As shown below this property is of great importance to quantum tunneling and therefore to fusion. Generally, it can be considered that the Coulomb potential is reduced by a constant value, , referred to as the screening energy. Including this screening effect, the Schrodinger equation becomes
Equation (8) is identical to (1) if E in (1) is replaced with (E +). As a result, we can use the same formula as in (2) and obtain the penetration probability with screening effects as
The screened cross section, such as (4), can be written as
The screening energy can thus affect the fusion cross section, especially when it is close to or higher than the particle energy. Figure 1 shows the cross sections for p-11B reaction using (10) along with p-B Gamow energy EG = 2.29 MeV and the following empirical astrophysical cross section factor [6] with screening energy up to = 45 keV,
where S(E) is in MeV-barn and E in MeV.
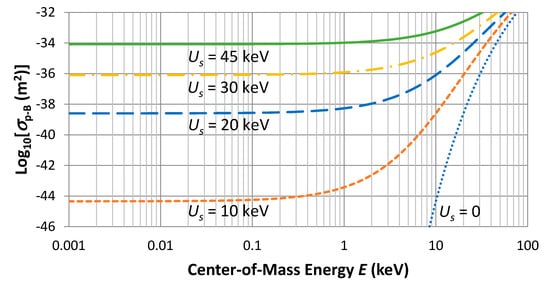
Figure 1.
p-11B cross section as function of particle energy for the screening electron densities up to = 45 keV. The cross section below E = 1 keV grows over 10 orders of magnitude (from 10−44 to 10−34 m2) when increases from 10 to 45 keV.
Without screening ( = 0), the cross sections drop quickly when the particle energy goes below a few tens of keV. With the screening effect, the cross sections turn nearly flat below 1 keV of E since the screening energy dominates over the particle energy in this region. It shows that the cross section rises very quickly with the screening energy (from 10−44 m2 to ~10−34 m2 as increases from 10 to 45 keV). In Section 3, we will show how to create an environment for fusion enhancement with high screening energies from plasma oscillations.
2.2. Plasma Rotation and Negative Ions
The rotation chamber consists of two coaxial cylinders with a positively biased center electrode and a grounded outer wall (Figure 2). An axial magnetic field is imposed along the cylinder coupled with a radial electric field produced by the positively biased center electrode. The ExB field between the two cylinders will act on any charged particles and drive them in the counterclockwise direction. The charge particles will collide with the neutrals and bring them along in the circular motion [7]. The rotation will push all particles toward the wall due to the centrifugal force; each species has a density profile that depends on its mass and temperature.
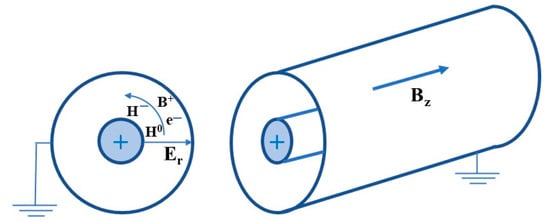
Figure 2.
Rotation chamber configuration with coaxial cylinders and axial magnetic field Bz. With outer wall grounded, the positively biased center electrode produces a radial electric field Er. The ExB forces drive the positive and negative ions and the electrons in a counterclockwise motion. The plasma oscillations of H− and B+ occur in the gap between two cylinders.
At low temperatures (<0.75 eV) in the rotating frame, electrons readily attach to hydrogen atoms and create negative ions H− [8]. The coexistence of negative and positive ions produces a much stabler plasma system compared to the electron-ion plasma [9]. In contrast to the muon-catalyzed fusion [10,11], where the fusion enhancement is due to the field created by each individual muon, the plasma oscillations can benefit the fusion process through collective effect of ion motions; like and unlike charges can bunch together every half cycle. Higher ion densities drive up the number of fusion events. The effect of the plasma oscillations on the screening process will be quantified in the next section.
3. Results
As shown in Figure 1, the screening energy Us needs approximately ten or more keV to achieve a significant fusion cross section so that sufficient fusion events occur for practical application. Therefore, the electrostatic fields generated by the collective oscillations should be high enough to provide such barrier reduction between the two reactants. For plasma oscillations in a two-component system, the dynamics of the positive charge sheet (p) and the negative charge sheet (n) can be described by the following 1-D Equation (12) [12].
Continuity equations:
Momentum equations:
Poisson’s equation
Here and are the fluxes of positive and negative ions. It is most likely that two plasmas of opposite charges will oscillate out of phase. One of the most interesting solutions here is the oscillation modes in standing waves. In the small amplitude approximation, the modes can be written as
Here k is the oscillation wave number, ω is the oscillation frequency, is the average density, and is the amplitude of the density oscillation. The electrostatic field generated by the density oscillation and the associated potential can be found from the Poisson’s equation.
Here and are the oscillation amplitudes of the electric field and potential, n1 = (np1+nn1) is the sum of the density oscillation amplitudes, and is the plasma frequency. The potential is chosen such that the value is zero when x = t = 0 or the density of positive ions is at its peak. Using , we have the values of and as
Here Λ = 2π/k is the wavelength of the plasma oscillation. For some typical parameters, = 1022 m−3 and Λ = 50 μm, the oscillation amplitudes of field and potential energy are found to be around and . The fluxes can also be derived from (12–13) and (18–19) as
Here the fluxes have difference sign since they are traveling in opposite directions. Considering the energy of the ions is negligible comparing to the screening energy ( = −eV >> E), we have the time- and space-dependent reaction rate per unit volume as
Here, S is the astrophysical cross section factor of the nuclear reaction. Since is small compared to , Equation (26) can be safely simplified as
Using (29), it is possible to calculate the reaction rate at any location and time. It is interesting to note that the reaction rate is zero whenever = = nπ, since the density fluctuations are stationary (fluxes are zero) at these locations and times. The corresponding screening energy in (28) thus varies between the value 0 and 2= 23 keV. The average reaction rate per unit volume can be obtained by averaging (30) over x and t.
Using the values of EG = 2.29 MeV, S = 195 MeV-barn (for the p-B reaction) and = 11.5 keV, the average cross section over x and t can be calculated to be about 0.7 pico-barn
For = 1023 m−3, the plasma frequency is . Using this value and (32) in (31), we obtain the average fusion reaction rate per unit volume as
In our gaseous experiment, it is expected the plasma oscillations will occur in the region near the outer wall. The volume of a table-top plasma region should be in the order of one cubic centimeter. Therefore, the reaction rate is expected to be in a few tens of thousands per second. Of course, this rate will change with the fusion parameters, such as plasma densities, oscillation amplitudes, and wavelengths.
4. Discussion
Conceptually we have found that the high-frequency oscillations are compatible with fusion events which take place in space-time of 10′s femto-seconds and femto-meters. However, these electric fields are not optimal for ionization which requires temporal and spatial scales of 10′s nano-seconds and nano-meters. The ionization of atoms and molecules depends on the amplitude and frequency of the exciting electric field. The velocity of the ionizing electron is proportional to eEτ/m where τ is either the period of the oscillation or the mean free time between collisions (whichever is smaller). We have chosen high densities of 1026/m3 for neutrals and 1023/m3 for ions in order to have high-frequency oscillations. The amplitude of velocity oscillations is only 10% since what is important is the collective behavior by many ions together. The Poisson equation governing the electric field depends on only the coherent motion of many ions and not on their temperature. Therefore, we can be judicious in the choice of plasma parameters to focus on increasing the fusion output.
Secondly the temperatures of all atoms, ions, and electrons in our rotating system are the same since they are all in thermal contact with the heated (1900 °K) “bulky” outer electrode. Multiple emitters of electrons formed from LaB6 (Lanthanum Hexaboride) maintain a significant (1023/m3) population of negative charges of electron and negative ions. Our thesis of providing negative charges to lower the Coulomb barrier comes from these hot surfaces which are also cooled by circulating water lines to a desired temperature below the melting point of metal. As a result, the high-frequency oscillating electric fields, or their recombination, will not affect the average temperature of this outer structure. While MeV fusion particles produced in this region do impart energy to this outer electrode, the heat is carried out by designed water circuits and contributes to the overall output of this fusion system. The consequence of maintaining low temperatures below 0.75 eV is the production of negative hydrogen ions by electron attachment to atomic hydrogen. This is an exothermic process.
5. Conclusions
A concept involving plasma oscillations of two opposite-charge species has been explored. It takes the advantage of stable negative and positive ion systems which produce fast oscillations of low damping [9]. The high electric fields and associated high potentials generated by oscillating high-density plasmas produce the needed screening energy for the enhancement of fusion reactions. Since the fusion reactants are also the oscillating media, the cycling motion of the ions ensures their interactions are repeated at high frequencies, resulting in higher efficiency of the overall process.
Although the examples given in this paper are based on the proton Boron reaction, the concepts can also be applied to other nuclear fusion reactions, such as D-D, 3He-3He, and p-7Li. Experiments based on these concepts have been conducted in the lab and the effects of fusion enhancement have been observed. Some of the experimental and computational results which motivated the present theoretical concept have been reported in papers [13,14,15]. A more complete summary will be forth coming.
Author Contributions
Conceptualization, A.Y.W. and C.-C.S.; formal analysis, A.Y.W. and C.-C.S.; funding acquisition, A.Y.W.; investigation, A.Y.W. and C.-C.S.; methodology, A.Y.W. and C.-C.S.; visualization, A.Y.W. and C.-C.S.; writing—original draft, A.Y.W. and C.-C.S.; writing—review and editing, A.Y.W. and C.-C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was fully funded by private individual investors and venture capital firm. No other external funding was received. The APC was waived by Plasma.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
This study did not report any data.
Acknowledgments
We wish to acknowledge discussion with Mason Guffey and Allan Chen on the experimental verification of this concept. We thank Belinda Mei for her help in editing this manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Lawson, J.D. Some criteria for a power producing thermonuclear reactor. Proc. Phys. Soc. Sect. B 1956, 70, 6–10. [Google Scholar] [CrossRef]
- Glasstone, S. Controlled Nuclear Fusion; US Atomic Energy Commission: Washington, DC, USA, 1974. [Google Scholar]
- Labaune, C.; Baccou, C.; Depierreux, S.; Goyon, C.; Loisel, G.; Yahia, V.; Rafelski, J. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat. Commun. 2013, 4, 2506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schiff, L.I. Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1968; Section 21. [Google Scholar]
- Ichimaru, S.; Kitamura, H. Pycnonuclear reactions in dense astrophysical and fusion plasmas. Phys. Plasmas 1999, 6, 2649. [Google Scholar] [CrossRef]
- Becker, H.W.; Rolfs, C.; Trautvetter, H.P. Low-Energy Cross Sections for 11B(p, 3α). Z. Phys. 1987, A 327, 341. [Google Scholar]
- Lee, K.H.; Lee, L.C.; Wong, A.Y. Acceleration of ions and neutrals by a traveling electrostatic wave. Phys. Plasmas 2018, 25, 023113. [Google Scholar] [CrossRef]
- Rau, A.R.P. The negative ion of hydrogen. J. Astrophys. Astron. 1996, 17, 113. [Google Scholar] [CrossRef]
- Wong, A.Y.; Mamas, D.L.; Arnush, D. Negative ion plasmas. Phys. Fluids 1975, 18, 1489. [Google Scholar] [CrossRef]
- Alvarez, L.W.; Bradner, H.; Crawford, F.S.; Crawford, J.A.; Falk-Vairant, P.; Good, M.L.; Gow, J.D.; Rosenfeld, A.H.; Solmitz, F.; Stevenson, M.L.; et al. Catalysis of nuclear reactions by µ mesons. Phys. Rev. 1957, 105, 1127. [Google Scholar] [CrossRef]
- Jackson, J.D. Catalysis of nuclear reactions between hydrogen isotopes by µ-mesons. Phys. Rev. 1957, 106, 330. [Google Scholar] [CrossRef]
- Stix, T.H. The Theory of Plasma Waves; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Wong, A.Y.; Shih, C.C. Approach to Nuclear Fusion Utilizing Dynamics of High-Density Electrons and Neutrals. arXiv 2019, arXiv:1908.11068. [Google Scholar]
- Wong, A.Y.; Gunn, A.; Chen, A.X.; Shih, C.C.; Guffey, M.J. Enhanced D-D Fusion Rates when the Coulomb Barrier Is Lowered by Electrons. arXiv 2021, arXiv:2106.12988. [Google Scholar]
- Guffey, M.J.; Wong, A.Y. Ponderomotive Screening of Nuclear Fusion Reactions Based on Localized Surface Plasmon Resonance. arXiv 2020, arXiv:2106.08127. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).