Abstract
In hot plasmas, such as the ones encountered in astrophysics or laser-fusion studies, the number of ionic excited states may become huge, and the relevant electron configurations cannot always be handled individually. The Super Transition Array approach enables one to calculate the massic photo-absorption cross-section (or radiative opacity) in a statistical manner consisting of grouping configurations close in energy into superconfigurations. One of the main issues of the method, beyond its spectral resolution, is the determination of the most relevant configurations that contribute to opacity. In this work, we discuss different aspects of the generation of superconfigurations in a hot plasma and propose a new adaptive algorithm.
1. Introduction
The radiative opacity is an essential quantity governing the structure and evolution of stars. In plasmas of medium to high-Z elements, some of the electrons remain bound to the ions even at very high temperature (this is for instance the case of iron in the center of the sun). Among the different contributions to opacity of plasmas at local thermodynamic equilibrium (LTE), the photo-excitation process (also called sometimes “line absorption” or bound–bound opacity), consisting of transitions between electronic states of the ions, is of particular importance.
The methods for the evaluation of the line absorption coefficient, in hot dense plasmas, even in non-LTE conditions, involve a compromise between the needed spectral resolution and the available computer resources. At one extremity one finds the uncompromising method of detailed line accounting (DLA), yielding a highly resolved (or detailed) spectrum, including all photo-absorption lines of all configuration-to-configuration transition arrays. For complex configurations, the numerical cost resulting from the huge number of transitions becomes prohibitive. In this case, one may turn to the unresolved transition arrays (UTA) method [1], which assumes that all lines in the spectrum of each configuration-to-configuration excitation merge into a single effective (super-) line, which can be depicted by a Gaussian function. The efficiency of the UTA method comes from the fact that compact formulas are available for the three lowest energy moments (orders 0, 1 and 2) of the line-strength weighted line energies of a transition array. Such moments are expressed in terms of reduced matrix elements of the dipole operator, Slater integrals, and subshell occupation numbers. The effect of higher-order moments was also investigated, using more sophisticated distributions [2,3]. Sometimes, the number of configurations is so high that the UTA approach and its relativistic counterpart the SOSA (Spin-Orbit Split Array) approach [4] are not tractable. For that reason, Bar-Shalom et al. developed the STA model, consisting of grouping the large number transition lines between an enormous number of configurations into large assemblies, called Super Transition Arrays (STAs) [5]. The STA moments are calculated analytically using a canonical partition function algebra, and can be split into smaller STAs until convergence (of the Rosseland mean for instance) is achieved.
The method was implemented in the SCO code, and combined to DLA calculations in the SCO-RCG code [6,7,8,9], which is used to interpret high-resolution spectra (see for instance Ref. [10]). The SCO code was developed in two versions, the first one in the Local Density Approximation [11], the second one in the statistical Hartree–Fock theory [12,13,14].
The STA approach was successfully applied to the interpretation of photo-absorption spectra [9,15,16,17,18,19,20], to solar physics [21,22,23,24] and equation of state [25,26,27,28,29,30,31,32,33]. The plasma modeling was extended to mixtures [29,34]. Much work was done on the optimization of the canonical partition functions, in the independent-particle approximation [35,36,37,38,39,40,41], and for a better inclusion of electron-electron interactions [42,43] in the Gibbs-Bogolyubov or Jensen-Feynman approach.
The STA formalism was recently improved by Kurzweil and Hazak within the framework of the CRSTA (Configurationally Resolved Super Transition Array) model [44,45,46], which enables one to refine the STAs to reveal the underlying structure. The basic idea is an adaptation of the Liouville evolution operator technique to the photo-absorption spectra.
Whatever the variant of the method that we consider, the choice of the superconfigurations that must be included in the calculation is an important issue. In order to obtain converged Rosseland mean opacities, the best completeness as possible has to be ensured. This is a difficult point because each opacity code has its own balance between accuracy (trying to use the most accurate models as possible), and completeness (including as many excited states as possible [7,47]). Since it is not realistic to calculate a full-range opacity spectrum for a trial list of superconfigurations, and then add a superconfiguration and calculate the spectrum again, etc. until convergence of the latter, one has to be predictive. In the present work, we discuss different ways of generating superconfigurations at a given temperature and plasma density, and propose in particular an adaptive “divide and conquer” algorithm.
The estimate of configuration probabilities, based on the average-atom model and/or involving correlated or uncorrelated binomial distributions, are presented in Section 2. The superconfiguration approach is described in Section 3 and the way the superconfigurations can be populated by electrons is described in Section 4. Our adaptive algorithm is presented in Section 5, and results are analyzed in Section 6. Finally, two alternative methods are briefly mentioned and discussed in Section 7—a first one consisting of generating superconfiguration using the correlated Gaussian approximation for configurations and the algorithm used in the SCROLL model—emphasizing the novelty of our approach.
2. Estimating Configuration Probabilities
2.1. Configuration Probabilities Based on the Average-Atom Model
The real ions in the plasma are in various multi-electron configurations, each one corresponding to a specific set of integer occupation numbers in the bound subshells. Starting from the average-atom picture, it is possible to build a law for the abundance of such ionic species, assuming that
- The configurations are statistically independent,
- A configuration C is entirely defined by the integer occupation numbers in each subshell i, .
- The total energy of C in terms of the occupation numbers can be expressed using quantities provided by the average-atom calculation.
In the grand canonical ensemble, knowing the form of the configuration energy with , ( is the degeneracy of subshell i), the probability law of the configurations reads:
where is the partition function and the chemical potential; we also set , where denotes Boltzmann’s constant and T the temperature. represents the usual binomial coefficient. The direct summation over all the configurations can become intractable when the number of subshells increases, in particular for large atomic numbers. It is, therefore, essential to make approximations to perform such summations. The energy can be formulated as a quadratic form of the subshell occupation numbers:
with the deviation of the integer with respect to its average-atom average value , where denotes the Fermi-Dirac factor:
The quantity is an interaction matrix element including the dominant Coulomb interaction between states i and j and an exchange-correlation contribution [48]. All the quantities entering Equation (2), except the occupation numbers , are given by the average-atom calculation.
The modeling of occupation-number fluctuations in a hot plasma, based on average-atom results and determination of correlations, has a long history [49,50,51,52,53]. An interesting approach consists of handling the sums over all configurations at once [48,54]. It allows one to calculate the statistical properties of a whole transition array representing a mono-electronic jump. The determination of such statistical properties relies on knowing the correlations between the subshell occupation numbers. In this method, the Gaussian approximation to the binomial coefficients of the configuration degeneracy
is used to gather the binomial coefficients and the Boltzmann factor in a single exponential. Using elementary matrix algebra on the argument of this exponential, the problem of finding the correlations reduces to the inversion of a matrix. This boils down to expressions of the configuration free energy, which are quadratic forms of the occupation numbers.
2.1.1. Uncorrelated Probability Law
The simplest possible approximation amounts to neglect the interaction terms in the energy. The consequence is that the probability reduces to a product of independent binomial laws, which presents the following advantages:
- The average occupation number of each subshell is a direct result of the average-atom calculation,
- The probability can be factorized shell by shell, making the calculation of averages simple. For instance, the variance of the total number of bound electrons is
2.1.2. Correlated Probability Law: Integral Transformation and High Temperature Limit
To deal with the statistical mechanics of systems associated with the quadratic energy in Equation (2), a clever method was proposed, making use of an integral transformation [55,56]. The quadratic term in the Boltzmann factor in Equation (1) is replaced with a linear one, at the cost of a multiple integration over auxiliary variables , . The consequence is that the Boltzmann factor has the same form as in the uncorrelated case, and the probability can be written as a product of factors, each one corresponding to one subshell. However, the method can thus be useful if the multiple integral is easily approximated, but reaches its numerical limits when accurate results are needed. Green proposed a treatment of the interacting system applicable to high temperatures when [57,58], consisting of computing the correlation factors up to second order in . The technique, rather cumbersome to implement, can lead to serious practical issues since the accuracy of the obtained expressions decreases as the electron correlations increase. If the temperature is too low, the occupation-number variances can even become negative, which of course makes the method inapplicable.
2.1.3. Correlated Gaussian Approximations
The correlated Gaussian approximations avoid the difficulties of the previous approaches. They treat the occupation-number deviations as continuous variables, which is equivalent to replace the binomial law by its Gaussian continuous limit, an approximation justified when the degeneracies of the electron subshells are large and if the number of electrons in a subshell is neither too close to zero nor to its degeneracy (in virtue of the central-limit theorem [59]). In that case, the probability law of Equation (1) becomes
where is the vector with components and the correlation matrix. The elements of the positive definite matrix are [48,56]:
and its eigenvalues are noted . Equation (7) becomes
where is defined as , being the unitary transformation diagonalizing . The equivalent of Equation (5) then reads
The correlated Gaussian approximation described above is very easy to implement. Its results are in excellent agreement with the exact calculation. For instance, in the case of a plasma at an electronic temperature = 100 eV and solid density, Wilson found that it is accurate to better than 1% [55]. We confirmed such an estimate, and found that in most usual situations encountered in laser-fusion experiments or stellar physics, the accuracy is usually of the order of a few percent. The method can be improved by combining the discrete variation of integer occupation numbers in a small number of subshells (the active ones and spectator subshells strongly coupled to them) and the continuous variation of occupation numbers in the other (spectator) subshells.
3. The Superconfiguration Method
3.1. Subshells, Configurations
Let us consider the ensemble of potential bound subshells for electronic configurations of ions in LTE conditions. The occupation numbers of the subshells satisfy and . We define
the ionization corresponding to that configuration.
3.2. Supershells, Superconfigurations
Let be a partition of the ensemble of bound states into supershells:
with , , , , . A supershell gathers an ensemble of subshells satisfying a given criterion. For instance, two subshells i and j belong to the same supershell if their energies are sufficiently (to be precisely defined) close: if and , where and are the energies of subshells i and j, and is the “width” (in reduced energy, i.e., energy divided by or multiplied by ) of the supershell of median energy .
A superconfiguration is defined by a set of integer occupation numbers of the supershells. The occupation numbers satisfy , where represents the degeneracy of supershell and
We write
the ionization corresponding to that superconfiguration .
A superconfiguration is then an ensemble of configurations that are close in energy. In practice, a good choice is to group configurations C with energies differing by less than . The superconfigurations are made of supershells containing several ordinary shells. The total occupation number of each supershell is fixed. For instance
is a superconfiguration for which the first three supershells coincide with the normal lowest shells while each one of the others contains three shells supposed to be close in energy. The choice of the shells to group in a supershell is done on the basis of the average-atom eigenvalues. In each supershell of , the total number of electrons is fixed. For instance, contains 20 configurations, corresponding to the number of possibilities to distribute seven electrons in subshells , and , i.e.,
and micro-states. The total number of configurations represented by the superconfiguration in Equation (15) is 3960 and the total number of micro-states 3,427,826,688!
3.3. Linearization of the Energy of a Superconfiguration
In Section 2, the energy of any configuration of the plasma was written as a quadratic form of the occupation numbers, its coefficients being obtained from a single self-consistent average-atom calculation. The difficulty relied on the statistical description of the system, while the electronic structure was obtained at a low numerical cost. The superconfiguration method relies on another choice: instead of keeping a unique quadratic expression for the total energy of any configuration, it uses several linear expressions, each one being valid for a superconfiguration (an ensemble of configurations), for which the electronic structure is computed independently. With this assumption, the statistical mechanics of the problem is simpler, thanks to the partition function algebra, but calculating the electronic structure becomes much more expensive, especially if a self-consistent calculation (similar to the average-atom one but with integer occupation numbers) is performed for each superconfiguration. An advantage of the method is that the refinement of the electronic structure description also improves the accuracy of the spectral opacity.
3.4. Number of Configurations, Weight of a Superconfiguration
A superconfiguration gathers all the possible configurations . The total number of micro-states (i.e., nondegenerate ion states), noted , satisfies, for each supershell (and using Vandermonde identity for the second equality):
where represents the list of degeneracies of the subshells belonging to the supershell . Therefore, the total number of micro-states in that superconfiguration is equal to
The probability that a superconfiguration takes into account the thermodynamics at LTE can be expressed through the Boltzmann factors of the subshells. Its statistical weight is proportional to the quantity
where the partition functions are defined by the relation
The number of configurations contained in , where contains subshells of respective degeneracies , , …, , is (see Ref. [60]):
Let us consider the case where is made of orbitals with the same degeneracy and orbitals with the same degeneracy , with . For instance correspond to = 6, = 10, = 3, = 2 and N = 10. One has
If we generalize and gather the subshells of degeneracy , the subshells of degeneracy , …, the subshells of degeneracy (with therefore ) [60], we obtain
The latter Formulas (21)–(23) show that it is possible to resort to an explicit formula for the number of configurations, avoiding the multiple nested summations (see Equation (16)) which become numerically costly for a large number of supershells containing many subshells. The most efficient way to compute the number of configurations consists of resorting to recurrence relations (see for instance Ref. [60]). Although the combinatoric number of configurations can be huge even for mid-Z elements, the number of configurations which have non-negligible occupation numbers is much lower and depends on temperature and density. Krief recently published two useful methods for the estimation of the number of populated configurations: the first one relies on an exact calculation of the total combinatoric number of configurations within superconfigurations in a converged STA calculation, and the second one involves an estimate for the multidimensional width of the probability distribution for electronic occupation number over bound subshells [61]. The latter work presents a detailed discussion about the effects of temperature and density on the number of populated configurations.
3.5. Number of Superconfigurations Associated with a Partition
For a given partition in fixed supershells, the number of possible superconfigurations is
4. Populating a Partition in Superconfigurations from the Average-Atom Results
For a fixed partition , we estimate from the average-atom results, obtained a priori. We assume that the ensemble of possible subshells for any configuration is included in the average-atom one. The average-atom calculation consists of a self-consistent computation of the energies of the subshells , the average (fractional) occupation numbers of the subshells and their associated variances and the chemical potential , connected to each other by the relations
where depends only on and (see Equation (3)).
4.1. Calculation of
For each subshell of the partition , we define, for the average atom, the degeneracy, the average occupation number and the variance, by summing over the subshells it contains:
We try to generate the possible (integer) occupation numbers under the constraints and . Since the superconfigurations to generate are at local thermodynamic equilibrium, one can restricts the first constraint to an interval around the average occupation number of the average atom, characterized by an integer number of standard deviations :
In practice, one defines
where is the total number of ways to choose integer satisfying , and the total number of possible superconfigurations for the partition is
The quantity in Equation (29) represents the number of essentially populated superconfigurations, while the quantity in Equation (24) denotes the total number of superconfigurations, irrelevant to their populations. It is important to note that the number of superconfigurations accounted according to Equations (28) and (29) is excessive. If the occupation numbers of several supershells are simultaneously close to or determined from Equation (28), the populations of corresponding superconfigurations are negligible and the latter can be safely disregarded.
4.2. Estimating Statistical Weights
In each superconfiguration calculated self-consistently, the energy is accurately approximated by the linear form
is an average energy independent of the occupation numbers, and is the self-consistent one-electron energy in subshell i of . In the grand canonical ensemble, the probability law takes the form
where is an uncorrelated probability relative to a specific superconfiguration . In analogy with the ideal electron gas partition functions, Bar-Shalom et al. have derived recurrence relations for calculating analytically all the sums required in the averages needed [5]. Hole counting is used instead of electron counting in order to avoid loss of accuracy when the number of electrons is larger than half the total degeneracy of the supershell [12].
One of the limitations of the superconfiguration method is that every non-linear term in the configuration free energy has to be averaged over all configurations belonging to the same superconfiguration. Another limitation is that depending on the supershells that are considered, the superconfiguration set resulting from that choice can still be large.
The superconfigurations are generated by covering all the possible partitions of electrons in the supershells. For each superconfiguration , its statistical weight is estimated using
where
is the partition function for the set of occupation numbers of that superconfiguration. is an estimate of the free energy of that superconfiguration. A rigorous calculation of the statistical weight implies a self-consistent computation of the electronic structure of each superconfiguration, what we precisely wish to avoid at this stage. It is satisfactory to take an estimate of the statistical weight making the following assumptions:
- In the calculation of the statistical sum , the one-electron energies (and subsequently the Boltzmann factors ) are approximated by the ones of the average atom.
- The free energy of the superconfiguration is estimated by the relation , being its ionization and the average-atom chemical potential.
The superconfigurations are then sorted by decreasing weights. Finally, the list can be truncated by eliminating the superconfigurations with a weak weight, either using a criterion based on a maximum number, or on a minimum weight.
5. Adaptive Algorithm
5.1. Algorithm “Divide and Conquer”
We are looking for a partition of the ensemble of bound states in supershells, providing a compromise between constraints on the energies of the subshells of the kind: , for while generating a reasonable number of superconfigurations. We are looking for such as be minimum under the constraint , where is the maximum number that we do not want to override. For a fixed partition , let us define
where are the energies of the average-atom model. For a fixed value of , we try to find a partition such that
For , we have therefore . It is worth mentioning that the condition
is equivalent, at first order, to . We set two mechanisms:
- A procedure consisting of splitting (“Split”) of a supershell into two supershells and :Such a mechanism will be activated if (unverified energy criterion). Its effect is to reduce the energy differences, but it increases by one the size of the partition. The number of superconfigurations to generate is multiplied by
- A concatenation (gathering) mechanism of consecutive and supershells (“Merge”)Such a mechanism will be activated if . Its effect is to reduce by one the size of the partition and the number of superconfigurations to generate is divided by the factor (38), but increases the energy differences inside the resulting supershell:
5.2. Algorithm “Divide and Conquer”: General Procedure
- Phase 1: gathering the supershells. As far as the number of superconfigurations to generate is larger than an imposed maximal value , we try to reduce the number of supershells of the partition. More precisely, we look for two consecutive supershells such that the energy dispersion (spread) be minimal, i.e.,If , we gather the states of these two supershells into a unique supershell , with characteristicsorOtherwise, end of phase 1.
- Phase 2: splitting the supershells. As far as there are supershells such that , and that the number of supershells remains smaller than an imposed maximum value , we look for the supershell such that the energy dispersion be maximum:The supershell is then split into two supershells, each one containing half of the states.
- Phase 3: relaxation of criterion: . This phase is necessary if there is no partition of the subshells that ensures several superconfigurations (but less than the critical value ).
5.3. Energy Criterion
It is possible to define an alternative criterion to replace Equation (35). The partition function reads
Linearizing
we obtain
which can be put in the form
where represents the number of micro-states introduced in Equation (17):
Applying the relation
one can write
yielding
or
leading itself to
The condition becomes therefore
Such a formulation is interesting since it provides an insight into the way the partition function is involved in the criterion. It is also of practical interest, since is arbitrary and can therefore help avoiding numerical problems. Finally, on the contrary to Equation (35), the subshells have to be scrolled only once.
5.4. Link to the Master Theorem
The above-mentioned procedure belongs to the class of “divide and conquer” algorithms, which structure and complexity are governed by the so-called “Master theorem” [62]. Consider a problem that can be solved using a recursive algorithm which divides the problem into several sub-problems recursively, each sub-problem being of size . The master theorem always yields asymptotically tight bounds to recurrences from divide and conquer algorithms that partition an input into smaller sub-problems of equal sizes, solve the sub-problems recursively, and then combine the sub-problem solutions to give a solution to the original problem. The master theorem states that the time for such an algorithm can be expressed by adding the work that they perform at the top level of their recursion (to divide the problems into sub-problems and then combine the sub-problem solutions) together with the time made in the recursive calls of the algorithm.
If denotes the total time for the algorithm on an input of size n, and denotes the amount of time taken at the top level of the recurrence then the time can be expressed by a recurrence relation that has the form
Here n is the size of an input problem, a is the number of sub-problems in the recursion, and b is the factor by which the sub-problem size is reduced in each recursive call (). This equation can be successively substituted into itself and expanded to obtain an expression for the total amount of work done.
6. Examples and Results
Let us consider the case of an iron plasma at eV and 0.01 g/cm. Table 1 represents, for the initial value , the final supershell partition, the number of iterations, the final value of the parameter and the number of effective superconfigurations found for different values of the maximum number of superconfigurations authorized (respectively 10, 100, 500, 1000, 5000, 10,000 and 50,000), in the case where the initial value of is 0.05 (which is our usual default value). The initial supershell partition reads
yielding 28,311,552 superconfigurations.

Table 1.
Final supershell partitions, number of iterations, final value of and number of effective superconfigurations found for different maximum numbers , in the case where our initial value of has its default value 0.05. The initial number of superconfigurations, obtained with the supershell partition of Equation (57), is 28,311,552.
In the way the algorithm is computed, it is important to start with a small value of . However, if the value is too low, the number of required iterations to reach convergence will be very large. For instance, in the case of , if we start with , the initial supershell partition is
yielding 9,223,372,036,854,775,807 superconfigurations, and the final one, obtained after 1643 iterations (and a final value of of 0.79):
represents 864 superconfigurations. In the case of (as can be seen in Table 1), the initial supershell partition (given in Equation (57)), yields 28,311,552 superconfigurations and the supershell partition (59) together the subsequent 864 superconfigurations are obtained after 31 iterations (and a final value of of 0.80). In the case where , one has
yielding 1296 superconfigurations, reduced finally with partition (59) to the 864 superconfigurations after 2 iterations (and a final value of of 1). If is too big, the algorithm will stop, because the number of superconfigurations is likely to be already below the critical value . In that case, initial and final supershell partition are the same. For instance, with , one obtains
and the number of superconfigurations is 15 (the final value of being 10). The algorithm could be easily improved by introducing a threshold (minimum) value of the number of superconfigurations, or to impose the final number of superconfigurations to be sufficiently (according to a particular criterion) close to , thus allowing to decrease. Table 2 contains the Rosseland and Planck means obtained with the different maximum numbers of superconfigurations asked (see Table 1) and Figure 1 shows the corresponding spectral opacities. Of course, the spectrum is not sufficiently resolved for = 10, but the purpose of our algorithm is to provide the best “sampling” of superconfigurations as possible for a specific maximum authorized number of superconfigurations (and therefore a maximum authorized computation time). We can see that in that case, the convergence as concerns the Planck and Rosseland mean is achieved for 5000 superconfigurations, but that acceptable values are already obtained for 500 ones.

Table 2.
Planck and Rosseland means in the different cases displayed in Table 1. The average ionization is 15.45.
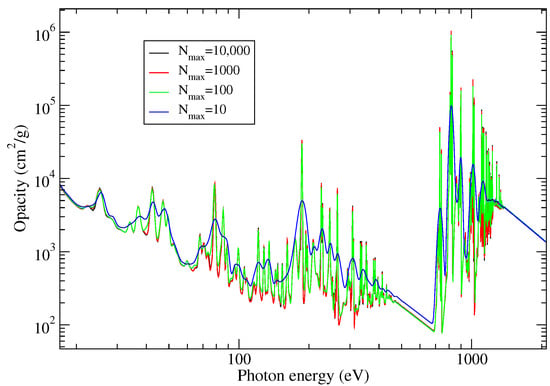
Figure 1.
Total opacity of an iron plasma at eV and g/cm computed in the different cases = 10, 100, 1000 and 10,000, which characteristics are provided in Table 1. The black ( = 10,000) and red ( = 1000) curves are almost superimposed.
Figure 2 displays a comparison between the experimental opacity deduced from an absorption-spectroscopy experiment performed on ASTERIX IV laser facility (Garching, Germany) [9,15,16] and different STA calculations, involving 3, 56, 385 and 2000 superconfigurations, respectively. The temperature is 22 eV and the density of 0.01 g/cm. The two calculations corresponding to 385 and 2000 superconfigurations are almost superimposed. Opacity measurements are of crucial importance to test the models. However, such experiments are difficult and subject to many uncertainties [63]. Moreover, they obviously concentrate on a narrow spectral range, which is not necessarily in the vicinity of the maximum of the Planck distribution or of its derivative with respect to the temperature. Therefore, a convergence criterion focusing on the spectrum in this finite range is not equivalent to a convergence of the Rosseland mean.
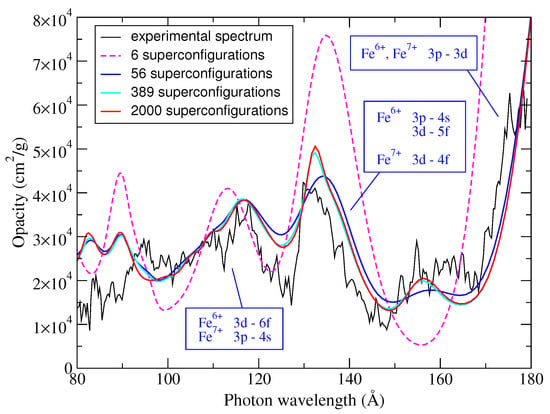
Figure 2.
Interpretation of an experimental spectrum measured on ASTERIX IV laser facility (Garching, Germany) by Winhart et al. [9,15,16]. The areal mass of the iron sample is 20 μg/cm. The best agreement was obtained at a temperature of 22 eV and a density 0.01 g/cm. The calculations have been carried out with 3, 56, 385 and 2000 superconfigurations, corresponding to 2, 3, 4 and 9 supershells respectively.
7. Other Possible Algorithms and Discussion
7.1. Generating Superconfigurations Using the Correlated Gaussian Approximation for Configurations
The following algorithm was suggested by Faussurier ([36] and private communication). The charge state distribution can be put in the form
with and [48,64,65]
The idea is to keep the ions between and , where represent the integer part of x. For each supershell, the occupation number is allowed to vary between and defined as
where
To define the supershells, one has to find the intersection point between the modeled energy distributions of the subshells i and :
and
yielding
with
The physical meaning of Equations (66) and (67) may seem questionable, since they are energy distribution and the variance and are occupation-number variances. This approximation, however, can be justified considering the continuous variation of the energy of the occupied subshell as proportional to its occupation number. If , the overlap tends to be weak and if it becomes difficult to distinguish between the two distributions and . The chain is broken in increasing order of the . Let us consider that the length of link i is . At each step, the supershell containing the largest link is cut (see Figure 3).
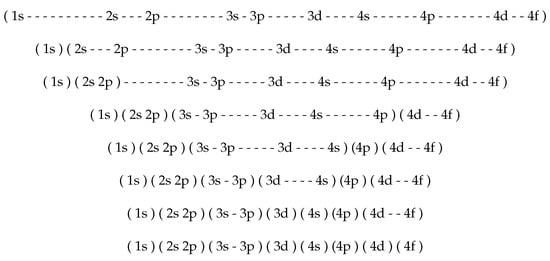
Figure 3.
Illustration of the method described in Section 7.1.
The advantage of such an approach is that the average-atom model and the fluctuation theory enable one to know a priori the order in which the supershells will be built, as well as the number of superconfigurations obtained at each step. Therefore, a proper estimate of the electronic correlations is required in order to avoid an underestimate of the energy separation between subshells and an overestimate of the number of superconfigurations. The parameter (typically between 1 and 10) must be chosen by the user. The relative population of a superconfiguration can be estimated by the product of Gaussian distributions such as the one of Equation (62) attributed to the different supershells. If the population is smaller than a given small parameter, then it can be disregarded, although it belongs to the initial set resulting from Equations (28) and (29).
7.2. The Scroll Algorithm
The following algorithm was proposed by Bar-Shalom et al. It was designed for the collisional-radiative superconfiguration code SCROLL (Super Configuration Radiative cOLLisional) [66,67,68]. The code takes into account the numerous excited and autoionizing states using superconfigurations. These are split systematically until the occupation numbers converge. The superconfigurations are refined in a stepwise manner until some convergence is reached. When the superconfiguration structure is fixed, the occupation numbers of the superconfigurations are obtained by solving the collisional-radiative-model rate equations:
where are the superconfiguration populations and are the superconfiguration transition rates, averaged over the initial configurations and summed over all final configurations . A basic initial assumption (relaxed in the course of the computation) in this model is that within a superconfiguration, the configuration occupation numbers are estimated by a Boltzmann factor. The superconfiguration-averaged rates can thus be written as
where are the configuration-to-configuration rates and the configuration partition functions. In the case of one-electron jumps, we have
where is the radial integral associated with the transition and computed with HULLAC (Hebrew University Lawrence Livermore Atomic Code) [69]. The assumption of LTE within superconfigurations is relaxed by a convergence procedure where at each step, supershells are split, giving rise to a new set of superconfigurations in Equation (70). This splitting is done in a systematic manner following a “binary tree” algorithm. The initial occupation numbers of these new superconfigurations are taken as proportional to their partition functions. All the necessary new rates are then computed. Actually, only the occupation-number factor needs to be re-evaluated, since the are taken from a pre-computed database. Then the steady state collisional-radiative-model matrix is rebuilt and solved. A sparse matrix algorithm is used, since the superconfigurations belonging to charge states differing by more than one unit are not connected. The resulting occupation numbers are then compared to the initial ones. The superconfigurations are split in this way, repeatedly, until all converge. This convergence process eliminates gradually the explicit dependence of the rates on the LTE Boltzmann factors in . In the configuration limit it disappears completely. In order to accelerate the convergence of this process, the temperature assumed for the LTE occupation numbers within the superconfiguration is not the electron temperature , but an effective ionization temperature defined by Busquet [70].
7.2.1. Effective (Ionization) Temperature
The algorithm starts with a guess for the ionization temperature . The idea behind such a concept is that the non-LTE spectrum at is very close to an LTE calculation at . For that guess, Busquet’s model can be used [70,71,72], or one can simply start with . With this temperature, an average-atom calculation is performed to obtain and an initial potential. The latter is used in a version of the HULLAC code with hydrogenic configurations [69], to obtain the orbital rates. At this point, a crude supershell structure is defined. A loop is described over pairs of superconfigurations and for each pair all the average rates are added to the rate matrix. A sparse matrix method is used to solve the rate equations for the occupation numbers (with the internal convergence iterations splitting supershells as mentioned above) and calculate .
The STA code is now run to find the temperature that produces this average charge state in LTE. At this point, one has to go back to the calculation of rates and so on until convergence [68].
7.2.2. Binary Supershell Split Algorithm
A central point in the splitting procedure is that unlike the LTE case, it is crucial to work with the minimal matrix size. This restricts the number of supershells. The authors have therefore adopted an algorithm based on a binary tree approach.
A node represents a supershell. Starting with a single node of all bound shells, one begins splitting nodes to two daughter nodes. For each node indexed by n, the left and right daughters are indexed by and , respectively. One goes down the tree splitting the left daughters while keeping all the other nodes fixed until convergence of that route. At this point, one must go back up the tree to the lowest unconverged parent node, take its right node and go down again splitting left daughters. We proceed in this way until all the nodes are locally converged with all other nodes fixed. At this point, the final supershell structure is constructed from all the converged nodes and a single splitting on each final node is performed separately to check the total convergence.
This algorithm, together with the one described in Section 7.1, proceeds in a unidirectional way (although the SCROLL models offer the possibility to go back in the tree, once a branch comes to its end it is not modified anymore, and other branches of the tree are explored). In other words, such algorithms consist of splitting supershells, but not gathering them. We do not pretend that our adaptive algorithm is more efficient that the above-mentioned ones. The most important points are that it is designed to ensure an optimal representation of atomic states for a given maximum authorized number of superconfigurations, and that its specificity is to rely on successive splitting and grouping.
8. Conclusions
We presented different algorithms for the generation of superconfigurations, which constitute the first step of an opacity calculation (for local thermodynamic equilibrium or non-local-thermodynamic-equilibrium plasmas) relying on the Super Transition Array approach. This is a critical issue of opacity calculations, which necessarily have to make a compromise between accuracy and completeness, which often turns out to be a real dilemma. It is difficult to assert without hesitation which algorithm is the best. Among the ones discussed above, the adaptive “divide and conquer” algorithm, which constitutes the main new result of the present work, is probably the most efficient one, since it provides the best sampling for a fixed maximal number of superconfigurations. However, the “ideal” algorithm would probably take into account the most important transitions in the plasmas, at the given temperature and density, i.e., the transitions which will contribute to the Rosseland mean.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy and ethical restrictions.
Acknowledgments
The author is indebted to P. Arnault, T. Blenski, C. Bowen, M. Busquet, P. Cossé, G. Dejonghe, G. Faussurier, F. Gilleron, M. Poirier and B. G. Wilson for fruitful discussions on the subject over the past 20 years. The authors would also like to thank the anonymous referees for useful suggestions and comments.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CRSTA | Configurationally Resolved Super Transition Array |
| DLA | Detailed Line Accounting |
| HULLAC | Hebrew University Lawrence Livermore Atomic Code |
| LTE | Local Thermodynamic Equilibrium |
| SCO | Superconfiguration Code for Opacity |
| SCROLL | Super Configuration Radiative cOLLisional |
| SOSA | Spin-Orbit Split Array |
| STA | Super Transition Array |
| UTA | Unresolved Transition Array |
References
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- Gilleron, F.; Pain, J.-C.; Bauche, J.; Bauche-Arnoult, C. Impact of high-order moments on the statistical modeling of transition arrays. Phys. Rev. E 2008, 77, 026708. [Google Scholar] [CrossRef] [PubMed]
- Pain, J.-C.; Gilleron, F.; Bauche, J.; Bauche-Arnoult, C. Effect of third- and fourth-order moments on the modeling of unresolved transition arrays. High Energy Density Phys. 2009, 5, 294–301. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. III. Case of spin-orbit-split arrays. Phys. Rev. A 1985, 31, 2248–2259. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Goldstein, W.H.; Shvarts, D.; Zigler, A. Super-transition-arrays: A model for the spectral analysis of hot, dense plasmas. Phys. Rev. A 1989, 40, 3183–3193. [Google Scholar] [CrossRef]
- Porcherot, Q.; Pain, J.-C.; Gilleron, F.; Blenski, T. A consistent approach for mixed detailed and statistical calculation of opacities in hot plasmas. High Energy Density Phys. 2011, 7, 234–239. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F. Accounting for highly excited states in detailed opacity calculations. High Energy Density Phys. 2015, 15, 30–42. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Blenski, T. Detailed computation of hot-plasma atomic spectra. Laser Part. Beams 2015, 33, 201–210. [Google Scholar] [CrossRef]
- Pain, J.-C. Super Transition Arrays: A Tool for Studying Spectral Properties of Hot Plasmas. Plasma 2021, 4, 42–64. [Google Scholar] [CrossRef]
- Bailey, J.; Nagayama, T.; Loisel, G.; Rochau, G.A.; Blancard, C.; Colgan, J.; Cosse, P.; Faussurier, G.; Fontes, C.J.; Gilleron, F.; et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 2015, 517, 56–59. [Google Scholar] [CrossRef]
- Blenski, T.; Grimaldi, A.; Perrot, F. A superconfiguration code based on the local density approximation. J. Quant. Spectroc. Radiat. Transf. 2000, 65, 91–100. [Google Scholar] [CrossRef]
- Blenski, T.; Grimaldi, A.; Perrot, F. A Hartree-Fock statistical approach to atoms in plasmas-electron and hole countings in evaluation of statistical sums. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 495–500. [Google Scholar] [CrossRef]
- Blenski, T.; Grimaldi, A.; Perrot, F. Hartree-Fock statistical approach to atoms and photoabsorption in plasmas. Phys. Rev. E 1997, 55, R4889–R4892. [Google Scholar] [CrossRef]
- Pain, J.-C. Koopmans’ theorem in the statistical Hartree-Fock theory. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 145001. [Google Scholar] [CrossRef]
- Winhart, G.; Eidmann, K.; Iglesias, C.A.; Bar-Shalom, A.; Minguez, E.; Rickert, A.; Rose, S.J. XUV opacity measurements and comparison with models. J. Quant. Spectrosc. Radiat. Transf. 1995, 54, 437–446. [Google Scholar] [CrossRef]
- Winhart, G.; Eidmann, K.; Iglesias, C.A.; Bar-Shalom, A. Measurements of extreme uv opacities of hot dense Al, Fe and Ho. Phys. Rev. E 1996, 53, R1332–R1335. [Google Scholar] [CrossRef]
- Merdji, H.; Missalla, T.; Blenski, T.; Perrot, F.; Gauthier, J.-C.; Eidmann, K.; Chenais-Popovics, C. Absorption spectroscopy of a radiatively heated samarium plasma. Phys. Rev. E 1998, 57, 1042–1046. [Google Scholar] [CrossRef]
- Blenski, T.; Loisel, G.; Poirier, M.; Thais, F.; Arnault, P.; Caillaud, T.; Fariaut, J.; Gilleron, F.; Pain, J.-C.; Porcherot, Q.; et al. Opacity of iron, nickel and copper plasmas in the X-ray wavelength range: Theoretical interpretation of the 2p-3d absorption spectra measured at the LULI2000 facility. Phys. Rev. E 2011, 84, 036407. [Google Scholar] [CrossRef]
- Lee, T.-G.; Jarrah, W.; Benredjem, D.; Pain, J.-C.; Busquet, M.; Klapisch, M.; Schmitt, A.J.; Bates, J.W.; Giuliani, J. Super-transition-array calculations for synthetic spectra and opacity of high-density, high-temperature germanium plasmas. High Energy Density Phys. 2020, 35, 100742. [Google Scholar] [CrossRef]
- Kurzweil, Y.; Polack-Schupper, N. Accuracy analysis of opacity models from transmission measurements in laser-produced plasmas. Phys. Plasmas 2022, 29, 012704. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A. The effect of first order superconfiguration energies on the opacity of hot dense matter. High Energy Density Phys. 2015, 15, 59–66. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. Solar opacity calculations using the super-transition-array method. Astrophys. J. 2016, 821, 45–59. [Google Scholar] [CrossRef]
- Pain, J.-C. Detailed Opacity Calculations for Astrophysical Applications. Atoms 2017, 5, 22. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas. Atoms 2018, 6, 35. [Google Scholar] [CrossRef]
- Pain, J.-C. Sur la Physique Atomique des Ions Dans les Plasmas en Présence de L’écrantage. Ph.D. Thesis, Université Paris Sud XI, Orsay, France, 2002. (In French). [Google Scholar]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. A self-consistent model for the study of electronic properties of hot dense plasmas in the superconfiguration approximation. J. Quant. Spectroc. Radiat. Transf. 2006, 99, 451–468. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. Quantum mechanical model for the study of pressure ionization in the superconfiguration approach. J. Phys. A Math. Gen. 2006, 39, 4659–4666. [Google Scholar] [CrossRef]
- Pain, J.-C. A model of dense-plasma atomic structure for equation-of-state calculations. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1553–1573. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. Equation of State of Dense Plasma Mixtures: Application to the Sun Center. Contrib. Plasma Phys. 2012, 52, 23–27. [Google Scholar] [CrossRef]
- Busquet, M. Pressure ionization in partition function algebra. High Energy Density Phys. 2013, 9, 535–541. [Google Scholar] [CrossRef]
- Ovechkin, A.A.; Loboda, P.A.; Novikov, V.G.; Grushin, A.S.; Solomyannaya, A.D. RESEOS-A model of thermodynamic and optical properties of hot and warm dense matter. High Energy Density Phys. 2014, 13, 20–33. [Google Scholar] [CrossRef]
- Ovechkin, A.A.; Loboda, P.A.; Falkov, A.L. Transport and dielectric properties of dense ionized matter from the average-atom RESEOS model. High Energy Density Phys. 2016, 20, 38–54. [Google Scholar] [CrossRef]
- Ovechkin, A.A.; Loboda, P.A.; Falkov, A.L. Plasma opacity calculations using the Starrett and Saumon average-atom model with ion correlations. High Energy Density Phys. 2019, 30, 29–40. [Google Scholar] [CrossRef]
- Pain, J.-C.; Blenski, T. Self-consistent approach for the thermodynamics of ions in dense plasmas in the superconfiguration approximation. J. Quant. Spectroc. Radiat. Transf. 2003, 81, 355–369. [Google Scholar] [CrossRef]
- Oreg, J.; Bar-Shalom, A.; Klapisch, M. Operator technique for calculating superconfiguration-averaged quantities of atoms in plasmas. Phys. Rev. E 1997, 55, 5874–5882. [Google Scholar] [CrossRef]
- Faussurier, G. Superconfiguration accounting approach versus average-atom model in local-thermodynamic-equilibrium highly ionized plasmas. Phys. Rev. E 1999, 59, 7096–7109. [Google Scholar] [CrossRef]
- Wilson, B.; Chen, M.H. A revised algorithm for the computation of super-transition array spectra of hot dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1999, 61, 813–823. [Google Scholar] [CrossRef]
- Gilleron, F.; Pain, J.-C. Stable method for the calculation of partition functions in the superconfiguration approach. Phys. Rev. E 2004, 69, 056117. [Google Scholar] [CrossRef]
- Wilson, B.G.; Gilleron, F.; Pain, J.-C. Further stable methods for the calculation of partition functions in the superconfiguration approach. Phys. Rev. E 2007, 76, 032103. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Porcherot, Q. Generating functions for canonical systems of fermions. Phys. Rev. E 2011, 83, 067701. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Wilson, B.G. Optimized recursion relation for the computation of partition functions in the superconfiguration approach. High Energy Density Phys. 2020, 37, 100891. [Google Scholar] [CrossRef]
- Faussurier, G.; Wilson, B.G.; Chen, M.H. Generalization of super-transition-array methods to hot dense plasmas by using optimum independent particle reference systems. Phys. Rev. E 2002, 65, 016403, Erratum in Phys. Rev. E 2002, 65, 049901. [Google Scholar] [CrossRef] [PubMed]
- Pain, J.-C.; Gilleron, F.; Faussurier, G. Jensen-Feynman approach to the statistics of interacting electrons. Phys. Rev. E 2009, 80, 026703. [Google Scholar] [CrossRef] [PubMed]
- Kurzweil, Y.; Hazak, G. Summation of the spectra of all partially resolved transition arrays in a supertransition array. Phys. Rev. E 2016, 94, 053210. [Google Scholar] [CrossRef] [PubMed]
- Hazak, G.; Kurzweil, Y. A Configurationally-Resolved-Super-Transition-Arrays method for calculation of the spectral absorption coefficient in hot plasmas. High Energy Density Phys. 2012, 8, 290–297. [Google Scholar] [CrossRef]
- Kurzweil, Y.; Hazak, G. Inclusion of UTA widths in the Configurationally Resolved Super-Transition-Arrays (CRSTA) method. High Energy Density Phys. 2013, 9, 548–552. [Google Scholar] [CrossRef]
- Wilson, B.G.; Iglesias, C.A.; Chen, M.H. Partially resolved super transition array method. High Energy Density Phys. 2015, 14, 67–73. [Google Scholar] [CrossRef]
- Perrot, F. Correlated fluctuations of electron populations in high temperature plasmas. Phys. A Stat. Mech. Appl. 1988, 150, 357–370. [Google Scholar] [CrossRef]
- Mayer, H. Methods of Opacity Calculations; Report LA-647; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1947.
- Grimaldi, F.; Grimaldi-Lecourt, A. Quasi-static electron density fluctuations of atoms in hot compressed matter. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 373–385. [Google Scholar] [CrossRef]
- Grimaldi, F.; Grimaldi-Lecourt, A. Fluctuations of a hot system of electrons in a static potential. In Proceedings of the 2nd International Conference on Radiative Properties of Hot Dense Matter, Sarasota, FL, USA, 31 October–4 November 1983; Davis, J., Hooper, C., Lee, R., Merts, A., Rozsnyai, B., Eds.; World Scientific: Singapore, 1985. [Google Scholar]
- Grimaldi, F.; Grimaldi-Lecourt, A. The calculation of the opacity of hot dense plasmas. In Proceedings of the 2nd International Conference on Radiative Properties of Hot Dense Matter, Sarasota, FL, USA, 31 October–4 November 1983; Davis, J., Hooper, C., Lee, R., Merts, A., Rozsnyai, B., Eds.; World Scientific: Singapore, 1985. [Google Scholar]
- Grimaldi, F. Electron Density Fluctuations in Hot Matter: A Method to Calculate Statistical Correlation Factors, p. 145 in Radiative Properties of Hot Dense Matter. In Proceedings of the 4th International Workshop, Sarasota, FL, USA, 22 October 1990; Goldstein, W., Hooper, C., Gauthier, J., Seely, J., Lee, R., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- Perrot, F.; Blenski, T. Electronic structure and statistical mechanics of ionic configurations in hot plasmas. J. Phys. IV Fr. 2000, 10, 473–480. [Google Scholar] [CrossRef]
- Wilson, B. Evaluating orbital occupation number correlations in high-temperature plasmas. J. Quant. Spectrosc. Radiat. Transf. 1993, 49, 241–258. [Google Scholar] [CrossRef]
- Faussurier, G. Traitement Statistique des Propriétés Spectrales des Plasmas à L’équilibre Thermodynamique Local Dans le Cadre du Modèle Hydrogénique Écranté. Ph.D. Thesis, Ecole Polytechnique, Paris, France, 1996. (In French). [Google Scholar]
- Green, J.M. The statistical mechanics of the interdependent electrons in the screening constant model of the many-electron-atom. J. Quant. Spectrosc. Radiat. Transf. 1964, 4, 639–662. [Google Scholar] [CrossRef]
- Green, J. An Explicit Expression for the Grand Partition Function of Interacting Particles in the High Temperature Limit; R&D Associates Report RDA-TR-135302-001; R&D Associates: Marina Del Rey, CA, USA, 1989. [Google Scholar]
- Fischer, H. A History of the Central Limit Theorem from Classical to Modern Probability Theory; Springer: New York, NY, USA, 2011. [Google Scholar]
- Pain, J.-C.; Poirier, M. Analytical and numerical expressions for the number of atomic configurations contained in a supershell. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 115002. [Google Scholar] [CrossRef]
- Krief, M. Number of populated electronic configurations in a hot dense plasma. Phys. Rev. 2021, 103, 033206. [Google Scholar] [CrossRef]
- Drmota, M.; Szpankowski, W. A Master Theorem for Discrete Divide and Conquer Recurrences. J. ACM 2013, 60, 1–49. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F. A quantitative study of some sources of uncertainty in opacity measurements. High Energy Density Phys. 2020, 34, 100745. [Google Scholar] [CrossRef]
- Faussurier, G.; Blancard, C.; Decoster, A. Laser Interaction with Matter (Proceedings of the 23rd European Conference, St. Johns College, Oxford, UK, 1923 September 1994); Rose, S.J., Ed.; Rutherford Laboratory: Chilton/Didcot, UK, 1995; p. 239. [Google Scholar]
- Faussurier, G.; Blancard, C.; Decoster, A. Statistical treatment of radiative transitions in local thermodynamic equilibrium plasmas. Phys. Rev. E 1997, 56, 3488–3497. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M. Non-LTE superconfiguration collisional radiative model. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 427–439. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M. Collisional radiative model for heavy atoms in hot non-local-thermodynamical-equilibrium plasmas. Phys. Rev. E 1997, 56, R70–R73. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M. Recent developments in the SCROLL model. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 43–55. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Klapisch, M.; Oreg, J. HULLAC, an integrated computer package for atomic processes in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 169–188. [Google Scholar] [CrossRef]
- Busquet, M. Radiation-dependent ionization model for laser-created plasmas. Phys. Fluids B Plasma Phys. 1993, 5, 4191–4206. [Google Scholar] [CrossRef]
- Klapisch, M.; Bar-Shalom, A. Checking the validity of Busquet’s ionization temperature with detailed collisional radiative models. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 687–697. [Google Scholar] [CrossRef]
- Cossé, P. Contribution à L’étude de la Cinétique Ionique des Plasmas Chauds: Mise en Évidence de Pseudo-Équilibres Thermodynamiques. Ph.D. Thesis, Université Paris Sud XI, Orsay, France, 2001. (In French). [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).