The Effect of Magnetic Field Strength and Geometry on the Deposition Rate and Ionized Flux Fraction in the HiPIMS Discharge
Abstract
:1. Introduction
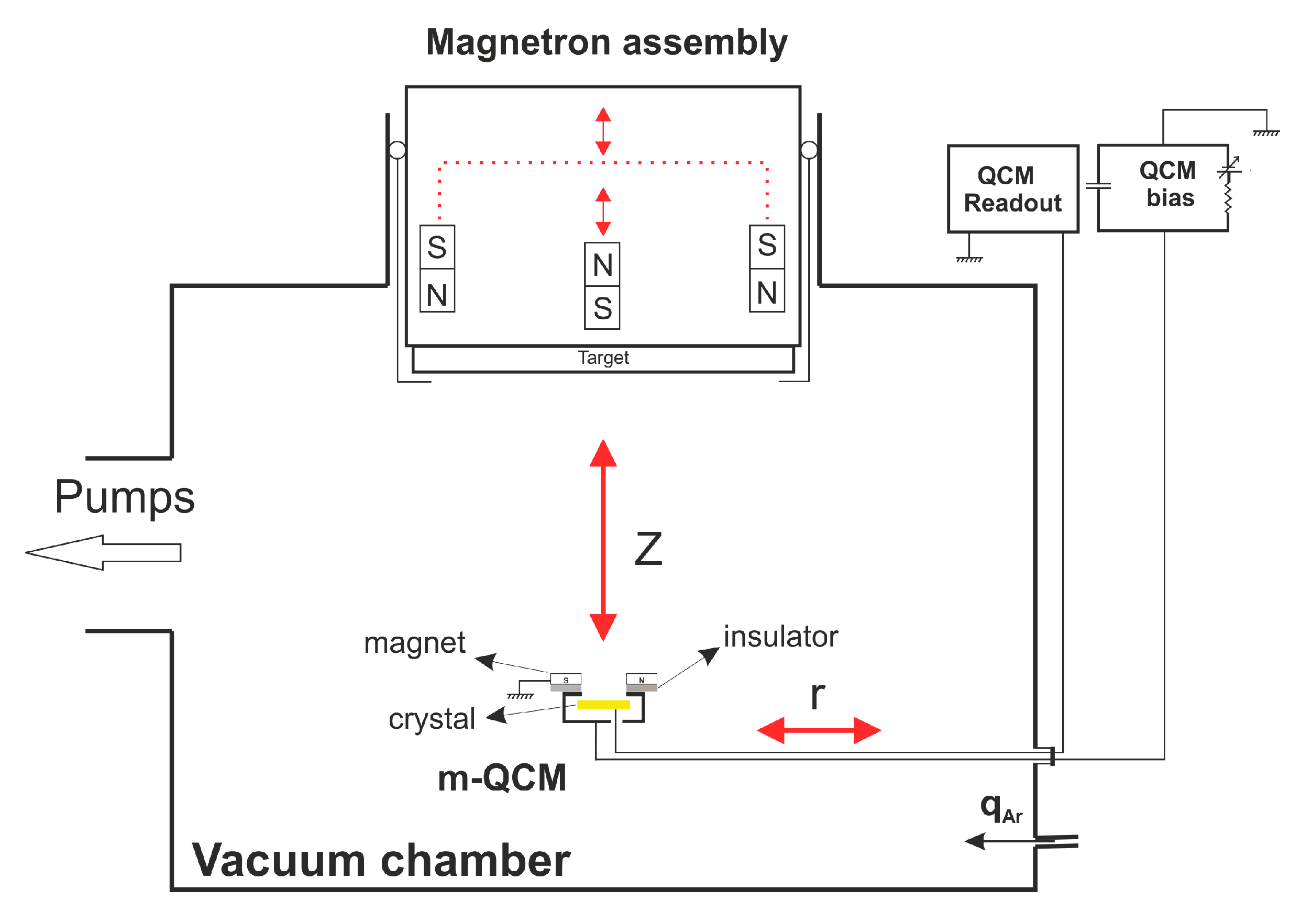
2. Materials and Methods
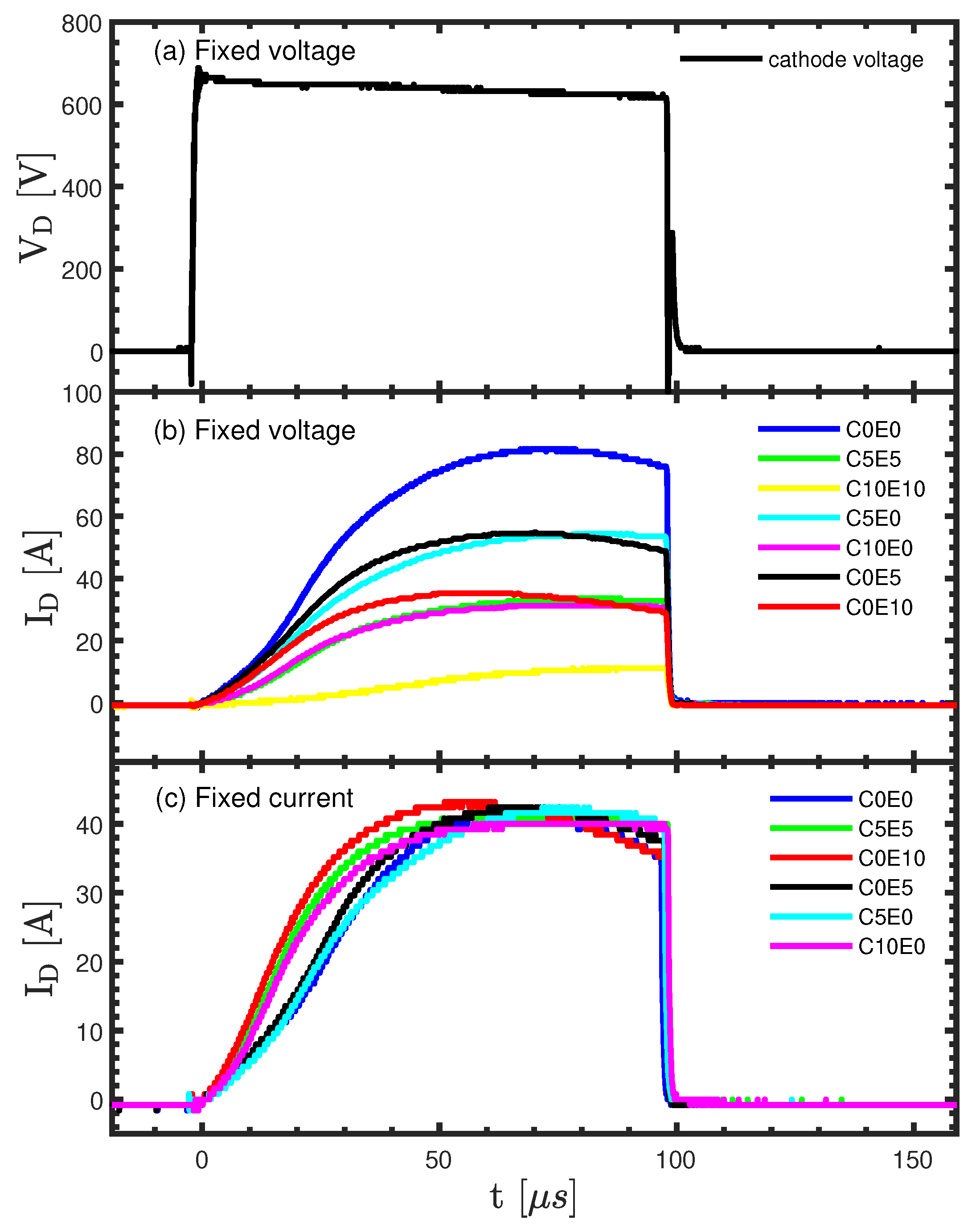
3. Results
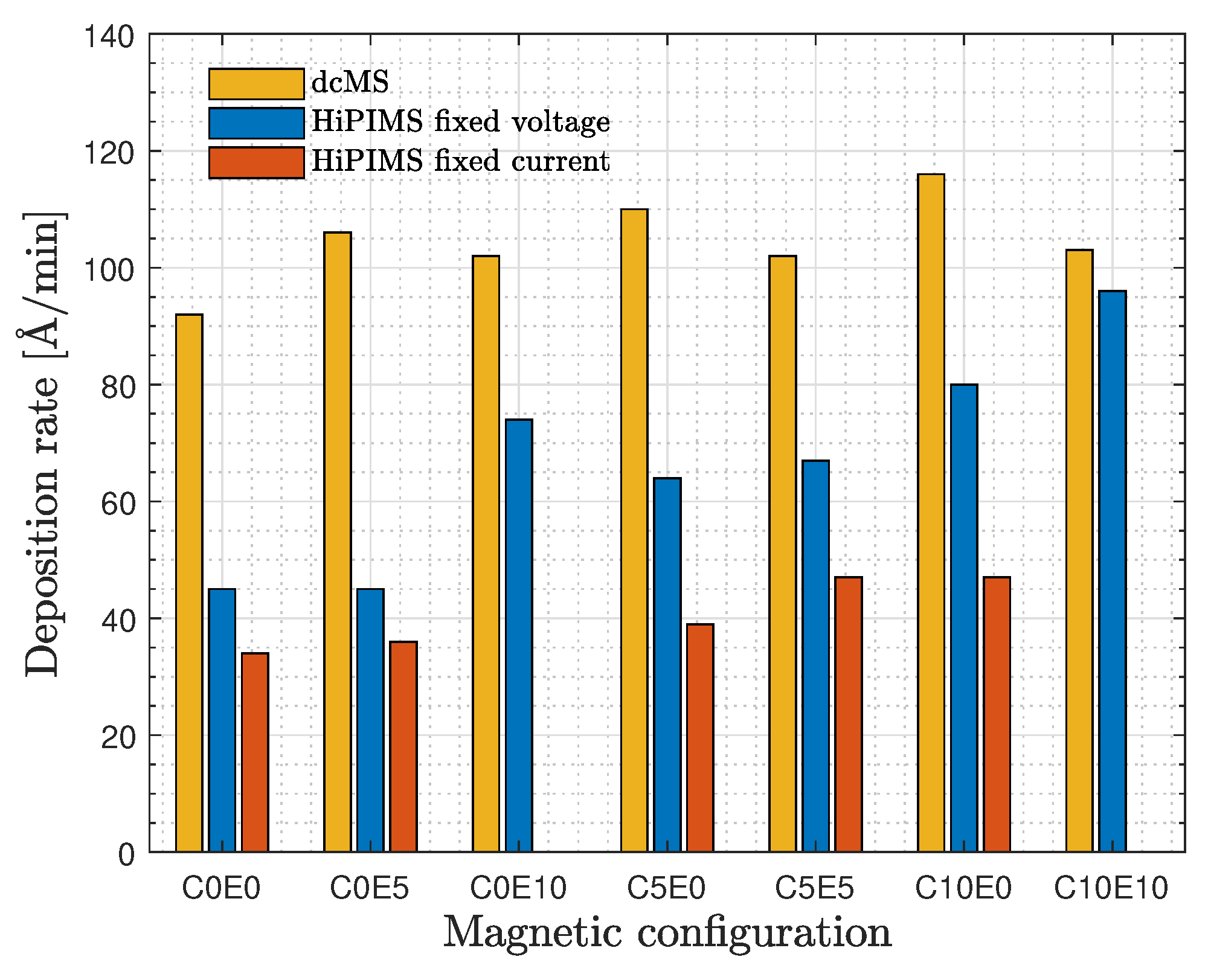
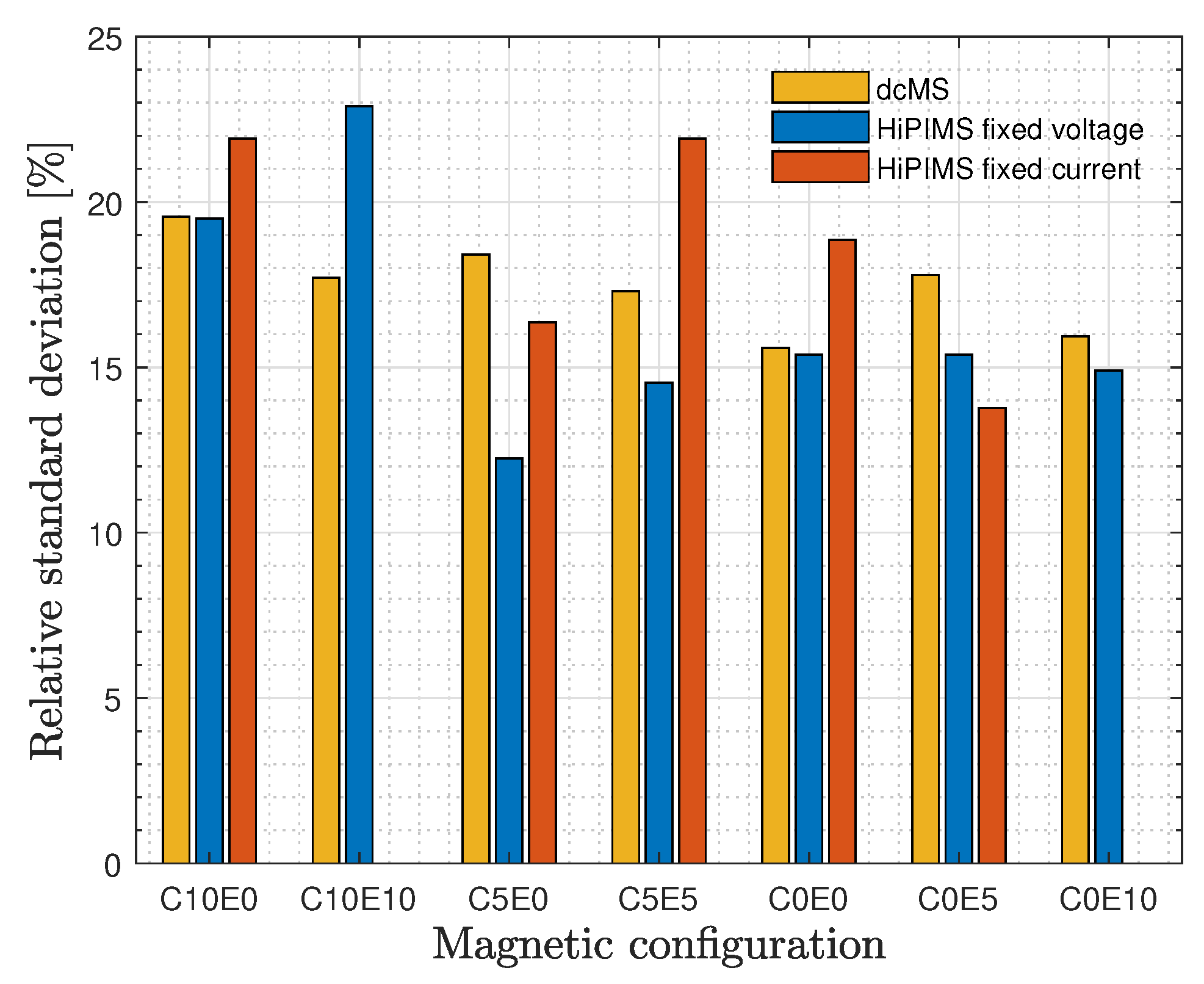
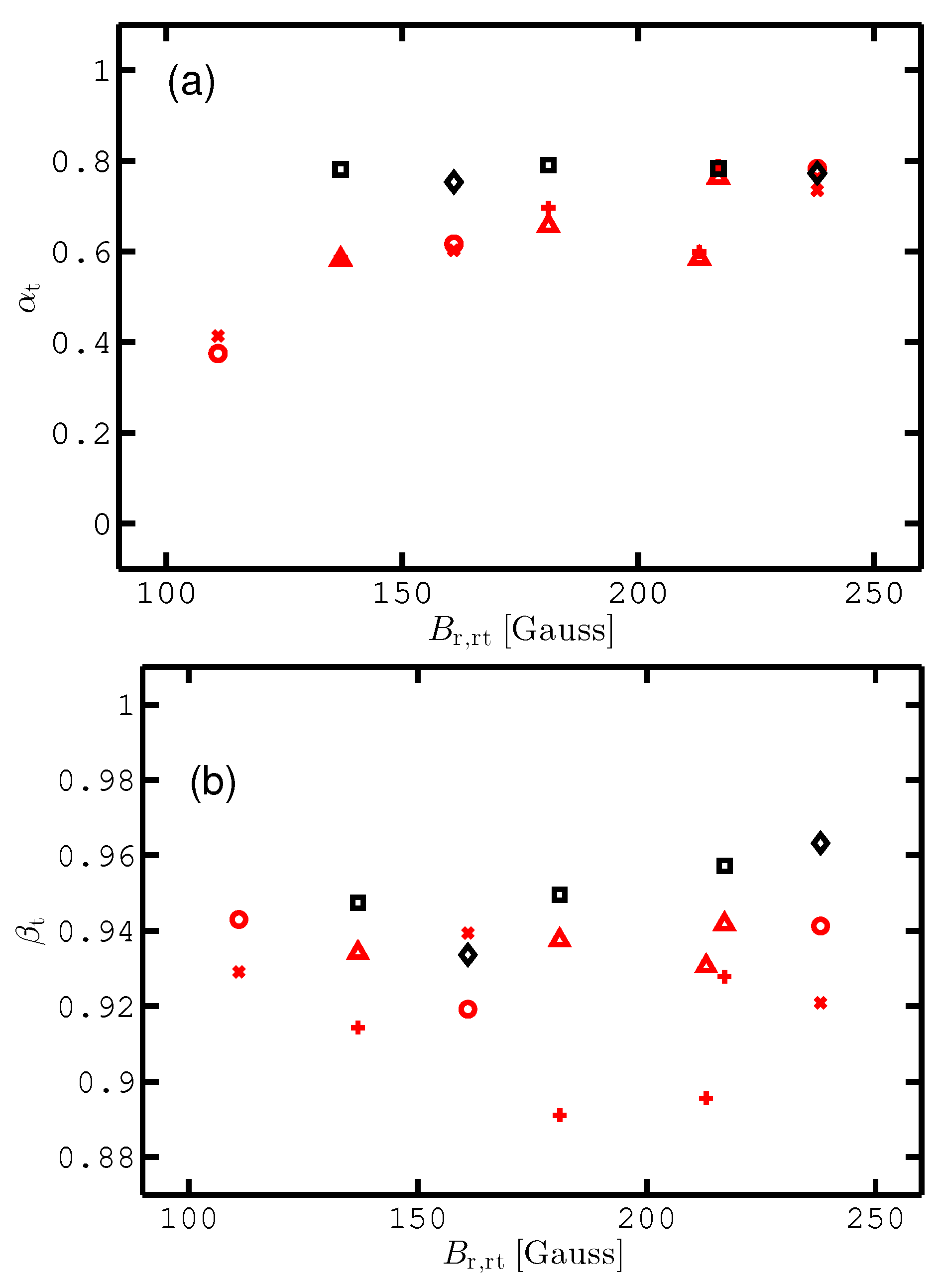
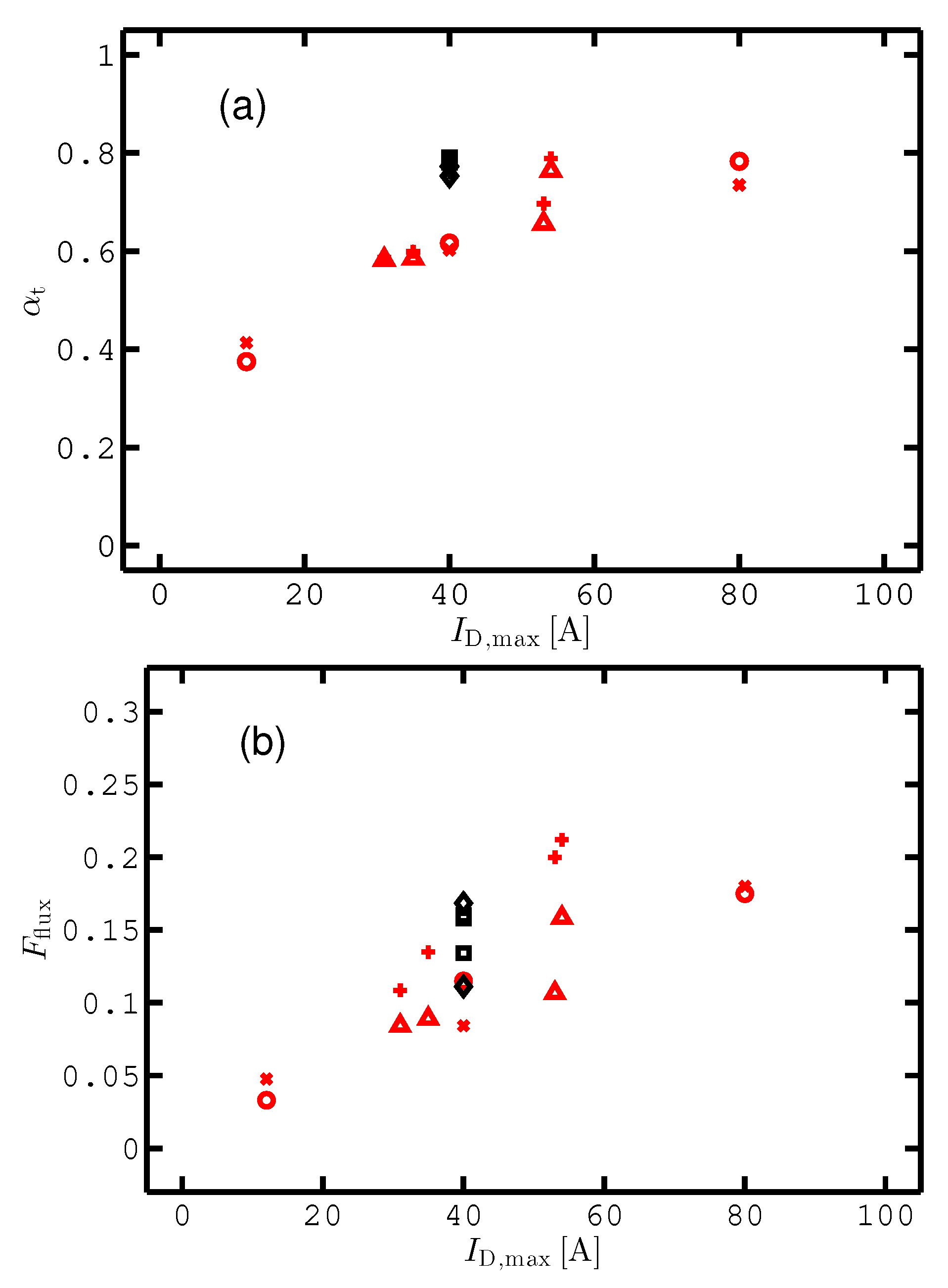
3.1. Deposition Rate
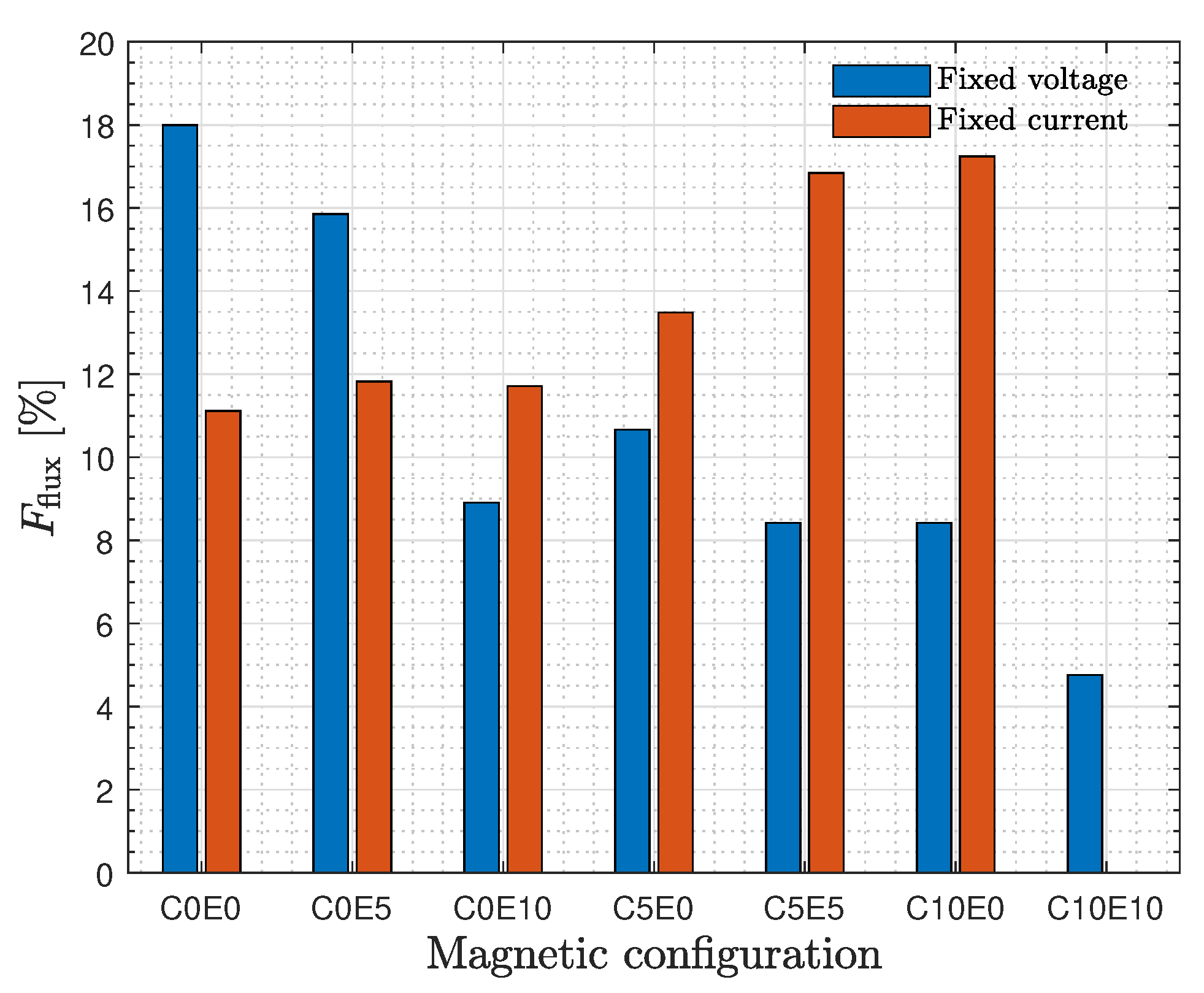
3.2. Ionized Flux Fraction
4. Discussion
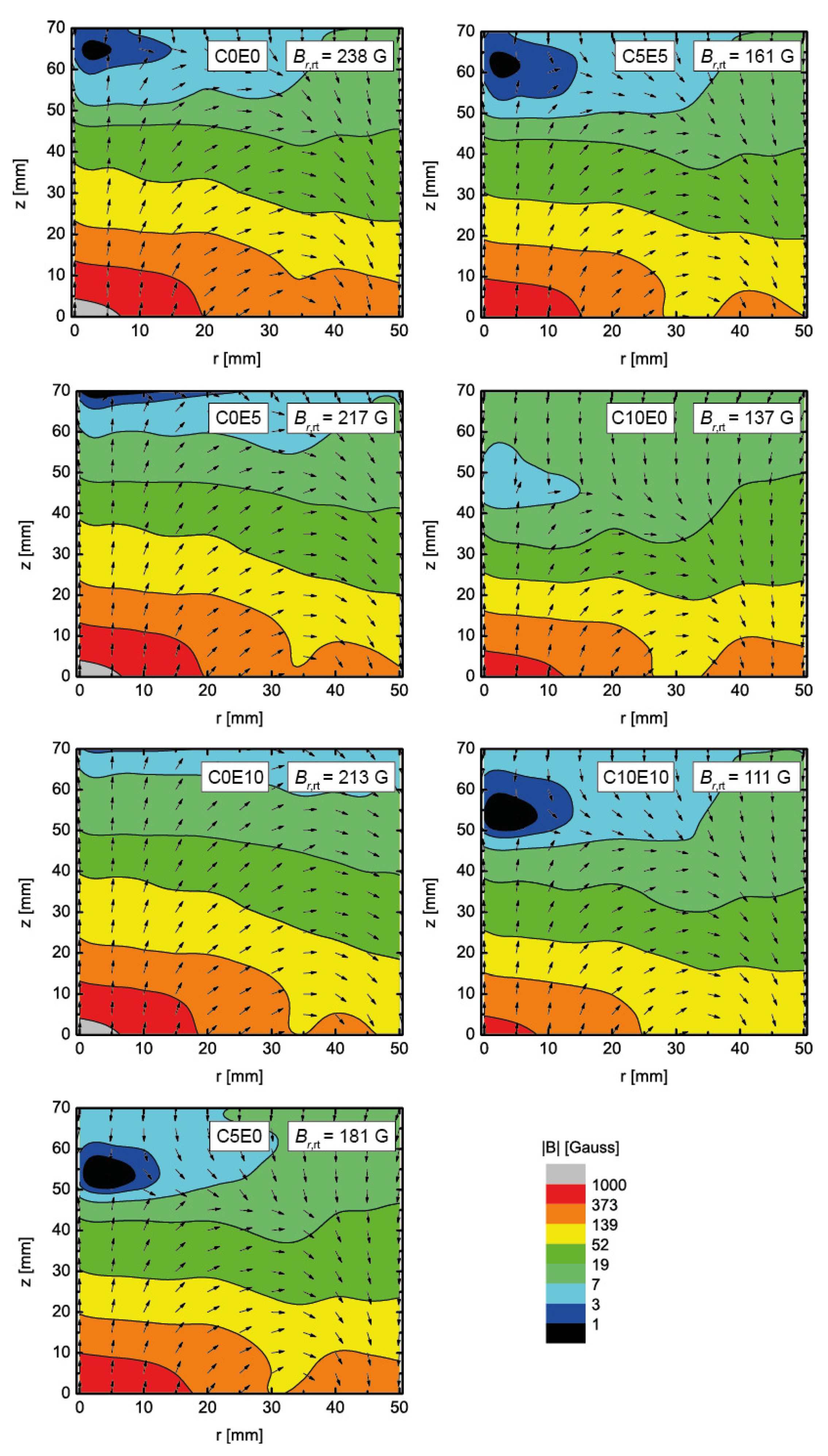
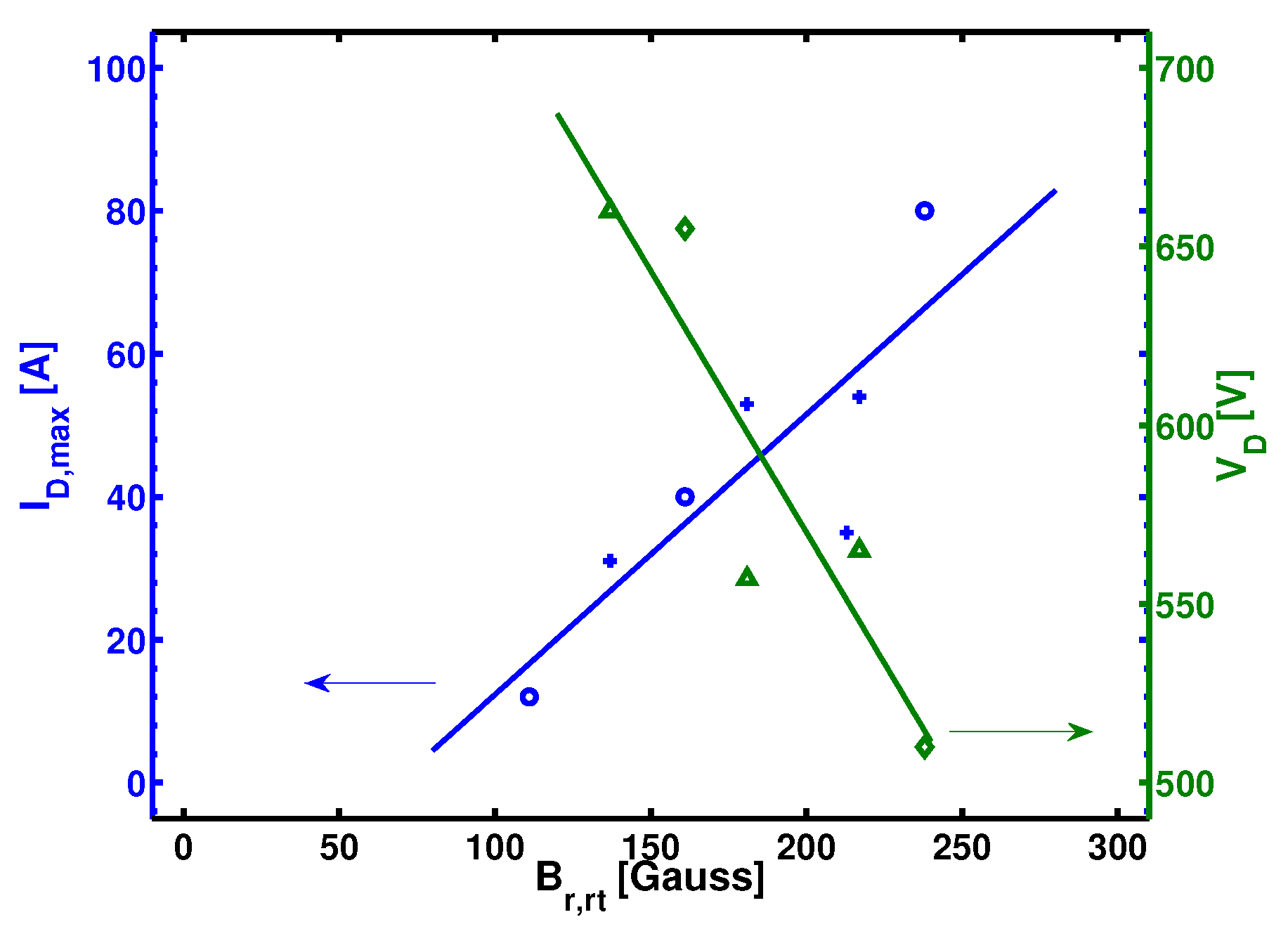
4.1. Discharge Physics
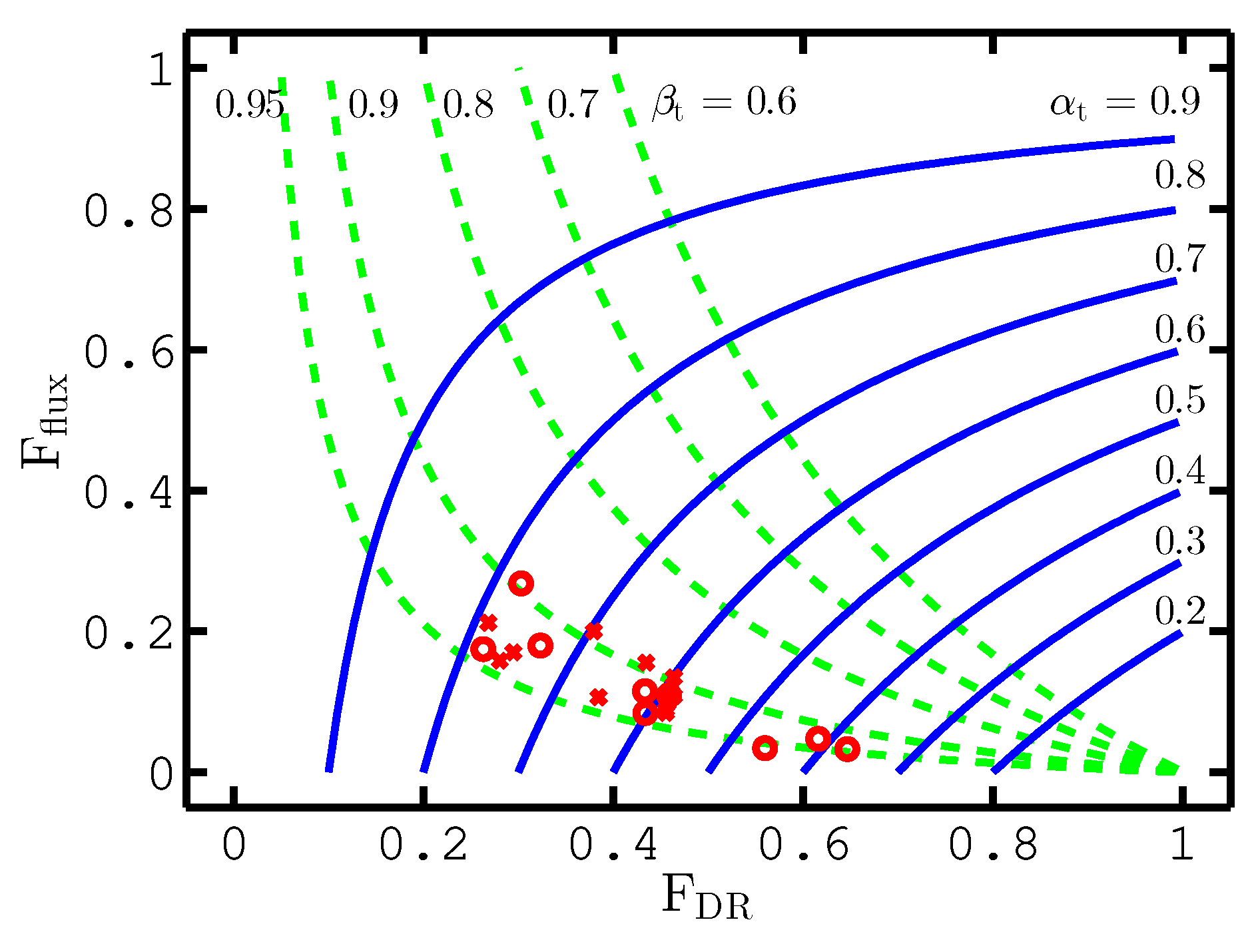
4.2. Deposition Rate and Ionized Flux Fraction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Helmersson, U.; Lattemann, M.; Bohlmark, J.; Ehiasarian, A.P.; Gudmundsson, J.T. Ionized physical vapor deposition (IPVD): A review of technology and applications. Thin Solid Films 2006, 513, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Gudmundsson, J.T.; Brenning, N.; Lundin, D.; Helmersson, U. The high power impulse magnetron sputtering discharge. J. Vac. Sci. Technol. A 2012, 30, 030801. [Google Scholar] [CrossRef]
- Kouznetsov, V.; Macák, K.; Schneider, J.M.; Helmersson, U.; Petrov, I. A novel pulsed magnetron sputter technique utilizing very high target power densities. Surf. Coat. Technol. 1999, 122, 290–293. [Google Scholar] [CrossRef]
- Kubart, T.; Čada, M.; Lundin, D.; Hubička, Z. Investigation of ionized metal flux fraction in HiPIMS discharges with Ti and Ni targets. Surf. Coat. Technol. 2014, 238, 152–157. [Google Scholar] [CrossRef]
- Lundin, D.; Čada, M.; Hubička, Z. Ionization of sputtered Ti, Al, and C coupled with plasma characterization in HiPIMS. Plasma Sources Sci. Technol. 2015, 24, 035018. [Google Scholar] [CrossRef]
- Lundin, D.; Sarakinos, K. An introduction to thin film processing using high power impulse magnetron sputtering. J. Mater. Res. 2012, 27, 780–792. [Google Scholar] [CrossRef]
- Anders, A. Deposition rates of high power impulse magnetron sputtering: Physics and economics. J. Vac. Sci. Technol. A 2010, 28, 783–790. [Google Scholar] [CrossRef]
- Samuelsson, M.; Lundin, D.; Jensen, J.; Raadu, M.A.; Gudmundsson, J.T.; Helmersson, U. On the film density using high power impulse magnetron sputtering. Surf. Coat. Technol. 2010, 202, 591–596. [Google Scholar] [CrossRef]
- Christie, D.J. Target material pathways model for high power pulsed magnetron sputtering. J. Vac. Sci. Technol. A 2005, 23, 330–335. [Google Scholar] [CrossRef]
- Bradley, J.W.; Thompson, S.; Gonzalvo, Y.A. Measurement of the plasma potential in a magnetron discharge and the prediction of the electron drift speeds. Plasma Sources Sci. Technol. 2001, 10, 490–501. [Google Scholar] [CrossRef]
- Rauch, A.; Mendelsberg, R.J.; Sanders, J.M.; Anders, A. Plasma potential mapping of high power impulse magnetron sputtering discharges. J. Appl. Phys. 2012, 111, 083302. [Google Scholar] [CrossRef] [Green Version]
- Sigurjónsson, P. Spatial and Temporal Variation of the Plasma Parameters in a High Power Impulse Magnetron Sputtering (HiPIMS) Discharge. Master’s Thesis, University of Iceland, Reykjavik, Iceland, 2008. [Google Scholar]
- Mishra, A.; Kelly, P.J.; Bradley, J.W. The evolution of the plasma potential in a HiPIMS discharge and its relationship to deposition rate. Plasma Sources Sci. Technol. 2010, 19, 045014. [Google Scholar]
- Liebig, B.; Bradley, J.W. Space charge, plasma potential and electric field distributions in HiPIMS discharges of varying configuration. Plasma Sources Sci. Technol. 2013, 22, 045020. [Google Scholar] [CrossRef]
- Konstantinidis, S.; Dauchot, J.P.; Ganciu, M.; Hecq, M. Influence of pulse duration on the plasma characteristics in high-power pulsed magnetron discharges. J. Appl. Phys. 2006, 99, 013307. [Google Scholar] [CrossRef]
- Velicu, I.L.; Tiron, V.; Popa, G. Dynamics of the fast-HiPIMS discharge during FINEMET-type film deposition. Surf. Coat. Technol. 2014, 250, 57–64. [Google Scholar] [CrossRef]
- Ferrec, A.; Kéraudy, J.; Jouan, P.Y. Mass spectrometry analyzes to highlight differences between short and long HiPIMS discharges. Appl. Surf. Sci. 2016, 390, 497–505. [Google Scholar] [CrossRef]
- Čapek, J.; Hála, M.; Zabeida, O.; Klemberg-Sapieha, J.E.; Martinu, L. Deposition rate enhancement in HiPIMS without compromising the ionized fraction of the deposition flux. J. Phys. D Appl. Phys. 2013, 46, 205205. [Google Scholar]
- Bradley, J.W.; Mishra, A.; Kelly, P.J. The effect of changing the magnetic field strength on HiPIMS deposition rates. J. Phys. D Appl. Phys. 2015, 48, 215202. [Google Scholar] [CrossRef]
- Yu, H.; Meng, L.; Szott, M.M.; Meister, J.T.; Cho, T.S.; Ruzic, D.N. Investigation and optimization of the magnetic field configuration in high-power impulse magnetron sputtering. Plasma Sources Sci. Technol. 2013, 22, 045012. [Google Scholar] [CrossRef]
- Raman, P.; Shchelkanov, I.A.; McLain, J.; Ruzic, D.N. High power pulsed magnetron sputtering: A method to increase deposition rate. J. Vac. Sci. Technol. A 2015, 33, 031304. [Google Scholar] [CrossRef]
- Raman, P.; Shchelkanov, I.; McLain, J.; Cheng, M.; Ruzic, D.; Haehnlein, I.; Jurczyk, B.; Stubbers, R.; Armstrong, S. High Deposition Rate Symmetric Magnet Pack for High Power Pulsed Magnetron Sputtering. Surf. Coat. Technol. 2016, 293, 10–15. [Google Scholar] [CrossRef]
- Ganesan, R.; Akhavan, B.; Dong, X.; McKenzie, D.R.; Bilek, M.M.M. External magnetic field increases both plasma generation and deposition rate in HiPIMS. Surf. Coat. Technol. 2018, 352, 671–679. [Google Scholar] [CrossRef]
- Antonin, O.; Tiron, V.; Costin, C.; Popa, G.; Minea, T.M. On the HiPIMS benefits of multi-pulse operating mode. J. Phys. D Appl. Phys. 2015, 48, 015202. [Google Scholar] [CrossRef]
- Barker, P.M.; Lewin, E.; Patscheider, J. Modified high power impulse magnetron sputtering process for increased deposition rate of titanium. J. Vac. Sci. Technol. A 2013, 31, 060604. [Google Scholar] [CrossRef]
- Tesař, J.; Martan, J.; Rezek, J. On surface temperatures during high power pulsed magnetron sputtering using a hot target. Surf. Coat. Technol. 2011, 206, 1155–1159. [Google Scholar] [CrossRef]
- Alami, J.; Maric, Z.; Busch, H.; Klein, F.; Grabowy, U.; Kopnarsk, M. Enhanced ionization sputtering: A concept for superior industrial coatings. Surf. Coat. Technol. 2014, 255, 43–51. [Google Scholar] [CrossRef]
- Hajihoseini, H.; Gudmundsson, J.T. Vanadium and vanadium nitride thin films grown by high power impulse magnetron sputtering. J. Phys. D Appl. Phys. 2017, 50, 505302. [Google Scholar] [Green Version]
- McLain, J.; Raman, P.; Patel, D.; Spreadbury, R.; Uhlig, J.; Shchelkanov, I.; Ruzic, D.N. Linear magnetron HiPIMS high deposition rate magnet pack. Vacuum 2018, 155, 559–565. [Google Scholar] [CrossRef]
- Poolcharuansin, P.; Bowes, M.; Petty, T.J.; Bradley, J.W. Ionized metal flux fraction measurements in HiPIMS discharges. J. Phys. D Appl. Phys. 2012, 45, 322001. [Google Scholar] [CrossRef]
- Raman, P.; Weberski, J.; Cheng, M.; Shchelkanov, I.; Ruzic, D.N. A high power impulse magnetron sputtering model to explain high deposition rate magnetic field configurations. J. Appl. Phys. 2016, 120, 163301. [Google Scholar] [CrossRef] [Green Version]
- Vlček, J.; Burcalová, K. A phenomenological equilibrium model applicable to high-power pulsed magnetron sputtering. Plasma Sources Sci. Technol. 2010, 19, 065010. [Google Scholar]
- Window, B.; Savvides, N. Charged particle fluxes from planar magnetron sputtering sources. J. Vac. Sci. Technol. A 1986, 4, 196–202. [Google Scholar] [CrossRef]
- Wu, L.; Ko, E.; Dulkin, A.; Park, K.J.; Fields, S.; Leeser, K.; Meng, L.; Ruzic, D.N. Flux and energy analysis of species in hollow cathode magnetron ionized physical vapor deposition of copper. Rev. Sci. Instrum. 2010, 81, 123502. [Google Scholar] [CrossRef] [PubMed]
- Green, K.M.; Hayden, D.B.; Juliano, D.R.; Ruzic, D.N. Determination of flux ionization fraction using a quartz crystal microbalance and a gridded energy analyzer in an ionized magnetron sputtering system. Rev. Sci. Instrum. 1997, 68, 4555–4560. [Google Scholar] [CrossRef]
- Huo, C.; Lundin, D.; Gudmundsson, J.T.; Raadu, M.A.; Bradley, J.W.; Brenning, N. Particle-balance models for pulsed sputtering magnetrons. J. Phys. D Appl. Phys. 2017, 50, 354003. [Google Scholar] [CrossRef]
- Butler, A.; Brenning, N.; Raadu, M.A.; Gudmundsson, J.T.; Minea, T.; Lundin, D. On three different ways to quantify the degree of ionization in sputtering magnetrons. Plasma Sources Sci. Technol. 2018, 27, 105005. [Google Scholar]
- Huo, C.; Lundin, D.; Raadu, M.A.; Anders, A.; Gudmundsson, J.T.; Brenning, N. On sheath energization and Ohmic heating in sputtering magnetrons. Plasma Sources Sci. Technol. 2013, 22, 045005. [Google Scholar] [CrossRef]
- Brenning, N.; Gudmundsson, J.T.; Lundin, D.; Minea, T.; Raadu, M.A.; Helmersson, U. The Role of Ohmic Heating in dc Magnetron Sputtering. Plasma Sources Sci. Technol. 2016, 25, 065024. [Google Scholar]
- Thornton, J.A. Magnetron sputtering: Basic physics and application to cylindrical magnetrons. J. Vac. Sci. Technol. 1978, 15, 171–177. [Google Scholar] [CrossRef]
- Brenning, N.; Gudmundsson, J.T.; Raadu, M.A.; Petty, T.J.; Minea, T.; Lundin, D. A unified treatment of self-sputtering, process gas recycling, and runaway for high power impulse sputtering magnetrons. Plasma Sources Sci. Technol. 2017, 26, 125003. [Google Scholar] [CrossRef]
- Huo, C.; Lundin, D.; Raadu, M.A.; Anders, A.; Gudmundsson, J.T.; Brenning, N. On the road to self-sputtering in high power impulse magnetron sputtering: Particle balance and discharge characteristics. Plasma Sources Sci. Technol. 2014, 23, 025017. [Google Scholar] [CrossRef]
- Bohlmark, J.; Lattemann, M.; Gudmundsson, J.T.; Ehiasarian, A.P.; Gonzalvo, Y.A.; Brenning, N.; Helmersson, U. The ion energy distributions and ion flux composition from a high power impulse magnetron sputtering discharge. Thin Solid Films 2006, 515, 1522–1526. [Google Scholar] [CrossRef]
- Andersson, J.; Ehiasarian, A.P.; Anders, A. Observation of Ti4+ ions in a high power impulse magnetron sputtering plasma. Appl. Phys. Lett. 2008, 93, 071504. [Google Scholar]

| Magnet | dcMS | HiPIMS | HiPIMS | HiPIMS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fixed Voltage | Fixed Peak Current | Fixed Peak Current | |||||||||||
| [Gauss] | [mm] | [V] | [A] | [V] | [A] | [Hz] | [V] | [A] | [Hz] | [V] | [A] | [Hz] | |
| C0E0 | 238 | 66 | 339 | 0.885 | 625 | 80 | 54 | 510 | 40 | 143 | 555 | 80 | 60 |
| C0E5 | 217 | 70 | 308 | 0.974 | 625 | 54 | 76 | 565 | 40 | 123 | 580 | 80 | 56 |
| C0E10 | 213 | 74 | 311 | 0.964 | 625 | 35 | 115 | 650 | 40 | 111 | |||
| C5E0 | 181 | 53 | 317 | 0.946 | 625 | 53 | 80 | 557 | 40 | 129 | 582 | 80 | 58 |
| C5E5 | 161 | 59 | 334 | 0.926 | 625 | 36 | 97 | 655 | 40 | 97 | 649 | 80 | 295 |
| C10E0 | 137 | 43 | 312 | 0.961 | 625 | 31 | 134 | 660 | 40 | 99 | 636 | 80 | 295 |
| C10E10 | 111 | 52 | 330 | 0.909 | 625 | 12 | 450 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajihoseini, H.; Čada, M.; Hubička, Z.; Ünaldi, S.; Raadu, M.A.; Brenning, N.; Gudmundsson, J.T.; Lundin, D. The Effect of Magnetic Field Strength and Geometry on the Deposition Rate and Ionized Flux Fraction in the HiPIMS Discharge. Plasma 2019, 2, 201-221. https://doi.org/10.3390/plasma2020015
Hajihoseini H, Čada M, Hubička Z, Ünaldi S, Raadu MA, Brenning N, Gudmundsson JT, Lundin D. The Effect of Magnetic Field Strength and Geometry on the Deposition Rate and Ionized Flux Fraction in the HiPIMS Discharge. Plasma. 2019; 2(2):201-221. https://doi.org/10.3390/plasma2020015
Chicago/Turabian StyleHajihoseini, Hamidreza, Martin Čada, Zdenek Hubička, Selen Ünaldi, Michael A. Raadu, Nils Brenning, Jon Tomas Gudmundsson, and Daniel Lundin. 2019. "The Effect of Magnetic Field Strength and Geometry on the Deposition Rate and Ionized Flux Fraction in the HiPIMS Discharge" Plasma 2, no. 2: 201-221. https://doi.org/10.3390/plasma2020015
APA StyleHajihoseini, H., Čada, M., Hubička, Z., Ünaldi, S., Raadu, M. A., Brenning, N., Gudmundsson, J. T., & Lundin, D. (2019). The Effect of Magnetic Field Strength and Geometry on the Deposition Rate and Ionized Flux Fraction in the HiPIMS Discharge. Plasma, 2(2), 201-221. https://doi.org/10.3390/plasma2020015






