Radial Kick in High-Efficiency Output Structures
Abstract
:1. Introduction
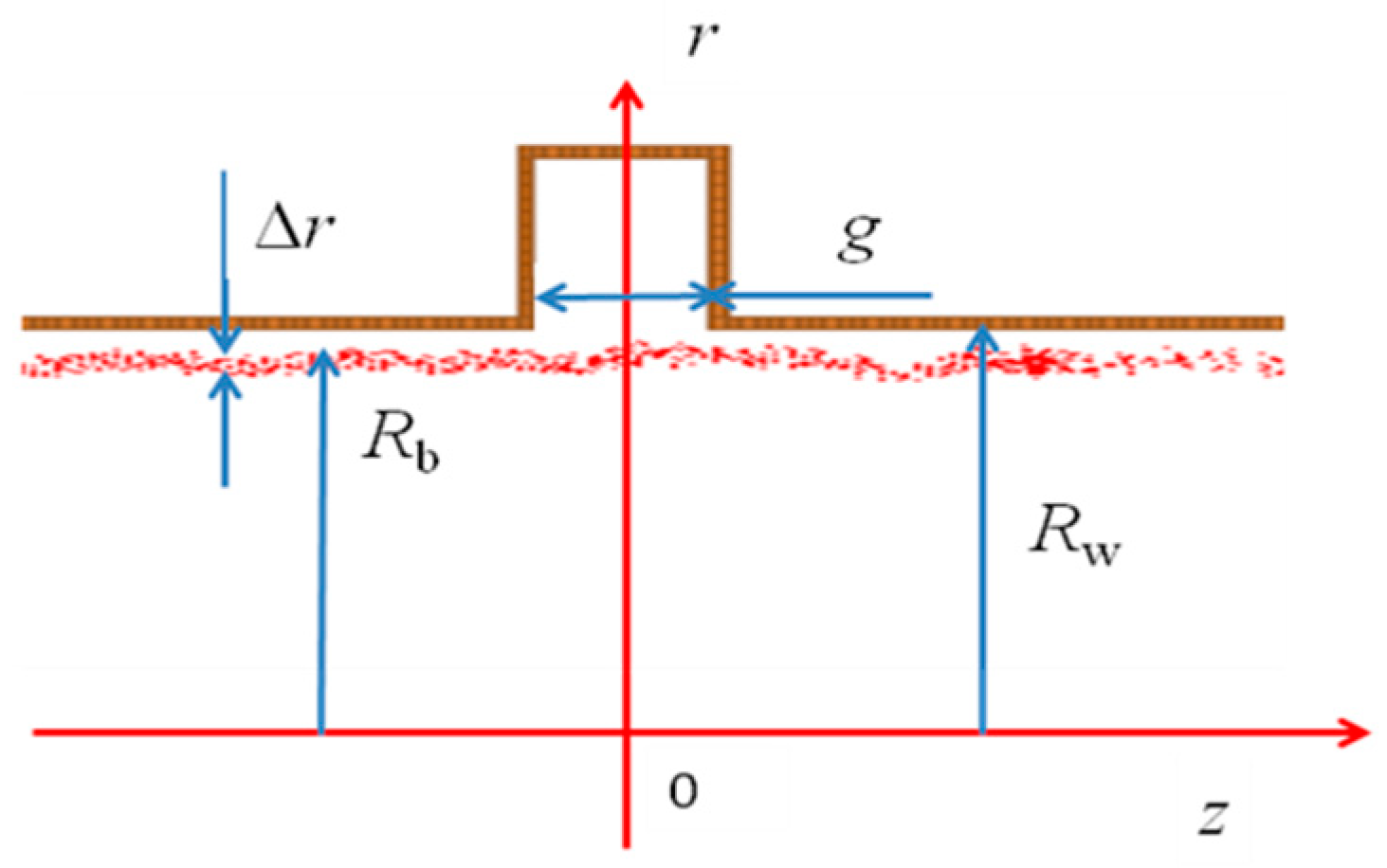
2. Formulation of the Model
3. Effective Radial Force
4. Discussion
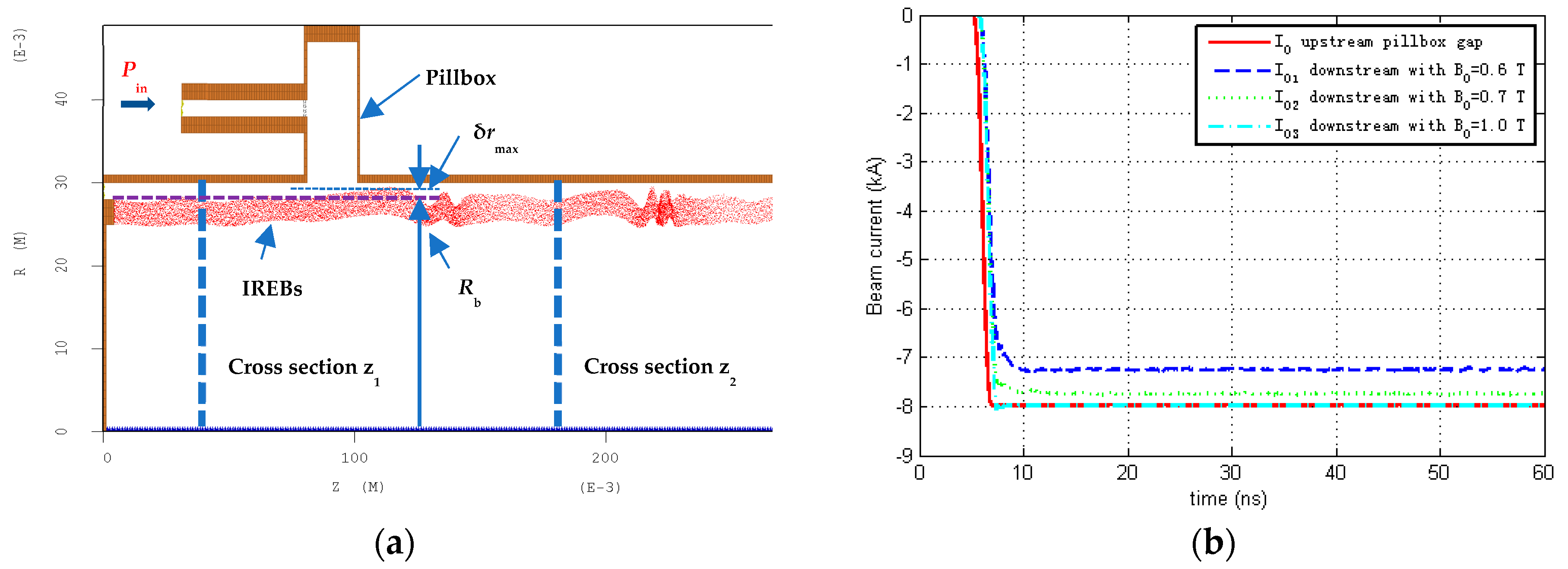
- For beam stability, it is required that the relativistic cyclotron frequency is significantly larger than the relativistic plasma frequency . In all of the expressions so far, we considered the average beam density, but we need to keep in mind that high-efficiency energy conversion is facilitated by a highly bunched beam; thus local density may exceed the averaged value by a factor of or even higher. Consequently, it will be more realistic to adopt a more stringent constraint on the magnetic field .
- The radial transverse kick, , is proportional to the amplitude of the radial oscillation.
- In case of a quasi-periodic structure whereby electrons lose a significant fraction of their energy , the magnetic field is tapered , the bunch density varies , and assuming that there are no reflected electrons, then on the first order, we may assume that the radial oscillation as a function of the location is:
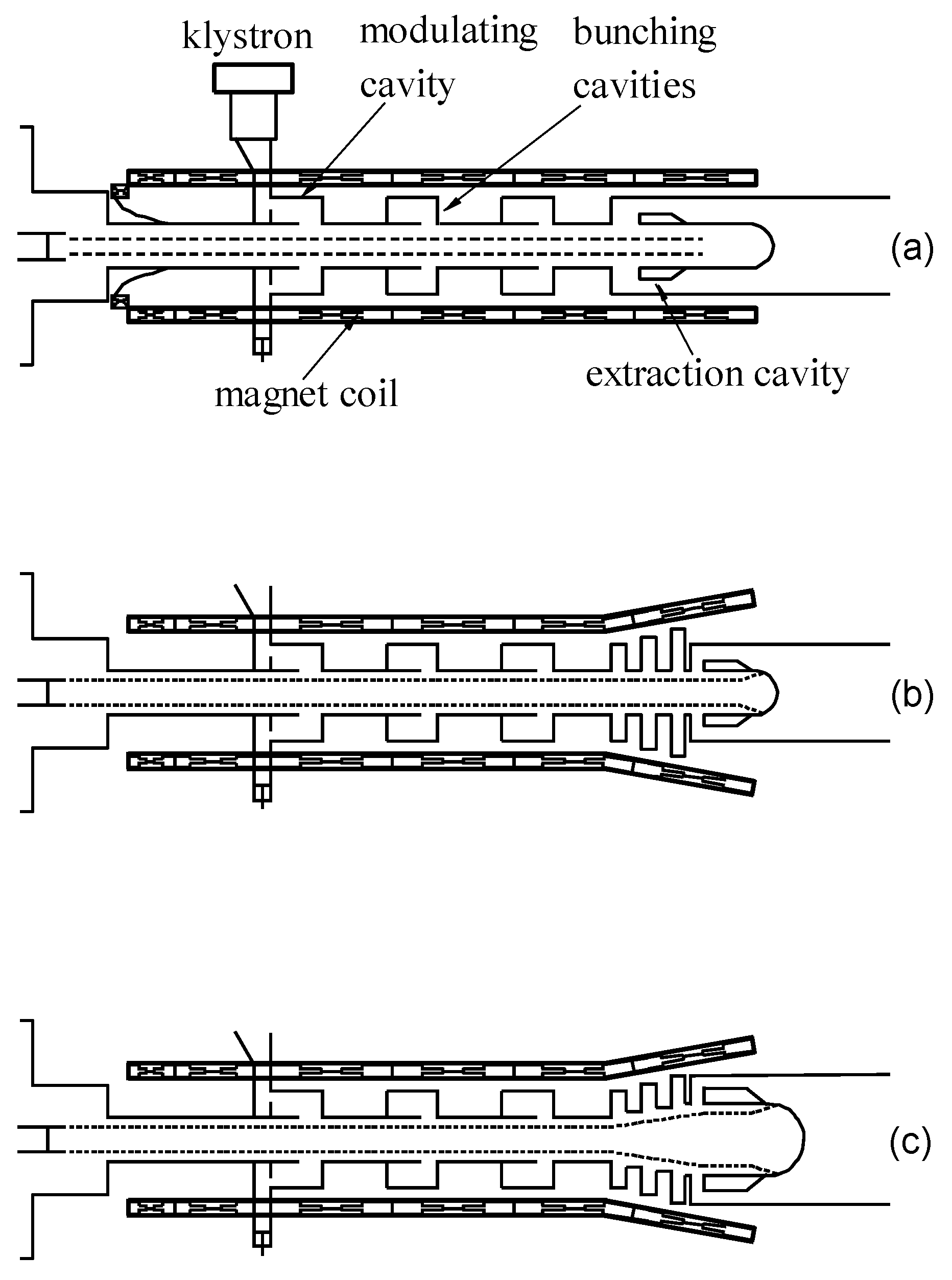
- According to the last result, there are several possibilities to taper the structure. Two are the most plausible: (i) Keeping the radius of the waveguide constant, but varying the guiding magnetic field and the external radius of the cavities (see in Figure 1b), such that the phase of the radial oscillation is preserved:(ii) Varying the waveguide radius, and thus the volume of the constraint on the guiding field may be weakened:
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andrews, M.L.; Davitian, H.; Hammer, D.A.; Fleischmann, H.H.; Nation, J.A.; Rostoker, N. On the propagation of high-current beams of relativistic electrons in gases. Appl. Phys. Lett. 1970, 16, 98–100. [Google Scholar] [CrossRef]
- Nation, J.A. On the coupling of a high-current relativistic electron beam to a slow wave structure. Appl. Phys. Lett. 1970, 17, 491–494. [Google Scholar] [CrossRef]
- Nation, J.A. A simple technique for single shot, microwave spectrum analysis. Rev. Sci. Instrum. 1970, 41, 1097–1098. [Google Scholar] [CrossRef]
- Andrews, M.L.; Davitian, H.; Fleischmann, H.H.; Kusse, B.; Kribel, R.E.; Nation, J.A. Generation of Astron-Type E Layers Using Very High-Current Electron Beams. Phys. Rev. Lett. 1971, 27, 1428–1431. [Google Scholar] [CrossRef]
- Carmel, Y.; Nation, J.A. Application of intense relativistic electron beams to microwave generation. J. Appl. Phys. 1973, 44, 5268–5274. [Google Scholar] [CrossRef]
- Carmel, Y.; Nation, J.A. Microwave emission from an anisotropy instability in a high-current relativistic electron beam. Phys. Rev. Lett. 1973, 31, 806–808. [Google Scholar] [CrossRef]
- Carmel, Y.; Nation, J.A. Instability of an unneutralized relativistic electron beam. Phys. Rev. Lett. 1973, 31, 286–289. [Google Scholar] [CrossRef]
- Carmel, Y.; Ivers, J.; Kribel, R.E.; Nation, J. Intense coherent cherenkov radiation due to the interaction of a relativistic electron beam with a slow-wave structure. Phys. Rev. Lett. 1974, 33, 1278–1282. [Google Scholar] [CrossRef]
- Granatstein, V.L.; Herndon, M.; Sprangle, P.; Carmel, Y.; Nation, J.A. Gigawatt microwave from an intense relativistic electron beam. Plasma Phys. 1975, 17, 23–28. [Google Scholar] [CrossRef]
- Providakes, G.; Nation, J.A.; Read, M.E. Microwave Generation Using Sheet Relativistic Electron Beams. IEEE Trans. Microw. Theory Tech. 1977, 25, 563–566. [Google Scholar] [CrossRef]
- Gammel, G.; Nation, J.A.; Read, M.E. Technique for the measurement of the amplitude and phase velocity of a slow space charge wave on a relativistic electron beam. Rev. Sci. Instrum. 1978, 49, 507–509. [Google Scholar] [CrossRef] [PubMed]
- Gammel, G.; Nation, J.A.; Read, M.E. Slow space-charge wave propagation on a relativistic electron beam. J. Appl. Phys. 1979, 50, 5603–5608. [Google Scholar] [CrossRef]
- Providakes, G.; Nation, J.A. Excitation of the slow cyclotron and space-charge waves in a relativistic electron beam. J. Appl. Phys. 1979, 50, 3026–3030. [Google Scholar] [CrossRef]
- Ivers, J.D.; Nation, J.A. Compact 1-GW pulse power source. Rev. Sci. Instrum. 1983, 54, 1509–1510. [Google Scholar] [CrossRef]
- Greenwald, S.; Kerslick, G.; Nation, J.A. Space-charge wave growth and propagation on a relativistic electron beam. IEEE Trans. Nucl. Sci. 1985, 32, 3497–3499. [Google Scholar] [CrossRef]
- Anselmo, A.; Kerslick, G.; Nation, J.A.; Providakes, G. Space-charge wave propagation in inhomogeneous waveguides. Phys. Fluids 1985, 28, 358–365. [Google Scholar] [CrossRef]
- Anselmo, A.; Nation, J.A. Parametric growth of space charge waves using a self-biased electrostatic wiggler. Phys. Fluids 1988, 31, 2037. [Google Scholar] [CrossRef]
- Shiffler, D.; Nation, J.A.; Wharton, C.B. High-power traveling-wave tube amplifier. Appl. Phys. Lett. 1989, 54, 674–676. [Google Scholar] [CrossRef]
- Shiffler, D.; Nation, J.A.; Kerslick, G.S. A high-power, traveling wave tube amplifier. IEEE Trans. Plasma Sci. 1990, 18, 546–552. [Google Scholar] [CrossRef]
- Schachter, L.; Nation, J.A.; Kerslick, G. On the bandwidth of a short traveling wave tube. J. Appl. Phys. 1990, 68, 5874–5882. [Google Scholar] [CrossRef]
- Schachter, L.; Nation, J.A. Analysis of a traveling wave tube tuned by a cavity. J. Appl. Phys. 1991, 70, 5186–5192. [Google Scholar] [CrossRef]
- Shiffler, D.; Ivers, J.D.; Kerslick, G.S.; Nation, J.A.; Schachter, L. Sideband development in a high-power traveling-wave tube microwave amplifier. Appl. Phys. Lett. 1991, 58, 899–901. [Google Scholar] [CrossRef]
- Schächter, L.; Nation, J.A.; Shiffler, D.A. Theoretical studies of high-power Cerenkov amplifiers. J. Appl. Phys. 1991, 70, 114–124. [Google Scholar] [CrossRef]
- Shiffler, D.; Nation, J.A.; Schachter, L.; Ivers, J.D.; Kerslick, G.S. A high-power two stage traveling-wave tube amplifier. J. Appl. Phys. 1991, 70, 106–113. [Google Scholar] [CrossRef]
- Schächter, L.; Nation, J.A. Slow-wave amplifiers and oscillators: A unified study. Phys. Rev. A 1992, 45, 8820–8832. [Google Scholar] [CrossRef]
- Kuang, E.; Davis, T.J.; Kerslick, G.; Nation, J.A.; Schächter, L. Transit time isolation of a high power microwave amplifier. Phys. Rev. Lett. 1993, 71, 2666–2669. [Google Scholar] [CrossRef] [PubMed]
- Davis, T.J.; Schächter, L.; Nation, J.A. High power microwaves at 9 GHz from an extended length cavity in a coaxial beam geometry. Appl. Phys. Lett. 1993, 63, 1854–1856. [Google Scholar] [CrossRef]
- Schächter, L.; Nation, J.A. Analytical method for studying a quasiperiodic disk loaded waveguide. Appl. Phys. Lett. 1993, 63, 2441–2443. [Google Scholar] [CrossRef]
- Davis, T.J.; Schächter, L.; Nation, J.A. Results from an X-band coaxial extended length cavity. IEEE Trans. Plasma Sci. 1994, 22, 504–510. [Google Scholar] [CrossRef]
- Kuang, E.; Davis, T.J.; Ivers, J.D.; Kerslick, G.; Nation, J.A.; Schächter, L. Low group velocity traveling wave tube amplifiers. IEEE Trans. Plasma Sci. 1994, 22, 511–517. [Google Scholar] [CrossRef]
- Schächter, L.; Nation, J.A. On the coupling between a quasiperiodic structure and an asymmetric output arm. IEEE Trans. Microw. Theory Tech. 1995, 43, 42–47. [Google Scholar] [CrossRef]
- Schachter, L.; Nation, J.A.; Schächter, L.; Nation, J.A. Propagation of electromagnetic and space-charge waves in quasiperiodic structures. Phys. Plasmas 1995, 2, 889–901. [Google Scholar] [CrossRef]
- Naqvi, S.A.; Kerslick, G.S.; Nation, J.A.; Schachter, L. Axial extraction of high-power microwaves from relativistic traveling wave amplifiers. Appl. Phys. Lett. 1996, 69, 1550–1552. [Google Scholar] [CrossRef]
- Naqvi, S.A.; Kerslick, G.S.; Nation, J.A.; Schächter, L. Resonance shift in relativistic traveling wave amplifiers. Phys. Rev. E 1996, 53, 4229–4231. [Google Scholar] [CrossRef]
- Naqvi, S.A.; Nation, J.A.; Schächter, L.; Wang, Q. High-efficiency TWT design using traveling-wave bunch compression. IEEE Trans. Plasma Sci. 1998, 26, 840–845. [Google Scholar] [CrossRef]
- Schächter, L.; Nation, J.A. Beam-quality and guiding-magnetic-field requirements for a high-power traveling-wave amplifier operating at 35 GHz. Phys. Rev. E 1998, 57, 7176–7183. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Z.; Ivers, J.D.; Nation, J.A.; Naqvi, S.; Schachter, L. Efficient operation of a high-power X-band traveling wave tube amplifier. Appl. Phys. Lett. 1999, 75, 2506–2507. [Google Scholar] [CrossRef]
- Banna, S.; Nation, J.A.; Schächter, L.; Wang, P. The interaction of symmetric and asymmetric modes in a high-power traveling-wave amplifier. IEEE Trans. Plasma Sci. 2000, 28, 798–811. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Z.; Nation, J.A.; Banna, S.; Schachter, L. Symmetric and asymmetric mode interaction in high-power traveling wave amplifiers: Experiments and theory. IEEE Trans. Plasma Sci. 2000, 28, 2262–2271. [Google Scholar] [CrossRef]
- Banna, S.; Schachter, L.; Nation, J.A.; Wang, P. Coupling of symmetric and asymmetric modes in a high-power, high-efficiency traveling-wave amplifier. Phys. Rev. E 2000, 61, 4445–4449. [Google Scholar] [CrossRef]
- Schachter, L. Beam Wave Interaction in Periodic and Quasi-Periodic Structures, 2nd ed.; Springer: Heidleberg, Germany, 2011; ISBN 978-3-642-19848-9. [Google Scholar]
- Friedman, M. Another approach to the injection of relativistic electrons into an astronlike device. Phys. Rev. Lett. 1970, 25, 567–570. [Google Scholar] [CrossRef]
- Friedman, M. Passage of an Intense Relativistic Electron Beam through a Cusped Magnetic Field. Phys. Rev. Lett. 1970, 24, 1098–1100. [Google Scholar] [CrossRef]
- Friedman, M.; Ury, M. Production and focusing of a high power relativistic annular electron beam. Rev. Sci. Instrum. 1970, 41, 1334–1335. [Google Scholar] [CrossRef]
- Friedman, M. A new diode for the production of high power relativistic electron beams. Rev. Sci. Instrum. 1971, 42, 1255–1256. [Google Scholar] [CrossRef]
- Friedman, M.; Herndon, M. Emission of coherent microwave radiation from a relativistic electron beam propagating in a spatially modulated field. Phys. Rev. Lett. 1972, 29, 55–58. [Google Scholar] [CrossRef]
- Friedman, M.; Ury, M. Microsecond duration intense relativistic electron beams. Rev. Sci. Instrum. 1972, 43, 1659–1661. [Google Scholar] [CrossRef]
- Friedman, M.; Herndon, M. Microwave emission produced by the interaction of an intense relativistic electron beam with a spatially modulated magnetic field. Phys. Rev. Lett. 1972, 28, 210–213. [Google Scholar] [CrossRef]
- Friedman, M.; Hammer, D.A. Catastrophic disruption of the flow of a magnetically confined intense relativistic electron beam. Appl. Phys. Lett. 1972, 21, 174–177. [Google Scholar] [CrossRef]
- Friedman, M.; Sprangle, P. Conditions for the production of rotational annular beams of relativistic electrons using a cusped magnetic field. Plasma Phys. 1972, 14, 207–210. [Google Scholar] [CrossRef]
- Friedman, M.; Herndon, M. Generation of intense infrared radiation from an electron beam propagating through a rippled magnetic field. Appl. Phys. Lett. 1973, 22, 658–660. [Google Scholar] [CrossRef]
- Friedman, M.; Herndon, M. Emission of coherent microwave radiation from a relativistic electron beam propagating in a spatially modulated field. Phys. Fluids 1973, 16, 1982–1995. [Google Scholar] [CrossRef]
- Friedman, M.; Hammer, D.A.; Manheimer, W.M.; Sprangle, P. Enhanced microwave emission due to the transverse energy of a relativistic electron beam. Phys. Rev. Lett. 1973, 31, 752–755. [Google Scholar] [CrossRef]
- Friedman, M.; Vitkovitsky, I.M. Implosion of an unneutralized drifting relativistic electron beam. Appl. Phys. Lett. 1974, 25, 259–260. [Google Scholar] [CrossRef]
- Friedman, M. Formation of a virtual cathode by a relativistic electron beam flowing through a cavity. Appl. Phys. Lett. 1974, 24, 303–305. [Google Scholar] [CrossRef]
- Friedman, M. Emission of intense microwave radiation from an automodulated relativistic electron beam. Appl. Phys. Lett. 1975, 26, 366–368. [Google Scholar] [CrossRef]
- Friedman, M. Unstable Flow of a Magnetically Focused Unneutralized Relativistic Electron Beam. Phys. Rev. Lett. 1975, 35, 572–574. [Google Scholar] [CrossRef]
- Friedman, M.; Siambis, J.G.; Bacon, D.P. Conditions for the self-destruction of a pulsed intense relativistic electron beam. Appl. Phys. Lett. 1976, 28, 308–311. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Conversion of the energy of intense relativistic electron beams into high-power electrical pulses. Rev. Sci. Instrum. 1983, 54, 1764–1766. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V.; Drobot, A.; Seftor, L. Propagation of intense relativistic electron beams through drift tubes with perturbed walls. Phys. Rev. Lett. 1983, 50, 1922–1925. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V.; Drobot, A.; Seftor, L. Self-modulation of an intense relativistic electron beam. J. Appl. Phys. 1984, 56, 2459–2474. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Generation of a modulated intense relativistic electron beam with a frequency tunable by a magnetic field. Rev. Sci. Instrum. 1984, 55, 1074–1076. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Interaction of a modulated intense relativistic electron beam with a cavity. Appl. Phys. Lett. 1984, 44, 394–395. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Modulation of intense relativistic electron beams by an external microwave source. Phys. Rev. Lett. 1985, 55, 2860–2863. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M.; Serlin, V. Parametric interaction of modulated intense relativistic electron beams with high-voltage gaps. Phys. Rev. Lett. 1985, 54, 2018–2021. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M.; Serlin, V. Behavior of high-voltage gaps in the presence of large space-charge fields. J. Appl. Phys. 1985, 58, 1460–1465. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Particle accelerators powered by modulated intense relativistic electron beams. Appl. Phys. Lett. 1986, 49, 596–598. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Generation of a high-power rf pulse in a rectangular waveguide. Rev. Sci. Instrum. 1987, 58, 58–59. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V. Electrostatic insulation of a high-voltage gap. IEEE Trans. Electr. Insul. 1988, 23, 51–56. [Google Scholar] [CrossRef]
- Lau, Y.Y.; Friedman, M.; Serlin, V.; Krall, J. Nonlinear Space-Charge Waves on an Intense Relativistic Electron Beam. IEEE Trans. Plasma Sci. 1988, 16, 249–257. [Google Scholar] [CrossRef]
- Friedman, M.; Krall, J.; Lau, Y.Y.; Serlin, V. Externally modulated intense relativistic electron beams. J. Appl. Phys. 1988, 64, 3353–3379. [Google Scholar] [CrossRef]
- Friedman, M.; Serlin, V.; Lau, Y.Y.; Krall, J. Electron accelerators driven by modulated intense relativistic electron beams. Phys. Rev. Lett. 1989, 63, 2468–2471. [Google Scholar] [CrossRef] [PubMed]
- Lau, Y.Y.; Friedman, M.; Krall, J.; Serlin, V. Relativistic Klystron amplifiers driven by modulated intense relativistic electron beams. IEEE Trans. Plasma Sci. 1990, 18, 553–569. [Google Scholar] [CrossRef]
- Krall, J.; Friedman, M.; Lau, Y.Y.; Serlin, V. Simulation Studies of a Klystronlike Amplifier Operating in the 10–100 GW Regime. IEEE Trans. Electromagn. Compat. 1992, 34, 222–228. [Google Scholar] [CrossRef]
- Friedman, M.; Fernsler, R.; Slinker, S.; Hubbard, R. Intense Relativistic Electron Beams into rf Waves. Phys. Rev. Lett. 1995, 75, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M.; Serlin, V.; Lampe, M.; Hubbard, R.; Colombant, D.; Slinker, S. Intense electron beam modulation by inductively loaded wide gaps for relativistic klystron amplifiers. Phys. Rev. Lett. 1995, 74, 322–325. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M.; Serlin, V. Generation of a large diameter intense relativistic electron beam for the triaxial relativistic klystron amplifier. Rev. Sci. Instrum. 1995, 66, 3488–3493. [Google Scholar] [CrossRef]
- Friedman, M. Propagation of an intense relativistic electron beam in an annular channel. J. Appl. Phys. 1996, 80, 1263–1267. [Google Scholar] [CrossRef]
- Friedman, M.; Pasour, J.; Smithe, D. Modulating electron beams for an X band relativistic klystron amplifier. Appl. Phys. Lett. 1997, 71, 3724–3726. [Google Scholar] [CrossRef]
- Friedman, M.; Fernsler, R.F. Guiding radio frequency waves on metallic foils. Appl. Phys. Lett. 1999, 74, 3468–3470. [Google Scholar] [CrossRef]
- Friedman, M.; Swanekamp, S.; Obenschain, S.; Chan, Y.; Ludeking, L.; Smithe, D. Stability of large-area electron-beam diodes. Appl. Phys. Lett. 2000, 77, 1053–1055. [Google Scholar] [CrossRef]
- Friedman, M. Extraction of radio frequency from electromagnetic surface waves guided by metallic strips. Rev. Sci. Instrum. 2000, 71, 551–553. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, D.; Liao, C.; Li, Z. CHIPIC: An Efficient Code for Electromagnetic PIC Modeling and Simulation. IEEE Trans. Plasma Sci. 2009, 37, 2002–2011. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, H.; Schächter, L. Radial Kick in High-Efficiency Output Structures. Plasma 2019, 2, 15-26. https://doi.org/10.3390/plasma2010003
Hua H, Schächter L. Radial Kick in High-Efficiency Output Structures. Plasma. 2019; 2(1):15-26. https://doi.org/10.3390/plasma2010003
Chicago/Turabian StyleHua, Huang, and Levi Schächter. 2019. "Radial Kick in High-Efficiency Output Structures" Plasma 2, no. 1: 15-26. https://doi.org/10.3390/plasma2010003
APA StyleHua, H., & Schächter, L. (2019). Radial Kick in High-Efficiency Output Structures. Plasma, 2(1), 15-26. https://doi.org/10.3390/plasma2010003



