Effect of (Ba1/3Nb2/3)4+ Substitution on Microstructure, Bonding Properties and Microwave Dielectric Properties of Ce2Zr3(MoO4)9 Ceramics
Abstract
1. Introduction
2. Experimental Section
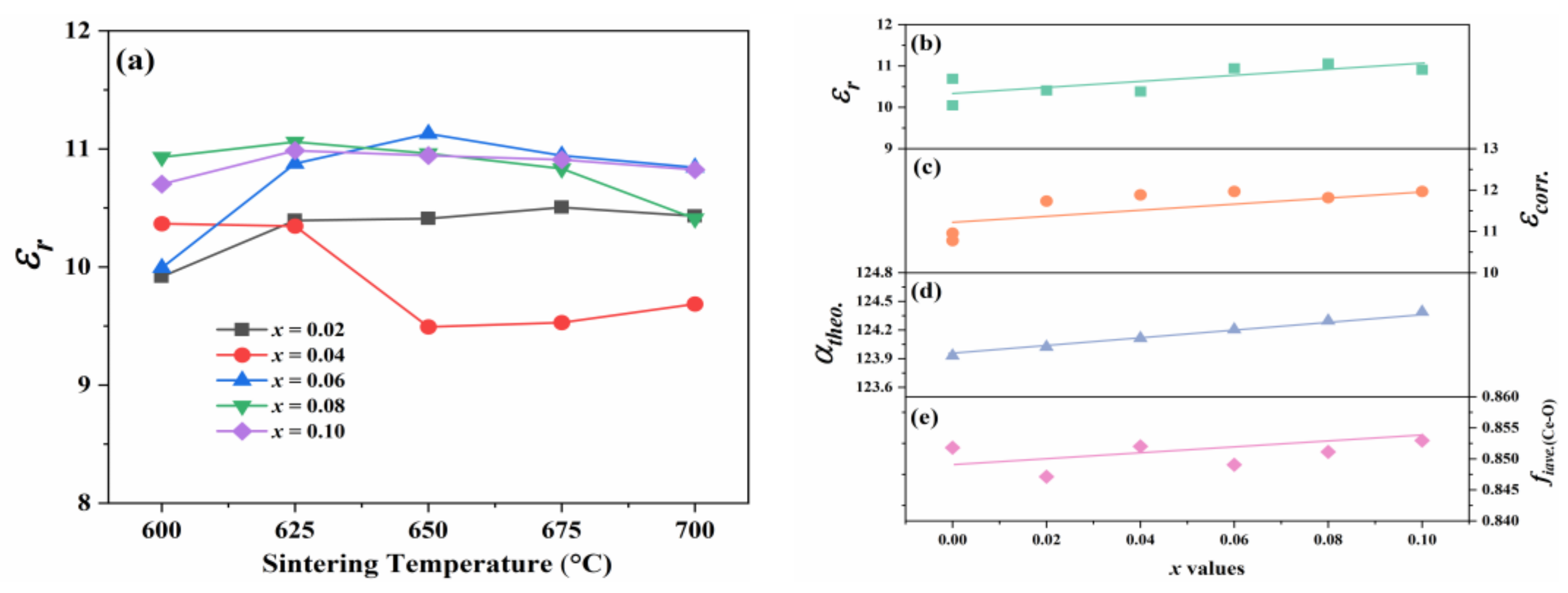
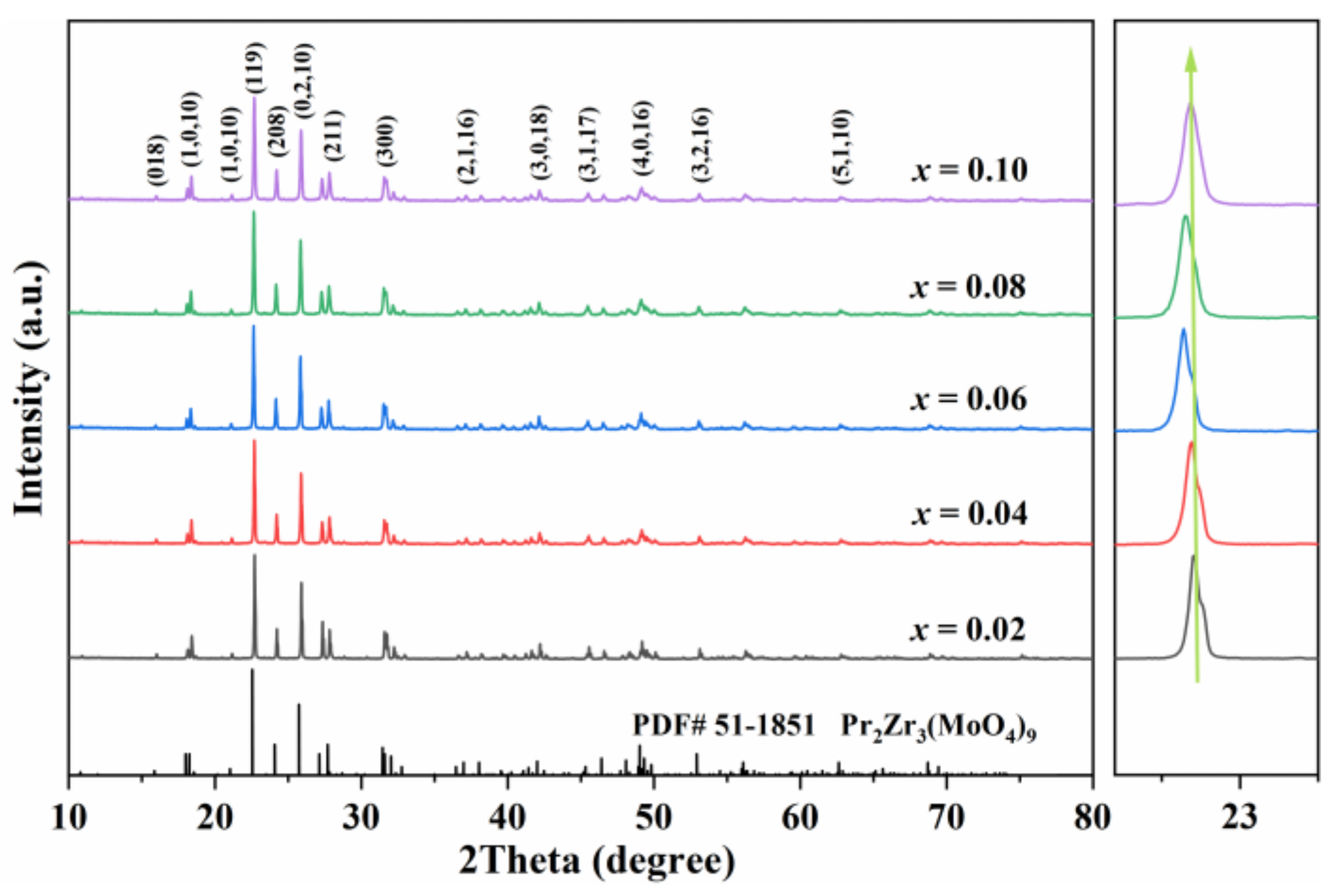
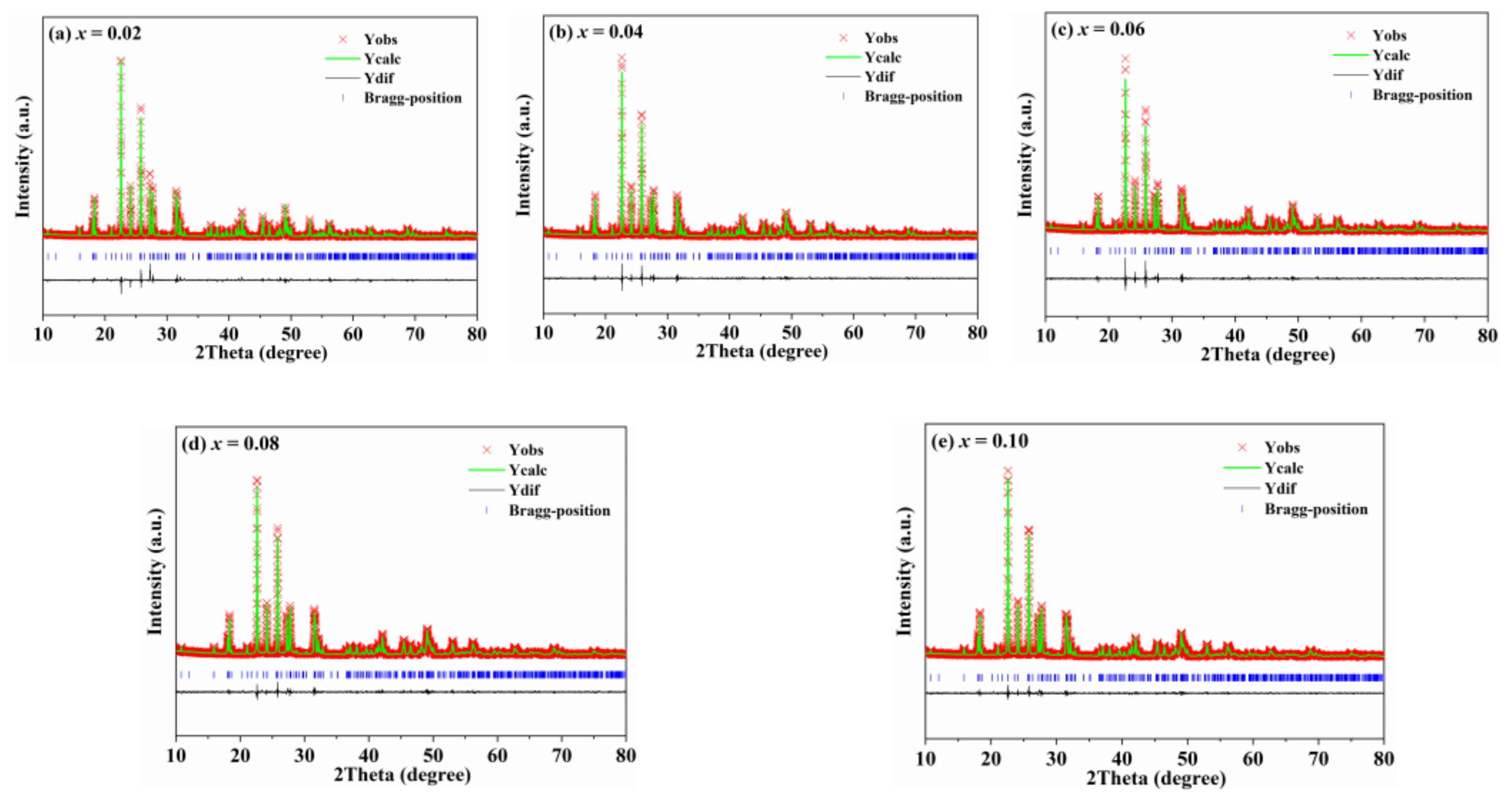
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; Silva, P.D.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A tutorial overview of standards, trials, challenges, deployment, and practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.D.; Zhao, S. 5G Internet of Things: A survey. J. Ind. Inf. Integr. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Yao, G.; Yan, J.; Tan, J.; Pei, C.; Liu, P.; Zhang, H.; Wang, D. Structure, chemical bond and microwave dielectric characteristics of novel Li3Mg4NbO8 ceramics. J. Eur. Ceram. Soc. 2021, 41, 6490–6494. [Google Scholar] [CrossRef]
- Luo, W.; Yan, S.; Zhou, J. Ceramic-based dielectric metamaterials. Interdiscip. Mater. 2022, 1, 11–27. [Google Scholar] [CrossRef]
- Tan, K.; Song, T.; Shen, T.; Yu, H.; Zhang, Y.; Cui, K.; Xu, X.; Li, W.; Wang, H. Research progress of low permittivity microwave dielectric ceramics. Adv. Ceram. 2022, 43, 11–29. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, J.; Tang, Y.; Xiang, H.; Li, J.; Fang, L. Relationship between bond characteristics and microwave dielectric properties of REVO4 (RE = Yb, Ho) ceramics. Ceram. Int. 2023, 49, 875–881. [Google Scholar] [CrossRef]
- Pei, C.; Hou, C.; Li, Y.; Yao, G.; Ren, Z.; Liu, P.; Zhang, H. A low εr and temperature-stable Li3Mg2SbO6 microwave dielectric ceramics. J. Alloys Compd. 2019, 792, 46–49. [Google Scholar] [CrossRef]
- Pei, C.; Tan, J.; Li, Y.; Yao, G.; Jia, Y.; Ren, Z.; Liu, P.; Zhang, H. Effect of Sb-site nonstoichiometry on the structure and microwave dielectric properties of Li3Mg2Sb1−xO6 ceramics. J. Adv. Ceram. 2020, 9, 588–594. [Google Scholar] [CrossRef]
- Huang, X.; Guo, H.; Zhu, P.; Liu, L.; Xiao, J.; Tang, D.; Lin, C.; Wu, X.; Zheng, X. Microwave dielectric properties of CaCu3Ti4O12 ceramics: A clue to its intrinsic dielectric response. J. Adv. Dielectr. 2023, 13, 2344001–2344006. [Google Scholar] [CrossRef]
- An, Z.; Lv, J.; Wang, X.; Xu, Y.; Zhang, L.; Shi, F.; Guo, H.; Zhou, D.; Liu, B.; Song, K. Effects of LiF additive on crystal structures, lattice vibrational characteristics and dielectric properties of CaWO4 microwave dielectric ceramics for LTCC applications. Ceram. Int. 2022, 48, 29929–29937. [Google Scholar] [CrossRef]
- Zhou, D.; Pang, L.; Wang, D.; Guo, H.; Yang, F.; Qi, Z.; Li, C.; Jin, B.; Reaney, I.M. Crystal structure, impedance and broadband dielectric spectra of ordered scheelite-structured Bi(Sc1/3Mo2/3)O4 ceramic. J. Eur. Ceram. Soc. 2018, 38, 1556–1561. [Google Scholar] [CrossRef]
- Tao, B.J.; Xing, C.F.; Wang, W.F.; Wu, H.T.; Zhou, Y.Y. A novel Ce2Zr3(MoO4)9 microwave dielectric ceramic with ultra-low firing temperature. Ceram. Int. 2019, 45, 24675–24683. [Google Scholar] [CrossRef]
- Liu, W.; Zuo, R. Low temperature fired Ln2Zr3(MoO4)9 (Ln = Sm, Nd) microwave dielectric ceramics. Ceram. Int. 2017, 43, 17229–17232. [Google Scholar] [CrossRef]
- Liu, W.; Zuo, R. A novel low-temperature firable La2Zr3(MoO4)9 microwave dielectric ceramic. J. Eur. Ceram. Soc. 2018, 38, 339–342. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Sun, J.J.; Dai, N.; Wu, Z.C.; Wu, H.T.; Yang, C.H. Crystal structure, infrared spectra and microwave dielectric properties of novel extra low-temperature fired Eu2Zr3(MoO4)9 ceramics. J. Eur. Ceram. Soc. 2019, 39, 1127–1131. [Google Scholar] [CrossRef]
- Shi, L.; Liu, C.; Zhang, H.; Peng, R.; Wang, G.; Shi, X.; Wang, X.; Wang, W. Crystal structure, Raman spectroscopy, metal compatibility and microwave dielectric properties of Ce2Zr3(MoO4)9 ceramics. Mater. Chem. Phys. 2020, 250, 122954. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, Y.; Tao, B.; Zhang, Q.; Wu, H.; Zhang, X. Crystal structure and optimised microwave dielectric properties of Ce2(Zr1−xTix)3(MoO4)9 solid solutions. Ceram. Int. 2021, 47, 5624–5630. [Google Scholar] [CrossRef]
- Xu, X.; Xi, Z.; Feng, Z.; Zhang, X.; Du, W.; Shan, L.; Du, J.; Wu, H.; Wangsuo, X. Microstructure, bonding characteristics, far-infrared spectra and microwave dielectric properties of co-substituted Ce2[(Zr1−x(Zn1/3Sb2/3)x]3(MoO4)9 ceramics. Ceram. Int. 2024, 50, 24769–24780. [Google Scholar] [CrossRef]
- Pan, H.; Yan, S.; Zhang, Y.; Du, J.; Zhang, X.; Gong, P.; Wu, H.; Tian, H.; Wübbenhorst, M. Crystal structure, bond characteristics and microwave dielectric properties of Ce2[Zr1−x(Sr1/3B2/3)x]3(MoO4)9 (B = Ta, Sb) solid solutions. Ceram. Int. 2023, 49, 24038–24046. [Google Scholar] [CrossRef]
- Du, K.; Zhou, M.; Li, C.; Yin, C.; Cai, Y.; Cheng, M.; Zhu, W.; Wei, G.; Wang, S.; Lei, W. Ultralow-permittivity and temperature-stable Ba1−xCaxMg2Al6Si9O30 dielectric ceramics for C-Band patch antenna applications. ACS Appl. Mater. Interfaces 2024, 16, 23505–23516. [Google Scholar] [CrossRef]
- Siragam, S. Synthesis and fabrication of proto-type microstrip patch antenna by using microwave dielectric ceramic nanocomposite material for C-band application. Optik 2024, 306, 171787. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Found. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- McCusker, L.; Von Dreele, R.; Cox, D.; Louër, D.; Scardi, P. Rietveld refinement guidelines. J. Appl. Crystallogr. 1999, 32, 36–50. [Google Scholar] [CrossRef]
- Yang, H.; Chai, L.; Liang, G.; Xing, M.; Fang, Z.; Zhang, X.; Qin, T.; Li, E. Structure, far-infrared spectroscopy, microwave dielectric properties, and improved low-temperature sintering characteristics of tri-rutile Mg0.5Ti0.5TaO4 ceramics. J. Adv. Ceram. 2023, 12, 296–308. [Google Scholar] [CrossRef]
- Bao, J.; Zhang, Y.; Kimura, H.; Wu, H.; Yue, Z. Crystal structure, chemical bond characteristics, infrared reflection spectrum, and microwave dielectric properties of Nd2(Zr1−xTix)3(MoO4)9 ceramics. J. Adv. Ceram. 2023, 12, 82–92. [Google Scholar] [CrossRef]
- Wang, X.; Liu, T.; Cao, Z.; Li, Z.; Xu, Y.; Shi, F.; Zhang, L.; Qi, Z.-m. Lattice vibrational characteristics and structure-property relationships of Ca(Mg1/2W1/2)O3 microwave dielectric ceramics with different sintering temperatures. Ceram. Int. 2022, 48, 1415–1422. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Guo, Y.; Ran, S. Influences of substituting of (Ni1/3Nb2/3)4+ for Ti4+ on the phase compositions, microstructures, and dielectric properties of Li2Zn[Ti1−x(Ni1/3Nb2/3)x]3O8 (0 ≤ x ≤ 0.3) microwave ceramics. J. Adv. Ceram. 2023, 12, 760–777. [Google Scholar] [CrossRef]
- Shannon, R.D. Dielectric polarizabilities of ions in oxides and fluorides. J. Appl. Phys. 1993, 73, 348–366. [Google Scholar] [CrossRef]
- Phillips, J.C.; Van Vechten, J.A. Charge redistribution and piezoelectric constants. Phys. Rev. Lett. 1969, 23, 1115–1117. [Google Scholar] [CrossRef]
- Levine, B.F. Bond susceptibilities and ionicities in complex crystal structures. J. Chem. Phys. 1973, 59, 1463–1486. [Google Scholar] [CrossRef]
- Wu, Z.J.; Meng, Q.B.; Zhang, S.Y. Semiempirical study on the valences of Cu and bond covalency in Y1−xCaxBa2Cu3O6+y. Phys. Rev. B 1998, 58, 958–962. [Google Scholar] [CrossRef]
- Stepan, S.B. Dielectric methods of studying the chemical bond and the concept of electronegativity. Russ. Chem. Rev. 1982, 51, 684. [Google Scholar] [CrossRef]
- Berkov, D.V. Evaluation of the energy barrier distribution in many-particle systems using the path integral approach. J. Phys. Condens. Matter 1998, 10, L89. [Google Scholar] [CrossRef]
- Fang, W.; Chen, J.; Yang, Y.; Ao, L.; Tang, Y.; Li, J.; Fang, L. Anomalous microwave dielectric behaviour induced by the orthorhombic-tetragonal phase transition in CaLaGaO4 ceramics. J. Eur. Ceram. Soc. 2022, 42, 1474–1479. [Google Scholar] [CrossRef]
- Sun, Y.; Xiang, H.; Tang, Y.; Li, J.; Fang, L. Constructing the cationic rattling effect to realize the adjustability of the temperature coefficient in Nd2-xSmxO3 microwave dielectric ceramics. J. Eur. Ceram. Soc. 2024, 44, 2859–2865. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, D.; Li, J.; Gan, G.; Rao, Y.; Huang, X.; Yang, Y.; Shi, L.; Liao, Y.; Liu, C.; et al. Crystal structure, bond energy, Raman spectra, and microwave dielectric properties of Ti-doped Li3Mg2NbO6 ceramics. J. Am. Ceram. Soc. 2020, 103, 4321–4332. [Google Scholar] [CrossRef]
- Li, F.; Li, Y.; Li, S.; Luo, Y.; Lu, Y.; Tang, T.; Liao, Y.; Zhang, J.; Wen, Q. All-ceramic array patch for 5G signal enhancement based on B-site substituted zinc-cobalt molybdate low temperature co-fired ceramics. Chem. Eng. J. 2023, 466, 143325. [Google Scholar] [CrossRef]
- Wu, F.F.; Zhou, D.; Du, C.; Xu, D.M.; Li, R.T.; Shi, Z.Q.; Darwish, M.; Zhou, T.; Jantunen, H. Design and fabrication of a satellite communication dielectric resonator antenna with novel low loss and temperature stabilized (Sm1−xCax)(Nb1−xMox)O4 (x = 0.15–0.7) microwave ceramics. Chem. Mater. 2023, 35, 104–115. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, X.; Zhang, Z.; Liu, Y.; Wu, H. Low-permittivity LiLn(PO3)4 (Ln = La, Sm, Eu) dielectric ceramics for microwave/millimeter-wave communication. J. Adv. Ceram. 2024, 13, 602–620. [Google Scholar] [CrossRef]
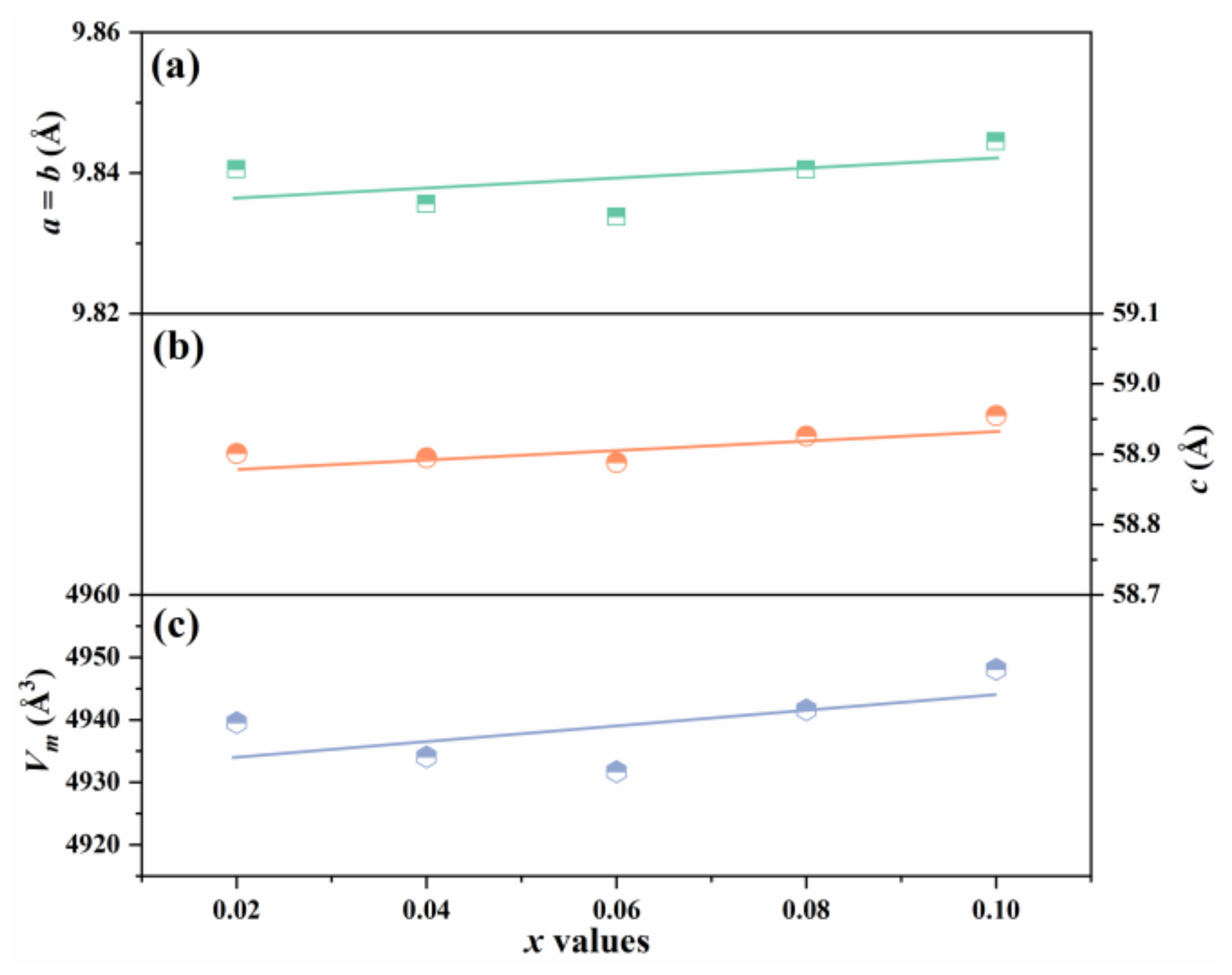
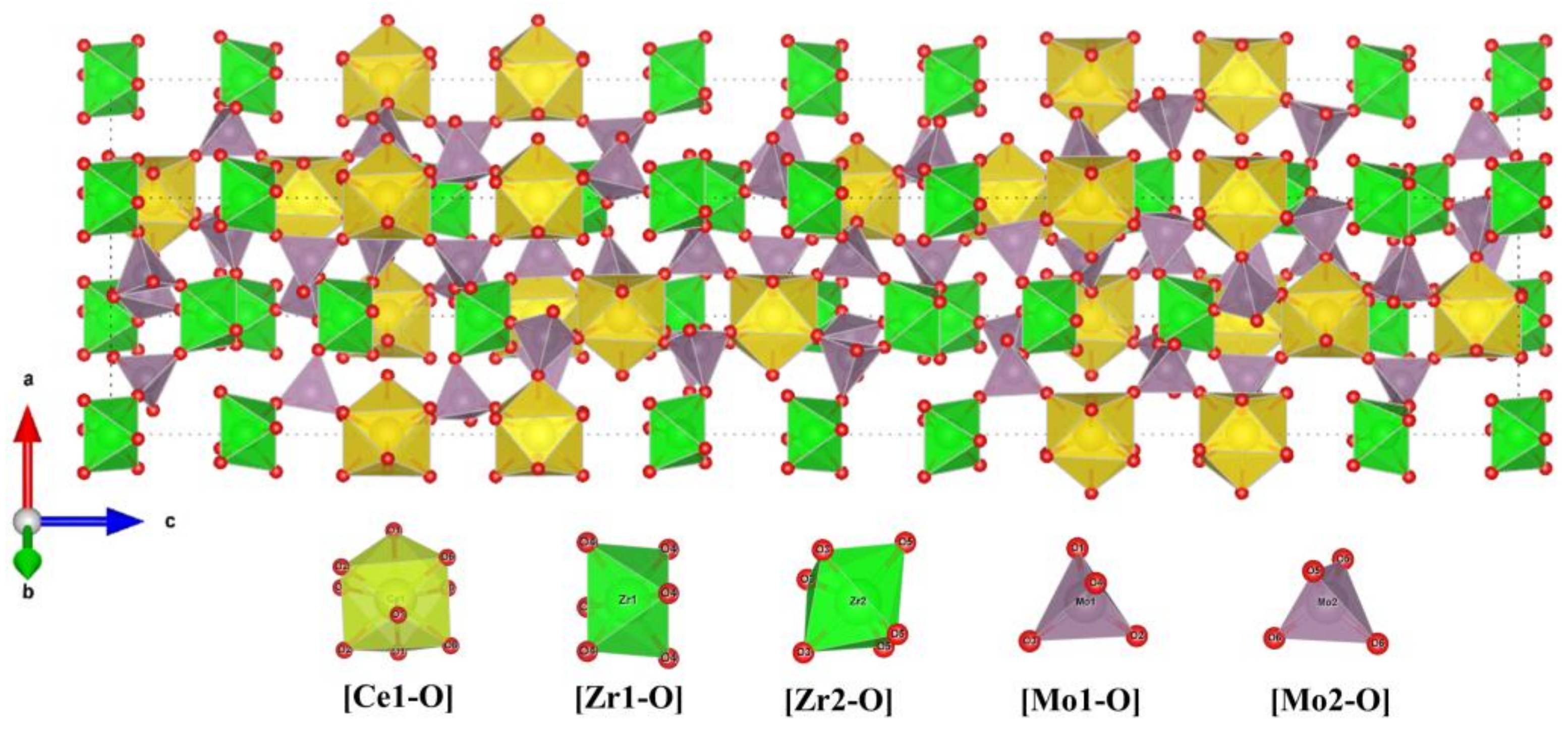
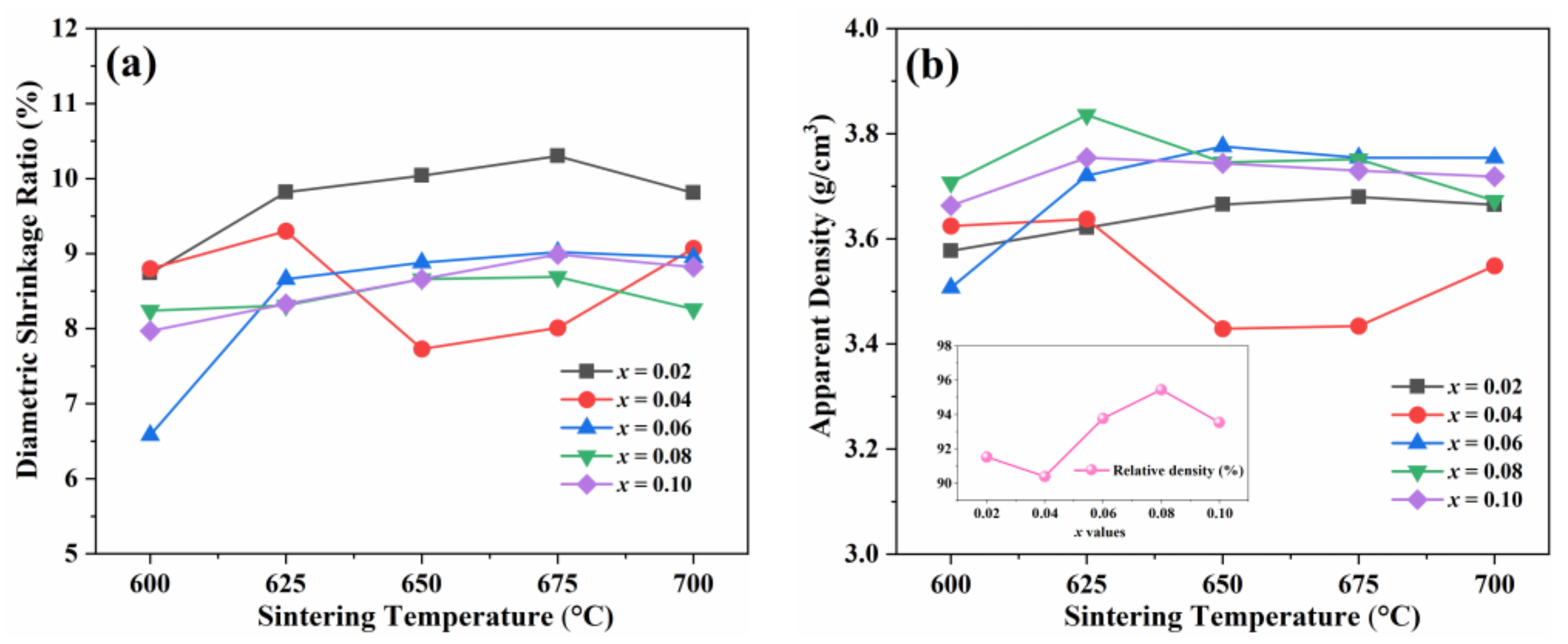
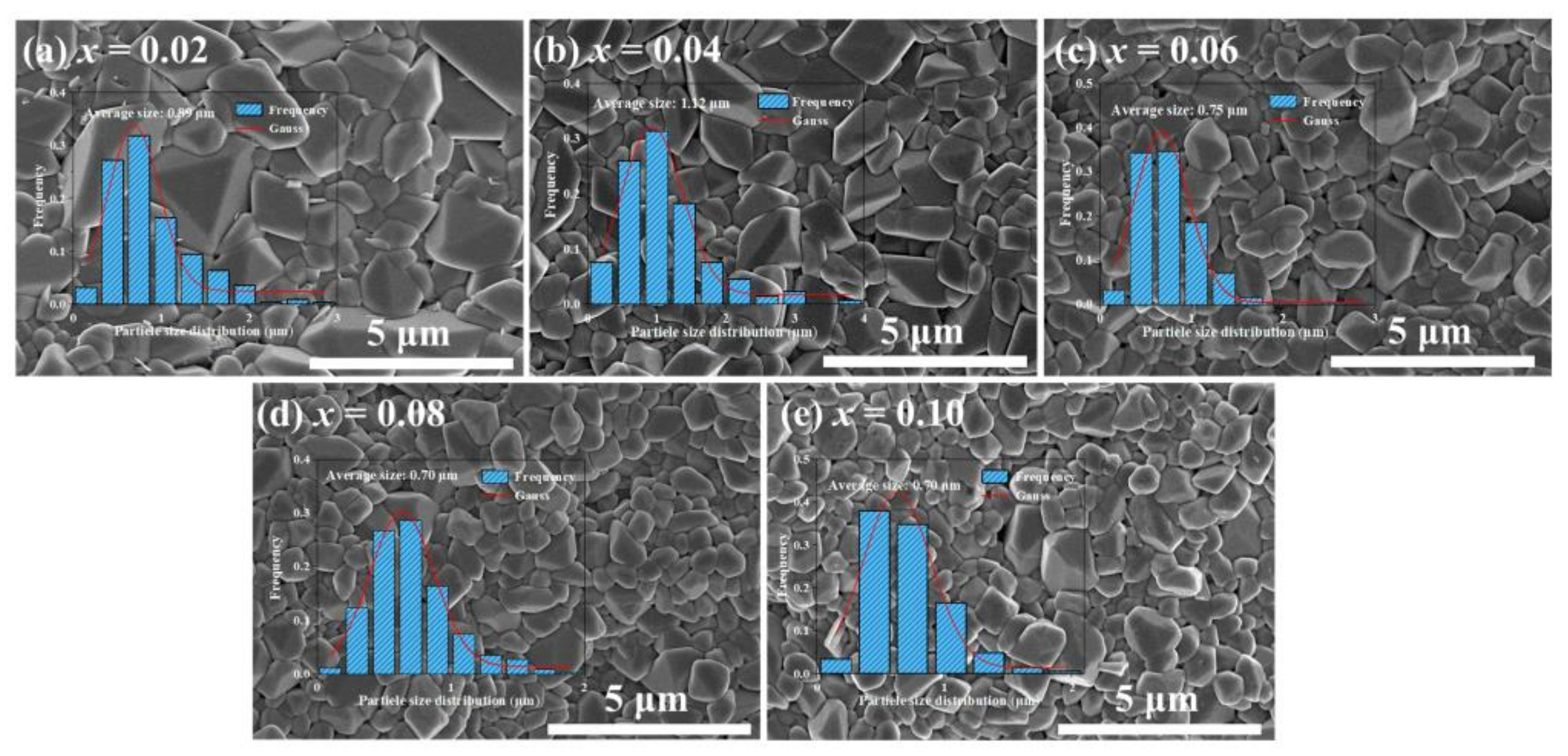
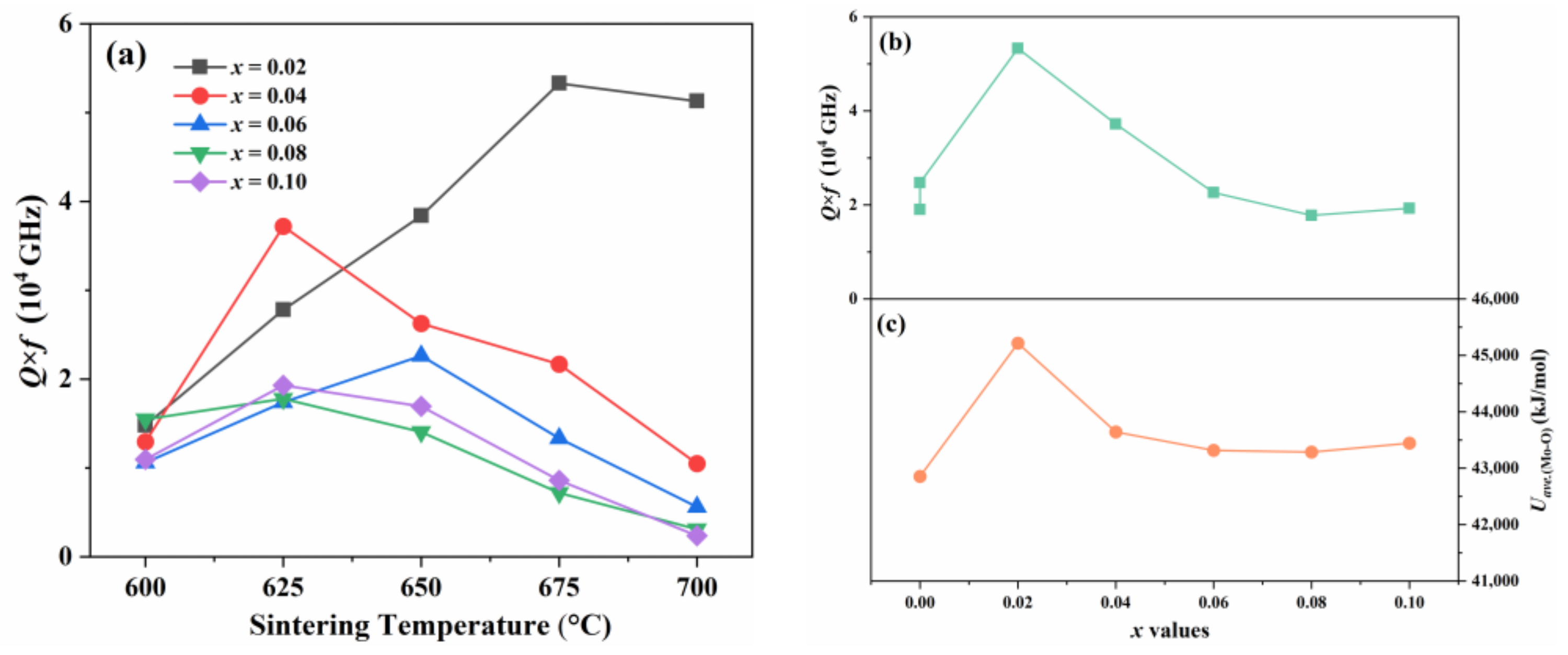
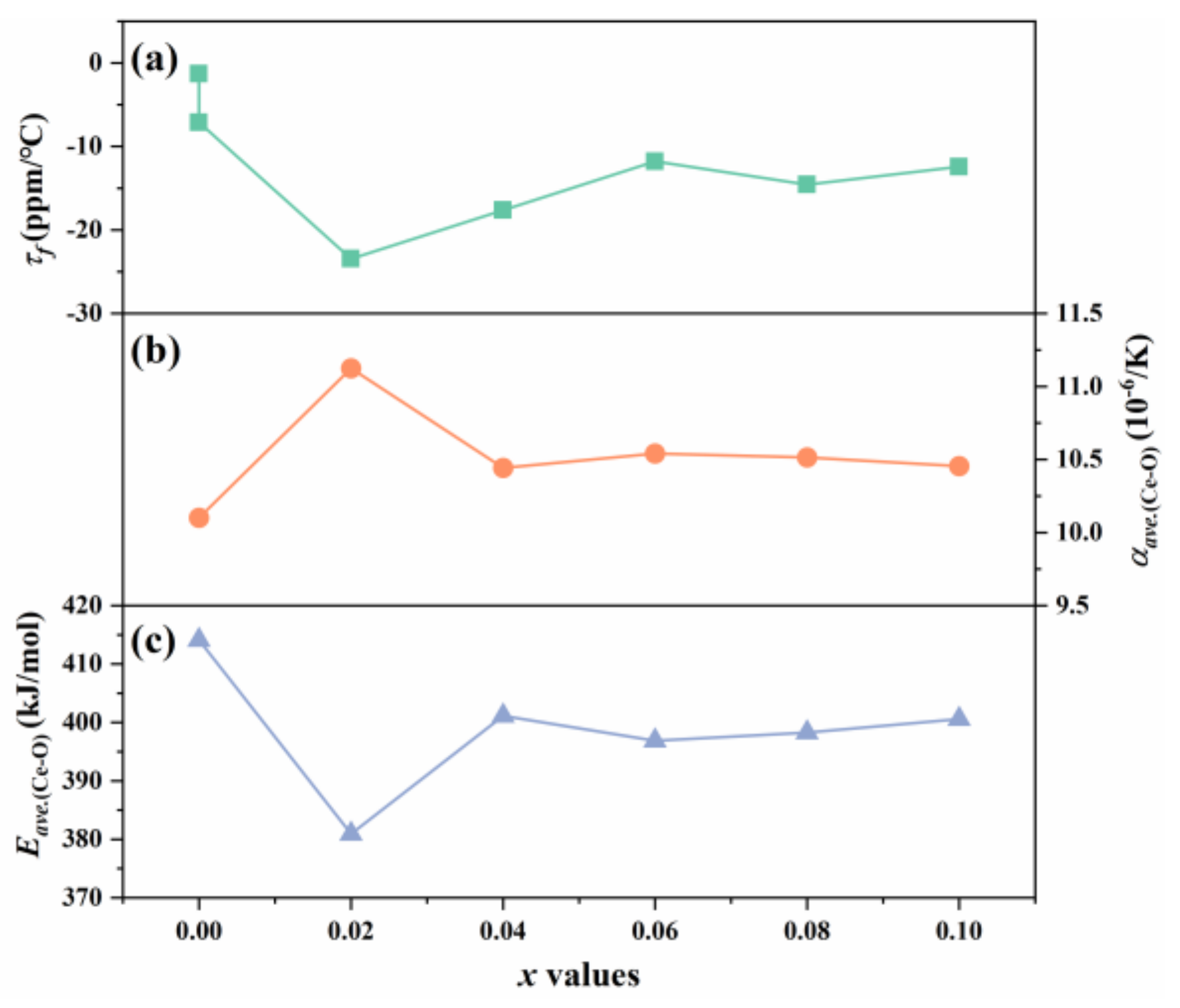
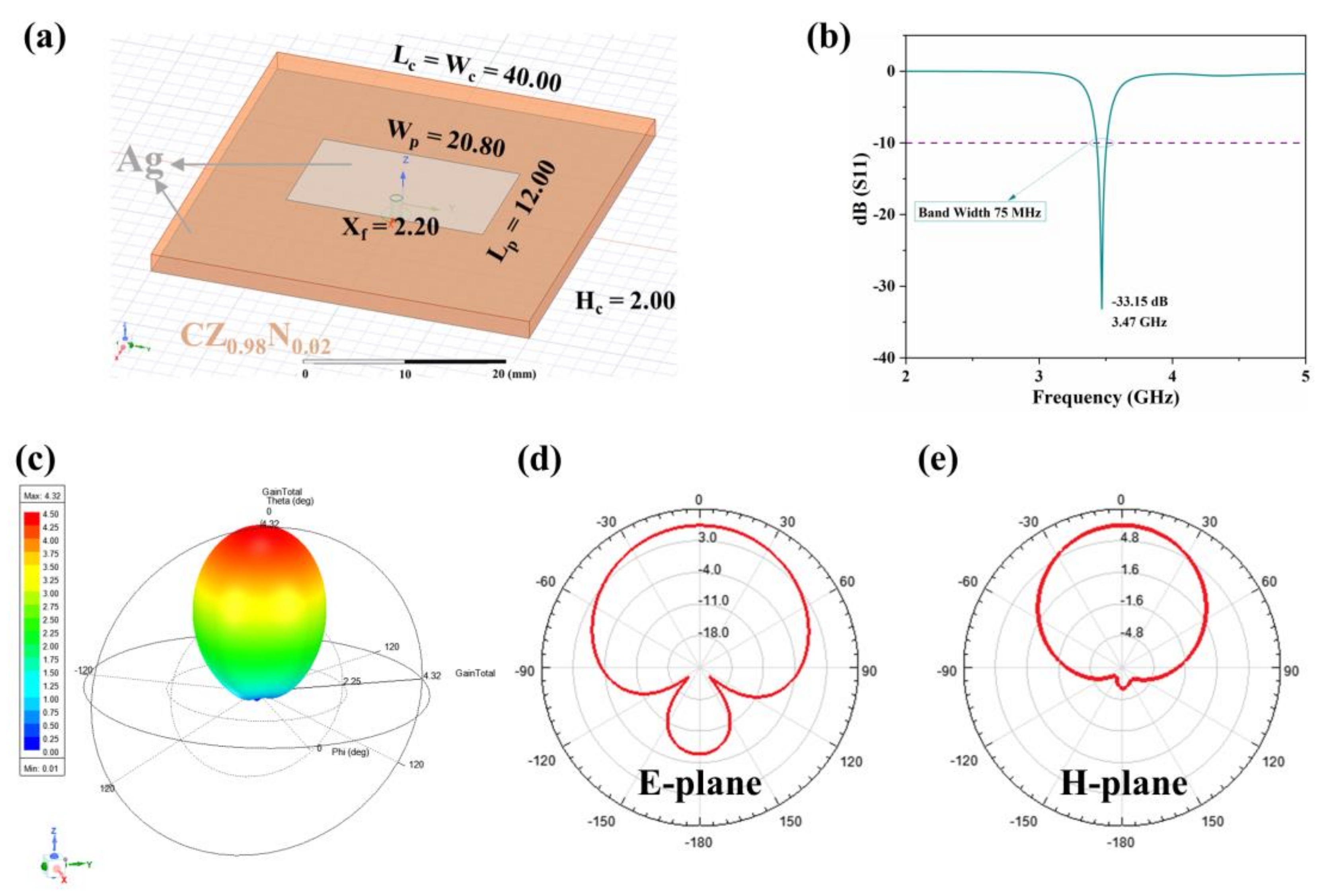
| x | Lattice Parameter | Reliability Factors | ||||||
|---|---|---|---|---|---|---|---|---|
| a = b (Å) | c (Å) | α = β (°) | γ (°) | Vm (Å3) | Rp (%) | Rwp (%) | χ2 | |
| 0.02 | 9.8405 | 58.9013 | 90 | 120 | 4939.56 | 6.17 | 8.07 | 2.52 |
| 0.04 | 9.8356 | 58.8950 | 90 | 120 | 4934.08 | 5.25 | 6.65 | 1.70 |
| 0.06 | 9.8337 | 58.8883 | 90 | 120 | 4931.71 | 5.60 | 7.06 | 1.85 |
| 0.08 | 9.8404 | 58.9261 | 90 | 120 | 4941.58 | 4.96 | 6.31 | 1.49 |
| 0.10 | 9.8445 | 58.9552 | 90 | 120 | 4948.08 | 4.76 | 6.08 | 1.49 |
| Bond Type | x = 0.02 | x = 0.04 | x = 0.06 | x = 0.08 | x = 0.10 |
|---|---|---|---|---|---|
| Ce-O(1) a | 0.8393 | 0.8490 | 0.8476 | 0.8506 | 0.8517 |
| Ce-O(1) b | 0.8393 | 0.8490 | 0.8476 | 0.8506 | 0.8518 |
| Ce-O(1) c | 0.8393 | 0.8490 | 0.8476 | 0.8507 | 0.8518 |
| Ce-O(2) a | 0.8382 | 0.8509 | 0.8485 | 0.8493 | 0.8533 |
| Ce-O(2) b | 0.8382 | 0.8509 | 0.8485 | 0.8493 | 0.8533 |
| Ce-O(2) c | 0.8382 | 0.8510 | 0.8485 | 0.8494 | 0.8533 |
| Ce-O(6) a | 0.8638 | 0.8561 | 0.8511 | 0.8534 | 0.8538 |
| Ce-O(6) b | 0.8638 | 0.8561 | 0.8511 | 0.8534 | 0.8538 |
| Ce-O(6) c | 0.8639 | 0.8561 | 0.8511 | 0.8534 | 0.8539 |
| Zr(BaNb)1-O(4) × 6 | 0.7865 | 0.7913 | 0.7952 | 0.7923 | 0.7913 |
| Zr(BaNb)2-O(3) a | 0.7666 | 0.7817 | 0.7781 | 0.7821 | 0.7835 |
| Zr(BaNb)2-O(3) b | 0.7666 | 0.7817 | 0.7781 | 0.7821 | 0.7836 |
| Zr(BaNb)2-O(3) c | 0.7666 | 0.7817 | 0.7782 | 0.7820 | 0.7836 |
| Zr(BaNb)2-O(5) a | 0.7643 | 0.7876 | 0.7762 | 0.7803 | 0.7836 |
| Zr(BaNb)2-O(5) b | 0.7644 | 0.7877 | 0.7762 | 0.7803 | 0.7836 |
| Zr(BaNb)2-O(5) c | 0.7644 | 0.7877 | 0.7763 | 0.7803 | 0.7837 |
| Mo1-O(1) | 0.7021 | 0.7170 | 0.7046 | 0.7103 | 0.7117 |
| Mo1-O(2) | 0.7095 | 0.7191 | 0.7062 | 0.7179 | 0.7198 |
| Mo1-O(3) | 0.7161 | 0.7370 | 0.7289 | 0.7312 | 0.7390 |
| Mo1-O(4) | 0.7048 | 0.7315 | 0.7222 | 0.7267 | 0.7280 |
| Mo2-O(5) × 2 | 0.7104 | 0.7251 | 0.7268 | 0.7307 | 0.7317 |
| Mo2-O(6) × 2 | 0.6281 | 0.7037 | 0.7006 | 0.7030 | 0.7104 |
| Bond Type | x = 0.02 | x = 0.04 | x = 0.06 | x = 0.08 | x = 0.10 |
|---|---|---|---|---|---|
| Ce-O(1) a | 1095 | 1100 | 1080 | 1076 | 1085 |
| Ce-O(1) b | 1095 | 1100 | 1080 | 1075 | 1085 |
| Ce-O(1) c | 1095 | 1100 | 1080 | 1075 | 1085 |
| Ce-O(2) a | 1103 | 1086 | 1074 | 1084 | 1074 |
| Ce-O(2) b | 1102 | 1085 | 1074 | 1084 | 1074 |
| Ce-O(2) c | 1102 | 1085 | 1074 | 1084 | 1074 |
| Ce-O(6) a | 906 | 1048 | 1055 | 1056 | 1070 |
| Ce-O(6) b | 906 | 1048 | 1055 | 1056 | 1070 |
| Ce-O(6) c | 906 | 1048 | 1055 | 1056 | 1070 |
| Zr(BaNb)1-O(4) × 6 | 10,161 | 10,653 | 10,145 | 10,476 | 10,702 |
| Zr(BaNb)2-O(3) a | 3726 | 3711 | 3676 | 3665 | 3696 |
| Zr(BaNb)2-O(3) b | 3726 | 3709 | 3676 | 3665 | 3696 |
| Zr(BaNb)2-O(3) c | 3726 | 3709 | 3675 | 3666 | 3695 |
| Zr(BaNb)2-O(5) a | 3761 | 3613 | 3707 | 3694 | 3695 |
| Zr(BaNb)2-O(5) b | 3761 | 3612 | 3707 | 3694 | 3695 |
| Zr(BaNb)2-O(5) c | 3760 | 3611 | 3706 | 3694 | 3694 |
| Mo1-O(1) | 43,587 | 44,245 | 45,021 | 44,810 | 45,295 |
| Mo1-O(2) | 42,314 | 43,919 | 44,773 | 43,585 | 44,009 |
| Mo1-O(3) | 41,121 | 40,777 | 40,864 | 41,257 | 40,646 |
| Mo1-O(4) | 43,133 | 41,786 | 42,088 | 42,075 | 42,641 |
| Mo2-O(5) × 2 | 42,157 | 42,900 | 41,254 | 41,343 | 41,993 |
| Mo2-O(6) × 2 | 53,631 | 46,310 | 45,640 | 45,941 | 45,491 |
| Bond Type | x = 0.02 | x = 0.04 | x = 0.06 | x = 0.08 | x = 0.10 |
|---|---|---|---|---|---|
| Ce-O(1) a | 10.2227 | 10.1619 | 10.4087 | 10.4592 | 10.3461 |
| Ce-O(1) b | 10.2227 | 10.1619 | 10.4087 | 10.4719 | 10.3461 |
| Ce-O(1) c | 10.2227 | 10.1619 | 10.4087 | 10.4719 | 10.3461 |
| Ce-O(2) a | 10.1256 | 10.3337 | 10.4846 | 10.3586 | 10.4846 |
| Ce-O(2) b | 10.1377 | 10.3461 | 10.4846 | 10.3586 | 10.4846 |
| Ce-O(2) c | 10.1377 | 10.3461 | 10.4846 | 10.3586 | 10.4846 |
| Ce-O(6) a | 13.0163 | 10.8233 | 10.7304 | 10.7173 | 10.5356 |
| Ce-O(6) b | 13.0163 | 10.8233 | 10.7304 | 10.7173 | 10.5356 |
| Ce-O(6) c | 13.0163 | 10.8233 | 10.7304 | 10.7173 | 10.5356 |
| Zr(BaNb)1-O(4) × 6 | 3.8445 | 3.5103 | 3.8340 | 3.6024 | 3.4493 |
| Zr(BaNb)2-O(3) a | 3.2064 | 3.2224 | 3.2734 | 3.2828 | 3.2189 |
| Zr(BaNb)2-O(3) b | 3.2064 | 3.2258 | 3.2734 | 3.2828 | 3.2189 |
| Zr(BaNb)2-O(3) c | 3.2064 | 3.2258 | 3.2751 | 3.2811 | 3.2207 |
| Zr(BaNb)2-O(5) a | 3.1471 | 3.3957 | 3.2195 | 3.2322 | 3.2207 |
| Zr(BaNb)2-O(5) b | 3.1471 | 3.3976 | 3.2195 | 3.2322 | 3.2207 |
| Zr(BaNb)2-O(5) c | 3.1488 | 3.3994 | 3.2212 | 3.2322 | 3.2224 |
| Mo1-O(1) | −0.4054 | −0.4465 | −0.4934 | −0.4808 | −0.5096 |
| Mo1-O(2) | −0.3223 | −0.4263 | −0.4786 | −0.4053 | −0.4319 |
| Mo1-O(3) | −0.2397 | −0.2150 | −0.2213 | −0.2494 | −0.2055 |
| Mo1-O(4) | −0.3763 | −0.2863 | −0.3070 | −0.3061 | −0.3441 |
| Mo2-O(5) × 2 | −0.3117 | −0.3612 | −0.2492 | −0.2554 | −0.3005 |
| Mo2-O(6) × 2 | −0.9229 | −0.5679 | −0.5297 | −0.5470 | −0.5211 |
| Bond Type | x = 0.02 | x = 0.04 | x = 0.06 | x = 0.08 | x = 0.10 |
|---|---|---|---|---|---|
| Ce-O(1) a | 406.8505 | 410.6544 | 401.4945 | 399.9166 | 404.4490 |
| Ce-O(1) b | 406.7539 | 410.5723 | 401.4004 | 399.8233 | 404.3694 |
| Ce-O(1) c | 406.6895 | 410.5067 | 401.3377 | 399.7611 | 404.3058 |
| Ce-O(2) a | 410.0645 | 404.6082 | 398.7994 | 403.8610 | 399.6523 |
| Ce-O(2) b | 410.0155 | 404.5445 | 398.7530 | 403.8133 | 399.6057 |
| Ce-O(2) c | 409.9500 | 404.4967 | 398.6911 | 403.7499 | 399.5435 |
| Ce-O(6) a | 326.0845 | 388.2832 | 390.5555 | 391.2096 | 397.8577 |
| Ce-O(6) b | 326.0742 | 388.2539 | 390.5109 | 391.1798 | 397.8269 |
| Ce-O(6) c | 326.0224 | 388.1952 | 390.4516 | 391.1053 | 397.7653 |
| Zr(BaNb)1-O(4) × 6 | 459.2762 | 489.8926 | 461.1076 | 481.5940 | 496.2735 |
| Zr(BaNb)2-O(3) a | 518.9672 | 518.3938 | 512.9597 | 512.3371 | 519.4946 |
| Zr(BaNb)2-O(3) b | 518.8108 | 518.2381 | 512.9597 | 512.3623 | 519.3393 |
| Zr(BaNb)2-O(3) c | 518.7847 | 518.2122 | 512.7823 | 512.5390 | 519.3134 |
| Zr(BaNb)2-O(5) a | 525.3543 | 500.8407 | 518.6251 | 517.7693 | 519.3134 |
| Zr(BaNb)2-O(5) b | 525.2741 | 500.7680 | 518.5733 | 517.7177 | 519.2358 |
| Zr(BaNb)2-O(5) c | 525.1139 | 500.6227 | 518.4178 | 517.5632 | 519.1066 |
| Mo1-O(1) | 592.0846 | 602.8673 | 619.4640 | 614.6348 | 623.9548 |
| Mo1-O(2) | 567.3968 | 596.3924 | 614.4154 | 590.1899 | 598.0154 |
| Mo1-O(3) | 544.9440 | 536.5641 | 538.9721 | 545.7791 | 534.0395 |
| Mo1-O(4) | 583.1916 | 555.2862 | 561.8104 | 561.0780 | 571.3516 |
| Mo2-O(5) × 2 | 564.4201 | 576.4860 | 546.1831 | 547.3699 | 559.0432 |
| Mo2-O(6) × 2 | 820.3593 | 645.2379 | 632.2044 | 637.9052 | 627.9761 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Xu, X.; Liu, X.; Zhang, X.; Li, M.; Du, J.; Wu, H. Effect of (Ba1/3Nb2/3)4+ Substitution on Microstructure, Bonding Properties and Microwave Dielectric Properties of Ce2Zr3(MoO4)9 Ceramics. Ceramics 2024, 7, 1172-1186. https://doi.org/10.3390/ceramics7030077
Gao H, Xu X, Liu X, Zhang X, Li M, Du J, Wu H. Effect of (Ba1/3Nb2/3)4+ Substitution on Microstructure, Bonding Properties and Microwave Dielectric Properties of Ce2Zr3(MoO4)9 Ceramics. Ceramics. 2024; 7(3):1172-1186. https://doi.org/10.3390/ceramics7030077
Chicago/Turabian StyleGao, Huamin, Xiangyu Xu, Xinwei Liu, Xiaoyu Zhang, Mingling Li, Jialun Du, and Haitao Wu. 2024. "Effect of (Ba1/3Nb2/3)4+ Substitution on Microstructure, Bonding Properties and Microwave Dielectric Properties of Ce2Zr3(MoO4)9 Ceramics" Ceramics 7, no. 3: 1172-1186. https://doi.org/10.3390/ceramics7030077
APA StyleGao, H., Xu, X., Liu, X., Zhang, X., Li, M., Du, J., & Wu, H. (2024). Effect of (Ba1/3Nb2/3)4+ Substitution on Microstructure, Bonding Properties and Microwave Dielectric Properties of Ce2Zr3(MoO4)9 Ceramics. Ceramics, 7(3), 1172-1186. https://doi.org/10.3390/ceramics7030077







