A Molecular Dynamics Simulation Study of Crystalline and Liquid MgO
Abstract
1. Introduction
2. Simulations
2.1. Ab Initio Molecular Dynamics Simulations
2.2. Classical Molecular Dynamics Simulations and Fitting Parameters Optimization
3. Results and Discussion
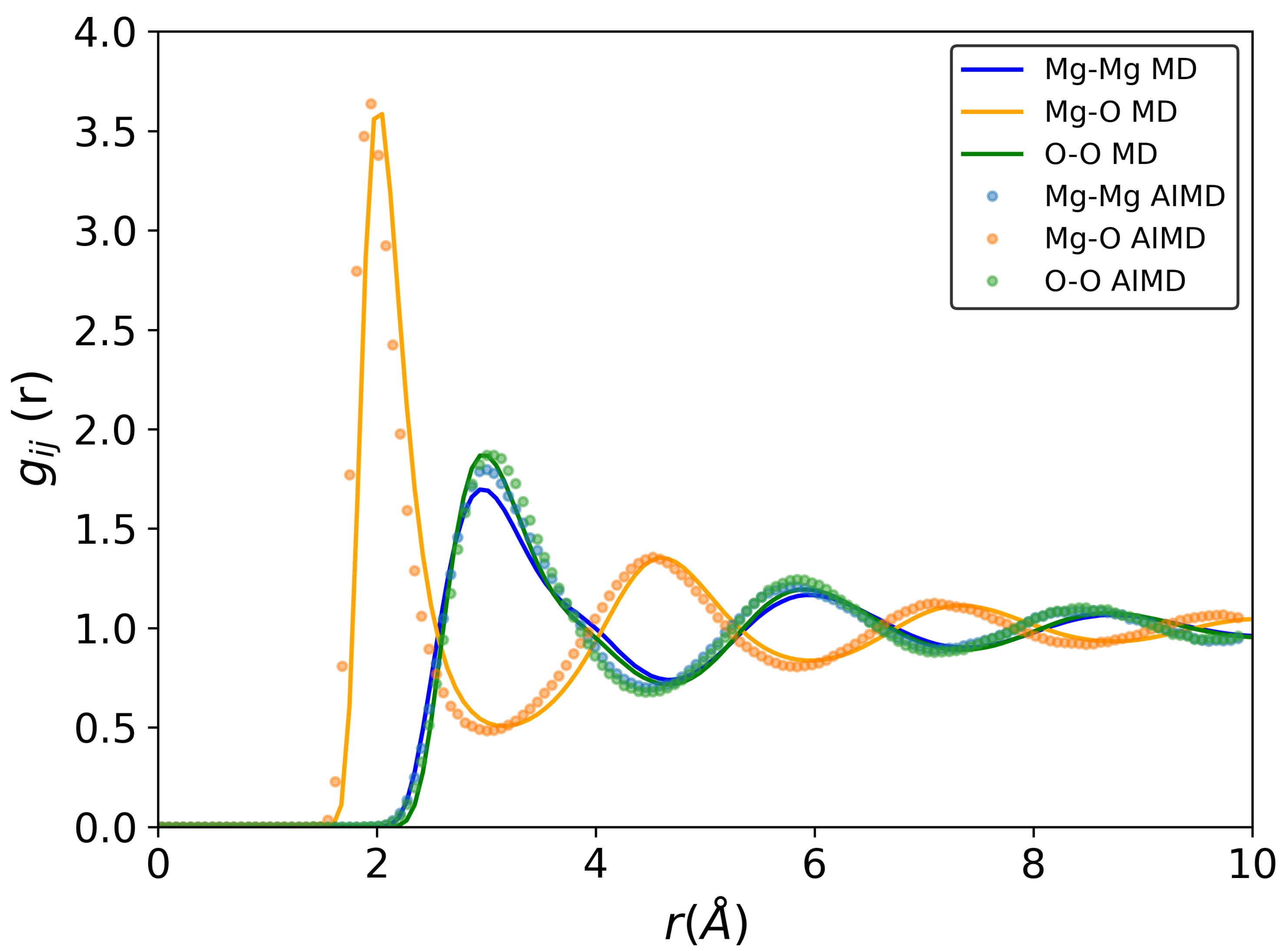
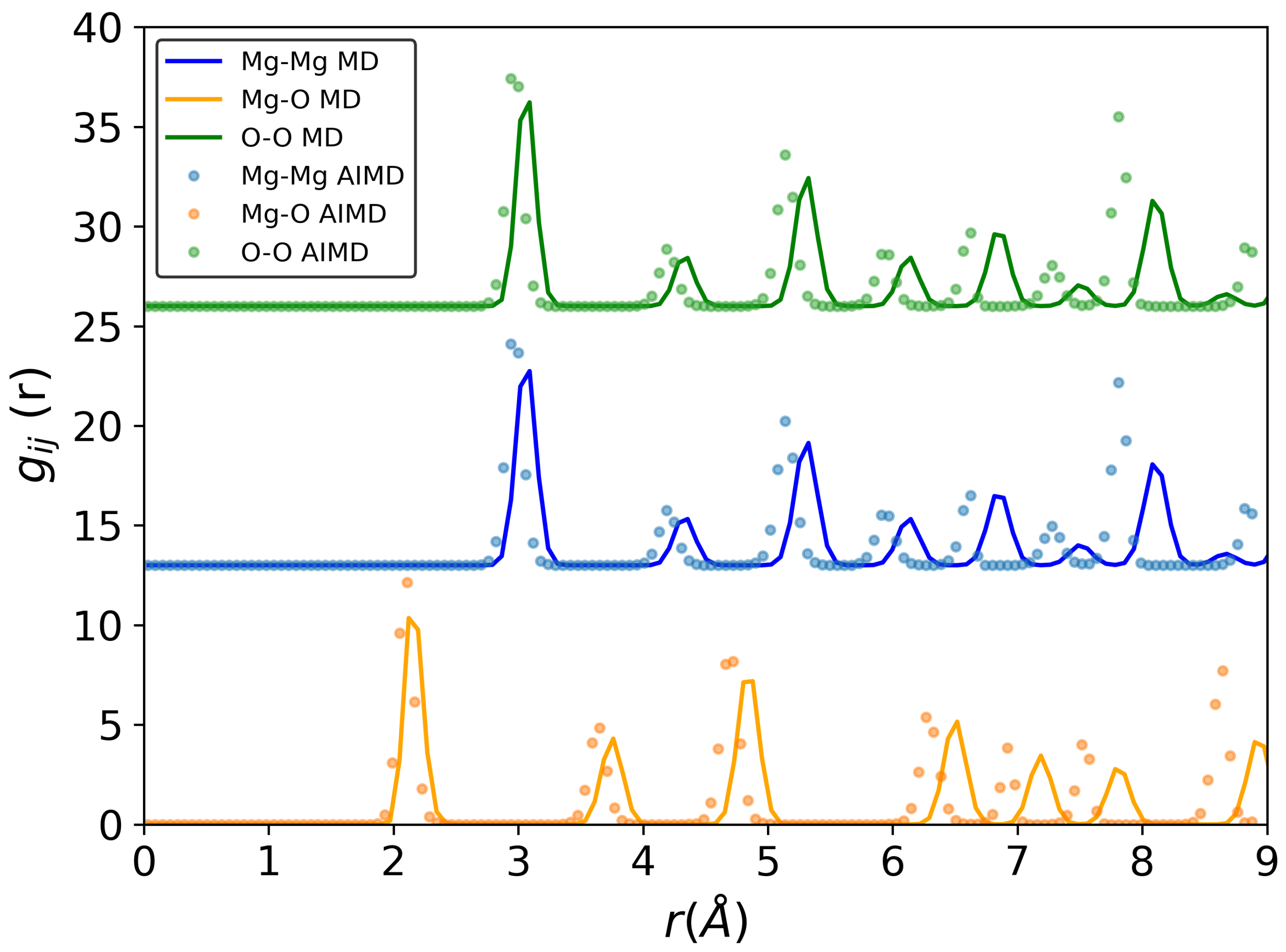
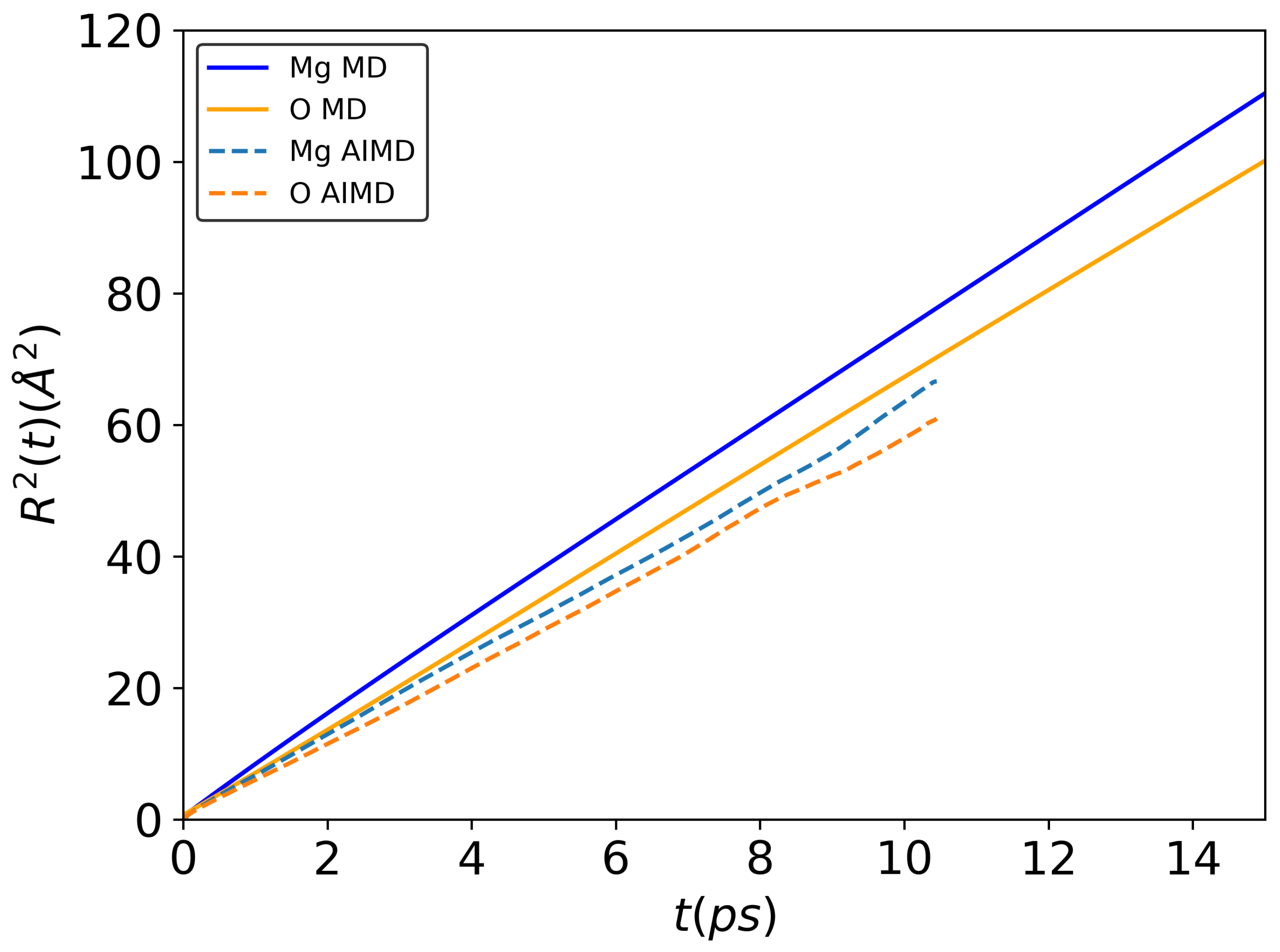
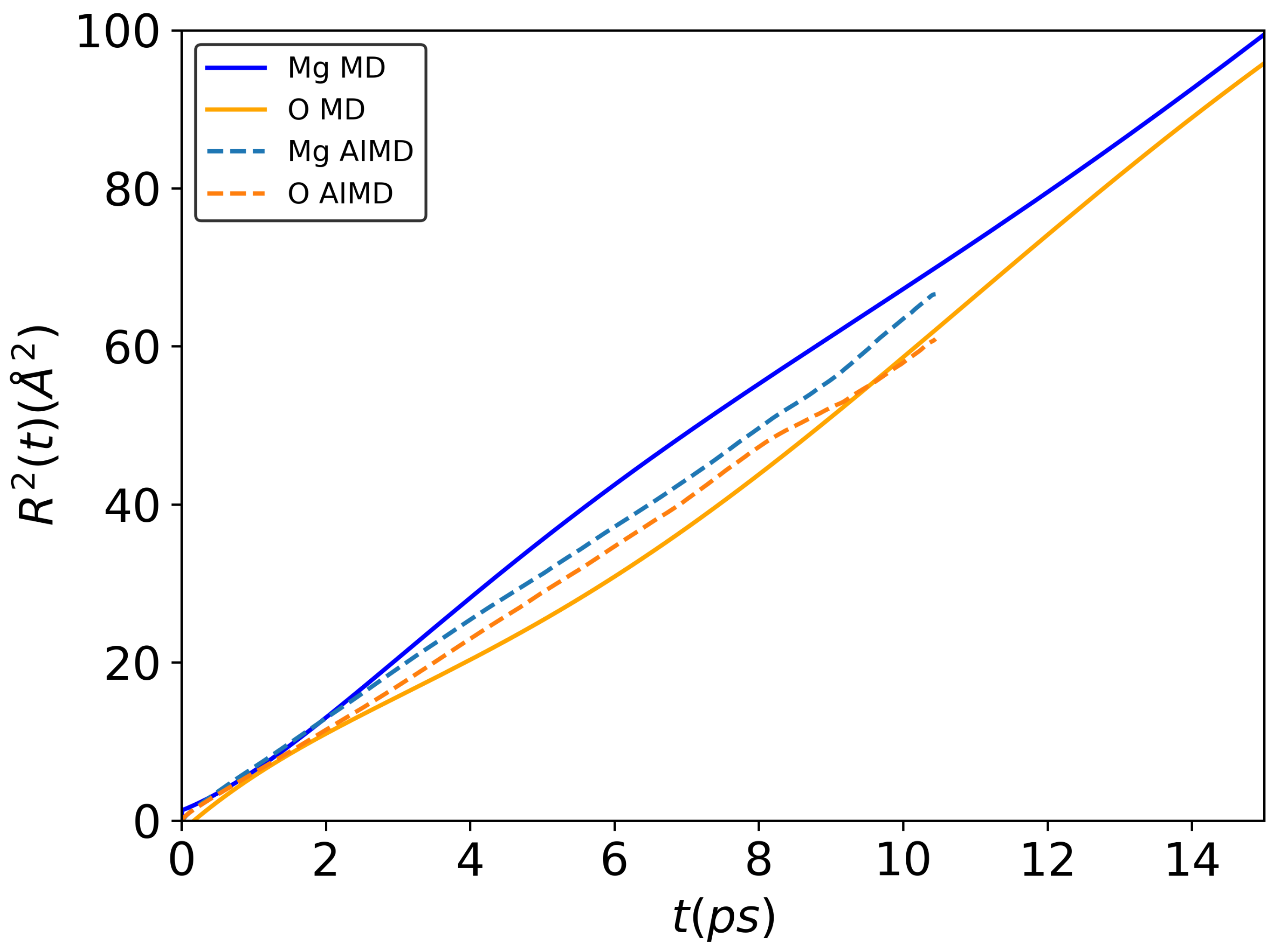
3.1. Structure and Diffusion
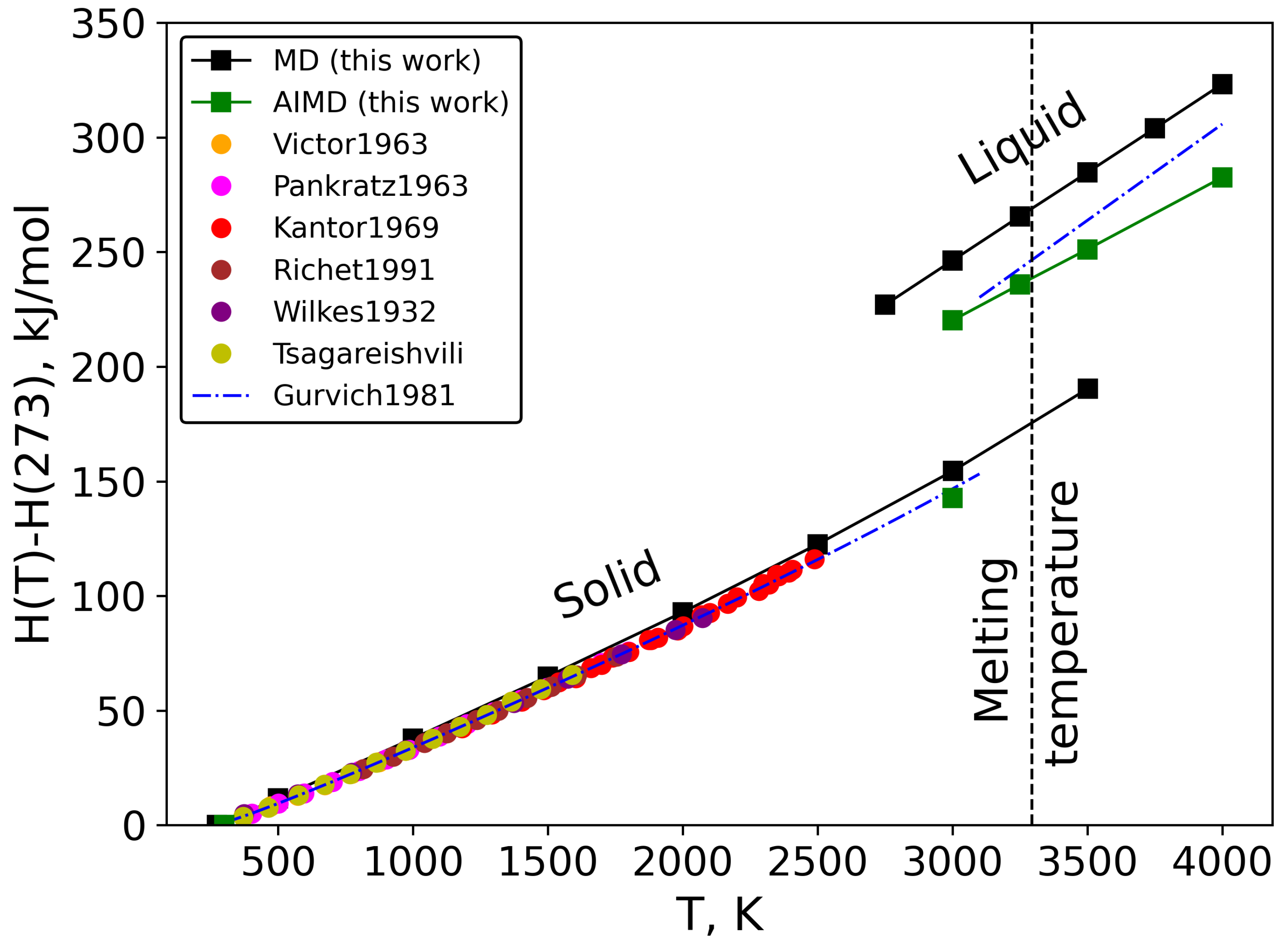
3.2. Thermodynamic Properties and Melting Temperature
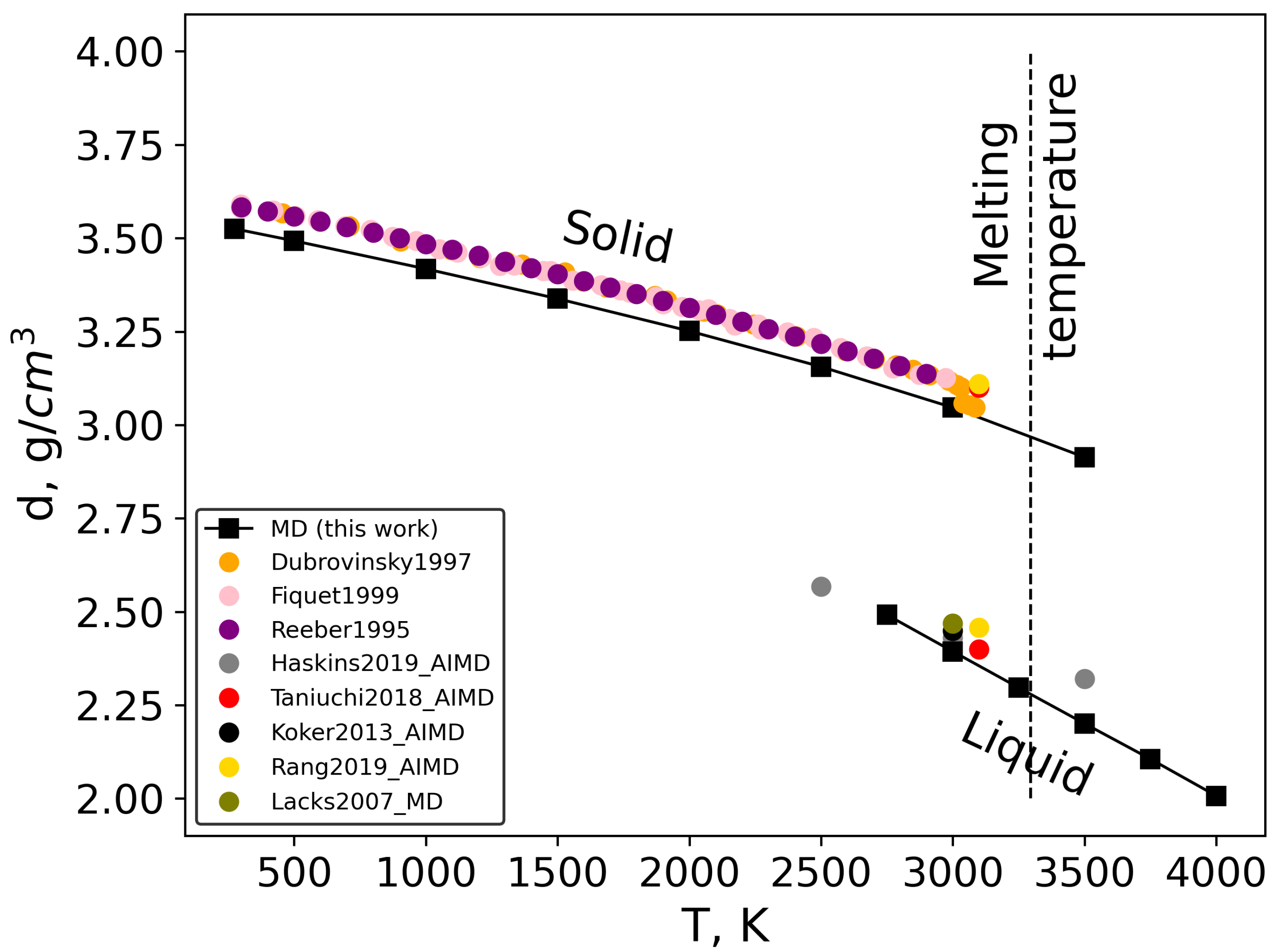
3.3. Density
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zerr, A.; Boehler, R. Constraints on the melting temperature of the lower mantle from high-pressure experiments on MgO and magnesioüstite. Nature 1994, 371, 506–508. [Google Scholar] [CrossRef]
- Riley, B. Determination of melting points at temperatures above 2000° Celcius. Rev. Int. Hautes Temp. Refract. 1966, 3, 327–336. [Google Scholar]
- Ronchi, C.; Sheindlin, M. Melting point of MgO. J. Appl. Phys. 2001, 90, 3325–3331. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Saxena, S.K. Thermal expansion of periclase (MgO) and tungsten (W) to melting temperatures. Phys. Chem. Miner. 1997, 24, 547–550. [Google Scholar] [CrossRef]
- Chernyshev, A.P.; Petrov, V.A.; Titov, V.E.; Vorobyev, A.Y. Thermal radiative properties of magnesium oxide at high temperatures. Thermochim. Acta 1993, 218, 195–209. [Google Scholar] [CrossRef]
- McNally, R.N.; Peters, F.I.; Ribbe, P.H. Laboratory furnace for studies in controlled atmospheres; melting points of MgO in a N2 atmosphere and of Cr2O3 in N2 and in air atmospheres. J. Am. Ceram. Soc. 1961, 44, 491–493. [Google Scholar] [CrossRef]
- Panek, Z. Melting Temperatures of CaO and MgO. Silikaty 1979, 23, 97–102. [Google Scholar]
- Zhang, L.; Fei, Y. Melting behavior of (Mg,Fe)O solid solutions at high pressure. Geophys. Res. Lett. 2008, 35, L13302. [Google Scholar] [CrossRef]
- Kimura, T.; Ohfuji, H.; Nishi, M.; Irifune, T. Melting temperatures of MgO under high pressure by micro-texture analysis. Nat. Commun. 2017, 8, 15735. [Google Scholar] [CrossRef]
- Du, Z.; Lee, K.K. High-pressure melting of MgO from (Mg,Fe)O solid solutions. Geophys. Res. Lett. 2014, 41, 8061–8066. [Google Scholar] [CrossRef]
- Leu, A.L.; Ma, S.M.; Eyring, H. Properties of molten magnesium oxide. Proc. Natl. Acad. Sci. USA 1975, 72, 1026–1030. [Google Scholar] [CrossRef]
- Vočadlo, L.; Price, G.D. The melting of MgO—Computer calculations via molecular dynamics. Phys. Chem. Miner. 1996, 23, 42–49. [Google Scholar] [CrossRef]
- Ferneyhough, R.; Fincham, D.; Price, G.D.; Gillan, M.J. The melting of MgO studied by molecular dynamics simulation. Model. Simul. Mater. Sci. Eng. 1994, 2, 1101. [Google Scholar] [CrossRef]
- Liu, Z.-J.; Cheng, X.-L.; Zhang, H.; Cai, L.-C. Molecular dynamics study for the melting curve of MgO at high pressure. Chin. Phys. 2004, 13, 384. [Google Scholar] [CrossRef]
- Lacks, D.J.; Rear, D.B.; Van Orman, J.A. Molecular dynamics investigation of viscosity, chemical diffusivities and partial molar volumes of liquids along the MgO–SiO2 join as functions of pressure. Geochim. Cosmochim. Acta 2007, 71, 1312–1323. [Google Scholar] [CrossRef]
- Jahn, S. Atomic structure and transport properties of MgO-Al2O3 melts: A molecular dynamics simulation study. Am. Mineral. 2008, 93, 1486–1492. [Google Scholar] [CrossRef]
- Alfè, D. Melting curve of MgO from first-principles simulations. Phys. Rev. Lett. 2005, 94, 235701. [Google Scholar] [CrossRef]
- Rang, M.; Kresse, G. First-principles study of the melting temperature of MgO. Phys. Rev. B 2019, 99, 184103. [Google Scholar] [CrossRef]
- Karki, B.B.; Bhattarai, D.; Stixrude, L. First-principles calculations of the structural, dynamical, and electronic properties of liquid MgO. Phys. Rev. B 2006, 73, 174208. [Google Scholar] [CrossRef]
- Aguado, A.; Madden, P.A. New Insights into the Melting Behavior of MgO from Molecular Dynamics Simulations: The Importance of Premelting Effects. Phys. Rev. Lett. 2005, 94, 068501. [Google Scholar] [CrossRef]
- Haskins, J.B.; Stern, E.C.; Bauschlicher, C.W.; Lawson, J.W. Thermodynamic and transport properties of meteor melt constituents from ab initio simulations: MgSiO3, SiO2, and MgO. J. Appl. Phys. 2019, 125, 235102. [Google Scholar] [CrossRef]
- Taniuchi, T.; Tsuchiya, T. The melting points of MgO up to 4 TPa predicted based on ab initio thermodynamic integration molecular dynamics. J. Phys. Condens. Matter 2018, 30, 114003. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Arapan, S.; Martonak, R.; Rosengren, A. MgO phase diagram from first principles in a wide pressure-temperature range. Phys. Rev. B 2010, 81, 054110. [Google Scholar] [CrossRef]
- de Koker, N.; Karki, B.B.; Stixrude, L. Thermodynamics of the MgO–SiO2 liquid system in Earth’s lowermost mantle from first principles. Earth Planet. Sci. Lett. 2013, 361, 58–63. [Google Scholar] [CrossRef]
- Strachan, A.; Çağin, T.; Goddard, W.A., III. Phase diagram of MgO from density-functional theory and molecular-dynamics simulations. Phys. Rev. B 1999, 60, 15084. [Google Scholar] [CrossRef]
- Carré, A.; Ispas, S.; Horbach, J.; Kob, W. Developing empirical potentials from ab initio simulations: The case of amorphous silica. Comput. Mater. Sci. 2016, 124, 323–334. [Google Scholar] [CrossRef]
- Alvares, C.; Deffrennes, G.; Pisch, A.; Jakse, N. Thermodynamics and structural properties of CaO: A molecular dynamics simulation study. J. Chem. Phys. 2020, 152, 084503. [Google Scholar] [CrossRef]
- Jakse, N.; Alvares, C.M.S.; Pisch, A. Ab initio based interionic interactions in calcium aluminotitanate oxide melts: Structure and diffusion. J. Phys. Condens. Matter 2021, 33, 285401. [Google Scholar] [CrossRef]
- Guillot, B.; Sator, N. A computer simulation study of natural silicate melts. Part I: Low pressure properties. Geochim. Cosmochim. Acta 2007, 71, 1249–1265. [Google Scholar] [CrossRef]
- Mitchell, P.J.; Fincham, D. Shell model simulations by adiabatic dynamics. J. Phys. Condens. Matter 1993, 5, 1031. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Huggins, M.L.; Mayer, J.E. Interatomic distances in crystals of the alkali halides. J. Chem. Phys. 1933, 1, 643–646. [Google Scholar] [CrossRef]
- Bouhadja, M.; Jakse, N. Structural and dynamic properties of aluminosilicate melts: A molecular dynamics study. J. Phys. Condens. Matter 2019, 32, 104002. [Google Scholar] [CrossRef] [PubMed]
- Bouhadja, M.; Jakse, N.; Pasturel, A. Structural and dynamic properties of calcium aluminosilicate melts: A molecular dynamics study. J. Chem. Phys. 2013, 138, 224510. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Morris, J.R.; Wang, C.Z.; Ho, K.M.; Chan, C.T. Melting line of aluminum from simulations of coexisting phases. Phys. Rev. B 1994, 49, 3109–3115. [Google Scholar] [CrossRef]
- Agrawal, P.M.; Rice, B.M.; Thompson, D.L. Molecular dynamics study of the melting of nitromethane. J. Chem. Phys. 2003, 119, 9617–9627. [Google Scholar] [CrossRef]
- Solca, J.; Dyson, A.J.; Steinebrunner, G.; Kirchner, B.; Huber, H. Melting curves for neon calculated from pure theory. J. Chem. Phys. 1998, 108, 4107–4111. [Google Scholar] [CrossRef]
- Jakse, N.; Pasturel, A. Molecular-dynamics study of liquid nickel above and below the melting point. J. Chem. Phys. 2005, 123, 244512. [Google Scholar] [CrossRef]
- Victor, A.C.; Douglas, T.B. Thermodynamic properties of magnesium oxide and beryllium oxide from 298 to 1200 K. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1963, 67, 325. [Google Scholar] [CrossRef]
- Pankratz, L.B.; Kelley, K.K. Thermodynamic Data for Magnesium Oxide (Periclase); U.S. Bureau of Mines Report of Investigations 6295; U.S. Bureau of Mines: Washington, DC, USA, 1963.
- Richet, P.; Fiquet, G. High-temperature heat capacity and premelting of minerals in the system MgO-CaO-Al2O3-SiO2. J. Geophys. Res. Solid Earth 1991, 96, 445–456. [Google Scholar] [CrossRef]
- Wilkes, G.B. The specific heat of magnesium and aluminum oxides at high temperatures. J. Am. Ceram. Soc. 1932, 15, 72–77. [Google Scholar] [CrossRef]
- Tsagareishvili, D.S.; Gvelisiani, G.G. Entalpiya i teploemkost okisi magniya pri visokih temperaturah. Teplofiz. Visok. Temp. 1974, 1, 208–210. [Google Scholar]
- Kantor, P.B.; Fomichev, E.N. Izmerenie entalpii i teploemkosti okisi magniya i dvuokisi tsirkoniya v intervale temperatur 1200-2500 K. Teplofiz. Svoystva Tverd. Visok. Temp. 1969, 1, 406–408. [Google Scholar]
- Glushko, V.P.; Gurvich, L.V.; Bergman, G.A.; Veyts, I.V.; Medvedev, V.A.; Khachkuruzov, G.A.; Yungman, V.S. Thermodynamic Properties of Individual Substances; Nauka: Moscow, Russia, 1981; Volume III. [Google Scholar]
- Saxena, S.K.; Zhang, J. Thermochemical and pressure-volume-temperature systematics of data on solids, examples: Tungsten and MgO. Phys. Chem. Miner. 1990, 17, 45–51. [Google Scholar] [CrossRef]
- Stebbins, J.F.; Carmichael, I.S.E.; Moret, L.K. Heat capacities and entropies of silicate liquids and glasses. Contrib. Mineral. Petrol. 1984, 86, 131–148. [Google Scholar] [CrossRef]
- Lange, R.A.; Navrotsky, A. Heat capacities of Fe2O3-bearing silicate liquids. Contrib. Mineral. Petrol. 1992, 110, 311–320. [Google Scholar] [CrossRef]
- Fiquet, G.; Richet, P.; Montagnac, G. High-temperature thermal expansion of lime, periclase, corundum and spinel. Phys. Chem. Miner. 1999, 27, 103–111. [Google Scholar] [CrossRef]
- Reeber, R.R.; Goessel, K.; Wang, K. Thermal expansion and molar volume of MgO, periclase, from 5 to 2900 K. Eur. J. Mineral. 1995, 7, 1039–1048. [Google Scholar] [CrossRef]


| q | A (eV) | (Å) | (Å) | C (eV ) | |
|---|---|---|---|---|---|
| Mg | 1.2 1 | ||||
| O | −1.2 1 | ||||
| Mg-Mg | 38,868.5 2 | 0.2066 2 | 0.0 2 | 43.773 2 | |
| Mg-O | 12,655.4 2 | 0.2089 2 | 0.0 2 | 36.798 2 | |
| O-O | 0.01015 1 | 0.2140 1 | 3.2678 1 | 5.0840 1 |
| Source | 3000 K | 3250 K | 3500 K | 4000 K | |
|---|---|---|---|---|---|
| D(Mg) | AIMD (this work) | 75 | 87 | 104 | 140 |
| MD (this work) | 82 | 102 | 122 | 168 | |
| [21] | 77 | 97 | 119 | 169 | |
| [22] | 110 (at 3100 K) | ||||
| D(O) | AIMD (this work) | 69 | 75 | 97 | 133 |
| MD (this work) | 73 | 96 | 112 | 161 | |
| [21] | 76 | 93 | 112 | 154 | |
| [22] | 120 (at 3100 K) | ||||
| Total D | [19] | 75 | 97 | 120 | 170 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arkhipin, A.S.; Pisch, A.; Uspenskaya, I.A.; Jakse, N. A Molecular Dynamics Simulation Study of Crystalline and Liquid MgO. Ceramics 2024, 7, 1187-1203. https://doi.org/10.3390/ceramics7030078
Arkhipin AS, Pisch A, Uspenskaya IA, Jakse N. A Molecular Dynamics Simulation Study of Crystalline and Liquid MgO. Ceramics. 2024; 7(3):1187-1203. https://doi.org/10.3390/ceramics7030078
Chicago/Turabian StyleArkhipin, Anatoly S., Alexander Pisch, Irina A. Uspenskaya, and Noël Jakse. 2024. "A Molecular Dynamics Simulation Study of Crystalline and Liquid MgO" Ceramics 7, no. 3: 1187-1203. https://doi.org/10.3390/ceramics7030078
APA StyleArkhipin, A. S., Pisch, A., Uspenskaya, I. A., & Jakse, N. (2024). A Molecular Dynamics Simulation Study of Crystalline and Liquid MgO. Ceramics, 7(3), 1187-1203. https://doi.org/10.3390/ceramics7030078