Near-Zero Thermal Expansion in Freeze-Cast Composite Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Methods
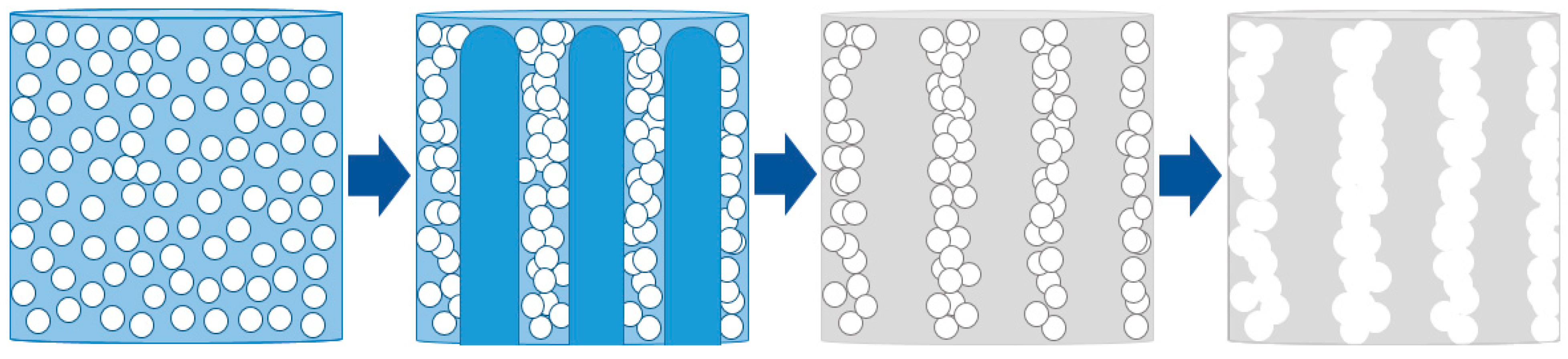
2.2.1. Preparation of Aluminum Tungstate Particles
2.2.2. Preparation of Aluminum Tungstate Scaffold
2.2.3. Preparation of Aluminum Tungstate/PMMA Composite
2.3. Characterization
2.3.1. Thermal Expansion
2.3.2. Thermogravimetric Analysis
2.3.3. Scanning Electron Microscopy
2.3.4. Density
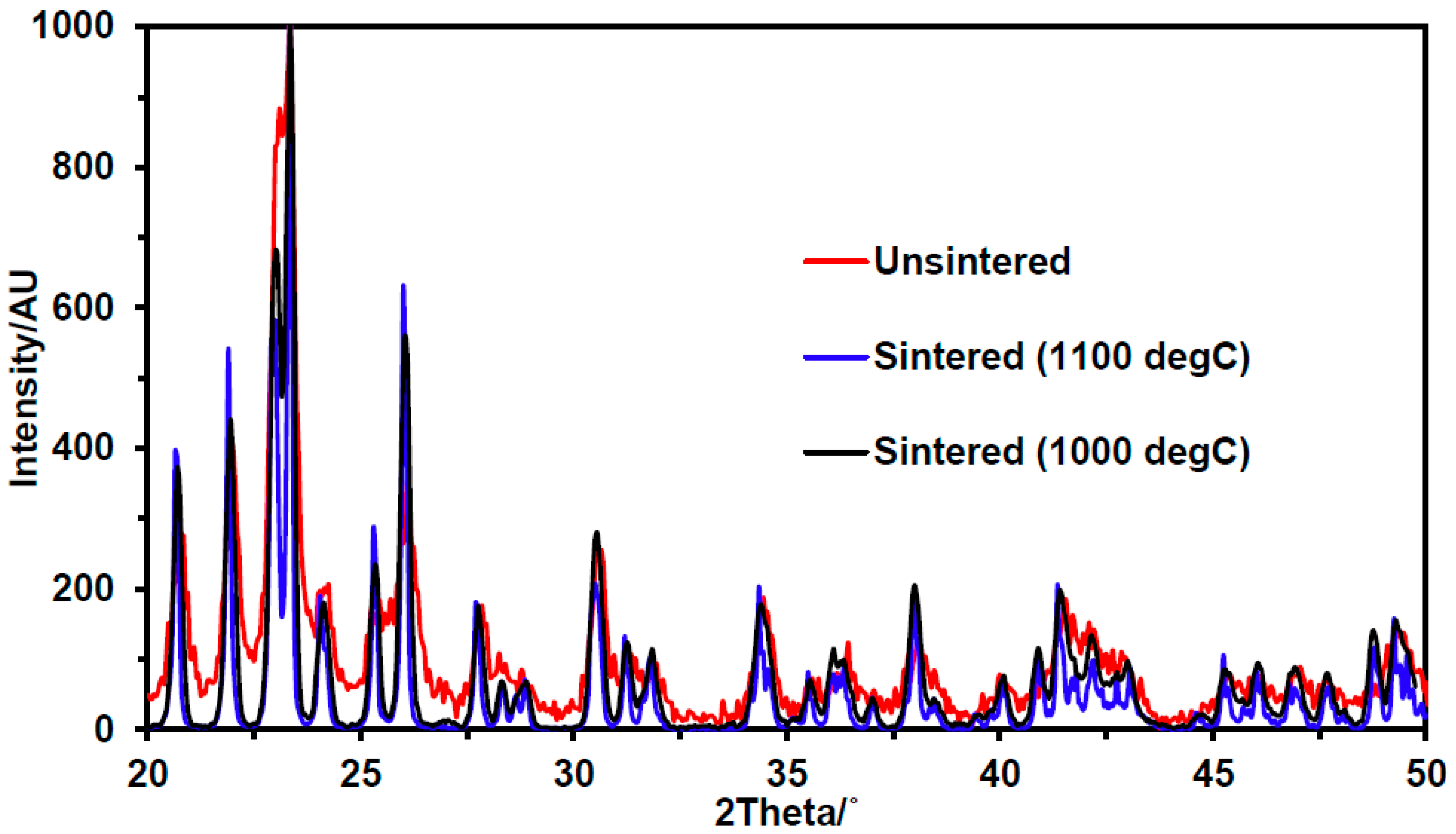
2.3.5. X-ray Diffraction
2.3.6. Vickers Indentation
3. Results and Discussion
3.1. Scaffold Synthesis
3.2. Structural Characterization of Scaffolds and Composites
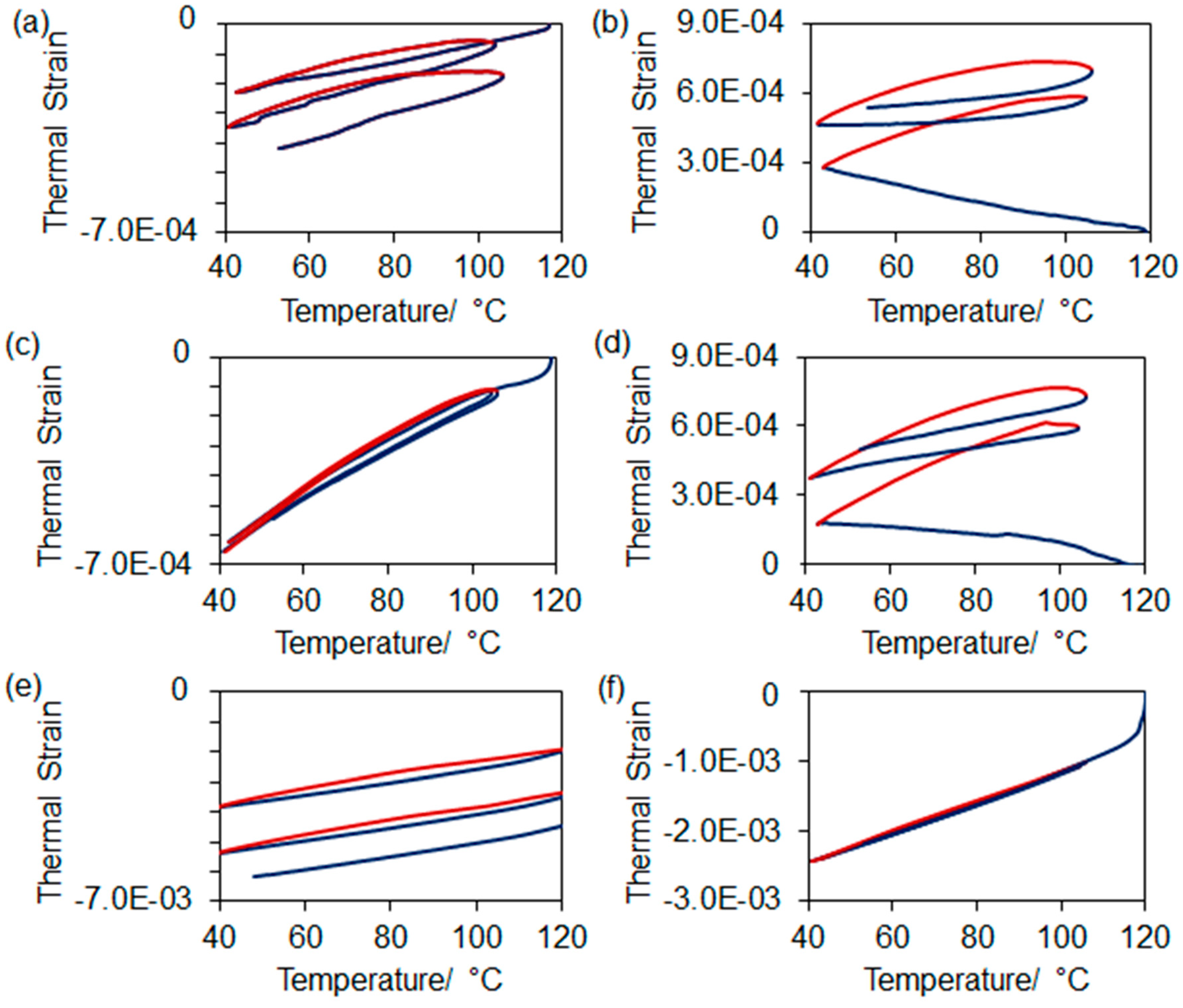
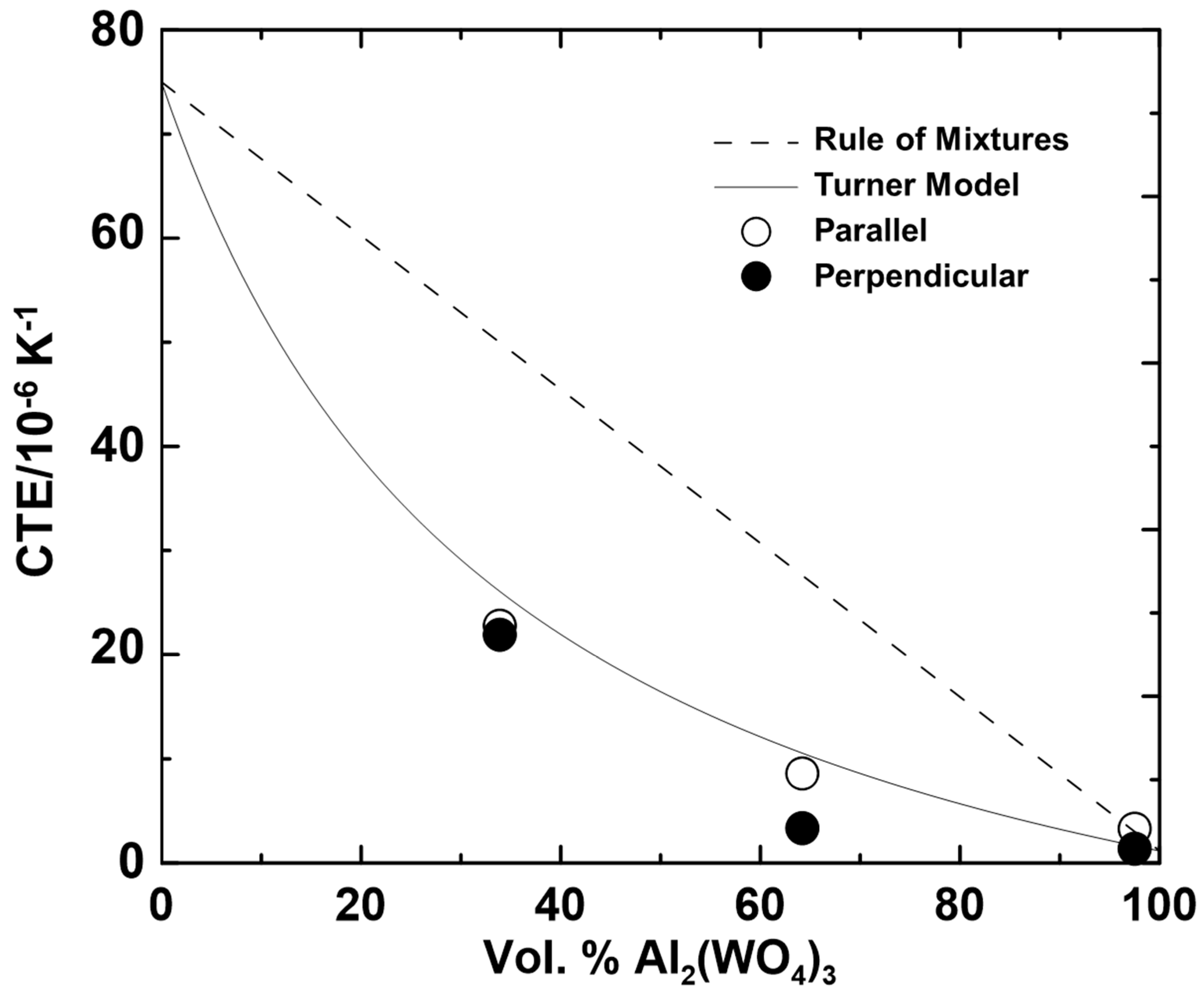
3.3. Thermal Expansion of Composites
3.4. Hardness Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Romao, C.P.; Miller, K.J.; Whitman, C.A.; White, M.A.; Marinkovic, B.A. Comprehensive Inorganic Chemistry II; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Oxford, UK, 2013; Volume 4, pp. 128–151. [Google Scholar]
- Miller, W.; Smith, C.W.; Mackenzie, D.S.; Mackenzie, D.S.; Evans, K.E. Negative thermal expansion: A review. J. Mater. Sci. 2009, 44, 5441–5451. [Google Scholar] [CrossRef]
- Lind, C. Two decades of negative thermal expansion research: Where do we stand? Materials 2012, 5, 1125–1154. [Google Scholar] [CrossRef] [PubMed]
- Mary, T.A.; Evans, J.S.O.; Vogt, T.; Sleight, A.W. Negative thermal expansion from 0.3 to 1050 kelvin in ZrW2O8. Science 1996, 272, 90–92. [Google Scholar] [CrossRef]
- Evans, J.S.O.; Mary, T.A.; Sleight, A.W. Negative thermal expansion in Sc2(WO4)3. J. Solid State Chem. 1998, 137, 148–160. [Google Scholar] [CrossRef]
- Marinkovic, B.M.; Jardim, P.M.; de Avillez, R.R.; Rizzo, F. Negative thermal expansion in Y2Mo3O12. Solid State Sci. 2005, 7, 1377–1383. [Google Scholar] [CrossRef]
- Romao, C.P.; White, M.A. Negative stiffness in ZrW2O8 inclusions as a result of thermal stress. J. Appl. Phys. 2016, 109, 031902. [Google Scholar] [CrossRef]
- Meyer, G. Rigid biological systems as models for synthetic composites. Science 2005, 310, 1144–1147. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Nalla, R.K.; Tomsia, A.P. Freezing as a path to build complex composites. Science 2006, 311, 515–518. [Google Scholar] [CrossRef]
- Deville, S. The lure of ice-templating: Recent trends and opportunities for porous materials. Scripta Materialia 2018, 147, 119–124. [Google Scholar] [CrossRef]
- Soares, A.R.; Ponton, P.I.; Mancic, L.; d’Almeida, J.R.M.; Romao, C.P.; White, M.A.; Marinkovic, B.A. Al2Mo3O12/polyethylene composites with reduced coefficient of thermal expansion. J. Mater. Sci. 2014, 49, 7870–7882. [Google Scholar] [CrossRef]
- Ponton, P.I.; Prisco, L.P.; Marinkovic, B.A. Effects of low contents of A2M3O12 submicronic thermomiotic-like fillers on thermal expansion and mechanical properties of HDPE-based composites. Polym. Compos. 2018, 39, E1821–E1833. [Google Scholar] [CrossRef]
- Bouville, F.; Maire, E.; Meille, S.; Van de Moortèle, B.; Stevenson, A.J.; Deville, S. Strong, tough and stiff bioinspired ceramics from brittle constituents. Nat. Mater. 2014, 13, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Munch, E.; Launey, M.E.; Alsem, D.H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Tough, bio-inspired hybrid materials. Science 2008, 322, 1516–1520. [Google Scholar] [CrossRef] [PubMed]
- Schiffres, S.N.; Harish, S.; Maruyama, S.; Shiomi, J.; Malen, J.A. Tunable electrical and thermal transport in ice-templated multilayer graphene nanocomposites through freezing rate control. ACS Nano 2013, 7, 11183–11189. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Yao, Y.; Gong, Z.; Wang, F.; Sun, R.; Xu, J.; Wong, C.P. Ice-templated assembly strategy to construct 3D boron nitride nanosheet networks in polymer composites for thermal conductivity improvement. Small 2015, 16, 6205–6213. [Google Scholar] [CrossRef] [PubMed]
- Wicklein, B.; Kocjan, A.; Salazar-Alvarez, G.; Carosio, F.; Camino, G.; Antonietti, M.; Bergström, L. Thermally insulating and fire-retardant lightweight anisotropic foams based on nanocellulose and graphene oxide. Nat. Nanotech. 2015, 10, 277. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Ye, L.; Yu, S.; Sun, R.; Xu, J.; Wong, C.P. Facile preparation of superelastic and ultralow dielectric boron nitride nanosheet aerogels via freeze-casting process. Chem. Mater. 2015, 27, 5849–5855. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, Y.; Zhang, D.; Bowen, C.R. Porous PZT ceramics with aligned pore channels for energy harvesting applications. J. Am. Ceram. Soc. 2014, 98, 2980–2983. [Google Scholar] [CrossRef]
- Shao, Y.; El-Kady, M.F.; Lin, C.W.; Zhu, G.; Marsh, K.L.; Hwang, J.Y.; Zhang, Q.; Li, Y.; Wang, H.; Kaner, R.B. 3D Freeze-Casting of Cellular Graphene Films for Ultrahigh-Power-Density Supercapacitors. Adv. Mater. 2016, 28, 6719–6726. [Google Scholar] [CrossRef]
- White, M.A.; Conrad, J.; Chen, R.; Romao, C.; Pereira, A.; Hill, I. Applications of ice-templated ceramics. Int. J. Appl. Ceram. Technol. 2018, 15, 1075–1084. [Google Scholar] [CrossRef]
- Romao, C.P.; Donegan, S.P.; Zwanziger, J.W.; White, M.A. Relationships between elastic anisotropy and thermal expansion in A2Mo3O12 materials. Phys. Chem. Chem. Phys. 2016, 18, 30652–30661. [Google Scholar] [CrossRef] [PubMed]
- Kreher, W.S. Modeling of random microstructural stresses and grain boundary damage in polycrystals. Comp. Mater. Sci. 1996, 7, 147–153. [Google Scholar] [CrossRef]
- Dhainaut, J.; Piana, G.; Deville, S.; Guizard, C.; Klotz, M. Freezing-induced ordering of block copolymer micelles. Chem. Comm. 2014, 50, 12572–12574. [Google Scholar] [CrossRef]
- Ghosh, D.; Banda, M.; Kang, H.; Dhavale, N. Platelets-induced stiffening and strengthening of ice-templated highly porous alumina scaffolds. Scripta Materialia 2016, 125, 29–33. [Google Scholar] [CrossRef]
- Martoïa, F.; Cochereau, T.; Dumont, P.J.J.; Orgéas, L.; Terrien, M.; Belgacem, M.N. Cellulose nanofibril foams: Links between ice-templating conditions, microstructures and mechanical properties. Mater. Design 2016, 104, 376–391. [Google Scholar]
- Sigmund, O.; Torquato, S.J. Design of materials with extreme thermal expansion using a three-phase topology optimization method. Mech. Phys. Solids. 1997, 45, 1037–1067. [Google Scholar] [CrossRef]
- Qu, J.; Kadic, M.; Naber, A.; Wegener, M. Micro-structured two-component 3D metamaterials with negative thermal-expansion coefficient from positive constituents. Sci. Rep. 2017, 7, 40643. [Google Scholar] [CrossRef]
- Imanaka, N.; Hiraiwa, M.; Adachi, G.; Dabkowska, H.; Dabkowski, A. Thermal contraction behavior in Al2(WO4)3 single crystal. J. Cryst. Growth 2000, 200, 176–179. [Google Scholar] [CrossRef]
- Romao, C.P.; Perras, F.A.; Werner-Zwanziger, U.; Lussier, J.A.; Miller, K.J.; Calahoo, C.M.; Zwanziger, J.W.; Bieringer, M.; Marinkovic, B.A.; Bryce, D.L.; et al. Zero thermal expansion in ZrMgMo3O12: NMR crystallography reveals origins of thermoelastic properties. Chem. Mater. 2015, 27, 2633–26476. [Google Scholar] [CrossRef]
- Prisco, L.P.; Romao, C.P.; Fernando, R.; White, M.A.; Marinkovic, B.A. The effect of microstructure on thermal expansion coefficients in powder-processed Al2Mo3O12. J. Mater. Sci. 2013, 48, 2986–2996. [Google Scholar] [CrossRef]
- Romao, C.P.; Miller, K.J.; Johnson, M.B.; Zwanziger, J.W.; Marinkovic, B.A.; White, M.A. Thermal, vibrational, and thermoelastic properties of Y2Mo3O12 and their relations to negative thermal expansion. Phys. Rev. B 2014, 90, 024305. [Google Scholar] [CrossRef]
- Chen, R.; Johnson, M.B.; Plucknett, K.P.; White, M.A. Thermal conductivity of tunable lamellar aluminum oxide/polymethyl methacrylate hybrid composites. J. Mater. Res. 2012, 27, 1869–1876. [Google Scholar] [CrossRef]
- Kashiwagi, T.; Inaba, A.; Brown, J.E.; Hatada, K.; Kitayama, T.; Masuda, E. Effects of weak linkages on the thermal and oxidative degradation of poly(methyl methacrylates). Macromol. 1986, 19, 2160–2168. [Google Scholar] [CrossRef]
- Ivanova, D.; Nikolov, V.; Peshev, P. Solvents for growing Al2(WO4)3 single crystals from high-temperature solutions. J. Alloys Compd. 2007, 430, 356–360. [Google Scholar] [CrossRef]
- Poly(methyl methacrylate); SDS 200336; Millipore Sigma: Saint Louis, MO, USA, 22 January 2019.
- Deville, S.; Saiz, E.; Tomsia, A.P. Ice-templated porous alumina structures. Acta Mater. 2007, 55, 1965–1974. [Google Scholar] [CrossRef]
- Plucknett, K.P.; Munro, C.D. Aqueous Colloidal Characterization and Forming of Multimodal Barium Titanate Powders. J. Am. Cer. Soc. 2009, 92, 2537–2543. [Google Scholar]
- Batista, F.M.C.; La Porta, F.A.; Gracia, L.; Cerdeiras, E.; Mestres, L.; Li, M.S.; Bastista, N.C.; Andres, J.; Longo, E.; Cavalcante, L.S. A joint experimental and theoretical study on the electronic structure and photoluminescence properties of Al2(WO4)3 powders. J. Mol. Struct. 2015, 1081, 381–388. [Google Scholar] [CrossRef]
- Nihtianova, D.; Velichkova, N.; Nikolova, R.; Koseva, I.; Yordanova, A.; Nikolov, V. Characterization of nanosized Al2(WO4)3. Mater. Res. Bull. 2011, 46, 2125–2130. [Google Scholar] [CrossRef]
- Prisco, L.P.; Pontón, P.I.; Guamán, M.V.; Avillez, R.R.; Romao, C.P.; Johnson, M.B.; White, M.A.; Marinkovic, B.A. Assessment of the Thermal Shock Resistance Figures of Merit of Al2W3O12, a Low Thermal Expansion Ceramic. J. Am. Cer. Soc. 2016, 99, 1742–1748. [Google Scholar] [CrossRef]
- Prisco, L.P.; Marzano, M.; Pontón, P.I.; Costa, A.M.L.M.; Neto, C.C.; Sweet, G.; Romao, C.P.; White, M.A.; Marinkov, B.A. Relationship between sintering methods and physical properties of the low positive thermal expansion material Al2W3O12. Int. J. App. Ceram. Tech. 2019, 16, 346–356. [Google Scholar] [CrossRef]
- Gökmen, M.T.; du Prez, F.E. Porous polymer particles: A comprehensive guide to synthesis, characterization, functionalization and applications. Prog. Polym. Sci. 2012, 37, 365–405. [Google Scholar] [CrossRef]
- White, M.A. Thermal Expansion. In Physical Properties of Materials, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 173–186. [Google Scholar]
- Kingery, W.D.; Bowen, H.K.; Uhlmann, D.R. Introduction to Ceramics; John Wiley & Sons: New York, NY, USA, 1960. [Google Scholar]
- Varga, T.; Wilkinson, A.P.; Lind, C.; Bassett, W.A.; Zha, C.-S. High pressure synchrotron x-ray powder diffraction study of Sc2Mo3O12 and Al2W3O12. J. Phys. Condens. Matter 2005, 27, 4271–4283. [Google Scholar] [CrossRef]
- Sinha, M.; Buckley, D.J. Acoustic Properties of Polymers. In Physical Properties of Polymers; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007; pp. 1021–1031. [Google Scholar]
- Romao, C.P. Anisotropic thermal expansion in flexible materials. Phys. Rev. B 2017, 96, 134113. [Google Scholar] [CrossRef]
- Tani, J.; Kimura, H.; Hirota, K.; Kido, H. Thermal expansion and mechanical properties of phenolic resin/ZrW2O8 composites. J. App. Pol. Sci. 2007, 106, 3343–3347. [Google Scholar] [CrossRef]
- Sullivan, L.M.; Lukehart, C.M. Zirconium Tungstate (ZrW2O8)/Polyimide Nanocomposites Exhibiting Reduced Coefficient of Thermal Expansion. Chem. Matter. 2005, 17, 2136–2141. [Google Scholar] [CrossRef]
- Lind, C.; Coleman, M.R.; Kozy, L.C.; Sharma, G.R. Zirconium tungstate/polymer nanocomposites: Challenges and opportunities. Phys. Status Solidi B 2010, 248, 123–129. [Google Scholar] [CrossRef]
- Liu, Q.; Ye, F.; Gao, Y.; Liu, S.; Yang, H.; Zhou, Z. Fabrication of a new SiC/2024Al co-continuous composite with lamellar microstructure and high mechanical properties. J. Alloy Compd. 2014, 585, 146–153. [Google Scholar] [CrossRef]
- Gurbuz, S.N.; Dericioglu, A.F. Effect of reinforcement surface functionalization on the mechanical properties of nacre-like bulk lamellar composites processed by a hybrid conventional method. Mater. Sci. Eng. C 2013, 33, 2011–2019. [Google Scholar] [CrossRef]




| Proportion of Al2W3O12/vol % | Porosity 1/% | Density/(g cm−3) | |||
|---|---|---|---|---|---|
| In Slurry | In Composite 2 | Scaffold | Composite | Scaffold | Composite |
| 53 | 98 | 38.0 | 3.4 | 3.1 | 3.6 |
| 41 | 64 | 57.6 | 34.0 | 2.2 | 2.4 |
| 15 | 34 | 84.4 | 53.9 | 0.9 | 1.2 |
| Linear CTE a/(10−6 K−1) | |||||||
|---|---|---|---|---|---|---|---|
| Composition Al2W3O12/% | Orientation | Cool 1 | Heat 2 | Cool 2 | Heat 3 | Cool 3 | Mean |
| 34 | ‖ | 28.4 ± 0.7 | 20 ± 1 | 26.0 ± 0.5 | 22.3 ± 0.6 | 26.7 ± 0.5 | 25 ± 1 |
| Ʇ | 24.6 ± 0.5 | 21.58 ± 0.07 | 21.35 ± 0.06 | 21.62 ± 0.08 | 21.9 ± 0.8 | 22.2 ± 0.4 | |
| 64 | ‖ | 8.41 ± 0.06 | 8.8 ± 0.2 | 8.17 ± 0.06 | 9.6 ± 0.2 | 7.97 ± 0.04 | 8.6 ± 0.3 |
| Ʇ | −2.13 ± 0.09 | 7.0 ± 0.3 | 3.12 ± 0.02 | 7.2 ± 0.3 | 4.07 ± 0.07 | 3.8 ± 0.3 | |
| 98 | ‖ | 2.65 ± 0.03 | 3.2 ± 0.1 | 4.1 ± 0.04 | 3.4 ± 0.2 | 4.45 ± 0.05 | 3.6 ± 0.2 |
| Ʇ | −3.93 ± 0.02 | 5.4 ± 0.2 | 1.07 ± 0.04 | 4.2 ± 0.3 | 1.72 ± 0.02 | 1.7 ± 0.2 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellis, S.N.; Romao, C.P.; White, M.A. Near-Zero Thermal Expansion in Freeze-Cast Composite Materials. Ceramics 2019, 2, 112-125. https://doi.org/10.3390/ceramics2010011
Ellis SN, Romao CP, White MA. Near-Zero Thermal Expansion in Freeze-Cast Composite Materials. Ceramics. 2019; 2(1):112-125. https://doi.org/10.3390/ceramics2010011
Chicago/Turabian StyleEllis, Sarah N., Carl P. Romao, and Mary Anne White. 2019. "Near-Zero Thermal Expansion in Freeze-Cast Composite Materials" Ceramics 2, no. 1: 112-125. https://doi.org/10.3390/ceramics2010011
APA StyleEllis, S. N., Romao, C. P., & White, M. A. (2019). Near-Zero Thermal Expansion in Freeze-Cast Composite Materials. Ceramics, 2(1), 112-125. https://doi.org/10.3390/ceramics2010011






