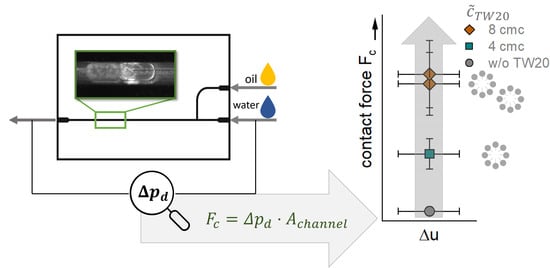
A Microfluidic Approach to Investigate the Contact Force Needed for Successful Contact-Mediated Nucleation
Abstract
1. Introduction
2. Materials and Methods
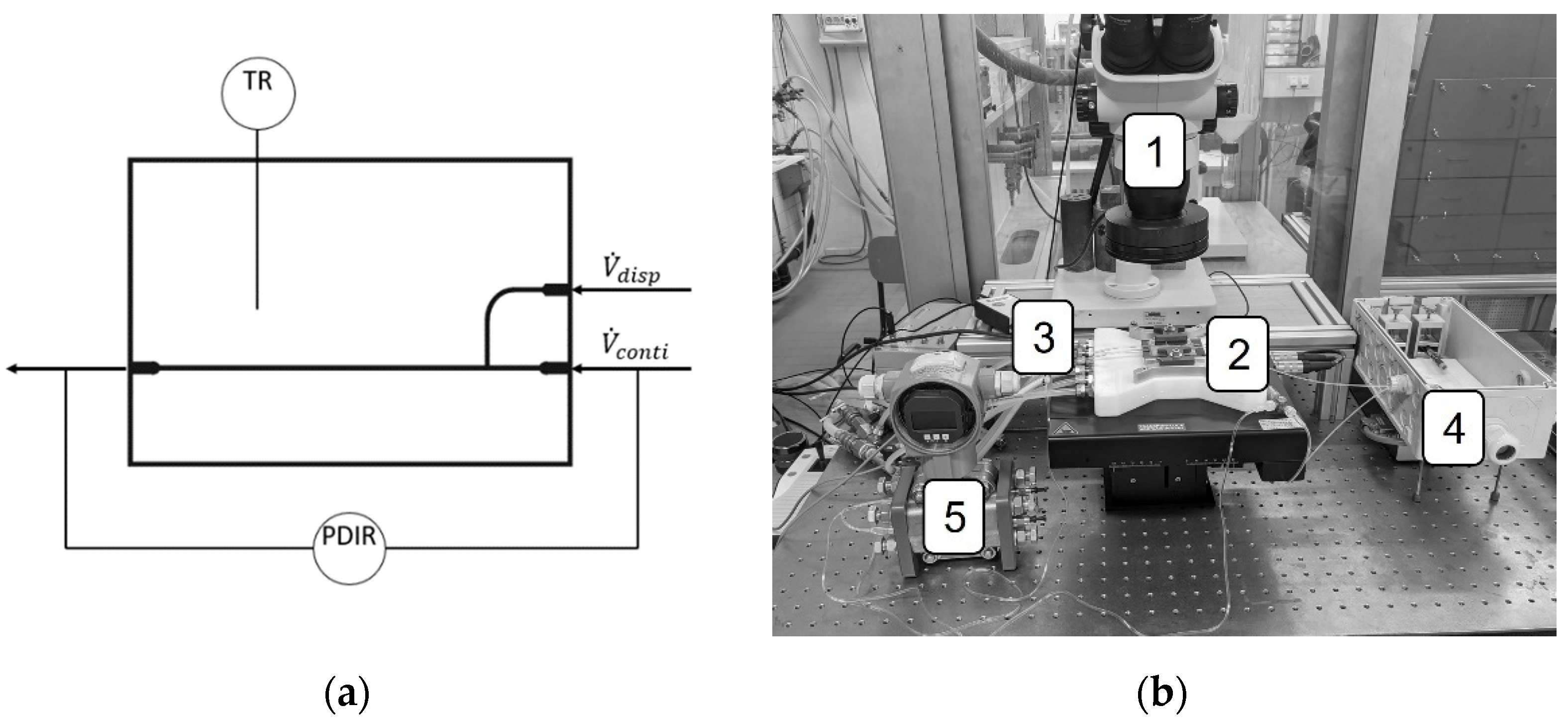
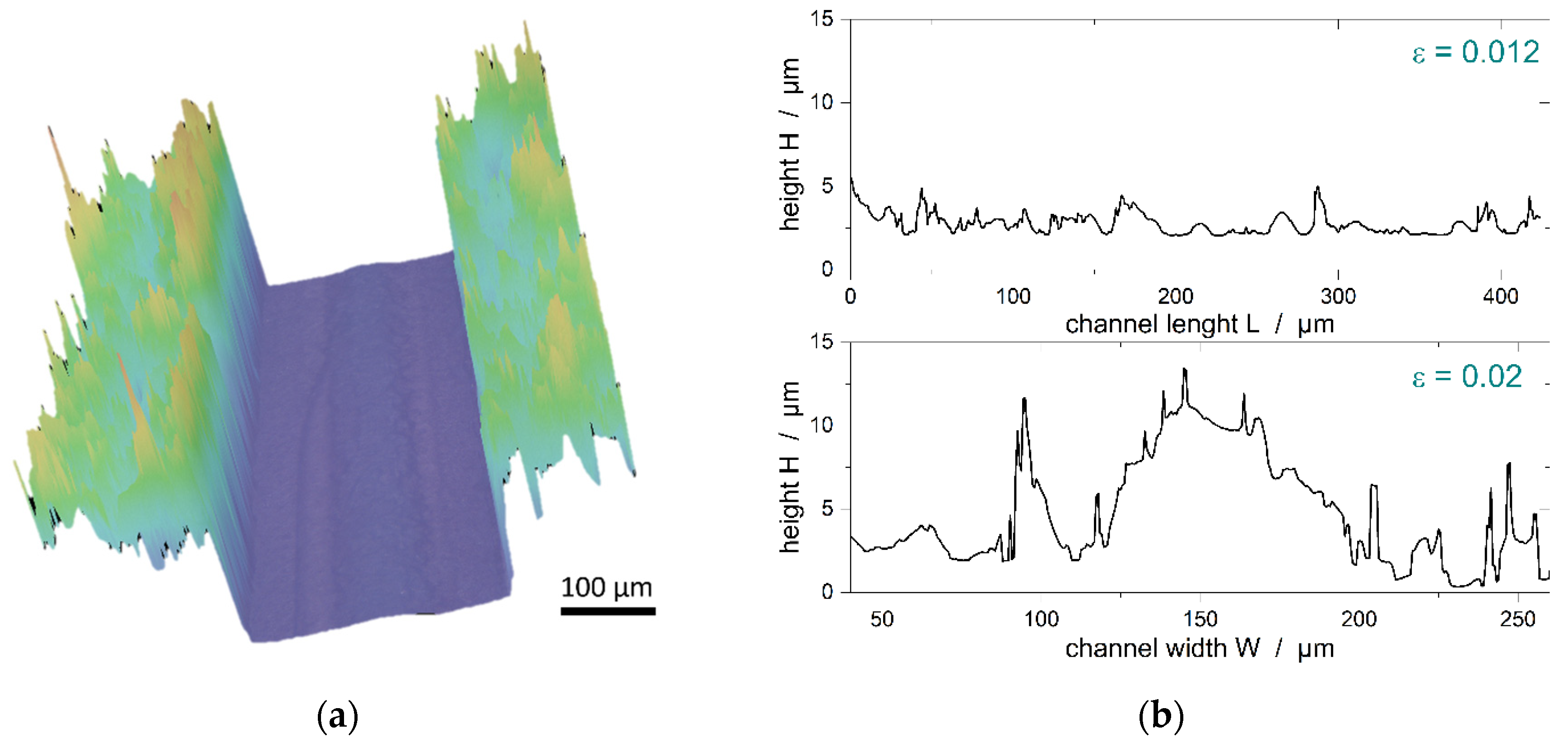
2.1. Microfluidic Setup
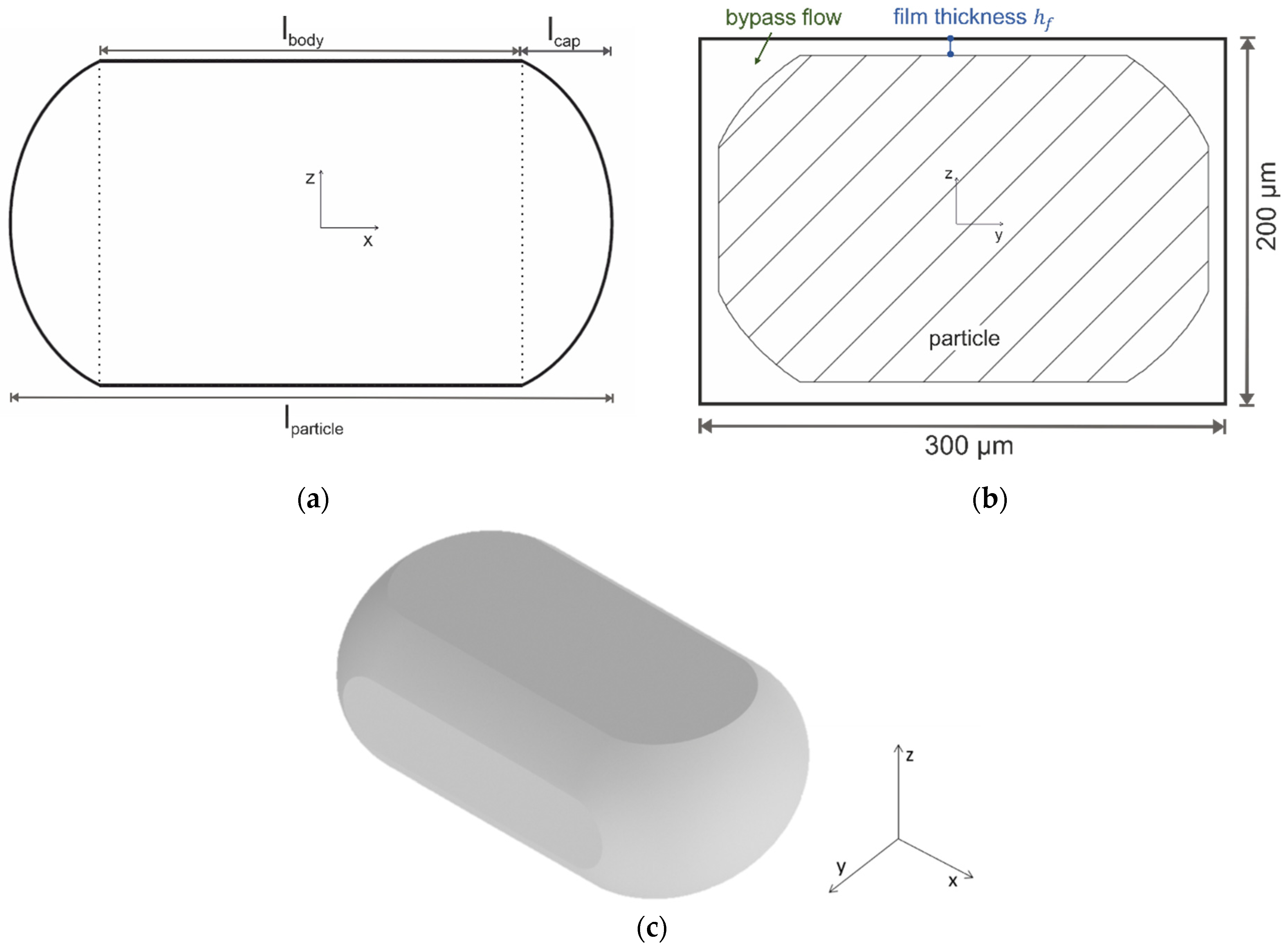
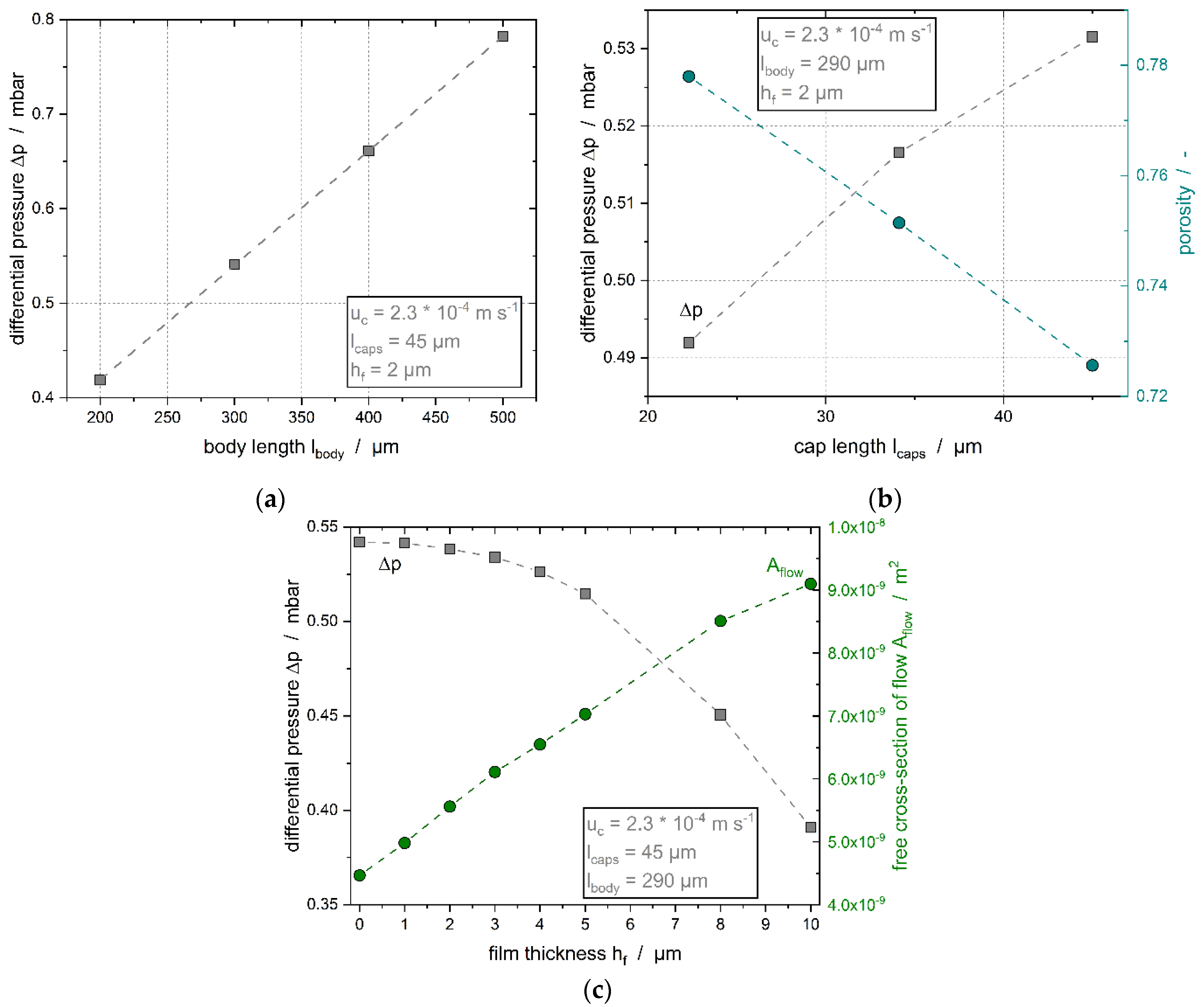
2.2. Numeric Flow Simulations
- length of the particle body ,
- length of the caps of the particles , and
- distance between the particle boundary and the channel wall, i.e., film thickness .
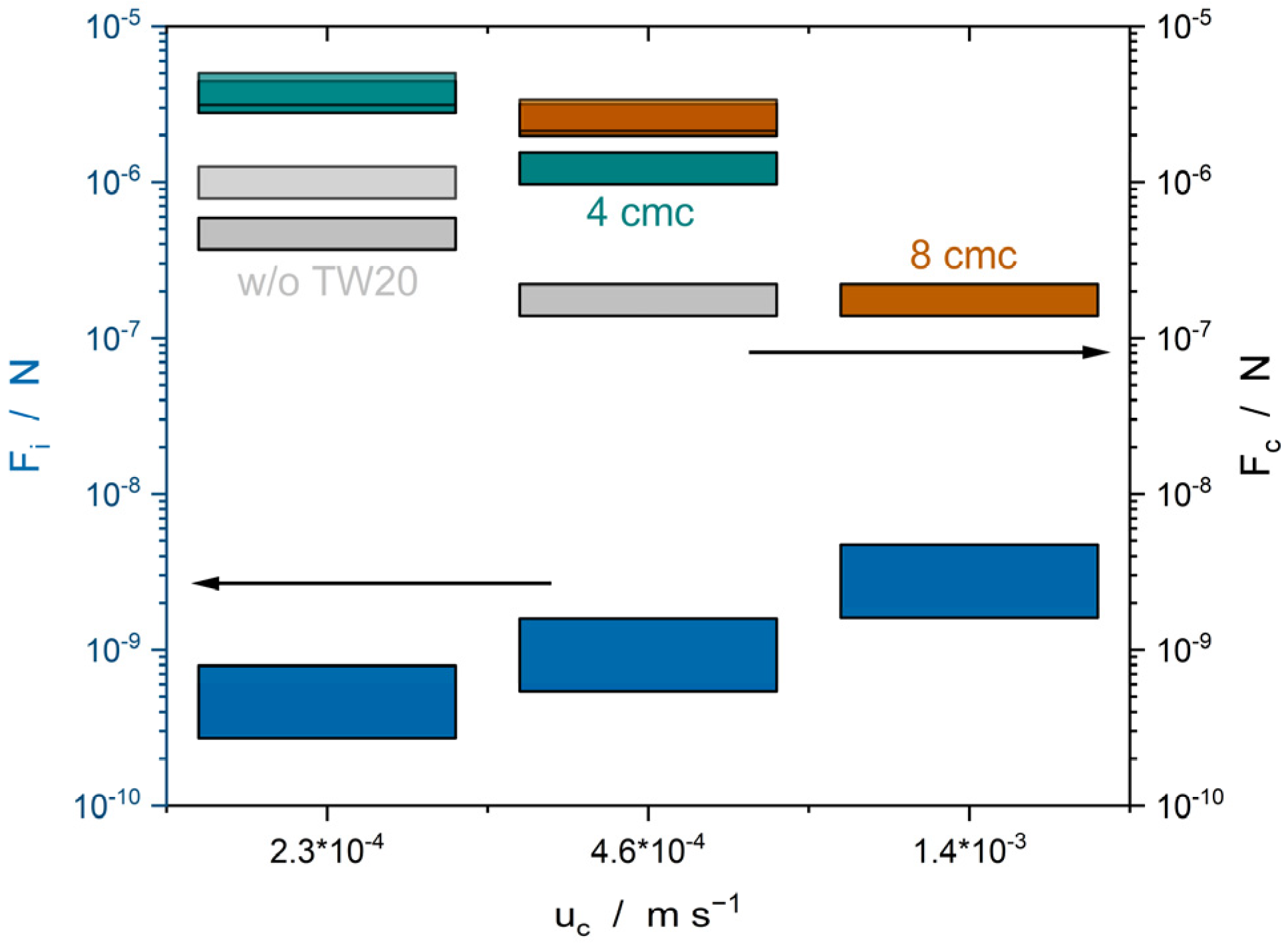
3. Results and Discussion
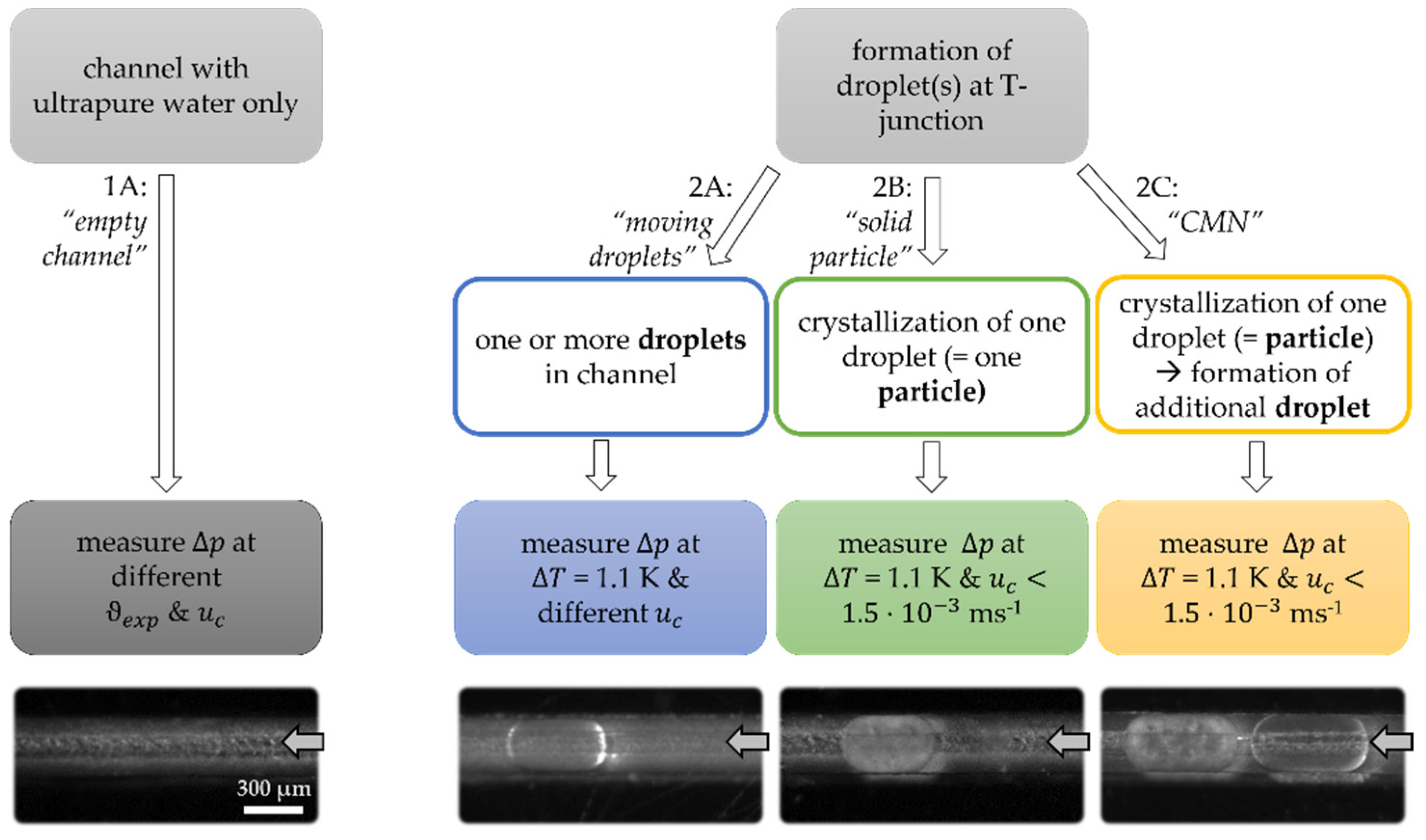
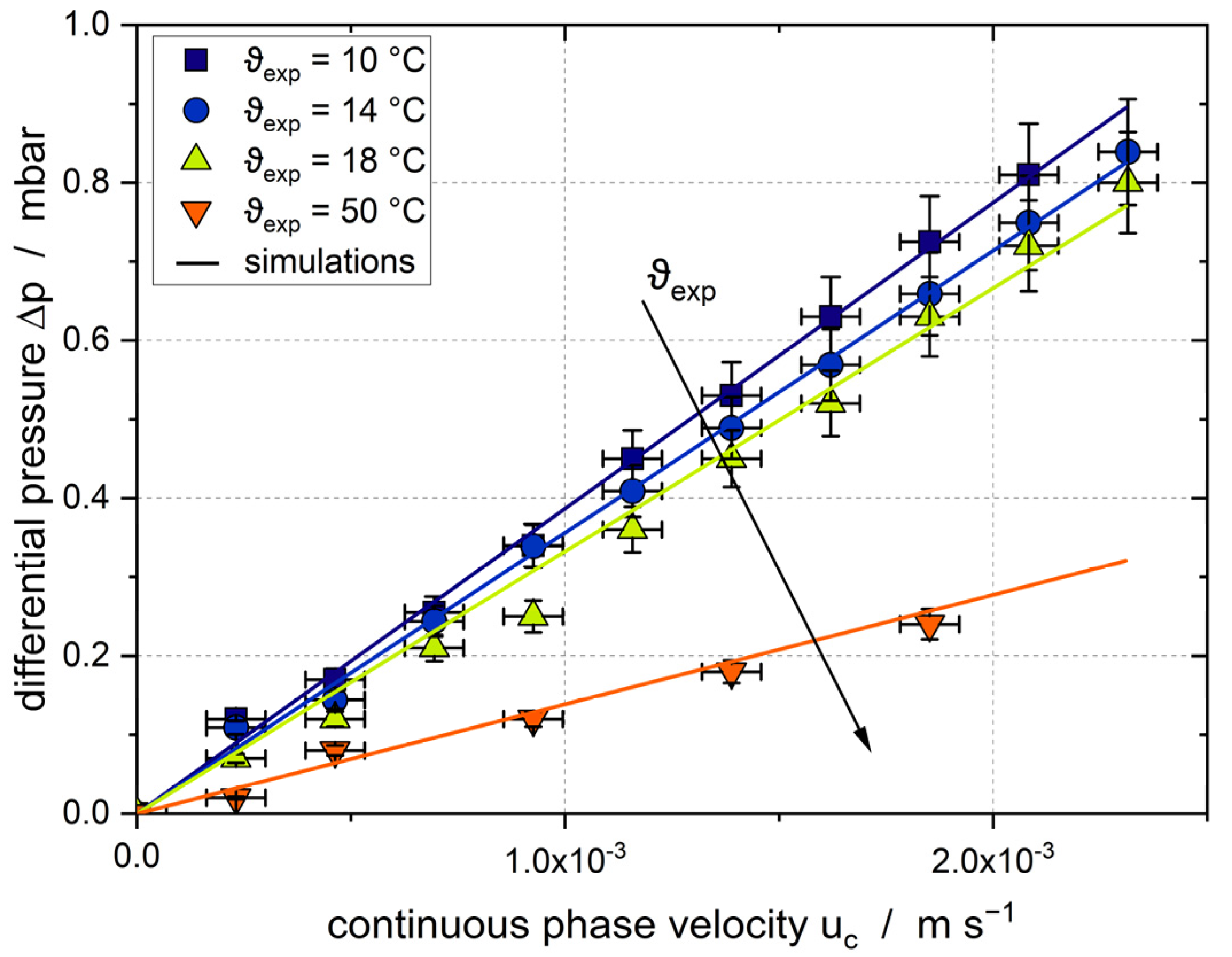
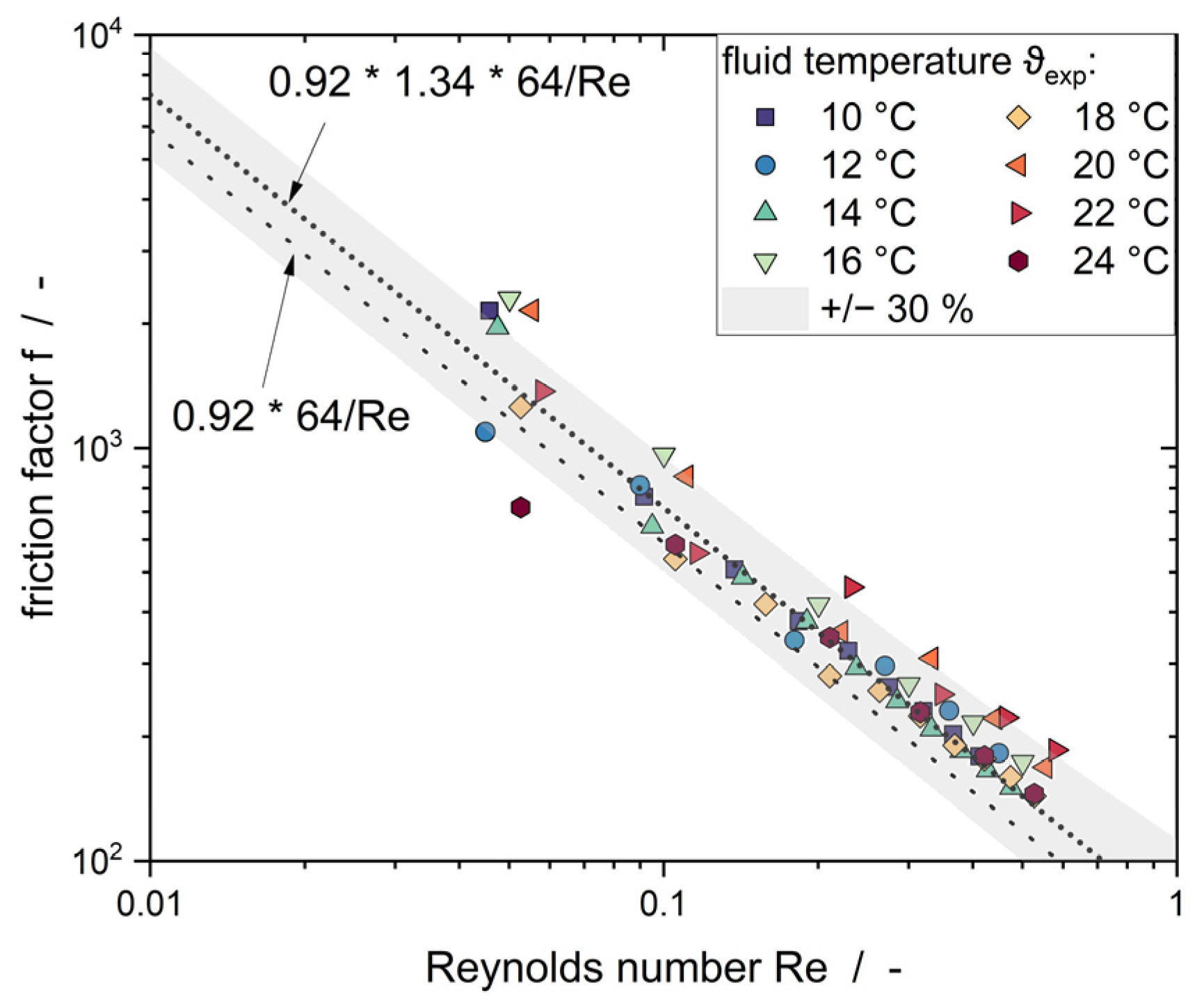
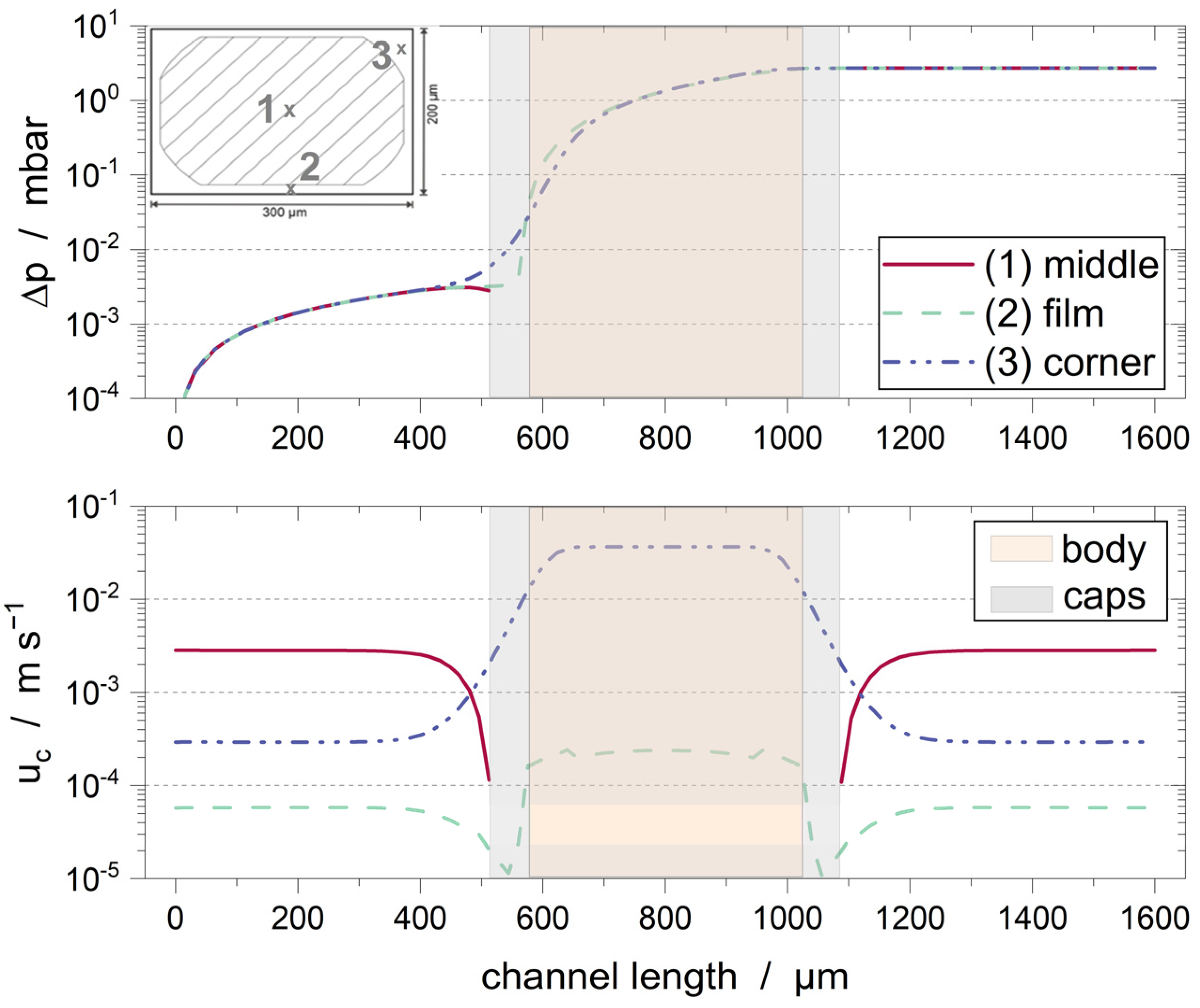
3.1. Empty Channel
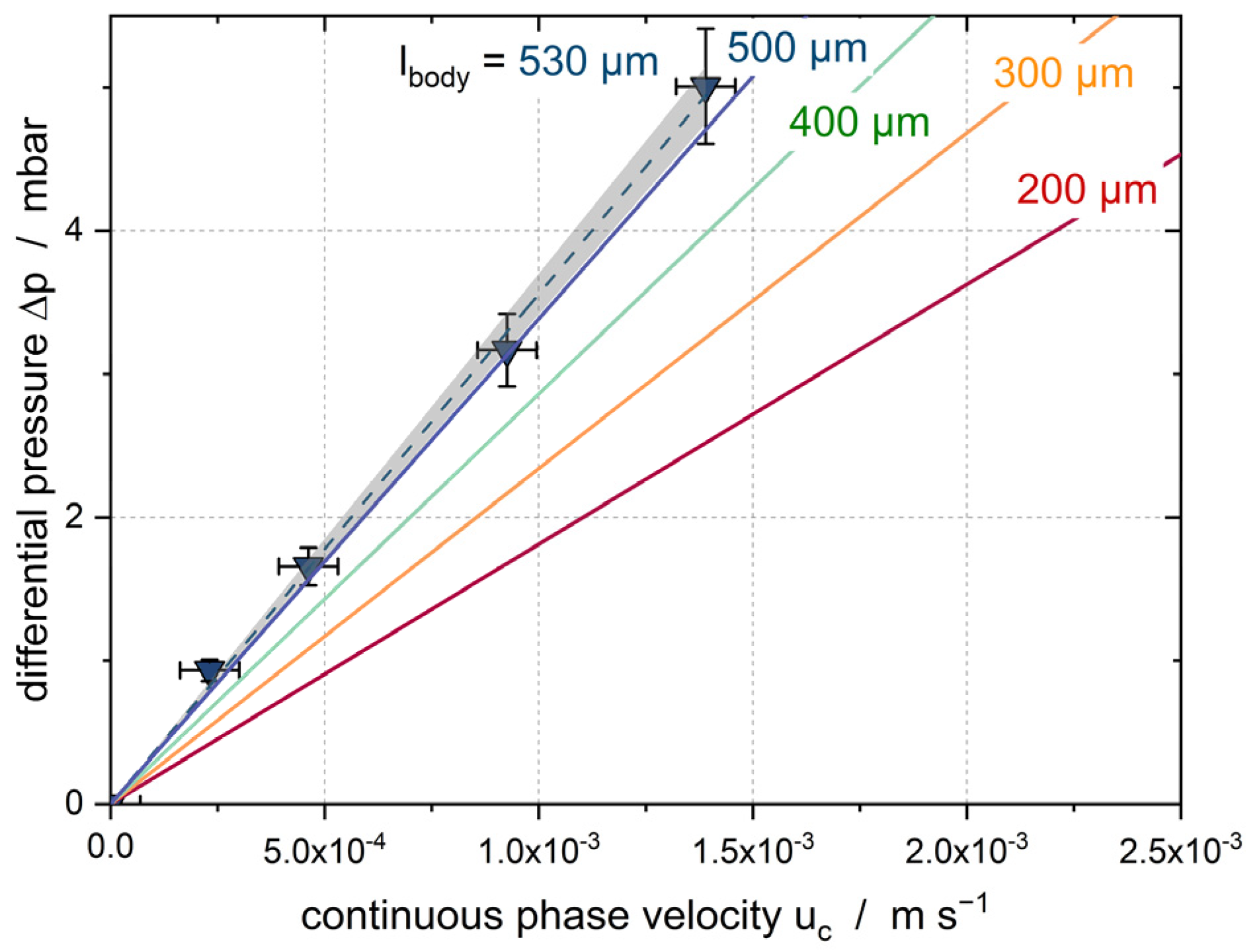
3.2. Solid Particle in Channel
3.3. Moving Droplets
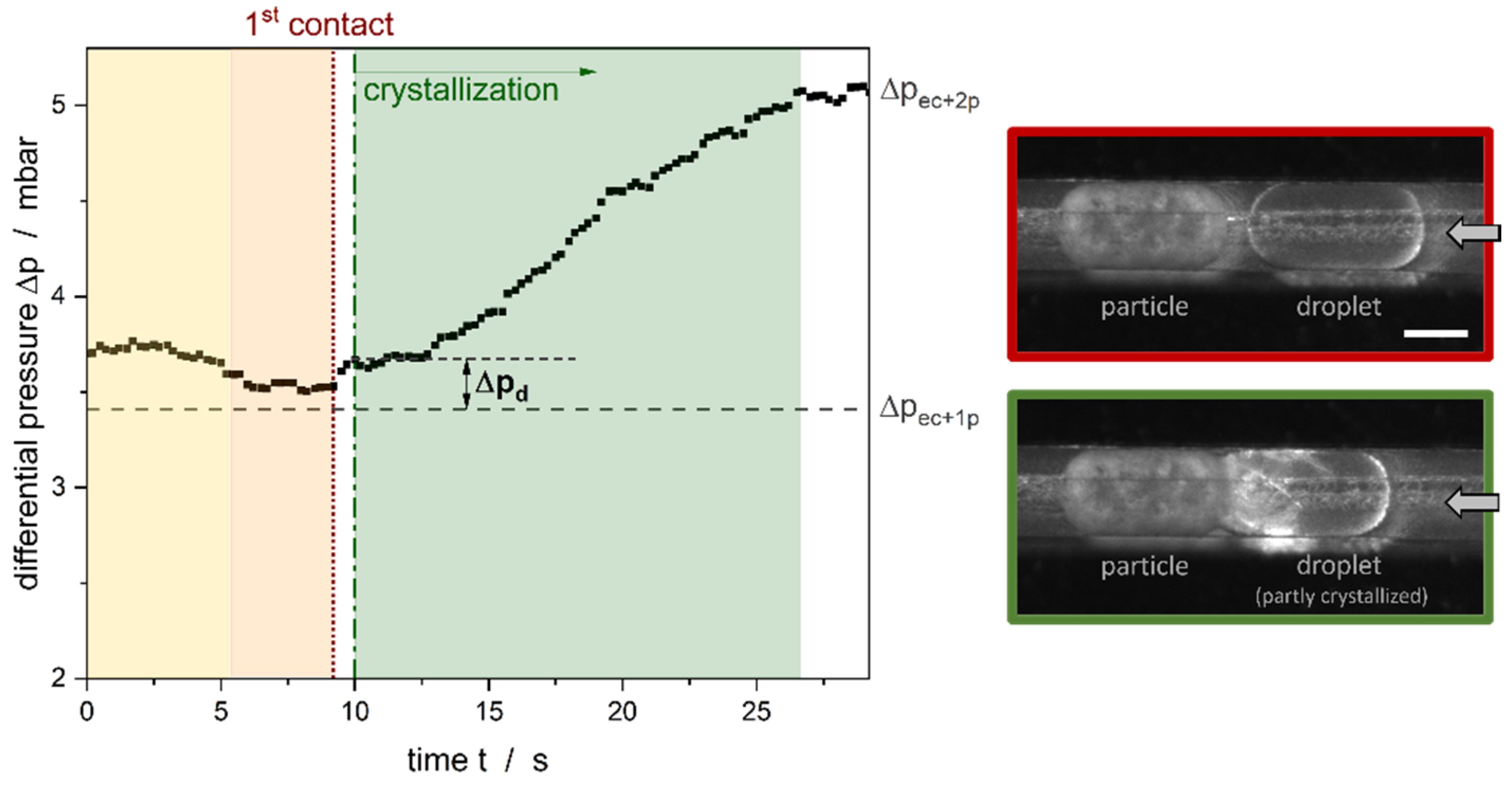
3.4. Differential Pressure during Crystallization
- t < 0: One solid particle can already be found in the channel. The corresponding is the sum of the pressure loss due to the fluid flow of the continuous phase around the particle and the empty channel.
- Yellow region: In addition to the solid particle, one liquid droplet is formed at the T-junction of the channel and is inserted into the main channel.
- Orange region: The formation of the liquid droplet is finished, and the droplet is moving towards the solid particle along the rectangular channel. As the previous results stated, the moving droplet resulted in an additional pressure loss. That is why in this region. The first contact between the liquid and the solid particles happened at the end of this region.
- The time between the first visible contact and the visible start of the crystallization is called the induction time and describes the time needed for the successful inoculation of the subcooled, liquid droplet. We were able to show in a previous work that the induction time is a function of the aqueous surfactant concentration and the relative velocity between the two collision partners [7]. Moreover, nucleation is possible because the solid particle seems to have a partial interfacial coverage with surfactant molecules compared to the fully covered interface of liquid droplets [46]. The surfactant molecules are moveable on the interface of the droplet, therefore, a molecular contact between these two partners can be given.
- Green region: After the crystallization starts, the crystal strands grow through the subcooled droplet until the droplet is completely crystallized. The speed of growth strongly depends on the subcooling (here: ~ 1.1 K). The speed of growth increases as the temperature decreases. The increase of can be explained by the change in the elasticity of the droplet as the latter becomes solid and due to the deformation of the liquid part of the droplet as it is pushed to the particle.
- As soon as the droplet is completely crystallized, becomes constant at the level indicated as (empty channel + two solid particles). As has been shown previously, the pressure loss due to the particle depends strongly on the size of the particle.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calculation of Dimensionless Numbers
- Reynolds number Re
- Capillary number Ca
| Fluid Properties | Symbol | Value | |
|---|---|---|---|
| Density/kg m−3 | water | 998.7 | |
| n-hexadecane | 775.1 | ||
| Dynamic viscosity/mPa s | water | 1.07 | |
| n-hexadecane | 3.70 1 | ||
| Interfacial tension/ N m−1 | with TW20 | 0.004 2 | |
| without TW20 | 0.047 3 | ||
| without TW20 | with TW20 | ||
References
- Bunjes, H.; Koch, M.H.J.; Westesen, K. Influence of emulsifiers on the crystallization of solid lipid nanoparticles. J. Pharm. Sci. 2003, 92, 1509–1520. [Google Scholar] [CrossRef] [PubMed]
- Kalnin, D.; Schafer, O.; Amenitsch, H.; Ollivon, M. Fat Crystallization in Emulsion: Influence of Emulsifier Concentration on Triacylglycerol Crystal Growth and Polymorphism. Cryst. Growth Des. 2004, 4, 1283–1293. [Google Scholar] [CrossRef]
- Maruyama, J.M.; Soares, F.A.S.D.M.; D’Agostinho, N.R.; Gonçalves, M.I.A.; Gioielli, L.A.; Da Silva, R.C. Effects of emulsifier addition on the crystallization and melting behavior of palm olein and coconut oil. J. Agric. Food Chem. 2014, 62, 2253–2263. [Google Scholar] [CrossRef] [PubMed]
- Miskandar, M.S.; Man, Y.C.; Rahman, R.A.; Aini, I.N.; Yusoff, M. Effects of Emulsifiers on Crystal Behavior of Palm Oil Blends On Slow Crystallization. J. Food Lipids 2007, 14, 1–18. [Google Scholar] [CrossRef]
- Kashchiev, D.; Clausse, D.; Jolivet-Dalmazzone, C. Crystallization and Critical Supercooling of Disperse Liquids. J. Colloid Interface Sci. 1994, 165, 148–153. [Google Scholar] [CrossRef]
- Mastai, Y. Advanced Topics in Crystallization; IntechOpen: London, UK, 2015; ISBN 9789535121251. [Google Scholar]
- Kaysan, G.; Rica, A.; Guthausen, G.; Kind, M. Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach. Crystals 2021, 11, 1471. [Google Scholar] [CrossRef]
- McClements, J.D.; Dickinson, E.; Povey, M. Crystallization in hydrocarbon-in-water emulsions containing a mixture of solid and liquid droplets. Chem. Phys. Lett. 1990, 172, 449–452. [Google Scholar] [CrossRef]
- Dickinson, E.; Kruizenga, F.-J.; Povey, M.J.; van der Molen, M. Crystallization in oil-in-water emulsions containing liquid and solid droplets. Colloids Surf. A Physicochem. Eng. Asp. 1993, 81, 273–279. [Google Scholar] [CrossRef]
- McClements, D.J.; Dungan, S.R. Effect of Colloidal Interactions on the Rate of Interdroplet Heterogeneous Nucleation in Oil-in-Water Emulsions. J. Colloid Interface Sci. 1997, 186, 17–28. [Google Scholar] [CrossRef]
- Povey, M.J.W.; Awad, T.S.; Huo, R.; Ding, Y. Quasi-isothermal crystallisation kinetics, non-classical nucleation and surfactant-dependent crystallisation of emulsions. Eur. J. Lipid Sci. Technol. 2009, 111, 236–242. [Google Scholar] [CrossRef]
- Kaysan, G.; Schork, N.; Herberger, S.; Guthausen, G.; Kind, M. Contact-mediated nucleation in melt emulsions investigated by rheo-nuclear magnetic resonance. Magn. Reason. Chem. 2022, 60, 615–627. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. 1883, 174, 935–982. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Single-phase liquid flow in minichannels and microchannels. In Heat Transfer and Fluid Flow in Minichannels and Microchannels; Kandlikar, S.G., Garimella, S., Li, D., Colin, S., King, M., Eds.; Elsevier: London, UK, 2006; pp. 87–136. ISBN 9780080445274. [Google Scholar]
- Kast, W.; Gaddis, E.S.; Wirth, K.-E.; Stichlmair, J. L1 Pressure Drop in Single Phase Flow. In VDI Heat Atlas; VDI e.V., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1053–1116. ISBN 978-3-540-77876-9. [Google Scholar]
- Kandlikar, S.G.; Grande, W.J. Evolution of Microchannel Flow Passages--Thermohydraulic Performance and Fabrication Technology. Heat Transf. Eng. 2003, 24, 3–17. [Google Scholar] [CrossRef]
- Kockmann, N. Transport Phenomena in Micro Process Engineering; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-74616-4. [Google Scholar]
- Chan, D.Y.C.; Horn, R.G. The drainage of thin liquid films between solid surfaces. J. Chem. Phys. 1985, 83, 5311–5324. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I.; Lee, S.-Y.; Wereley, S.T. Experimental and Computational Investigation of Flow Development and Pressure Drop in a Rectangular Micro-channel. J. Electron. Packag. 2006, 128, 1–9. [Google Scholar] [CrossRef]
- Xu, B.; Ooti, K.T.; Wong, N.T.; Choi, W.K. Experimental investigation of flow friction for liquid flow in microchannels. Int. Commun. Heat Mass Transf. 2000, 27, 1165–1176. [Google Scholar] [CrossRef]
- Mohiuddin Mala, G.; Li, D. Flow characteristics of water in microtubes. Int. J. Heat Fluid Flow 1999, 20, 142–148. [Google Scholar] [CrossRef]
- Mirmanto, M. Prediction and Measurement of Pressure Drop of Water Flowing in a Rectangular Microchannel. DTM 2017, 3, 75–82. [Google Scholar] [CrossRef]
- Ghajar, A.J.; Tang, C.C.; Cook, W.L. Experimental Investigation of Friction Factor in the Transition Region for Water Flow in Minitubes and Microtubes. Heat Transf. Eng. 2010, 31, 646–657. [Google Scholar] [CrossRef]
- Steinke, M.E.; Kandlikar, S.G. Single-phase liquid friction factors in microchannels. Int. J. Therm. Sci. 2006, 45, 1073–1083. [Google Scholar] [CrossRef]
- Selzer, D.; Spiegel, B.; Kind, M. A Generic Polycarbonate Based Microfluidic Tool to Study Crystal Nucleation in Microdroplets. J. Cryst. Process Technol. 2018, 8, 1–17. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, S.W.; Tan, J.; Wang, Y.J.; Luo, G.S. Preparation of highly monodisperse droplet in a T-junction microfluidic device. AIChE J. 2006, 52, 3005–3010. [Google Scholar] [CrossRef]
- Musterd, M.; van Steijn, V.; Kleijn, C.R.; Kreutzer, M.T. Calculating the volume of elongated bubbles and droplets in microchannels from a top view image. RSC Adv. 2015, 5, 16042–16049. [Google Scholar] [CrossRef]
- Fuerstman, M.J.; Lai, A.; Thurlow, M.E.; Shevkoplyas, S.S.; Stone, H.A.; Whitesides, G.M. The pressure drop along rectangular microchannels containing bubbles. Lab Chip 2007, 7, 1479–1489. [Google Scholar] [CrossRef] [PubMed]
- Ransohoff, T.; Radke, C. Laminar flow of a wetting liquid along the corners of a predominantly gas-occupied noncircular pore. J. Colloid Interface Sci. 1988, 121, 392–401. [Google Scholar] [CrossRef]
- Linke, D. Detergents. In Guide to Protein Purification, 2nd ed.; Burgess, R., Deutscher, M., Eds.; Elsevier: London, UK, 2009; pp. 603–617. ISBN 9780123745361. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Salome, Version 9.3.0.; Open Cascade SA: Guyancourt, France, 2019.
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Chesters, A.A. The modelling of coalescence processes in fluid-liquid dispersions: A review of current understanding. Chem. Eng. Res. Des. 1991, 69, 259–270. [Google Scholar]
- Kaysan, G.; Spiegel, B.; Guthausen, G.; Kind, M. Influence of Shear Flow on the Crystallization of Organic Melt Emulsions—A Rheo-Nuclear Magnetic Resonance Investigation. Chem. Eng. Technol. 2020, 43, 1699–1705. [Google Scholar] [CrossRef]
- Moody, L.F. Friction Factors for Pipe Flow. Trans. Am. Soc. Mech. Eng. 1944, 66, 671–678. [Google Scholar] [CrossRef]
- Krishnamoorthy, C.; Ghajar, A.J. Single-Phase Friction Factor in Micro-Tubes: A Critical Review of Measurement, Instrumentation and Data Reduction Techniques From 1991–2006. In Proceedings of the ASME 2007 5th International Conference on Nanochannels, Microchannels, and Minichannels, Puebla, Mexico, 18–20 June 2007; pp. 813–825, ISBN 0-7918-4272-X. [Google Scholar]
- Tam, L.M.; Tam, H.K.; Ghajar, A.J.; Ng, W.S.; Wong, I.W.; Leong, K.F.; Wu, C.K. The Effect of Inner Surface Roughness and Heating on Friction Factor in Horizontal Micro-Tubes. In Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference: Symposia—Parts A, B, C, and D, Hamamatsu, Japan, 24–29 July 2011; Volume 1, pp. 2971–2978, ISBN 978-0-7918-4440-3. [Google Scholar]
- Gloss, D.; Herwig, H. Microchannel Roughness Effects: A Close-Up View. Heat Transf. Eng. 2009, 30, 62–69. [Google Scholar] [CrossRef]
- Reinelt, D.A.; Saffman, P.G. The Penetration of a Finger into a Viscous Fluid in a Channel and Tube. SIAM J. Sci. Stat. Comput. 1985, 6, 542–561. [Google Scholar] [CrossRef]
- Hazel, A.L.; Heil, M. The steady propagation of a semi-infinite bubble into a tube of elliptical or rectangular cross-section. J. Fluid Mech. 2002, 470, 91–114. [Google Scholar] [CrossRef]
- Schwartz, L.W.; Princen, H.M.; Kiss, A.D. On the motion of bubbles in capillary tubes. J. Fluid Mech. 1986, 172, 259–275. [Google Scholar] [CrossRef]
- Baroud, C.N.; Gallaire, F.; Dangla, R. Dynamics of microfluidic droplets. Lab Chip 2010, 10, 2032–2045. [Google Scholar] [CrossRef] [PubMed]
- Adzima, B.J.; Velankar, S.S. Pressure drops for droplet flows in microfluidic channels. J. Micromech. Microeng. 2006, 16, 1504–1510. [Google Scholar] [CrossRef]
- Jousse, F.; Lian, G.; Janes, R.; Melrose, J. Compact model for multi-phase liquid-liquid flows in micro-fluidic devices. Lab Chip 2005, 5, 646–656. [Google Scholar] [CrossRef]
- Kaysan, G.; Kräling, R.; Meier, M.; Nirschl, H.; Guthausen, G.; Kind, M. Investigation of the surfactant distribution in oil-in-water emulsions during the crystallization of the dispersed phase via nuclear magnetic resonance relaxometry and diffusometry. Magn. Reson. Chem. 2022, 60, 1131–1147. [Google Scholar] [CrossRef]
- Dudek, M.; Fernandes, D.; Helno Herø, E.; Øye, G. Microfluidic method for determining drop-drop coalescence and contact times in flow. Colloids Surf. A Physicochem. Eng. Asp. 2020, 586, 124265. [Google Scholar] [CrossRef]
- Christov, N.C.; Danov, K.D.; Zeng, Y.; Kralchevsky, P.A.; von Klitzing, R. Oscillatory structural forces due to nonionic surfactant micelles: Data by colloidal-probe AFM vs theory. Langmuir 2010, 26, 915–923. [Google Scholar] [CrossRef]
- Kinoshita, H.; Kaneda, S.; Fujii, T.; Oshima, M. Three-dimensional measurement and visualization of internal flow of a moving droplet using confocal micro-PIV. Lab Chip 2007, 7, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Rott, N. Note on the History of the Reynolds Number. Annu. Rev. Fluid Mech. 1990, 22, 1–12. [Google Scholar] [CrossRef]
- Bretherton, F.P. The motion of long bubbles in tubes. J. Fluid Mech. 1961, 10, 166–188. [Google Scholar] [CrossRef]
- van der Graaf, S.; Schroën, C.G.P.H.; van der Sman, R.G.M.; Boom, R.M. Influence of dynamic interfacial tension on droplet formation during membrane emulsification. J. Colloid Interface Sci. 2004, 277, 456–463. [Google Scholar] [CrossRef] [PubMed]



| 15 µm | 11.6 µm | 9 µm | |||
|---|---|---|---|---|---|
| empty channel (no particle) | 44.21 | 44.63 | 44.94 | 0.0329 | 0.0242 |
| Parameters Influencing CMN in Stirred Systems 1 | Parameters Investigated in the Microfluidic Approach | Condition for Successful CMN in Stirred Systems |
|---|---|---|
| Collision frequency | - | - |
| Contact force | minimum contact force for CMN | |
| Contact time | induction time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaysan, G.; Hirsch, T.; Dubil, K.; Kind, M. A Microfluidic Approach to Investigate the Contact Force Needed for Successful Contact-Mediated Nucleation. Colloids Interfaces 2023, 7, 12. https://doi.org/10.3390/colloids7010012
Kaysan G, Hirsch T, Dubil K, Kind M. A Microfluidic Approach to Investigate the Contact Force Needed for Successful Contact-Mediated Nucleation. Colloids and Interfaces. 2023; 7(1):12. https://doi.org/10.3390/colloids7010012
Chicago/Turabian StyleKaysan, Gina, Theresa Hirsch, Konrad Dubil, and Matthias Kind. 2023. "A Microfluidic Approach to Investigate the Contact Force Needed for Successful Contact-Mediated Nucleation" Colloids and Interfaces 7, no. 1: 12. https://doi.org/10.3390/colloids7010012
APA StyleKaysan, G., Hirsch, T., Dubil, K., & Kind, M. (2023). A Microfluidic Approach to Investigate the Contact Force Needed for Successful Contact-Mediated Nucleation. Colloids and Interfaces, 7(1), 12. https://doi.org/10.3390/colloids7010012