Abstract
It was reported in many papers that the magnetic field (MF) affects properties of water, and, among others, its surface tension. Thus, it should be reflected in changes of the wetting contact angle of a water droplet deposited on the solid surface. In this study, the water contact angles were measured on the glass and mica surface. The water was first exposed to the static magnetic field (MF) (15 mT or 0.27 T) for 1, 5, and 10 min under dynamic conditions. Then applying the van Oss et al. approach (LWAB), it was found that the MF effect is reflected in the changes of the calculated acid-base components of the solids, especially the electron donor parameter. However, the total surface free energy of the solids remained practically unchanged. Moreover, the apparent surface free energy of the solids calculated from the water contact angle hysteresis (CAH), i.e., the difference between the advancing and receding contact angles, changes in the same way as the electron donor parameter does. Since the solid surfaces were not magnetically treated, the acid-base components, which are mainly results from hydrogen bonding interactions, may be indirect evidence of the water structure changed by the MF action. All of the mentioned changes are greater for the glass than for a more hydrophilic mica surface and depend upon the time of MF exposure and its strength. The magnetic field effect on the changes of the surface-free energy parameters for the mica and glass is opposite what may be due to the difference in the surface hydrophilicity. A “magnetic memory” effect was also found. The effect of MF on the water surface tension depends on the circulation time. It increases with the field duration. Moreover, the changes in the work of water adhesion indicate the possibility of solid surface wettability changes by the external MF water treatment. However, these are preliminary results that need further confirmation by other techniques.
1. Introduction
The magnetic field (MF) influence on water and water solutions has been investigated for decades [1]. This is due to the possible usage of both magnetic and electromagnetic fields as a non-chemical method of water treatment. Therefore, the MF studies were focused mainly on the effect of the magnetic field on the calcium carbonate precipitating from the aqueous solutions, as the principal component of limescale [2,3,4]. However, the question of whether MF influences properties of water itself is interesting as well, especially in practical aspects of wetting processes such as mineral processes, agriculture, chemical protection of plants, and others [1]. Although the MF effects on water properties, such as surface tension [5,6,7], viscosity [5,8], rate of water evaporation [9,10,11,12], heat capacity [13], changes in the IR and Raman spectra [14], and others, have been described many times. However, a full understanding of them remains an open issue. Yet, as follows from the literature data, the magnetic field can affect the water structure. The latest approaches to the magnetic field effects have been reviewed in the recent review paper [1].
Among different approaches concerning the MF effects, one of them is the field action on the hydrogen-bonded structure of water [5,15,16,17]. Chang and Weng [16] found that the increase in the strength of the magnetic field from 1 to 10 T causes the number of hydrogen bonds to increase by about 0.34%. In addition, Hosoda et al. [15] suggested that 10 T MF can cause an increase in the hydrogen bonds strength via delocalization of electrons in the hydrogen-bonded molecules. Based on the viscosity, surface tension results, and H1-NMR measurements, Cai et al. [5] suggested an increase of average size of the water clusters after magnetic treatment. If the external magnetic field changes the structure of water clusters and, thus, water properties as well, one can also expect some changes in the processes occurring at the solid-liquid interfaces, i.e., wetting using the magnetized water.
Surface-free energy determines the energetic and wetting properties of solid surfaces and is important in many processes at the interfaces. Its magnitude results from the kind of intermolecular interactions present at the interface and their strength. Van Oss et al. [18] proposed to express the surface-free energy of a solid (s) or a liquid (l) as the sum of apolar () and polar () components.
The first component expresses the Lifshitz-van der Waals interactions (LW) and the other results from the Lewis acid-base (AB) interactions, mainly hydrogen bonding. The polar component is expressed as the geometric mean of the electron donor () and electron acceptor () parameters.
In the case of solid/liquid interface, the interfacial free energy (γSL) can be written as:
where WA is the work of liquid adhesion to the solid surface and using the Van Oss et al. [18] approach, it is expressed:
Combining the above equation with the Young equation:
where is the contact angle, the work of adhesion (WA) of the solid-liquid interface is calculated using the equation below.
From Equation (6), the surface-free energy of a solid can be calculated if the advancing contact angles for three probe liquids, including one apolar and two polar, have been measured.
Chibowski proposed another approach to surface-free energy determination [19,20,21]. It is based on the surface tension of the liquid () and the contact angle hysteresis, which is the difference between the advancing () and receding () contact angles.
It should be stressed that the solid surface-free energy values determined from the contact angles of different probe liquids, using both the Van Oss et al.’s (LWAB) or hysteresis contact angle (CAH) approaches, are apparent ones. They depend on the kind and strength of the interactions occurring at the solid-liquid interface, which differ for different probe liquids. Based on this assumption, the changes in the MF-treated water properties should be reflected in the contact angle changes and in the calculated solid surface-free energy values. Moreover, if the MF caused changes in the water hydrogen bond network, it should be reflected in the acid-base interactions calculated from the LWAB approach. The aim of this study was verifying this assumption by measuring the water contact angles of the magnetized water on two solid surfaces, which are glass and mica, and calculation of their surface-free energy using the LAWB and CAH approaches. The surface-free energy of these solids and quartz was investigated many times [22,23,24,25,26]. Since the purpose of this paper was not investigation of the surface-free energy of these solids, it will not be discussed in detail.
2. Materials and Methods
2.1. Materials
The water was from a Milli–Q system with resistivity 18.2 MΩ cm (Merck Millipore, Warsaw, Poland). Formamide (≥99.5% (GC), BioReagent) and diiodomethane (99%, contains copper as a stabilizer) were from Sigma Aldrich (Poznan, Poland). They were used as received. The probe liquids surface tension and its components can be found in Reference [27].
The microscopic glass slides (AS Polonia, Ltd., Warsaw, Poland) of 26 × 76 × 1 mm and mica muscovite type (Continental Trade, Warsaw, Poland) of 26 × 76 mm were used. Before the contact angle measurements, the glass and mica plates were washed with a commercial detergent, flowing tap water, and distilled water. Next, they were washed in the sequence with ethanol for 30 min and three times with Milli-Q water for 15 min using the ultrasonic bath. Lastly, the samples were dried at 100 °C.
2.2. Methods
The contact angles were measured using the contact angle meter with a video-camera system (GBX, Bourg-de-Peage, France). The advancing contact angle of the probe liquid was measured after settling 6 μL droplets on the solid surface. Then, 2 μL volume from the droplet was sucked into the syringe and the receding contact angle was measured. All measurements were performed at 20 °C ± 3 °C by taking readings on the left and right sides of the droplets. For each liquid, the contact angles were measured for at least nine droplets. The obtained results were statistically analysed with the unpaired student’s t-test and p < 0.05.
The surface tension of water was measured by means of the tensiometer (Kruss K100, Kruss, Hamburg, Germany) using the du Nuoy ring method at 20 ± 3 °C.
To magnetize water, two types of magnets were used in the experiments. The details of the setup can be found in our previous papers [10,28]. Briefly, a magnetic stack (B = 15 mT) of 3.5 cm diameter and 41 cm long composed of 29 magnets and nonmagnetic separating elements arranged convertibly (Feniks, Gliwice, Poland (patent PL 155856)) were used. Water circulated by means of a peristaltic pump inside a Teflon tube was wrapped around the magnetic stack. Due to the rigidity of the Teflon tube, about 30 cm of a polyethylene tube instead of the Teflon one was used for water circulation. The length of the tubing being in touch with the stack was 95 cm. As a reference system (without MF), the tube of the same length and diameter was twisted around a glass cylinder with the same diameter as the magnetic stack. As the second source of magnetic field, a neodymium magnet N-S (0.27 T) attached to the reference system was applied. The MF water treatment was carried out at 20 °C ± 3 at the water flow rate of 2.8 mL/s. The circulation system was sealed to avoid CO2 dissolution. The volume of the circulating water was approximately 100 mL.
3. Results and Discussion
The total surface-free energy and its components of the investigated solid surfaces were first calculated from the van Oss et al. (LWAB) approach using the advancing contact angles of three probe liquids: apolar (diiodomethane) and polar, water, and formamide (Table 1). The values refer to the MF untreated water. The relatively big contact angle values of polar liquids are likely due to the glass surface (the information from the manufacturer). Since, in this study, we were interested in whether MF influences wettability of the same surfaces by water (magnetized and non-magnetized), such a glass surface seemed to be the best for these experiments. Nevertheless, to confirm these results, in the near future, similar experiments will be conducted using different solid samples.

Table 1.
Advancing contact angles (in degrees) of the probe liquids on the glass and mica surfaces.
The calculated surface-free energy values from the contact angles in Table 1 are listed in Table 2. It can be seen that the total surface-free energy and its components are higher for the mica surface. While the electron donor parameter is significant for both solid surfaces, the electron acceptor is meaningless, particularly for the glass surface. The slight electron acceptor interactions are characteristic of most solid surfaces. These results show clearly that the mica surface is more polar than that of glass.

Table 2.
Values in mJ/m2 of the surface free energy () and its components: Lifshitz-van der Waals (, electron acceptor (, electron donor (, and acid-base () of glass and mica calculated from the LWAB approach.
The values of advancing and receding contact angles of water on the mica and glass surfaces for the magnetized and non-magnetized water are presented in Figure 1. Figure 2 presents the photos of typical water droplets on the glass and mica surfaces. As can be seen in Table 1, the advancing contact angle of MF untreated water (denoted as no MF) on the glass is much higher than those on the mica surface, 62° and 47°, respectively.
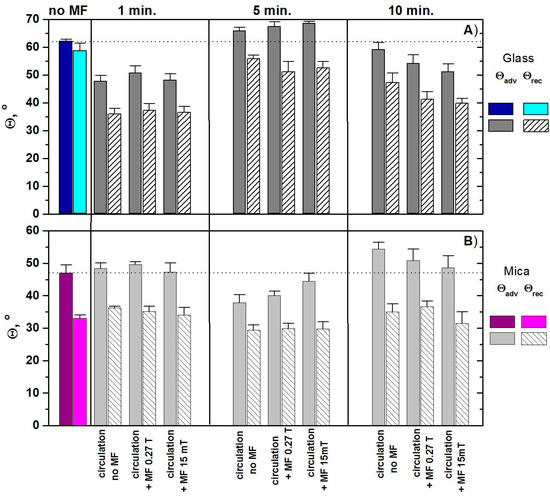
Figure 1.
Advancing and receding contact angles of non-magnetized and magnetized water on: (A) glass and (B) mica.

Figure 2.
Water droplets on the glass and mica surfaces. Water circulated for 5 min.
As follows from Figure 1, on both the glass and mica surfaces, the receding contact angles are smaller than the advancing ones, which occurs commonly. The MF effects on the water contact angles are measured immediately after circulation for 1, 5, or 10 min in the presence of 15 mT or 0.5 T MF. These contact angle values differ significantly from those of the untreated water. In the case of glass surface, 5 min treatment leads to reduction of contact angles whereas 1-min or 10-min treatment results in their increase. In the case of the mica surface, the effect is reverse. Moreover, larger changes were observed for the glass surface. Possible changes in the water properties due to the MF treatment may influence its interactions with the solid surface, mainly via the acid-base interactions. The acid-base component () of the surface-free energy was found to be five times greater for mica than for glass. It seems that this could be the reason for the opposite changes. Nevertheless, to confirm it, further studies with solids having a different polarity are needed. It is worth noticing (Figure 1) that even the circulation without the MF presence affects the contact angle. This may be due to the presence of CO2 and/or oxygen dissolved during the sample preparation. Hamadi et al. [29] showed that the water contact angle on the glass surface depends on the solution pH. Hihashitani et al. [30] investigated the magnetic field effect on the calcium carbonate precipitation and found that this effect resulted mainly from the magnetic exposure of Na2CO3 solutions rather than CaCl2 solution. The results obtained by us seem to originate from a combination of both effects during the water circulation, i.e., the dissolved gas (air) and the magnetic field influence on a possible formation in the water including some carbonate and bicarbonate ions.
The values of measured water contact angles were estimated statistically using the unpaired student’s t-test. It can be seen in Table 3 that, besides the receding angles on mica obtained using the water circulated for 10 min without the MF and in the presence of 0.27 T MF as well as the water circulated for 1 min in the presence of the 15 mT MF, the other results are statistically significant.

Table 3.
Analysis of probabilities. Statistically insignificant results are in italic.
Next, the advancing water contact angles were used to determine the surface-free energy and its components from the LWAB approach. The contact angles of diiodomethane and formamide were the same as in Table 1. In the calculations, it was assumed that the Lifshitz-van der Waals component ( of glass and mica remained unchanged regardless of the fact that magnetized or non-magnetized water contact angles are applied, i.e., 36.3 mJ/m2 and 42.7 mJ/m2 for glass and mica, respectively. The obtained results are presented in Table 4.

Table 4.
Values in mJ/m2 of the surface-free energy () and its components: Lifshitz-van der Waals (, electron acceptor (, electron donor (, and acid-base () of glass and mica calculated from the LWAB approaches using the MF treated water.
In the case of glass surface treated for 1 min and 10 min, the square root of the electron acceptor parameter is negative and then the calculations have no physical sense. Such cases are known in the literature. However, they cannot always be assigned to an experimental error of the contact angle measurement. Van Oss suggested that the root value should be zero.
In Table 4, one can see that using the contact angles of MF-treated water, the determined values of the total surface-free energy are practically the same. However, there are changes in the electron donor parameter (Figure 2) and, hence, in the acid-base component. It is worth stressing that, because the solid surfaces were exactly the same when the untreated and MF-treated water was used, the changes in can be caused by those in the water structure. It was assumed that the magnetic field affects the hydrogen bonding network in water, which causes different water molecule arrangements in the intermolecular clusters and solid surface/water hydrogen bonding interactions. To confirm that MF does not change the Lifshitz-van der Waals component ( of water, the contact angles of water after the MF treatment were measured on the polytetrafluoroethylene (PTFE) surface, which is nonpolar. The obtained results (not given here) showed that the contact angles of MF treated and untreated water were the same within the standard deviation. Based on this, one can conclude that the apolar component of water surface tension remains unchanged after the MF treatment.
Figure 3 also presents the total surface-free energy values calculated from the contact angle hysteresis (CAH) of water together with the electron donor () parameter calculated from the LWAB approach.
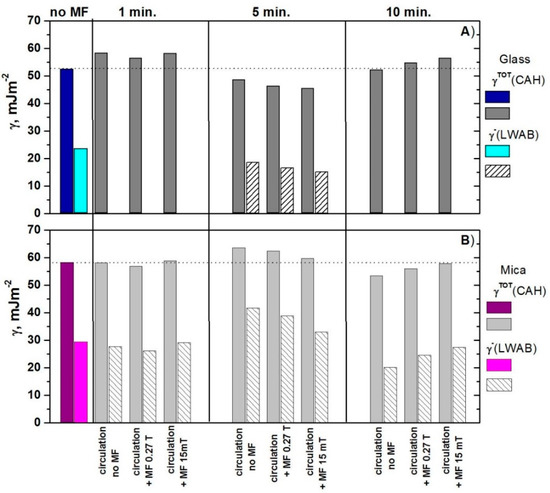
Figure 3.
Total surface-free energy calculated from the water contact angle hysteresis (CAH) and the electron donor () parameter calculated from the LWAB approach for (A) glass and (B) mica surfaces.
As can be seen in Figure 3, the electron donor parameter calculated from the LWAB approach changes in the same way as the energy calculated from the water contact angle hysteresis using the CAH. However, the trend of these changes for glass is opposite to those for mica, i.e., if the value increases for mica, it decreases for glass. Moreover, the magnitude of the changes depends on the time of water circulation with or without the MF presence as well its strength. However, there is no straight relation of these parameters. In the case of glass surface, the biggest changes appeared if the water was treated for 1 and 5 min whereas, for the mica surface, it was for 5 and 10 min.
Comparing the advancing contact angles (Figure 1) and the values of apparent surface-free energy calculated from the water contact angle hysteresis (Figure 3), it can be seen that, if the duration of water treatment is extended to 5 and 10 min, the presence of MF enhances the effect caused by circulation for glass and weakens it for mica. For both surfaces, the effectiveness of the magnetic stack (15 mT) is greater than that of the single neodymium magnet (0.27 T). This can be related to a different arrangement and density of the field lines. In the case of shorter operating time (1 min), the presence of 0.15 mT MF enhances the effect caused by only the circulation if the contact angle was measured on the mica surface and weakens if on the glass surface. For 15 mT MF, the effect is reverse.
As reported many times in the literature [10,17], the changes of water properties caused by the magnetic field can last for some time. This phenomenon is called the ‘memory effect.’ To examine this effect, the contact angles of MF-treated water for 10 min were measured directly after the treatment and after 24 h. The results of advancing contact angles are shown in Figure 4.
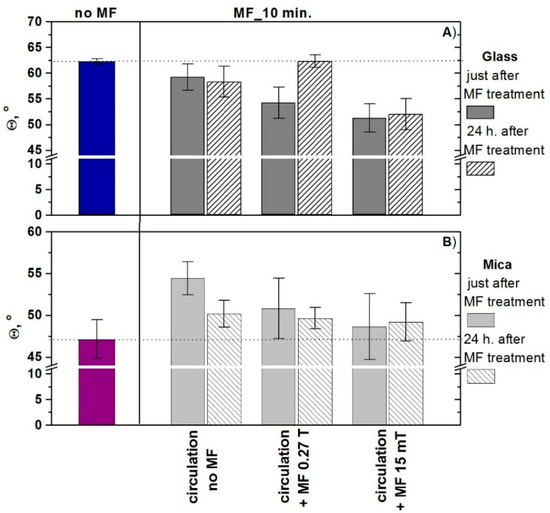
Figure 4.
Advancing contact angles of water were measured immediately after exposition to MF and 24 h later for (A) glass and (B) mica surfaces. The obtained results were statistically analysed with the unpaired student’s t-test and, except for the circulation and circulation + MF 0.27 T, the other results were statistically insignificant.
It can be seen that, after 24 h, the values of contact angles tend to those measured for the MF-untreated water, particularly if 0.27 T MF was applied. The memory effect for 15 mT MF seems to last longer.
In the next step, the surface tension (γ) of water magnetically treated and untreated was measured (Figure 5A). For each sample, the surface tension was measured before and after the MF treatment. Since the obtained changes were very small, it seemed better to present them as the differences between the surface tension before and after treatment. The mean value of the surface tension of water without any treatment in these experiments was 70.1 ± 0.3 mN/m. The circulation without and with MF causes reduction of the surface tension regardless of the MF action time. Although these changes are insignificant and do not exceed 0.35 mN/m, they correlate with the changes of the water contact angles measured on glass and mica (Figure 1). The circulation itself lowers the surface tension and these changes increase with the increasing circulation time. The presence of the magnetic field during the circulation additionally strengthens or weakens this effect. In the case of circulations lasting 1 min, the impact of the field is small and the changes are within the range of the standard deviation. The effect of magnetic field acting 5 min causes a greater reduction of the surface tension. However, during the 10-min circulation, the presence of a magnetic field causes a decrease in the effect of circulation alone on the surface tension, which likely causes strengthening of hydrogen bonds and, hence, a small increase of surface tension.
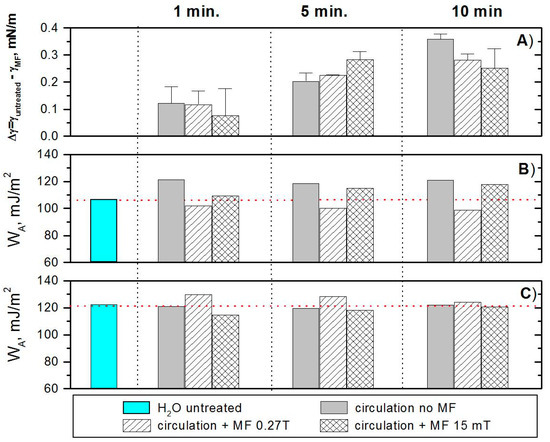
Figure 5.
Changes in water surface tension caused by the exposition to MF (A), and the work of water adhesion to the glass (B) and mica (C) surfaces.
Based on the obtained values of water surface tension and advancing contact angles, the work of adhesion (WA) values were calculated using Equation (6).
Knowledge of WA allows us to evaluate wettability of the investigated surface. It can be seen that the work of adhesion of untreated water is higher for mica than for the glass surface, which means that mica is more hydrophilic. Circulation of water without MF does not change WA for mica but it increases in the case of glass. From these results, one can conclude that the magnetic treatment of water changes its work of adhesion to a solid surface but the change depends on the kind of solid surface, the magnetic type, and the treatment time. The treatment with the Neodymium magnet (0.27 T) causes a decrease of WA to the glass but an increase to the mica surface. Moreover, for the glass surface, the MF effect increases with the prolonged circulation time in the MF. However, for the mica surface, it decreases. Additionally, the magnetic-stack (15 mT) treatment leads to reverse changes, i.e., if MF acts for a longer time, the water on the glass surface behaves since the surface would be a more hydrophilic (WA increases) and, on the mica surface, it behaves since it would be less hydrophilic. However, this effect decreases with the increasing MF action time.
To depict the contact angle changes better, the changes in the water advancing contact angles on the examined surfaces are plotted in Figure 6. It can be seen that their values depend largely on the magnetic field duration with the maximum appearing for 5 min of MF operation. However, if these changes are compared with the water contact angle obtained for the untreated water (denoted as “no treatment”), they are no longer so clear, particularly for the glass surface. Nevertheless, it is evident that the changes are greater for the glass, whose surface is more hydrophobic than that of mica. This finding is in agreement with the results obtained by Ozeki et al. [31] who used static MF from 1 to 9.6 kG at 30 °C. They found that MF affected water adsorption at the surface coverage >1 regardless of the solid type. This indicates that the magnetic field acts on the water molecules interacting weakly via the hydrogen bonds than on the strongly adsorbed first layer. They also showed that MF can affect the first adsorbed layer of water molecules interacting with the hydrophobic surfaces. Otsuka and Ozeki [32] measured the magnetized and non-magnetized water contact angles on the Pt plate and found no changes for the de-aerated magnetically-treated water. If magnetically-treated water contained dissolved oxygen, the measured contact angle decreased from 65° to 56°.
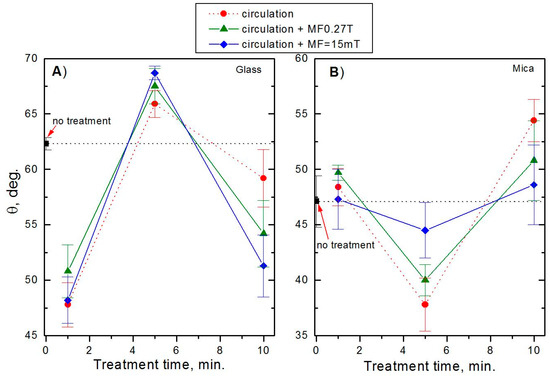
Figure 6.
Changes in the advancing contact angels of water on (A) glass and (B) mica surfaces.
Similarly, when compared to experiments, the solid surfaces remained unchanged. Therefore, it can be suggested that the all-calculated changes in the apparent free energy at the water/solid interface originated from those in the properties of water itself. From the obtained results, it can be seen that circulation itself can affect water properties. This may be due to some weakening of the hydrogen bonds and/or a decreased amount of the dissolved gases from the atmosphere. One can also conclude that the magnetic field can affect the gas/water interface. Hence, to find an unambiguous answer, more experiments are needed under the static MF conditions with degassed water.
4. Conclusions
In the study, it was shown that the static magnetic field acting under the dynamic conditions causes changes in the values of the water contact angle measured on the mica and glass surfaces and, thus, influences the surface wettability. However, the contact angles of water after its circulation without MF also change. MF strengthens or weakens the contact angle changes and this effect depends on the MF strength and time of action being larger for a more hydrophobic surface. Although the total apparent surface energy calculated using the LWAB approach practically remains unchanged, a significant MF effect is reflected in the values of the acid-base component, mainly in its electron-donor parameter. The changes of this parameter are parallel to the apparent surface-free energy calculated from the water contact angle hysteresis using the CAH approach. All mentioned changes are greater for the glass surface than mica surface and depend on the time of exposure to the magnetic field and its strength. Moreover, the MF effect on the electron donor interactions calculated for the glass and mica surfaces is opposite. Existence of the ‘magnetic memory’ effect was also demonstrated. Since the solid was not subjected to magnetization, all changes must result from those in the water structure. It seems that the MF effect on water depends on the gas/water interface because of some air dissolved in it. Hence, in the next paper, the experiments under the static conditions using degassed water will be carried out. Moreover, to find an unambiguous answer, more experiments are needed in which different techniques for measurements of water surface tensions and its components can be applied. Since the solid surfaces remain unchanged during all experiments, it can be suggested that the changes in the apparent free energy at the water/solid interface can result from those in the properties of water itself. Even though one can question the applied method and the results’ interpretation, it is believed that the magnetic field effects on water properties have been demonstrated. Moreover, it was shown that the magnetic field treatment of water can affect the water wettability of solids and this can find a practical application.
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, E.R.; validation, A.S., E.C. and E.R.; formal analysis, A.S. and E.C.; investigation, E.R.; resources, A.S.; data curation, A.S. and E.C.; writing—original draft preparation, A.S.; writing—review and editing, A.S. and E.C.; visualization, A.S.; supervision, E.C.; project administration, E.C.; funding acquisition, E.C. All authors have read and agreed to the published version of the manuscript.
Funding
The National Science Centre based on the decision number DEC-2016/21/B/ST4/00987 financed this project.
Acknowledgments
We express our thanks to Jerzy Ważny for his kind supply of the magnetic device used in these experiments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Chibowski, E.; Szcześ, A. Magnetic water treatment-a review of the latest approaches. Chemosphere 2018, 203, 54–67. [Google Scholar] [CrossRef] [PubMed]
- Madsen, H.E.L. Crystallization of calcium carbonate in magnetic field in ordinary and heavy water. J. Cryst. Growth 2004, 267, 251–255. [Google Scholar] [CrossRef]
- Alimi, A.; Tlili, M.; Gabrielli, C.; Georges, M.; Ben Amor, M. Effect of a magnetic water treatment on homogeneous and heterogeneous precipitation of calcium carbonate. Water Res. 2006, 40, 1941–1950. [Google Scholar]
- Alimi, F.; Tlili, M.; Ben Amor, M.; Maurin, G. Influence of magnetic field on calcium carbonate precipitation. Desalination 2007, 206, 163–168. [Google Scholar] [CrossRef]
- Cai, R.; Yang, H.; He, J.; Zhu, W. The effects of magnetic fields on water molecular hydrogen bonds. J. Mol. Struct. 2009, 938, 15–19. [Google Scholar] [CrossRef]
- Iino, M.; Fujimura, Y. Surface tension of heavy water under high magnetic fields. App. Phys. Lett. 2009, 94, 261902. [Google Scholar] [CrossRef]
- Amor, H.B.; Elaoud, A.; Salah, N.B.; Elmoueddeb, K. Effect of magnetic treatment on surface tension and water evaporation. Int. J. Adv. Ind. Eng. 2017, 5, 119–124. [Google Scholar]
- Ghauri, S.A.; Ansari, M.S. Increase of water viscosity under the influence of magnetic field. J. App. Phys. 2006, 100, 066101. [Google Scholar] [CrossRef]
- Nakagawa, J.; Hirota, N.; Kitazawa, K.; Shoda, M. Magnetic field enhancement of water vaporization. J. App. Phys. 1999, 86, 2923–2925. [Google Scholar] [CrossRef]
- Szcześ, A.; Chibowski, E.; Hołysz, L.; Rafalski, P. Effects of static magnetic field on water at kinetic condition. Chem. Eng. Process. 2011, 50, 124–127. [Google Scholar] [CrossRef]
- Guo, Y.-Z.; Yin, D.-C.; Cao, H.-L.; Shi, J.-Y.; Zhang, C.-Y.; Liu, Y.-M.; Huang, H.-H.; Liu, Y.; Wang, Y.; Guo, W.-H.; et al. Evaporation rate of water as a function of a magnetic field and field gradient. Int. J. Mol. Sci. 2012, 13, 16916–16928. [Google Scholar] [CrossRef]
- Seyfi, A.; Afzalzadeha, R.; Hajnorouzi, A. Increase in water evaporation rate with increase in static magnetic field perpendicular to water-air interface. Chem. Eng. Process. 2017, 120, 195–200. [Google Scholar] [CrossRef]
- Zhou, K.X.; Lu, G.W.; Zhou, Q.C.; Song, J.H.; Jiang, S.T.; Xia, H.R. Monte carlo simulation of liquid water in a magnetic field. J. Appl. Phys. 2000, 88, 1802–1805. [Google Scholar] [CrossRef]
- Pang, X.F.; Deng, B. Investigation of changes in properties of water under the action of a magnetic field. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 1621–1632. [Google Scholar] [CrossRef]
- Hosoda, H.; Mori, H.; Sogoshi, N.; Nagasawa, A.; Nakabayashi, S. Refractive indices of water and aqueous electrolyte solutions under high magnetic fields. J. Phys. Chem. A 2004, 108, 1461–1464. [Google Scholar] [CrossRef]
- Chang, K.T.; Weng, C.I. The effect of an external magnetic field on the structure of liquid water using molecular dynamics simulation. J. App. Phys. 2006, 100, 043917. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, K.; Yang, Z. Changes of water hydrogen bond network with different externalities. Int. J. Mol. Sci. 2015, 16, 8454–8489. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Interfacial lifshitz-van der Waals and Polar interactions in macroscopic systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Chibowski, E.; Perea-Carpio, R.; Ontiveros-Ortega, A. On the interpretation of contact angle hysteresis. J. Adhes. Sci. Technol. 2002, 16, 1367–1404. [Google Scholar] [CrossRef]
- Chibowski, E. Surface free energy of a solid from contact angle hysteresis. Adv. Colloid Interface Sci. 2003, 103, 149–172. [Google Scholar] [CrossRef]
- Chibowski, E. Surface free energy and wettability of silyl layers on silicon determined from contact angle hysteresis. Adv. Colloid Interface Sci. 2005, 113, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Staszczuk, P.; Jańczuk, B.; Chibowski, E. On the determination of the surface free energy of quartz. Materials Chem. Phys. 1985, 12, 469–481. [Google Scholar] [CrossRef]
- Chibowski, E.; Delgado, A.V.; Rudzka, K.; Szcześ, A.; Hołysz, L. Surface modification of glass plates and silica particles by phospholipid adsorption. J. Colloid Interface Sci. 2011, 353, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Jurak, M.; Chibowski, E. Topography and surface free energy of DPPC layers deposited on a glass, mica, or PMMA support. Langmuir 2006, 22, 7226–7234. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.S.; Schmidt, M.; Laanait, N.; Sturchio, N.C.; Fenter, P. Investigation of structure, adsorption free energy, and overcharging behavior of trivalent yttrium adsorbed at the muscovite (001)-water interface. J. Phys. Chem. C 2013, 117, 23738–23749. [Google Scholar] [CrossRef]
- Gao, S.; Ma, L.; Wei, D.; Shen, Y. Wettability of quartz particles at varying conditions on the basis of the measurement of relative wetting contact angles and their flotation behaviour. Physicochem. Probl. Miner. Process. 2019, 55, 278–289. [Google Scholar]
- Hołysz, L. Surface free energy components of silica gel determined by the thin layer wicking method for different layer thicknesses of gel. J. Mater. Sci. 1998, 33, 445–452. [Google Scholar] [CrossRef]
- Hołysz, L.; Szcześ, A.; Chibowski, E. Effects of a static magnetic field on water and electrolyte solutions. J. Colloid Interface Sci. 2007, 316, 996–1002. [Google Scholar] [CrossRef]
- Hamadi, F.; Latrache, H.; Zekraoui, M.; Ellouali, M.; Bengourram, J. Effect of pH on surface energy of glass and teflon and theoretical prediction of staphylococcus aureus adhesion. Mater. Sci. Eng. C 2009, 29, 1302–1305. [Google Scholar] [CrossRef]
- Higashitani, K.; Kage, A.; Katamura, S.; Imai, K.; Hatade, S. Effects of a magnetic field on the formation of CaCO3 particles. J. Colloid Interface Sci. 1993, 156, 90–95. [Google Scholar] [CrossRef]
- Ozeki, S.; Wakai, C.; Ono, S. Is a magnetic effect on water adsorption possible? J. Phys. Chem. 1991, 95, 10557–10559. [Google Scholar] [CrossRef]
- Otsuka, I.; Ozeki, S. Does magnetic treatment of water change its properties? J. Phys. Chem. B 2006, 110, 1509–1512. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).