Abstract
In view of emerging research on forced wetting under complex applied forces, a simple model for a droplet shape evolution is developed here. In particular, the model refers to droplet spreading under quasisteady conditions. The corresponding linearized two-dimensional Young–Laplace equation is solved analytically resulting in a system of two equations that relates the droplet shape features to each other. Despite its simplicity, the final model produces a wealth of droplet behaviors when combined with the physical requirement that the contact angle should be within a particular range of values. Indicative results of the droplet behavior under several forces scenarios are examined here exhibiting why the present model is useful for designing experimental campaigns on forced spreading.
1. Introduction
Wetting behavior of liquids on solid surfaces affects the process effectiveness in several unit processes of chemical technology (e.g., condensation [1], flotation [2]). Whereas, on a small-size scale, wetting behavior is completely determined by molecular forces, the situation is different for larger-size scales where body and surface forces are of importance [3]. The transition size from the one to the other dependence is affected by the magnitude of external forces and is typically of the order of hundreds of micrometers for common forces met in practice (e.g., induced by acceleration fields with values of up to tens of g). Spreading is a term typically employed to describe the partial motion of a droplet contact line under the influence of external forces whereas the term sliding refers to the motion of the whole droplet. The transition from spreading to sliding has been an evergreen research topic over the years. The spreading behavior in case of a slowly varying external body force (compared to the droplet hydrodynamic time scale) depends only on the external force magnitude and on the molecular forces (as expressed by surface tension and contact angles). The experimental campaigns on the subject until recently have been restricted to either tangential or normal forces and to specific combinations of the two forces arising by tilting droplets in the earth gravitational field [4,5,6]. Only recently have more complex combinations and scenarios of applied forces have been tested [7,8,9].
The exploitation of these data (and also additional data of this type to emerge in the literature in the future) requires employment of corresponding mathematical models. The physics of the particular problem is well-founded and the basic mathematical tool for the droplet shape is the three dimensional Young–Laplace equation [10]. Whereas the prediction of the droplet shape for a given contact line contour is well established, the prediction of the contact line evolution during forced wetting is rather based on empirical arguments. An extensive analysis on the subject can be found in [11]. The droplet equilibrium shape can be found using global energy minimization approaches (e.g., Surface Evolver) [12], finite element solvers [13], perturbation expansion methods (only for small deformations) [14], intelligent dimensionality reduction approaches (only for specific contact line shapes) [15,16] and boundary collocation (only for the linearized problem and omniphilic surfaces) [11]. The computation effort ratio from the first to the last method is of the order of millions.
According to [17], there are two limiting categories of models: the first attempts to include as many details as possible at the cost of complexity and specificity, whereas the second attempts to integrate general features and behaviors in the simplest possible way. Here, a model of the second type is developed for the wetting behavior of droplets on omniphilic surfaces (i.e., contact angle smaller than 90°) under combined evolving tangential and normal body forces. The model is a two-dimensional linearized one and is the only one that admits analytical solution. In the following section, the solution of the model is described in detail. Then it is applied to demonstrate several interesting results on the droplet behavior for some scenarios of combined applied forces.
2. Theoretical Analysis
Up to now, experimental studies on forced spreading refer to one of two effects: either to simple tilting plates or to centrifugal devices with varying tangential force applied to a droplet lying horizontally. Hence, theoretical studies also refer to similar conditions [4,5,6]. The generalized simultaneous variation of both effects requires new theoretical analysis. Earlier [18], an oversimplified model for the drop shape was introduced. It is based on the combination of a two-dimensional (planar) geometry and linearization of the Young–Laplace equation. Such a model is expected to give only qualitative information but it has the major advantage that it permits analytical solution retaining the essential physics of the process. In that earlier work, the model has been developed and results are presented for the case of only normal or only tangential force. Here, it is expanded for arbitrary variation of both forces and results are presented for both idealized and realistic variation scenarios. The reference set up considered for the theoretical analysis consists of a droplet lying on a plate which can be rotated and tilted simultaneously, as displayed in Figure 1. The ratio of droplet size to the distance from the rotation axis is so small that the exercised body force can be assumed uniform along the droplet.
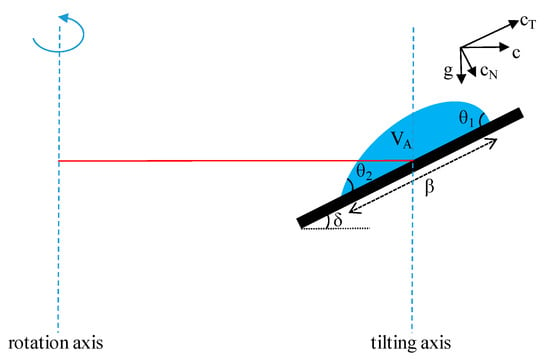
Figure 1.
A schematic of the reference set-up showing the parameters used in the model.
Let us denote as f(x) the shape of the droplet, σ the liquid surface tension, ρ the liquid density and CN, CT the global (rotational plus gravitational) normal and tangential acceleration field values, respectively. The problem has not a unique intrinsic characteristic length (in general the droplet length is unknown) so usually the capillary length is used for non-dimensionalization [19]. Recently, the problem of defining a relevant Bond number is reconsidered revealing that at least five different characteristic lengths have been employed in the literature [20]. Even in the case of a known droplet radius, its use as characteristic length does not usually offer a meaningful non-dimensionalization. For example, in the case of normal force, the droplet height and not the droplet length is responsible for the effect of gravity. The new Bond number proposed in [21] depends on force direction. For the above reasons it is found more convenient to use as characteristic length a size scale simply relevant to the actual one, instead of using the capillary length or a droplet dimension. This choice in the present work is L = 1 mm. The major advantage of this definition of Bond number is that it is a property of the external forcing field and is not related to the specific droplet studied.
The dimensionless linearized (i.e., exact in the limit df/dx << 1) two-dimensional Young–Laplace equation for simultaneous normal and tangential forces, with the corresponding Bond numbers denoted as BoN (=ρCNL2/σ) and BoT (=ρCTL2/σ), takes the form (f and x are normalized by L):
The parameter G is related to the pressure in the droplet and it is an unknown quantity which has to be found from the solution of the mathematical problem. Let us call β the contact line length of the droplet. The origin of the x axis (x = 0) is designated to the rear (with respect to tangential acceleration direction) droplet edge. The following conditions must be fulfilled by the function f:
where θ1 and θ2 are the front and rear contact angle, respectively, and VA is the area under the droplet profile (i.e., two-dimensional “volume” or alternatively volume per unit length in the third dimension).
f(0) = 0
f(β) = 0
The general solution of the equation can be found as the sum of the homogeneous solution and of a particular solution:
where the symbols A = (BoN)0.5 and E = BoT/BoN have been introduced for clarity of presentation. Substitution of Equation (7) in Equations (2)–(4) leads to the following Equations (8)–(10), respectively:
Eliminating G between Equations (8) and (9) leads to:
The Equations (10) and (11) constitute a linear system for c1 and c2 which can be solved to yield:
Finally, substituting Equation (7) in (6) and eliminating G using Equation (8) leads to the following compatibility condition:
The above system of equations can be explicitly solved for θ1 to give:
where
The angle θ2 can be found from the condition (5) as:
Equation (15) relates θ1 το VA, β and Equation (16) relates θ2 το θ1, β. In any case, if two of the above four variables are known, the other two can be found from these equations. A partial validation of the analytical model arises as follows: The following compatibility conditions were previously found [19] in case of only a tangential force applied:
By putting θ1 and θ2 equal to the advancing θa and the receding θr angle, respectively, the droplet is exactly at the critical condition for the onset of sliding so BoT should take its critical value BoTc. Eliminating β from the above equations leads after some algebra to the relation:
Expanding the trigonometric terms to a Taylor series and keeping the first terms (valid in the limit of small angles) results in:
This equation is exactly the same with the one taken by expanding the well-known sliding condition [7]:
in Taylor series for small angles.
It is noted that above conditions have no droplet size dependence of the critical sliding force. This dependence appears when the area VA is assumed to be the ratio of the droplet volume to droplet width in order to account for the third dimension.
3. Indicative Model Results and Discussion
In general, the literature work associates the motion of the rear droplet edge with sliding which is true for past experimental procedures by earlier researchers. Nevertheless, this is not true in the present case of a general force variation in which the rear droplet edge motion can be due to normal force reduction occurring simultaneously with a tangential force increase. The cases of only one force component examined before [18] are based on the existence of a fixed point in the physical space (droplet center for normal force and rear contact line edge for tangential force). Therefore, the combination of forces leaves us with no fixed point in space (as is the case when a single force component increases). Let us assume that there is a valid droplet configuration with parameters βo, θ1o, θ2o and the forces suddenly change to new values of ΒοΝ, ΒοΤ. The procedure of droplet shape variation is in general non-reversible and non-conservative so the exact trajectory BoN-BoT must be considered (i.e., there is no way to find directly what happens at the final conditions since the droplet evolution is history depended). In particular, the non-reversibility comes for setting limits θa and θr to the angle values (however, as far as the angles remain in-between the limiting values θa and θr, reversibility holds). The trajectory BoN, BoT must be followed by considering (infinitely small in theory but very small in calculations) small variation steps.
At the first step, Equation (15) is employed for calculation of θ1 setting β = βο. Then, θ2 is computed from Equation (16). In case of θr ≤ θ1, θ2 ≤ θa, the new droplet configuration is acceptable. If one of the angles overrides θa, then the exact point (force values) at which this angle takes the value θa must be found. For this, Equation (15) is solved for θ = θa having β as unknown. A similar procedure is followed if an angle becomes smaller than θr. The point with θ = θr must be found and then Equations (15) and (16) are solved for β. In general, the system of Equations (15) and (16) admits as input β or θ1 or θ2 and returns as output values of θ1, θ2 or β, θ2 or β, θ1, respectively. The above procedure is repeated for each step along the BoT–BoN trajectory. Of particular interest is the handling of the motion in the physical space. If a contact angle (or both) has the value θa or θr then the variation of β (positive for value θa, negative for value θr) is assigned to the motion of the corresponding contact line edge (or to both contact line edges in equal parts).
Let us first present what are the predictions of the model for some simple scenarios regarding the two forces. The case of a droplet with VA = 5 mm2, θa = 60° and θr = 40° with an increasing tangential force is examined. This case has been previously studied for zero normal force [18], so the effect of non-zero normal force is examined here. It is found that the main effect of the normal force is just to elongate the droplet with a negligible effect to the shape at the two edges. The normal force does not influence the critical Bond number BoTc and, thus, the critical detachment force which is compatible to the independency of force from the droplet size according to the present model (see Equation (19)). It is reminded that this independency refers only to two dimensions (extension to the third dimension leads to the proportionality of critical force to the droplet size appearing in the well-known Furmidge equation). The BoN is expected to affect the critical force for sliding in three dimensions through the droplet width dependence. Figure 2 shows the increase of droplet length as BoT increases for an initial angle θ0 equal to the advancing one. The evolution of the droplet profiles is quite similar to those for zero normal force [18]. In addition, introducing an oscillation of the tangential force (i.e., BoT varies periodically between 0 and BoTc), a similar periodic behavior of droplet shape is taken independently of the normal force. In particular, after the initial transient the droplet shape retains its length (taken at BoTc) and its two angles θ1 and θ2 oscillate following certain curves already found for BoN = 0 in a previous study (e.g., see [18] for details).
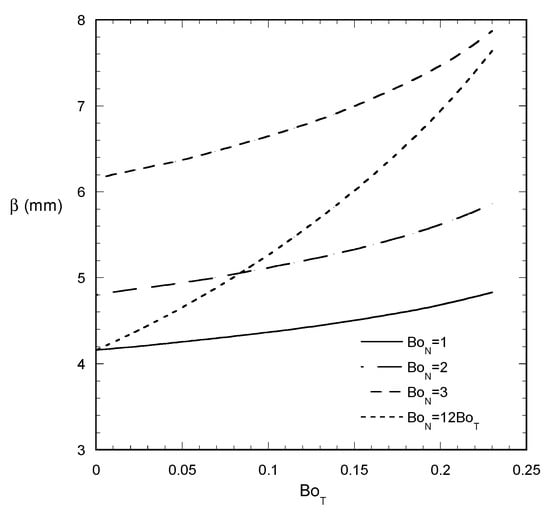
Figure 2.
Evolution of droplet length β with BoT and for several scenarios for BoN variation (constant or proportional to BoT). (VA = 5 mm2, θa = 60°, θr = 40°, θο = 60°, starting transient).
A more interesting scenario is the simultaneous increase of both force components (in the case of absence of gravity it corresponds to increasing the rotation speed at a fixed tilting angle). Considering exactly the same set of parameters as for a constant normal force plus the relation of BoN = 12 BoT, very interesting results are obtained. At the starting transient the droplet length increases crossing the lines of constant BoN (Figure 2). Under the particular conditions of the transient, a function β(ΒοΝ,ΒοΤ) can be constructed which can give directly β for arbitrary BoN–BoT trajectory. The idea behind the proposed scenarios is not the direct imitation of practical situations but the allowance to understand better the droplet shape evolution process in order to create models for any practical situation.
The oscillating force scenario is examined next. It is noted that the imparted oscillations are simultaneous for both components in order to keep their ratio constant (i.e., increasing and decreasing rotation speed for constant tilting angle in the absence of gravity). After the initial transient, the droplet gets into a steady periodic behavior. Interestingly enough, this behavior is quite different than the one found for constant BoN since not only the contact angles but also the droplet length varies periodically. The evolution of droplet length β, front angle θ1 and rear angle θ2 for periodic forces oscillation is shown in Figure 3, Figure 4 and Figure 5, respectively. The periodic cycle advancing part (i.e., increasing forces) contains a part in which the droplet length is constant and the angle θ1 increases. As the point θ1 reaches the value θa (advancing contact angle), the drop length starts increasing up to the critical point for sliding. Then, at the receding cycle, the length of the droplet decreases and the angle θ1 goes from the advancing angle to the receding angle value. Even more interesting is the behavior of the angle θ2 which at the receding cycle retains always the value θr. At the advancing cycle, it increases as far as length β remains constant acquiring a maximum at the point of β transition (from constant to increasing) and then decreases up to the critical point for sliding.
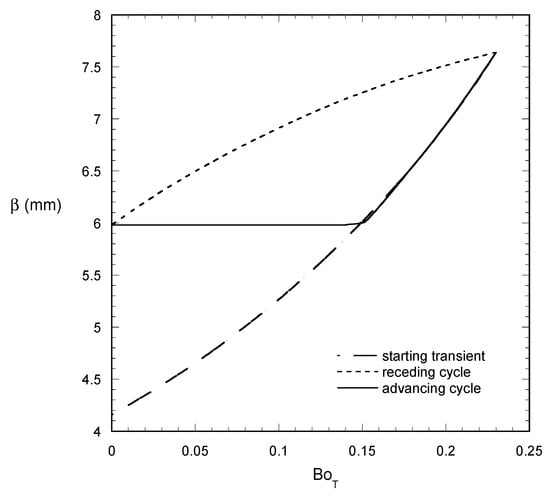
Figure 3.
Evolution of droplet length β with BoT for BoN = 12 BoT and periodic forcing (VA = 5 mm2, θa = 60°, θr = 40°, θο = 60°).
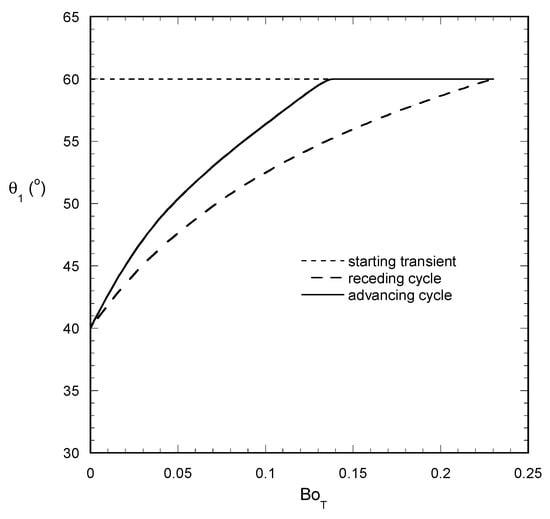
Figure 4.
Evolution of droplet front angle θ1 with BoT for BoN = 12 BoT and periodic forcing (VA = 5 mm2, θa = 60°, θr = 40°, θο = 60°).
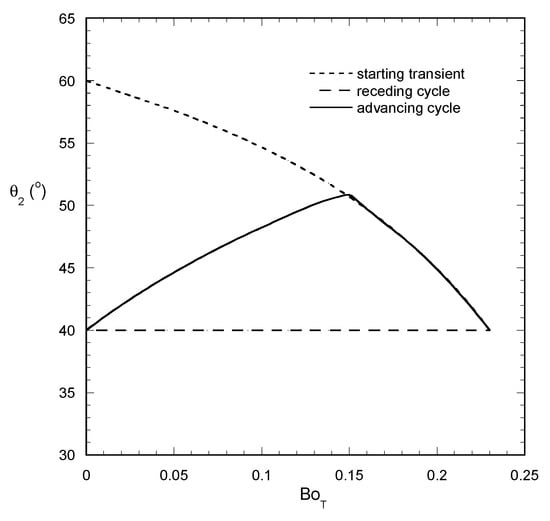
Figure 5.
Evolution of droplet front angle θ2 with BoT for BoN = 12 BoT and periodic forcing (VA = 5 mm2, θa = 60°, θr = 40°, θο = 60°).
Typical droplet profiles that correspond to the results shown in Figure 3, Figure 4 and Figure 5 are presented in Figure 6 for periodic forcing and BoN = 12 BoT. It must be noted that for clarity in the presentation the scales at the two axes are different leading to distorted views of the droplet profiles. Figure 6a refers to the starting transient. As BoT increases, the symmetry is destroyed but also the length increases due to increase of BoN. The receding cycle profiles are shown in Figure 6b. The angle θ2 has the value θr at the beginning of the cycle. The reduction of tangential force leads to increase of the angle θ2, but the reduction of the normal force leads to its decrease which overall prevails leading to retraction of the rear contact line edge. Therefore, the rear contact line retraction is due to the reduction of the normal force. The front contact line does not retract due to the higher value of θ1 than θ2 in the beginning of the receding cycle. The cycle ends with a symmetric drop (zero tangential force) with angles at their receding values. The profiles for the advancing cycle are shown in Figure 6c. Initially, the droplet retains its length and both angles increase. At some point, the front angle reaches the advancing value, so the droplet length starts increasing and the rear angle starts decreasing. The front contact line edge moves leading, at the end of the cycle, to the same droplet shape as in the start of the cycle but at a different physical (spatial) position (see the x values of both edges). Such a behavior cannot be identified by the parameter variation appearing in Figure 3, Figure 4 and Figure 5. To better identify the situation, the variation of the physical position of the two contact line edges of the droplet during one cycle is presented in Figure 7. The region between the two lines in this figure (for each cycle) corresponds to the physical space occupied by the droplet. From this figure, it is clear how the droplet initially expands, then, when it gets in the oscillating regime, retracts and, finally, expands again but with a different fixed point. This motion pattern appears in each oscillation cycle leading to an effective overall droplet motion (shift by 1.66 mm per cycle) which is exclusively due to the simultaneous variation of BoN with BoT. The situation arising here has a very interesting sequence: The macroscopic motion of the drop cannot be identified as spreading (dominated by surface energy) or sliding (dominated by hydrodynamics) in case of complex force scenarios.
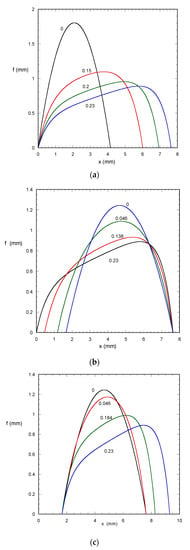
Figure 6.
Evolution of droplet profile for periodic forcing and BoN = 12 BoT (VA = 5 mm2, θa = 60°, θr = 40°, θο = 60°) (a) starting transient (b) receding cycle (c) advancing cycle. The corresponding BoT numbers are shown in the figures.
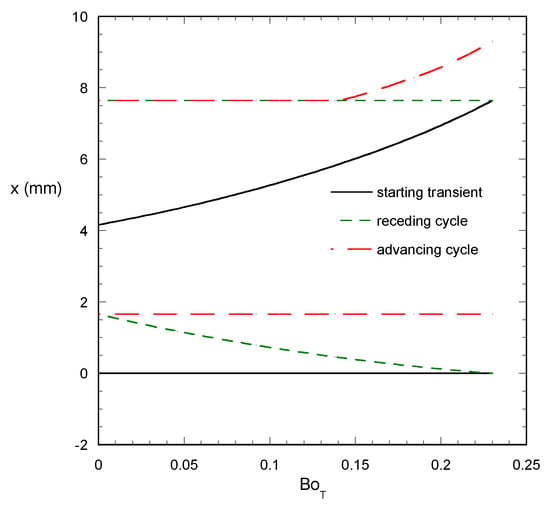
Figure 7.
Motion of droplet basis for periodic forcing and BoN = 12 BoT (VA = 5 mm2, θa = 60°, θr = 40°, θο = 60°). The curves above x = 3 mm denote the motion of front edge and the curves below x = 3 mm denote the motion of the rear edge of the droplet.
The scenarios of BoN–BoT variation examined up to now appear idealized in the absence of gravity but in practice terrestrial gravity is always present so their realization is rather cumbersome. Let us consider the very basic case of increasing the normal force while keeping zero the tangential force. To realize this in the absence of gravity the tilting angle should be 90° (vertical substrate parallel to axis of rotation). However, in the presence of gravity, the tilting angle must vary simultaneously with the rotation speed in order for the tangential component of gravity and rotation to be counterbalanced. This implies a tilting angle of 90° in which the tangential acting of gravity is present. Let C be the rotational acceleration magnitude and δ the inwards tilting angle. The condition of zero tangential force leads to C/g = tan (δ) which means that the rotation speed and the tilting angle must evolve simultaneously satisfying always this condition. The normal acceleration is given by CN/g = cos (δ) + tan (δ) sin (δ).
The scenario of constant ratio of acceleration components examined above is discussed next. In the absence of gravity this corresponds to a constant value of δ as already noticed. An analysis in the presence of gravity leads to
The required variation of δ with C for two values of the component ratio is shown in Figure 8. The general shape of the δ vs. C curve is similar to the case of zero CT. The normal acceleration component is also shown in the figure. The form of the function δ vs. C indicates that the required trajectory is technically quite difficult to be exactly followed. There is large sensitivity with respect to rotational speed for small speeds and with respect to the tilting angle for large speeds. In practice, the trajectory can be followed only in discrete steps which, even if they are small, they still create excess forces. The influence of these forces can be assessed employing the analytical droplet model. In order to demonstrate the procedure a very coarse (four steps) stepwise approximation of the continuous δ–C curve for zero tangential force is considered. There are two routes to achieve this: (i) first vary the tilting angle δ and then vary C (i.e., rotational velocity) in each step (blue line at the left of continuous curve in Figure 9) and (ii) first vary C and then vary δ (red line at the right of continuous curve in Figure 9). Computations show that the second route leads to larger tangential forces so droplet profiles are shown only for the first route. The same droplet parameters as before are considered except for θr which is assumed to be zero to avoid droplet sliding. It is also assumed that BoN = CN/2.5. Some profiles for specified positions along the blue route are shown in Figure 10.
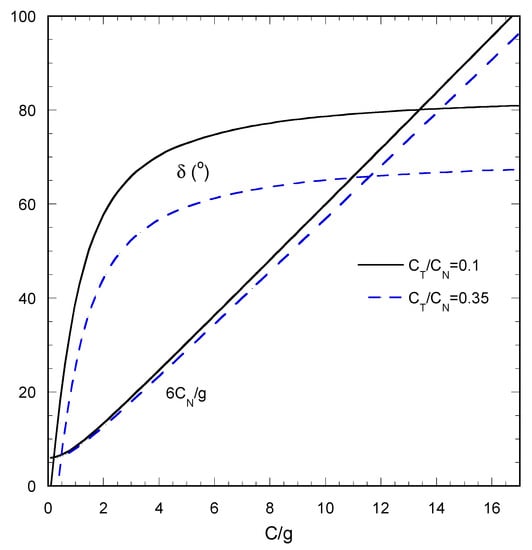
Figure 8.
The required centrifugal acceleration C- tilting angle δ trajectory to ensure a constant ratio of acceleration components; in practice for two values of this ratio. The value of normal component CN is also shown.
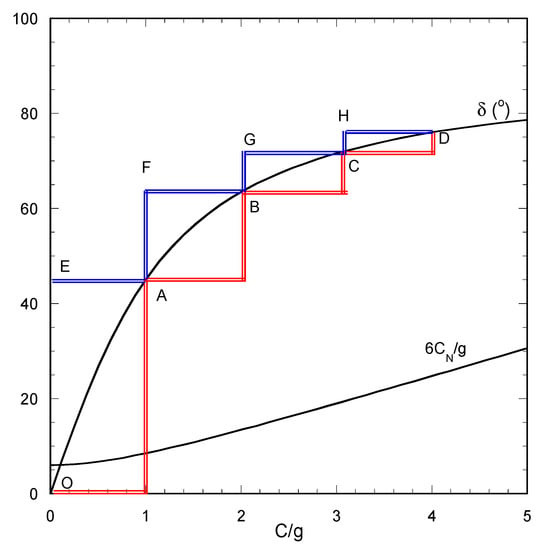
Figure 9.
The required centrifugal acceleration C- tilting angle δ trajectory to ensure zero tangential acceleration in practice and the corresponding normal acceleration component CN. Alternative stepwise trajectories (with names A-H, O given at key positions) are shown.
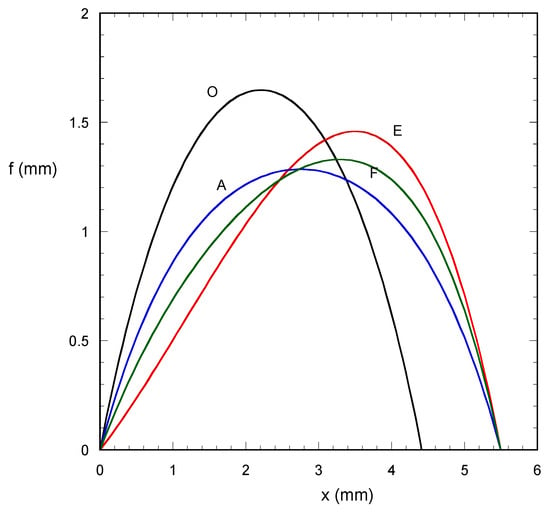
Figure 10.
Droplet profiles at different positions along the blue (left) stepwise trajectory in Figure 9 (VA = 5 mm2, θa = 60°, θo = 60°, BoN = CN/2.5).
At position E, the variation of δ without the counterbalancing effect of C leads to a significant tangential force which for θr = 40° would lead to droplet sliding. The tangential force increases the contact line length of the droplet. At the other displayed positions (A, F), the droplet length remains constant whereas the shape alternates between symmetric (A position at the continuous curve in Figure 9) and asymmetric (F position outside the continuous curve in Figure 9) with a decreasing difference between the two states as C increases.
The comparison of droplet profiles at positions B and D reached through the continuous curve and through the left stepwise one (blue line in Figure 9) is presented in Figure 11. The difference between the two routes in position B (red curves) is very large since the droplet has been elongated abruptly by the tangential force raised by the stepwise route. As the normal force increases the droplet, the following continuous route is progressively elongated leading to small differences between the profiles from the two trajectories at position D. The above case study reveals the complexity of the problem combining the technical limitations on applied forces variation and the physicochemical aspect of droplet spreading. This is why the simple model presented herein is useful to assess different experimental procedures and as a starting point for more detailed calculations. A partially qualitative confirmation of the resulting behavior regarding the oscillations of tangential force and the force step scenarios can be found in [8].
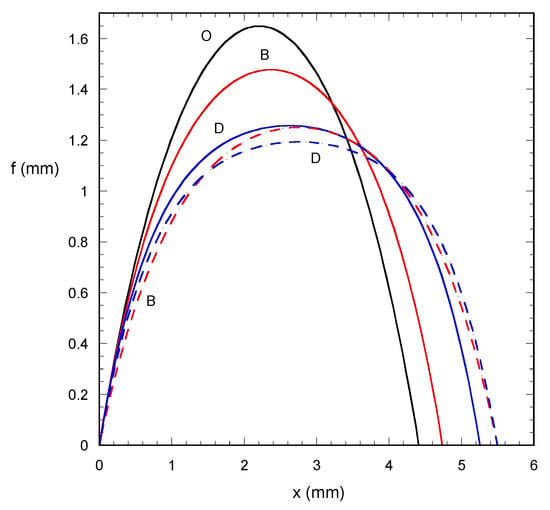
Figure 11.
Comparison between droplet profiles at positions B (red lines) and D (blue lines) following the continuous (solid lines) or the left stepwise (dashed lines) C–δ trajectories shown in blue in Figure 9 (VA = 5 mm2, θa = 60°, θo = 60°, BoN = CN/2.5).
The main aspect of the model that creates the droplet evolution is the interaction between the applied forces scenario and the onset of motion condition (θ ≤ θa and θ ≥ θr). In this respect, the conclusions are expected to be qualitatively valid for real droplets. However, in pursuing a quantitative analysis it has been implied, [8], that the main deviation of the present approximation from reality is due to the linearization of the Young–Laplace equation and not due to the reduced dimensionality. It is reminded that the linearization is valid in the limit of very omniphilic surfaces. The present model serves the scope of being the simplest case (and the only analytic one) capable of reproducing the qualitative droplet behavior under complex force scenarios. Our final aim is to relax the simplifications using approximate solutions of the governing equations.
4. Conclusions
It is shown that the two-dimensional linearized Young–Laplace equation for a sessile droplet on a omniphilic surface under a uniform body force of arbitrary direction can be solved analytically to give an explicit shape profile function. The particular simplification has been used extensively in the past to model sliding behavior [22]. In case of nontrivial scenarios of the force magnitude and direction evolution under quasisteady conditions (evolution characteristic time much smaller than droplet hydrodynamic characteristic time), the complete droplet dynamics is described by two algebraic equations combined to the requirement that the two contact angles must always have values between the receding and the advancing one. Several scenarios of force evolution are examined (mainly based on the rotating-tilting configuration) and it is found that very interesting drop behavior emerge even by using a so primitive model. It is expected that the model can qualitative describe the actual droplet behavior but further research is needed to account for its quantitative performance with respect to more complicated models.
Author Contributions
Conceptualization, M.K. and T.D.K.; methodology, M.K.; software, M.K.; formal analysis, M.K.; investigation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, T.D.K.; project administration, T.D.K.; funding acquisition, T.D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Marie-Curie ITN ‘Complex Wetting Phenomena, CoWet’ (FP7-PEOPLE2013-ITN, Grant Agreement No.: 607861).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sikarwar, B.S.; Muralidhar, K.; Khandekar, S. Effect of drop shape on heat transfer during dropwise condensation underneath inclined surfaces. Interfacial Phenom. Heat Transf. 2013, 1, 339–356. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Schulze, H.J. Colloidal Science of Flotation; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Hartland, S. Interfacial Tension: Measurement, Theory and Applications; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Bikerman, J.J. Sliding of droplets from surfaces of different roughnesses. J. Colloid Sci. 1950, 5, 349–359. [Google Scholar] [CrossRef]
- Goodwin, R.; Rice, D.; Middleman, S. A model for the onset of motion of a sessile liquid drop on a rotating disk. J. Colloid Interface Sci. 1988, 125, 162–169. [Google Scholar] [CrossRef]
- ElSherbini, A.I.; Jacobi, A.M. Liquid droplets on vertical and inclined surfaces: I. An experimental study of droplet geometry. J. Colloid Interface Sci. 2004, 273, 556–565. [Google Scholar] [CrossRef] [PubMed]
- Ríos-López, I.; Evgenidis, S.; Kostoglou, M.; Zabulis, X.; Karapantsios, T.D. Effect of initial droplet shape on the tangential force required for spreading and sliding along a solid surface. Colloids Surf. A Physicochem. Eng. Asp. 2018, 549, 164–173. [Google Scholar] [CrossRef]
- Ríos-López, I.; Petala, M.; Kostoglou, M.; Karapantsios, T.D. Sessile droplets shape response to complex body forces. Colloids Surf. A Physicochem. Eng. Asp. 2019, 572, 97–106. [Google Scholar] [CrossRef]
- De la Madrid, R.; Garza, F.; Kirk, J.; Luong, H.; Snowden, L.; Taylor, J.; Vizena, B. Comparison of the Lateral Retention Forces on Sessile, Pendant, and Inverted Sessile Drops. Langmuir 2019, 35, 2871–2877. [Google Scholar] [CrossRef] [PubMed]
- Prabhala, B.R.; Panchagnula, M.V.; Vedantam, S. Three-dimensional equilibrium shapes of drops on hysteretic surfaces. Colloid Polym. Sci. 2013, 291, 279–289. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karapantsios, T. Contact Angle Profiles for Droplets on Omniphilic Surfaces in the Presence of Tangential Forces. Colloids Interfaces 2019, 3, 60. [Google Scholar] [CrossRef]
- Janardan, N.; Panchagnula, M.V. Effect of the initial conditions on the onset of motion in sessile drops on tilted plates. Colloids Surf. A Physicochem. Eng. Asp. 2014, 456, 238–245. [Google Scholar] [CrossRef]
- Brown, R.A.; Orr, F.M.; Scriven, L.E. Static drop on an inclined plate: Analysis by the finite element method. J. Colloid Interface Sci. 1980, 73, 76–87. [Google Scholar] [CrossRef]
- De Coninck, J.; Fernandez-Toledano, J.C.; Dunlop, F.; Huillet, T.; Sodji, A. Shape of pendant droplets under a tilted surface. arXiv 2020, arXiv:2001.11233. [Google Scholar]
- Higashine, M.; Katoh, K.; Wakimoto, T.; Azuma, T. Profiles of liquid droplets on solid plates in gravitational and centrifugal fields. J. Jpn. Soc. Exp. Mech. 2008, 8, s49–s54. [Google Scholar]
- Ríos-López, I.; Karamaoynas, P.; Zabulis, X.; Kostoglou, M.; Karapantsios, T.D. Image analysis of axisymmetric droplets in wetting experiments: A new tool for the study of 3D droplet geometry and droplet shape reconstruction. Colloids Surf. A Physicochem. Eng. Asp. 2018, 553, 660–671. [Google Scholar] [CrossRef]
- Aris, R. Mathematical Modeling Techniques; Dover: New York, NY, USA, 1994. [Google Scholar]
- Evgenidis, S.P.; Kalić, K.; Kostoglou, M.; Karapantsios, T.D. Kerberos: A three camera headed centrifugal/tilting device for studying wetting/dewetting under the influence of controlled body forces. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 38–48. [Google Scholar] [CrossRef]
- Pozrikidis, C. Fluid Dynamics: Theory, Computation, and Numerical Simulation; Kluwer: Boston, MA, USA, 2001. [Google Scholar]
- Berim, G.O.; Ruckenstein, E. Bond number revisited: Two-dimensional macroscopic pendant drop. J. Phys. Chem. B 2019, 123, 10294–10300. [Google Scholar] [CrossRef] [PubMed]
- Berim, G.O.; Ruckenstein, E. Bond number revisited: Axisymmetric macroscopic pendant drop. Langmuir 2020, 36, 6512–6520. [Google Scholar] [CrossRef] [PubMed]
- Hocking, L.M. Sliding and spreading of thin two-dimensional droplets. Q. J. Mech. Appl. Math. 1981, 34, 37–55. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).