Investigation of Single and Binary of “Sandwich” Type Convex Liquid Capillary Bridges, Stretched between Two Flat Surfaces (Experimental Approach)

Abstract

The interest to monophasic liquid capillary bridges (CB) has a long history. These shapes are attractive not only because of their interesting surface properties but also because of the possibility of their behavior to be analytically predicted by the equations of differential geometry. In the current paper we extend our previous studies by implementation of an approach for prediction of liquid gravityless CB behavior during their quasi-static stretching. It was found, that a simple linear relation, $\frac{h}{r_m}~\ln \frac{R}{r_m}$, is valid the case of good wetting, 0° ≤ θ ≤ 90°, where h is the height of CB, R is the radius at the contact surface, r_m is the CB waist radius, and θ is the solid/liquid (static, receding) contact angle. We experimentally studied the geometrical properties evolution of monophasic cedar oil and water CBs between two glass plates during their quasi-static (stepwise with equilibration after each step for 1–2 min.) stretching. In addition, we investigated a binary CB of a new type, resembling “sandwich”. There, due to the stronger glass wetting by the water, the oil phase is adhered at the water/gas interface, partially engulfed with a tendency to stand in the zone around the waist (minimal surface energy). During the stretching, it tends to replace the water in the CB waist region. A simple mechanism for interaction of the two immiscible liquids leading to creation of “sandwich” like binary structures, is proposed. Experiments of capillary bridges (CB) stretching between two flat surfaces have been carried for all liquids at different volume proportions. The investigation is extended also to identification of CB profile generatrix shape. We experimentally found that for monophasic CB, it can be described by a circle during the quasi-static stretching. If the CB height is increased, before the rupture, the shape evolves consecutively to an ellipse, parabola, or possibly to a hyperbola. The investigated binary CB evolves a similar way. Conclusions are drawn and directions for further investigations are given.

1. Introduction

The capillary structures that are subject to our analysis belong to a class of axially symmetrical surfaces of constant mean curvature [1]. The classical approach for analysis of capillary structure lies through integration of the Young–Laplace equation $\mathsf{\Delta }P=const$ in the case of axial symmetry [2]. The obtained solution in the form $z=\pm z\left(r\right)$ is usually expressed by incomplete elliptic integrals of first, $F\left(\varphi |m\right)$, and second, $E\left(\varphi |m\right)$, kind, where $\varphi$ is the angle and m is a parameter. Originally, the elliptic integrals are discussed in computing the lengths of basic plane curves $F\left(\varphi |m\right)$ for Bernoulli’s lemniscate and $E\left(\varphi |m\right)$ for an ellipse, [3]. Despite their practical importance, the solutions involving linear combination of these integrals always is exposed to problems because of complex relations, resulted from $F\left(\varphi |m\right)$ and relation to Jacobian elliptic functions, [4]. According to [4], there are three groups of methods for computing of these integrals: series expansion formulas, implementation of Landen transformations, and methods using duplication theorems. All of these methods have their advantages and disadvantages. We will further outline our method for the solution of capillary bridges (CB) which avoids the above-mentioned problems. It was presented in detail in [5].

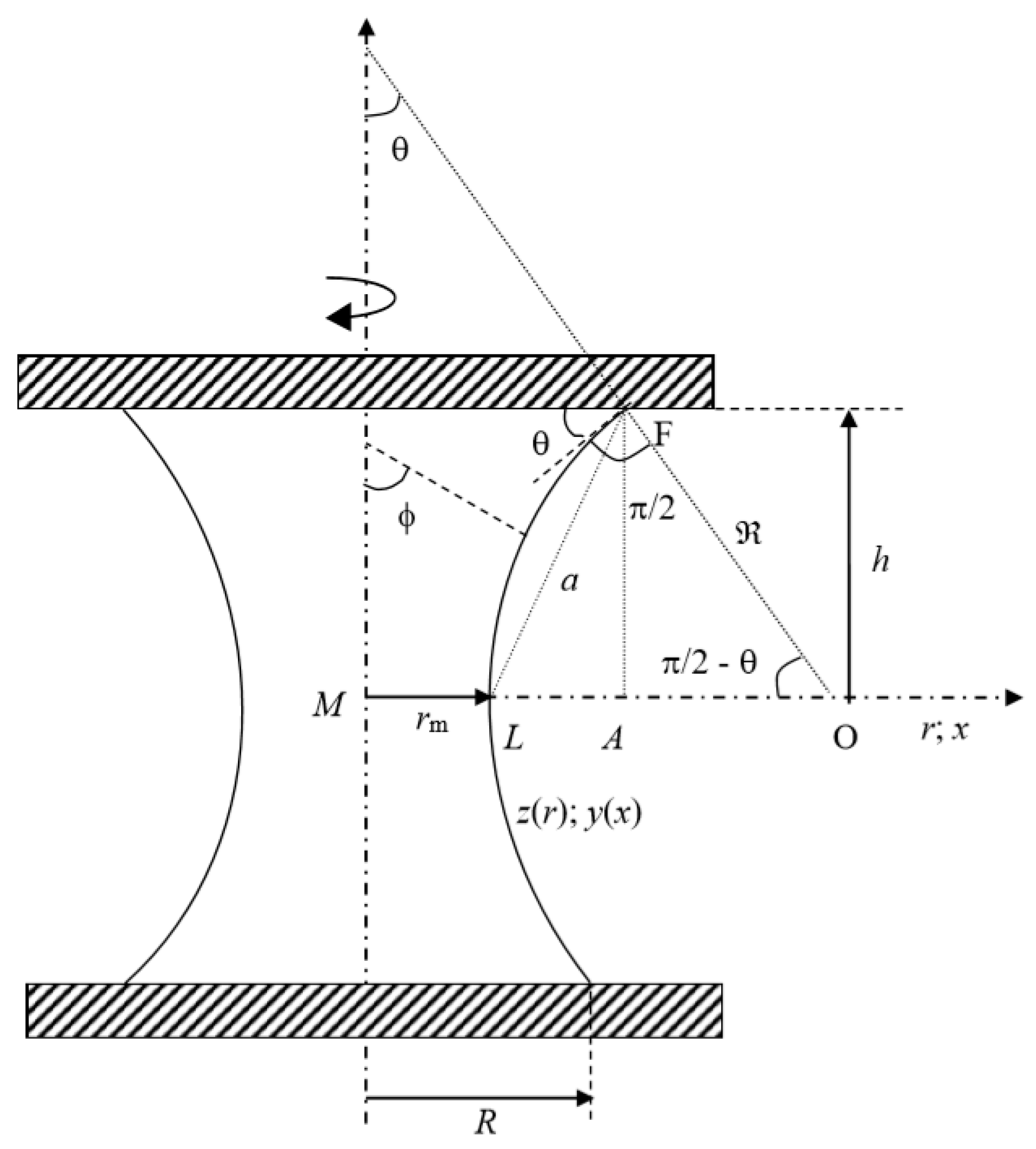
The subject of our investigation is CB in conditions of lack of gravity, sketched in Figure 1. The geometry equation that needs to be solved, was formulated by Princen, [6] and in dimensionless form, [5] is:

$$\frac{dy}{dx}=\mp \frac{C\left(x^2-1\right)+1}{\sqrt{x^2-{\left[C\left(x^2-1\right)+1\right]}^2}}$$

(1)

where $x=\frac{r}{r_m}$ and $y=\frac{z}{r_m}$ are dimensionless cylindrical coordinates, r is the current radius, z is the axial coordinate, both scaled by $r_m$ (the CB waist radius). The parameter C is the dimensionless capillary pressure: $C=\frac{X\sin \theta -1}{X^2-1}\equiv \Delta P\frac{r_m}{2\sigma }$, where σ is the surface tension [5].

Previously, we developed a theoretical approach for analysis of stretching behavior of a capillary bridge between two flat surfaces. We derived two important equations, related to the dimensionless dependence of height and volume from the radius. We introduced two integrals, presented below, as follows:

$$I_0\left(X,C\right)={\int }_1^X\frac{1+\left[{\xi }^2\left(C-1\right)\right]}{\sqrt{{\xi }^2-{\left[{\xi }^2\left(C-1\right)\right]}^2}}d\xi ,$$

(2)

$$I_2\left(X,C\right)={\int }_1^X\frac{1+\left[{\xi }^2\left(C-1\right)\right]}{\sqrt{{\xi }^2-{\left[{\xi }^2\left(C-1\right)\right]}^2}}{\xi }^{2}d\xi ,$$

(3)

where the dimensionless contact line radius is $X=\frac{R}{r_m}$, and R is dimensional contact line radius. Independent integration parameter is $\xi \equiv x=\frac{r}{r_m}$. The generalized form of the integrals from Equations (2) and (3) is:

$$I_n\left(X,C\right)={\int }_1^X\frac{1+\left[{\xi }^2\left(C-1\right)\right]}{\sqrt{{\xi }^2-{\left[{\xi }^2\left(C-1\right)\right]}^2}}{\xi }^{n}d\xi$$

(4)

The relation of the integrals in Equations (2) and (3) with dimensional parameters is: $I_0\left(X,C\right)=\frac{h}{r_m}$ and $I_2\left(X,C\right)=\frac{V}{r_m^3}$, where 2h and V are correspondingly the CB dimensional height and volume. Integration of these equations for gravityless CBs yields:

$$I_0\left(X,C\right)=\frac{\pi }{4C}-\frac{1}{2C}\mathrm{asin}\left[\frac{\frac{\left(1-2C\right)}{2C^2}-\left(X^2-1\right)}{\frac{\left(1-2C\right)}{2C^2}}\right]-{\int }_1^X\frac{\sqrt{x-\left[x^2\left(C-1\right)+1\right]}}{\sqrt{x+\left[x^2\left(C-1\right)+1\right]}}dx$$

(5)

$$\begin{array}{ll}{I}_2\left(X,C\right)=& \left[1+\frac{\left(1-2C\right)}{2C^2}\right]\frac{\pi }{4C}-\left[1+\frac{\left(1-2C\right)}{2C^2}\right]\frac{1}{2C}\mathrm{asin}\left[\frac{\frac{\left(1-2C\right)}{2C^2}-\left(X^2-1\right)}{\frac{\left(1-2C\right)}{2C^2}}\right]\\ & \hspace{1em}\hspace{1em}\hspace{1em}-\frac{1}{2C}\sqrt{\frac{\left(1-2C\right)}{C^2}\left(X^2-1\right)\left[1-\left(X^2-1\right)\right]}-{\int }_1^X\frac{\sqrt{x-\left[x^2\left(C-1\right)+1\right]}}{\sqrt{x+\left[x^2\left(C-1\right)+1\right]}}{x}^{2}dx\end{array}$$

(6)

The dimensionless parameter $I_0\left(X,C\right)$ represents the height of the axisymmetric capillary structure and the dimensionless integral $I_2\left(X,C\right)$ is the dimensionless volume. We divide the original integrals on two parts: Part one is complicated and irregular but integrable analytically and one obtains in this way the exact solution. Part two is a regular integral but we cannot integrate it analytically. However, suitable numerical methods for integration can be applied. Thus, our approach is a reliable alternative to the traditional solution as mentioned in Equation (1), where incomplete elliptic integrals [1,7,8] are involved.

Based on these equations, we developed a set of curves for CB constant solid/liquid static receding contact angles, called isogones. They represent the domain of existence of capillary bridges. These curves outline the capillary bridges characteristics at static and quasi-static stretching conditions. In our previous papers [5,9], we performed the experimental verification of this approach.

The paper presents some theoretical background in Section 2, where the previously obtained data is added to the new experimental information. The scientific question that we discuss in the current paper was stated in the literature but not answered previously: If the CB is created on surfaces without it contact radius to be pinned, how can their behavior be predicted during the stretching? To answer this question we present a theoretical formula in Section 3 that predicts a linear-like relation of liquid CB evolution with a constant contact solid/liquid static receding angle in the case of quasi-static stretching. Section 3 also presents a theoretical analysis that, in our opinion, allows the stretching behavior of a liquid CB to be predicted. We further discuss the three types of liquid CBs, made of water, cedar oil, and binary cedar oil/water, investigated at three different initial volumes of 8 μL, 10 μL, and 12 μL. The experimental approach, required materials, and equipment is justified in Section 4. The same section describes in detail the applied methods and limitations: The study is justified to solid/liquid static receding contact angles below or equal to 45°. The experimental confirmation of the theory is presented in Section 5. Some additional results from the experimental investigation also are presented and discussed: (1) determination of profile generatrix, y(x), shape of the investigated CB structures, and (2) justification of the linear-like dependence, $\frac{h}{r_m}~\ln \frac{R}{r_m}$, during CB stretching. A simple mechanism for interaction of the two immiscible liquids, leading to the creation of “sandwich”-like binary structures, is proposed. We also try to analyze the breakage kinetics: In our previous CB kinetics report [5] we found a boundary of the CB definition domain and now we apply this to count the time to the first picture taken after passing this boundary. It helps us to obtain suitable information about the CB viscous properties. Finally, a conclusion is drawn that the proposed linear-like dependence resulted not only from the circular shape of the profile generatrix but also from other types of closed curves.

2. Theoretical Background

The original analysis, reported in [5], showed theoretically-obtained isogones and experimentally-measured values, in such a way that a plot $\frac{2h}{R}=\frac{2h}{R}\left(\frac{1}{X}\right)$ was created, where 2h is the CB height and R is the contact radius. It is seen from the plot, shown in Figure 2, that the solid/liquid static receding contact angles cannot be evaluated despite the fact that the observed evolution of CB goes around an isogone. The direct measurement of the contact angle can provide some approximate values. In Figure 2 is seen that the contact angle can be estimated from the plot only qualitative way, because of the exhibited non-linear behavior of the isogones.

The previous studies of monophasic liquid CBs [5,9] presented experimental verification of the isogones in the proposed coordinates. At that time the CB was created between two microscope slides with droplets of ~1 mm³ made of deionized water [5] (D1 sequence in Figure 3). We apply the same scale for the newly obtained data of CBs of different initial volumes: 8 μL, 10 μL, and 12 μL, made of water or cedar oil (sequence D2 in Figure 2). The data show that the behavior of pure water and pure cedar oil CBs is remarkably identical with the same liquid/solid static receding contact angles despite the different nature of the liquids.

3. Theoretical CBs Analysis and Prediction of Their Stretching Behavior

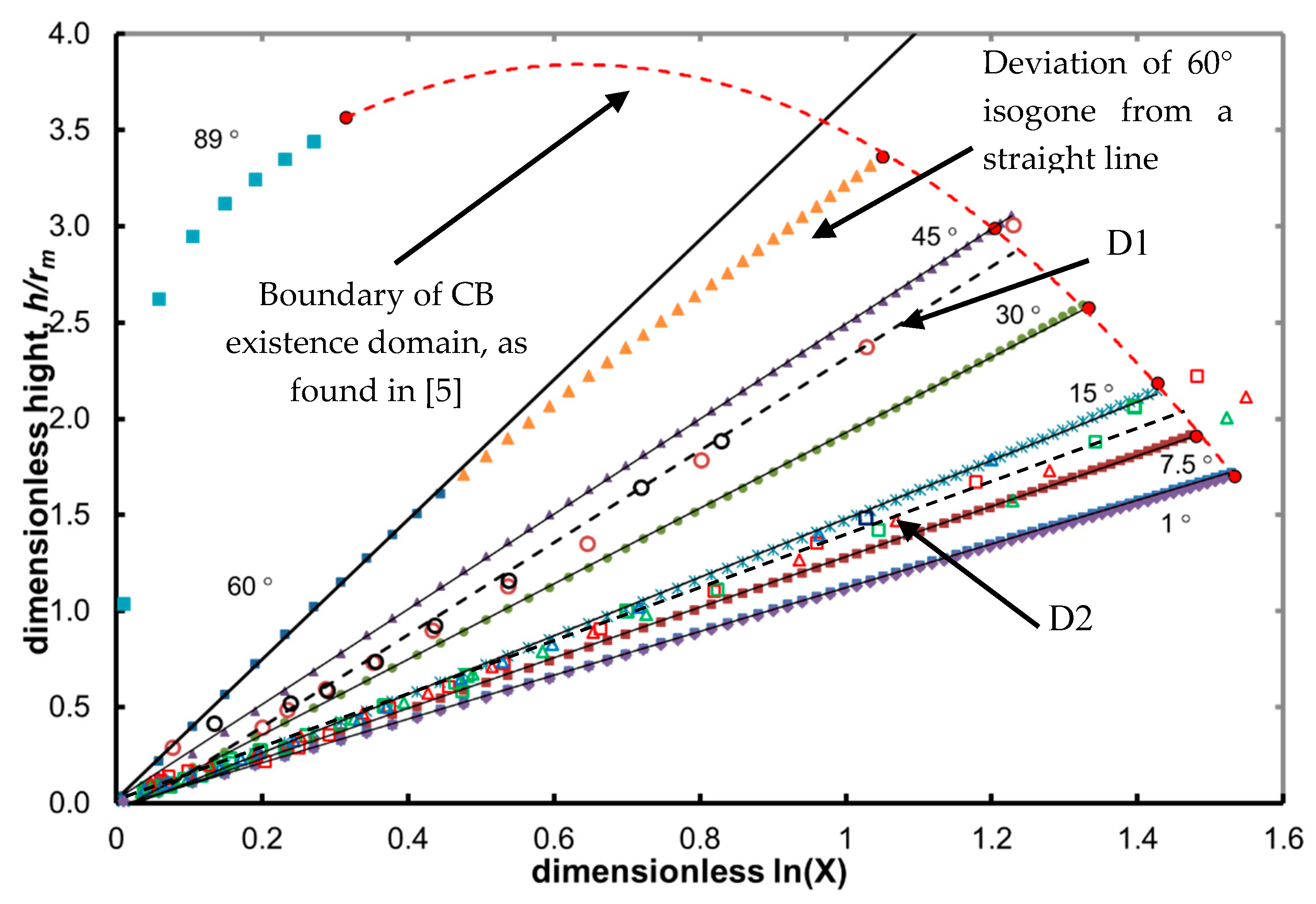
During theoretical studies, we found that the way of presentation of the obtained isogones for CBs is not helpful, if we want to identify precisely the wetting properties through the contact angles. Because of this, we looked for an alternative way for prediction of the stretching behavior of capillary bridges. Our initial hypothesis is that if we are able to linearize somehow the isogones for Figure 2, then we could estimate the contact angles during CB stretching and we could also measure the degree of deviation from the linearity.

It was found, that for equilibrium (static) states, a simple linear relation, $\frac{h}{r_m}~\ln \frac{R}{r_m}$ is valid, where the proportionality coefficient is related to the solid/liquid static receding contact angle. To analyze this experimental observation, we used the same data of theoretically obtained curves, presented in Figure 2, i.e., we made the corresponding plot $\frac{h}{r_m}$ vs. $\ln \frac{R}{r_m}$ of them. The results are presented in Figure 3. The new experiments of stretching with cedar oil and water at different volume proportions (see Section 4, further) are also plotted at the same scale in Figure 3, D2 along with the old data, D1 (data taken from [5]).

The theoretically obtained isogones by Equations (5) and (6) now show linear like dependence. There is exhibited full linear like dependence for 1°, 7.5°, 15°, 30°, 45° or partial for 60°, 89° within the range of concave CB existence domain. This simplifies the further analysis. The deviation from a single straight line increases for angles higher than 45°. For the isogone of 60° solid/liquid static receding contact angle, the deviation from a line is significant. Finally, close to 90° the linear behavior is almost lost. The static receding contact angle of linear-like dependence, ranging between 0° and 45°, corresponds to a “good” wetting [10,11,12,13]. Due to the isogones’ good linearization, the contact angles within the range: 0° < θ < 45°, will be further the main subject of our analysis. As a result, we obtain the following semi-empirical relation:

$$\frac{H}{r_m}=A\left(\theta \right)\ln \frac{R}{r_m}$$

(7)

If comparison between the contact angle for isogones in Figure 2, Ref. [5] and inclination angles of theoretical lines in Figure 3 is made, an empirical linear dependence is revealed: $\mathrm{atan}\left[A\left(\theta \right)\right]=0.444\theta +48.797$. The linearization indicates that the stretching between two glass surfaces results in CB evolution with a constant contact angle. The tangent of inclination angle of the D1 sequence is obtained numerically from the plot in Figure 3: $A\left(\theta \right)=2.392$. The empirical relation in Equation (7), gives a solution for the contact angle, θ = 41.07°. Approximately, the same value was measured over the capillary bridges stretching and reported in [5]. Based on this, we estimated the solid/liquid static receding contact angle for sequence D2 (Figure 3) to be ~11°.

The advantage of the newly proposed approach is that macroscopic parameters, provide sufficient information to be identified the contact angle during CB stretching with unpinned solid/liquid contact line. This empirical relation is in agreement by our previous theory, reported in [5], where we proved that for very thin CBs (h<<R), the generatrix evolved to a part of a circle. We obtained analytically an equation [14], ((A3), Appendix A), and now it can be modified to:

$$\frac{H}{r_m}=\sqrt{\frac{1+\sin \theta }{1-\sin \theta }}\ln \frac{R}{r_m}$$

(8)

The approximate term $\left(\frac{R}{r_m}-1\right)$ in Equation (A3), may result from $\ln \frac{R}{r_m}$ expansion by Taylor series. Therefore, the analytically obtained Equation (8) shows that the linear like dependence during CB stretching may come from retaining a circular arc (or a part of similar closed curve) generatrix of the CB profile during the quasi-static stretching process. The proposed generatrix range expansion to other circular shapes, is based on ”ln(…)” expansion, as will be seen below. The same example for A(θ) = 2.392 was recalculated again according to the Equation (8) and produces relative error of 19%. Therefore, the theoretical relation $A\left(\theta \right)=f\left(\theta \right)\sqrt{\frac{1+\sin \theta }{1-\sin \theta }}$ is valid, where $f\left(\theta \right)$ is an unknown function. In fact, the closer is the contact angle to the complete wetting, the deviation of Equation (8) from when Equation (7) diminishes. For complete wetting, Equation (8) becomes: $\frac{H}{r_m}\to \left(\frac{R}{r_m}-1\right)$.

4. Materials and Methods

The presented theory in Section 3 for capillary bridges requires a reliable experimental confirmation: The selection of liquid phases was done in such a way that: (1) The refraction indices must differ sufficiently, in order to distinguish liquids upon optical observation; (2) Mutual immiscibility of two selected liquid phases is also required. We found that optical grade cedar oil and water match these criteria and we selected them as a subject of our investigation.

4.1. Experimental Equipment and Materials

The following equipment was acquired and assembled for the purpose of the investigation: The specially designed table consists of two supporting plates: The lower, Figure 4(1), is fixed and the upper one, Figure 4(2) can be moved controlled way on z-axis (up and down) by a micrometer, Figure 4(3). On the plates are placed special type supporting tables, Figure 4(4), which in the current investigation hold pre-washed glass plates 18 × 18 mm of thickness: 0.13–0.16 mm (cover glass for microscopy by Deltalab, [15]). The glass plates are replaced before the each new droplet deposition for a CB creation. The recording camera is a Mustcam HDMI digital microscope [16], 3M censor, 1080 P output, 220× magnification and 30 fps speed. We used distilled water and natural cedar oil (Immersion Oil Natural, Juniperus virginiana, CAS no.: 8000-27-9). The cedar oil main constituents by the specification are thujopsene (27.6%), cedrol (15.8%), α-cedrene (27.2%), β-cedrene (7.3%), α-copaene (6.3%), and widrol (1%). The refractive index is n 20/D = 1.519, viscosity is 2000–5000 mPa∙s, and HLB = 16.7 [17]. We measured the oil surface tension by the Wilhelmy plate method to be 31.4 mN/m based on the methodology in [18,19]. The water/cedar oil surface tension was reported 0.5 mN/m in [17]. The experimental setup light system (see Figure 4(5)) and the supporting tables were designed by FreeCad software [20], and printed by a TRONXY X8, P802M3D printer, [21] using PLA (polylactic acid) as a printing material.

4.2. Experimental Methods for Investigation

The experimental method consists of two steps: During the first step we studied the quasi-static stretching of CB, created by mono-phase fluids. The second step of the experimental investigation involves a study of a binary CB of “sandwich” type, created from the same fluids, used in monophasic investigations.

4.2.1. Capillary Bridges Created by a Mono-Liquid Droplets

Each of the selected liquids (water, cedar oil) was investigated by the creation of a sequence of CBs of three different volumes: 8, 10, and 12 μL, as follows: A droplet of the selected volume was placed on the middle of the lower plate and the upper plate was moved down by the micrometer, until the droplet spread on its surface, bridging in this way both of the supporting table’s surfaces. The initial height of the just created CB was usually around 500–800 μm. The stretching of the bridge was performed on small steps. After each step there was allowed 1–2 min equilibration of the bridge, before continuing further with the stretching. The same procedure was repeated for each droplet with the selected volume. We call this approach quasi-static stretching.

4.2.2. Binary Capillary Bridges

The experimental procedure for binary capillary bridges differs from the described procedure in Section 4.2.1 by the positioning of two droplets (from each liquid phase), instead of a one. Consequently, the droplet of each liquid phase, was placed on the corresponding supporting table surface: The water droplet was placed on the upper surface as a pendant drop, not necessarily above the oil droplet, which was placed on the bottom surface. The CB was created when two supporting tables were approached such way that water and oil droplets bridged the surfaces, creating this way two independent but linked CBs. As a result, the oil CB was partially was engulfed into the water bridge. We tried the same experiments with different oil/water volume proportions, droplets of 4:4, 5:3, and 6:2 μL to 8 μL but we found that only 4:4 μL allows for the creation of the described binary structures. Further, upon the CB stretching, a binary CB is created (see Discussion section and the Supplementary Materials).

4.3. Contact Angle Measurements

Current investigation includes geometrical characteristics measurement (height, contact line, and neck radii) of CBs, contact angles at different stretched states, as well as fitting the generatrix profile with an oval that is a part of a circle or ellipse. The solid/liquid contact angle is a characteristics, related directly to wettability and it is important that it is determined correctly. Issues related to its measurement are discussed in [22,23]. As mentioned in [23], the equilibrium static contact angle of capillary shapes, according to the thermodynamics, contradicts the Laplace equation for the convex surfaces. The pressure inside any droplet (circular axisymmetric shape) differs from the surrounding vapor/air pressure. We believe that, because of the nature of the CB stretching process, the contact angle of the stretched CB quasi-static method corresponds to the static receding contact angle of a droplet, which is closer to the equilibrium contact angle as stated in [23]. Therefore, in this paper the appropriate qualification for the contact angle is static and receding.

5. Results

The presentation of the results from the experimental investigation is concentrated on the 8 μL CB behavior while stretching. CBs made by water of 10 μL and 12 μL behave in a similar way and the results confirm the generality of our observations.

5.1. Investigation of Water Capillary Bridges

Water capillary bridges were created by spreading water droplet on the lower table surface and bridging the upper surface by approaching of the upper table to the top of the droplet. The single droplet spreading static contact angle before and after CB creation was measured 12°. Figure 5 presents pictures of selected states, recorded during stretching of 8 μm CB. The generatrix profile was analyzed by adjustment of an oval at it edge by ImageJ software [22]. The oval matches a circle for each recorded state, until the stretching is approaching the initiation of the self-breakage, Figure 5a,e. At that point, as seen in Figure 5f, the shape of profile generatrix evolved to an ellipse, with slightly inclined major axis to the horizon.

This fact explains the substantiated linear like dependence, described by Equation (8) and expressed in Figure 3. It simplifies the identification of the contact angle at stretching based on geometrical considerations (see Discussion section) and justifies a pinned contact angle during CB stretching. The generatrix profile evolves to a part of an ellipse just before the self-initiation of breakage, Figure 5f. Figure 5g–i show the recorded moments from the self-initiated breakage kinetics. Considering the characteristics of the recording camera, the entire process of failure continues less than 0.333 sec. It is predeceased by a slow neck thinning, similar to the presented in the dynamics section of [2] until $r_m/h\approx 0.156$ is reached. Inclined regarding horizon major axis of the ellipse of the generatrix, may be associated with the gravity influence, which is distinguished by the difference between the projections of the upper and lower contact lines, Figure 5f,g.

5.2. Investigation of Cedar oil Capillary Bridge

Figure 6 shows stretching of CB made by 8 μL of cedar oil. The creation of CB and its stretching proceeded the same way as it was done for water CB. The initially spread droplet showed a static equilibrium contact angle of 20°. The analysis of pictures in Figure 6 indicates that, during the stretching, the CB behaves very much like a water made CB. In Figure 6a–f is seen that the generatrix is described very well by a circle, similarly to the water bridge generatrix.

The transformation of the generatrix from a circular to an elliptical shape resulted from the increased CB height. Due to gravity’s influence, there is a corresponding decrease/increase in the top/bottom contact lines (Figure 6g). In addition, at that point, the ellipse major radius is slightly inclined regarding the horizon. The stretching regime justifies a pinned contact angle during CB stretching (see the Discussion section), Figure 3.

Figure 6g shows the CB just before initiation of self-breakage. The process of self-initiated breakage goes slower than the one made from water. Figure 5g shows that the generatrix is transformed from circle to an ellipse at the initiation of the self-breakage. The breakage takes place in less than 0.667 sec, predeceased by a slow thinning, [2], until $r_m/h\approx 0.134$ is reached. Figure 6h shows the initiation of CB failure after continuous neck thinning

5.3. Investigation of Binary Capillary Bridges

The experimental approach is described in Section 4.2.2. The created binary CB behaves very much like a monophasic CBs.

The generatrix of the profile, after CB creation, is fitted with a part of a circle, Figure 7a,b. During the stretching, the circular generatrix, is transformed to a part of an ellipse, as shown in Figure 7c,d. This process takes place earlier than for the monophasic liquid CBs during their stretching (see Section 5.1 and Section 5.2).

The breakage appears in the viscous regime, as is seen in Figure 5f–h. The observed regime is very similar to the reported in [3], where we investigated viscous ionic liquids. The breakage takes place for less than 0.667 sec, predeceased by a slow neck thinning [2], until $r_m/h\approx 0.067$ is reached. Note that the thinning and the breakage of the binary CB, unlike the other cases, proceeds by formation a thin cylindrical neck, which resulted only from oil/water phase combination.

5.4. Uncertainty and Error Analysis

In order to ensure the quality of the obtained results, the intensity values of all images were analyzed by implementing quartile analysis in order to identify the percent of the intensities that appear as outliers and, thus, reduce the reliability of the images. We applied the ImageJ “Quartile Threshold” tool [24,25]. There where analyzed four quartiles, Q_n, of the picture intensity values (see a detailed description in Appendix B), [26]. In our case, 8-bit grey pictures (with intensity values generally vary within the range of 0–255) do not contain pixels with intensity 255, and thus avoided information losses because of pixel intensity oversaturation. The results indicate that, indeed, for low CB heights, about 25% of the intensities are outliers, but for sufficiently stretched CBs no outliers are observed (see Appendix B). Our image analysis indicates that outliers are produced manly by the presence of the upper support plate (see Figure 4(2)) in pictures, which is withdrawn from the recorded images during CB stretching. Therefore, the recorded pictures contain reliable results.

The uncertainty of the measured data from the pictures is also very important for qualification of the results. The experimental errors from the pictures are related to camera resolution, which is 24.4 µm (the distance between two pixels). The minimal dimension in our series of pictures is the initial CB height, which is stated in the paper to be minimum around 21 times longer. We consider a 22 pixel height to be sufficient for revealing the highly-pressed CB geometrical properties.

6. Discussion

Figure 8a is an extension of Figure 3 and summarizes the data from the three different types of CBs, according to the Equation (7). The results indicate that both oil and water CB retain constant solid/liquid static receding contact angle (the straight line in Figure 3) until the initiation of self-breakage takes place. This indicates that a naturally pinned contact angle regime is simultaneously valid if the solid/liquid contact line is not fixed. The conclusion is also supported by the binary CB of “sandwich” type. During its stretching, a deviation from the contact angle line, for the monophasic CBs, is observed. This resulted from the deviation of the generatrix profile from a circle with increasing of the CB height (see red squares in Figure 8a) due to the oil/water interaction. In order to support this conclusion, it is important to evaluate the uncertainty of $\frac{h}{r_m}$ and of $\ln \frac{R}{r_m}$ in Figure 8a. This is performed in the following way: The uncertainty range of the dependent variable is $\pm \Delta \left(\frac{h}{r_m}\right)=\left(\frac{\Delta h}{h}+\frac{\Delta r_m}{r_m}\right){\frac{h}{r_m}|}_{value}$, where $2\Delta h=2\Delta r_m=24.4$µm. The order of magnitude of the uncertainty range is estimated to be 10⁻² µm. The independent variable $\frac{R}{r_m}$ is scaled also by “ln(…)”. Therefore, for the uncertainty we obtain $\pm \Delta \ln \left(\frac{R}{r_m}\right)=\ln \left(\frac{R+\Delta R^{*}}{R-\Delta R^{*}}\right)$, where $\Delta R^{*}=\left(\frac{\Delta R}{R}+\frac{\Delta r_m}{r_m}\right)R$. The estimated uncertainty is in order of magnitude $\Delta \ln \left(\frac{R}{r_m}\right)\cong {10}^{-5}-{10}^{-4}$. Thus, the deviation in Figure 8a of the binary CB stretching properties cannot be qualified as uncertainty of measurements. In addition, based on the data, presented in Figure 8a, one can conclude that the linear like stretching behavior of a liquid CB, expressed in coordinates of $\frac{h}{r_m}~\ln \frac{R}{r_m}$, can be obtained for all liquid CBs that exhibit a generatrix profile to be a part of a closed curve. It appears that the rule is valid for a wide number of monophasic CBs, created between two flat surfaces with good wetting properties (with a contact angle less than 45°). The circular generatrix profile shape is necessary but not sufficient condition for the CB for a pinned contact angle stretching.

The relation between the Bond number (Bo) and CB height is presented in Figure 8b, which is plotted by the following:

$$\frac{H}{R}=f\left(\sqrt{\frac{\rho }{\sigma }}ℛ\right),$$

(9)

Bond number, $Bo=\frac{\rho {ℛ}^2}{\sigma }$, is calculated with selected characteristic length: the radius of generatrix, $ℛ$. In Figure 8b is presented the relation between $\sqrt{Bo}$ and dimensionless height 2h/R for the stretching range, where the generatrix profile was identified as a part of circle. This approach is similar to the expression of Bo number for pendant drops [27,28,29]. These plots indicate that if stretching the liquid water bridge, the increasing height causes an increase in the gravity influence to the generatrix profile. The cedar oil CBs behave in a very similar way because the three plots in Figure 8b do not show a distinguished sensitivity to the initial volume (mass). The water CBs are the more sensible to the initial volume (mass) of the liquid, Figure 8b, because of the increase of water quantity, leads to the increase of gravity’s influence (the inclination angle increases). The binary CBs exhibit low sensitivity to gravity with stretching due to the modification of the surface properties of both liquids.

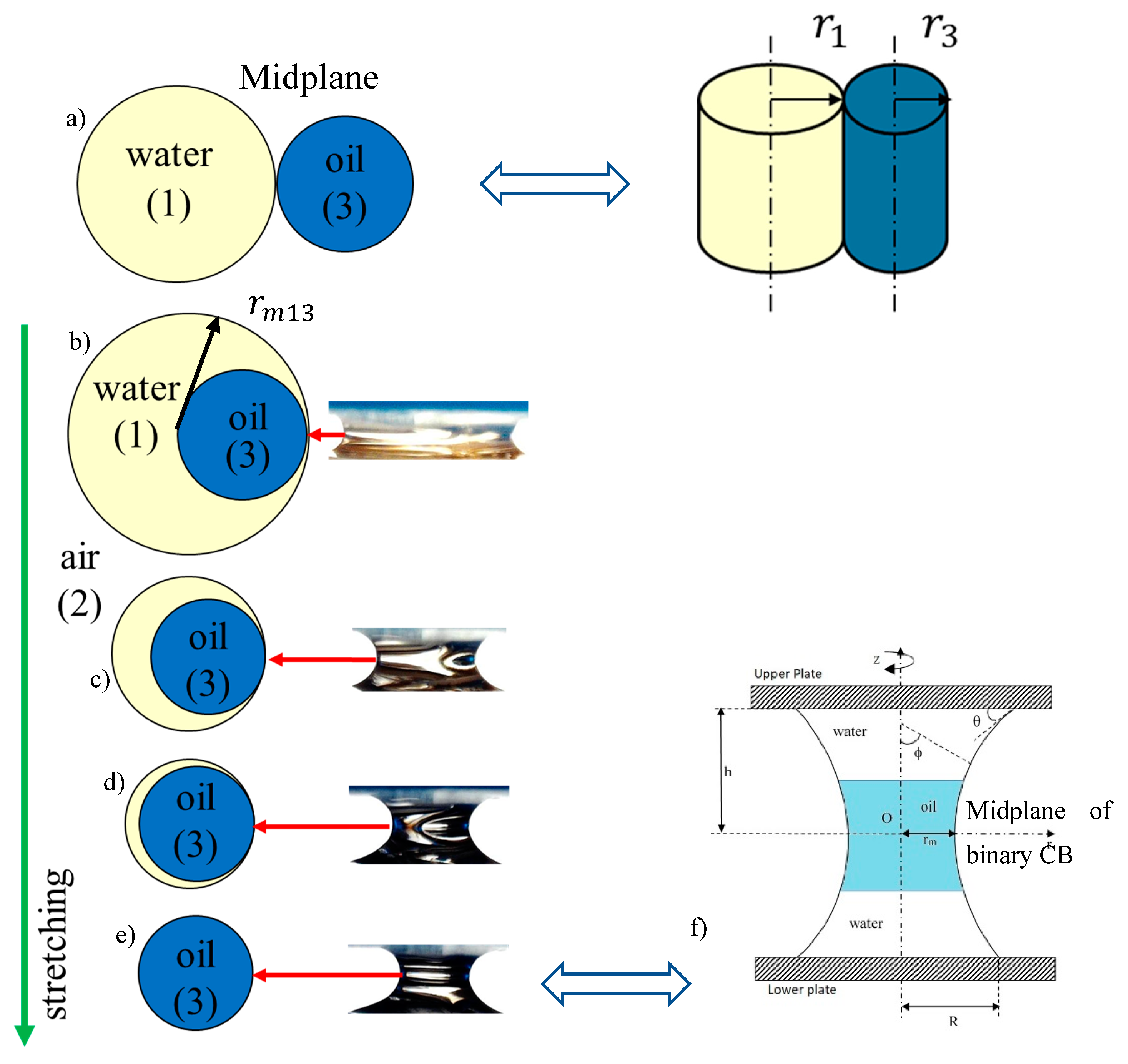
Investigation of binary CBs is a very complicated task but the efforts are worthwhile because these CBs provide further information about the surface interaction of two fluids. Figure 9 presents the proposed behavior and kinetics of binary liquid CB of a “sandwich” type. After completion of the steps, described in Section 4.2.2, at the initial moment, for relatively low heights between the supporting tables, two parallel CBs exist for a while, Figure 9a. Because of the R >> h, r_m>>h condition, at this stage, the CB can be presented as a liquid cylinders. This initiates oil to be engulfed (partially) into the water CB, creating this way a binary CB. Further, due to the stronger glass wetting by water, the oil phase is adhered at the water/gas interface with a tendency to stand in the zone around the waist (minimal surface energy), Figure 9b. During the stretching the CB waist is thinned, reducing this way the quantity of water around the oil droplet, Figure 9c,d. After stretching, at a certain height, the water escapes from the waist and only cedar oil droplet remains there. At this stage the water CB is considered broken, Figure 9e. However, the oil droplet links the two CB water parts. It keeps the entire structure intact, creating a sandwich-like CB, shown in Figure 9f. Due to the adhesion to the water phase, the oil phase stabilizes the entire structure. If manual stretching continues, soon afterwards a spontaneous waist thinning occurs and the bridge breaks. As we noticed previously, during our experiments, the self-initiated thinning behavior of binary CBs is different than the corresponding behavior of the pure systems (see the Supplementary Materials).

According to the work done by Torza and Mason, [30], and Israelashvilly, [31], the creation of binary CB resulted from engulfing of oil CB into the initially created water CB (the two liquid phases are immiscible):

$$\begin{gathered} S_1={\sigma }_{23}-\left({\sigma }_{12}+{\sigma }_{13}\right)=-41.13\mathrm{mN}/\mathrm{m}<0 \\ {S}_2={\sigma }_{13}-\left({\sigma }_{23}+{\sigma }_{21}\right)=-102.87\mathrm{mN}/\mathrm{m}<0 \\ {S}_3={\sigma }_{12}-\left({\sigma }_{31}+{\sigma }_{32}\right)=40.13\mathrm{mN}/\mathrm{m}>0 \end{gathered}$$

(10)

where the coefficients S₁, S₂, and S₃ are related to three fundamental types of wetting [32]: adhesion, immersion, and spreading (spreading coefficients). Each of these coefficients presents the corresponding free energy decrease. The classification of current case corresponds to “complete engulfing,” according to [30]. The geometrical characteristics of the binary CB are predictable by general capillary equations and interfacial tension relations. The structure is called an n-singlet, where n indicates the number of negative coefficients.

The process of engulfing is initiated when two initial droplets are pressed by the upper plate such way that $X_1\cong 1$ and $X_3\cong 1$, which means that the radius of curvature is sufficiently small, i.e., $2h_1\ll {ℛ}_1$ and $2h_3\ll {ℛ}_3$. The indices meaning is as follows: 1, water; 2, air; 3, cedar oil. There are two competitive processes that could initiate the engulfing:

• Penetration under capillary pressure difference (favored by large ${\sigma }_{12}$ and $r_1>r_3$);
• Spreading of phase three over phase one under the action of S₃ > 0.

The relation of capillary pressure difference, for 2-singlet according to [30] is:

$$\Delta P_{13}=\frac{{\sigma }_{12}}{r_1}-\frac{{\sigma }_{23}}{r_3}>0$$

(11)

where $\Delta P_{13}>0$ is required for the engulfing process to take place. Therefore, we can obtain the critical pressure condition for initiation of the engulfing:

$$\frac{r_3}{r_1}>\frac{{\sigma }_{23}}{{\sigma }_{12}}=2.29$$

(12)

Due to the specific nature of interactions and relation in Equation (12), there could be suggested that the spreading of phase 3 over phase one mechanism (Figure 9), leads to engulfing. If the engulfing occurs at the most pressed state of CB, shown in Figure 9a, upon stretching a sufficient quantity from the oil CB enters into the water CB. This resulted in further modification of the CB stretching and breakage properties.

Our investigation of three different CBs indicates that three possible shapes of generatrix profiles could be considered. Two of them, described in [33], can be summarized as “circular/elliptical” and parabolic profiles take place during self-initiated breakage [3]. If for a CB, h << R ≈ r_m is valid, then indeed a circular generatrix profile is formed, proven mathematically and experimentally verified in [5,14]. Further, upon stretching, it reaches an elliptical form at the initiation of the self-breakage kinetics. Finally, the generatrix takes a parabolic shape. Following this information, obtained from the current investigation, we obtain:

$${\left[r\left(z\right)-\left(r_c+ℛ\right)\right]}^2+z^2={ℛ}^2$$

(13)

which further transforms into an inclined ellipse that can be described by the equation [34]:

$$\frac{{\left\{\left[r\left(z\right)-\left(r_c+ℛ\right)\right]\cos \alpha +z\sin \alpha \right\}}^2}{A^2}+\frac{{\left\{\left[r\left(z\right)-\left(r_c+ℛ\right)\right]\sin \alpha +z\cos \alpha \right\}}^2}{B^2}=1$$

(14)

where α is the inclination of the ellipse regarding the horizon. If the ellipse is horizontal ($\alpha =0$), then the equation simplifies to:

$$\frac{{\left[r\left(z\right)-\left(r_c+ℛ\right)\right]}^2}{A^2}+\frac{z^2}{B^2}=1$$

(15)

The shape evolves to parabolic during the CB breakage, as previously stated in [3]. Then Equation (14) in a more general form will be:

$$\begin{array}{l}{\left\{\left[r\left(z\right)-\left(r_c+ℛ\right)\right]\sin \alpha +z\cos \alpha \right\}}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=B^2+\left(e^2-1\right){\left\{\left[r\left(z\right)-\left(r_c+ℛ\right)\right]\cos \alpha +z\sin \alpha \right\}}^2\end{array}$$

(16)

where $e=\sqrt{1-{\left(\frac{B}{A}\right)}^2}$ is the ellipse eccentricity. If $e=0$, then $ℛ=B=A$ and a circle is formed with a radius $ℛ$. For the axis inclination α > 0° and $0<e<1$, the circle is transformed to an inclined ellipse with constants A and B. The transformation to an parabola takes place for $e=1$, and $B^2=p\left\{\left[r\left(z\right)-\left(r_c+ℛ\right)\right]\cos \alpha +z\sin \alpha \right\}$. Finally, for $e>1$, the CB generatrix possibly evolves to a hyperbola (note that the process of stretching itself is not an equilibrium action). We observed in our experiments that the most probable form of generatrix profile during the quasi-static stretching is circular. It is possible to verify that the obtained shape is correctly identified as a circle.

The identified circular shape in our measurements (section three) can be verified by the usage of relation, $ℛ=2h/\cos \theta$, [32]. The results from this verification indicate a less than 5% deviation of the calculated solid/liquid contact angles from the analytically estimated values of ~11° (Figure 3), for all identified generatrix circular shapes.

7. Conclusions

We proposed a new relation $\frac{h}{r_m}~\ln \frac{R}{r_m}$ that shows a linear-like dependence for contact angles 0° ≤ θ ≤ 45° during CB stretching. Based on its implementation, the behavior of CBs becomes predictable. If there are no other limiting conditions on solid/liquid surface wetting, the contact angle at this process is constant (pinned) during the CB stretching. This is demonstrated by the inclination of linear-like, numerically-obtained data for all calculated isogones. The profile generatrix of all created CBs at low heights, is initially a part of a circle or further evolves to an ellipse during the stretching. If a self-initiation breakage begins, the generatrix may be transformed to a parabola or possibly to a hyperbola, [9].

The presented approach easily allows the contact angle to be calculated by applying the relation $ℛ=2h/\cos \theta$, due to the easy identification of the macroscopic geometrical characteristics of CB.

The CBs stretching properties can be engineered by the creation of a binary CB of “sandwich” type. This way one can design a combination of a particular surface solid/liquid properties and breakage behavior.

The remaining part of the 45° < θ < 90° wetting region is planned to be investigated in the future. However, due to limited linearity, there may be some complications in the implementation of the presented approach (see Figure 3).