Impact of a Linear Array of Hydrophilic and Superhydrophobic Spheres on a Deep Water Pool
Abstract
1. Introduction
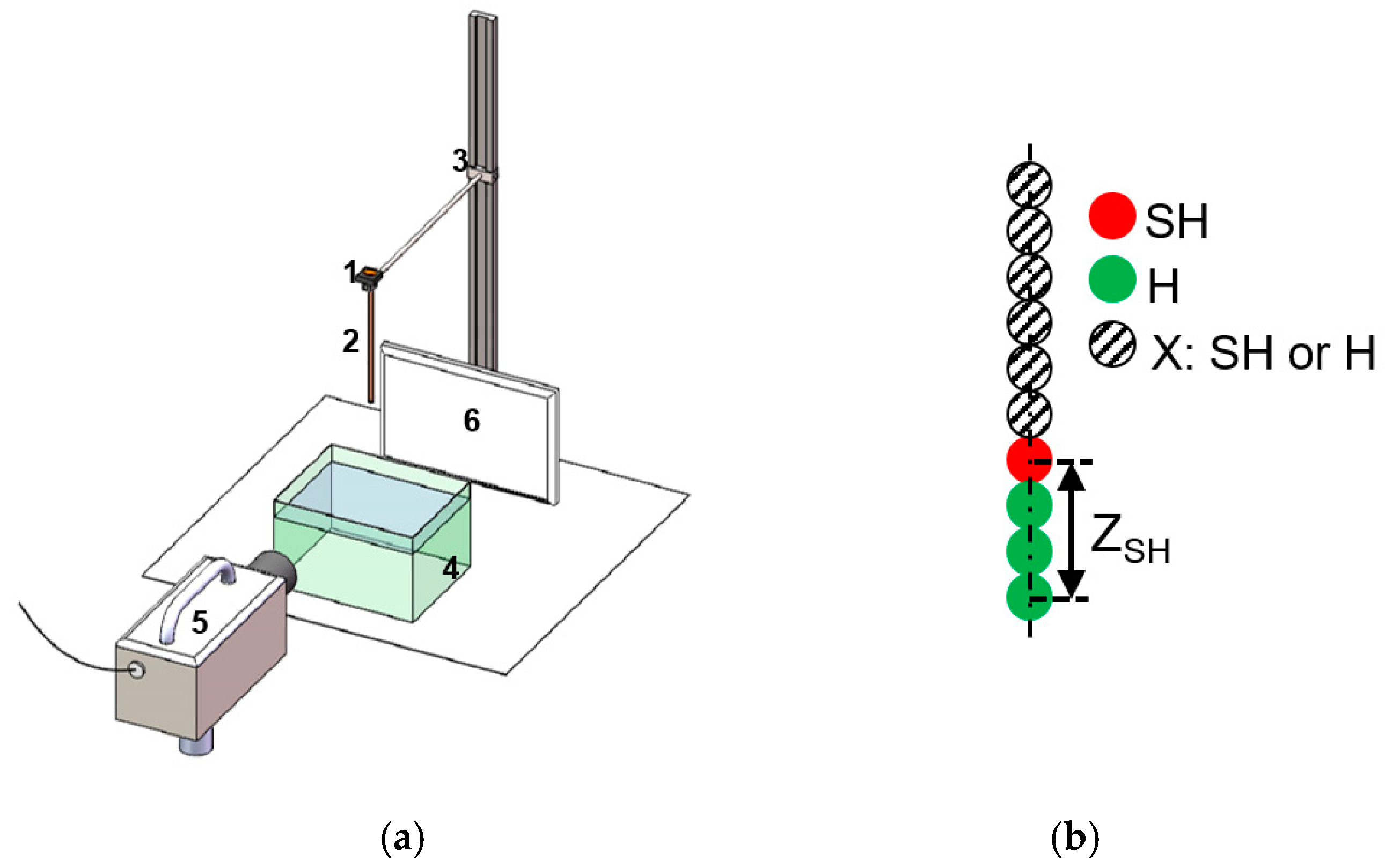
2. Materials and Methods
3. Results and Discussion
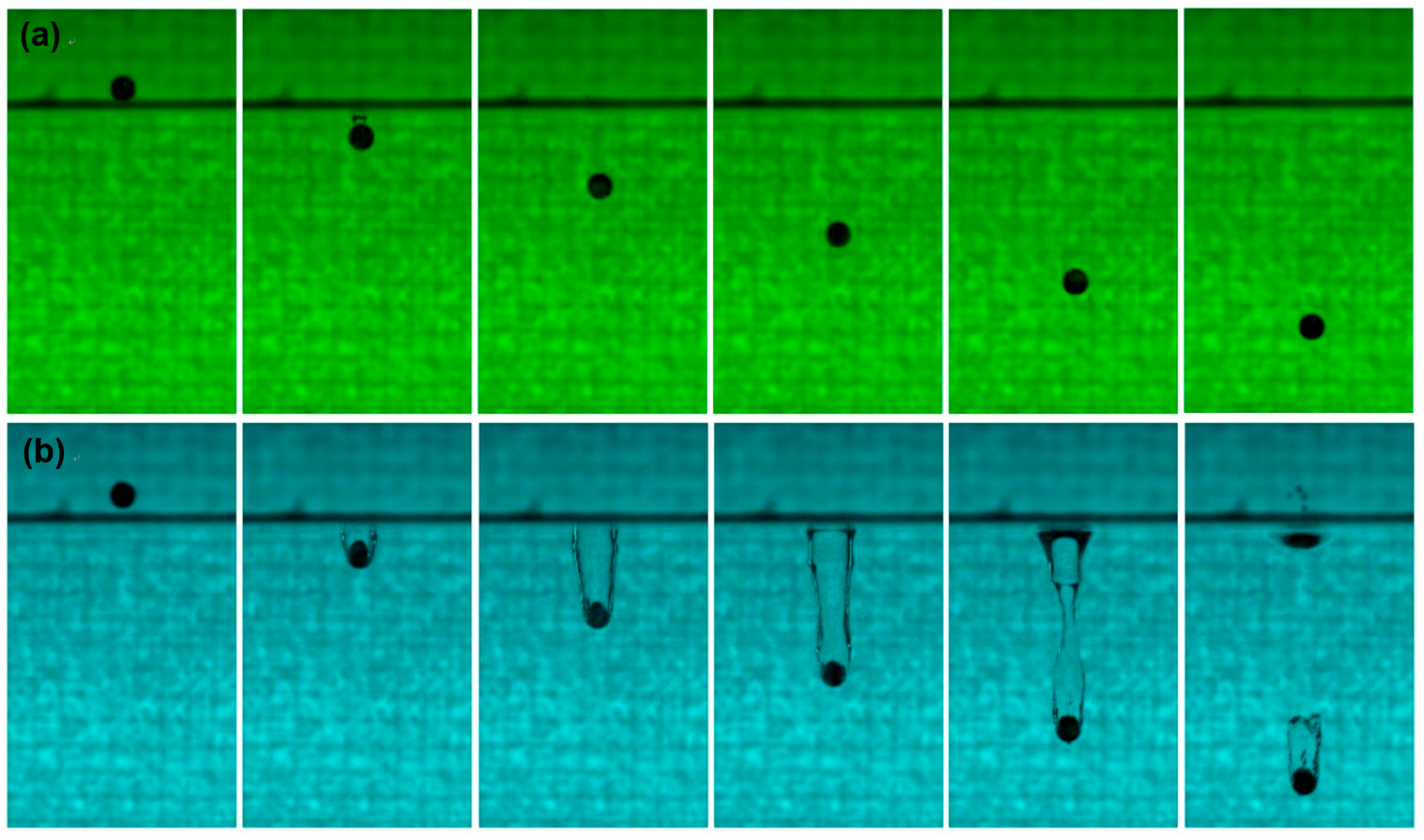
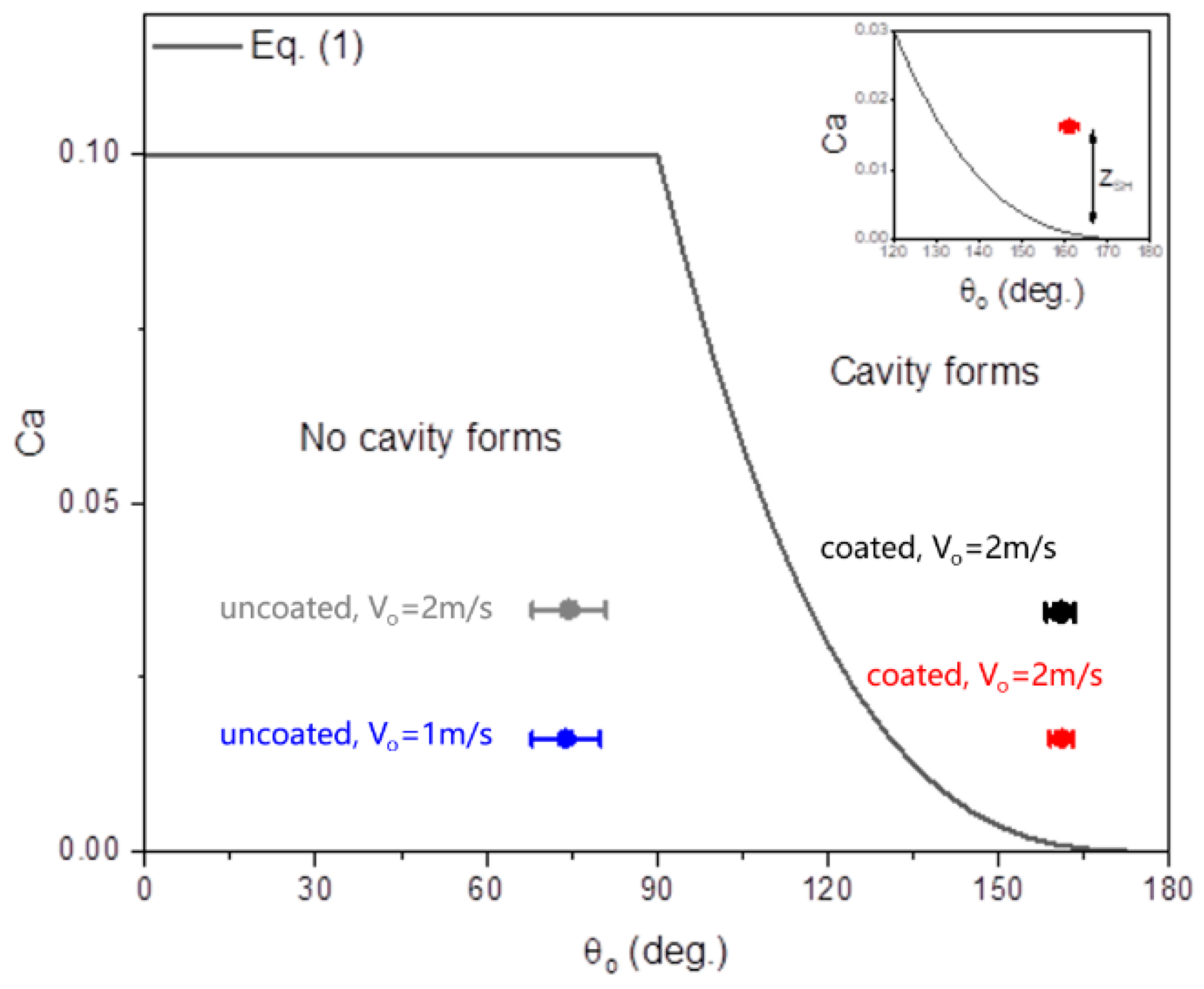
3.1. Cavity Evolution
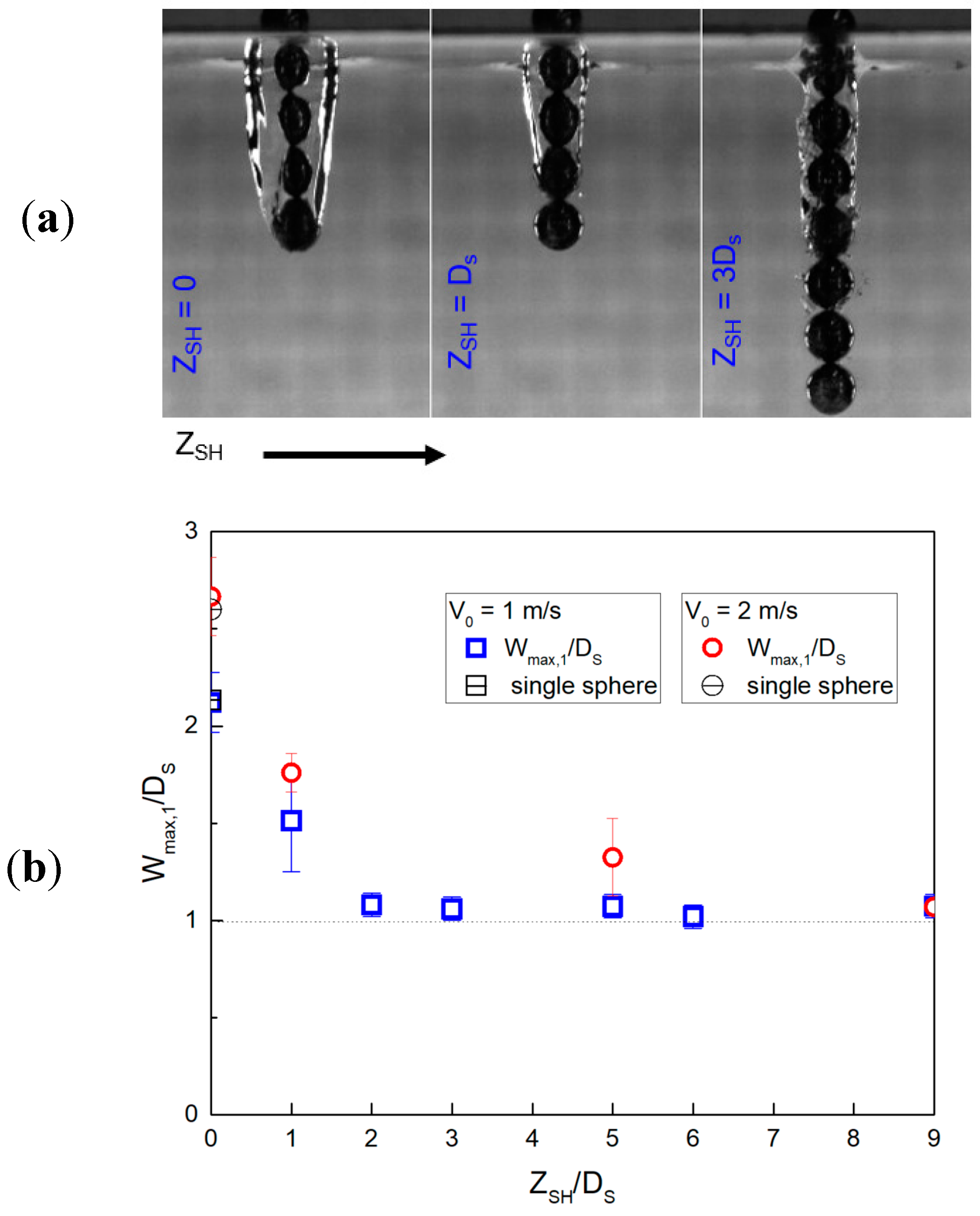
3.2. Maximum Cavity Width
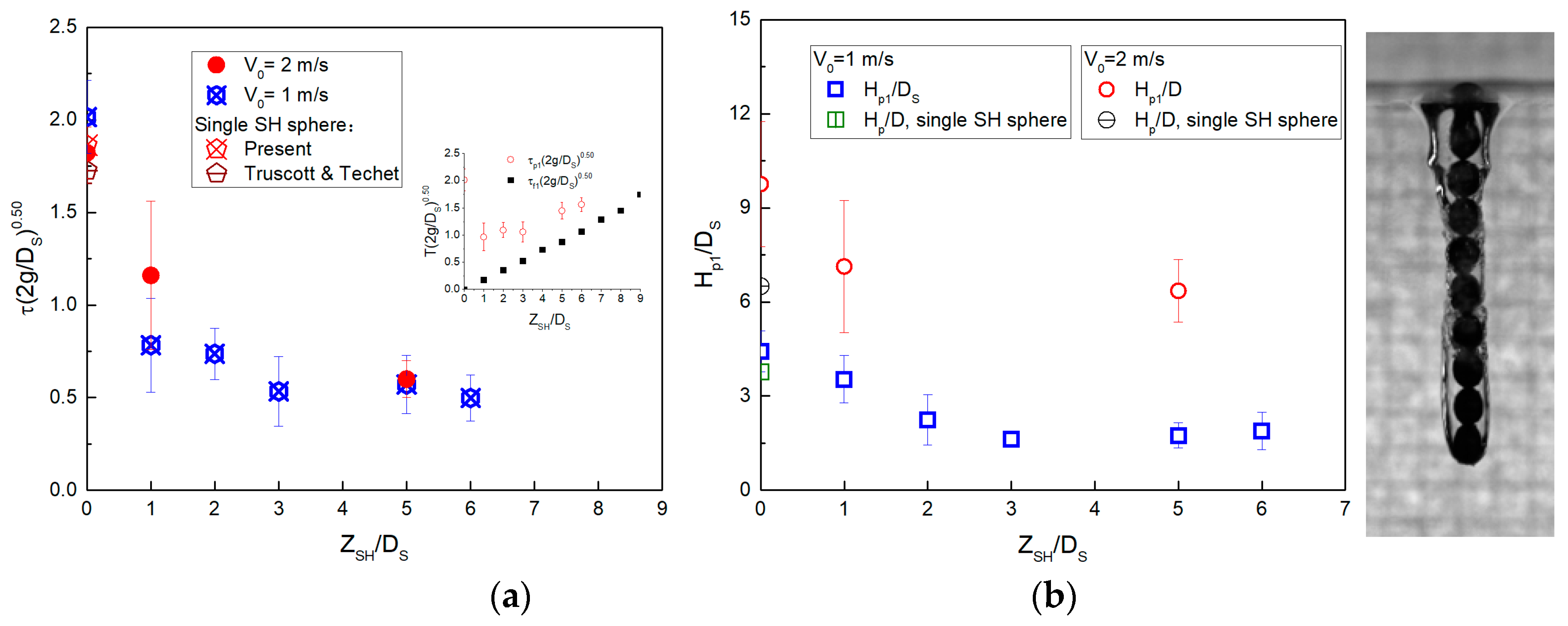
3.3. First Pinch-Off
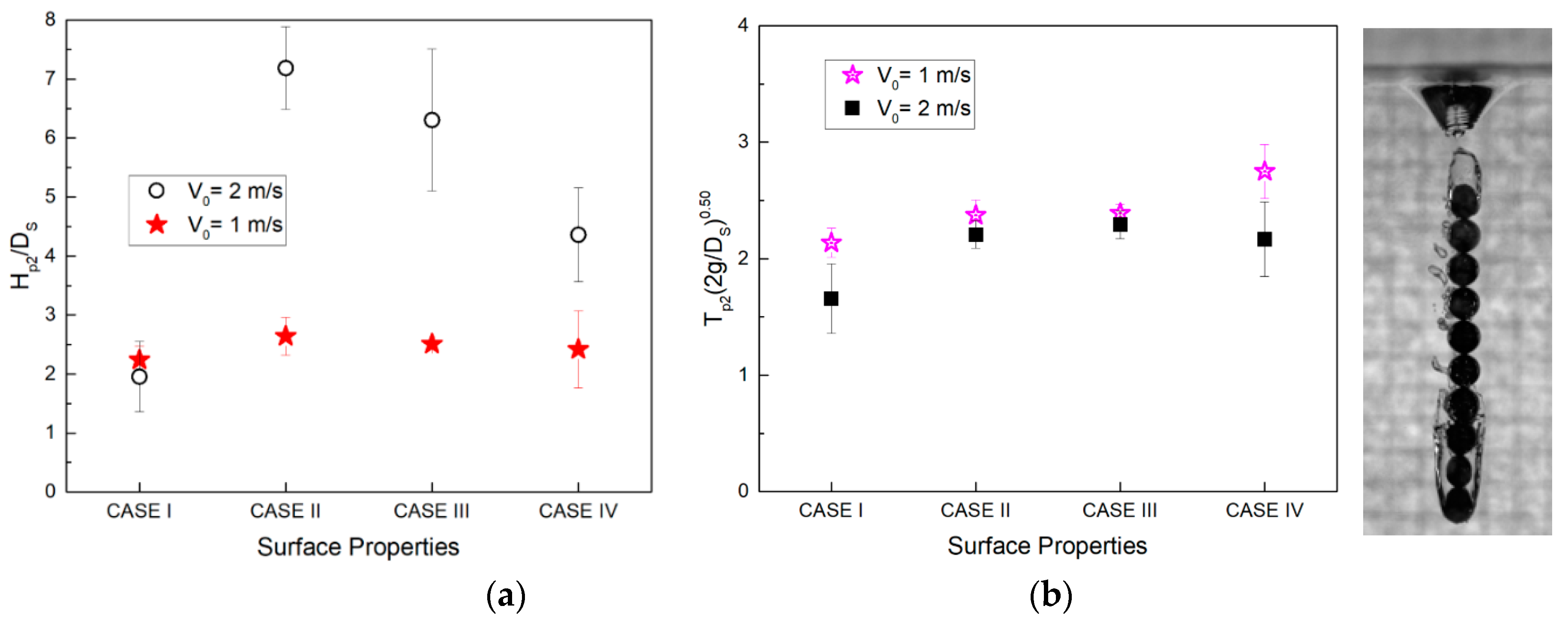
3.4. Second Pinch-Off
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B
References
- Worthington, A.M.; Cole, R.S. Impact with a liquid surface, studied by the aid of instantaneous photography. Phil. Trans. A 1897, 189, 137–148. [Google Scholar] [CrossRef]
- Worthington, A.M.; Cole, R.S. Impact with a liquid surface, studied by the aid of instantaneous photography—Paper II. Phil. Trans. A 1900, 194, 175–200. [Google Scholar] [CrossRef]
- Truscott, T.T.; Epps, B.P.; Belden, J. Water entry of projectiles. Annu. Rev. Fluid Mech. 2014, 46, 355–378. [Google Scholar] [CrossRef]
- Tan, B.C.W.; Thomas, P.J. Influence of an upper layer liquid on the phenomena and cavity formation associated with the entry of solid spheres into a stratified two-layer system of immiscible liquids. Phys. Fluids 2018, 30, 064104. [Google Scholar] [CrossRef]
- Duez, C.; Ybert, C.; Clanet, C.; Bocquet, L. Making a splash with water repellency. Nat. Phys. 2007, 3, 180–183. [Google Scholar] [CrossRef]
- Truscott, T.T.; Techet, A.H. A spin in cavity formation during water entry of hydrophobic and hydrophilic spheres. Phys. Fluids 2009, 21, 121703. [Google Scholar] [CrossRef]
- Aristoff, J.M.; Bush, J.W. Water entry of small hydrophobic spheres. J. Fluid Mech. 2009, 619, 45–78. [Google Scholar] [CrossRef]
- Speirs, N.B.; Mansoor, M.M.; Belden, J.; Truscott, T.T. Water entry of spheres with various contact angles. J. Fluid Mech. 2019, 862, 3. [Google Scholar] [CrossRef]
- Hurd, R.C.; Belden, J.; Jandron, M.A.; Fanning, D.T.; Bower, A.F.; Truscott, T.T. Water entry of deformable spheres. J. Fluid Mech. 2017, 824, 912–930. [Google Scholar] [CrossRef]
- Li, J.C.; Wei, Y.J.; Wang, C.; Xia, W.X. Cavity formation during water entry of heated spheres. Chin. Phys. B 2018, 27, 094703. [Google Scholar] [CrossRef]
- Speirs, N.B.; Mansoor, M.M.; Hurd, R.C.; Sharker, S.I.; Robinson, W.G.; Williams, B.J.; Truscott, T.T. Entry of a sphere into a water-surfactant mixture and the effect of a bubble layer. Phys. Rev. Fluids 2018, 3, 104004. [Google Scholar] [CrossRef]
- Gupta, R.; Vaikuntanathan, V.; Sivakumar, D. Superhydrophobic qualities of an aluminum surface coated with hydrophobic solution NeverWet. Colloid Surf. A 2016, 500, 45–53. [Google Scholar] [CrossRef]
- Yang, G.; Vaikuntanathan, V.; Terzis, A.; Weigand, B.; Helmig, R. Impact of a linear array of hydrophilic and superhydrophobic spheres on water pool. In Gallery of Fluid Motion, 71st Annual Meeting of the APS Division of Fluid Dynamics, Atlanta, GA, USA, 18–20 November 2018; The Division of Fluid Dynamics of the American Physical Society: College Park, MD, USA, 2018. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Vaikuntanathan, V.; Terzis, A.; Cheng, X.; Weigand, B.; Helmig, R. Impact of a Linear Array of Hydrophilic and Superhydrophobic Spheres on a Deep Water Pool. Colloids Interfaces 2019, 3, 29. https://doi.org/10.3390/colloids3010029
Yang G, Vaikuntanathan V, Terzis A, Cheng X, Weigand B, Helmig R. Impact of a Linear Array of Hydrophilic and Superhydrophobic Spheres on a Deep Water Pool. Colloids and Interfaces. 2019; 3(1):29. https://doi.org/10.3390/colloids3010029
Chicago/Turabian StyleYang, Guang, Visakh Vaikuntanathan, Alexandros Terzis, Xin Cheng, Bernhard Weigand, and Rainer Helmig. 2019. "Impact of a Linear Array of Hydrophilic and Superhydrophobic Spheres on a Deep Water Pool" Colloids and Interfaces 3, no. 1: 29. https://doi.org/10.3390/colloids3010029
APA StyleYang, G., Vaikuntanathan, V., Terzis, A., Cheng, X., Weigand, B., & Helmig, R. (2019). Impact of a Linear Array of Hydrophilic and Superhydrophobic Spheres on a Deep Water Pool. Colloids and Interfaces, 3(1), 29. https://doi.org/10.3390/colloids3010029




