1. Introduction
The wetting and spreading of aqueous surfactant solutions over porous materials is currently used in a wide range of applications (shampoos, sponges, cleaning, application of drugs on skin and hair) and in near infinite examples in the natural world, from the absorption of water through the xylem of plants, to allowing insects to move on the surface of water.
Scientific interest in wetting and spreading behaviour has increased exponentially in recent years, primarily due to the expanding range of medical and biological science, and environmental engineering applications [
1], for example, maintaining biodiversity in soil ecology [
2]. Much of the experimental research and theory published related to contact angle characteristics has focussed on smooth and homogenous substrates. In such cases, when a liquid is deposited on the solid’s surface, the three-phase dynamic contact angle will reach an equilibrium value in accordance with Young’s equation [
3,
4]. Dynamic contact angles and hysteresis have been extensively investigated, and the general consensus is that for impermeable solids, contact angle and spreading behaviour depend on the degree of surface roughness, heterogeneity and hydrophobicity [
5]. For example, rough surfaces effectively have multiple barriers to liquid spreading.
More recently, investigations into the wetting properties of porous media specifically have become more prominent. The latter is because numerous real-world substrates exhibit a porosity throughout their structure, or have a thin porous sub-layer [
6]. These include sponges, filters and biomedical tissue scaffolds. It has been highlighted that the mechanism for the wetting and spreading of liquids on porous substrates differs from non-porous solids because two competing processes of surface spreading and imbibition into porous substrate are occurring simultaneously. There have been some successful attempts to develop hydrodynamic models for spreading over both dry and saturated porous substrates [
6], using Brinkman’s equations [
7] to predict inter-porous layer flows. Other theoretical works of the spreading, wetting and dewetting have been conducted by Bonn et al. [
8] and Dietrich et al. [
9], and the wetting of real surfaces has also been investigated by Bormashenko [
10].
The research below is focussed on characterising the wetting and spreading behaviour of droplets of aqueous surfactant solutions using commercially available surfactants deposited on porous substrates under different degrees of saturation. The latter process is of great interest for multiple industries for understanding how surfactant products interact with porous media. For example, in enhanced oil recovery, where surfactant solutions are used to extract oil or gas, the rocks where the oil/gas is located are usually porous. The relationship between contact angle characteristics and foam production is significant when assessing the conditions in which the surfactant products are most effective.
The influence of surfactants on wettability is well understood; however, it has also been established that employing surfactants to enhance spreading on solid porous substrates substantially modifies the wetting process [
4,
11,
12]. The rate of surface spreading increases as the surfactant concentration increases [
4] on a smooth homogeneous surface; however, it could be more complicated in the case of spreading over porous materials. It is easy to distinguish between complete and partial wetting in the case of smooth homogeneous substrates: in the case of complete spreading, the final contact angel tends to zero over time, while in the case of partial wetting the droplet stops after reaching a static advancing contact angle, which is different from a zero value [
1]. However, a definition of complete and partial wetting in the case of spreading over a porous substrate is not so straightforward and has been given in [
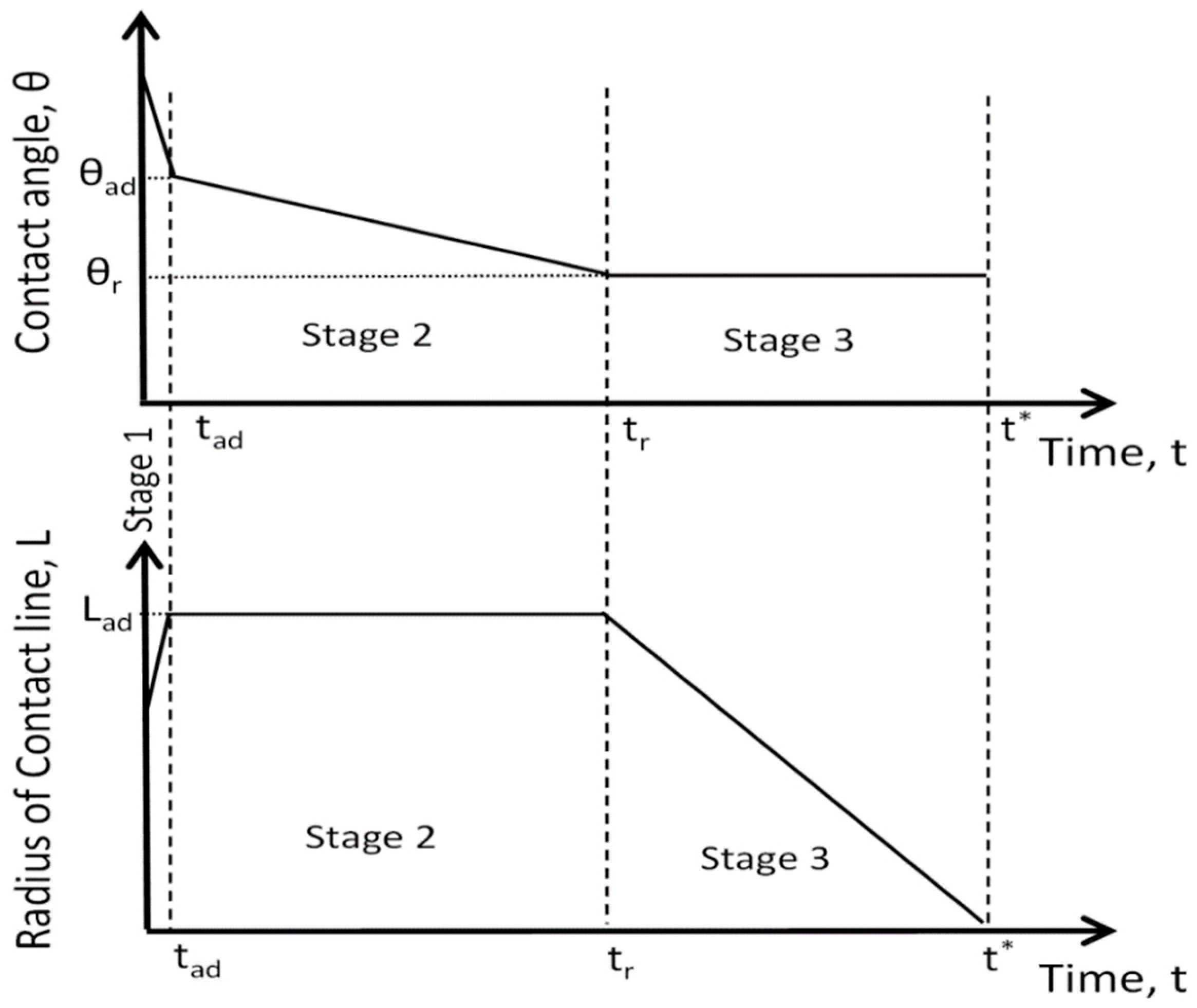
1]. In the case of partial wetting (
Figure 1), there are three stages of spreading/imbibition of droplet over porous substrate: (i) during the first stage the droplets spread out until the maximum radius of droplet base, L
ad, is reached at moment t
ad; during this stage the contact angle decreases until the static advancing contact angle, θ
ad, is reached at the same moment t
ad; (ii) during the second stage, which lasts from t
ad to t
r, the droplet base does not change but the contact angle decreases linearly from the static advancing contact angle θ
ad to static receding contact angle θ
r; (iii) during the third stage the contact angle remains constant and equal to the static receding contact angle, while the droplet base decreases until the complete penetration of the droplet at t* (
Figure 1).
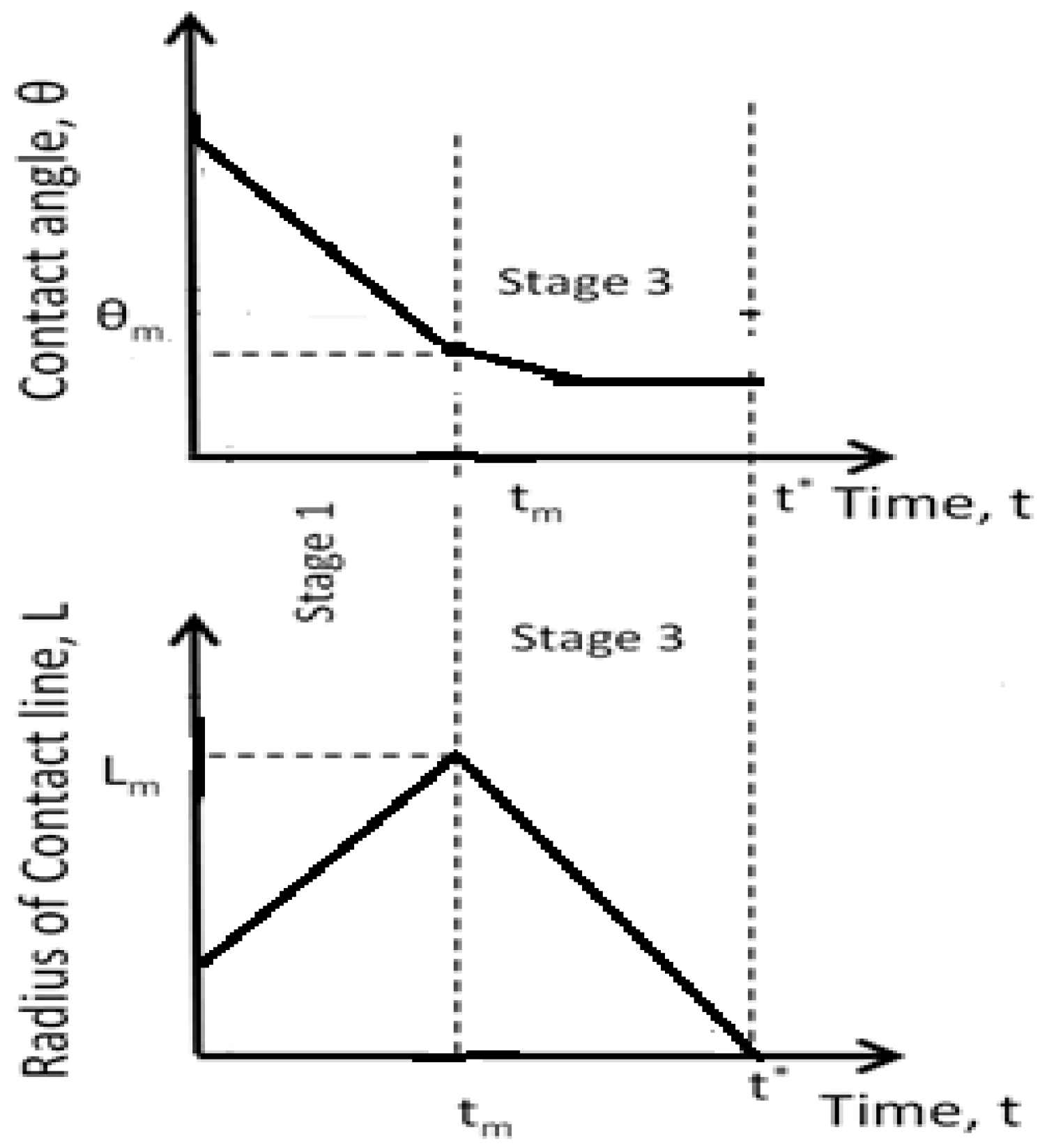
In the case of complete wetting, the spreading behaviour is different from the partial wetting case (
Figure 2). In this case: (i) stage 2 is absent, (ii) the duration of the stage 1 is much longer, and (iii) the constancy of the contact angle over the duration of stage 3 is only approximately satisfied [
1].
Common sponges such as those studied below are often made of polyester and other polymers. They have a soft porous structure, allowing them to be easily compressed to absorb liquids. The wettability of sponges is an important factor that can vary between synthetic sponges. Other important properties include structural properties such as porosity and pore size.
2. Materials and Methods
2.1. Preparation of Surfactant Solutions
A commercially available surfactant solution is used during the investigation, wherein a serial dilution was carried out for 0–100% (w/w). The CMC point of the commercial surfactant was found to be 0.2% and the concentration of all solutions used was above CMC. The surface tension was constant and equal to 25 mN/m.
2.2. Experimental Apparatus
The wetting data (contact angle and spreading diameter) were collected using a KRUSS (Hamburg, Germany) DSA100 drop-shape analyser.
It was operated via a purpose-designed ‘ADVANCE (KRUSS software, Hamburg, Germany)’ interfacial software package.
2.3. Sponge Characteristics
Three porous sponge types were tested: a dish sponge (Spondex(France) Washup sponge), a car sponge (Tesco (Hertfordshire, England) car sponge) and an audio sponge (used in sound proofing, Basotect acoustic foam). The sponges used in this investigation are made out of 100% polyester; they are all soft, approximately 3–4 cm in height, and swell slightly when water is absorbed. The contact angle of distilled water was found to be 128.9° ± 2.8° on the dish sponge and 106.9° ± 2.1° on the car sponge; that is, both sponges show non-wetting behavior. The audio sponge completely absorbed the water droplet immediately after deposition.
A scanning electron microscope was used to analyse the pore characteristics of each type of sponges; the porosity was calculated using Matlab (Massachusetts, U.S.A.) by comparing the total area of the image to the combined area of the dark contrast pores. The results of this study are presented in
Table 1, which shows that all three sponges have similar porosity but the pore size is smaller in the audio sponge as compared with the dish and car sponges.
2.4. Dry/Wet Sponge
All three sponge samples used (see below) were cut into uniform cylinders using an aluminium cutting tool. A 10–100 µL ‘Finnipipette’ micropipette was used to deposit droplets of surfactant solution (approx. 40 µL) onto a sponge sample placed on the platform in the KRUSS device. Once the droplet had been fully absorbed into the sponge, the recording was stopped, and the recorded data were exported to Microsoft Excel for analysis. When recording liquid droplets on sponges that were fully or partially wetted, there was an additional preparatory phase arranged. First, a beaker of distilled water was filled and weighed. A cylinder of the sponge sample being tested was thoroughly soaked in the distilled water. The beaker of water was then weighed again. The difference between the initial and final measurements equated to the mass of water contained within a fully saturated sponge sample. This information could then be used to create sponge samples of known percentage saturation (in this case 10% and 50%), by weighing out fractions of the saturated mass of water and using a dry sponge to soak the water onto the sponge surface. The amount of water used was 30 g for complete saturation; this was the amount of water observed to completely saturate the sponge without drainage being observed. The data recording technique was the same as for a dry sponge.
3. Results and Discussion
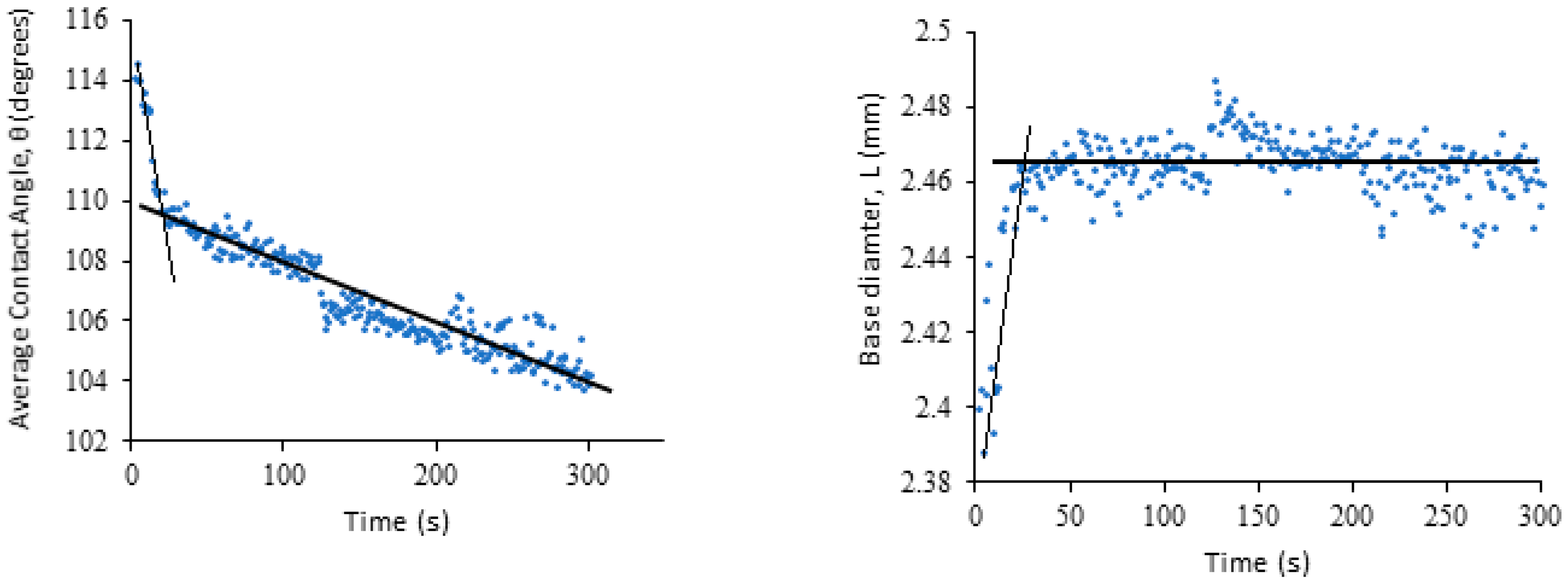
Initially the droplet dynamics of pure water on each of the sponge types was investigated to identify the relative degrees of hydrophobicity. In
Figure 3 the obtained time dependencies of contact angle and droplet base, determined in the case of the dry dish sponge, are presented. For the dish sponge (
Figure 3), it is evident that the initial contact is high, at approximately 116°. The contact angle reduces quite rapidly during the first 30 s. Mirroring this, the droplet base diameter increases quickly as the water begins to spread. This stage is followed by the second stage, when the contact angle decreases linearly, while the droplet base remains constant. Comparison of the data presented in
Figure 3 shows that the case under consideration corresponds to the partial wetting. However, we did not reach the third and final stage, when the contact angle reaches the static receding value. The droplet is still very stable on the surface after 5 min has passed, with a contact angle of 104° when recording ceased, and only a 0.1 mm increase in diameter. Hence, it is evident that the dish sponge exhibits a high degree of hydrophobicity.
The car sponges exhibited very similar partial wetting behaviour to that in
Figure 3 when distilled water droplets were applied. The average initial contact angle for the car sponge was 111°, reducing to 102° after 5 min. Therefore, the car sponge is highly hydrophobic since the initial contact angle is over 90° [
5]. The dish sponge is the most hydrophobic, closely followed by the car sponge. When distilled water droplets were introduced to the audio sponge, they did not finish in spherical shapes with a non-zero contact angle at the surface of the sponge but were very quickly absorbed. The differences in hydrophobicity (initial contact angle) of the four sponges mentioned are determined by the difference in the polymers that the sponges were manufactured from.
The data presented in
Figure 4 show complete wetting behaviour according to
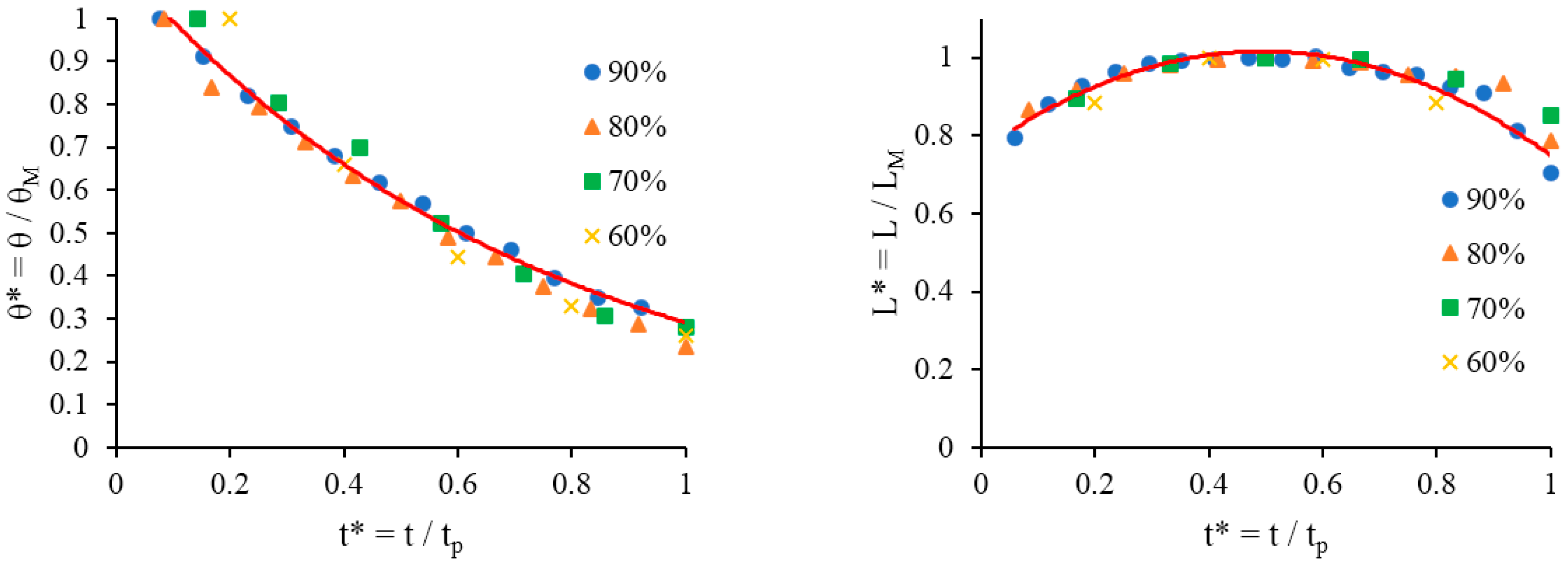
Figure 2. The experimental data from all experimental runs across the range of dry sponges using various surfactant concentrations have been compiled into dimensionless plots such as those shown in
Figure 5 using the following procedure: the contact angle values are divided by the maximum contact angle θ
M and the base diameter is divided by the maximum base diameter L
M, changing them into dimensionless values θ* and L*, respectively. Both θ* and L* are plotted against dimensionless time, t*, which is calculated by dividing the time values by the total time period of the process t
p, where the time period is determined by the point where the droplet absorbs into the substrate
. In all cases the initial contact angle is around 107° and the rate at which the contact angle decreases also decreases over time. The measurement of contact angles below 25° is impossible due to surface heterogeneity; the curves in
Figure 4 do not go below this point because, once a certain contact angle is reached, the droplets rapidly absorb into the substrate.
The droplet base diameter time dependency in
Figure 4 gives an indication of the relative rates of surface spreading and absorption or capillary imbibition into the porous structure of the sponge. The total time over which spreading and absorption occurs reduces as the surfactant concentration increases. Comparison of the data presented in
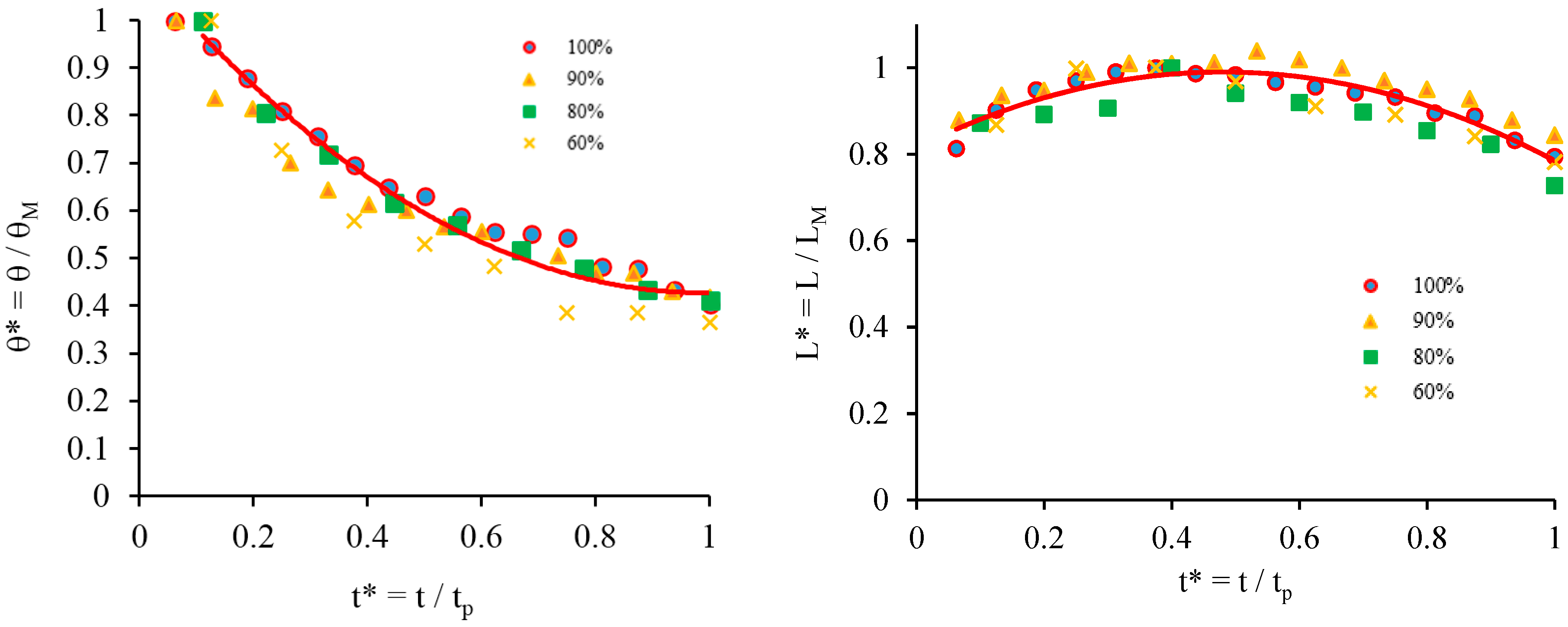
Figure 5 proves that at all concentrations of surfactants considered compete wetting is observed The same dimensionless form was used to present the experimental data on spreading of surfactant solutions over the dish sponge in
Figure 6. The data were converted to a dimensionless form, giving universal profiles for contact angle and spreading diameter such as those shown in
Figure 6, which confirms that the spreading/imbibition of surfactant solutions shows the complete wetting behaviour of the dish-washing sponge.
Despite the dish and audio sponges having significantly different pore sizes and hydrophilicities, the overall wetting characteristics are very similar. The dish sponge raw data (not shown) follows the same trend as in
Figure 4, whereby contact angle reduction and spreading occur faster for lower concentrations of surfactant. The initial contact angle for surfactant droplets is around 95°.
Figure 6 demonstrates that dish sponge data for contact angle and spreading diameter align to universal dimensionless profiles and show complete wetting. Again, it is evident that the rate at which the contact angle is decreasing reduces over time. The dimensionless diameter profile in
Figure 6 shows that the dish sponge encourages significant surface spreading of surfactant solutions before absorption, and that the final stages of droplet imbibition transpired relatively quickly.
The raw data for the car sponge also match the same trend of the contact angle reducing faster for lower concentrations of surfactant solution and show universal complete wetting behaviour if the same dimensionless variables are used. The data on spreading of surfactant solutions over a car sponge (not shown) demonstrate similarly complete wetting behaviour, as shown in
Figure 5 and
Figure 6.
Wet Sponge Results
Following the dry sponge analysis, the sponges were tested whilst being subjected to three different degrees of saturation: 10%, 50%, and 100%, where 100% saturation is 30 g of water absorbed into the porous media. The addition of water to the sponges prior to the deposition of surfactant droplets increases the speed of the wetting and spreading processes significantly. Despite this, the overall trends in contact angle and spreading diameter showed the same behaviour as for the dry sponges described above. For this reason, the figures and graphs from this part of the investigation are not included, but the key findings are summarised by
Table 2. When any quantity of water is used to pre-wet the sponge, it is no longer possible to observe the contact angle or spreading diameter for droplets of pure distilled water such as in
Figure 3. These are very quickly absorbed into the sponge structure. When any amount of surfactant is present in the droplets, it demonstrates complete wetting (
Figure 2).
Table 2 shows that for any degree of saturation the process time (time drop remains on the surface) is significantly reduced; the process time between different degrees of saturation is similar, indicating that increasing the saturation of an already wet sponge does not increase the spreading rate. The maximum droplet base diameter increases from a dry sponge to a wet sponge. The base diameter increases as saturation increases until after 50%; once the sponge is saturated, the base diameter decreases to a value similar to that of a dry sponge.
Initial contact of the droplet decreases as the degree of saturation increases and, in the case of the car sponge, increases as the sponge becomes saturated, whereas for the dish sponge the initial contact angle decreases only slightly and still lies within the error range of a droplet on a dry sponge. All the sponges, wet or dry, display a minimum contact angle after which the droplet rapidly absorbs into the porous media. For the car sponge the contact angle at which this phenomenon occurs decreases as the saturation increases. This is unlike the dish sponge, where this point of rapid absorption occurs at a larger contact angle, indicating that the initial contact angle and complete absorption contact angle are more heavily affected by the material and structural behaviour of the media than by the degree of saturation of the media.
4. Conclusions
When distilled water droplets are deposited on porous sponges, we have a case of partial wetting; when any concentration of commercial surfactant solution is used, on both wet and dry sponges, there is a change to a complete wetting scenario.
The methods used are proven to be effective at characterising the overall wetting and spreading characteristics of the sponges via the generation of universal dimensionless dependences in each case.
Pre-wetting the sponges to any degree increases the speed of spreading and the rate of contact angle reduction. Partially wetting the sponge increases the base diameter, whereas with saturated sponges the base diameter is the same as that of a dry sponge.
All the sponges, no matter the saturation, display a minimum contact angle after which the droplet absorbs rapidly into the porous media.
Initial contact angle and complete absorption contact angle are more dependent on the material and structural behaviour of the media than the degree of saturation of the media.