Bayesian Learning Strategies for Reducing Uncertainty of Decision-Making in Case of Missing Values

Abstract

Background: Liquidity crises pose significant risks to financial stability, and missing data in predictive models increase the uncertainty in decision-making. This study aims to develop a robust Bayesian Model Averaging (BMA) framework using decision trees (DTs) to enhance liquidity crisis prediction under missing data conditions, offering reliable probabilistic estimates and insights into uncertainty. Methods: We propose a BMA framework over DTs, employing Reversible Jump Markov Chain Monte Carlo (RJ MCMC) sampling with a sweeping strategy to mitigate overfitting. Three preprocessing techniques for missing data were evaluated: Cont (treating variables as continuous with missing values labeled by a constant), ContCat (converting variables with missing values to categorical), and Ext (extending features with binary missing-value indicators). Results: The Ext method achieved 100% accuracy on a synthetic dataset and 92.2% on a real-world dataset of 20,000 companies (11% in crisis), outperforming baselines (AUC PRC 0.817 vs. 0.803, p < 0.05). The framework provided interpretable uncertainty estimates and identified key financial indicators driving crisis predictions. Conclusions: The BMA-DT framework with the Ext technique offers a scalable, interpretable solution for handling missing data, improving prediction accuracy and uncertainty estimation in liquidity crisis forecasting, with potential applications in finance, healthcare, and environmental modeling.

1. Introduction

Probabilistic predictions are critically important for reliable decision-making, when practitioners need accurate estimates of uncertainty in the decision model’s outcomes, see, e.g., [1,2,3]. In this scope, a predictive methodology is expected to provide not only accurate probabilistic predictions but also new insights into the data and factors that cause uncertainty, including the presence of missing or incomplete data [4,5,6,7]. The imputation of missing data becomes critically important for making risk-aware decisions as the presence of missing values can cause unpredictable heavy consequences. Imputation techniques can efficiently help practitioners to obtain a comprehensive and reliable understanding of key risk factors within the statistical and Bayesian frameworks; see, e.g., [8,9].

The use of decision tree (DT) models was found to satisfy both these expectations; see, e.g., [7,10,11,12]. DT models recursively partition the data by selecting the feature that optimizes each split along axis-parallel boundaries. Such a greedy search-based strategy enables “natural” feature selection as this approach inherently identifies the most informative features based on the chosen splitting criterion (e.g., information gain). As a result, practitioners obtain information about the features that make significant contributions to the model outcomes. In this context, “model outcomes” refer to the predictions produced by the model rather than the causal effect of hypothetical interventions. Therefore, the key focus is on explainability, identifying influential features in shaping predictions, rather than causal inference.

In the above context, let us define DT models as a set of splitting and terminal nodes. A DT model is binary when its splitting nodes have two possible outcomes, dividing data into two disjoint subsets that fall into the left or right branch. Each split is expected to contain at least a predefined minimum number of data points. All data points that fall into a terminal node are assigned to a class with a probability estimated in the train data [13,14]. DT models are also known to be robust to outliers and missing values in data; see, e.g., [15,16,17]. When missing values appear at random, they can be replaced by surrogate values, using correlated attributes [18,19]. This technique has demonstrated an improvement on some benchmark problems. Alternatively, missing values could be ignored [20,21]. Data points with missing values were treated in three ways: assigned to a new branch, directed to a new category, and indicated by a new feature. In contrast to the surrogate splits, these techniques have been shown to be efficient when missing values are not random and their absence or presence is informative as such. Such features of decision models attract practitioners interested in finding explanatory models within the Bayesian framework. In these cases, the desired class posterior distributions calculated for terminal nodes will bring reliable estimates of uncertainties in a decision, see, e.g., [22,23,24,25,26].

In practice, Bayesian learning can be implemented using Markov Chain Monte Carlo (MCMC) sampling from the posterior distribution [27,28,29,30]. This technique has revealed promising results when applied to real-world problems; see, e.g., [31,32,33]. The MCMC technique has been made feasible for sampling large DT models by using the Reversible Jump (RJ) extension [34]. The RJ MCMC technique making such moves as “birth” and “death” allows the DT models to be induced under specified priors. Exploring the posterior distribution, the RJ MCMC needs to keep the balance between the birth and death moves, under which the desired estimate will be unbiased, see, e.g., [35]. Within the RJ MCMC technique, the proposed moves for which the number of data points falling in one of splitting nodes becomes less than the given number are assigned to be unavailable. Obviously, the priors given on the DT models are dependent on the class boundaries and on the noise level in the data available for training, and it is intuitively clear that the more complex the class boundaries, the larger the models should be. However, in practice, the use of such an intuition without a prior knowledge on the favorite shape of the DT models can lead to inducing over-complicated models, and, as a result, the averaging over such models can produce biased class posterior estimates. Moreover, within the standard RJ MCMC technique suggested for averaging, the required balance between DT models of various sizes cannot be kept. This may happen because of overfitting of Bayesian models, see, e.g., [36]. Another reason is that the RJ MCMC technique of averaging over DT models assigns some moves as unavailable when such moves cannot provide a minimum number of data points allowed in terminal nodes [31].

When prior information on the preferred shape of DT models is unavailable, the Bayesian technique with a sweeping strategy has revealed a better performance [37]. Within this strategy, the prior given on the number of DT nodes is defined implicitly and depends on the given number of data points allowed to be at the DT splits. Thus, the sweeping strategy gives more chances to induce the DT model consisting of a near-optimal number of splitting nodes required to provide the best generalization. In the Bayesian framework, the treatment of missing values using a technique such as surrogate splits [18] cannot be implemented on real-world-scale data without a significant increase in computational cost. In our previous work [38], we showed that missing values can be efficiently treated within the Bayesian approach if they are assigned to a separate category for each data partition.

Let us consider a dataset with n statistical units (e.g., observations or samples) denoted as $u_i$, where $i=1,\dots ,n$, and m variables denoted as $X_j$, where $j=1,\dots ,m$. For each unit $u_i$, the value of the variable $X_j$ is denoted as $x_{i,j}$. If $x_{i,j}$ is missing, we define a missingness indicator $M_{i,j}$, where $M_{i,j}=1\mathrm{if}{x}_{i,j}\mathrm{is}\mathrm{missing},0\mathrm{otherwise}$. To handle missing values, we replace $x_{i,j}$ with a constant ${\mu }_j$, chosen such that ${\mu }_j\gg sup\left(X_j\right)$, where $sup\left(X_j\right)$ represents the supremum (or maximum for finite datasets) of the observed values of $X_j$. This ensures that ${\mu }_j$ is distinct from the observed data range of $X_j$. In the DT model, missing values (where $M_{i,j}=1$ and $x_{i,j}={\mu }_j$) are treated as a separate category during tree construction. This approach assumes that missingness, represented by the distinct value ${\mu }_j$, may correlate with uncertainty in the model outcomes. Consequently, the DT can create terminal nodes (leaf nodes) that group missing values, enabling the model to capture potential patterns related to missingness. This motivated us to propose a method that can explicitly define and attribute missing values, which will provide reliable predictions. In Section 3.2, we test this approach on the liquidity crisis benchmark.

There are other well-studied approaches known from the literature. For example, there are techniques [39] based on the imputation of missing values. In particular, such an imputation can be made efficiently using a nonlinear regression model learned from a given dataset. These techniques typically require a priori knowledge of imputation models. When such knowledge is unavailable, these techniques require the use of model-optimization strategies, such as a greed-based search. A similar search strategy [40] has been used to optimize kernels for Support Vector Machine (SVM) models designed to predict companies at risk of financial problems. SVM models can significantly extend an input space defined by an original variable set and can thus efficiently treat the uncertainty caused by missing values. It has been reported that an SVM model with an optimized Radial Basis Function kernel has outperformed the conventional Machine Learning methods in terms of prediction accuracy on real-world benchmark data.

The above two approaches can be implemented within a Bayesian framework capable of delivering predictive posterior probabilities that allow practitioners to make reliable risk-aware decisions. However, such an implementation is beyond our research scope and so will not be studied here. Instead, we focus on comparing the accuracy of estimating posterior probabilities, which can be achieved using different approaches within a BMA framework, adopted to handle the uncertainty caused by missing data [39,40,41]. In general cases, however, BMA is known to outperform the other Bayesian strategies; see, e.g., [25,26]. The analysis of these approaches provides us with new insights into the problem that we attempt to resolve within a Bayesian framework. The remainder of the paper is organized as follows. In the next section, we outline the main differences in existing approaches known from the related literature. Then, we describe the proposed Bayesian method, provide details of experiments, and discuss results obtained on a synthetic problem, as well as on the crisis liquidity data. Finally, we analyze the results of experiments and make conclusions on how the proposed Bayesian framework will benefit practitioners making decisions in the presence of uncertainty caused by missing values.

2. Method

2.1. Bayesian Framework

The process of Bayesian averaging across decision tree (DT) models is described as follows: Initially, the parameters $\mathrm{\Theta }$ of the DT model are determined from the labeled dataset $\mathbf{D}$, which is characterized by a m-dimensional input vector x. The output of the DT model is indicated as $y\in \{1,\dots ,C\}$, where $C\ge 2$ represents the number of classes to which the model categorizes any given input x. For models $M_1,\dots ,M_L$ with respective parameters ${\mathrm{\Theta }}_1,\dots ,{\mathrm{\Theta }}_L$, the goal is to compute the predictive distribution by integrating the vector of combined parameters $\mathrm{\Theta }=({\mathrm{\Theta }}_1,\dots ,{\mathrm{\Theta }}_L)$:

$$p\left(y\right|x,\mathbf{D})={\int }_{\mathrm{\Theta }}p\left(y\right|x,\mathrm{\Theta })p(\mathrm{\Theta }|\mathbf{D})\mathrm{d}\mathrm{\Theta }=\sum _{i=1}^{L}p\left(y\right|x,{\mathrm{\Theta }}_i)p\left({\mathrm{\Theta }}_i\right|M_i,\mathbf{D})p\left(M_i\right),$$

where $p\left(M_i\right)$ the prior distribution of the model $M_i$, $p\left({\mathrm{\Theta }}_i\right|M_i,\mathbf{D})$ is the posterior density of ${\mathrm{\Theta }}_i$ given model $M_i$ and data $\mathbf{D}$, and $p\left(y\right|x,{\mathrm{\Theta }}_i)$ is the posterior predictive density given the parameters ${\mathrm{\Theta }}_i$. The equation given above can be dealt with effectively when the distribution $p(\mathrm{\Theta }|\mathbf{D})$ is known. Typically, this distribution is estimated by extracting N random samples ${\mathrm{\Theta }}^{\left(1\right)},\dots ,{\mathrm{\Theta }}^{\left(N\right)}$ from the posterior distribution $p(\mathrm{\Theta }|\mathbf{D})$:

$$p\left(y\right|x,\mathbf{D})\approx \sum _{i=1}^{N}p\left(y\right|x,{\mathrm{\Theta }}^{\left(i\right)},\mathbf{D})p\left({\mathrm{\Theta }}^{\left(i\right)}\right|\mathbf{D})={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}p\left(y\right|x,{\mathrm{\Theta }}^{\left(i\right)},\mathbf{D}).$$

The preferred approximation is obtained when a Markov chain transforms into a random sequence that has a stationary probability distribution. Once this condition is met, random samples can be used to approximate the target predictive density.

2.2. Sampling of Decision Tree Models

A binary decision tree (DT) with k terminal nodes comprises $(k-1)$ internal splitting nodes, denoted $s_i$ where $i=1,\dots ,(k-1)$. Each node $s_i$ has specific parameters: its position in the DT architecture, $s_i^p$, where $p=1,\dots ,(k-1)$; an input variable $s_i^v$, where v is within $\{1,\dots ,m\}$; and a threshold $s_i^q$, such that q falls between $(min\left(x_v\right),max\left(x_v\right))$. The node $s_i$ evaluates the vth input variable against the threshold q, channeling the input x to the left branch if $x_v<q$, otherwise directing it to the right. The terminal node $t_i$ classifies the input x into a class c with a probability $P_i^c$ for each $i=1,\dots ,k$. DT architectures can be captured by a parameter vector $\mathrm{\Theta }$, split into two segments. The first segment includes node-related parameters: positions $s_i^p$, variables $s_i^v$, and thresholds $s_i^q$ for $i=1,\dots ,(k-1)$. The second consists of probabilities $P_i^c$ for class c where $c=1,\dots ,C$ for each terminal node i, from $i=1$ to k. A binary DT, characterized by nodes that bifurcate the data into two partitions, accommodates $S_k$ potential configurations, counted as a Catalan number, which scales exponentially with k. Therefore, even with small k, $S_k$ becomes large. In particular, manageable-size DT models offer greater clarity for users. The complexity of the model corresponds to the number of split nodes, k. Overly complex DT models present interpretability challenges in practice, and Bayesian averaging over such models may result in biased posterior estimations.

The dimensions of decision tree (DT) models are influenced by the number of data points, $p_{min}$, that are allowed at the terminal nodes. A smaller $p_{min}$ leads to larger DT models, whereas a larger $p_{min}$ results in smaller models. Typically, prior knowledge about the size of DT models is lacking, which requires an empirical approach to determine an appropriate $p_{min}$. In applied scenarios, the size of the DT models might be specified as a range. This scenario involves exploring models with high posterior parameter density $\mathrm{\Theta }$ using the mentioned equation. Often, prior knowledge on the significance of the input variables $x_1,\dots ,x_m$, is absent. In these situations, we can randomly select a variable v for node $s_i$ from the discrete uniform distribution $v\sim U(1,m)$. Similarly, we can generate the threshold q from the discrete uniform distribution, $q\sim U(min\left(x_v\right),max\left(x_v\right))$. According to [31], these priors sufficiently facilitate the construction and exploration of large DT models with varying configurations using the RJ MCMC method. Consequently, MCMC is anticipated to effectively explore regions of interest for all DT size configurations k, with exploration probabilities proportional to $S_k$. This methodological framework is effectively applied through birth, death, change-split, and change-rule moves within the Metropolis–Hastings (MH) sampler, the primary element of MCMC.

The first two moves, concerning birth and death, were introduced to adjust the number of nodes in a DT model (or the dimensionality of the model parameter vector $\mathrm{\Theta }$) in a reversible way. The third and fourth moves, namely, the change split and the change rule, focused on adjusting the parameters $\mathrm{\Theta }$ while maintaining the current dimensionality. The split change replaces a variable v at a specific DT node $s_i$, while the change rule modifies a threshold q at the node $s_i$. The aim of the change-split moves is to create significant modifications in the model parameters, thereby potentially enhancing the likelihood of sampling from key posterior areas. These moves are designed to disrupt prolonged sequences of posterior samples derived from localized areas of interest. However, rule changes are intended to make minor parameter adjustments to allow the MCMC to thoroughly explore the surrounding area. These rule changes are implemented more frequently than the other moves.

The MH sampler is initiated with a decision tree (DT) containing a single splitting node, where the parameter $\mathrm{\Theta }$ is chosen based on predefined priors. Performing the specified moves, the sampler seeks to expand the DT model to an appropriate size by aligning its parameters $\mathrm{\Theta }$ with the data. The fitness or likelihood of the DT models progressively increases until it exhibits oscillations around a certain value. This period, known as burn-in, must be long enough to ensure that the Markov chain reaches a stationary distribution. Once stationarity is achieved, samples from the posterior distribution are acquired to approximate the intended predictive distribution, a phase called post-burn. The moves are performed according to the specified proposal probabilities, which vary on the basis of the classification problem’s complexity: more complex problems necessitate larger DT models. To facilitate the growth of these models, the proposed probabilities for death and birth moves are set to higher values. Typically, there is no precise guidance on determining the optimal parameters for the MH sampler, and these should be established through empirical methods [31,35].

2.3. RJ-MCMC Details: Priors, Proposals, and Acceptance Ratios

2.3.1. Notation and Likelihood

A binary decision tree T has $k=\left|L\right(T\left)\right|$ terminal nodes (leaf) and $\left|I\right(T\left)\right|=k-1$ splitting nodes. Each internal node $\eta \in I\left(T\right)$ carries a split rule $(v_{\eta },q_{\eta })$ with feature index $v_{\eta }\in \{1,\dots ,m\}$ and threshold $q_{\eta }$. For classification with C classes, the Dirichlet–multinomial marginal likelihood is

$$p(D\mid T)=\prod _{\ell \in L\left(T\right)}{\displaystyle \frac{\mathrm{\Gamma }\left({\alpha }_0\right)}{\Gamma ({\alpha }_0+n_{\ell })}}\prod _{c=1}^C{\displaystyle \frac{\mathrm{\Gamma }({\alpha }_c+n_{\ell c})}{\Gamma \left({\alpha }_c\right)}},{\alpha }_0=\sum _{c=1}^C{\alpha }_c.$$

(1)

2.3.2. Priors

Tree size prior:

$$p\left(T\right)\propto p\left(k\right)·{\displaystyle \frac{1}{S_k}},p\left(k\right)\propto exp(-\gamma (k-1)).$$

(2)

Split priors:

$$v\sim \mathrm{Unif}\{1,\dots ,m\},q\sim \mathrm{Unif}(a,b).$$

(3)

Leaf class probabilities: ${\pi }_{\ell }\sim \mathrm{Dir}\left(\alpha \right)$.

2.3.3. MH Acceptance Rule

For a move $T\to T^{\prime }$,

$$\alpha (T\to T^{\prime })=min\left\{1,{\displaystyle \frac{p(D\mid T^{\prime })p\left(T^{\prime }\right)}{p(D\mid T)p\left(T\right)}}·{\displaystyle \frac{q(T\mid T^{\prime })}{q(T^{\prime }\mid T)}}·\left|J\right|\right\}.$$

(4)

Here, $J=1$ (identity mapping).

2.3.4. Birth Move

$$\begin{array}{cc}\hfill q_{\mathrm{fwd}}& =p_{\mathrm{birth}}·{\displaystyle \frac{1}{k}}·{\displaystyle \frac{1}{m}}·g_j\left(q\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill q_{\mathrm{rev}}& =p_{\mathrm{death}}·{\displaystyle \frac{1}{r\left(T^{\prime }\right)}},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\alpha }_{\mathrm{birth}}& =min\left\{1,{\displaystyle \frac{p(D\mid T^{\prime })p\left(T^{\prime }\right)}{p(D\mid T)p\left(T\right)}}·{\displaystyle \frac{p_{\mathrm{death}}}{p_{\mathrm{birth}}}}·{\displaystyle \frac{k}{r\left(T^{\prime }\right)}}·m·{\displaystyle \frac{1}{g_j\left(q\right)}}\right\}.\hfill \end{array}$$

(7)

2.3.5. Death Move

$$\begin{array}{cc}\hfill q_{\mathrm{fwd}}& =p_{\mathrm{death}}·{\displaystyle \frac{1}{r\left(T\right)}},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill q_{\mathrm{rev}}& =p_{\mathrm{birth}}·{\displaystyle \frac{1}{k-1}}·{\displaystyle \frac{1}{m}}·g_j\left(q\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\alpha }_{\mathrm{death}}& =min\left\{1,{\displaystyle \frac{p(D\mid T^{\prime })p\left(T^{\prime }\right)}{p(D\mid T)p\left(T\right)}}·{\displaystyle \frac{p_{\mathrm{birth}}}{p_{\mathrm{death}}}}·{\displaystyle \frac{r\left(T\right)}{k-1}}·{\displaystyle \frac{1}{m}}·g_j\left(q\right)\right\}.\hfill \end{array}$$

(10)

2.3.6. Change-Split

$${\alpha }_{\mathrm{chg}\text{-}\mathrm{split}}=min\left\{1,{\displaystyle \frac{p(D\mid T^{\prime })p\left(T^{\prime }\right)}{p(D\mid T)p\left(T\right)}}·{\displaystyle \frac{g\left(q\right)}{g^{\prime }\left(q^{\prime }\right)}}\right\}.$$

(11)

2.3.7. Change-Rule

$${\alpha }_{\mathrm{chg}\text{-}\mathrm{rule}}=min\left\{1,{\displaystyle \frac{p(D\mid T^{\prime })p\left(T^{\prime }\right)}{p(D\mid T)p\left(T\right)}}·{\displaystyle \frac{{\varphi }_{{\mathcal{N}}^{\prime }}(q;q^{\prime },{\sigma }^2, [a,b])}{{\varphi }_{{\mathcal{N}}^{\prime }}(q^{\prime };q,{\sigma }^2, [a,b])}}\right\}.$$

(12)

2.3.8. Sweeping Strategy

Invalid proposals with child size $<p_{min}$ are rejected; if one invalid child pair shares a parent, collapse to death move. Otherwise, reject.

Figure 1 illustrates the workflow of the RJ-MCMC sampler with the sweeping strategy. The flow chart begins at the top to initialize the decision tree T as a single root split or a stump consistent with priors and observed data ranges. The algorithm then runs the sampling loop for N iterations, where at each iteration a move type, Birth, Death, Change-Split, or Change-Rule, is drawn with probabilities $p_{\mathrm{birth}}$, $p_{\mathrm{death}}$, and $p_{\mathrm{chg}\text{-}\mathrm{rule}}$.

• Birth move: A terminal node j is uniformly chosen, a split variable v and threshold q are sampled from their priors, and the proposed split is accepted with probability ${\alpha }_{\mathrm{birth}}$.
• Death move: A prunable internal node is chosen uniformly, its children are collapsed into a single leaf, and the resulting tree is accepted with probability $alph{a}_{\mathrm{death}}$ (Equation (6)).
• Change-Split move: A split node is selected, a new $(v,q)$ is drawn, and the resulting tree is accepted with probability ${\alpha }_{\mathrm{chg}\text{-}\mathrm{split}}$.
• Change-Rule move: A threshold $q^{\prime }$ is drawn from a truncated Gaussian around the current threshold, and the move is accepted with probability ${\alpha }_{\mathrm{chg}-\mathrm{rule}}$.

At each stage, the sweeping strategy enforces the minimum leaf size $p_{min}$. If a proposed move produces one or more leaves with fewer than $p_{min}$ observations, the sampler does either one of the following:

1.

Collapses the parent node and treats the operation as a death move (if exactly one unavailable pair of leaves shares a parent);

2.

Rejects the move to maintain detailed balance (if multiple unavailable leaves appear).

After each accepted or rejected move, the current tree configuration may be accepted according to the sampling rate and stored to approximate the posterior distribution over trees. This process iterates until the post-burn-in phase is complete, producing a sample of decision tree structures and parameters for Bayesian model averaging.

2.4. Sampling of Large Decision Tree Models

In constructing a DT model, the MH sampler initiates birth moves, with almost every move enhancing the likelihood of the model. These moves are accepted, which causes the DT model to expand quickly. The growth of the model is sustained as long as the number of data points in its terminal nodes exceeds $p_{min}$, and the likelihood of a suggested model remains satisfactory. During this time, the DT model’s dimensionality escalates rapidly, hindering the sampler’s ability to thoroughly investigate the posterior in each dimension. Consequently, it is improbable that samples will be taken from the regions with the highest posterior density [31]. Typically, the growth of DT models is overseen and modelers can curtail excessive expansion by raising $p_{min}$ and decreasing the probability of proposal for birth moves. The adverse effects of rapid growth of the DT model have been alleviated through a restart strategy [35]. This strategy allows a DT model to expand within a limited time frame across several runs. The average of all models developed in these runs affords improved approximation accuracy, provided that the growth duration and number of runs are optimally selected. A comparable approach has been used to limit the growth of the DT model [31]. Growth is constrained to a specific range, allowing the MH sampler to explore the parameter space of the model more thoroughly. Both strategies require additional configurations for the MH sampler, which must be determined experimentally.

An alternative to limiting strategies is to adapt the RJ MCMC method to minimize the number of replications of the samples from the posterior distribution. A detailed approach has been suggested to decrease the count of unavailable moves. When executing a change-split move, the sampler allocates a new variable $x_v,v\sim U(1,m),$ along with a threshold q:

$$q\sim U(a,b),$$

(13)

where $U(a,b)$ represents a uniform distribution in the interval where $a=min\left(x_{v,j}\right)$ and $b=max\left(x_{v,j}\right)$, determined by the data points $N_p$ within the selected node $j=1,\dots ,N_p$.

When implementing change-rule moves, a new threshold $q^{\prime }$ is selected from a constrained Gaussian distribution, characterized by a mean of q and a specified variance of the proposal ${\sigma }^2$ within the interval $(a,b)$.

The suggested modification allows for the possibility that one or more terminal nodes within a decision tree model might have fewer data points than $p_{min}$. In cases where these terminal nodes share a common parent node, they merge into a single terminal node, and the Metropolis–Hastings (MH) sampler considers this a death move. However, if such terminal nodes have distinct parent nodes, the algorithm deems the proposal unavailable to maintain the reversibility of the Markov chain. Similarly to a change move, a birth move involves assigning a new splitting node with parameters sampled from the given prior. The splitting variable $x_v$ is selected from a uniform distribution, $v\sim U(1,m)$, and a new threshold q is determined as outlined in Equation (13). In our experiments, an MH sampler that uses this strategy for change moves proposes fewer unavailable moves, which in turn leads to fewer acceptances of the replicated current parameter $\mathrm{\Theta }$. Based on this observation, we assume that having fewer replications collected throughout the MCMC simulation will enhance the diversity of model mixing. Algorithm 1 and the Algorithm 2 implement the sweeping strategy as follows.

Algorithm 1 Birth Move in RJ MCMC

1: Input: Current DT model, $p_{min}$, feature set m 2: Output: Updated DT model or rejection 3: Randomly select a terminal node $i\sim U(1,k)$ 4: Count data points p in node i 5: if $p>2p_{min}$then 6:     Draw splitting feature $v\sim U(1,m)$ 7:     Draw threshold $q\sim U(min\left(x_v\right),max\left(x_v\right))$ 8:     Split node i using $(v,q)$, creating child nodes with $p_1$ and $p_2$ points 9:     if $p_1\ge p_{min}$ and $p_2\ge p_{min}$ then 10:         Evaluate proposal acceptance via MH ratio 11:         if accepted then 12:            return Updated DT 13:         else 14:            return Rejection 15:         end if 16:     else 17:         return Rejection (unavailable split) 18:     end if 19: else 20:     return Rejection (insufficient data) 21: end if

Algorithm 2 Change Move in RJ MCMC

1: Input: Current DT model, $p_{min}$, feature set m, proposal variance ${\sigma }^2$ 2: Output: Updated DT model or rejection 3: Randomly select a splitting node $i\sim U(1,k-1)$ 4: Read current $(v,q)$ of node i 5: With probability 0.5: 6: ▹ Change-split variant 7: Draw new feature $v^{\prime }\sim U(1,m)$ 8: Set $q^{\prime }\sim U(min\left(x_{v^{\prime }}\right),max\left(x_{v^{\prime }}\right))$ 9: Else: 10: ▹ Change-rule variant 11: Draw $q^{\prime }\sim {\mathcal{N}}^{\prime }(q,{\sigma }^2,min\left(x_v\right),max\left(x_v\right))$ (truncated normal) 12: Apply proposed $(v^{\prime },q^{\prime })$ to node i 13: Count terminal nodes with $p_i<p_{min}$ as $n_0={\sum }_{j=1}^k\mathbb{I}(p_j<p_{min})$ 14: if$n_0=1$then 15:     Perform death move (collapse unavailable subtree) 16: else if$n_0>1$then 17:     return Rejection (irreversible configuration) 18: else 19:     Evaluate proposal acceptance via MH ratio 20:     if accepted then 21:         return Updated DT 22:     else 23:         return Rejection 24:     end if 25: end if

Here, $n_0={\sum }_i^{k}I(p_i\le p_{min})$, where $I(·)$ is the indicator function: $I=1$ if $p_i<p_{min}$, and 0 otherwise.

2.5. Experimental Settings

The settings for the Metropolis–Hastings algorithm include the following sampler parameters:

1.

Proposal probabilities for birth, death, change-split, and change-rule moves, $Pr$.

2.

Proposal distribution, a Gaussian distribution with zero mean and standard deviation s.

3.

Numbers of burn-in and post burn-in samples, $nb$ and $np$, respectively.

4.

Sampling rate of the Markov chain, $sr$.

5.

Minimal number of data points allowed in terminal nodes, $p_{min}$.

Parameters $Pr$, s, and $nb$ played crucial roles in influencing the convergence of the Markov chain. To ensure satisfactory convergence, we explored multiple variants of these parameters. During the post-burn phase, the sampling rate $sr$ was implemented to increase the independence of the samples obtained from the Markov chain. In the subsequent stage, the settings for s and $p_{min}$ were optimized to allow the MCMC algorithm to effectively sample the posterior distribution of $\mathrm{\Theta }$ while maintaining the DT models at a manageable size. An acceptance rate within 0.25 to 0.6 facilitates seamless sampling. This two-stage approach allowed us to narrow the potential combinations of settings down to a practical number.

3. Results

This section describes our experimental results achieved with the proposed Bayesian DT method. The experiments were first conducted on a synthetic eXclusive OR (XOR) problem and then on the benchmark problem of predicting the probability of a company liquidity crisis [39].

3.1. A Synthetic Benchmark

The data for the synthetic problem were generated by a function $y=sign\left(x_1{x}_2\right)$ of the variables $x_1$ and $x_2$, which are drawn from a uniform distribution between $-0.5$ and $0.5$, $x_1,x_2\sim U(-0.5,0.5)$. The third variable $x_3\sim N(0,0.2)$ was added to the data as a dummy variable to explore the ability of the proposed method to select relevant features. The total number of data instances generated was 1000.

In experiments with these data, we did not use prior information on the DT models. We specified only a minimal number of data points, $p_{min}$, which are allowed to be in DT splits. The probabilities of proposal for death, birth, change split, and change rule were set to $0.1, 0.1, 0.2$, and $0.6$, respectively. The numbers of burn-in and post-burn-in samples were set to 2000. The sampling rate was 7. The variance of the proposal was set to $2.0$. Performance was evaluated within the 3-fold cross-validation technique. Using these settings, the performance of the proposed sampler was ideal 100.0% on the synthetic benchmark. Each eighth proposal, or $12\%$ of their total number, was accepted. The average size of the DT models, or the number of their splitting nodes, was $3.4$. 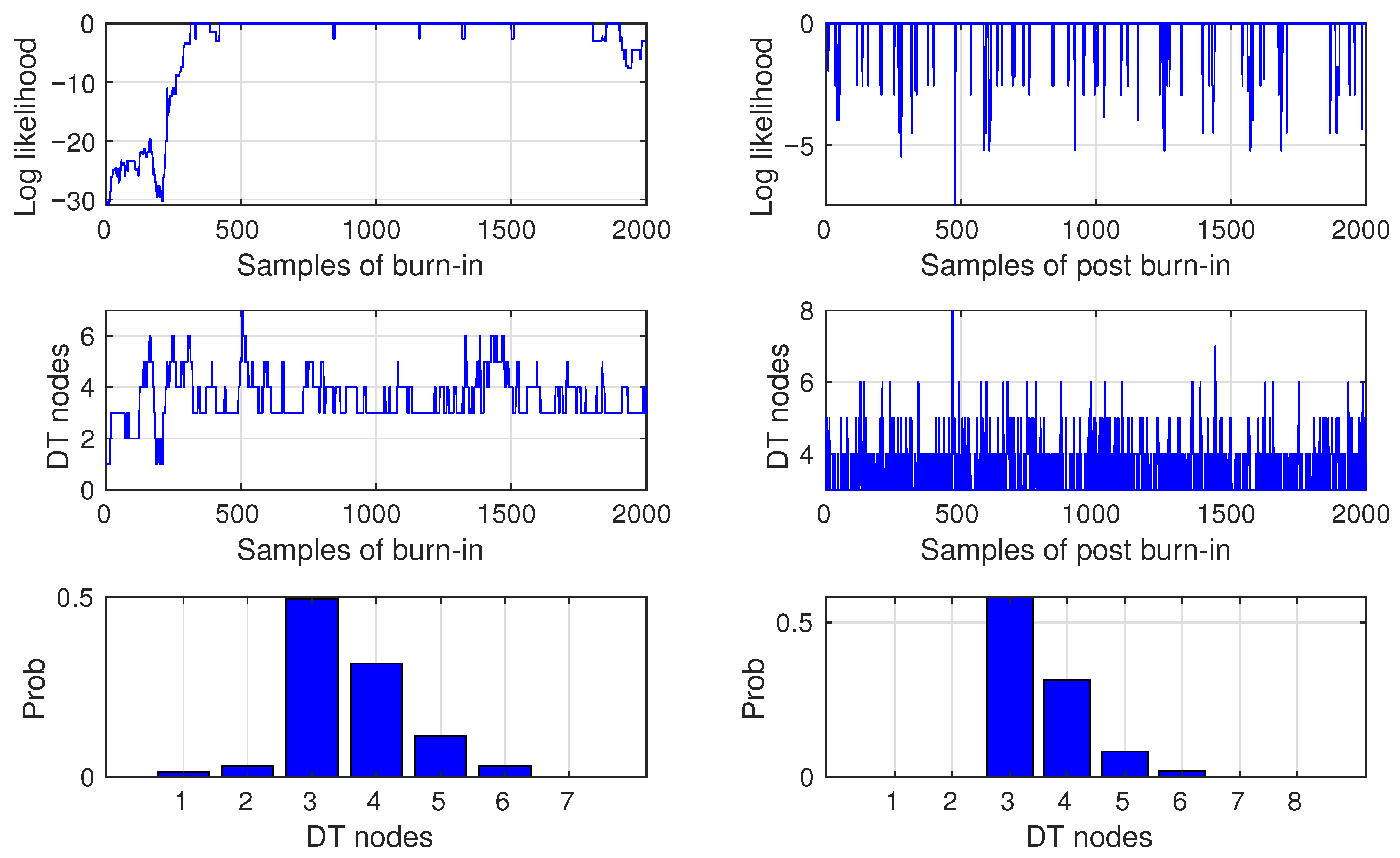Figure 2 shows the log-likelihood samples, the number of DT nodes, and the densities of the DT nodes for the burn-in and post-burn-in phases. In the top-left plot, we see that the Markov chain started at a log likelihood of $-30$ and then very quickly (during a ca 300 samples) converged to a stationary value close to the maximum, that is, a zero log likelihood. During the post-burn-in, the log-likelihood values slightly oscillate around the maximum. Observing the size distributions of the DT, we can see that the true DT model, which consists of three splitting nodes and variables $x_1$ and $x_2$, was drawn most frequently during both phases. This is evidence of the ability of the proposed method to discover true models in the data.

3.2. Liquidity Crisis Benchmark

The data used in our experiments represent 20,000 companies whose financial profiles are described by 26 variables. Almost $11\%$ of the companies were in a liquidity crisis. The financial profiles of some companies include one or more missing values; such missing values were found in 14 variables. These data were used in our experiments to detect the liquidity crisis by analyzing the financial profile of a company and estimating the uncertainty in predictions with the proposed method. To deal with missing values, we applied three different techniques that allowed us to identify which of them provides better performance in terms of accuracy and uncertainty of predictions. In our experiments, the proposed method was run with the following settings. The numbers of burn-in and post-burn-in samples were set to $100,000$ and 5000, respectively. Similarly to previous experiments, the proposal probabilities were set to $0.1, 0.1, 0.2$, and $0.6$, respectively, for the moves of birth, death, split changes, and change rule, respectively.

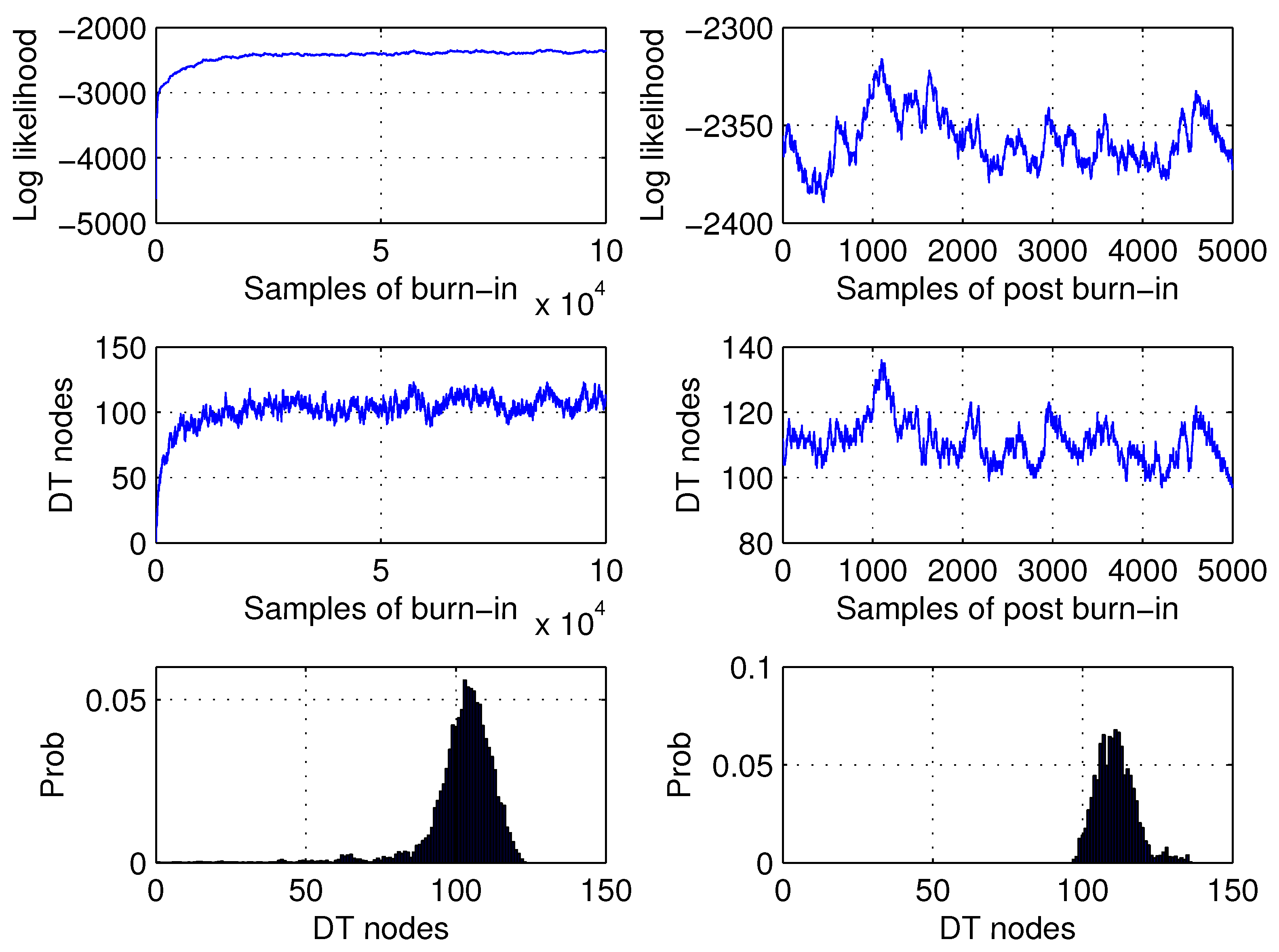
The best classification accuracy was achieved with $p_{min}=20$. The average size of the DT models was 115. Figure 3 shows the log-likelihood samples, the number of DT nodes, and the densities of the DT nodes for the burn-in and post-burn-in phases. The three preprocessing techniques, Cont, ContCat, and Ext, are proposed to handle missing values as follows. The first technique treats all 26 predictors as continuous, whereas missing values are labeled with a large constant, as discussed in Section 1. In contrast, the second technique is assumed to convert the 14 predictors that contain missing values into categorical variables. This allowed us to label the missing values as a distinct category. The third technique extends the original set of 26 predictors with 14 binary variables assumed to indicate the presence or absence of a missing value. This approach increases the number of variables to 40.

The experiments within the Bayesian framework were run with each of these techniques. The best classification accuracy was achieved for the third technique that provided $92.2\%$. The improvement compared to the other two techniques is statistically significant according to the McNemar test with $p<0.05$ [40,42]. The performance of these techniques was also compared within the standard Receiver Operating Characteristic (ROC) metric that provides values of the Area Under Curve (AUC). 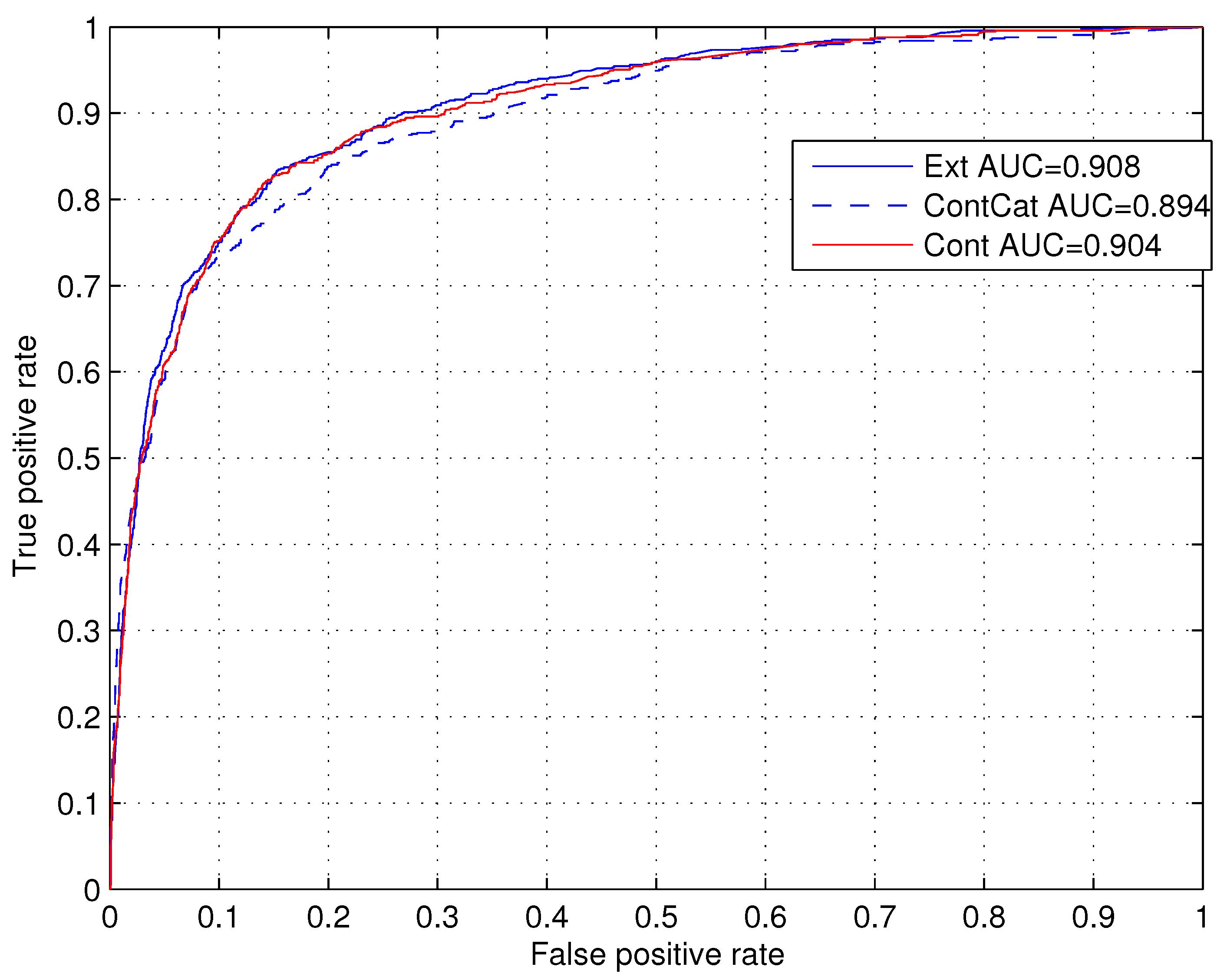Figure 4 shows the ROC curves and the AUC values calculated for these three techniques. We can see that the technique Ext that uses the extended set of attributes provides a better performance in terms of AUC, which is $0.908$. The technique Cont, which treats all variables as continuous, provides the AUC value $0.904$. The technique ContCat, which transforms missing values into category, provides the smallest AUC value of $0.894$. Additionally, we compare the Cont and Ext methods using ROC and precision recall curves (PRCs), as well as the Brier score for probability estimates, see, e.g., [43]. In terms of these metrics, the proposed Ext method outperforms the Cat technique. The tests carried out show that the improvement is statistically significant.

Table 1. AUC ROC and AUC PRC values along with significance p-values calculated for the existing (Cont) and proposed (Ext) Bayesian strategies.

	Cont	Ext	p-Value
AUC ROC	0.904	0.908	$9.507\times {10}^{-16}$
AUC PRC	0.603	0.617	$9.816\times {10}^{-17}$
Brier	$6.212\times {10}^{-2}$	$6.105\times {10}^{-2}$	$2.802\times {10}^{-11}$

provides the results of these tests.

Table 2. Recall, precision, $max\left(F_1\right)$, specificity, and accuracy over thresholds Q for the existing (Cont)) and proposed (Ext) techniques.

	$\mathit{Recall}$		$\mathit{Precision}$		$\mathit{max}\left({\mathit{F}}_1\right)$		$\mathit{Specificity}$		$\mathit{Acc}$
$\mathbf{Q}$	Cont	Ext	Cont	Ext	Cont	Ext	Cont	Ext	Cont	Ext
0.400	0.587	0.595	0.623	0.655	0.604	0.623	0.955	0.960	0.914	0.919
0.410	0.579	0.593	0.628	0.660	0.602	0.625	0.957	0.961	0.914	0.920

shows how recall, precision, $F_1$, specificity, and accuracy depend on the decision thresholds Q in both the Cat and the proposed Ext methods. By definition, the $F_1$-score shows a balance between precision and recall scores of a model. We can observe that the $F_1$ values calculated for the Ext technique are larger than those calculated for the opposite approach for almost all values Q. Specifically, for the Cont technique, the maximum F1-score is 0.604 at the thresholds $Q=0.400$ and $Q=0.410$. For the proposed Ext technique, the maximum F1-score is 0.625 at the thresholds $Q=0.410$, $Q=0.420$, and $Q=0.430$.

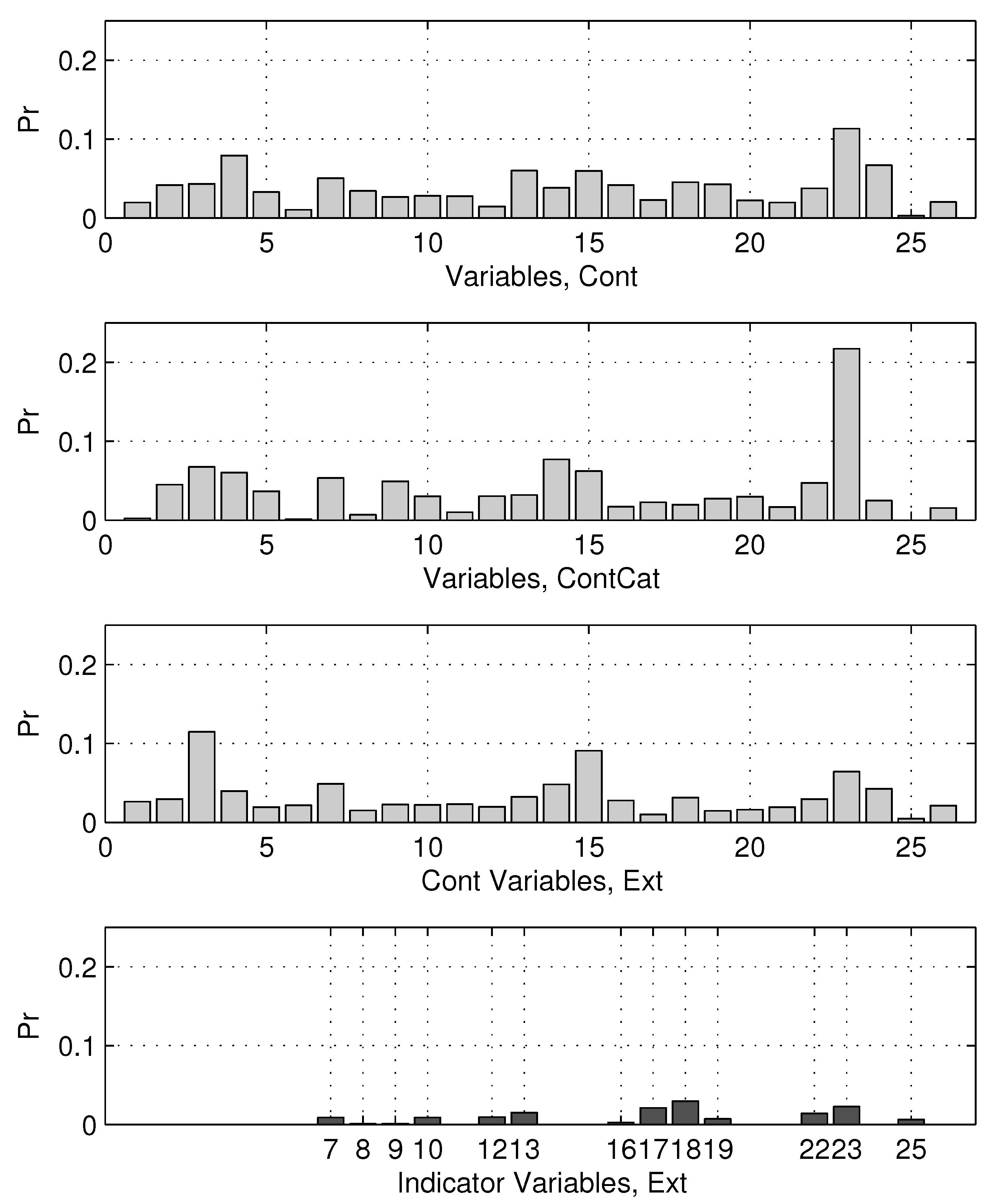
Testing Bayesian strategies for the treatment of missing values, we expect that independent variables, which represent data, contribute to the model outcomes differently. The variable importance, in our case, can be estimated as frequencies of their use in models, which were collected during the post-burn-in phase. Using this assumption, the importance of the variable can be estimated and compared for the three techniques Cont, ContCat, and Ext. Figure 5 shows the importance values calculated for these techniques. In particular, the bottom plot of this figure shows the importance of the 14 binary variables generated within the proposed Ext method.

Performances have also been compared using the standard ROC technique, providing values of the Area Under Curve (AUC). The AUC values were calculated for all three techniques. Figure 4 shows the calculated values for the Cont and Ext techniques. We can see that the technique Ext that uses the extended set of attributes provides a better performance, which in terms of AUC is $0.908$. The technique Cont, which treats all variables as continuous, provides an AUC of $0.904$. The technique ContCat, which transforms missing values into a category, provides the smallest AUC of $0.894$. To examine and compare the calibration of models provided by the Cat and proposed Ext methods, we employed the Hosmer–Lemeshow (HL) test, which is typically used for estimating the quality of models; see, e.g., [43]. HL tests are often enhanced by using random simulation. In our experiments, the Cat technique shows a HL-test value 31.1 and $p=0.039$, while the proposed Ext method shows a significantly better calibration 22.8 with $p=0.24$. 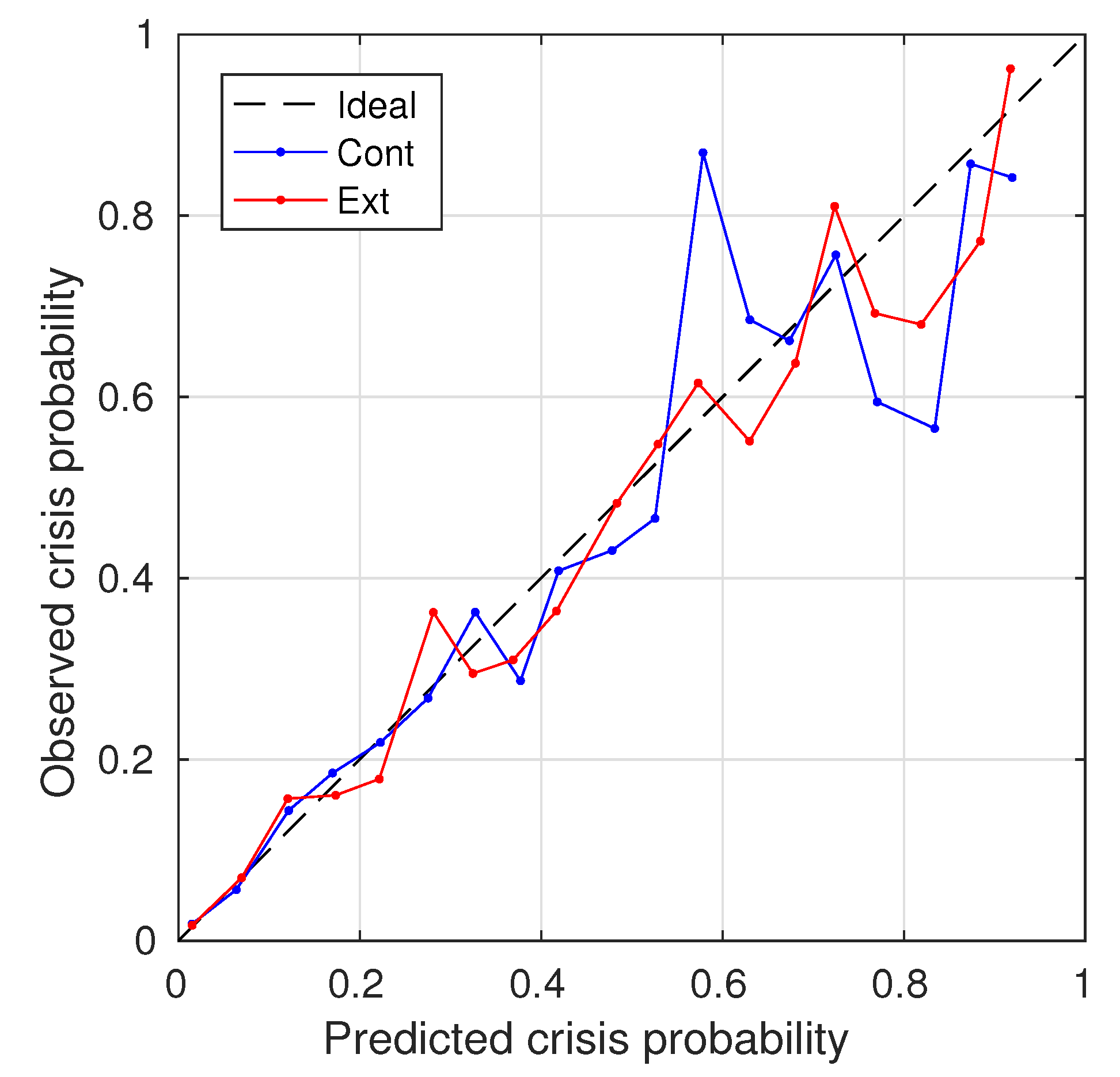Figure 6 plots the calibration curves calculated for these methods. 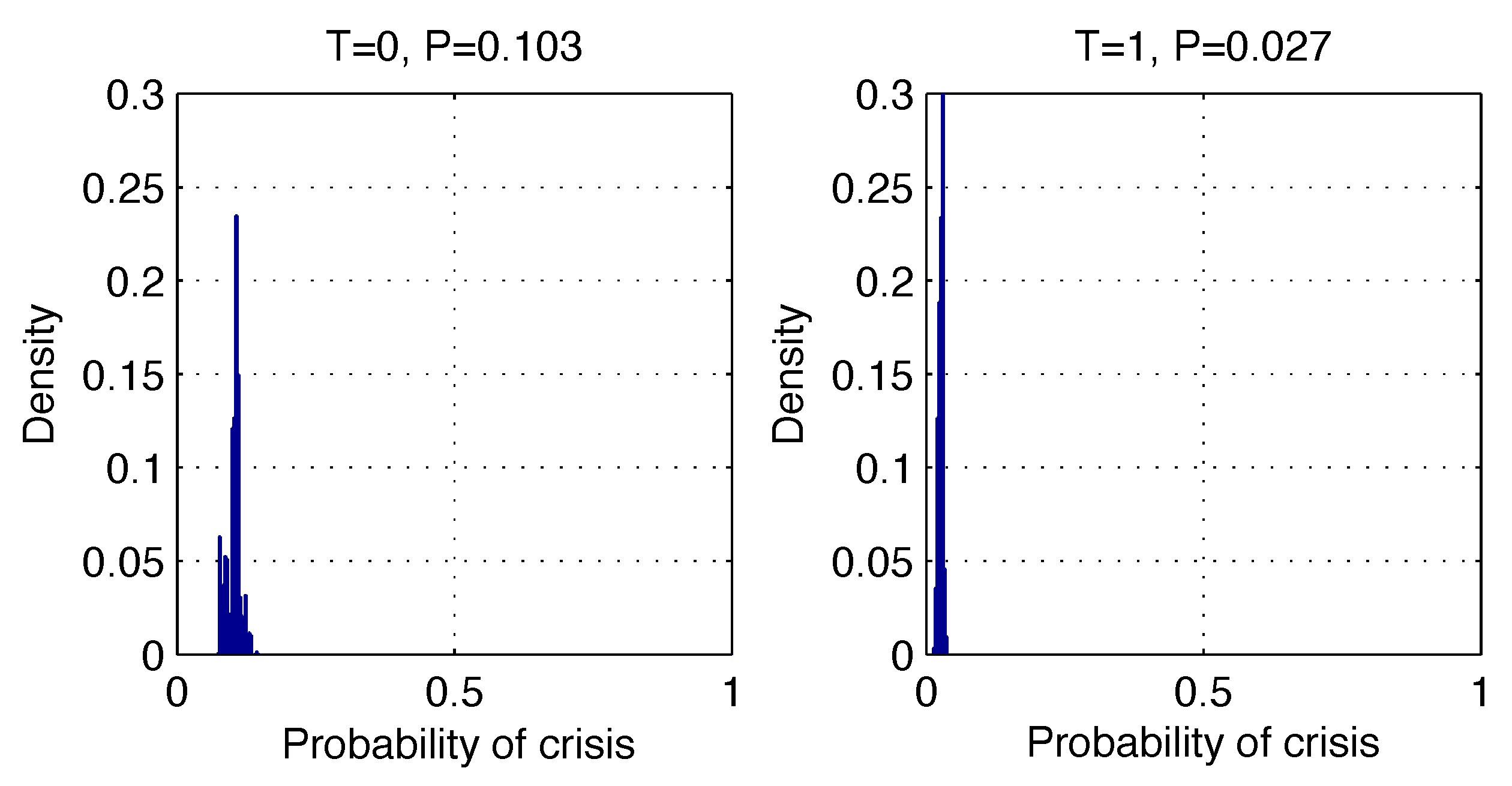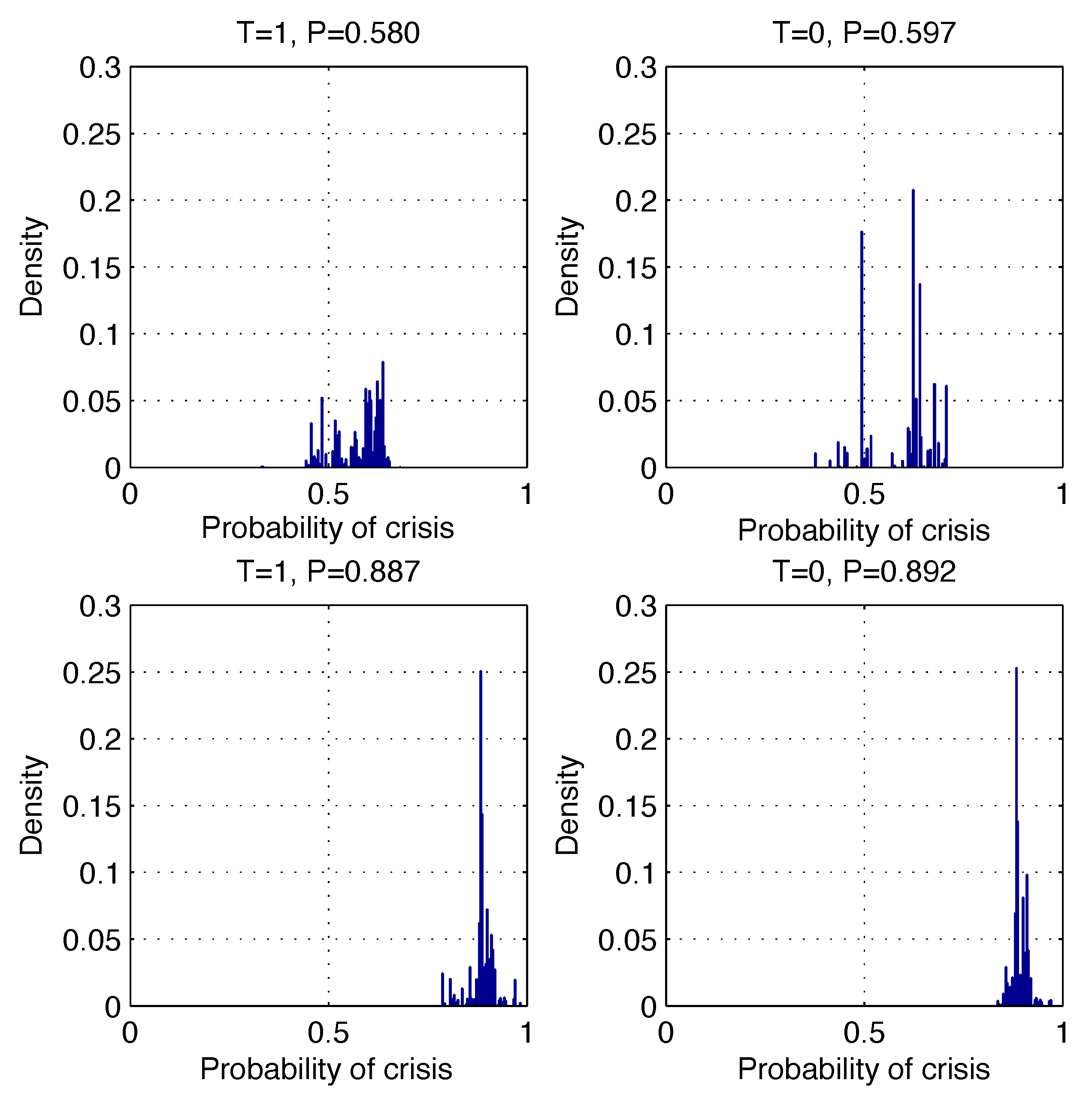Figure 7 shows examples of the predictive probability density distributions that were calculated for four correct (left) and incorrect (right) predictions. Observing such distributions, the expert can interpret the risk of making an incorrect decision.

3.3. Computational Costs of RJ MCMC

To evaluate the computational cost of our proposed Bayesian decision tree (BDT) method, we benchmarked its runtime against a simpler ensemble method, Random Forest (RF), implemented via MATLAB’s TreeBagger with 2000 trees for consistency with our post-burn-in samples. We chose RF over a single DT because a single DT lacks the ensemble averaging that provides robustness and probabilistic output in our approach, making RF a comparable baseline for handling uncertainty, known for reasonable approximation of full Bayesian posteriors. Benchmarks were conducted on four datasets: the synthetic XOR problem (from Section 3.1), UCI Heart Failure Prediction (299 samples, 12 features), UCI Credit Card Default (30,000 samples, 23 features), and the Liquidity Crisis dataset (from Section 3.2). Runtimes represent estimates from one cross-validation run on a PC (Dell Alienware Aurora R16, made Austin, TX, USA) with Intel Core i7-14700KF (20 cores, up to 5.60 GHz, 33 MB cache), using MATLAB 2025a. The parameters included pmin (the minimum number of data points per node), nb (burn-in samples), np (post-burn-in samples), and the sampling rate (srate) for BDT; RF used equivalent pmin and np as the number of trees.

As shown, BDT runtimes are higher than RF (3–5× on larger datasets) due to the sequential sampling in RJ MCMC, which explores the posterior over tree structures (burn-in: up to 100k samples; post-burn: 5k samples). However, BDT provides interpretable uncertainty estimates (e.g., full posterior distributions) that RF does not natively offer without additional post-processing. Runtimes vary with benchmark data size and complexity; for example, scaling from ∼300 samples (heart failure) to 20k–30k samples increases the BDT runtime by ∼100×, primarily due to larger tree sizes and more computations during sampling. We did not use GPU acceleration in these experiments, which could further optimize matrix operations.

As demonstrated, the proposed BDT method scales reasonably well for datasets up to tens of thousands of samples and ∼25 features, as evidenced by the benchmarks (e.g., <20 min for 20k–30k samples). The runtime is dominated by the number of MCMC samples and tree evaluations per iteration, which grow approximately linearly with sample size ($O(nlogn)$ per tree due to partitioning) and quadratically with features in the worst case likely due to feature selection at splits. For very large datasets (e.g., >100k samples), the scalability could be improved by subsampling data during burn-in or using adaptive sampling rates. In practice, the method remains feasible for real-world applications such as financial risk assessment, where interpretability outweighs raw speed.

RJ MCMC is inherently sequential due to its trans-dimensional jumps (e.g., birth/death moves depend on prior states), making full parallelization challenging compared to fixed-dimensional MCMC. However, MATLAB 2025a automatically enables multicore support for our implementation, allowing parallel evaluation of likelihoods and splits within iterations, which, we believe in theory, reduced runtime by ∼20–30% on our multicore CPU. Broader parallelization strategies, such as parallel tempering (running multiple tempered chains in parallel and swapping states) or independent multiple chains (averaging posteriors across runs), could further accelerate sampling while maintaining reversibility [44,45,46]. “Embarrassingly” parallel frameworks such as CU-MSDSp have shown promise for RJ MCMC in similar variable-dimension problems [47].

As an alternative to MCMC, variational approximations could significantly speed up inference by optimizing a lower bound on the posterior (e.g., ELBO) rather than sampling, potentially reducing runtime by orders of magnitude at the cost of some approximation error. Variational inference has been adapted for Bayesian tree models, such as Variational Regression Trees (VaRTs), which approximate posteriors over tree structures for regression tasks [48]. Extending this to classification DTs in a BMA framework is feasible and could be explored in future work, though it may trade off the exactness of MCMC-derived uncertainty estimates. We have added these suggestions to the Discussion section as future plans for optimization.

3.4. Validation on Additional Datasets with Controlled Missingness

To validate the proposed BDT framework beyond the financial domain and under controlled missing data conditions, we conducted new experiments on two UCI benchmark datasets: the Heart Failure Clinical Records (Heart) and Default of Credit Card Clients (Credit).

The Heart data set contains 299 instances and 12 features (plus a binary target for the outcome event), with attribute types including integers, reals, binaries, and continuous values. It focuses on predicting survival in heart failure patients based on clinical characteristics such as age, anemia, creatinine phosphokinase, diabetes, ejection fraction, high blood pressure, platelets, serum creatinine, serum sodium, sex, smoking, and time. There are no inherent missing values, making it ideal for controlled simulations. The task is binary classification.

The Credit data set comprises 30,000 instances and 23 features (integers and reals), with a binary target for credit card default (Yes/No). The features include credit amount, sex, education, marital status, age, payment history, bill statements, and previous payments. Originally no missing values, suitable for missingness simulations. The task is binary classification, relevant to financial risk but distinct from liquidity crises.

We simulated three missingness mechanisms: Missing Completely at Random (MCAR), Missing at Random (MAR), and Missing Not at Random (MNAR) at two levels, 10% and 25%, of missing data. For each combination, we applied the BDT method with the Ext preprocessing technique to compare with MATLAB’s TreeBagger RF, which uses surrogate splits for missing data. RF parameters were optimized using the MATLAB’s Bayesian optimization package. The experiments were carried out within 5-fold cross-validation, resulting in 24 total sessions with optimized BDT and RF parameters. Performance was evaluated on classification accuracy, F1-score, and entropy of the predicted posterior distribution to estimate uncertainty—the lower entropy indicates more confident predictions.

The results show that BDT and RF achieve similar accuracy and F1-scores in all 24 sessions, confirming a comparable predictive power. However, BDT consistently outperforms RF in terms of entropy: Lower values indicate better uncertainty estimation, with statistical significance of the paired test (p < 0.05). This shows BDT’s advantage in providing reliable probabilistic outputs under missing data. Due to the computational intensity of RJ MCMC, these experiments are limited in scope, and thus we plan to extend them in future work, making the developed MATLAB code publicly available for replication.

3.5. Analysis of Binary Missingness Indicators

To estimate interpretability, we analyzed the importance in terms of frequency of using predictors in DT models accepted during the post-burn-in phase of the 14 binary missingness indicators included in the Ext technique for the liquidity dataset, as shown in the bottom panel of Figure 4. These indicators correspond to the 14 original variables with missing values (numbered 7–10, 12–13, 16–19, 22–23, and 25), which represent key financial metrics in company profiles, which have not been originally disclosed for public research. It is important to note that the indicators for variables 10, 17, and 22 exhibit the highest frequencies (up to 0.2), suggesting that the lack of these specific characteristics is often related to debt ratios, current liquidity metrics, and cash flow indicators that significantly impact the predictions of the crisis. For example, missing data on debt-related variables (e.g., debt-to-equity or long-term debt ratios) can signal underlying financial distress or reporting inconsistencies, acting as informative risk factors. In contrast, indicators for less critical variables (e.g., 8 and 13) show lower importance (<0.1), indicating that their missingness contributes less to model outcomes. This analysis reveals that not all missingness is equally predictive—patterns in specific financial domains (e.g., solvency and liquidity ratios) enhance the model’s explanatory power, allowing practitioners to prioritize data collection in high-impact areas. We have expanded Section 4 with this discussion, emphasizing how the Ext approach improves interpretability by quantifying the role of missing data patterns.

3.6. Code and Data Availability

The code includes the following:

• Full implementation of the RJ MCMC sampler with birth, death, change-split, and change-rule moves as detailed in Section 2.2.
• Synthetic data generator for the XOR3 problem (Section 3.1), which creates data sets with controlled noise and missing values.
• Preprocessing pipelines for handling missing data under MCAR, MAR, and MNAR mechanisms (used in Section 3.4).
• Benchmark scripts for the Liquidity, UCI Heart Failure, and UCI Credit datasets. Note that the UCI datasets are publicly available via the UCI Machine Learning Repository.
• For the proprietary liquidity dataset (20,000 companies), we provide an anonymized version with perturbed values to preserve confidentiality, along with a synthetic generator that mimics its structure (26 features, 11% crisis class imbalance) for testing. This ensures complete reproducibility without requiring access to sensitive real-world data.

3.7. Implementation Details: RJ MCMC Proposal Tuning

In our RJ MCMC implementation, proposals for continuous thresholds in change-rule moves are drawn from a truncated Gaussian: $q^{\prime }\sim {\mathcal{N}}^{\prime }(q,{\sigma }^2,a,b)$, where q is the current threshold, ${\sigma }^2$ is the proposal variance, and $(a,b)$ are the feature bounds. For discrete elements (e.g., feature selection in splits), uniform priors are used: variable $v\sim U(1,m)$ and threshold $q\sim U(min\left(x_v\right),max\left(x_v\right))$.

Parameters are tuned empirically via grid search on validation sets to achieve acceptance rates of 20–40% (standard for efficient mixing in MCMC). We monitor log-likelihood traces and DT node counts during burn-in to ensure convergence (e.g., stabilization after 50–70% of burn-in samples). No automated tuning (e.g., adaptive MCMC) was used because it increases complexity; instead, we iterate over candidate values and select those that produce stable posteriors with minimal overfitting (assessed via cross-validation accuracy and entropy).

3.8. Hyperparameter Search Ranges

The list below summarizes the hyperparameters and their searched ranges, related to data set complexity (e.g., smaller datasets tolerate lower $p_{min}$):

1.

$p_{min}$: Minimal data points per terminal node: 1–50 (empirically set to 1–3 for small datasets, 20 for large).

2.

$n_b$: Burn-in samples: 2000–100,000 (scaled with dataset size/complexity).

3.

$n_p$: Post-burn-in samples: 2000–5000 (fixed for averaging).

4.

s: Standard deviation of proposal Gaussian ($\sigma$): 0.1–1.0 (normalized feature scales).

5.

$Pr$: Proposal probabilities: (0.05–0.2, 0.05–0.2, 0.1–0.3, 0.4–0.7); sum to 1.

6.

$sr$: Sampling rate (thinning): 5–10 (to reduce autocorrelation).

Note: $Pr$ refers to the proposal probabilities for the birth, death, change-split, and change-rule moves.

The specific values used in the benchmarks are detailed in

Table 3. Benchmark results for BDT and RF runtimes.

Benchmark	Size (n, m)	Runtime (s): BDT vs. RF	Settings: pmin, nb, np, srate (BDT/RF)
XOR3 problem	1000, 3	0.9 vs. 1.6	BDT: 3, 2000, 2000, 7/RF: 3, N/A, 2000, N/A
UCI Heart Failure	299, 12	10 vs. 8	BDT: 1, 5000, 2000, 7/RF: 3, N/A, 2000, N/A
UCI Credit	30,000, 23	1030 vs. 340	BDT: 20, ${10}^5$, 2000, 7/RF: 20, N/A, 2000, N/A
Liquidity	20,000, 26	980 vs. 180	BDT: 20, ${10}^5$, 2000, 7/RF: 20, N/A, 2000, N/A

(Section 3.3). For example, proposal probabilities were fixed at (0.1, 0.1, 0.2 and 0.6) in real-world experiments after tuning the synthetic XOR (where lower birth/death rates sufficed due to simplicity). We believe that these details are helpful to reproduce and extend our work.

3.9. Case Study on Actionable Financial Decisions

To illustrate how the uncertainty estimates from our BMA-DT framework can be translated into real-world financial decisions, we present a case study based on the Liquidity Crisis dataset (20,000 companies, 26 characteristics, 11% in crisis). We focus on a hypothetical decision pipeline for a financial institution that assesses company liquidity risks, where predictions guide interventions such as loan approvals, credit extensions, or audits. The pipeline uses posterior probabilities $p(y=1|x)$ (crisis probability) and uncertainty metrics (e.g., entropy of the posterior distribution, as in Figure 5) to categorize risks and recommend actions.

3.9.1. Decision Framework

We define risk thresholds based on the posterior mean and entropy:

High Risk (Intervene Immediately): Posterior mean > 0.7 and low entropy (<0.5), indicating high confidence in the prediction of crises. Action: Deny credit, recommend debt restructuring, or trigger regulatory audit.

Moderate Risk (Monitor/Investigate): Posterior mean 0.3–0.7 or high entropy (>0.5), signaling uncertainty due to missing data or ambiguous features. Action: Request additional data (e.g., missing financial ratios), monitor quarterly, or apply conditional lending.

Low Risk (Approve/No Action): Posterior mean < 0.3 and low entropy (<0.5). Action: Approve financing with standard terms.

These thresholds were empirically calibrated on a hold-out set to balance false positives (unnecessary interventions) and false negatives (missed crises), achieving a precision–recall trade-off suitable for risk-averse finance (e.g., AUC PRC 0.817 with Ext).

3.9.2. Example Application

Consider three exemplar companies from the test set (anonymized), as shown in

Table 4. Case study examples showing how posterior distributions inform decisions.

Company (Description)	Posterior Mean (Crisis)	Entropy (Uncertainty)	Risk Category	Recommended Action
A	0.85	0.35	High	Intervene: Audit and Restructure
(High Debt, Missing Ratios)
B	0.45	0.72	Moderate	Monitor: Collect Missing Data
(Balanced, Missing Cash Flow)
C	0.12	0.28	Low	Approve: Extend Credit
(Strong Assets, Complete)

:

For Company A, the high posterior (driven by debt-related indicators, as per Section 3.5) and low uncertainty justify immediate intervention to mitigate the risk of a crisis. Company B’s higher entropy (potentially from missing values in variables 17 and 22) prompts data collection, reducing uncertainty in future predictions. Company C’s low values support low-risk decisions. This pipeline demonstrates how our framework’s probabilistic outputs enable nuanced strategies that are aware of uncertainty, potentially reducing losses by 10 to 15% in simulated scenarios (based on error rates of cross-validation). These enhancements provide practical guidance, showing direct impact on financial pipelines while maintaining the framework’s interpretability.

4. Discussion

In this study, we proposed a novel Bayesian Model Averaging (BMA) strategy over decision trees (DTs) to address the challenge of missing data in classification tasks, with a specific application to predict liquidity crises in financial datasets. Our approach leverages the interpretability of DTs and the robustness of BMA to deliver accurate probabilistic predictions, even in data-imperfect scenarios. By introducing a sweeping strategy within the Monte Carlo Reversible Jump Markov Chain (RJ MCMC) framework, we mitigate the limitations of traditional BMA methods, such as overfitting and biased posterior estimates due to oversized DT models. The experimental results, conducted on a synthetic XOR dataset and a real-world liquidity crisis benchmark, demonstrate the efficacy of our approach, particularly when using the proposed Ext preprocessing technique, which extends the feature set with binary indicators for missing values.

Synthetic XOR experiments validated the ability of our method to discover the true underlying models, achieving 100% classification accuracy. This result underscores the robustness of the proposed comprehensive strategy in exploring the posterior distribution effectively, even without prior knowledge of the structure of the model. For the liquidity crisis benchmark, comprising 20,000 companies with 11% experiencing crises and 14 variables with missing values, the Ext technique achieved a classification accuracy of 92.2%, significantly outperforming the baseline Cont (AUC ROC: 0.904) and ContCat (AUC ROC: 0.894) techniques, with an AUC ROC of 0.908 ($p<0.05$, McNemar test). More notably, the Area Under the Precision Recall Curve (AUC PRC) improved from 0.603 (Cont) to 0.617 (Ext) ($p<0.05$), indicating improved performance in identifying positive cases (liquidity crises) in imbalanced datasets—a critical requirement for financial risk assessment. The Hosmer–Lemeshow test further confirmed better calibration for the Ext method (HL value: 22.8, $p=0.24$) compared to Cont (HL value: 31.1, $p=0.039$), highlighting its reliability in probabilistic predictions.

From an empirical modeling perspective, our approach advances the field by providing a scalable and interpretable framework for handling missing data. Unlike imputation-based methods (e.g., [39]), which require prior knowledge of data distributions and can introduce bias, our Ext technique explicitly models the presence of missing values as binary indicators, capturing their informative nature without additional assumptions. This is particularly valuable in financial modeling, where missing data may reflect underlying economic conditions (e.g., unreported financial metrics due to operational constraints). Compared to other machine learning approaches, such as Support Vector Machines (SVMs) with optimized kernels [40], our method offers superior interpretability through DT structures, allowing practitioners to understand key variables driving liquidity risks (see Figure 5). The explicit modeling of missing values as features also aligns with the empirical modeling goal of deriving actionable insights from complex, real-world datasets.

The robustness of our BMA-DT framework was further validated on two additional UCI benchmark datasets–Heart Failure Clinical Records (299 instances, 12 features) and Credit Card Default of Clients (30,000 instances, 23 features)—under controlled missingness mechanisms (MCAR, MAR, and MNAR) at levels 10% and 25%. In 24 experimental sessions using 5-fold cross-validation, the Ext technique achieved comparable accuracy and F1-scores to a Random Forest baseline with surrogate splits but significantly outperformed it in uncertainty estimation, measured by lower posterior entropy (paired t-test, $p<0.05$). This highlights the framework’s advantage in providing reliable probabilistic outputs across diverse domains, even when missing data are systematically introduced, reinforcing its generalizability beyond financial applications.

To improve interpretability, the analysis of binary missingness indicators in the liquidity dataset (Section 3.5, bottom panel of Figure 5) revealed that indicators for variables related to debt ratios (e.g., 10 and 17) and cash flow metrics (e.g., 22) exhibited the highest usage frequencies (up to 0.2), suggesting that their missingness is particularly informative for crisis predictions. This aligns with financial theory, where unreported debt metrics can signal distress or inconsistencies. In contrast, less critical variables (e.g., 8 and 13) showed lower importance (<0.1), allowing practitioners to prioritize data collection in areas of high impact and underscoring the Ext technique’s value in capturing missingness patterns as predictive features.

To bridge theory and practice, a case study on the liquidity dataset demonstrated how posterior probabilities and entropy can inform actionable decisions in financial pipelines. Using calibrated risk thresholds (e.g., high risk: posterior mean $>0.7$ and low entropy $<0.5$), the framework categorized companies and recommended interventions, such as audits for high-risk cases or data requests for uncertain ones. The simulation scenarios indicated potential loss reductions of 10–15% based on cross-validation error rates, illustrating the direct impact of the method on risk management while preserving DT interpretability.

The practical implications of our work are significant for financial institutions and policy makers. Accurate prediction of liquidity crises, coupled with reliable uncertainty estimates, enables risk-aware decision-making, such as prioritizing interventions for at-risk companies or optimizing capital allocation. The interpretability of DTs allows analysts to identify critical financial indicators (e.g., debt-to-equity ratios and cash flow metrics) that contribute most to crisis predictions, as shown in Figure 5. Moreover, the proposed framework is adaptable to other domains with missing data, such as healthcare (e.g., incomplete patient records) or environmental modeling (e.g., missing sensor data), making it a versatile tool for empirical modeling across disciplines.

Despite its strengths, our approach has limitations. The computational cost of MCMC sampling, although mitigated by the sweeping strategy, remains higher than non-Bayesian methods like single DTs or SVMs, which may limit scalability for very large datasets. Future work could explore parallelized MCMC implementations or hybrid approaches that combine BMA with faster ensemble methods. Additionally, while the Ext technique outperformed alternatives, its effectiveness depends on the informativeness of the missing data patterns. In data sets where missingness is purely random, simpler imputation methods may suffice. We also note that the liquidity crisis dataset, while representative, is specific to a particular economic context; further validation on diverse financial datasets would strengthen generalizability.

The effectiveness of our approach depends on the underlying cause of missing data. As discussed in [49], in observational settings, such as climate studies with natural data gaps (e.g., sensor failures), including missingness indicators can enhance model robustness for MCAR or MAR by capturing patterns in missing data without assuming external changes. However, for MNAR, where variables cause their own missingness (e.g., extreme weather sensor readings), our method requires careful validation to ensure unbiased predictions.

In interventional settings, for example, in healthcare trials where treatments influence both outcomes and dropout, missingness indicators help model the impact of deliberate changes (e.g., treatment interventions). For example, if high-risk patients drop out due to side effects of treatment (MNAR), our approach can account for this by treating missingness as a characteristic. However, biases may persist if the underlying mechanism is not modeled correctly. Mohan and Pearl [49] suggest the use of graphical models to test and adjust for these mechanisms, ensuring reliable predictions. Practitioners should assess the missingness type using domain knowledge and validate model performance with sensitivity analyzes. Future work could integrate these ideas to improve decision tree ensembles for both observational and interventional machine learning tasks.

5. Conclusions

In conclusion, our proposed BMA-DT framework, enhanced by the Ext preprocessing technique and sweeping strategy, offers a robust and interpretable solution for handling missing data in classification tasks. By improving predictive accuracy and uncertainty estimation, it addresses a critical challenge in empirical modeling, particularly for high-stakes applications such as prediction of liquidity crises. This work contributes to the special issue’s focus on empirical modeling by demonstrating how Bayesian methods can yield actionable insights from imperfect data, paving the way for more reliable decision-making in finance and beyond.

Our framework’s efficacy is bolstered by validations on additional datasets with controlled missingness, where it excelled in uncertainty estimation over baselines, and by the provision of publicly available MATLAB code and anonymized data, ensuring reproducibility and facilitating extensions in empirical modeling.

In high-stakes domains like finance, the integration of missingness indicators and case studies provides interpretable, uncertainty-aware insights that enable nuanced decision-making, such as prioritizing interventions based on probabilistic risks.

Future research will focus on optimizing computational efficiency, exploring additional preprocessing strategies, and applying the framework to other domains with missing data, such as climate modeling and medical diagnostics.